Population pharmacokinetics of darbepoetin alfa in healthy subjects

Abstract

Aim

To develop and evaluate a population pharmacokinetic (PK) model of the long-acting erythropoiesis-stimulating protein, darbepoetin alfa in healthy subjects.

Methods

PK profiles were obtained from 140 healthy subjects receiving single intravenous and/or single or multiple subcutaneous doses of darbepoetin alfa (0.75–8.0 µg kg⁻¹, or either 80 or 500 µg). Data were analysed by a nonlinear mixed-effects modelling approach using NONMEM software. Influential covariates were identified by covariate analysis emphasizing parameter estimates and their confidence intervals, rather than stepwise hypothesis testing. The model was evaluated by comparing simulated profiles (obtained using the covariate model) to the observed profiles in a test dataset.

Results

The population PK model, including first-order absorption, two-compartment disposition and first-order elimination, provided a good description of data. Modelling indicated that for a 70-kg human, the observed nearly twofold disproportionate dose–exposure relationship at the 8.0 µg kg⁻¹-dose relative to the 0.75 µg kg⁻¹-dose may reflect changing relative bioavailability, which increased from ∼48% at 0.75 µg kg⁻¹ to 78% at 8.0 µg kg⁻¹. The covariate analysis showed that increasing body weight may be related to increasing clearance and central compartment volume, and that the absorption rate constant decreased with increasing age. The full covariate model performed adequately in a fixed-effects prediction test against an external dataset.

Conclusion

The developed population PK model describes the inter- and intraindividual variability in darbepoetin alfa PK. The model is a suitable tool for predicting the PK response of darbepoetin alfa using clinically untested dosing regimens.

Introduction

Erythropoiesis-stimulating proteins (ESPs) are successfully used for the treatment of anaemia, which is associated with, and is a complication of a variety of chronic diseases, such as chronic kidney disease, cancer and chronic heart failure. Darbepoetin alfa (Aranesp®) is a hyperglycosylated ESP which contains two additional N-linked carbohydrate chains compared with the primary sequence of recombinant human erythropoietin (rHuEPO) [1]. Although darbepoetin alfa stimulates erythropoiesis in the same manner as endogenous erythropoietin, the increased carbohydrate content of the protein results in an approximately threefold longer serum half-life and greater in vivo biological activity, allowing for more convenient dosing intervals compared with rHuEPO [2]. Currently, darbepoetin alfa is approved for the treatment of anaemia secondary to chronic kidney disease [3–5] and anaemia associated with chemotherapy treatment of nonmyeloid cancers in adults [6, 7]. In these patient populations, darbepoetin alfa effectively and safely maintains haemoglobin levels and, as shown in patients with chronic kidney disease [8, 9], can be administered at dosing intervals of once monthly compared with more frequently dosed rHuEPO.

In addition to the approved indications, darbepoetin alfa is being explored as a treatment option for anaemia associated with other chronic diseases. Darbepoetin alfa has been shown to elevate haemoglobin levels in patients with anaemia associated with chronic heart failure [10] or human immunodeficiency virus (HIV) infection [11], or in patients with anaemia secondary to ribavirin therapy for hepatitis C virus infection [12]. In addition to investigating anaemia treatment in other disease settings, more convenient dosing regimens of darbepoetin alfa, such as monthly administration or prefilled syringe-based (i.e. nonweight-based, flat) dosing, are being explored [7].

The potential application of darbepoetin alfa in other patient populations with different anaemia aetiologies or the design of new dosing paradigms requires an understanding of the molecule’s dose–pharmacokinetics (PK) relationship, the interindividual variability (IIV) in PK and the covariates affecting PK variability. Therefore, we have developed a population PK model of darbepoetin alfa in healthy subjects using nonlinear mixed-effects modelling techniques. Model development in healthy subjects is useful because detailed PK profiles over a wide dose range are available in this population, and mean PK characteristics of darbepoetin alfa appear to be similar in healthy subjects and in patients diagnosed with certain chronic diseases with which anaemia is associated, e.g. chronic heart failure, as indicated by previous data [10]. The model will be an important tool in improving our understanding of the PK of darbepoetin alfa and, through clinical trial simulations, in selecting the appropriate doses and dosing frequencies of darbepoetin alfa in a variety of anaemic disease populations.

Methods

Clinical studies and study populations

Data from healthy subjects (N = 140) were collected from six Amgen-sponsored clinical studies. The study protocols were approved by the institutional review boards of the individual study sites. All subjects gave written informed consent after full explanation of study details and before any study-related procedures were carried out.

Darbepoetin alfa was administered as a single intravenous (i.v.) dose (0.75 µg kg⁻¹), as single/multiple subcutaneous (s.c.) doses (ranging from 0.75 to 8.0 µg kg⁻¹), or as multiple s.c. doses of either 80 µg or 500 µg. Intensive PK sampling after the first dose was performed in all studies with a minimum of 10 blood samples collected from each subject in the first 1–3 weeks. Sparse and/or intensive sampling after multiple doses was also done in a subset of subjects. Before commencement of the modelling, a subset of the data (50% of subjects) was randomly selected and set aside for model evaluation (test dataset).

Key inclusion criteria for healthy subjects enrolled in the studies were age ≥18 years; normal physical examination and free of any clinically significant disease or condition requiring a physician’s care; normal 12-lead electrocardiogram; adequate iron stores (transferrin saturation ≥15%); normal levels of serum vitamin B₁₂ and folate. Exclusion criteria included infection with HIV, hepatitis B or C virus; clinically significant cardiovascular disease, hepatic or renal impairment; pregnancy; major surgery within the last 12 months; primary haematological disorder; screening haemoglobin >15.0 g dl⁻¹; exposure to any erythropoiesis-stimulating product (e.g. rHuEPO or anabolic steroids, except for oral iron), or blood donation/transfusion within 90 days (30 days in one trial) before randomization; heavy smoking. Subjects were prohibited from taking any medications other than oral contraceptives, hormone replacement therapy in postmenopausal women, or vitamin and iodine supplements.

Table 1 summarizes the dosing and sampling data used in this analysis along with the clinical studies from which they were obtained. Table 2 describes the baseline characteristics of the study population selected for the development and testing of the PK model.

Table 1.

Dosing and sampling schema for studies used in model development and model evaluation

Dataset	Dose	Dosing schedule (no. of doses)	No. of samples, n (sampling schedule)	Subjects (n)	Study number
Model development	i.v. 0.75 µg kg−1	Once	12 (5 min to 17 days)	4 (cross-over, 28 days apart)	20010262
	s.c. 0.75 µg kg−1	Once	11 (2 h to 17 days)
	s.c. 1.0 µg kg−1	Q6W (2)	17 (1 h to 14 days)*	28	990134
	s.c. 2.0 µg kg−1	Once	12 (2 h to 17 days)	6	20010198
	s.c. 3.0 µg kg−1	Once	12 (2 h to 17 days)	6
	s.c. 5.0 µg kg−1	Once	12 (2 h to 17 days)	6
	s.c. 6.5 µg kg−1	Once	19 (2 h to 21 days)	10	20010174
	s.c. 8.0 µg kg−1	Once	19 (2 h to 21 days)	10
Model evaluation	s.c. 80 µg	Q4W (2)	17 (1 h to 17 days)*	30	20030163
	s.c. 2.0 µg kg−1	QW (4)	14 (1st dose)(2 h to 7 days)	10	20000250
			2 (2nd dose) (3 and 7 days)
			2 (3rd dose) (3 and 7 days)
			16 (4th dose) (2 h to 21 days)
	s.c. 3.0 µg kg−1	Q3W (2)	18 (1st dose)	10
			16 (2nd dose) (2 h to 21 days)
	s.c. 6.5 µg kg−1	Q3W (2)	18 (1st dose)	10
			16 (2nd dose) (2 h to 21 days)
	s.c. 500 µg	Q3W (2)	18 (2 h to 21 days)*	10

^*Sampling schedule applied to both doses. I.v., Intravenous; QW, once every week; Q3W, once every 3 weeks; Q4W, once every 4 weeks; Q6W, once every 6 weeks; s.c., subcutaneous.

Table 2.

Baseline clinical characteristics of the study population

Clinical data	Model development	Model evaluation
Number of subjects	70	70
Sex
Male	31 (44)	31 (44)
Female	39 (56)	39 (56)
Age (years)	47 ± 17	55 ± 18
Height (cm)	168 ± 10	167 ± 10
Weight (kg)	68.6 ± 10.3	71.0 ± 10.8
Haemoglobin (g dl−1)	14.0 ± 1.0	14.0 ± 1.2
Creatinine clearance (ml min−1)	94 ± 27	90 ± 23

Data are n (%) or means±SD.

Analytical methods

Concentrations of darbepoetin alfa in the serum were measured by MDS Pharma Services (Montreal, Quebec, Canada) using the validated Quantikine IVD human erythropoietin enzyme-linked immunosorbent assay (ELISA; R&D Systems, Minneapolis, MN, USA). The standard curve range was from 0.125 to 5.0 ng ml⁻¹ and the lower limit of quantification was 0.14 ng ml⁻¹. The assay has been validated previously with demonstrated recovery of spike experiments, parallelism, accuracy, interassay precision (coefficient of variation was 5–7%), and stability [13]. Endogenous erythropoietin (EPO) cross-reacted in the ELISA and was therefore included in darbepoetin alfa serum concentration measurements.

Modelling methodology

Nonlinear mixed-effects modelling techniques were used to conduct the population PK analysis. Fixed-effect parameters, representing the typical population estimates, consisted of structural PK parameters (e.g. clearance, volume of distribution) and parameters characterizing their hypothesized relationship to baseline covariates. Random IIV in the PK parameters and random residual (unexplained) variability (RRV) were also estimated.

For any parametric, nonlinear mixed-effects model, it is necessary to assume parametric distributions for the random effects. In this analysis, all interindividual variances were described by an exponential error model, as follows:

(1)

where P_i is the estimated parameter value for individual i, TVP is the typical population value (geometric mean) of the parameter, η^Pi are individual-specific interindividual random effects for individual i and parameter P, and are assumed to be normally distributed: η∼ N(0, ω²) with interindividual variance–covariance matrix Ω.

For PK observations, the residual error model was initially described by an exponential error model as follows:

(2)

where C_ij is the j^th measured observation (serum drug concentration) in individual i, 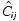is the j^th model predicted value (total serum drug concentration) in individual i, ɛ_ij is residual random error for individual i and measurement j, assumed to be independently and identically distributed: ɛ∼NID(0, σ₁²). Each subject’s endogenous EPO concentration was assumed to remain constant during the study and its contribution to the measured total drug level in the serum was therefore modelled as an individual-specific constant. Thus, 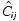, the j^th predicted total drug level in the serum of each individual, consists of two components: 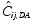, the predicted darbepoetin alfa level, and 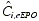, the estimated endogenous EPO level in individual i. 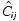is a single fixed-effect parameter with associated random effects:

(3)

Pharmacokinetic models with increasing number of disposition compartments were used to describe the data and the best model was chosen based on goodness-of-fit criteria including diagnostic plots, minimum objective function value (MOFV) after accounting for the number of fitted parameters, and precision and plausibility of parameter estimates. Each subject’s endogenous EPO concentration was assumed to remain constant during study duration and its contribution to measured serum darbepoetin alfa levels was therefore modelled as an individual-specific constant. A covariate modelling approach emphasizing parameter estimation rather than stepwise hypothesis testing was implemented [14, 15]. First covariate–parameter relationships were identified based on exploratory graphics, scientific interest, mechanistic plausibility or prior knowledge, and a full covariate model was constructed. Correlation or collinearity in predictors was avoided. Population covariate coefficients were also estimated for any remaining effects revealing evidence of a relationship. Inferences about clinical relevance of parameters were then based on the resulting parameter estimates and the estimation precision–bootstrap 95% confidence intervals (95% CI) [16]. Presence or absence of a covariate effect would be concluded based on effect size calculations using the estimate and 95% CI of the covariate coefficient in the case of precise parameter estimates. Poor precision of parameter estimates would indicate lack of information on an effect rather than lack of effect. No hypothesis testing was conducted. This approach is a simplification of the global model approach described by Burnham and Anderson [17] and allowed for the direct assessment of the clinical relevance of covariate effects [15, 18, 19]. It also differentiated between true lack of an effect vs. lack of information about that effect, thus providing some explanation for the apparent absence of a covariate effect. The limitations of stepwise hypothesis testing using likelihood approximations have been previously discussed [20–22]. The approach outlined above has been proposed as an alternative to overcome the limitations of the stepwise regression methods [14, 22, 23]. The following covariates were evaluated in this analysis: body weight, height, lean body mass, body mass index, age, gender, race, creatinine clearance and baseline haemoglobin.

The effects of covariates were modelled using a normalized power model:

(4)

where the estimated individual parameter θ_n was described as a function of m individual, continuous covariates (cov_m) and the typical value of the model parameter (TVP) such that θ_n has the estimated population typical PK parameter value for an individual i with covariates equal to the reference covariate values (cov_mi = ref_m), and r_m were estimated parameters (covariate coefficients) describing the magnitude of the covariate–parameter relationships.

The population PK model was evaluated by performing a prediction with the fixed-effect parameters of the full covariate model against the test dataset. The precision and bias in the typical predicted PK profiles compared with the observations in the test dataset were evaluated by calculating the mean percent prediction error (MPPE) and root mean square percent error (RMSPE) at the nominal 48-h time point, respectively, as follows:

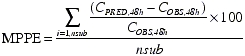(5)

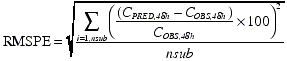(6)

where C_PRED,48h is the serum concentration predicted using typical population PK parameter values (θ_1−m+n in equation 4), C_OBS,48h is the observed serum concentration in the external dataset; the summation is over all subjects (nsub). The PK assessment at the nominal 48-h time point was used to calculate MPPE and RMSPE since the time of maximum serum concentration of darbepoetin alfa after a s.c. dose is typically ∼48 h (Figure 1). The extent of the possible impact, i.e. effect size, of the influential covariates identified in this analysis was evaluated by performing deterministic simulations with the full model fixed-effect–parameters. For each covariate, the bootstrap point estimates and 95% CI of the covariate coefficients of each covariate–PK parameter relationship were used to obtain the PK parameter values at the extremes of the covariate range. Simulations were performed with these calculated parameter values and the rest of the PK parameters and covariates fixed to their population-typical values. Differences in the single-dose exposure (measured by the area under the serum concentration–time curve, AUC_0–∞) at the extremes of the covariate range were estimated. The procedure was repeated to obtain the effect size of each covariate separately.

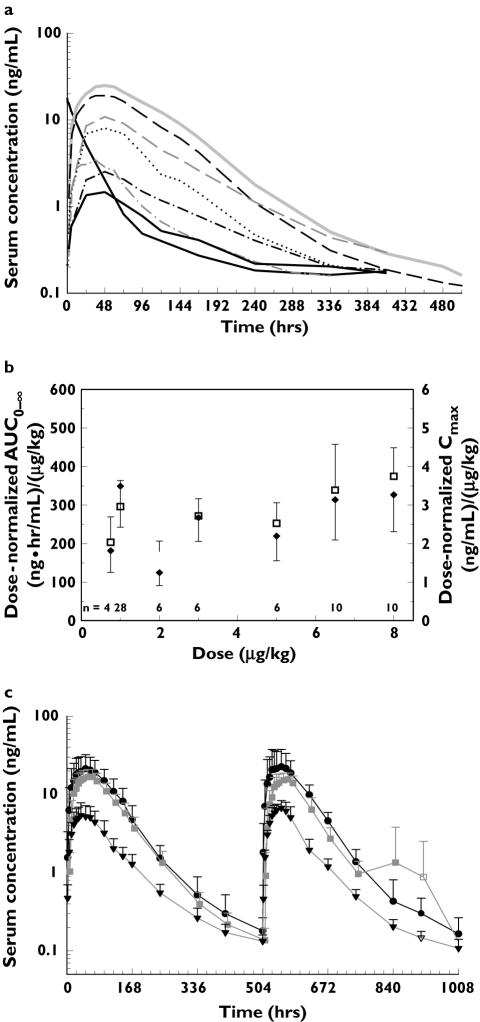
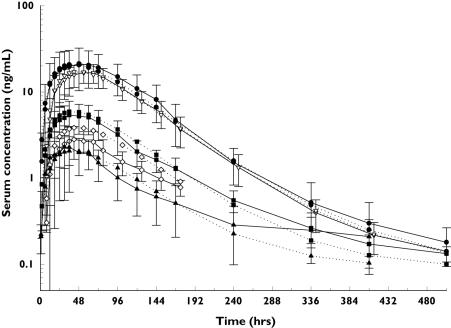
Figure 1.

Exploratory graphics analysis of data. (a) Mean of model development dataset serum darbepoetin alfa concentration profiles, 0.75 µg/kg SC, IV (n = 4) (), 8 µg/kg (n = 10) (), 6.5 µg/kg (n = 10) (), 5 µg/kg (n = 6) (), 3 µg/kg (n = 6) (), 2 µg/kg (n = 6) (), 1 µg/kg (n = 28) (), (b) change in exposure measured by dose-normalized AUC_0–∞ (□) and C_max (✦), along with the standard deviations and number of subjects are plotted against administered darbepoetin alfa s.c. dose; (c) mean (+ SD) of model evaluation dataset serum concentration–time profiles after first and second doses for selected dose groups. 500 µg (n = 4–10) (•), 6.5 µg/kg (n = 5–10) (), 3 µg/kg (n = 5–10) (▾). n, Number of individual observations at each time point

Nonlinear mixed-effects modelling was performed using the NONMEM software version V, level 1.2; NMTRAN version III, level 1.0; and PREDPP version IV, level 1.0 running on a Clustered Array of Processors (CAP; ClinApps, San Diego, CA, USA) and on a standalone laptop (Compaq Evo running Microsoft Windows 2000, Pentium IV 1.8-MHz processor, Compaq Visual Fortran v6.6 compiler) [24]. The first-order conditional estimation (FOCE) method (with interaction between the IIV and RRV terms) was used for PK parameter estimation. Graphing was performed using SigmaPlot (version 8.02; SPSS Inc., Chicago, IL, USA) and S-Plus (version 6.2; Insightful Corporation, Seattle, WA, USA). Assembly of clinical trials data was accomplished using SAS (version 8.0; SAS Institute Inc., Cary, NC, USA) and S-Plus software.

Results

PK model

A total of 1664 plasma samples from 70 subjects were available for the development of the population PK model. Exploratory graphical analysis of the data (Figure 1a–c) revealed that the mean serum concentration–time profile of darbepoetin alfa after i.v. dosing was biphasic, whereas those after s.c. administration were generally monophasic. The exposure after administration of a 1.0 µg kg⁻¹ dose was uncharacteristically high, compared with other doses (Figure 1a). There was a tendency towards increased dose-normalized exposure (nAUC_0–∞) at doses >5.0 µg kg⁻¹ (Figure 1b). Furthermore, the serum concentration–time profile after the first dose was similar to that after subsequent doses following s.c. administration of 3.0 µg kg⁻¹, 6.5 µg kg⁻¹ or 500 µg (Figure 1c).

We attempted to describe the dose-disproportionate increase in exposure using (i) concentration-dependent (Michaelis–Menten type) clearance, or (ii) using dose-dependent bioavailability (linear and power equations) with constant clearance, or (iii) concentration-dependent clearance and dose-dependent bioavailability. Models corresponding to strategies (i) and (iii) did not converge successfully during our analysis. The final model, which provided the best description of the PK data, was a two-compartment disposition model parameterized with constant clearance (CL), central volume of distribution (V₁), intercompartmental clearance (Q) and peripheral volume of distribution (V₂), with first-order absorption rate constant (K_a) and bioavailability fraction (F). Bioavailabilities of the s.c. doses, relative to the 0.75 µg kg⁻¹ i.v. dose, were best fit using a linear equation:

(7)

where F₀ and p₁ were estimated fixed-effects parameters, and Dose was the individual µg dose. The random IIV was obtained for CL and V₁. Because i.v./s.c. crossover PK data were available in only a few subjects (N = 4), IIV of F₀ and p₁ were not estimated. Furthermore, it was not possible to estimate the IIV of Q and V₂. This model was used as the base model for subsequent covariate analysis.

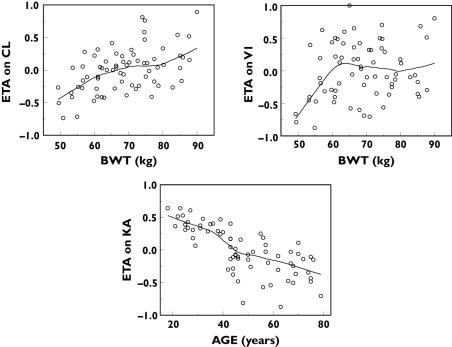
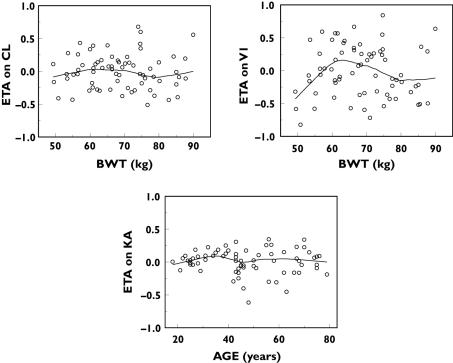
When the empirical Bayes PK parameter estimates were plotted against covariates of interest, it appeared that CL and V₁ increased with increasing body weight, while K_a decreased with increasing age (Figure 2). Even though the relationship between V₁ and body weight was not pronounced in these data, this relationship was explored based on scientific plausibility – distribution of macromolecules such as darbepoetin alfa is typically confined to the plasma volume, which in turn is known to increase with body weight – and prior knowledge [13, 25]. These covariate–PK parameter relationships were parameterized in the full covariate model as follows:

(8)

(9)

(10)

where 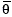is the estimated individual PK parameter value given individual covariates, TV are the population typical value estimates at reference covariate values, BWT is body weight and r₁₋₃ (covariate coefficients) are fitted parameters characterizing the covariate–PK parameter relationships.

Figure 2.

Pharmacokinetic (PK) parameter–covariate relationships in the base PK model. ETA (η) is the interindividual variance parameter (see equation 1)

The estimated PK parameters for the full covariate model are shown in Table 3. The observed median and 95% CI were obtained for each estimated parameter from the distribution of parameter estimates from 500 NONMEM estimation runs. The linear equation fit (equation 7) to the F vs. Dose relationship was chosen over a power equation based on precision of parameter estimates.

Table 3.

Final population covariate model parameter estimates

	Estimate (%SEP)*	Asymptotic(95% CI)†	Bootstrap median (95% CI)
PK parameters; typical values
Clearance, CL (l h−1)	0.164 (11.6)	(0.127, 0.201)	0.166 (0.138, 0.25)
Central compartment volume, V1 (l)	5.98 (13.7)	(4.37, 7.59)	6.13 (4.96, 10.2)
Peripheral compartment volume, V2 (l)	1.21 (40.4)‡	0.252, 2.17)	1.22 (0.721, 28.2)
Central to peripheral compartment clearance, Q (l h−1)	0.0153 (38.1)‡	(0.00387, 0.0267)	0.0192 (0.013, 0.0396)
First-order absorption rate constant, Ka (h−1)	0.0212 (3.54)	(0.0197, 0.0227)	0.0211 (0.0194, 0.0225)
Bioavailability equation: F = F0 + p1 × Dose
F0	0.448 (10.2)‡	(0.358, 0.538)	0.450 (0.389, 0.702)
p1	0.000586 (37.2)‡	(0.000159, 0.00101)	0.000576 (0.000225, 0.00109)
eEPO concentration (ng ml−1)	0.0867 (4.19)	(0.0796, 0.0938)	0.0872 (0.0795, 0.0958)
Covariate coefficients
r1 (BWT on CL)	1.19 (21.9)	(0.678, 1.70)	1.19 (0.668, 1.74)
r2 (BWT on V1)	0.983 (44.9)	(0.119, 1.85)	1.01 (0.0572, 1.93)
r3 (Age on Ka)	−0.951 (7.48)	(−1.09, −0.812)	−0.953 (−1.12, −0.823)

Interindividual variances	Estimate (%SEP)	∼ CV%§	Asymptotic (95% CI)	Bootstrap median (95% CI)
ωCL2	0.075 (25.3)	27.4	(0.0378, 0.112)	0.0707 (0.0398, 0.112)
ωV12	0.227 (20.1)	47.6	(0.137, 0.317)	0.215 (0.136, 0.32)
ωKa2	0.0832 (24.2)	28.8	(0.0438, 0.123)	0.0785 (0.0413, 0.117)
ωeEPO2	0.132 (28.5)	36.3	(0.0583, 0.206)	0.122 (0.0524, 0.222)
σ12, RRV	0.324 (3.64)¶	56.9	(0.301, 0.347)	0.323 (0.299, 0.345)

^*%SEP, Standard error of parameter estimate defined as the standard error of prediction/predicted value × 100% (measure of uncertainty in the parameter estimate).

^†Asymptotic 95% CI is calculated as parameter estimates ± 1.96 × standard error of prediction.

^‡Interindividual random variance was fixed at 0 in the PK model.

^§Approximate CV% is calculated as the square root of the variances.

^¶σ₁ is assumed to have mean 0. BWT, Body weight; CI, confidence interval; CV, coefficient of variation; RRV, random residual variability; eEPO, endogenous erythropoietin.

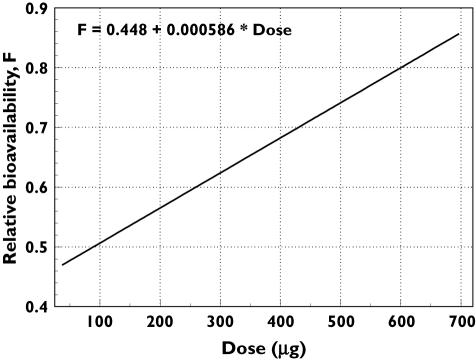
Assuming constant CL, based on equation 7, the relative bioavailability increased from ∼48% at 0.75 µg kg⁻¹ to ∼78% at 8.0 µg kg⁻¹ (Table 3, Figure 3). All fixed- and random-effects parameters were precisely estimated [standard error of prediction (SEP), calculated as standard error ÷ parameter estimate × 100, was <30% for all parameters except Q, V₂ and p₁]. The approximate interindividual coefficient of variation (%CV) of the PK parameters ranged from ∼27% to 48% for all parameters. The endogenous EPO concentration typical for the study population was estimated at 0.0867 ng ml⁻¹ (SEP = 4.19%), indicating that it contributed little to the measured darbepoetin alfa serum levels. The absorption half-life [ln(2)/K_a; 33 h] was longer than the elimination half-life [ln(2)/(CL/V_c); 25 h], suggesting flip-flop kinetics for this molecule.

Figure 3.

Plot of estimated bioavailability vs. dose from the full covariate pharmacokinetic model. Bioavailability was estimated at 0.75, 1.0, 2.0, 3.0, 5.0, 6.5 and 8.0 µg kg⁻¹ doses using the linear equation fit to the data

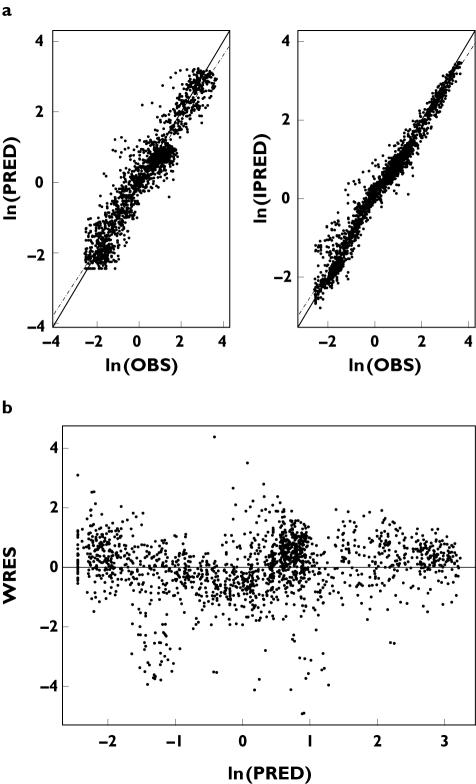
We used diagnostic plots to assess model goodness-of-fit visually (Figure 4a,b). The plot of predicted and observed concentrations (Figure 4a) indicated that the model adequately described the observations over the entire dose range. An exponential residual error model (variance of residual error: σ₁² in equation 2) provided an adequate fit to the residual variability in the PK data. A combination error model (additive + proportional) was also attempted; however, the contribution of the additive error was negligible compared with that of the proportional error term, and was therefore discarded. Most of the weighted residuals were within a standard deviation (SD) of ±2 normalized units (Figure 4b).

Figure 4.

Diagnostic plots of the full pharmacokinetic model. (a) Mean predicted (PRED) and individual predicted (IPRED) vs. observed (OBS) serum darbepoetin alfa concentrations are plotted on a log scale. The data points represent individual observations. (b) Plot of the weighted residuals (WRES) vs. PRED

The final estimates of the covariate coefficients and asymptotic standard errors obtained from the full covariate model in NONMEM are shown in Table 3. Addition of the covariates reduced the MOFV by 67 points, decreased the random IIV on CL by ∼36%, on V₁ by ∼32% and on K_a by ∼62% (Table 3; data not shown for base model). The bootstrap 95% CI of estimates of covariate coefficients r₁, r₂ and r₃ did not overlap their NULL values (Table 3). However, the precision of the r₂ estimate was relatively poor (%SEP = 44.9), indicating that there was insufficient information in the data to characterize this relationship precisely (i.e. lack of information about covariate effect). The distribution of the empirical Bayes estimates after inclusion of the covariate effects in the full model are shown in Figure 5.

Figure 5.

Pharmacokinetic (PK) parameter–covariate relationships in the full covariate PK model. ETA (η) is the interindividual variance parameter (see equation 1)

Full covariate model evaluation using predictions

The mean serum darbepoetin alfa levels as predicted using the full covariate model, and the observed levels for the test dataset, are shown in Figure 6. The MPPE and RMSPE at the nominal 48-h time point in the test dataset were 20% and 52%, respectively. In comparison, the MPPE and RMSPE of the base model against the same test dataset were 32% and 69%, respectively.

Figure 6.

Summary of the fixed-effects prediction. Mean predicted (dotted line) and mean (±SD) observed (solid line) serum darbepoetin alfa concentration–time profiles at the dose levels in the test dataset are shown. 500 µg (•), 6.5 µg/kg (▿), 3 µg/kg (▪), 2 µg/kg (◊), 80 µg (▴), Mean predicted (), Mean (SD) observed (——)

Assessment of the effect size of covariates

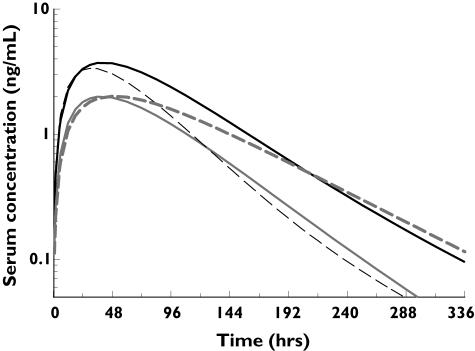
A 100-µg s.c. dose of darbepoetin alfa was used to estimate the effect size of the covariates body weight and age (Figure 7). Simulations indicated that at this dose, the AUC_0–∞ for a person weighing 50 kg is likely to be 101% (95% CI 48, 179) higher than that in a person weighing 90 kg. The simulated exposure for a 30- and an 80-year-old person is likely to be the same, but because of flip-flop kinetics, the lower K_a in an older person is likely to result in a 43% (95% CI 34, 52) longer terminal half-life of darbepoetin alfa.

Figure 7.

Evaluation of effect size of influential covariates. Darbepoetin alfa serum concentration profiles after a 100-µg fixed dose, simulated using the full covariate model fixed-effect parameters at the extremes of the ranges of the covariates body weight (solid line) and age (hashed line). 50 kg (), 90 kg (), 30 yr (), 80 yr ()

Discussion

We developed a population PK model of darbepoetin alfa in healthy subjects and evaluated the model using a test dataset. The dose-disproportionate increase in darbepoetin alfa exposure (less than twofold) at doses >5.0 µg kg⁻¹ was explained by increased relative bioavailability at those doses. Increasing body weight correlated with increased darbepoetin alfa clearance and central compartment volume of distribution, while increasing age correlated with a reduced absorption rate constant after s.c. administration. These covariate–PK parameter relationships need to be investigated further and their clinical significance evaluated in different disease settings under different dosing regimens.

Previous noncompartmental analyses of PK data of darbepoetin alfa in patient populations with chronic kidney disease and chemotherapy-induced anaemia have indicated dose-linear PK at the therapeutic dose range (0.45–4.5 µg kg⁻¹) in these patient populations [26]. Recent data have also indicated PK dose linearity in patients with chronic heart failure [10]. Here, we have investigated darbepoetin alfa PK over a dose range of 0.75–8.0 µg kg⁻¹ by analysing, via a population approach, combined data derived from healthy subjects enrolled in different Amgen-sponsored clinical studies that applied various dosing and sampling regimens. Furthermore, this is the first study exploring the effect of baseline covariates on the PK variability of darbepoetin alfa in any subject population.

The full covariate PK model reported here provided an adequate description of the data. The goodness-of-fit plots and standard errors (Figure 4, Table 3) indicated that the estimates were precise and unbiased. The downward biased weighted residuals in Figure 4b reflect the uncharacteristically high concentrations seen in the 1.0 µg kg⁻¹-dose cohort.

A potentially confounding factor in our analysis is the variability in the concentration of endogenous EPO, which cross-reacted in the darbepoetin alfa assay and is believed to exhibit up to twofold diurnal variation in healthy subjects [27]. In our model, the endogenous EPO levels were described by an individual-specific constant value. At the lowest dose, the estimated typical population endogenous level of EPO (0.0867 ng ml⁻¹) was <10% of the mean observed maximum serum concentration (1.47 ng ml⁻¹), indicating that even with the diurnal fluctuations the impact of endogenous EPO on this analysis is likely to be small.

For an average 70-kg human, the estimated mean s.c. relative bioavailability increased from ∼48% at 0.75 µg kg⁻¹ to ∼78% at 8.0 µg kg⁻¹, similar to the trend reported for rHuEPO [28]. Saturable injection site loss, which has been observed for many proteins including rHuEPO [29, 30], and/or saturable degradation by proteolytic enzymes in the lymph may contribute to this phenomenon [31]. It is also possible that this dose-disproportionate exposure increase is due to concentration-dependent clearance; however, in our analysis the parameters of such a clearance could not be estimated, possibly because the serum concentration profile after s.c. dosing is determined mainly by the molecule’s absorption rate (flip-flop kinetics) and therefore provides little information for precisely estimating parameters of concentration-dependent clearance. Serum concentration–time profiles after higher i.v. doses are required to characterize fully a potential concentration-dependent clearance. Previous analyses [28] have reported combined zero- and first- order absorption kinetics for rHuEPO. However, we were not able to estimate the parameters of this combined absorption model, presumably due to the small number of data points available from the absorption phase.

Our analysis indicated that body weight and age may be important covariates influencing PK parameter variability in healthy subjects. The relationship between body weight and V₁ was estimated with poor precision, indicating that the significance of this relationship should be confirmed using data analysis covering a wider range of weights. Previous analyses of rHuEPO PK also identified body weight as an influential covariate on clearance and volume of distribution [32, 33]. Other body weight-derived factors such as body mass index and lean body mass did not correlate better than body weight with clearance and volume of distribution. Graphical analysis indicated no discernible effect of gender, baseline haemoglobin or creatinine clearance on the clearance of darbepoetin alfa (plots not shown). The absorption rate constant declined with age. This relationship has not been previously reported for erythropoietic agents. In their graphical analysis, Chakraborty et al.[33] reported an apparent decline of erythropoietin K_a with body weight; however, the result was not statistically significant. Age-dependent reduction in lymphatic flow rate as observed in rats and hypothesized in humans may explain the apparent decrease in absorption rate constant with age [34, 35].

The effect sizes of these covariate relationships were estimated by performing deterministic simulations and comparing the exposures at the extremes of the covariate ranges. The mean predicted AUC_0–∞ in a person weighing 50 kg was approximately 101% greater than that in a person weighing 90 kg. However, clinical trials showed no difference in the mean haemoglobin response across different body weight groups after a darbepoetin alfa fixed-dosing (325 µg s.c.) regimen of once every 3 weeks (Q3W) in patients with chemotherapy-induced anaemia [7]. Our simulations indicated that the terminal half-life following s.c. dosing of darbepoetin alfa in an 80-year-old person might be expected to increase by a mean of 43% (95% CI 34, 52) compared with a 30-year-old person; however, this difference should be viewed in light of the approximate two- to threefold variability in half-life typically observed in a given population. Therefore, the covariate–PK parameter relationships identified in this analysis should be investigated in more detail in different disease populations and their effect sizes evaluated at the dosing regimen of interest before conclusions are drawn regarding their clinical significance. Nevertheless, these results provide a convenient starting point for such analyses, while possibly providing insights into the mechanism of absorption and disposition of darbepoetin alfa in healthy subjects.

The fixed-effects predictions of serum concentrations at 48 h in the test set using the full covariate model had a MPPE of 20% and a RMSPE of 52%. In comparison, predictions using the base model had values of 32% and 69% for the two parameters, respectively, indicating that a significant proportion of the variability in PK was unaccounted for even after the inclusion of the two covariates body weight and age. Therefore, further exploration of covariates influencing darbepoetin alfa PK variability is necessary. The bias in the fixed-effects prediction for both the base and the full model is presumably exaggerated by the uncharacteristically high concentrations observed in the 1.0 µg kg⁻¹-dose cohort in the training dataset – a fixed-effects prediction using a model developed without the 1.0 µg kg⁻¹-data in the training set resulted in MPPE of −15% against the same test dataset. However, in order to obtain the most general population PK model, the 1.0 µg kg⁻¹-data were included in the training dataset. In light of the typically observed C_max variability after administration of darbepoetin alfa (CV ∼100%), the MPPE and RMSPE indicate that the model is adequately predictive.

We developed a population PK model of darbepoetin alfa in healthy subjects using data obtained over a wide dose range. This model is a suitable starting point for the development of pharmacokinetic–pharmacodynamic models and simulations in various disease settings. The observed, modestly disproportionate dose-exposure relationship at doses >5.0 µg kg⁻¹ (less than twofold) may reflect increased relative bioavailability at the higher doses. A covariate analysis indicated that the clearance and volume of distribution may be related to increasing body weight and the absorption rate constant decreased with increasing age in these subjects.