Abstract
What is already known about this subject
Effects of size, renal function, age (postnatal age, gestational age and postmenstrual age) as predictors of vancomycin clearance in premature neonates are established, but the relative contribution of each component remains poorly quantified, largely because these variables are closely correlated.
We have quantified the covariates contributing to vancomycin clearance population parameter variability in order to establish the major covariates required for dosing predictions. Size, standardized using allometric models, was the primary covariate used in our analysis.
What this study adds
Size explained 49.8%, postmenstrual age 18.2% and renal function 14.1% of clearance variability.
Descriptors of the relationship between age and clearance in premature neonates vary.
The use of a variable slope sigmoidal model to describe the relationship between clearance and postmenstrual age predicted an adult clearance of 3.79 l h−1 70 kg−1 (95% confidence interval 2.76, 4.98) from premature neonatal data.
Aim
To identify and quantify factors describing the variability of vancomycin clearance in premature neonates.
Methods
Population pharmacokinetics were estimated (NONMEM) in 214 neonates [postmenstrual age (PMA) 30.4 weeks, range 24–34 weeks; postnatal age 11.9 days, range 1–27 days; weight 1.30 kg, range 0.42–2.6 kg] using therapeutic drug monitoring data. Covariate analysis included weight, PMA, serum creatinine, use of inotropes or ibuprofen, positive blood culture and respiratory support. A one-compartment linear disposition model with zero order input and first-order elimination was used to describe the data (604 observations).
Results
The population estimate for volume of distribution (V) was 39 l 70 kg−1 (coefficient of variation 19.4%). Clearance (CL) increased from 0.897 l h−1 70 kg−1 at 24 weeks PMA to 2.02 l h−1 70 kg−1 by 34 weeks PMA. The between-subject variability for CL was 18.6% and the between-occasion variability was 12.2%. The use of ibuprofen reduced clearance, but this effect was attributable to reduced renal function. Overall, 82% of the variability of CL was predictable. Size explained 49.8%, PMA 18.2% and renal function 14.1%. The use of a variable slope sigmoidal model to describe the relationship between clearance and PMA predicted an adult clearance of 3.79 l h−1 70 kg−1 (95% confidence interval 2.76, 4.98).
Conclusions
Size, renal function and PMA are the major contributors to clearance variability in premature neonates. The small (18%) unexplained variability in clearance suggests target concentration intervention is unnecessary if size, age and renal function are used to predict the dose. Extrapolation to an adult clearance from neonatal data is possible using allometric size models and a function describing clearance maturation.
Keywords: allometry, drug interactions, pharmacokinetics, premature infants, vancomycin
Introduction
Premature neonates remain susceptible to nosocomial infections during their stay in the neonatal intensive care unit (NICU), in part due to a relative immunological incompetence and in part due to invasive techniques commonly used in this environment (e.g. central venous catheters, endotracheal intubation). Coagulase-negative staphylococci and Staphylococcus aureus are the most prominent nosocomial bacterial pathogens involved in this age group. Vancomycin is currently the first-choice antibiotic for treatment of these infections. Although there is no clear relationship between serum concentrations and a given clinical response, vancomycin dosing is commonly titrated to obtain peak serum concentrations of 20–40 mg l−1 and serum trough concentrations of 5–10 mg l−1[1]. Low concentrations may result in less effective therapy and an increased propensity to bacterial resistance, whereas high concentrations are reported to be associated with nephrotoxicity and ototoxicity, although these toxic effects are rare in neonates and bear no obvious relationship to serum concentrations [2].
Effects of size, renal function, age (postnatal age, gestational age and postmenstrual age) as predictors of vancomycin clearance are established [3–6] but the relative contribution of each component remains poorly quantified, largely because these variables are closely correlated. Concomitant drug therapy [e.g. nonsteroidal anti-inflammatory drugs (NSAIDs)] also influences clearance. We have undertaken a covariate analysis from therapeutic monitoring data in a cohort of neonates resident in a NICU. Covariate data included weight, postmenstrual age (PMA), postnatal age (PNA), serum creatinine, inotrope use, positive blood culture result, use of respiratory support, administration of a NSAID as well as maternal betamethasone administration from a cohort of neonatal intensive care residents. We have attempted to quantify the covariates contributing to vancomycin clearance population parameter variability in order to establish the major covariates required for dosing predictions.
Methods
Patients
Premature neonates with a PMA of <35 weeks and a PNA of <29 days who were treated with vancomycin during admission to the NICU of the University Hospital, Gasthuisberg, Leuven between January 2002 and October 2005 were considered for inclusion in this retrospective study if at least one vancomycin serum concentration was assayed for therapeutic drug monitoring (TDM). Maternal and neonatal characteristics of these premature neonates (PMA, PNA, weight, antenatal betamethasone, use of respiratory support, blood culture-proven infection, coadministration of dopamine or ibuprofen, serum creatinine concentration) were extracted from a prospectively collected database while observations on vancomycin dose and interval were extracted from the daily nursing progress reports. It was possible to extract a further group requiring endotracheal positive pressure ventilation from the respiratory support group that included those neonates given nasal continuous positive airway pressure (CPAP).
Ethics
All reported data were available in a prospectively collected clinical database. Vancomycin analyses were performed for TDM and these data used for pharmacokinetic (PK) analysis. The Institutional Review Board of the University Hospital Gasthuisberg agrees on the general concept of prospective collection of clinical characteristics for quality of care assessment. All parents of neonates admitted to the NICU receive written information about this prospective data collection and that these data are collected for quality control and clinical performance studies.
Vancomycin drug administration and sampling
Vancomycin (Vancocin®; Elli Lilly, Brussels, Belgium) and amikacin (Amukin®; Bristol Myers Squibb, Waterloo, Belgium) were the standard empirical treatment for suspected nosocomial bacterial infection. Vancomycin (15 mg kg−1 per dose) was administered as an intravenous infusion over 60 min by syringe driver (SIMS Graseby®; Watford, UK). The time interval between consecutive administrations was 12 h but was increased to 24 h in neonates younger than 7 days PNA and in those with a serum creatinine >71 µmol l−1 (0.8 mg dl−1). Blood samples for TDM were collected from an indwelling arterial line or by venous puncture just before (‘trough’) and within 5 min of finishing the second or third dose infusion (‘peak’).
Assay
Vancomycin plasma concentration assays were performed using a homogeneous particle enhanced turbidimetric inhibition immunoassay method (PETINIA on Dimension RxL; Dade Behring Holding GmbH, Liederbach, Germany) within 12 h following sample collection and were reported in mg l−1. Laboratory performance characteristics of the assay are: linearity up to a concentration of 50 mg l−1, reproducibility assessed at different levels (5, 10 and 30 mg l−1) yielded a within-run and a total coefficient of variation (CV%) of ≤3%, internal quality assessment on levels covering the therapeutic concentration range showed typically a long-term CV of ≤6%. Based on user experiments, the minimal quantifiable concentration was set at 2 mg l−1 defined by a CV of <15%.
Pharmacokinetic analysis
Population parameter estimations
A one-compartment linear disposition model with zero order input (1-h i.v. infusion) and first-order elimination was used to describe the data. Population parameter estimates were obtained using a nonlinear mixed effects approach (NONMEM) [7]. This model can account for population parameter variability (between and within subjects) and residual variability (random effects) as well as parameter differences predicted by covariates (fixed effects). The between-subject variability in model parameters was modelled by exponentiating random effects (equivalent to assuming a log-normal distribution). Residual unexplained variability was modelled using a combined proportional and additive error model.
The population parameter variability is modelled in terms of random effect (η) variables. Each of these variables is assumed to have mean 0 and a variance denoted by ω2, which is estimated. We report the estimate of ω for each variability component. The covariance between two elements of η (e.g. CL and V) is a measure of statistical association between these two variables. Their covariance is related to their correlation, i.e.
The covariance of clearance and distribution volume variability was estimated.
Covariate analysis
The parameter values were standardized for a body weight of 70 kg using an allometric model [8, 9]:
where Wi is the weight in the ith individual. Allometric scaling has a strong theoretical and empirical basis with a PWR exponent of 0.75 for clearance and 1 for distribution volume [10–14]. We have chosen a standard weight of 70 kg to enable comparison with adult values and other paediatric studies.
Creatinine clearance (CLcr) was predicted using PMA (weeks) as a covariate to predict creatinine production rate (CPR) with a scaling constant (Kage) for age. This is based on assuming a CPR of 516 µmol h−1 in a 70-kg, 40-year-old male [15]:
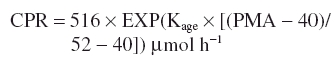 |
Renal function (RF) was standardized to a creatinine clearance of 6 l h−1 70 kg−1. Vancomycin clearance was predicted by assuming all elimination is renal.
An indicator variable was applied to those subjects given ibuprofen. The effect of coadministration of ibuprofen on vancomycin clearance was investigated by applying a scaling factor (FNSAID) to clearance in those neonates given a NSAID. The influence of prenatal betamethasone, use of dopamine (Finotope), positive pressure ventilation (Fventilation), CPAP, sepsis and a positive blood culture were investigated in a similar manner.
Alternative models for clearance maturation
Covariate analysis included a linear model investigating age-related changes for clearance:
where FPMA is centred on 40 weeks PMA (full-term gestation), PMA is the postmenstrual age in weeks and SLPCL is a parameter describing changes of clearance with PMA.
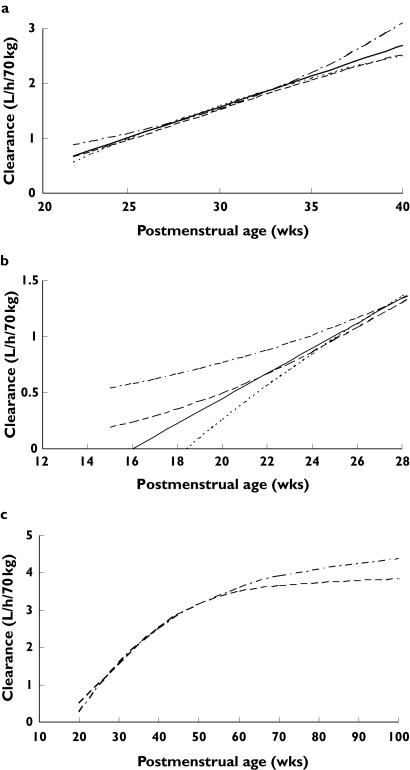
We investigated three alternative models to relate maturation of clearance to age. These three models (exponential, first order, variable slope sigmoidal) can approximate the linear model over the age range of the neonatal population studied (Figure 1a). Maturation of clearance must develop before birth and extrapolation of a linear function does not allow this. Consequently, an exponential function was investigated in order to allow for a gradual increase in clearance at earlier postmenstrual ages (Figure 1b). This exponential function was used by Kimura et al. in their study of vancomycin PK in neonates [4]:
This exponential function, in common with the linear model, predicts increasing clearance with age. This model is empirical and does not extrapolate to adult values because, physiologically, clearance must rise and plateau at some age. A first-order model, common in biological systems, has been previously used to investigate clearance maturation of other drugs during infancy [14]. A ‘mature’ clearance can be estimated (Figure 1c) at plateau:
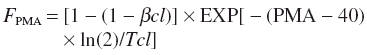 |
where βcl is parameter estimating the fractional CLstd at 40 weeks PMA and Tcl describe the maturation half-life of the age-related changes of CL. We were unable to estimate Tcl from our current data but assumed a prior of 19 weeks from study investigating morphine metabolite clearance [16]. This model also suffers because it assumes zero clearance at the x-intercept (Figure 1b).
Figure 1.
(a) The four models used to investigate the relationship between age and clearance maturation are similar in the age range of the population studied. (b) The first-order and linear models intercept the abscissa before 0. This seems unlikely as organogenesis is occurring during the second trimester of pregnancy. The exponential and variable slope sigmoidal models (Hill equation) allow for gradual clearance maturation which starts early in fetal life. (c) The first-order and variable slope sigmoidal models predict a ‘mature’ vancomycin clearance. The first-order model shows that 80% of the ‘mature’ value at 62 weeks postmenstrual age (PMA), whereas the variable slope sigmoidal model is at 90% of the ‘mature’ value at 62 weeks PMA. Exponential (.––.); first order (......); Hill (––); liner (——)
A variable slope sigmoidal model (Hill equation) allows gradual maturation of clearance in early life and a ‘mature’ clearance to be achieved at a later age (Figure 1c):
where EMATCL50 is the PMA at which clearance is 50% that of the mature value and HillCL is the Hill coefficient for clearance.
Group clearance was predicted for infants sharing similar covariates from:
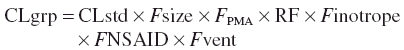 |
Individual clearance was predicted from the group clearance and an exponential random effect:
Parameter estimation was performed using NONMEM version V release 1.1 with the first-order conditional method and the interaction option and a convergence criterion of three significant digits. Models were compiled with Compaq Visual Fortran Version 6.6 update C and executed on an Intel Pentium processor under Windows XP. The quality of fit of the PK model to the data was judged by NONMEM’s objective function and by visual examination of plots of observed vs. predicted concentrations. Models were nested and an improvement in the objective function was referred to the χ2 distribution to assess significance, e.g. an objective function change (OBJ) of 3.84 is significant at α = 0.05 with one additional parameter in the model.
Results
Data from 604 drug assay samples in these 214 subjects were available to study the PK of vancomycin. The covariates size (weight), postmenstrual age, renal function and ventilation influenced clearance (Table 1a, linear model; Table 1b variable slope sigmoidal model). Confidence intervals for the variable slope sigmoidal model (Table 1c) were estimated using bootstrap statistics [17]. It should be noted that the way renal function has been included in the model is independent of body size. Postmenstrual age was superior to postnatal age (Table 2). The coadministration of ibuprofen resulted in an 18% reduction in clearance, but this effect was no longer observed after renal function was accounted for. There was no effect attributable to prenatal betamethasone, inotrope use, sepsis or a positive blood culture result.
Table 1a.
Vancomycin population pharmacokinetic parameter estimates using a linear model relating postmenstrual age (PMA) to clearance (CL)
| Parameter | Estimate | BSV | BOV | %SE |
|---|---|---|---|---|
| CLstd (lh−170kg−1) at 40weeks PMA and RF=1 | 2.19 | 0.187 | 0.122 | 15.3 |
| Vstd (l70kg−1) | 39.0 | 0.194 | – | 2.5 |
| SLPCL (1week−1) | 0.0216 | – | – | 17.2 |
| Fventilation (on CL) | 0.942 | – | – | 3.5 |
| Finotrope (on V) | 1.17 | – | – | 9.9 |
| Kage | 0.0096 | – | – | 40.4 |
| Residual unidentified variability additive | 1.4mgl−1 | – | – | 30.6 |
| proportional | 0.23% | – | – | 10.7 |
BSV and BOV are the between-subject and between-occasion variability expressed as the square root of their variance; SE is the standard error of the structural estimate. V = Vstd × (Wt/70) × Finotrope × Inot l. CL = CLstd × (Wt/70)0.75 × [1+SLPCL × (PMA−40)] × RF × Fventilation × Vent)lh−1 where Vstd and CLstd are the population estimates for V and CL, respectively, standardized to a 70-kg person using allometric models; PMA is the postmenstrual age in weeks; SLPCL is the factor relating PMA to developmental changes in CL; Finotrope and Fventilation are scaling factors applied for the use of inotropes (Inot) or positive pressure artificial ventilation (Vent); Inot and Vent have a value of 1 if present and 0 if absent. The calculation of renal function (RF) is explained in the text.
Table 1b.
Vancomycin population pharmacokinetic parameter estimates using a variable slope sigmoidal model relating postmenstrual age (PMA) to clearance (CL)
| Parameter | Estimate | BSV | BOV | %SE |
|---|---|---|---|---|
| CLstd ‘mature’ (lh−170kg−1) and RF=1 | 3.79 | 0.209 | 0.122 | 20.2 |
| Vstd (l70kg−1) | 39.4 | 0.197 | – | 2.6 |
| EMATCL50 (weeks) | 33.3 | – | – | 28.3 |
| HillCL | 3.68 | 37.2 | ||
| Fventilation (on CL) | 1.03 | – | – | 3.6 |
| Finotrope (on V) | 1.18 | – | – | 10.8 |
| Kage | 0.00789 | – | – | 64.9 |
| Residual unidentified variability additive | 1.5mgl−1 | – | – | 32.1 |
| proportional | 0.23% | – | – | 11.7 |
BSV and BOV are the between-subject and between-occasion variability expressed as the square root of their variance, SE is the standard error of the structural estimate. V = Vstd×(Wt/70) × Finotrope × Inot l. CL=CLstd × (Wt/70)0.75 × [PMAHillCL/(PMAHillCL + EMATCL50HillCL)]×RF×Fventilation×Vent lh−1where Vstd and CLstd are the population estimates for V and CL, respectively, standardized to a 70-kg person using allometric models; PMA is the postmenstrual age in weeks; EMATCL50 is the PMA at which clearance is 50% that of the mature value; HillCL is the Hill coefficient for clearance; Finotrope and Fventilation are scaling factors applied for the use of inotropes (Inot) or positive pressure artificial ventilation (Vent); Inot and Vent have a value of 1 if present and 0 if absent. The calculation of renal function (RF) is explained in the text.
Table 1c.
Bootstrap statistics for vancomycin population pharmacokinetic parameter estimates using a variable slope sigmoidal model relating postmenstrual age (PMA) to clearance (CL)
| Parameter | Median | 5% centile | 95% centile | % SE |
|---|---|---|---|---|
| CLstd ‘mature’ (lh−170kg−1) and RF=1 | 3.83 | 2.76 | 4.98 | 19.1 |
| Vstd (l70kg−1) | 39.4 | 37.8 | 41.1 | 2.6 |
| EMATCL50 (weeks) | 33.3 | 33.3 | 33.3 | – |
| HillCL | 3.68 | 3.68 | 3.68 | – |
| Fventilation on CL | 1.03 | 0.976 | 1.1 | 3.6 |
| Finotrope on V | 1.19 | 0.995 | 1.421 | 11.2 |
| Kage for CPR maturation | 0.00823 | 0 | 0.0148 | 59.6 |
| BSVCL | 0.208 | 0.144 | 0.271 | 18.4 |
| BSVV | 0.195 | 0.125 | 0.259 | 21.7 |
| BOVCL | 0.110 | 5.01×10−5 | 0.169 | 43.5 |
| Residual unexplained variability additive | 1.47 | 1.10 | 1.88 | 16.4 |
| proportional | 0.227 | 0.203 | 0.248 | 6.0 |
BSVCL, between-subject variability for CL; BSVV, between-subject variability for V; BOVCL, between-occasion variability for CL.
Table 2.
Effect of covariate analysis on variance of clearance (ω2) – impact of each covariate analysis when added sequentially to the model
| Individual covariate alone | PPVt2 | BSVR2 | BOV2 | PPVP2 | PPVP2/PPVt2 | OBJ |
|---|---|---|---|---|---|---|
| No covariates | 0.279 | 0.279 | 0 | 0 | 0 | 2835.261 |
| Allometric scaling | 0.279* | 0.0538 | 0.0862 | 0.139 | 0.498 | 2632.123 |
| Age | ||||||
| PMA linear | 0.279* | 0.0449 | 0.0443 | 0.190 | 0.680 | 2515.136 |
| exponential | 0.279* | 0.0443 | 0.0456 | 0.189 | 0.678 | 2519.390 |
| first order | 0.279* | 0.0446 | 0.0450 | 0.189 | 0.679 | 2515.461 |
| variable slope sigmoidal | 0.279* | 0.0452 | 0.0450 | 0.189 | 0.677 | 2514.865 |
| PNA linear | 0.279* | 0.0734 | 0.0373 | 0.1683 | 0.603226 | 2579.162 |
| Renal function | 0.279* | 0.0362 | 0.0137 | 0.230 | 0.821 | 2418.198 |
| Ventilation scaling factor | 0.279* | 0.0356 | 0.0137 | 0.230 | 0.823 | 2413.725 |
Assumed from no covariate model estimate. PPVt2, Total population parameter variability estimated without covariate analysis; BSVP2, between-subject variability predictable from covariates, BSVR2, random BSV2 estimated on a parameter when covariate analysis is included; BOV2, between-occasion variability (PPVt2 = BSVP2 + BSVR2 + BOV2). The ratio of the population parameter variability predictable from covariates (PPVP2) to the total population parameter variability obtained without covariate analysis (PPVt2) (i.e. PPVP2/ PPVt2) indicates the fraction of the total variability in the parameter that is predictable from covariates. OBJ, Objective function value measuring the goodness of fit.
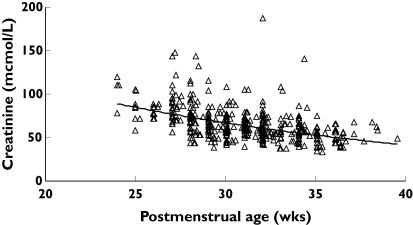
Figure 2 shows the observed and predicted relationship between PMA and maximum a posteriori Bayesian individual predictions of CL. Serum creatinine was observed to decrease with age in the raw data (Figure 3). This was expected, as maternal creatinine is eliminated and renal function matures. There was almost no change in predicted CPR within the premature neonatal cohort over the range of PMA studied, but we were reassured because Kage was similar to an estimate from a study examining morphine metabolite clearance in infants [16]. CPR is about 73% of adult values at birth in a term neonate.
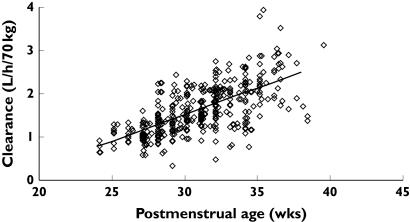
Figure 2.
Individual predicted vancomycin clearances (CL), standardized to a 70-kg person, from the NONMEM post hoc step, are plotted against postmenstrual age. The solid line represents the linear relation between clearance and age
Figure 3.
Creatinine concentrations in those neonates greater than 2 days postnatal age are plotted against postmenstrual age. Creatinine concentration is a function of both production and renal clearance
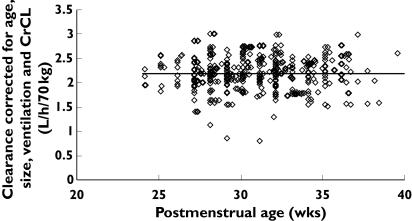
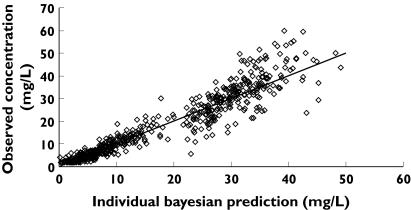
Figure 4 shows the observed and predicted relationship between PMA and maximum a posteriori Bayesian individual predictions of CL with contribution from covariate information. Individual Bayesian concentration predictions from the linear PMA model based on values of the parameters for the specific individual are compared with those observed in Figure 5. The population parameter estimate for volume of distribution (V) was 39 l 70 kg−1 (CV 19.4%). The use of an inotrope increased V by 17%. We were unable to demonstrate any relationship between V and PMA or PNA.
Figure 4.
Individual predicted vancomycin clearances (CL) from the linear postmenstrual age (PMA) model, standardized to a 70-kg person, from the NONMEM post hoc step, and corrected for age, creatinine clearance and ventilation, are plotted against PMA. The horizontal line represents clearance in an average neonate (30 weeks PMA)
Figure 5.
Individual Bayesian concentration predictions from the linear postmenstrual age model based on values of the parameters for the specific individual are compared with those observed. The line x = y is the line of identity
The correlation of between-subject variability (BSV) for CL and V was 0.96 for the linear model and 0.896 for the variable slope sigmoidal model. CL increased from 0.897 l h−1 70 kg−1 at 24 weeks PMA to 2.02 l h−1 70 kg−1 by 34 weeks PMA using the linear PMA model. The BSV for CL was 18.6% and the between-occasion variability (BOV) was 12.2%. The difference between BSV without covariates and with covariates is a measure of the predictable decrease in BSV due to covariates. The ω2 estimates for the different components contributing to variability are shown in Table 2. The ratio of the between-subject variability predictable from covariates (BSVP2) to the total population parameter variability obtained without covariate analysis (PPVt2) gives an indication of how important covariate information is. For example, the ratio of 0.823 achieved for clearance in this current study indicates that 82.3% of the overall variability in clearance is predictable from covariate information. Weight explained 49.8%, PMA 18.2% and renal function 14.1%.
Mean age-related PK predictions based on the covariate models are shown in Table 3. Parameters were estimated based on a standard adult weight of 70 kg to enable comparison with other glycopeptide and aminoglycoside studies. Table 3 also expresses PK parameters per kg, based on the expected weight for each age group. The linear model best described the maturation of clearance with PMA (Table 2), although all models predicted similar mean clearance values for the age range observed. Both the first-order model asymptotic (‘mature’) clearance estimate (4.6 l h−1 70 kg−1, SE 5.8%) and variable slope sigmoidal model asymptotic clearance estimate (3.9 l h−1 70 kg−1, SE 52.5%) (Figure 1c) were similar to adult estimates (3–5.5 l h−1 70 kg−1) [18–21]. The variable slope sigmoidal model estimated an EMATCL50 of 33.3 (SE 28.3%) and a HillCL of 3.68 (SE 37.2%). The estimate for EMATCL90 was 62 weeks PMA.
Table 3.
Weight- and age-related vancomycin parameters predicted using the allometric ‘1/4 power’ model (70 kg−1) and linear per kilogram model (kg−1)
| Age | Weight (kg) | CL (l h−1 70 kg−1) | CL (l h−1) | CL (l h−1 kg−1) | V (l) | V (l kg−1) |
|---|---|---|---|---|---|---|
| 24 weeks PMA | 0.5 | 0.897 | 0.022 | 0.044 | 0.279 | 0.557 |
| 25 weeks PMA | 0.6 | 1.009 | 0.028 | 0.047 | 0.334 | 0.557 |
| 26 weeks PMA | 0.8 | 1.121 | 0.039 | 0.045 | 0.446 | 0.557 |
| 27 weeks PMA | 0.9 | 1.233 | 0.047 | 0.052 | 0.501 | 0.557 |
| 28 weeks PMA | 1 | 1.346 | 0.056 | 0.056 | 0.557 | 0.557 |
| 29 weeks PMA | 1.15 | 1.458 | 0.067 | 0.058 | 0.641 | 0.557 |
| 30 weeks PMA | 1.3 | 1.57 | 0.079 | 0.061 | 0.724 | 0.557 |
| 34 weeks PMA | 2.4 | 2.019 | 0.161 | 0.067 | 1.337 | 0.557 |
| 40 weeks PMA | 3.3 | 2.692 | 0.272 | 0.084 | 1.838 | 0.557 |
The linear PMA model was used for these predictions. PMA, Postmenstrual age.
Discussion
Size, PMA, renal function and ventilation are important covariates influencing clearance variability in neonates with presumed sepsis in a NICU. Parameter estimates compare well with those from other publications [2–6]. Vancomycin is almost exclusively cleared by renal elimination and PMA is a predictor of vancomycin clearance, presumably because it predicts the time course of development of the glomerular filtration rate (GFR). Our current estimates for vancomycin clearance mirror GFR estimates in premature neonates [22, 23]. GFR matures during infancy and approaches an adult rate (6 l h−1 70 kg−1) by 6 months post natal age [24, 25]. The administration of ibuprofen, to enhance closure of a symptomatic patent ductus arteriosis (PDA), was associated with a reduction of vancomycin clearance by 18%. This reduction is similar to that reported for an NSAID effect on amikacin clearance at birth [26]. This observation in the current cohort with a mean PNA of 11.9 days (SD 5.9) suggests an effect attributable to the NSAID and not the PDA and that this effect is not restricted to the first few days of life.
Creatinine concentration decreases with age (Figure 3). Consequently, vancomycin clearance estimates have been estimated using only an inverse relationship to creatinine concentration [3]. Weight and age were excluded in the study by Grimsley [3], whereas Capparelli used only weight and creatinine concentration [6]. Kimura also invoked an inverse relationship with creatinine concentration, but showed the addition of PMA and weight improved estimates [4]. We wished to standardize our estimates to a 70-kg person. Attempts to use the Cockcroft and Gault models [15] to predict creatinine production rate failed, as expected. The increase CPR in neonates is assumed to be a consequence of increasing muscle bulk with age as opposed to the decrease in muscle bulk that occurs with age in adults. An empirical formula based on age to predict creatinine production was used instead because creatinine production increases with age in premature neonates as opposed to adults, in whom production decreases with age. Collinearity between ibuprofen use and renal function exists and the use of a predicted renal function empirical formula removed the need for a factor to account for ibuprofen. Correction for renal function accounted for 14.1% of clearance variability.
Size, postmenstrual age and renal function accounted for 82% of clearance variability, suggesting that TDM may be unnecessary if changes in weight, PMA and creatinine are monitored. Creatinine in the first few days of life reflects maternal concentrations more than neonatal renal function and subsequent concentrations are influenced by tubular reabsorption [27]. Septic patients are often catabolic with increased muscle breakdown and creatinine production. However, creatinine concentration remains an important marker of renal function and consequent dosing.
We were unable to demonstrate any effect attributable to sepsis, inotrope use or the presence of positive blood cultures on clearance. The absence of any dopamine effect on vancomycin clearance has been reported by others in a similar neonatal population [3, 28]. Positive pressure ventilation had a small effect on CL which was model dependent. Although Van der Heijden [23] has documented an absence of any effect of ventilation on renal clearance in premature neonates at PNA 3 days, others [22, 29, 30] have demonstrated a reduction of renal clearance in premature neonates in their first 2 weeks of life. This reduction may be mediated through lowered renal function due to decreased atrial natriuretic peptide and increased antidiuretic hormone production attributable to right atrial pressure receptors which are influenced by altered thoracic pressures during positive pressure ventilation.
There was no relationship between PNA or PMA and V, indicating that the initial dose is independent of age. We anticipated disease markers to have an impact on V. Lingvall et al. reported that blood culture-proven infections were associated with a 14% increase in V of gentamicin in neonates [31]. Only inotrope use was associated with 17% increased V in our cohort of patients [28]. Inotrope use is a surrogate marker of severity of illness and may be a more sensitive marker than blood culture positivity, which indicates only the presence of a pathogen, not pathological effects such as compromised haemodynamics caused by sepsis.
Van den Anker et al. have reported on the impact of maternal administration of betamethasone before birth on inulin clearance on days 3 and 10 of postnatal life [32]. We were unable to confirm these observations in either a population PK study on maturation of amikacin pharmacokinetics (24–30 weeks PMA at birth) or in the current study examining the first month of life. De Hoog [2] and Allegaert [33] have also been unable to document this effect.
Size was the primary covariate used in our analysis of the effects of age and weight. This deliberate choice was based on known biological principles. A great many physiological, structural and time-related variables scale predictably within and between species with weight exponents of 0.75, 1 and 0.25, respectively [12]. We have used these ‘1/4 power models’ in the current study rather than centred weight, or some other function of weight, because the ‘1/4 power models’ have a sound theoretical and observational basis in biology [10, 11]. The 3/4 power law for metabolic rates was derived from a general model which describes how essential materials are transported through space-filled fractal networks of branching tubes. By choosing weight as the primary covariate, all parameter estimates could be standardized to a weight of 70 kg to facilitate comparison with adult values and the secondary effects of PMA and creatinine clearance could be investigated.
Clearance maturation begins before birth. We investigated the variable slope sigmoidal model because this model allows for gradual maturation in the immature neonate and also predicts a ‘mature’ clearance value that we might expect in an adult (3–5.5 l h−1 70 kg)−1[18–21]. The EMATCL50 of 33.3 weeks (SE 28.3%) is in reasonable agreement with the known time course of maturation of renal function. GFR matures during infancy and approaches an adult rate (6 l h−1 70 kg−1) within 6 months post natal age (Figure 1c), consistent with our EDMAT90 estimate of 62 weeks PMA. The ‘mature’ estimate of CLstd 3.9 l h−1 70 kg−1 (95% confidence interval 2.76, 4.98) predicted by this variable slope sigmoidal model is similar to reported values in adults. There is currently considerable debate about the estimation of paediatric parameter estimates from adult data [34, 35]. Use of a variable slope sigmoidal model may allow prediction of adult parameter estimates from premature neonatal data.
Acknowledgments
The clinical research of K.A. is supported by the Fund for Scientific Research, Flanders (Belgium) by a Clinical Doctoral Grant (A6/5–KV–G1). The research of J.N.v.d.A. is supported by grant 5 U10 HD045993-03, National Institute of Child Health and Development, Bethesda, MD, USA. We gratefully acknowledge the assistance of Koen Desmet, Department of Laboratory Medicine, University Hospital, Gasthuisberg, for analysing the vancomycin samples
References
- 1.de Hoog M, Mouton JW, van den Anker JN. New dosing strategies for antibacterial agents in the neonate. Semin Fetal Neonatal Med. 2005;10:185–94. doi: 10.1016/j.siny.2004.10.004. [DOI] [PubMed] [Google Scholar]
- 2.de Hoog M, Mouton JW, van den Anker JN. Vancomycin: pharmacokinetics and administration regimens in neonates. Clin Pharmacokinet. 2004;43:417–40. doi: 10.2165/00003088-200443070-00001. [DOI] [PubMed] [Google Scholar]
- 3.Grimsley C, Thomson AH. Pharmacokinetics and dose requirements of vancomycin in neonates. Arch Dis Child Fetal Neonatal Ed. 1999;81:F221–7. doi: 10.1136/fn.81.3.f221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kimura T, Sunakawa K, Matsuura N, Kubo H, Shimada S, Yago K. Population pharmacokinetics of arbekacin, vancomycin, and panipenem in neonates. Antimicrob Agents Chemother. 2004;48:1159–67. doi: 10.1128/AAC.48.4.1159-1167.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Frattarelli DA, Ergun H, Lulic-Botica M, Lehr VT, Aranda JV. Vancomycin elimination in human infants with intrauterine growth retardation. Pediatr Infect Dis J. 2005;24:979–83. doi: 10.1097/01.inf.0000186283.95728.34. [DOI] [PubMed] [Google Scholar]
- 6.Capparelli EV, Lane JR, Romanowski GL, McFeely EJ, Murray W, Sousa P, Kildoo C, Connor JD. The influences of renal function and maturation on vancomycin elimination in newborns and infants. J Clin Pharmacol. 2001;41:927–34. doi: 10.1177/00912700122010898. [DOI] [PubMed] [Google Scholar]
- 7.Beal SL, Sheiner LB, Boeckmann A. Nonmem User’s Guide. San Francisco: Division of Pharmacology, University of California; 1999. [Google Scholar]
- 8.Anderson BJ, Meakin GH. Scaling for size: some implications for paediatric anaesthesia dosing. Paediatr Anaesth. 2002;12:205–19. doi: 10.1046/j.1460-9592.2002.00616.x. [DOI] [PubMed] [Google Scholar]
- 9.Holford NHG. A size standard for pharmacokinetics. Clin Pharmacokinet. 1996;30:329–32. doi: 10.2165/00003088-199630050-00001. [DOI] [PubMed] [Google Scholar]
- 10.West GB, Brown JH, Enquist BJ. A general model for the origin of allometric scaling laws in biology. Science. 1997;276:122–6. doi: 10.1126/science.276.5309.122. [DOI] [PubMed] [Google Scholar]
- 11.West GB, Brown JH, Enquist BJ. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science. 1999;284:1677–9. doi: 10.1126/science.284.5420.1677. [DOI] [PubMed] [Google Scholar]
- 12.Peters HP. Physiological correlates of size. In: Beck E, Birks HJB, Conner EF, editors. The Ecological Implications of Body Size. Cambridge: Cambridge University Press; 1983. pp. 48–53. [Google Scholar]
- 13.Rajagopalan P, Gastonguay MR. Population pharmacokinetics of ciprofloxacin in pediatric patients. J Clin Pharmacol. 2003;43:698–710. [PubMed] [Google Scholar]
- 14.Anderson BJ, Woollard GA, Holford NHG. A model for size and age changes in the pharmacokinetics of paracetamol in neonates, infants and children. Br J Clin Pharmacol. 2000;50:125–34. doi: 10.1046/j.1365-2125.2000.00231.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cockcroft DW, Gault MH. Prediction of creatinine clearance from serum creatinine. Nephron. 1976;16:31–41. doi: 10.1159/000180580. [DOI] [PubMed] [Google Scholar]
- 16.Bouwmeester NJ, Anderson BJ, Tibboel D, Holford NH. Developmental pharmacokinetics of morphine and its metabolites in neonates, infants and young children. Br J Anaesth. 2004;92:208–17. doi: 10.1093/bja/aeh042. [DOI] [PubMed] [Google Scholar]
- 17.Parke J, Holford NH, Charles BG. A procedure for generating bootstrap samples for the validation of nonlinear mixed-effects population models. Comput Meth Programs Biomed. 1999;59:19–29. doi: 10.1016/s0169-2607(98)00098-4. [DOI] [PubMed] [Google Scholar]
- 18.Pou L, Rosell M, Lopez R, Pascual C. Changes in vancomycin pharmacokinetics during treatment. Ther Drug Monit. 1996;18:149–53. doi: 10.1097/00007691-199604000-00007. [DOI] [PubMed] [Google Scholar]
- 19.Rodvold KA, Blum RA, Fischer JH, Zokufa HZ, Rotschafer JC, Crossley KB, Riff LJ. Vancomycin pharmacokinetics in patients with various degrees of renal function. Antimicrob Agents Chemother. 1988;32:848–52. doi: 10.1128/aac.32.6.848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Le Normand Y, Milpied N, Kergueris MF, Harousseau JL. Pharmacokinetic parameters of vancomycin for therapeutic regimens in neutropenic adult patients. Int J Biomed Comput. 1994;36:121–5. doi: 10.1016/0020-7101(94)90102-3. [DOI] [PubMed] [Google Scholar]
- 21.Guay DR, Vance-Bryan K, Gilliland S, Rodvold K, Rotschafer J. Comparison of vancomycin pharmacokinetics in hospitalized elderly and young patients using a Bayesian forecaster. J Clin Pharmacol. 1993;33:918–22. doi: 10.1002/j.1552-4604.1993.tb01922.x. [DOI] [PubMed] [Google Scholar]
- 22.Sonntag J, Prankel B, Waltz S. Serum creatinine concentration, urinary creatinine excretion and creatinine clearance during the first 9 weeks in preterm infants with a birth weight below 1500 g. Eur J Pediatr. 1996;155:815–9. doi: 10.1007/BF02002914. [DOI] [PubMed] [Google Scholar]
- 23.van der Heijden AJ, Grose WF, Ambagtsheer JJ, Provoost AP, Wolff ED, Sauer PJ. Glomerular filtration rate in the preterm infant: the relation to gestational and postnatal age. Eur J Pediatr. 1988;148:24–8. doi: 10.1007/BF00441807. [DOI] [PubMed] [Google Scholar]
- 24.Bergstein JM. Introduction to glomerular diseases. In: Behrman RE, Kliegman RM, Jenson HB, editors. Nelson Textbook of Pediatrics. 16. Philadelphia: W.B. Saunders Co.; 2000. pp. 1574–5. [Google Scholar]
- 25.Arant BS., Jr Developmental patterns of renal functional maturation compared in the human neonate. J Pediatr. 1978;92:705–12. doi: 10.1016/s0022-3476(78)80133-4. [DOI] [PubMed] [Google Scholar]
- 26.Allegaert K, Anderson BJ, Cossey V, Holford NH. Limited predictability of amikacin clearance in extreme premature neonates at birth. Br J Clin Pharmacol. 2006;61:39–48. doi: 10.1111/j.1365-2125.2005.02530.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guignard JP, Drukker A. Why do newborn infants have a high plasma creatinine? Pediatrics. 1999;103:e49. doi: 10.1542/peds.103.4.e49. [DOI] [PubMed] [Google Scholar]
- 28.Seay RE, Brundage RC, Jensen PD, Schilling CG, Edgren BE. Population pharmacokinetics of vancomycin in neonates. Clin Pharmacol Ther. 1994;56:169–75. doi: 10.1038/clpt.1994.120. [DOI] [PubMed] [Google Scholar]
- 29.Leslie GI, Philips JB, 3rd, Work J, Ram S, Cassady G. The effect of assisted ventilation on creatinine clearance and hormonal control of electrolyte balance in very low birth weight infants. Pediatr Res. 1986;20:447–52. doi: 10.1203/00006450-198605000-00014. [DOI] [PubMed] [Google Scholar]
- 30.Ross B, Cowett RM, Oh W. Renal functions of low birth weight infants during the first two months of life. Pediatr Res. 1977;11:1162–4. doi: 10.1203/00006450-197711000-00010. [DOI] [PubMed] [Google Scholar]
- 31.Lingvall M, Reith D, Broadbent R. The effect of sepsis upon gentamicin pharmacokinetics in neonates. Br J Clin Pharmacol. 2005;59:54–61. doi: 10.1111/j.1365-2125.2005.02260.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.van den Anker JN, Hop WC, de Groot R, van der Heijden BJ, Broerse HM, Lindemans J, Sauer PJ. Effects of prenatal exposure to betamethasone and indomethacin on the glomerular filtration rate in the preterm infant. Pediatr Res. 1994;36:578–81. doi: 10.1203/00006450-199411000-00006. [DOI] [PubMed] [Google Scholar]
- 33.Allegaert K, Cossey V, Rayyan M, vanHole C, Devlieger H. Administration of betamethasone before birth has no effect on the amikacin pharmacokinetics in preterm infants at birth. Paed Perinatal Drug Ther. 2005;6:149–54. [Google Scholar]
- 34.Bjorkman S. Prediction of cytochrome p450-mediated hepatic drug clearance in neonates, infants and children: how accurate are available scaling methods? Clin Pharmacokinet. 2006;45:1–11. doi: 10.2165/00003088-200645010-00001. [DOI] [PubMed] [Google Scholar]
- 35.Baber N, Pritchard D. Dose estimation for children. Br J Clin Pharmacol. 2003;56:489–93. doi: 10.1046/j.1365-2125.2003.01901.x. [DOI] [PMC free article] [PubMed] [Google Scholar]