Dose–response of minor analgesics in acute pain

An important question to ask about any drug is whether increasing the dose improves the effect. When licensing a new drug, regulatory authorities require manufacturers to provide data to support proposed dosage regimens. However, premarketing studies are generally too small and hence too insensitive to pick out real dose differences in effect. Surrogate outcomes often used to improve trial sensitivity usually predict more meaningful clinical outcomes poorly because the correspondence curves are rarely linear. Consequently, at the time of first marketing the dose–clinical response curve is poorly defined, for both efficacy and, more particularly, adverse effects. For older drugs, there is even less evidence base to rely on as they were licensed when drug regulation was laxer.

In this issue of the Journal, McQuay and Moore report on their attempt to define the dose–response curves for three commonly used minor analgesics in acute pain, through a meta-analysis of the available randomized controlled trial evidence. Although they found 50 trials, there were relatively few direct comparisons suitable for quantitative pooling; the largest number, 13, compared 400 mg vs. 800 mg ibuprofen. Seven trials compared paracetamol 500 or 650 mg with 1000 mg and eight trials compared aspirin 500 or 600 mg with 1000 or 1200 mg. However, for each of the three analgesics, the pooled comparisons included over 900 subjects, a large increase relative to the number of subjects in the individual trials. On average they estimated that for each of the three analgesics some 20% more patients would respond to the higher dose than the lower dose, corresponding to an absolute increase of about 10%[7% (aspirin), 9% (ibuprofen) and 12% (paracetamol)]. For those who find it easier to interpret, the number-needed-to-treat was about 10.

A meta-analysis is meant to improve precision and it may appear sacrilegious to approximate pooled results as roughly as we have just done. However, the success of the Oxford group, in their meta-analytic approach to summarizing pain relief data, resides in their not being afraid to sacrifice some precision for the sake of clarity. For example, while their outcome data are 50% pain relief, very few trials in fact report results as such. Instead, data are usually reported in terms of mean integrated total pain relief score over defined intervals (TOTPAR). Data at the individual patient level are rarely accessible. To arrive at their 50% pain relief data for each trial, McQuay and Moore first convert TOTPAR data to percentage pain relief relative to maximum pain relief score (%maxTOTPAR) using an approach described elsewhere in more detail [1, 2]. By calculating this value from a series of trials and with access to individual patient data, they are then able to derive a straight-line equation for the number of patients who have at least 50% pain relief from the %maxTOTPAR score [2, 3]. It is this equation which they use to estimate the number of patients obtaining at least 50% pain relief from any trial reporting TOTPAR data. While the approximation is acceptable (r² = 0.895), there is considerable scatter in the individual trial data [2–4]. Using other scores such as the sum of pain intensity difference (SPID) yields similar results [2]. Each trial point estimate of effect calculated using their equations is associated with an error. This is not carried forward into the meta-analysis except through weighting using the trial sample size for each treatment arm. Therefore, the true error associated with estimates from any new meta-analysis using the interpolated values, such as their current one, is larger than reported. However, the results are probably good enough for meaningful clinical interpretation.

How good is 50% pain relief as an outcome measure? Opinions will of course differ as to what level of pain relief is sufficient, given that the experience of pain is so subjective. In a recent study [5], using signal detection theory and individual patient meta-analysis, we estimated that if rescue analgesic were used as an outcome measure for inadequate pain relief in acute pain, the optimum pain relief score would be 44%, not far from the intuitive value of 50% often used in meta-analyses [1]. For chronic pain, Farrar et al.[6, 7] have reported a cut-off value of about 30% but with generally lower sensitivity and specificity than those we reported [5], probably because of differences in the types of pain studied.

So did McQuay and Moore find a dose–response? Only to the extent that some 20% more patients would respond to an increase in dose within the range they studied than would at the lower dose for each of their analgesics. While their finding is consistent with a rather flat dose–response curve for each of the three analgesics, as has long been suspected by many, the dose–response curve itself remains poorly defined, even after McQuay and Moore’s valiant effort. The dose range studied in published clinical trials, suitable for meta-analysis, are simply too narrow. Can we do better?

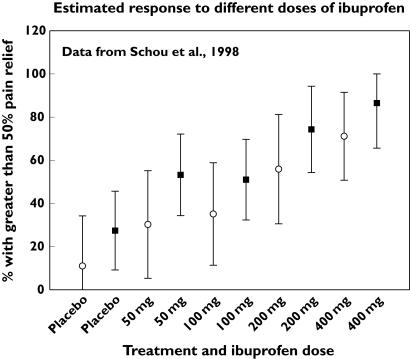
Schou et al.[8] investigated the dose–response of ibuprofen over the range 50–400 mg. Using their summary SPID and TOTPAR data, it is possible to derive the response rates using the equations of Moore et al.[2, 3]. The results are shown in Figure 1. It is obvious that despite considerable overlap in the 95% confidence intervals, there is a clear increase in the rate of response with increasing dose. Moreover, while the dose–response profiles are similar with both SPID and TOTPAR, there is a significant divergence in point estimates. This illustrates the loss of precision inherent in the approach adopted by McQuay and Moore, where different outcome measures are reduced to a common metric.

Figure 1.

Analgesic dose-response curve for ibuprofen

Meta-analysis is a useful approach to summarize apparently disparate data, but can be adversely reductionist. MacQuay and Moore’s study illustrates both points well. Thus, while the study summarizes the disparate studies of the common dosages of the three analgesics, it focuses on only narrow segments of the single dose–response curves. Neils Bohr, while grappling with understanding the apparently stochastic nature of subatomic particles, commented in what is now known as his Principle of Complementarity that ‘Evidence obtained under different experimental conditions cannot be comprehended within a single picture, but must be regarded as complementary in the sense that only the totality of the phenomena exhausts the possible information about the objects’. This principle of complementarity, which recognizes Heisenberg’s principle of uncertainty, applies even more so to the response of human beings to analgesics. Therefore, McQuay and Moore’s results should be viewed as another piece of useful evidence to construct the whole picture, to which the results of Schou et al.’s single, but broader study [8] also contribute.