Lack of correlation between exercise and sibenadet-induced changes in heart rate corrected measurement of the QT interval

Abstract

What is already known about this subject

• When this study was conducted it was already known that the ‘standard’ methods of correcting the QT interval for heart rate were not optimal and that bias could result in their use in certain circumstances, in particular when drugs or conditions also induced wide fluctuations in heart rate.

• The use of subject specific correction methods had been advocated and whilst these had been shown to apparently correct QT interval over usual physiological heart rates, they had not been tested under conditions where drugs could potentially increase heart rate and ‘standard’ correction methods gave apparent increases in QT interval. Furthermore, subject specific correction methods had usually been generated over a normal physiological heart rate range and made the assumption that the relationship remained linear outside of this usual range.

What this study adds

• A subject specific correction factor for QT correction can be calculated from a wide range of heart rates using exercise testing and the relationships between QT and RR are unique for a given individual.

• The generation of subject specific correction factors from ECGs collected under resting conditions is not a robust method.

• That subject specific correction factors derived from exercise testing are not appropriate to apply to drugs (with no evidence to suggest effects on the QT interval) that induce increases in heart rate and that the relationship between the QT and RR interval during exercise is clearly different to the QT/RR relationship of a drug that increases heart rate.

Aims

We sought to investigate subject specific QT interval correction factors (SSCF) determined at rest and after exercise and to determine the validity of these factors after the administration of a probe drug known to increase heart rate without directly affecting cardiac repolarization.

Methods

Thirty-two healthy volunteers underwent graded exercise, multiple recordings of electrocardiogram during rest over a day and a treatment phase administering inhaled placebo or sibenadet (a β₂-adrenoceptor/dopamine D₂-receptor agonist) at 250, 500 or one of 750 or 1000 µg. SSCF were determined from linear regression of plots of log RR interval vs. log QT after exercise (QTcX), rest (QTcR), and combined data (QTcC). The SSCFs along with Bazett & Fridericia corrections were applied to the ECGs after inhalation of sibenadet.

Results

SSCFs obtained from the combination of the exercise and resting day (mean QTcC = 0.41) and exercise alone (mean QTcX = 0.40) were similar with a good fit to the data (mean r² = 0.92 and 0.93, respectively) while data at rest resulted in a less pronounced slope (mean QTcR = 0.27) and poorer fit (mean r² = 0.52). After the administration of sibenadet, none of the SSCFs, Bazett or Fridericia corrections adequately corrected QT for heart rate induced changes.

Conclusions

Neither a SSCF from exercise, Bazett’s or Fridericia’s correction factors, adequately corrected the QT interval after the administration of a sympathomimetic agonist drug to increase heart rate in healthy volunteers demonstrating the potential need for QT/RR correction factors to be tailored for each drug studied.

Introduction

The evaluation of the potential for new drugs to affect cardiac repolarization is now an integral part of the drug development program. However, there is difficulty with the current methods of correcting QT interval for heart rate to assess whether a drug has a true effect on the QT interval when the drug also has an effect on heart rate.

The QT interval adapts to changes in heart rate and under normal conditions there is a general relationship that as heart rate increases, QT interval decreases. However, due to the variability of the QT interval with heart rate it is difficult to compare directly the QT interval in an individual or between individuals at different moments in time. This is particularly necessary when evaluating the potential effects on cardiac repolarization of new drugs in clinical development. Therefore it is recommended to correct the QT interval for heart rate. Many universal formulae have been proposed for the correction of QT for heart rate [1–4]. However, the use of these universal correction methods has been reviewed and it is suggested that such correction methods do not provide a best fit in all circumstances [5] and that bias in either direction can result when using a single correction formula especially in circumstances of high heart rates [6]. The use of the Bazett correction method [1] has been particularly criticized for showing the most variability and over-correction at high heart rates [7].

The relationship between the QT interval and heart rate is unique for any given individual and there is wide variation in this relationship between individuals [8]. The derivation of a subject-specific correction factor (SSCF) based on the individual’s relationship of QT interval vs. heart rate to ensure appropriate correction of the QT interval for changes in heart rate has been advocated [8, 9].

The approach for deriving a SSCF has relied on collecting ECGs during rest [9] or by 12–lead ambulatory monitoring [8]. ECGs collected at rest only allow determination of an individual’s specific correction during resting heart rates. This is not suitable to apply to a drug that increases heart rate outside this resting range as it assumes that the QT/heart rate relationship remains linear outside the resting range. The use of Holter collection of ECGs yields large amounts of ECG data but there are two drawbacks of this method. The large amount of data collected cannot practically be managed without sophisticated software to do the analysis, and manual over-reading of the data to assure accuracy of the automated analysis is not practicable. In addition, a delay in the duration of cardiac repolarization to respond to changes in heart rate (hysteresis) has been demonstrated [10]. The use of Holter recordings to derive the relationship between the QT interval and heart rate for an individual pairs the QT interval with the preceding beat RR interval and does not account for potential hysteresis between the QT interval and heart rate [10].

In this study we have investigated the use of exercise as a method to obtain ECGs from individuals across a wide range of steady heart rates in order to determine a SSCF. This SSCF was used to correct QT for heart rate with a probe drug, sibenadet, that increases heart rate. In particular, one of the objectives was to explore whether a graded exercise test provided a practical method for generating SSCFs from a wide range of heart rates and whether this method was useful in correcting QT in a clinical pharmacology setting.

Sibenadet is a dual β₂-adrenoceptor/dopamine D₂-receptor agonist [11], administered by inhalation, that can induce dose-dependent increases in heart rate as a result of its β₂-adrenoceptor agonist properties. Sibenadet has no effect on the hERG channel dog Purkinjke fibre action potential duration and did not prolong the corrected QT interval in dogs in vivo[12]. However, it is recognized that these criteria do not necessarily preclude sibenadet from having QT prolonging effects in a clinical setting. The characteristic of rapid effect on heart rate combined with the documented lack of effect on repolarization makes sibenadet ideally suited to study how our methodology of QT correction for drug induced-changes in heart rate performs.

Methods

Subject population

The study was conducted in 32 healthy volunteers (16 male and 16 female, mean age 37 years, range 25–58 years). The local Ethics Review Committee approved the study and all subjects gave informed consent before any study-related procedures were conducted.

At screening all subjects had normal physical examination and 24 h Holter ECG recordings and denied a history of cardiovascular or other clinically significant disease that would affect autonomic tone. From the time of screening, subjects withheld the use of any concomitant medications (except paracetamol, oral contraceptives, or hormone replacement therapy) until the end of the study.

Graded exercise test

The exercise test was conducted in two parts. Part one of the test was conducted at screening and was used to individualize the exercise test to each subject, so that in the second test the magnitude of heart rate changes would be matched to those predicted to be induced by the top dose of sibenadet. For each subject an ECG was recorded after resting while supine and standing, followed by mild graded exercise performed on a bicycle ergometer beginning at a workload of 50 W. Subjects cycled at a constant speed of 60 rev min⁻¹ throughout the test. Workload increased by 15 W every 2 min until a heart rate of 120 beats min⁻¹ was achieved. For each subject workload vs. heart rate was plotted. From this plot the workloads required for heart rates of 80, 95, 105 and 120 beats min⁻¹ were calculated. These workloads were used for the second formal exercise test.

For the formal exercise test three ECGs were collected at 1-min intervals at the following time points: after resting supine for 10 min; after standing for 2 min; after cycling at a constant speed of 60 rev min⁻¹ for 5 min at each workload to achieve heart rates of 80, 95, 105 and 120 beats min⁻¹ (a total of 7 min per exercise stage). If standing heart rates were greater than 80–95 beats min⁻¹, subjects progressed to the next workload level to start exercising to achieve heart rates of 95 or 105 beats min⁻¹, respectively. The data presented for the exercise period included the data recorded during the formal exercise test and the pre-exercise supine and standing measurements.

Collection of resting ECGs

Subjects attended the clinic on a separate day for recording of resting ECGs. ECGs were collected every 20 min, after 10 min supine rest, over a 14-h period with intermittent breaks for food. Forty ECGs were collected for each subject.

Evaluation of sibenadet effects – the treatment phase of the study

The study was a crossover design with subjects receiving a single dose by inhalation of either placebo or sibenadet at 250, 500 or one of 750 or 1000 µg at each visit in a random sequence. Subjects were initially dosed with 1000 µg sibenadet but many tolerated this dose poorly because of palpitations, and subsequently the highest dose was reduced to 750 µg. Since the highest dose of sibenadet was split between 750 and 1000 µg these two doses were pooled to give a dose group 750 µg*. Subjects attended the clinic for treatment visits on the evening before dosing and were fasted from midnight until the final ECG recording taken 6 h after dosing. On dosing days ECGs were recorded at the following time points: −20, −10, 5, 10, 15, 20, 30, 45, 60, 90 min, 2, 3, 4 and 6 h post dosing.

ECG interval analyses

ECGs were collected in a digital format using a PC based 12-Lead ECG and Stress Test System (PC-ECG 1200s, Norav Medical Ltd). From the exercise test ECGs a nominated precordial lead that easily delineated the ending of the T wave was chosen for analysis of interval. Where possible lead V5 was chosen. However, if this was unsuitable an alternative lead was used. The lead selected from the exercise visit was then used for the subject for all remaining ECGs collected in the study.

From each 10-s ECG recording the average RR interval was calculated from all of the complete complexes recorded. The QT interval was measured from the average beat constructed from all of the individual beats in the 10 s recording by the software program. All measurements were made by a technician and confirmed by an over-reading cardiologist. The QT interval of the average beat was measured by placing electronic calipers at the start of the QRS complex and at the point where the tangent of the T-wave intersected the isoelectric line.

Statistical analysis

Calculation of correction factors

The primary SSCF for each subject was calculated from linear regression on the log-transformed interval data relating the observed uncorrected QT interval to the RR interval from the ECGs collected from the exercise visit & the resting day.

Using the simplified model QTc = QT/(RR)^b re-arranging and logarithmic-transforming this equation leads to a linear model:

where Ln(QT) = observed QT (ms) values, Ln(QTc) = associated intercept of the linear model, Ln(RR) = observed RR (s) values and b = estimated subject-specific slope correction.

The linear model was fitted to obtain estimates of ‘b’ for each subject separately (i.e. the SSCF).

A SSCF was calculated from the exercise data alone (QTcX) and the resting day data alone (QTcR), and combining the exercise and resting data (QTcC) using the above model. In addition, a study-specific global correction factor (QTcG) was calculated by the log-log regression of all total RR vs. QT data obtained during the exercise and resting periods of the study. QT intervals for all subjects for all timepoints were also corrected using the Bazett (QTcB) and Fridericia (QTcF) formulae. All the correction formulae were applied to the ECG data for each subject obtained during the treatment phase of the study for comparison of ability to correct QT for heart rate. Linear regression lines were fitted through the data points of each plot of QTc vs. RR interval and a slope of zero represented appropriate correction of QT for heart rate.

Where least squares means (i.e. the means adjusted for the factors and covariates included in the statistical model) are presented, these are calculated from a linear mixed effects model with fixed effects for treatment, period and baseline covariate together with random effects for subject.

Results

Study disposition

Thirty-two subjects completed the exercise test and collection of resting day ECGs. For drug treatment visits 23 subjects completed placebo treatment and 22, 25 and 27 subjects completed 250, 500 and 750 µg* of sibenadet, respectively.

Evaluation of interval data from exercise and resting ECGs

Comparison of correction factors from exercise and resting ECG data

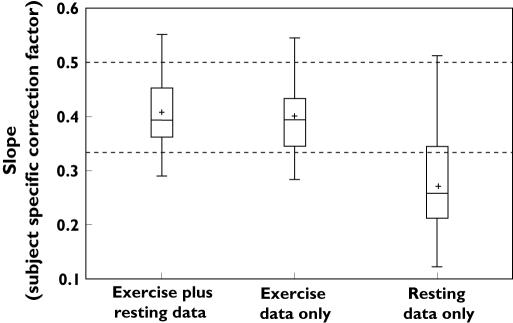
Individual plots of Ln(QT) against Ln(RR) interval for each subject (see Figure 1 for example) showed similar slopes for the exercise plus resting data and exercise data alone. From the exercise plus resting data (QTcC), the slopes for the 32 subjects ranged between 0.28 and 0.55 (mean ± SD, 0.41 ± 0.065 and median of 0.39) with correlation coefficients (r ²) of the slopes ranging from 0.74 to 0.98. This compared well with slopes using just the exercise phase (QTcX) which ranged between 0.28 and 0.54 (mean ± SD, 0.40 ± 0.067 and median 0.39, r² 0.85–0.98). This indicated that the fits of the plots combining exercise with data from a day at rest were no better than the exercise data alone. However, it was recognized that the more widely spread out exercise data were dominating the slope determination in these instances. Individual plots of resting data alone (QTcR) gave less pronounced slopes with more variability. Slopes ranged between 0.12 and 0.51 (mean±SD, 0.27 ± 0.089 and median 0.26) with r² ranging between 0.10 and 0.93 (Figure 2). All the data from the exercise phase and the resting day were combined to determine a study specific global correction factor (QTcG) of 0.41. This is summarized in Table 1.

Figure 1.

Example of a plot of Ln QT against Ln RR of exercise plus resting data (slope = 0.44, r² = 0.90), exercise data alone (slope = 0.38, r² = 0.92) and resting data alone (slope = 0.26, r² = 0.41) for an individual subject. The line through the points is a linear regression line the slope of which was the calculated subject-specific correction factor

Figure 2.

Box plot summarizing the calculated subject-specific correction factors for all 32 subjects of exercise plus resting data, exercise data alone and resting data alone. The upper dotted horizontal line represents the correction factor of the Bazett method and the lower dotted horizontal line represents the correction factor of the Fridericia method. + represents the mean

Table 1.

The range, mean, median and correlation coefficients of the different subject-specific correction factors

Correction factor	Range	Mean	Median	Range of r2	Mean r2
QTcC	0.28–0.55	0.41	0.39	0.74–0.98	0.92
QTcX	0.28–0.54	0.40	0.39	0.85–0.98	0.93
QTcR	0.12–0.51	0.27	0.26	0.10–0.93	0.52
QTcG		0.41

QTcC = subject-specific correction factor from combined exercise and resting day data, QTcX = a subject-specific correction method from exercise alone, QTcR = a subject-specific correction factor from resting day only and QTcG = a study-specific correction method.

During the exercise test, after cycling for 5 min at each work load, for each subject, the heart rate did not vary significantly between each of the three ECGs obtained for each exercise workload. For each subject’s given workload the maximum heart rate difference between the three ECGs varied by fewer than 5 beats min⁻¹ indicating that a stable heart rate had been achieved at each workload.

Effect of subject-specific correction factors at rest without treatment

The SSCF obtained from the exercise period (QTcX) was applied (along with Bazett & Fridericia corrections) to the ECGs obtained during the resting day and the administration of placebo during the treatment phase of the study. The same subjects participated in both the rest day and the treatment phase of the study, with a separation of between 2 weeks and 3 months between participation in the two parts of the study. This allowed us to compare the performance of the correction factors over the time period. We did not use QTcC or QTcR in this comparison, as it would have been inappropriate to compare the data used to derive the formula in making a comparison between the two treatment phases. In both situations, the subjects were at rest and the recordings were made in a similar clinical situation. As demonstrated in Figure 3, when the data from the resting and the placebo period were compared the correction formula showed similar trends, with the Fridericia correction method showing greater tendency to correct QT changes appropriately for heart rate and the Bazett method demonstrating the least tendency.

Figure 3.

Box plots showing the effect of correcting QT for RR with a subject specific correction factor derived from exercise testing (QTcX) compared to the Bazett (QTcB) and Fridericia (QTcF) methods after collection of supine ECGs in subjects on the resting day (a) and after placebo treatment (b). A regression slope of zero would indicate appropriate correction. + represents the mean

Evaluation of an exercise-derived SSCF to correct QT for the heart rate effects of sibenadet

Effect of sibenadet on heart rate and uncorrected QT interval

Sibenadet induced dose-dependent increases in heart rate after administration of a single dose giving least squares mean (95% CI) for maximum positive changes from baseline of 6 (2, 9), 13 (10, 17), 20 (17, 23) and 28 (25, 31) beats min⁻¹ for placebo, 250, 500 and 750 µg* of sibenadet, respectively. Maximum changes occurred in the first 10–15 min post dosing. As expected, there was a dose-dependent decrease in uncorrected QT interval with least squares mean (95% CI) for maximum negative changes from baseline of −9 (−16, −2), −20 (−27, −13), −30 (−36, −23) and −38 (−44, −32) ms for placebo, 250, 500 and 750 µg*, respectively. Similarly to the effects on heart rate the maximum changes occurred in the first 10–15 min post dosing.

Effect of sibenadet QT interval corrected by different formulae

The ECGs obtained after treatment were corrected utilizing the six different correction formulae for each subject. In order to have a significant range of heart rates, we combined all the data after treatment with sibenadet for each subject and regressed the RR interval against the corrected QT interval (Figure 4). An ideal correction factor would result in a regression slope of zero. As demonstrated, none of the correction factors performed as expected in that all the mean regression slopes were different from zero.

Figure 4.

Box plots showing the effect of using different correction factors of the QT interval in subjects after treatment with sibenadet. The different correction methods used were a subject-specific correction factor from combined exercise and resting day data (QTcC), a subject-specific correction method from exercise alone (QTcX), a subject-specific correction factor from resting day only (QTcR), Bazett’s method (QTcB), Fridericia’s method (QTcF) and a study-specific correction method (QTcG). A regression slope of zero would indicate appropriate correction. + represents the mean

The slope of Ln(QT) against Ln(RR) was calculated for each subject after each treatment period of exercise, rest day, placebo and their pooled data set of sibenadet treatment. This resulted in mean slope values of 0.40 (SD 0.07), 0.27 (SD 0.09), 0.19 (SD 0.11) and 0.19 (SD 0.13), respectively. This demonstrated that on average the slope values for rest day, placebo treatment and sibenadet treatment were essentially similar but the slope values after exercise were much steeper.

Discussion

Evaluation of a SSCF from exercise and resting ECGs

A SSCF from graded exercise

Using ECGs collected at steady heart rates during rest and exercise, each individual had a relationship between QT and heart rate that was unique. In this subject population, logarithmic transformation of the data resulted in an approximately linear relationship between the QT and RR intervals for all individuals across the range of heart rates obtained. Other workers have demonstrated that different mathematical models such as exponential models describe the relationship between QT and RR interval data [3, 4]. Recently it has been demonstrated that not only is the relationship between the QT interval and heart rate unique for a given individual but that the mathematical formula describing this relationship is also unique [8]. In this study we found that a log-log model gave a good fit of the data for all subjects and this provided a pragmatic approach for calculation of each SSCF. Although the slopes of the individual relationships were all different, they were generally within the range of the different generic correction factors that are used.

The slopes of the lines of QT against RR of the exercise plus resting day data and of the exercise data alone were very similar within individuals with good correlation coefficients. The addition of the greater number of ECGs at rest, all with a narrow range of heart rates, to the exercise data did little to improve the correlation of heart rate vs. QT interval. However, compared with the relationship at exercise the slopes of the resting day QT against RR relationships were much less steep and also showed much more variability. In some of the subjects, the correlation coefficients were so low (r² = 0.1) that little confidence could be placed in a correction factor obtained from these data. The range of heart rates at rest is narrow and therefore it is difficult to describe the relationship between QT and heart rate. In this scenario, a few outlier points determine the relationship between QT and heart rate for each individual. Other studies, collecting larger numbers of ECGs during resting periods, have also demonstrated shallower slope values [9] than those obtained from exercise.

Many workers have investigated the relationship of the QT/RR relationship during exercise [4, 6, 13–15]. As with all of these studies, we have also shown a linear relationship between the QT and RR interval, even though different mathematical models across the studies have been used. This linear relationship during exercise is suggested to be conserved within an individual even when different exercise methods are used [4]. However, none of these studies has proposed deriving a relationship for each individual to correct QT for rate when investigating potential effects on QT interval for a drug that also increases heart rate although some studies have suggested using the QT interval at nominal heart rates (e.g. QT60) after exercise to compare across different treatments and disease [4, 16].

Application of a subject-specific correction factor to QT intervals during rest and placebo treatment

The SSCF derived from the exercise data (QTcX) was used to correct the QT interval from the rest day ECGs and the placebo treatment ECGs for each individual. This correction method was compared with the Bazett and Fridericia methods. In both scenarios no correction method showed appropriate correction of the QT interval independent of heart rate as regression slopes of QTc against heart rate deviated from zero. The trend of the effect of correcting the QT interval by all three methods was similar for both the rest day and placebo treatment, with the Fridericia method demonstrating the nearest regression of slopes to zero.

The analysis between the resting day period and placebo treatment period gave us the opportunity to study the individual’s relationship between heart rate and cardiac repolarization over a period of between 2 weeks and 3 months. We were able to confirm the observation of Malik & coworkers that the individual’s relationship is stable over the period of observation [8].

Application of the subject-specific correction factor to heart rate changes induced by sibenadet

In this study no method of correcting QT for heart rate changes after treatment with sibenadet gave appropriate correction. Sibenadet has shown no effect in preclinical studies to increase QTc in vivo, or to affect the hERG channel or cardiac repolarization [12]. In this study the effects of sibenadet on QTc correlated with increasing heart rate. Therefore it is reasonable to postulate that the use of a SSCF derived from exercise was inappropriate and appeared to be over-correcting. Similarly, the use of an exercise-derived correction factor to correct QT interval for the heart rate effects of reboxetine was suggested to over-correct compared with the Fridericia method, which demonstrated little effect of reboxetine on QTc for heart rate effects [17].

The use of exercise to derive a SSCF may be inappropriate since different mechanisms may be responsible for drug-induced changes in heart rate compared with exercise-induced effects [18]. One possible explanation may be due to potential hysteresis between the QT and RR intervals. In order to overcome potential hysteresis effects we deliberately recorded ECGs during exercise at steady state heart rates. However, due to the pharmacokinetic profile of sibenadet steady state heart rates could never be achieved after inhaled administration. Increases in heart rate were rapid in onset, peaking at approximately 10–15 min and then returning to baseline over a 4–6-h period. Therefore the two scenarios for increasing heart rate where ECGs were collected during exercise and during drug treatment may not be compatible.

However, it cannot be ruled out from this study that as the SSCF had been determined when the QT interval and heart rate were in equilibrium during exercise, then applying this factor to a scenario when there is potentially no equilibrium may manifest as an increase in QTc.

Comparison with literature data

Although there are different mechanisms by which heart rate can be increased it would appear that the dynamics of the heart rate affect the way the QT interval adapts. The changes in QT for heart rate after autonomic stimuli such as a cold pressor response or Valsalva manoeuvre [19] or after atrial pacing [13] are of a much smaller magnitude than those seen after exercise.

Magnano & coworkers [14] explored the influence of the autonomic nervous system on cardiac repolarization. They plotted the relationship of heart rate to QT interval after the administration of the β-adrenoceptor agonist, isoproterenol and atropine and compared this with the relationship during exercise. They demonstrated that isoproterenol resulted in a shorter duration of QT interval for a given heart rate compared with other stimuli, and postulated that this was because of differences on the effects on the autonomic nervous system. Our results are completely consistent with these results and support the hypothesis that changes in the autonomic nervous system induced by sibenadet can influence cardiac repolarization differently from the changes produced by exercise. In addition, our results, taken together with the results of Magnano et al. [14] would suggest that it does not matter whether β-adrenoceptor stimulants reach constant or transient plasma exposures, the QT changes for given heart rates are still shorter than the changes observed at steady state exercise. Akhras et al. [13] suggested that the increased shortening of the QT interval during exercise was due to circulating catecholamines. However, the data generated from both Magnano et al. and our study would suggest a) that the QT shortening during exercise cannot be explained by circulating catecholamines alone and that other autonomic changes are also of contributing importance and b) that the differences in the QT/RR relation between the administration of β-adrenoceptor agonists and during exercise cannot be explained solely by hysteresis effects.

In other human studies, bolus injections of isoproterenol induced transient increases in heart rate with little change in QT interval [20] whereas intravenous infusion of isoproterenol resulted in steady state heart rate increases with a significant decrease in QT interval [21], possibly supporting the hypothesis of a contribution from the impact of hysteresis between the RR and QT intervals.

Akhras & coworkers claimed that they observed no hysteresis between the QT and RR intervals during exercise. However, a hysteresis does appear to be more apparent during the recovery period after exercise rather than during the onset of exercise period [22]. This may be due to differences in autonomic mechanisms between the onset and recovery periods of exercise.

During initial exercise it has been suggested that there is a reduction in parasympathetic innervation to the heart. Parasympathetic influences on the heart are suggested to have more profound effects on the QT interval than sympathetic innervation and atropine-induced tachycardia has been demonstrated to produce changes in QT similar to those seen during exercise [20, 21]. Perhaps the steep slopes of QT/RR plots observed during exercise are a combination of increased sympathetic tone and reduced sympathetic tone. Therefore the generation of a SSCF generated during steady state exercise cannot be applied to investigating the effects of drugs on the QT interval, or at least to the effects of β-adrenoceptor agonists on the QT interval, in the presence of an increased heart rate.

In conclusion, the application of an exercise derived SSCF for correcting the QT interval for drug-induced changes in heart rate after the sympathomimetic/D₂-receptor agonist sibenadet was not appropriate. This may be because the mechanisms involved in the autonomic control of the heart rate during exercise are different from the mechanisms involved when heart rate is increased by pharmacological methods. A method of deriving a SSCF from a wide range of heart rates in order to provide confident regression slopes is still to be achieved.