Abstract
The structure of a DNA octamer d(TTGGCCAA)2 complexed to chromomycin-A3 and a single divalent cobalt ion has been solved by using the pseudocontact shifts due to the unpaired electrons on the cobalt. A protocol was developed and critically evaluated for using the pseudocontact shifts in structure determination. The pseudocontact shifts were input as experimental restraints in molecular dynamics simulations with or without NOE constraints. Both the magnitude and orientation of the susceptibility anisotropy tensor required for the shift calculations were determined during the simulations by iterative refinement. The pseudocontact shifts could be used to define the structure to a very high precision and accuracy compared with a corresponding NOE-determined structure. Convergence was obtained from different starting structures and tensors. A structure determination using both NOE’s and pseudocontact shifts revealed a general agreement between the two data sets. However, some evidence for a discrepancy between NOE’s and pseudocontact shifts was observed in the backbone and terminal base pairs of the DNA. Violations in shift or NOE restraints remaining in the final structures were examined and may be a reflection of motional averaging of the constraints and evidence for flexibility. This work demonstrates that pseudocontact shifts are a powerful tool for NMR structure determination.
1. Introduction
Globular proteins with densely packed proton cores are successfully studied using the nuclear overhauser effect (NOE) in nuclear magnetic resonance (NMR). The NOE provides a short-range (<5 Å) constraint between proton pairs. NMR structures of DNA and RNA oligomers are of comparably lower precision because the extended nature of their structures precludes the measurement of large numbers of long-range (nonsequential) NOE’s. This problem is compounded by the difficulties associated with quantitating NOE’s to the exchangeable base protons, which usually provide the only interstrand NOE’s. Ideally, long-range constraints are needed to define characteristics such as DNA bending or the three-dimensional arrangement of domains in RNA structure.1
Several recent studies have shown that chemical shifts and relaxation rate enhancements induced by paramagnetic metals are valuable long-range structural constraints.2-6 The paramagnetic shift occurs in molecules containing tightly bound rapidly relaxing paramagnetic metal ions such as lanthanides or certain transition metals such as iron and cobalt. Usually, two components can contribute to the paramagnetic shift, a scalar contact shift (through bond), which propagates about five to six bonds from the paramagnetic center, and a dipolar pseudocontact shift (through space).
A large body of work exists on the application of pseudocontact shifts in conjunction with NOE’s to the structure determination of paramagnetic metalloproteins. Protocols have been designed that apply the pseudocontact shift as a restraint energy term in energy minimization3 and molecular dynamics (MD)5,6 calculations. These studies invariably showed that the additional restraints improve the quality of the convergence, especially around the region of the metal center where the pseudocontact shifts are sizable and the number of other conventional constraints could be reduced. The pseudocontact shifts were used to define the precise metal origin and the orientation of the susceptibility tensor. The susceptibility magnitudes were the only required input parameters.
In this work, we have developed and critically evaluated a systematic protocol for structure refinement of a DNA complex based on NMR pseudocontact shifts with or without the NOE’s. The susceptibility tensor (g-tensor), which is required for the calculation of pseudocontact shifts, is optimized during the course of MD refinement so that the final structure obtained is independent of the starting structure. We will show that it is possible to obtain and optimize both the magnitude and orientation of the susceptibility tensor without any a priori knowledge of the structure, that the final structure is independent of starting structure or tensor, and that, indeed, we are able to obtain the structure of this DNA–drug complex by the predominant use of pseudocontact shifts. In addition, the final structure is far more precise than that which could be obtained using traditional NOE methods. We show that, in extended structures with a limited number of NOE’s, the pseudocontact shift is a valuable constraint for structure definition.
The structure we have refined is a 1:2:1 complex of d(TTGGCCAA)2–chromomycin-A3–divalent metal ion. The metal ion is coordinated to the O1 and O9 atoms of the chromomycin chromophore, and the two chromomycin molecules bind in the minor groove of the DNA at the GC step. Complexes of this type have been extensively studied, including the determination of the solution structure of d(AAGGCCTT)2 with drug and Mg2+.7,8 We have obtained and assigned NMR spectra of the complex with Zn2+ and Co2+ 9 and used the pseudocontact shifts derived from the difference in chemical shifts in the Zn2+ and Co2+ complexes to carry out the structure determination described here.
2. Materials and Methods
2.1. Theory behind the Use of Pseudocontact Shifts in Structure Determination
The dipole moment generated by unpaired electrons in a magnetic field gives rise to the pseudocontact shift, which, because of the rapid reorientation of molecules in solution, and assuming the point dipole approximation, reduces to the isotropic dipolar shift, given by2
| (1) |
This equation describes the relationship between the isotropic dipolar shift and the polar spherical coordinates (ri,θi,φi) of a nucleus i in the principal axis system (PAS) of the magnetic susceptibility tensor. The magnitudes of the axial and rhombic susceptibility anisotropies Δχax and Δχeq are required to calculate the shifts. In addition, a single transformation describing the relative orientation of the susceptibility and molecular PAS needs to be known.
The pseudocontact shift is incorporated as an energy term in MD simulations using a simple flat well potential, which is zero for shifts lying within experimental error (tol) of the calculated shift and which grows quadratically outside that range:
| (2) |
Epc is the experimental energy contributed to the simulation from the pseudocontact shift data. δi,obs and δi,calc are the observed and calculated pseudocontact shifts, respectively, for nucleus i, and fi is the force constant in kcal mol−1 ppm−2. The pseudocontact shift is used directly as the constraint, with no assumptions about correlation times, motional properties, or isolated spin pair approximations being required as they are for the NOE. Equation 2, along with analytical expressions for the gradients of eq 2 in the x, y, and z directions of the molecular reference frame, has been programmed into X-PLOR.3 In our simulations, the dipolar eq 1 is assumed to hold for all protons in the complex, that is, δi,calc = δi,dip. It is known to break down for protons within 7 Å of a transition metal coordination site, due to electron delocalization.10 We will examine the effect of this approximation on protons in that range.
2.2. Determination of an Experimental Constraint Set
1H and 31P NMR experiments9 on d(TTGGCCAA)2 · (chromomycin)2 · Zn2+ and d(TTGGCCAA)2 · (chromomycin)2 · Co2+ have provided a set of 256 paramagnetic shifts for the complex, which contains 304 1H and 31P nuclei. These shifts were obtained as the difference in shift recorded in the Co2+ and Zn2+ spectra. Experiments have shown that no structural change occurs upon metal substitution.9 This was validated by the observation of negligible diamagnetic shift changes between the Zn2+ and Mg2+ complexes. The shift difference is therefore entirely due to the paramagnetic effect and may contain contact as well as pseudocontact contributions. Thirty protons on the chromomycin chromophore and parts of the C-sugar are excluded from the simulations because they lie within the range of the Fermi contact shift. This leaves 234 out of a possible 274 pseudocontact-shifted nuclei that can be used in the simulation. Missing protons include those closer than about 4.0 Å from the metal, as well as the rapidly exchanging base protons of the adenine and thymine base pairs and of the hydroxyl groups on the chromomycin sugar moieties. Protons of unknown stereospecific assignment, such as H5′, H5″ and H2′, H2″ protons of the DNA, were excluded from initial simulations and then included in later refinement. Their unique pseudocontact shifts made stereospecific assignment possible in both the diamagnetic (Zn2+) and paramagnetic (Co2+) spectra.
The tolerance or experimental error (tol) in eq 2 is obtained from the sum of the line widths of the resonances in the diamagnetic and paramagnetic spectra. The tolerance will be proportionately larger for nuclei closer to the metal, but so will their change in shift with displacement. The large change in frequency accompanying positional displacement for an inner sphere proton will counteract the inaccuracies of measuring a broad peak.
Additionally, NOE’s were obtained from the Zn2+ complex. Seven-hundred and eighty NOE’s were measured, consisting of 642 intramolecular NOE’s and 138 intermolecular NOE’s. These NOE’s were interpreted either using the two-spin approximation, in which NOE’s were classified as weak, medium, or strong and given distance ranges of 1.8–6, 1.8–4, and 1.8–3 Å, respectively; or by using a relaxation matrix approach to derive a distance set.11 In the latter case, a 4 ns isotropic correlation time was assumed, and the distance bounds were averaged over two starting structures, P and B (see text). Unless otherwise indicated, the two-spin approximation was used. This contrasts with the much larger NOE data set developed in the previous study of the d(AAGGCCTT)2 · (chromomycin)2 · Mg2+ complex, in which over 2000 NOE’s were obtained and relaxation matrix analyses were carried out to obtain the final structure.8
2.3. Restrained Energy Minimization and Molecular Dynamics Calculations
Pseudocontact shift restraints were introduced into the potential energy function in XPLOR through eq 2, from which the forces due to the shift energy penalty could be derived. Restrained energy minimization and molecular dynamics calculation on the Co2+-coordinated chromomycin-d(AAGGCCTT)2 complex with explicit hydrogen atoms were carried out using modified XPLOR 3.1 or XPLOR 3.8.12 The Co2+ metal center was fixed to the origin. The distances between O(9) and O(1) from chromomycin to the Co2+ metal center were restrained through a Square-Well function. Standard CHARMM22 parameters for nucleic acids were used. The partial charges for the saccharide components of the chromomycin were taken from the structurally related carbohydrates reported previously,13,14 while other parameters were deduced from CHARMM 22 carbohydrate parameters. The metal was parametrized using the values for Mg(II). High- to low-temperature simulated annealing (SA) refinements were carried out using a seed to generate random initial velocities. NOE restraints were applied as a square well potential with a force constant of 1000 kcal mol−1 Å−2. Pseudocontact shift restraints were used with varying force constants (see text). Molecular dynamics and simulated annealing runs were carried out from three different models for the DNA, an existing PDB file (1D83), canonical B-DNA, and canonical A-DNA. Resulting structures are always labeled with the prefixes P, B, and A, respectively, in the text. In the case of the A-DNA model structure, an initial minimization with NOE constraints was used prior to the simulated annealing protocol. Structures obtained from simulated annealing procedures were continuously refined to minimize the number of residual experimental violations. A final round of minimization with pseudocontact shift force constant fpc = 5 kcal mol−1 ppm−2 and NOE scale factor 50 kcal mol−1 Å −2 was carried out to relax the averaged minimized structures obtained from individual families. For the combined use of NOE and shift data, structures obtained with shift restraints were used as initial starting points.
3. Results and Discussion
3.1. Determination of the Magnetic Susceptibility Tensor
The knowledge of the susceptibility anisotropy (Δχ) and its orientation in the molecular frame is required for the calculation of pseudocontact shifts. The tensor Δχ itself is usually determined from some prescribed knowledge of structure.2 Therefore, our first goal is to develop a systematic method for determining a tensor, that is independent of the initial starting structure.
3.1.1. Initial Magnetic Susceptibility Tensor
As shown in eq 1, there are five variables contributing to pseudocontact shift calculation, that is, the axial and equatorial components of the susceptibility anisotropy, Δχax and Δχeq, and three Euler angles, α, β, and γ, which describe the relative orientation of susceptibility and molecular PAS. In this system, because of the 2-fold axis of symmetry, we define the molecular PAS as follows: the metal is placed at the origin; the Z-axis lies along the C2 symmetry axis; the Y axis is in the plane of the metal and two O1 oxygen atoms of the chromophore; and the X axis is perpendicular to both Y and Z. The angle β must be either 0°or 90°, because of the C2 axis of symmetry; by requiring Δχax > Δχeq, we obtain β = 90°, that is, the positive lobes of the tensor are perpendicular to the C2 symmetry axis. Thus α + γ is the angle to be determined. Since only the metal center is fixed during the simulated annealing process, the whole system rotates in space to achieve the best match with pseudocontact shifts. Therefore, the accuracy of the orientational parameters will not affect the final structure determination, although it does affect the speed of convergence. In summary, for this system, we only need to determine two parameters, that is, Δχax, and Δχeq. In the following, we show two different approaches to deriving the initial tensor. One is from the pre-existing NMR structure; the other is from NMR line broadening data. The purpose of this is to unequivocally demonstrate the independence of the final structure on the choice of initial tensor or structure.
3.1.1.1.Initial Tensor A: Derived from a Starting Structure
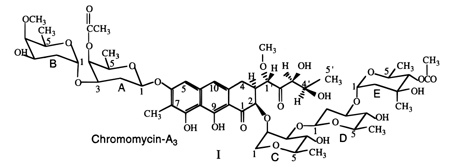
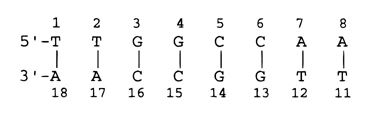
The published coordinates of d(AAGGCCTT)2 · (chromomycin)2 · Co2+, PDB accession number 1D83, were used for a starting structure.8 The adenine bases were modified to thymine and thymine bases to adenine, and a 500 step energy minimization was carried out to relax the structure. The base numbering is defined as follows:
In addition, the structure of the chromomycin is shown as structure I. It consists of di- and tri-saccharide segments and a hydrophilic side chain attached to a central aromatic chromophore. The drug residues B, A, chromophore, E, D, and C are numbered 21–26 and 31–36, respectively, for the two drug molecules in the complex. The protons that are closer than 7 Å from the metal or are less than six bonds from the O1 and O9 oxygen atoms of the chromophore were excluded from tensor refinement. One-hundred and seventy-three proton pseudocontact shifts were fit by a nonlinear least-squares method to calculated shifts from eq 1. The parameters varied were the magnetic susceptibility anisotropy amplitudes and Euler angles. The best fit parameters were used as an initial tensor for further refinement through molecular dynamics calculation, that is, Δχax = 3.58 × 10−3 cm3/mol, Δχeq = −0.606 × 10−3 cm3/mol, α = 80.0°, and γ = 0.8°.
3.1.1.2. Initial Tensor B: Derived from Pseudocontact Shift and Line Broadening Data
To demonstrate that a structure does not need to be known a priori to derive a susceptibility tensor or use the pseudocontact shifts in structure calculation, we have also devised a method for extracting the magnitudes of an initial tensor from experimental data that does not require any structural assumptions. This method simply makes use of a set of pseudocontact-shifted nuclei in a rigid plane where the relative geometry is known, such as the aromatic ring in a cytosine base in this system. Table 1 lists the line broadening data, the distance to the metal center, and the pseudocontact shift for CYT5. A standard cytosine aromatic ring was generated from SYBYL.15 Since the observed line broadening of the nucleus is related to the distance of that nucleus to the metal center, we are able to obtain the possible positions of this plane in space that satisfy all of the distance requirements for pseudocontact-shifted nuclei in that plane. Because measurement of line broadening is inaccurate, corresponding to a large range of upper and lower distance bounds, various positions of the plane are allowed by the data. Eight positions that satisfied all of the distance requirements to the metal center were selected on the basis of the distance constraints.
Table 1.
Line Broadening Data and Pseudocontact Shift for CYT5
| residue | Line Width
(Zn) (Hz) |
Line Width
(Co) (Hz) |
1/T2Ma (s−1) |
distanceb (Å) |
Pseudocontact
shift (ppm) |
|---|---|---|---|---|---|
| NH41 | 21. ± 4. | 39. ± 2. | 75.–38. | 7.6–8.5 | −5.73 ± 0.057 |
| NH42 | 21. ± 4. | 35. ± 5. | 72.–16. | 7.6–9.8 | −8.02 ± 0.057 |
| H5 | 20. ± 2. | 25. ± 2. | 28.–3. | 8.9–12.9 | −4.93 ± 0.051 |
| H6 | 18. ± 2. | 30. ± 3. | 53.–22. | 8.0–9.3 | −2.51 ± 0.073 |
| C5 | 52. ± 5. | 67. ± 9. | 91.–3. | 4.6–8.1 | −7.70 ± 0.200 |
| C6 | 58. ± 10. | 83. ± 10. | 141.–16. | 4.3–6.2 | −7.86 ± 0.200 |
Paramagnetic transverse relation rate.
Calculated from the Solomon equations assuming dipolar and Curie contributions to T2M.
For each set of coordinates, a C2 axis of symmetry was created by generating a second cytosine aromatic ring through negation of the coordinates of the first ring. The best tensor parameters were then calculated through nonlinear least-squares fitting to observed pseudocontact shift data. A value for β of ~90° was consistently obtained because of the C2 symmetry axis. The α and γ values are meaningless because of arbitrary principal axis system selection with Z along the metal to CYT5-H41 atom. Table 2 lists the susceptibility anisotropy amplitudes obtained from these eight ring positions. The initial tensor was chosen as the average value, that is, Δχax = 3.308 × 10−3 cm3/ mol and Δχeq = −0.168 × 10−3 cm3/mol.
Table 2.
Susceptibility Anisotropy Amplitudes for the Eight Orientations of the CYT5 Aromatic Ring Obtained from Line Broadening Dataa
| I | II | III | IV | V | VI | VII | VIII | |
|---|---|---|---|---|---|---|---|---|
| Δχax | 3.243 | 3.575 | 3.416 | 3.434 | 3.142 | 2.747 | 3.544 | 3.361 |
| Δχeq | −0.055 | −0.167 | −0.267 | −0.356 | −0.165 | −0.273 | −0.257 | −0.352 |
In 10−3 cm3/mole.
3.1.2. Refinements of the Structure and Magnetic Susceptibility Tensor Anisotropy
Both methods for the determination of the initial tensor leave a lot of room for refinement. As shown in the previous section, initial tensor A is highly dependent on the prescribed knowledge of structure, while a broad range of distance bounds leads to a large range of values in initial tensor B. To demonstrate conclusively that the final structures are dependent on neither the starting structure nor the initial tensor, it is necessary to develop a systematic protocol to optimize the tensor and the structure, and to derive a set of converged structures from different starting points.
We performed two sets of refinements from two different initial conditions. The first one started with the initial tensor A and the same structure 1D83 from which it was derived. We will refer it as model P_SHFT in this paper. The second one, called model B_SHFT in the following text, started from the initial tensor B and a canonical B-DNA model docked with chromomycin. To prevent the inner sphere of protons from dominating the refinement and driving the calculation at the expense of the more remote protons, we used a smaller set of pseudocontact shift constraints for the simulated annealing process; that is, the protons that are closer than 7 Å to the metal were excluded. We call this data set PS-S, which is distinguished from the full set of pseudocontact shift data PS-T, which we used for the final energy minimization process. We also included hydrogen bond constraints between the base pairs and distance constraints between the four metal-binding oxygen atoms and the metal. The detailed refinement protocol is as follows.
Step 1. Energy minimization for 500 steps with force constant fpc,i = 5 kcal mol−1 ppm−2 in PS-S.
Step 2. Simulated annealing from temperature Tinitial = 600 K to Tfinal = 20 K with temperature interval 20 K. At each temperature, 500 steps of molecular dynamics simulation were performed with fpc,i = 5 kcal mol−1 ppm−2 in PS-S.
Step 3. Energy minimization for 500 steps each with fpc,i = 5, 50, and 300 kcal mol−1 ppm−2 in PS-T, respectively.
Step 4. Nonlinear least-squares fitting to get new susceptibility anisotropy amplitudes. Go back to step 1 to perform refinement again using the new Δχ tensor until convergence is achieved.
Figure 1 shows the convergence of the magnetic susceptibility anisotropy amplitudes in the course of refinements for the two models. Model P_SHFT leads to Δχax = 2.625 × 10−3 cm3/ mol and Δχeq = 0, while model B_SHFT gives Δχax = 2.770 × 10−3 cm3/mol and Δχeq = 0. There is a 5% difference between the two resulting Δχax values, and the average value was used for the final structure refinements, that is, Δχax = 2.697 × 10−3cm3/mol and Δχeq = 0. Structures calculated with each of the two final tensors differed from each other by 1.04 Å rmsd for all non-H atoms (excluding the terminal base pairs). Additionally, we have performed studies that show that a 10% variation of Δχax produced negligible (< 1 Å) deviation between structures.
Figure 1.
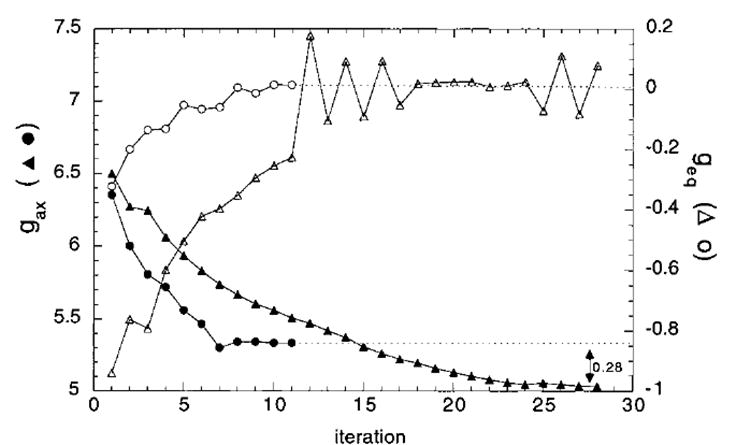
Convergence of the magnitudes of the axial and equatorial susceptibility tensor starting from the models P (▲, △) and B (●,○) (see text). The units along the susceptibility axes are given in gq = Δχq/[b2S(S + 1)/9kT], q = ax, eq. The gq values are not the true values of the electronic g tensor anisotropies.
3.2. Structure Refinements
By using the refined tensor, we carried out simulated annealing refinements for model P_SHFT and B_SHFT, as well as a third model, A_SHFT, derived by docking chromomycin onto canonical A-DNA. The detailed protocol is the same as the step 1 to step 3 in g tensor refinement, except for a range of fpc,i = 0.5, 5, 50 kcal mol−1 ppm−2. To evaluate the quality of the refinement on the basis of pseudocontact shifts, we also performed three sets of parallel refinements with NOE and pseudocontact shift restraints and three more with NOE restraints only. We will refer to them as models P_SHFT_NOE, B_SHFT_NOE, and A_SHFT_NOE and P_NOE, B_NOE, and A_NOE in the following text. A family of 20 structures was generated for each of the P and B runs, and 10 structures were generated for each of the A runs.
3.2.1. Analysis of Refined Structures
The structural statistics are listed in Table 3. Rmsd’s are a comparison between the minimized average structure for each family and the bundle of structures comprising the other families. Excluded from the calculation of rmsd is the difference between the minimized averaged structure and the bundle of structures within one family. The reason for this is that the bundles were found to be extremely tight regardless of type of constraint used. Variation of structures within a family averaged 0.27, 0.36, and 0.82 Å for SHFT, SHFT+NOE, and NOE constraint data, respectively. This may reflect poor sampling of conformational space, and true convergence can only be demonstrated from different starting points. For the same reason, all figures and tables display results from a single minimized average structure derived from each entire family of structures.
Table 3.
Analysis of the Restrained-MD Generated Structures of d(TTGGCCAA)2·Chr2·Co(II)
|
| |||||
| NMR Pseudocontact Shift Restraints | |||||
| total no. of measured paramagnetic shifts | 256 | ||||
| no. of pseudocontact shifts used in refinement | 234 | ||||
| no. of pseudocontact shifts for DNA | 168 | ||||
| no. of pseudocontact shifts for drug | 66 | ||||
| range of pseudocontact shifts | −45.42 to +42.50 | ||||
| NMR Distance Restraints | |||||
| total number of distance restraints | 788 | ||||
| intraresidue distance restraints | 492 | ||||
| interresidue distance restraints | 296 | ||||
| Empirical Restraints | |||||
| H-bonding restraints | 20 | ||||
| Co – O distance restraints | 4 | ||||
| Structural Statistics | |||||
|
| |||||
| SHFTa,b | NOEa,c | SHFT_NOEa,d | |||
|
| |||||
| rmsd of NOE violations (Å) | 0.34 ± 0.01 | 0.031 ± 0.005 | 0.036 ± 0.005 | ||
| no. of NOE violations >0.3 Å | 55 ± 2 | 0 | 0 | ||
| rmsd of shift violations (ppm) | 0.31 ± 0.01 | 7.93 ± 2.37 | 0.37 ± 0.04 | ||
| no. of shift violations >expt+grad. erre | 32 ± 4 | 227 ± 29 | 36 ± 5 | ||
| Pairwise rmsd over all non-H atomsf | |||||
| SHFTb,g | 0.95 ± 0.20 | 1.99 ± 0.19 | 1.11 ± 0.17 | ||
| NOEc,g | 1.93 ± 0.25 | 2.05 ± 0.27 | 1.85 ± 0.25 | ||
| SHFT+NOEd,g | 1.11 ± 0.17 | 1.90 ± 0.20 | 1.01 ± 0.04 | ||
| rmsd from ideal geometry | |||||
| bond length (Å) | 0.017 ± 0.0 | 0.016 ± 0.0 | 0.018 ± 0.001 | ||
| bond angle (deg) | 2.94 ± 0.04 | 3.15 ± 0.31 | 3.74 ± 0.01 | ||
| improper angle (deg) | 4.00 ± 0.17 | 3.65 ± 0.34 | 3.78 ± 0.30 | ||
|
| |||||
Three families of structures; P (20 structures), B (20 structures), and A (10 structures).
Three structures obtained using pseudocontact shift data.
Three structures obtained using NOE data.
Three structures obtained using both pseudocontact shift and NOE data.
Experimental error is the sum of the line widths in the paramagnetic and diamagnetic spectra (tol in eq 2). Gradient. error is the shift caused by a 0.3 Å displacement along the steepest gradient (eq 3).
Average of nine rmsd’s for comparison of structures obtained using different data sets, and of six rmsd’s for comparison of structures obtained with a given data set. Terminal base pairs are excluded.
Three minimized averaged structures for the three sets of restrained minimization, starting with P, B, and A (see text).
The final energy of the shift-restrained structures, −2407 ± 24 kcal/mol, is about as low as for the NOE structures, −2431 ± 95 kcal/mol, and only slightly higher than for unrestrained minimization, −2472 ± 81 kcal/mol. Structures refined with shift + NOE data exhibit more strain and van der Waal’s conflicts than SHFT or NOE structures and have higher total energy, −2097 kcal/mol. This is representative of a conflict between the NOE and shift data sets. Incompatibilities are limited to specific protons and contacts in the molecule, as will be shown below; 93% of the NOE’s are compatible with SHFT structures. It should also be noted that the initial unconstrained minimized structure from 1d83 shows very poor agreement to either the shift16 or NOE data set.
Table 3 demonstrates that convergence was obtained from three different starting models for SHFT and SHFT_NOE data sets. The structures also moved more than 2 Å from their initial starting points. Associated with structural convergence is an excellent agreement between observed and calculated pseudocontact shifts for the SHFT and SHFT_NOE structures. Individual shift violations are addressed in the next section. Residual NOE violations in the SHFT structures are satisfied in SHFT_NOE structures but at the expense of higher total energy (vide infra). However, the structures obtained using pseudocontact shifts show large deviations from the structures obtained from NOE data alone. The NOE data by themselves were also not able to define a unique structure from different starting structures, with almost 2 Å rmsd between P_NOE, B_NOE, and A_NOE.
Figure 2 shows the result of a residue-based comparison of the three final structures obtained from models P, B, and A with pseudocontact shift restraints, shift plus NOE restraints, or NOE restraints alone. This result shows that, for the DNA, the three structures derived with either shift or shift + NOE restraints are the best converged, at ≤0.8 Å rmsd. Exceptions occur at the ends of the DNA, specifically T1, A8, T11, and A18, which all show an rmsd of ≥1 Å, as well as at the chromophore residues 23 and 33 and sugars C26 and C36. These latter residues are not well defined by the pseudocontact shift data used in the simulations because they contain many contact-shifted protons.
Figure 2.
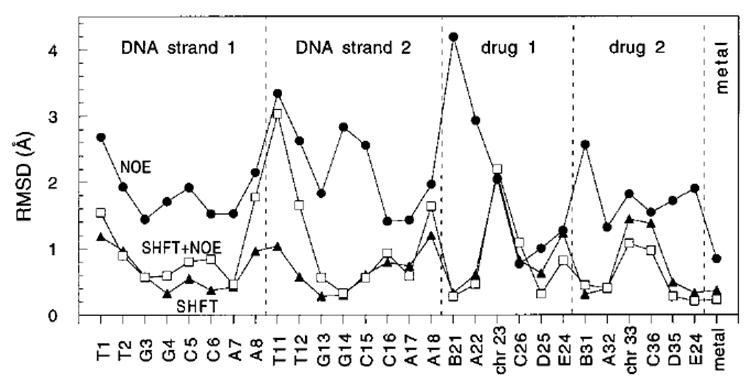
Plot of the per residue pairwise average deviation of three averaged minimized structures derived from A, B, or P starting structures for the cases where NOE’s (●), pseudocontact shifts (▲), or both (□) were used in the simulations.
The NOE structures are not well converged, although each independently has no NOE violations. This is a reflection of the fact that this number of NOE constraints, defined simply as distance ranges, is insufficient to describe a single possible structure. If only NOE constraints are available, the procedure normally used is to apply numerical and relaxation matrix analysis to the NOE data, as well as to fix dihedral angles from coupling constant data or from expected backbone geometry, to confine the structure. In this case, relaxation matrix analysis of the NOE intensities did not significantly improve the convergence between structures and lead to structures of much higher energy. Not enough long-range NOE’s are available to define the structure. Additionally, the C2 axis of symmetry results in a situation where NOE’s may consist of both intraand intermolecular components and hence cannot be readily interpreted using relaxation matrix analysis.
Figure 3 shows a superposition of the three structure families, starting from A, B, or PDB DNA, and refined using shift, shift and NOE, or NOE data. It illustrates the lack of resolution of the NOE structure, whereas the SHFT and SHFT_NOE structures are very well defined.
Figure 3.
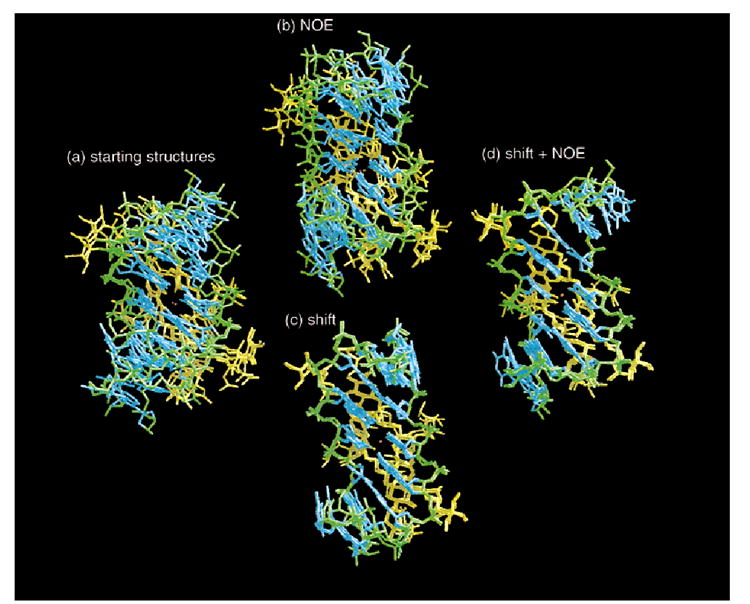
Superposition of three structures from each of the A, B, and P families, for (a) initial structures and (b–d) the three simulation conditions: (b) with NOE restraints, A_NOE, B_NOE, and P_NOE; (c) with pseudocontact shift restraints, A_SHFT, B_SHFT, and P_SHFT; and (d) with both shift and NOE restraints, A_SHFT_NOE, B_SHFT_NOE, and P_SHFT_NOE. The structures were superimposed at the central four DNA base pairs. The DNA backbone is shown in green, the DNA bases in cyan, and the two drug molecules in yellow. In b–d, minimized average structures from the full family of structures are shown.
3.2.2. Violations of Experimental Constraints
3.2.2.1. NOE Violations
There were no NOE violations in any of the NOE or SHFT_NOE structures that exceeded 0.1 Å. Figure 4 shows the minimized average structures for models P_SHFT, B_SHFT, P_SHFT_NOE, and B_SHFT_NOE. The NOE violations are depicted in red for P_SHFT and B_SHFT and are completely resolved in P_SHFT_NOE and B_SHFT_NOE.
Figure 4.
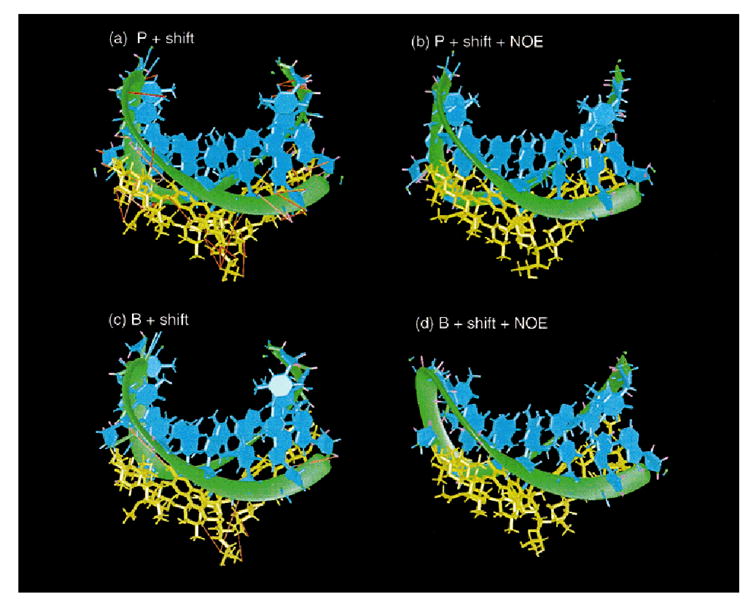
Pseudocontact shift (magenta) and NOE (red) violations shown on (a) P_SHFT, (b) P_SHFT_NOE, (c) B_SHFT, and (d) B_SHFT_NOE. The drug is shown in yellow, and the DNA is shown in green (backbone) and cyan (bases).
There are specific NOE violations (>0.5 Å) that occur in the SHFT structures (Table 4). Only NOE violations that occur in all or all but one structure are listed, as these are NOE’s that consistently disagree with shift restraints. One group of violations occurs between the A7 ribose protons and surrounding protons, including D sugar, C6, and A8 ribose and other A7 ribose protons. A second set of violations occurs between protons of the chromophore side chain and nearby protons, that is, other chromophore side chain or ring contacts as well as contacts to the C-sugar methyl proton. A third group of violations involving the terminal base pairs occurs. Additionally, a few violations of intermolecular contacts between the two drug molecules and a couple of other miscellaneous NOE violations are included in Table 4. There are a total of 51, 46, and 61 violations out of 780 NOEs in the P_SHFT, B_SHFT, and A-SHFT structures, respectively.
Table 4.
NOE Violations in SHFT Structuresa
| NOE | average
violation (Å) |
structures in
which found |
|---|---|---|
| terminal residues | ||
| T1(11)H6-T1(11)H2′ | −1.12 | A, B, P |
| T1(11)H6–H2″ | −0.60 | A, B, P |
| T2(12)H5–H3′ | −0.80 | A, B, P |
| T2H5-T1H1′ | −0.71 | A, B, P |
| A7(17)H1′–A8(18)H4′ | −1.10 | A, B, P |
| A7(17)H4′–A8(18)H8 | −0.64 | A, B |
| A8(18)H8–H2″ | −0.68 | B, P |
| adenine 7(17) | ||
| A7(17)H8–H2″ | −0.99 | A, B, P |
| A7(17)H8–H3′ | −0.66 | A, B, P |
| A7(17)H5″–C6(16)H1′ | −0.91 | A, P |
| A7(17)H5″–C6(16)H2′ | −1.10 | A, P |
| A7(17)H4′–D35(25)H2A | −0.95 | A, B, P |
| A7(17)H3′–D35(25)H2A | −0.58 | B, P |
| chromophore side chain | ||
| CPH23H1′OMe-C26HM6 | −2.30 | B, P |
| CPH23H1′–C26HM6 | −1.59 | B, P |
| C23(33)H4′–H4A/E | −2.56 | A, B, P |
| C23(33)H5′–H4A/E | −1.15 | B, P |
| C23(33)H1′–H4A/E | −0.61 | A, B, P |
| C23(33)H5′–H1′OMe | −0.93 | B, P |
| C23(33)H1′–H3′ | −1.19 | B, P |
| C23(33)H1′–H4′ | −1.40 | B, P |
| C16H4′–C23H4′ | −1.62 | B, P |
| C33H1′OMe-H10 | −0.88 | A, B, P |
| inter-drug | ||
| B21(31)H2E–A22(32)H4 | −0.64 | A, B, P |
| B21(31)H2E–A22(32)HM4 | −1.77 | A, B, P |
| C23(33)H10-A22(32)H1 | −0.63 | A, P |
| E24(34)HM6-A32(22)HM4 | −1.45 | A, B, P |
| miscellaneous | ||
| G3(13)H4′–H2′ | −0.86 | A, B, P |
| B21(31)HM6-G14(4)H5′ | −1.09 | A, P |
| C23(33)HM7-G13(3)H1′ | −0.63 | A, B, P |
Minimized average shift structures for each family, using fpc = 50 kcal mol−1 ppm−2.
The side chain of the chromophore is an example of a region that is inadequately defined by the pseudocontact shift, although the shift is very large. For example, the H5′ methyl at the end of the side chain has a pseudocontact shift of −4.49 ppm, yet the side chain adopts several conformations with the two end methyl groups being as much as 8 Å apart, with small residual shift violations of H3′, H4′, or H5′. The conformers are related by a ~180°rotation about the C3–C1′ bond. This is particularly apparent when overlaying the two symmetry-related halves of the molecule, in which excellent agreement is obtained for all regions with the exception of the side chain. The reason for the allowed conformational variation of this side chain is that it lies in the xy-plane, and the pseudocontact shift is insensitive to radial movement within that plane because of the axial symmetry. In addition, the number of available restraints to fix the side chain position is very low, with the H1′ and H1′ OMe groups excluded on the basis of possible contact shift components.
Inclusion of NOE’s as well as the noted absence of certain NOE’s improves the definition of the side-chain orientation but still allows more than one possible rotamer around the C3–C1′ bond.
3.2.2.2. Shift Violations
Following the concept of NOE violation, we need a function to describe the accuracy of pseudocontact shift refinement. A shift violation of a given magnitude does not carry equal weight over the whole molecule. The ratio of shift violation to shift gradient is a better indicator of accuracy, since it indicates how much a nucleus must be displaced to conform to the measured shift. The shift gradient varies across the molecule and along different directions from any given point. The pseudocontact shift deviation due to the displacement dl of an atom along the steepest gradient of the shift tensor is
| (3) |
where r, θ, and φ are the polar coordinates of the nucleus.17 Since the molecule is not rigid, we allow atoms “breathing” motion, which does not disrupt the structure, and define d(δpc) calculated at dl = 0.3 Å as the criterion for severe violation.
Table 5 lists the pseudocontact shift violations that were observed for the 6 minimized average structures for models P_SHFT, B_SHFT, A_SHFT, P_SHFT_NOE, A_SHFT_ NOE, and B_SHFT_NOE. Violations were defined by the condition that the difference between calculated and observed shifts exceeded the sum of the experimental error (tol in eq 2) and the gradient error (d(δpc) at dl = 0.3 Å, eqn. 3) or by the condition that the contribution to the total pseudocontact shift energy in the refined structure exceeded 1 kcal/mol.
Table 5.
Pseudocontact Shift Violations Occuring in the Final Structuresa
| atom | δpc violationb | Epc (kcal/mol)c | structures in which violations found |
|---|---|---|---|
| T1(11)H2′ | 0.12 | 0.12 | A-SHFT, B_SHFT, P_SHFT |
| T1(11)H3′ | −0.07 | 0.09 | A-SHFT, B_SHFT, P_SHFT, B_SHFT_NOE |
| T1(11)H4′ | −0.05 | 0.05 | A-SHFT, B_SHFT, P_SHFT, A_SHFT_NOE |
| T2H1′ | 0.07 | 0.27 | B_SHFT, P_SHFT_NOE, B_SHFT_NOE |
| T2(12)H2′ | 0.40 | 0.50 | B_SHFT_NOE, P_SHFT_NOE |
| T2(12)H4′ | −0.12 | 0.41 | all |
| T2(12)H5′ | −0.09 | 0.08 | all |
| T2(12)H5″ | −0.16 | 0.57 | P_SHFT, P_SHFT_NOE, B_SHFT_NOE |
| G3(13)H1′ | −0.36 | 1.22 | B_SHFT, P_SHFT |
| G3(13)H2′ | 0.63 | 1.90 | B_SHFT_NOE, P_SHFT_NOE |
| G3(13)H2″ | −0.35 | 0.72 | P_SHFT, B_SHFT_NOE, P_SHFT_NOE |
| G3(13)H3′ | −0.04 | 0.82 | A_SHFT_NOE, P_SHFT_NOE |
| G3(13)H4′ | −0.23 | 0.78 | A-SHFT, B_SHFT, P_SHFT |
| G4(14)H5′ | 0.45 | 1.80 | B_SHFT, B_SHFT_NOE |
| G4(14)H5″ | −0.50 | 6.28 | B_SHFT, B_SHFT_NOE |
| A7(17)H2″ | −0.43 | 2.31 | A_SHFT_NOE, B_SHFT_NOE, P_SHFT_NOE |
| A7(17)H3′ | −0.31 | 2.88 | all |
| A7(17)H4′ | 1.21 | 12.72 | A_SHFT_NOE, B_SHFT_NOE, P_SHFT_NOE |
| A7(17)H2 | 0.22 | 0.39 | B_SHFT, P_SHFT, B_SHFT_NOE, P_SHFT_NOE |
| A8(18)H1′ | −0.22 | 1.12 | A_SHFT, B_SHFT, P_SHFT, B_SHFT_NOE, P_SHFT_NOE |
| A8(18)H2″ | −0.16 | 0.22 | A-SHFT, P_SHFT, P_SHFT_NOE |
| A8(18)H3′ | −0.32 | 2.35 | P_SHFT_NOE |
| A8(18)H4′ | −0.34 | 1.19 | A-SHFT, P_SHFT, P_SHFT_NOE |
| A8(18)H8 | 0.02 | 0.65 | A-SHFT, B_SHFT, P_SHFT, B_SHFT_NOE, A_SHFT_NOE |
| A22(32)H4 | 0 | 1.01 | all |
| B21(31)H2E | −0.07 | 0.26 | B_SHFT |
| chr23H3′ | 0 | 1.09 | A_SHFT_NOE |
| chr23H4′ | 0 | 2.88 | A_SHFT_NOE |
Violations are defined as occurring when |δi,obs − δi,calc| > tol + d(δpc); dl = 0.3 Å (eqs 2 and 3 in the text) or when more than 1 kcal/mol is contributed to the total shift energy.
|δi,obs − δi,calc| − tol, in parts per million, averaged over the structures indicated. Shift violations of 0 imply that the shift error does not exceed tol + d(δpc).
Using fpc= 50 kcal mol−1 ppm−2(eq 2), averaged over structures indicated.
The violations in Tables 5 have several characteristics. First, violations at the terminal base pairs T1(11) and A8(18) can be attributed to fraying and will not be discussed further. Violations at the backbone of T2(12) and G3(13) appear to be consistent in many of the final structures. We have observed a secondary weak binding site for divalent metal at the T2-G3 step, observed as selective line broadening and shifting in the presence of excess Co2+.18 For this structural study, care was taken to ensure that Co2+ was not present in excess in the paramagnetic sample, but excess divalent metal or minute amounts of free Co2+ may contribute up to ~0.04 ppm in shift. This alone is not sufficient to account for the observed discrepancy, but the presence of different metals at this secondary site may cause differential local structural changes.
Almost all of the remaining protons listed in Table 5 occur in SHFT_NOE structures and result from an inconsistency between NOE’s and pseudocontact shifts. Pseudocontact shift violations of the adenine-7 residue, at H2″, H3′, H4′, and H2, arise or are exacerbated by the presence of conflicting NOE restraints. The violations at A7 are the hardest to explain, since this ribose is found to exist in a single pucker and is a point of significant intermolecular contact. However, the A7H3′ pseudocontact shift is violated in all structures, even those based on shift restraints alone. This is not a site for weak metal binding. The A7H5′ and H5″ protons were not assigned in the Co2+ spectrum, resulting in indetermination of the position of A7C5′ in the SHFT structures.
In Figure 4, the pseudocontact shift violations are displayed in the color magenta for two of the structure families. There are 32, 33, and 23 violations for the models P_SHFT, B_SHFT, and A_SHFT, respectively, and 33, 34, and 20 violations for the models P_SHFT_NOE, B_SHFT_NOE, and A_SHFT_NOE, respectively.
3.3. Precision of Structure Determination
Table 5 illustrates the fact that not all shift violations contribute equally to the shift energy of the molecule, a result of the shape of the susceptibility anisotropy tensor. Violations at T1 and T2 and parts of A8 are more readily tolerated by the simulation because they do not contribute significantly to the total energy. Increasing the force constant in eq 2 for these residues might improve determination of their positions but, in this case, was not considered feasible because their positions are averaged by the fraying at the ends of the DNA helix.
The most accurate way to assess the precision of structure determination is to determine the rmsd of the structural components in the various simulated annealing structures. A per-atom rmsd analysis of the three minimized averaged structures A_SHFT, B_SHFT, and P_SHFT is shown in Figure 5a. Apart from a few outliers, one observes a gradual decrease in precision with an increase in distance from the metal, with the precision always within 1.4 Å. The outliers include protons on A8(18), which show pseudocontact shift violations in the final structures (Table 5), as well as protons at T1(11) and T2.
Figure 5.
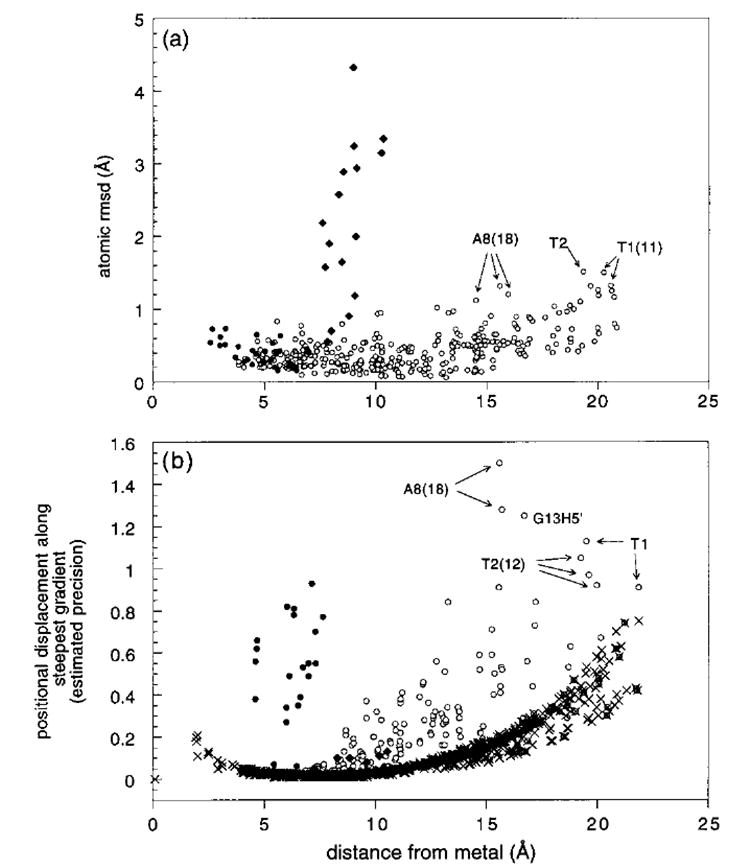
(a) Plot of the atomic rmsd (excluding hydrogens) between the three minimized averaged structures A_SHFT, B_SHFT, and P_SHFT as a function of distance from the metal: ●, regions of the chromomycin that are involved in contact shifts; ♦, the chromophore side chain; and ○, the rest of the molecule. (b) Plot of the allowed positional displacement along the steepest gradient that would not cause or exceed an observed shift discrepancy ((δcalc-δobs-tol) > 0 (see text)) as a function of distance from the metal for the model P_SHFT. The plot shows the positional displacement calculated assuming no violations between experimental and observed shifts (×) and for the actual experimental result for P_SHFT (○,●,♦): ●, protons of the chromomycin that are involved in contact shift effects; ♦, protons of the chromophore side chain; and ○, all other protons and phosphorus nuclei. The least well-defined protons are identified individually.
By far the most variable region is the chromophore side chain, which, as we have already indicated, adopts various conformations, allowed by pseudocontact shifts, in the different structures and across symmetry-related halves of an individual structure.
It is useful to be able to get an a priori assessment of how well a structure might be determined from a given magnetic susceptibility anisotropy, prior to carrying out extensive molecular dynamics simulations. We might use as a measure of precision the distance dl (equation 3) that an atom can migrate along its steepest gradient before the experimental error (d(δpc) = tol) is exceeded. In Figure 5b, the positional error dl is plotted as a function of distance from the metal ion in P_SHFT using eq 3 to calculate dl for d(δpc) equal to the maximum of (δobs − δcal − tol), tol, or the digital resolution, taken (generously) as 0.05 ppm. Also shown in Figure 5b is the estimated precision, assuming there are no violations between observed and calculated shifts. It can be seen that the presence of shift discrepancies lowers the estimated precision for individual atoms but that overall an estimated precision within 1 Å is obtained for all but a few atoms at the terminal base pairs, or at G13 (site of secondary metal binding). The limiting value of about 1 Å is in agreement with the experimental results in Figure 5a. The estimated precision has a strong dependence on distance from the metal and in general predicts coordinate determination within a fraction of an Ångstrom. In Figure 5a, on the other hand, the natural dynamics of the molecule averages the resulting rmsd to ~1 Å over most of the distance range.
One also expects that the contact-shifted protons would be definable to a much lower precision because the presence of the contact shift, which is not calculated into eq 1, results in large values of (δobs − δcal − tol). Nevertheless, these protons are still definable within 1 Å (Figure 5b), a consequence of the predominance of the pseudocontact shift. Indeed the chromophore position is fixed tightly in the MD simulations (Figure 5a) because it is attached to the metal, which is restrained to the origin.
The big discrepancy between estimated (Figure 5b) and observed (Figure 5a) precision occurs for the chromophore side chain protons. The large values of the steepest gradient for these protons would predict that the side chain would be very well defined. The failure of the prediction arises from choosing the steepest gradient to calculate the limiting dl. For isolated atoms, this is a best case scenario, since clearly positional displacements would be larger along a shallower gradient. However, the constraints of molecular bonding restrict the allowed movement of individual atoms, making the choice of steepest gradient a fairly realistic one for most of the complex. Nevertheless, we observe that this criterion fails when motion along a shallow gradient predominates, such as for the chromophore side chain. The failure of eq 3 to estimate severe violation, or, inversely, precision of coordinate determination, can be predicted to occur when a group is extended away from the structure and not constrained by bonding. In such a case, the precision must be directly assessed from the results of simulated annealing of different starting structures.
The estimate of precision is color coded into Figure 6 and correlates well with the observed scatter among the structures and with the orientation of the susceptibility anisotropy tensor. Apart from the contact-shifted atoms, other atoms falling within a 10 Å radius are extremely well defined. This demonstrates the sufficiency of eq 1 to describe the pseudocontact shift even though the dipole approximation breaks down below 7 Å. The reason for this is the likelihood that the large shift gradient in this region masks any error that results from making the dipole approximation.
Figure 6.
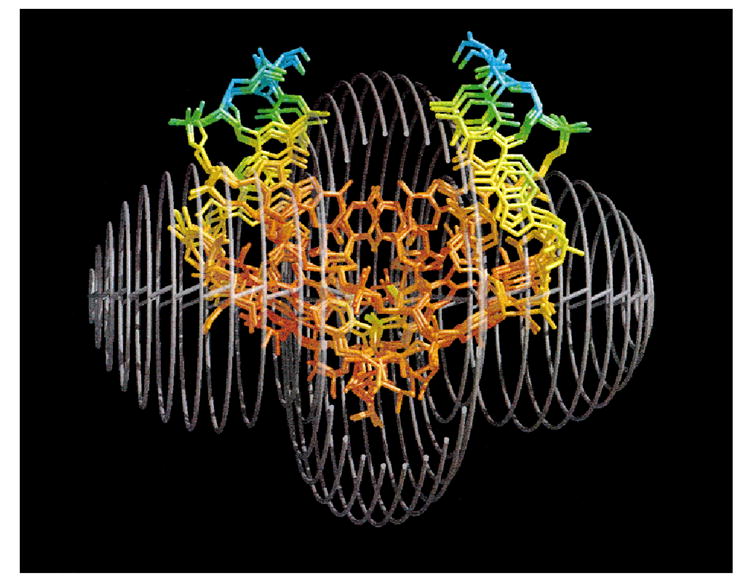
Superposition of A_SHFT, B_SHFT, and P_SHFT at the central 4 base pairs, shown in the cage of the susceptibility anisotropy tensor, drawn at a ± 1 ppm pseudocontact shift surface. The front of the tensor is cut off to show the molecules more clearly. The molecules are color coded for precision (see text). The red–blue color range depicts a range of estimated precision of 0–0.8 Å.
4. Conclusion
We have reported a detailed protocol for structure determination from pseudocontact shifts in the NMR spectrum by introducing experimental pseudocontact shifts as a restraint term in the potential energy function in XPLOR. We have demonstrated that we can obtain the magnetic susceptibility anisotropy tensor, independently of the prescribed structural information, through iterative refinement. We have observed that the final structure is insensitive to a 10% error in the susceptibility anisotropy values. We also show that structural convergence can be achieved from three different sets of starting structures. The precision of structure determination is extremely high, vastly superseding that available from NOE restraints alone. It varies across the molecule, because of the nature of the pseudocontact shift function, but extends more than 20 Å with sub-Ångstrom precision. We have found that the precision can be reliably estimated from knowledge of the susceptibility tensor anisotropy.
Ninety-three percent of the NOE’s and 84% of the pseudocontact shifts are satisfied by the shift-based structure determination. The discrepancies in NOE’s and pseudocontact shift restraints fall into certain categories. Several NOE’s and pseudocontact shifts are violated at the ends of the DNA and are likely to be a reflection of restraint and structural averaging due to fraying. A second group of violations is principally associated with a conflict between NOE’s from the drug protons to DNA backbone protons and corresponding shift restraints. In particular, the ribose ring of adenine-7(17) was found to be involved in several such shift or NOE violations. The reason for this is unknown, unless fraying of the DNA extends to the penultimate base pairs. Certainly, the A7(17)-ribose ring makes key contacts to the drug. In the absence of this ribose (i.e., for a truncated DNA), the chromomycin fails to form a tight complex with the DNA.18
Pseudocontact shifts alone were insufficient to define the conformation of the chromomycin chromophore side chain. This is an example of how the orientation of the susceptibility anisotropy tensor influences the ability of the shifts to determine structures. NOE’s alone also could not determine this side chain orientation, but the use of both pseudocontact shifts and NOE’s allowed it to be determined. In general, using the maximum amount of data is bound to give the best result, although we have observed that conflicts between the NOE and shift data sets give rise to higher molecular energies and structures of slightly increased strain. It is likely that these conflicts are due to some type of motional averaging, since the DNA backbone in particular is known to be flexible, and most of the conflicts that arise involve backbone atoms or the DNA termini. In this case, the use of a method such as time-averaged restraints19 or multiple conformer modeling20 could lead to more relaxed structures from the combined data sets. The precision of structure determination using the pseudocontact shift becomes limited by the presence of internal motions. This study indicates that localized motional averaging can apparently be detected by the disagreement between NOE’s and pseudocontact shift restraints.
Finally, we would like to report on the robustness of pseudocontact shift restraint-based simulations for determining a family of conformers representing the biomolecular structure. We have found rapid convergence with no data manipulation required and final structures with very low energies. Getting an NOE structure of comparable precision is probably impossible or would require substantial user manipulation. In this case, the NOE’s averaged more than 27 per residue, if they were uniformly distributed. Of course the problem is that the number of defining NOE’s is quite small in an elongated complex. Thus a paramagnetic probe can be particularly useful for examining extended structures or the orientation of subdomains. For this particular complex, a detailed study of the structure obtained using the pseudocontact shifts reveals significant differences from the earlier NMR structure derived from NOE’s (manuscript in preparation).
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health Grant GM53164. Additional support was obtained from NIH CA25644 to Peter Kollman. Use of the Computer Graphics Laboratory at UCSF, supported by NIH P41-RR01081, is acknowledged. This research was supported in part by a grant from the Pittsburgh Supercomputing Center through the NIH National Center for Research Resources cooperative agreement 2 P41-RR06009. The authors are grateful to Peter Kollman for valuable suggestions and helpful discussions.
Footnotes
Supporting Information Available: Listings of final energies obtained for each family of structures, rmsd’s between each of the nine families of structures as well as to the initial starting structures, and structural statistics for each family of structures. Coordinates and constraint files are deposited at PDB (accession number 1cqb; restraint file r1cqbmr); chemical shifts of Co(II) and Zn(II) forms are deposited at the Biomagnetic Resonance Data Bank (BMRB # 4361 and 4362, respectively). This material is available free of charge via the Internet at http://pubs.acs.org.
Note Added in Proof. Since this paper went to press, further NMR studies have revealed an error in the assignment of the A7H4′ and D-sugar H2a, H2e protons in the Co2+ complex. Correction of these shifts removed all discrepancies between NOE’s and pseudocontact shifts at the A7 ribose, accompanied by a slight local structural change at the backbone of A7.
Contributor Information
Kechuan Tu, Department of Pharmaceutical Chemistry, University of California, San Francisco, California 94143.
Miriam Gochin, Department of Microbiology, University of the Pacific School of Dentistry, San Francisco, CA 94115.
References
- 1.Pardi A, Hare DR, Wang C. Proc Natl Acad Sci USA. 1988;85:8785–8789. doi: 10.1073/pnas.85.23.8785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bertini I, Luchinat C. NMR of Paramagnetic Molecules in Biological Systems. Benjamin/Cummings; Menlo Park, CA: 1986. [Google Scholar]
- 3.Gochin M, Roder H. Protein Sci. 1995;4:296–305. doi: 10.1002/pro.5560040216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gochin M. J Am Chem Soc. 1997;119:3377–3378. [Google Scholar]
- 5.Banci L, Bertini I, Bren KL, Cremonini MA, Gray HB, Luchinat C, Turano P. J Bioinorg Chem. 1996;1:117–126. [Google Scholar]
- 6.Banci L, Bertini I, Savellini G, Romagnoli A, Turano P, Cremonini M, Luchinat C, Gray H. Proteins: Struct, Funct, Genet. 1997;29:68–76. doi: 10.1002/(sici)1097-0134(199709)29:1<68::aid-prot5>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 7.Gao XL, Patel DJ. Biochemistry. 1990;29:10940–10956. doi: 10.1021/bi00501a012. [DOI] [PubMed] [Google Scholar]
- 8.Gao XL, Mirau P, Patel DJ. J Mol Biol. 1992;223:259–279. doi: 10.1016/0022-2836(92)90730-8. [DOI] [PubMed] [Google Scholar]
- 9.Gochin M. J Biomol NMR. 1998;12:243–257. doi: 10.1023/a:1008289724077. [DOI] [PubMed] [Google Scholar]
- 10.Golding R, Stubbs L. J Magn Reson. 1979;33:627–647. [Google Scholar]
- 11.Liu H, Kumar A, Weisz K, Schmitz U, Bishop KD, James TL. J Am Chem Soc. 1993;115:1590–1591. [Google Scholar]
- 12.Brünger AT. X-PLOR 3.1. Yale University; 1992. [Google Scholar]
- 13.Baleja JD, Pon RT, Sykes BD. Biochemistry. 1990;29:4828–4839. doi: 10.1021/bi00472a012. [DOI] [PubMed] [Google Scholar]
- 14.Bruccoleri RE, Karplus M. Biopolymers. 1986;25:1767–1802. doi: 10.1002/bip.360250916. [DOI] [PubMed] [Google Scholar]
- 15.SYBYL 6.0. Tripos Associates, Inc; 1992. [Google Scholar]
- 16.Calculated using the refined tensor from 3. 1. 2. A better agreement to observed shifts is obtained using initial tensor A
- 17.Feng Y, Roder H, Englander SW. Biochemistry. 1990;29:3494–3504. doi: 10.1021/bi00466a011. [DOI] [PubMed] [Google Scholar]
- 18.Gochin, M., unpublished data.
- 19.Schmitz U, Kumar A, James TL. J Am Chem Soc. 1992;114:10564–10556. [Google Scholar]
- 20.Ulyanov NB, Schmitz U, Kumar A, James TL. Biophys J. 1995;68:13–24. doi: 10.1016/S0006-3495(95)80181-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.