Using mathematical modeling and control to develop structured treatment interruption strategies for HIV infection

Abstract

The goal of this article is to suggest that mathematical models describing biological processes taking place within a patient over time can be used to design adaptive treatment strategies. We demonstrate using the key example of treatment strategies for human immunodeficiency virus Type-1 (HIV) infection. Although there has been considerable progress in management of HIV infection using highly active antiretroviral therapies, continuous treatment with these agents involves significant cost and burden, toxicities, development of drug resistance, and problems with adherence; these latter complications are of particular concern in substanceabusing individuals. This has inspired interest in structured or supervised treatment interruption (STI) strategies, which involve cycles of treatment withdrawal and re-initiation. We argue that the most promising STI strategies are adaptive treatment strategies. We then describe how biological mechanisms governing the interaction over time between HIV and a patient’s immune system may be represented by mathematical models and how control methods applied to these models can be used to design adaptive STI strategies seeking to maintain long-term suppression of the virus. We advocate that, when such mathematical representations of processes underlying a disease or disorder are available, they can be an important tool for suggesting adaptive treatment strategies for clinical study.

1. Introduction

Adaptive treatment strategiesare a potentially powerful approach to operationalizing clinical decision-making (e.g.,Lavori and Dawson, 2003; Murphy et al., 2006). An adaptive treatment strategy is a set of sequential decision rules, each of which describes how and when the next step of treatment for a patient should proceed based on information on the patient in the form of tailoring variables, such as previous treatments received, response to those treatments, and adherence of the patient up to that point, with the goal of achieving some clinical outcome. Because the decision rules allow treatment to adapt to the state of the patient, such strategies offer a principled, systematic approach to individualization of therapy, and their value as a flexible tool in the management of chronic, relapsing disorders such as substance abuse is broadly recognized (e.g., Sobell and Sobell, 2000 ). Moreover, as noted by Rivera et al. (2006) , there is strong interest in the use of adaptive treatment strategies in numerous other disease and disorder areas.

A key challenge is the need for methods that can assist in the development of evidencebased adaptive treatment strategies. One emerging approach is to base formulation of adaptive treatment strategies on data collected under suitable experimental designs and analytical “learning” methods that synthesize the information into sequential decision rules (e.g.Collins et al., 2004;Lavori and Dawson, 2003;Murphy, 2005;Murphy et al., 2006). Another idea is to exploit mathematical modelsthat represent the patient as a “system” that is changing over time. The behavior of the system can be modified by controllinga variable or variables that can be manipulated (e.g., treatment) to achieve desired outcomes, possibly using feedbackfrom the system up to the current point, to deduce the next control (treatment) action to take. Based on such a representation, decision rules may be determined using mathematical control principles and simulation. Rivera et al. (2006) provide an excellent introduction to this approach. In this article, we focus on the promise of this second approach in situations where such a mathematical model is suggested by knowledge of or hypotheses about biological and physiological mechanisms underlying the disease or disorder, using HIV infection as a concrete example.

Potent antiretroviral therapy has led to a profound decrease in morbidity and mortality from HIV and AIDS-related illnesses (Detels et al., 1998; Murphy et al., 2001;Palella et al., 1998), but these treatments cannot completely eradicate the virus, so HIV-infected patients must continue these therapies for life (Finzi et al., 1999;Siliciano et al., 2003). However, lifelong commitment to anti-HIV therapy is often complicated by side-effects, toxicities, adherence issues, problems with drug resistance, high costs, and life style issues (Ledergerber et al., 1999;Martinez et al., 2001;Phillips et al., 2005;Richman et al., 2004;Smith, 2002). These difficulties have led to interest in developing treatment strategies known as structured or supervised treatment interruptions(STI), which involve having patients take antiretroviral therapy for some period of time, followed by treatment interruption and possible re-initiation, perhaps through several cycles of these steps. Many specific STI strategies, involving different interruption intervals and different decision rules for terminating/re-initiating therapy, have been proposed, mostly based on expert opinion, and have been studied in humans and animals (Lisziewicz et al., 1999;Lori et al., 2000;Lori and Lisziewicz, 2001;Rosenberg et al., 2000; Walker and Rosenberg, 2000;Wodarz et al., 2000); however, the potential benefits of STI are still not established. We contend that this is because the STI strategies studied were not developed based on a systematic, evidence-based approach.

Since Ho et al. (1996) demonstrated that the time course of HIV RNA load (or “viral load,” the concentration of copies of viral RNA present in the body) can be described by mathematical models, there has been vigorous development of such models to represent known and hypothesized interactions between HIV and the immune system taking place within a patient and in using them in conjunction with patient data to provide possible explanations for the mechanisms responsible for observed progression of the disease and for the effects of treatment (e.g.,Adams et al., 2005;DiMascio et al., 2004;Dixit and Perelson, 2004;Pereleson et al., 1997). We suggest that these mathematical models for the within-patient biological mechanisms of HIV infection can form the basis for principled, evidence-based formulation of adaptive STI strategies.

In the remainder of the article, after a review of current HIV treatment practices and STI, we give an introduction to such HIV dynamic modelsand their application to data, describe how control methods may be applied to them to design adaptive STI strategies, and how the strategies so derived may be evaluated via computer simulation from the mathematical model of “virtual” patients following the strategies to suggest the most promising for clinical study. Readers may find it beneficial to review Rivera et al.(2006), also in this issue, before proceeding.

2. HIV therapy and structured or supervised treatment interruption

Just as clinicians caring for substance abusing individuals must take into account factors reflecting stage of the disorder, such as chronicity, multiplicities of drugs used, and lifestyle changes; measures of progression such as frequency and type of use; relapse (e.g.,Finney et al., 1996); and co-occurring disorders (Kessler et al., 2003) in ongoing treatment decisions over time, clinicians managing HIV-infected patients must consider many analogous factors in deciding when therapy should be initiated or discontinued, what drugs should be used, and when to change regimen. Indeed, current clinical guidelines for treatment of HIV-infected patients (Yeni et al., 2004;DHHS, 2005) and current practice are based on monitoring HIV-infected patients over time for indications of disease stage and progression, relapse, and other outcomes.

CD4 T cell counts and viral load measurements are key factors used in monitoring and treatment decisions. CD4 T cell counts reflect immunologic status; lower CD4 cell counts are associated with higher mortality and increased risk of disease progression (Egger et al., 2002;Chene et al., 2003;Palella et al., 2003;Sterling et al., 2003). Magnitude of viremia at viral load “set-point” (a plateau typically reached within the first 6-12 months after infection) is highly prognostic for the rate of disease progression (Lyles et al., 2000), and viral load > 100,000 copies/ml plasma is associated with death (Wood et al., 2003b). Both measures are the most widely accepted surrogate markers for monitoring therapeutic response; the optimal response would be an increase in CD4 T cells and complete suppression of viral replication, reflected by “undetectable” viral load below the lower limit of quantification of the assay. In situations where a patient may have acquired drug resistant virus, the first indicator is the emergence of persistently detectable plasma viremia (analogous to relapse of a behavioral disorder previously under control). Frequently, the re-emergence of viremia results in a slow decline in CD4 T cell counts. Therefore, viral load measurements are the cornerstone in measuring therapeutic response to antiretroviral drugs while CD4 T cell counts are the ultimate indicator of disease stage and effect of therapy.

It is common to make changes to treatment regimens based on side effects to one or more drugs in a given combination, as these may be debilitating. Ability to adhere to complex antiretroviral regimens involving multiple drugs and high pill burden is also considered; adherence is a critical determinant of survival (Wood et al., 2003a). Nonadherence, particularly problematic in patients with co-occurring substance abuse issues (Hser et al., 1997), often leads to development of drug resistance, which can result in elimination of therapeutic options (discussed further below). Indeed, substance abusing individuals, especially intravenous drug users, are at risk both for acquiring HIV infection and for nonadherence, and many providers are reluctant to recommend antiretroviral therapy to patients with active drug issues, as their propensity for nonadherence is apt to lead to swift elimination of treatment options.

Ideally, for an HIV-infected patient experiencing sustained, optimal response to antiretroviral treatment with no adherence or side effect issues, a provider would continue with the current therapeutic regimen long-term. However, the complications involved in continuous administration of therapy discussed in Section 1 have inspired interest in STI strategies. As noted at the outset, despite several clinical investigations of STI strategies, the value of STI is still not established, which we conjecture is due in part to the fact that the specific STI strategies studied so far (i.e., the particular decision rules used) were conceived via “educated guesses” and informal review of empirical evidence rather than by a systematic approach. The importance of developing treatment strategies for HIV infection that address the problems with continuous administration, along with the inconclusive results for STI so far, suggest the need for an alternative, evidencebased approach to designing STI strategies for clinical study, as we propose in the sequel.

We now review the experience with and rationale for STI. Two types of STI strategies are possible, and there is experience with both types. For example, an STI strategy may specify that antiretroviral therapy continue for 16 weeks, followed by an interruption of 8 weeks and subsequent resumption for another 16 weeks. Such a regimen is an instance of a non-adaptive treatment strategyin that the treatment decisions (interruption and re-instatement of therapy here) are pre-specified and hence do not take into account (i.e., adaptto) the state of any patient following the strategy. In contrast, many STI strategies studied have been adaptive, where decisions to interrupt or re-initiate treatment are determined based on observation of tailoring variables such as magnitude of viremia or decline in CD4 cell count. For example, in the Strategies for Management of AntiRetroviral Therapy trial (El-Sadr and Neaton, 2006), an adaptive STI strategy was studied under which patients remained off therapy until their CD4 counts fell < 250 cells/mm³, at which point therapy was initiated and maintained until CD4 cell counts increased to at least 350 cells/mm³, which dictated re-interruption. Patients following this strategy cycled through periods of treatment interruption and re-instatement determined adaptivelybased on periodic observations of their CD4 cell counts according to these specific decision rules.

We consider the rationale for STI in two settings, first for managing chronic (long-term) HIV infection and second for managing acute (new) HIV infection. Both non-adaptive and adaptive STI strategies have been studied in individuals with chronic infection (Katlama et al., 2004;Lawrence et al., 2003;Ruiz et al., 2000;Ruiz et al., 2003;El-Sadr and Neaton, 2006), based on several rationales for interrupting therapy in these patients (Hirschel, 2001). One is to provide “drug holidays,” breaks from the burden and side effects of antiretroviral therapy (while hopefully not negating the benefits). For patients with multi-drug resistant virus, a further rationale is to allow “wild-type,” drug-sensitive viral quasi-species to repopulate the body and preferentially replicate over less susceptible, drug resistant virus. Lengthy therapy with antiretroviral agents may result in emergence of drug resistant virus, which is particularly likely if a patient is poorly adherent. The development of drug resistance may eliminate an entire drug class (or classes), limiting the number of treatment options. However, genotypic mutations, which alter susceptibility to antiretroviral therapy, may in theory “cost” the virus in terms of its “fitness” or ability to replicate (Croteau et al., 1997;Deeks et al., 2001;Nijhuis et al., 2001), and some studies have shown that cessation of therapy results in reversion of viral quasi-species back to wild-type virus. These observations have led to the hypothesis that an interruption in therapy eliminates drug pressure, resulting in reversion of viral populations to a more susceptible viral quasi-species, thus improving chances that subsequent salvage regimens will be effective. Although studies have demonstrated that virus harboring genotypic mutations can revert back to wild-type quasi-species and may improve virologic outcome (Katlama et al., 2004), clinical benefit of treatment interruption in chronically-infected patients leads has not been established (Antinori et al., 2005;Ghosn et al., 2005;Yeni et al., 2004).

The rationale for STI in acute infection is different from that for chronic infection. Acute HIV infection is the period from viral entry to formation and detection of HIV-specific antibodies. This time period may offer an opportunity to initiate therapy with the goal being preservation of HIV-specific immunity and treatment discontinuation (Kassutto and Rosenberg, 2004;Rosenberg et al., 1997;Rosenberg et al., 2000); the rationale is grounded in the biologic and immunologic events surrounding primary HIV infection. A hallmark of acute HIV infection is the extreme degree of viral replication, resulting in high levels of viremia, where the virus preferentially targets and infects HIV-specific CD4+ T helper cells (Douek et al., 2002), resulting in profound impairment in their function. These cells are believed to be critical in the normal generation and maintenance of effective cellular and humoral immune responses. One hypothesis is that treatment with antiretroviral therapy during acute HIV infection will limit viral replication and minimize impairment of T helper cells. Early treatment during acute HIV infection reliably restores HIV-specific T helper cells that would otherwise be lost (Oxenius et al., 2000;Rosenberg et al., 1997;Rosenberg et al., 2000), resulting in an immunological phenotype similar to that of individuals with long-term non-progressive (LTNP) infection (Rosenberg et al., 1997). The difference is that persons with LTNP HIV infection spontaneously control viral replication without antiretroviral therapy, whereas individuals treated during acute HIV infection require therapy to contain viremia. This immunological similarity has led investigators to question whether immune responses generated and maintained during treatment of acute infection would be adequate to control viral replication if therapy is subsequently discontinued. Anecdotal evidence suggests that viremia returns once therapy is discontinued but viral load set-point may be lower (Lisziewicz et al., 1999;Rosenberg et al., 2000). These observations have generated additional questions. For example, can cyclical treatment interruptions resulting in re-exposure to autologous virus further stimulate and augment immune responses? If so, will these enhanced immune responses result in improved viral control with each successive interruption? This concept of “autologous vaccination” via STI has been attempted in very limited trials with mixed success; in these studies, persons undergoing STI showed immunological control of viral replication but the duration was transient (Rosenberg et al., 2000;Kaufmann et al., 2004;Streeck et al., 2006).

It is clear that further investigation is needed to prove or discount these rationales for STI. In particular, a potentially unlimited number of practically feasible STI strategies, both nonadaptive and adaptive, may be conceived, raising the possibility that those studied so far, whose specific decision rules were developed on the basis of expert opinion and “educated guesses,” may have been unfortunately chosen. For example, the decision rules used in the “Strategies for Management of AntiRetroviral Therapy” study, which were based on particular CD4 cell count thresholds dictating interruption and re-initiation of therapy (chosen after much debate by a consensus of experts), may have been suboptimal; moreover, other critical measures, such as viral load, were not incorporated in the rules at all. Accordingly, it may be premature to dismiss the idea of STI on the basis of the inconclusive results of this study.

Our contention is that an approach to designing STI strategies based on combining biological knowledge and data in a principled way should be considered. Given the complexity of HIV infection, the immunologic and virologic basis underlying existing HIV treatment guidelines, and the need to provide clinicians with flexible options, STI strategies for which the decisions on interruption and re-initiation of treatment are made adaptivelyhold the most promise. We now turn to our main premise, that mathematical HIV dynamic models of the biological mechanisms underlying the interaction between virus and immune system and the effects of treatment on these processes within a patient are a potentially valuable tool for constructing new, evidence-based adaptive STI strategies worthy of further clinical study.

3. HIV dynamic models

HIV dynamic models are based on representing known and hypothesized processes involved in the virus-immune system interplay through a series of hypothetical “compartments” characterizing different populations of virus and constituents of the immune system. The collection of compartments so hypothesized is regarded as a “system” within the patient in which interactions take place among the populations in the various compartments over time.

One compartment usually included is the population of infectious virus particles, or virions, present in the body. Typical other compartments include the population of non-infected CD4 T cells, which are targets for infection by virus; the population of infected CD4 T cells, those that have already been infected; the population of non-infectious virus (e.g., virus that has been rendered incapable of infecting CD4 T cells via the effect of treatment); and populations of other cells that are involved in the immune system’s “counterattack” against the virus (e.g., cytotoxic T-lymphocytes, or CTLs, which are produced in response to the presence of infected cells). Over time, the size of the population in each compartment is assumed to change according to specific assumptions about how the virus interacts with the other populations. For example, it might be assumed that infectious viral particles infect non-infected target CD4 T cells at a constant rate per unit of time. When a CD4 T cell is infected, the virus uses it as a vehicle to replicate itself; thus, such infection causes more infectious viral particles to be produced and leads to the death of the infected T cell when the new viral particles produced are released. A model may suppose that these infected cells produce new infectious virions at a certain rate per unit time and then die at some rate. Virus also dies naturally; thus the model may assume that virus particles exit the system at some rate. One may make different assumptions about the number of compartments present and how they interact, which lead to different overall representations of the mechanisms thought to be occurring in HIV infection within a patient. With more compartments and interactions, models may be made more compatible with hypotheses about what are undoubtedly rather complicated biological processes; we discuss this further below.

Treatment may also be introduced into the system. The antiretroviral agents comprising typical combination therapy include reverse transcriptase inhibitors (RTI), which act to block new infections, and protease inhibitors (PI), which cause infected CD4 cells to produce non-infectious virus. These effects are often incorporated by assuming that, for example, in the presence of RTI therapy, the rate of production of new infectious virus is attenuated by some constant factor related to the efficacy of the therapy. The models can accommodate changes in the “input” of treatment into the system; e.g., treatment may be “turned on” or “off” over time. This feature may be exploited in the design and study of different STI strategies, elaborated in the next section.

As an example, Fig. 1 presents a schematic of a typical and fairly simple model. The model includes compartments for the populations of infected and non-infected CD4 T cells, which, when uninfected, are the main target for the virus and, when infected, are the main source of viral replication; and compartments for infectious and non-infectious virus populations. Also included are compartments representing infected and non-infected CD4 “memory cells,” which may be thought of as a “latent” population of CD4 cells that become infected and die at different rates from the main populations. These memory compartments represent in a simple way the belief that there is a reservoir of target cells that lie in a latent state in which they do not produce new virus and are responsible for the fact that the virus always can reemerge upon withdrawal of therapy. The arrows labeled “differentiation” indicate that target CD4 T cells may revert to latent status, becoming part of the reservoir, and the “activation” arrows allow latent cells to emerge and contribute to the main target population and, if infected, production of virus. The “immune effectors” compartment represents CTL cells that arise from the presence of infected CD4 T cells, indicated by the arrow pointing from the infected CD4 T cell compartment. These cells are part of the response of the immune system; the upper arrow pointing away from this compartment represents their action in killing infected CD4 cells. The arrows emerging from the infectious virus compartment depict hypothesized actions of the virus in stimulating and infecting CD4 cells; the “RTI” notation represents the interference of these therapeutic agents with the ability of the virus to transform non-infected target cells to infected status. The arrow from the infected CD4 compartment to the infectious virus compartment represents the release of new virus produced by infection; the arrow pointing to the non-infectious virus compartment with the “PI” notation incorporates the effect of protease inhibitors in leading to production of non-infectious virus. For all compartments, the outward arrows with no destination represent death of the cells in the respective populations, and inward arrows from outside represent birth of new cells into the indicated populations.

Fig 1.

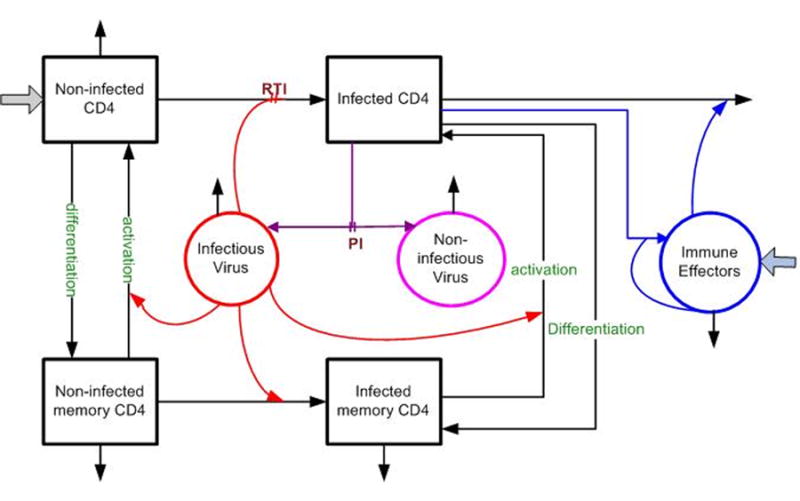
Schematic diagram of a typical HIV dynamic model for the mechanisms taking place within a single HIV-infected patient. The model has seven compartments representing infectious and non-infectious virus, infected and non-infected CD4 T cells, infected and non-infected latent memory CD4 T cells, and cytotoxic T-lymphocytes (CTLs) (immune effectors). The arrows depict interactions among the compartments; for example, the arrow from the non-infected CD4 compartment to the infected CD4 compartment indicates the transformation of the former type of cells to the latter as they are infected by infectious virus. The arrows leading into the non-infected CD4 and immune effector compartments indicate the natural processes of the birth of new cells into these populations. The “RTI” notation represents the effect of reverse transcriptase inhibitors in interfering with the infection process. Further description of the components of the model is given in the text.

Once a compartmental depiction is conceived, it may be formulated mathematically as a system of ordinary differential equations, or ODEs, in terms of variablesthat represent the size of the population in each compartment at each point in time, where time “0” represents the time at which virus is introduced into the body (i.e., the time of infection), and a set of initial conditions corresponding to the state of the system at time 0. The ODEs formalize how each variable representing the size of the population in each compartment changes as the processes of infection of target cells, production of new virus, stimulation of the immune system, and viral and cell death take place over time. Given a set of initial conditions, the system of ODEs may be solved using appropriate numerical techniques (e.g.,Hairer et al., 1996;Hindmarsh, 1983) to yield expressions for the size of the populations in each compartment at any time in terms of the rates of infection, production, death, etc., and, in the presence of antiretroviral therapy, the efficacies of the various agents (e.g., RTI and PI) given in combination.

An HIV dynamic model thus describes processes taking place over time within an HIV-infected individual under a specific set of assumptions on the virus-immune system interaction and the effects of treatment. It is natural to expect that, although the processes so represented might be similar across patients, they would not be identical because of the natural biological heterogeneity that is expected across individuals as well as due to identifiable characteristics of patients (e.g., gender, comorbidities). This is conceptualized by supposing that, while each patient follows the same system of ODEs, the values of rates of infection, viral production, cell and viral death; efficacies of treatment; and so on, are different for different patients. We refer to these quantities henceforth as the “model parameters.” The same system of ODEs will behave differently with different values of the model parameters. Thus, if the values of model parameters differ across patients, this would lead to different patients undergoing the same treatment regimen to exhibit heterogeneous responses (e.g., viral load and CD4 cell counts over time), as is observed in practice. From this perspective, then, taking a particular HIV dynamic model as an approximation to the processes taking place inside patients, the extent to which values of the model parameters vary across patients dictates the extent to which clinical outcomes vary across patients. Intuitively, if this variation could be quantified, it could lead to understanding of how responses to different treatment strategies might vary in the patient population; a feature we exploit in the next section.

Clearly, data from actual patients are critical for understanding not only how the parameters in a given model vary in the population but also for conceiving realistic models. All of the compartments that make up a fairly realistic such HIV dynamic model cannot be observed on a patient; typically, viral load and CD4 T cell count are the standard (and only) relevant measurements taken, as discussed in Section 2. In the context of the dynamic model in Fig. 1, for example, as viral assays cannot distinguish infectious and non-infectious virus, viral load may be viewed as a measurement of the sum of the sizes of the populations in the infectious and noninfectious virus compartments. Moreover, in the absence of data on viral genotype and “fitness,” it would be difficult to learn about components of a more complex model that includes hypothesized mechanisms involved in the development of drug resistant strains or reversion of susceptible viral quasi-species to wild-type. Thus, of necessity, HIV dynamic models to be used for practical purposes must strike a balance between realistic representation of complex mechanisms and feasibility given the data at hand; we discuss this further in the next section.

We now describe in more detail how data from a single patient and from many patients may be used to learn about the underlying processes taking place within patients, as represented by a particular HIV dynamic model, and how these processes vary across patients. First, consider a single patient. Given frequent clinical longitudinal observations of viral load and CD4 cell count only on a single patient, it is possible using appropriate mathematical and statistical methods (Banks and Kunisch, 1989;Davidian and Giltinan, 1995, 2003;Kelley, 1999;Vogel, 2002) to estimatethe values of his/her underlying model parameters in a model of the complexity of that in Fig. 1. For example, even when only total viral load is available, it is still possible to recover information on parameters connected with both the infectious and non-infectious virus compartments, such as rates of infection, viral production, and cell birth, and death. Once a patient’s parameters are estimated, the system may be solved numerically as described above using the estimated parameters to yield fitted values of, e.g., viral load and CD4 cell count predicted by the model at any time (including times beyond those under which the patient was observed).

Fig. 2 depicts for a single real patient acutely infected with HIV actual longitudinal viral load data and two different kinds of fitted values obtained from these viral loads and longitudinal CD4 counts (not shown) for this patient using a model similar to that in Fig. 1. The thick solid lines on the horizontal axis indicate time periods where the patient was undergoing antiretroviral therapy; note that the patient terminated therapy permanently at about day 825. The two model fits shown arise from estimating the model parameters two ways. The dashed line represents the fit when the model parameters were estimated based on all 1600 days of data, while the solid line gives the fit when the parameters were estimated based only on the first 800 days of data. Model fitting with viral load measurements in either case is complicated by the fact that, under therapy, these tend to drop below the lower limit of quantification of the viral load assay, so that their actual values are known only to lie below this limit. As is conventional, such viral load data values are plotted in Fig. 2 at the value of this known limit. The usual estimation techniques mentioned above were combined with methods for regression analysis for such so-called “censored” data to obtain the fits (see Adams et al., 2006), and the open circles in Fig. 2 indicate predictions of the actual values of viral load, based on the model fit using half the data, that would have been observed had there been no assay limit. Both the fit based on the all the data and that based on only half the data track the pattern of viral loads in the data well. That based on half the data does a good job predicting the trend in the subsequent viral load measurements. This demonstrates a key feature of the mathematical modeling approach that makes it attractive for designing treatment strategies, namely, that reasonable knowledge of a specific patient’s model parameters, e.g., obtained from early data, is sufficient to predict that patient’s future long-term progression.

Fig 2.

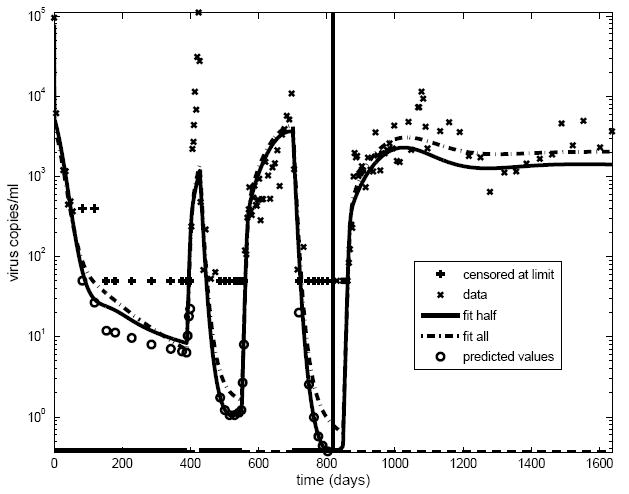
Longitudinal data on viral load measurements from a single patient acutely infected with HIV, with fitted time profiles obtained from a model similar to that depicted schematically in Fig. 1 superimposed. The “x” symbols indicate viral load measurements above the limit of quantification of the assay. The “+” symbols indicate that a viral load measurement at that time point is known only to lie below the limit of quantification of the assay used at that time point; in this case, symbols are plotted at the limit of quantification. The thick bars on the horizontal time axis correspond to time intervals when the patient was on antiretroviral therapy; note that this patient permanently interrupted therapy at about 825 days. The dashed line shows the fit using all the data for the entire 1600 days. The solid line shows another fit using only the data up to the time of permanent treatment interruption. The fit of the model takes into account the “censoring” of viral loads at the limit of quantification, with the open circles representing “predicted values” of viral loads known only to be below the limit.

The foregoing discussion applies to estimation of the model parameters, e.g., rates of infection, viral production, cell birth and death, for a single patient. When longitudinal data from each patient in a sample of patients are available, estimates of the model parameters for each patient may be obtained by these methods. These estimates may then be used collectively to construct a representation of the way in which model parameters vary across patients in the population of patients. This representation may be achieved by identifying and estimating a probability distributionthat approximates how this variation in the population takes place, based on the model parameter estimates from all patients in the sample.. As we now discuss, this, and further mathematical techniques, hold promise for facilitating the design of STI strategies.

4. Design of STI strategies using HIV dynamic models

The availability of HIV dynamic models and information from data on model parameters for individual patients or samples of patients suggests the use of a mathematical tool that can guide the design of both non-adaptive and adaptive STI treatment strategies. Control theoryis a body of mathematical theory and techniques for modifying, or controlling, the behavior of systems of ODEs like HIV dynamic systems through the manipulation of system inputs (Anderson and Moore, 1990;Camacho and Bordons, 2004;Rivera et al., 2006). Here, the input is antiretroviral therapy, and STI involves turning the input “on” or “off” at various points over time. Control theory seeks to specify the best strategies for treatment input over time for a particular model in order to control the system behavior so as to optimize a particular objective. For example, the objective may be to drive viral load set-point to a value below a specified low threshold while minimizing the treatment burden imposed on patients. Control theoretic methods have been used with HIV dynamic models to suggest “optimal” strategies for administering antiretroviral therapy over time (Adams et al., 2004,2005; Banks et al., 2005a;Brandt and Chen, 2001;Culshaw et al., 2004;Jeffrey et al., 2003;Kirschner et al., 1997;Wein et al., 1997). For example, inAdams et al. (2005), the authors considered a fairly complicated HIV dynamic model and used control theory to design non-adaptive STI strategies that involve a short-term pattern of several interruptions after infection. They showed that such strategies can, at least theoretically, lead to long-term control of the virus in some patients. However, to the knowledge of the authors, HIV dynamic models and control theory have mainly been used to deduce and study STI strategies hypothetically but have not been used in a systematic way to design STI strategies with the intention of implementing them in actual clinical trials. We now outline how we envision that HIV dynamic models, control theory, and information from data may be used for this purpose.

Under the assumption that a particular HIV dynamic model is a reasonable approximation to the processes underlying HIV disease within a patient, longitudinal data from existing patients may be used to estimate the model parameters for single patients and thus to approximate the probability distribution describing variation in the population of patients using mathematical and statistical methods. This facilitates the ability to simulatean entire population of “virtual patients” resembling the true population of existing patients. Specifically, a virtual patient may be simulated by randomly generating from the probability distribution a set of model parameters corresponding to the patient. This may be carried out repeatedly to produce a large number of patients. As discussed in Section 3, the values of the model parameters for a virtual patient will dictate how, for example, that patient’s viral load and CD4 cell count (as well as other features) would evolve over time if that patient followed different treatment strategies.

Given the values of model parameters, control theory may be used to derive promising STI strategies. A particular strategy may then be “followed” by each virtual patient, yielding from the dynamic model under the strategy the values of viral load and CD4 cell count at any time for the patient under the strategy. The results from many such virtual patients may be combined to provide a hypothetical picture of how the population of HIV-infected patients would fare if all were to follow the particular STI treatment strategy under consideration.

As a simple example, Fig. 3 presents viral load profiles generated for 100 such virtual patients who “followed” the simple non-adaptive STI strategy of starting antiretroviral therapy at time 0, with a terminal (no subsequent re-initiation of therapy) interruption of therapy at 6 months. The profiles for all 100 patients were simulated from the same HIV dynamic model (that in Fig. 1); however, as noted above, each patient had a different setting of the model parameters (each randomly generated from the probability distribution). Similar to the behavior for the real patient in Fig. 2, continuous treatment until six months results in very low viral load; when treatment is withdrawn at six months, all patients exhibit a rebound in viral load that eventually stabilizes at a set-point for each. The figure shows clearly how, although they all underwent the identical treatment strategy, patients vary considerably in the extent and steepness of decline in viral load under therapy and the eventual set-point to which their viral load stabilizes, reflecting the different values of their underlying model parameters.

Fig 3.

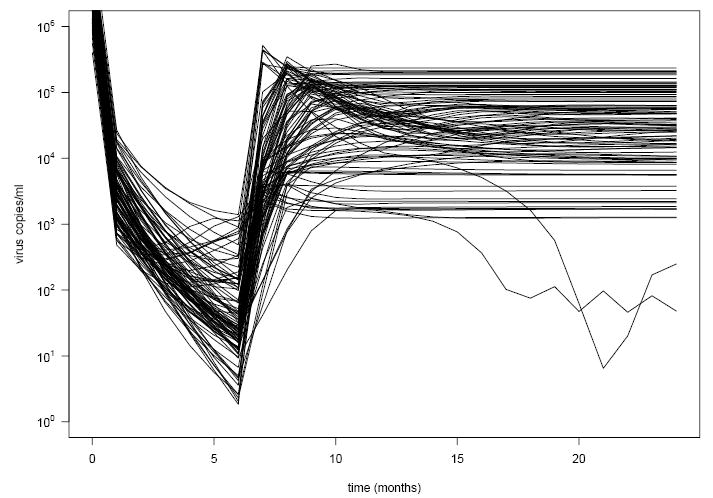
HIV RNA viral load time profiles for 100 “virtual patients,” each of whom followed the non-adaptive treatment strategy of initiating treatment at time 0 and then permanently interrupting treatment at 6 months. All profiles are based on the same HIV dynamic model, similar to that depicted in Fig. 1. To create a virtual patient, values of the model parameters were randomly generated from a probability distribution representing how the model parameters vary in the population of patients. The system of ordinary differential equations was then solved using these values of the model parameters under this treatment strategy to yield the time profile for that patient.

Such simulations have the potential to provide valuable insight into the relative benefits of different STI strategies based on, say, different objectives, different HIV dynamic models, and different assumptions about the population. As patients would naturally vary in their responses, the results from numerous “virtual patients” would provide important information on the extent to which the benefits of a strategy vary across patients as well. The facility to simulate “virtual patients” means that numerous strategies could be studied, albeit hypothetically, in real time without the commitment of actual patients or resources.

The foregoing procedure allows evaluation of STI strategies under “ideal” conditions where all patients show perfect adherence to the strategy under study over time and do not deviate it for any reason (e.g., behavioral issues, side effects). As noted in Section 2, some patients would fail to comply with the treatment steps dictated by a strategy at some point. Clearly, the use of STI strategies in substance abusing patients presents this challenge, and thus it would be critical to understand the implications of non-adherence on the success of a strategy and to design strategies that take prior non-compliance into account in decision rules for subsequent treatment steps. Because the model takes treatment as “input” at any time point, it would be possible to study by simulation the effects of different patterns of non-adherence on both individual “virtual” patients and on the entire population when some proportion of patients fails to comply with a strategy over time and to use this information to inform use of the strategies. If data on actual antiretroviral ingestion were available, probability modelsdescribing the likelihood of patients to show patterns of non-adherence over time could be developed and used in conjunction with the HIV dynamic model to design strategies that take non-adherence into account in the decision rules. In this regard, the models may be useful both for understanding the extent to which non-adherence can compromise outcomes among substance-abusing HIV-infected patients and for designing strategies that anticipate such non-adherence in these patients.

Of course, the advantages of using mathematical modeling and control theory in this way can only be confirmed through testing of the STI strategies so derived in actual patients. The authors of this article are part of a multidisciplinary team that is currently using these tools to develop STI strategies for the treatment of acutely-infected patients. The most promising of these will be studied in a clinical trial. An important component of the trial will be to collect detailed, frequent longitudinal data on not only HIV RNA load and CD4 cell counts but also on other quantities such as CTLs and results of viral “fitness” and viral genome sequencing assays. We will also attempt to collect accurate records on adherence to the strategy and on actual treatment use by participants. These rich data will contain critical information that will suggest improvements to the mathematical HIV dynamic model to render it more clinically relevant, e.g., by incorporating features that may explain drug resistance, and for developing models for adherence that may help inform modified strategies. The data may be used to estimate model parameters and probability distributions of model parameters in such improved HIV models that may be used to design improved STI strategies. These models will allow “virtual” and targeted study of issues such as the likelihood of developing drug resistance under different patterns of non-adherence.

5. Discussion

The goal of this paper is to promote the idea that, when available, mathematical models for biological mechanisms involved in disease, coupled with statistical methods for their application to data, may be a valuable tool for assisting in the design of adaptive treatment strategies. The development of STI regimens for HIV infection is a key setting where we believe that this approach is both feasible and has great potential. We envision that these mathematical and statistical tools could lead to an iterative approach to the clinical study of HIV infection and the development of STI treatment strategies through a series of small, proof-of-principle studies. This would proceed as follows. Existing data could be used to guide HIV dynamic model development and estimation of model parameters and their probability distribution. These could be combined with control theoretic methods to suggest new adaptive STI strategies that could then be evaluated by simulated application to the “virtual” target population. The most promising might be compared in small clinical trials, the data from which would both provide information on the benefits of the strategies studied and rich data to inform refinements to the model that may in turn be exploited to design new strategies. Strategies emerging from this sequence of trials would be worthy candidates for testing against conventional treatment regimens in large confirmatory trials. In a future report, we will recount the experience of our team implementing these ideas.

It is natural to question whether it is necessary to invoke complex mathematical models in order to undertake studies of how best to define the decision rules for adaptive STI strategies. We believe that HIV dynamic models, which can incorporate and exploit in a systematic way knowledge of biological mechanisms hold great promise, making contending with such complexity worthwhile. However, they are not the only approach to constructing STI strategies. As we noted in Section 1, trials to compare several strategies that both overlap and differ in the decision rules they involve may be designed according to principles such as those in Lavori and Dawson (2003) andMurphy (2005), and data from these studies may be used with empirical, statistical models to refine the decision rules, e.g., by incorporating more detailed information on tailoring variables, leading to a sequence of such trials. We believe that both approaches are worthwhile and complementary. A possible advantage of exploiting mathematical models is that they may focus attention quickly on specific aspects of the disease process that are important to acknowledge in decision rules; in fact, even if not used as the primary mechanism for constructing strategies, they may be a useful adjunct for designing such trials.

In many other disease and disorder settings, understanding of biological mechanisms is much less well developed. Indeed, a disorder like substance abuse involves very complex interactions among social, behavioral, biological and other phenomena, so that it is not possible to formulate a solely biological model capable of representing the underlying processes over time. However, empirically-based models, such as those described by Rivera et al. (2006), hold great promise in a similar spirit to inform the design of adaptive treatment strategies. In fact, in may be possible to combine such empirical and biological mathematical models in a single framework to suggest adaptive strategies for co-occurring disorders like HIV infection and substance abuse.

We hope that the ideas reviewed herein will inspire consideration of mathematical-statistical models as a potential tool for guiding the conception of adaptive treatment strategies in other settings where this is possible.