Abstract
We have developed a new Magnetic Resonance Electrical Impedance Tomography (MREIT) algorithm, RSM-MREIT algorithm, for noninvasive imaging of electrical conductivity distribution using only one component of magnetic flux density. The proposed RSM-MREIT algorithm uses Response Surface Methodology (RSM) algorithm for optimizing the conductivity distribution through minimizing the errors between the measured and calculated magnetic flux density. A series of computer simulations have been conducted to assess the performance of the proposed RSM-MREIT algorithm to estimate electrical conductivity values of the scalp, the skull, and the brain tissue, in a three-shell piece-wise homogeneous head model. Computer simulation studies were conducted in both a spherical and realistic geometry head model with a single variable (the brain-to-skull conductivity ratio) and three-variables (the conductivity of the brain, the skull, and the scalp). The relative error between the target and estimated head conductivity values were less than 12% for both the single-variable and three-variable simulations. These promising simulation results demonstrate the feasibility of the proposed RSM-MREIT algorithm in estimating electrical conductivity values in a piece-wise homogeneous head model of the human head, and suggest that the RSM-MREIT algorithm merits further investigation.
Keywords: Magnetic resonance electrical impedance tomography, Response Surface Methodology, current density imaging, electrical impedance tomography, conductivity, magnetic flux density
I. Introduction
Electrical impedance tomography (EIT) (Metheral et al., 1996; Saulnier et al., 2001) is an imaging modality that estimates the electrical properties at the interior of an object from measurements made on its surface. Typically, currents are injected into the object through electrodes placed on its surface, and the resulting voltages from other electrodes are measured. A reconstruction algorithm is then used to estimate the distribution of electrical conductivity and permittivity within the object, based on the knowledge of the applied current patterns and the measured surface voltages. In EIT, the current flow is determined by the impedance distribution within the object. Additionally, the problem is ill-posed, meaning that large changes in impedance at the interior of the object result in only small voltage changes on the surface of the object. Therefore, despite the substantial progress being made in the field, the spatial resolution of the conventional EIT is limited.
This problem is more serious when the object to be imaged is a human head. Accurate human head conductivity imaging is important for the diagnosis and therapy of brain disease. However, it is more challenging to apply EIT for head conductivity imaging due to the low conductivity skull, as compared with other organs.
Recently, Magnetic Resonance Electrical Impedance Tomography (MREIT) has been proposed to provide noninvasive high resolution imaging of electrical impedance within an object. MREIT is based upon the principles of Magnetic Resonance Current Density Imaging (MRCDI) technique (Joy et al., 1989; İder and Muftuler, 1997; Eyüboğlu et al., 1998) and EIT (Metheral et al., 1996; Saulnier et al., 2001). In MRCDI, a current is injected into the object through a pair of surface electrodes, and the induced magnetic flux density B inside the object is measured by means of MRI scanner. From Ampere’s law, the current density J inside the object can be obtained, . In MREIT, the conductivity distribution inside the object has then been estimated through the relationship between the electrical conductivity and the current density J, or the magnetic flux density B.
Early works on MREIT were based on minimization of the error between the current density measured by MRCDI and the current density as a function of the conductivity distribution (Zhang, 1992; Woo et al., 1994). A further extension on this idea was reported by Kwon et al (Kwon et al., 2002) to develop the “J-Substitution algorithm”, which uses (at least) two injected current patterns and a single set of voltage measurements to reconstruct the electrical impedance image. They also claim that at any point in the object, current density measured for the two current injection patterns should not be parallel. This requirement of at least two injected current patterns is proved later by Kim et al (Kim et al., 2002). Khang et al (Khang et al., 2002) have successfully applied the J-Substitution algorithm to data obtained from saline phantoms. Both methods in Woo et al (Woo et al., 1994) and Kwon et al (Kwon et al., 2002) are iterative. Another iterative method reported by Eyüboğlu et al (Eyüboğlu et al., 2001), is based on minimizing the error between measured and calculated current densities and peripheral voltages simultaneously. Recently Birgül et al (Birgül et al., 2003a) reported another iterative method in which a single voltage measurement and eight current injection patterns are used.
The MREIT algorithms discussed above all use internal current density estimate J to reconstruct conductivity distribution image. Using the current density to reconstruct conductivity images requires obtaining all three components of B(Bx, By, Bz). However, in MRCDI, only one component of magnetic flux density, which is parallel to the main magnetic field of MRI system, can be measured at one time (Joy et al., 1989). This means that we must rotate subject twice inside MRI in order to measure all three components of magnetic flux density. Such rotation presents a limitation for MREIT in clinical applications.
To overcome the rotation limitation when using MRCDI, MREIT algorithms using magnetic flux density measurement instead of current density measurement have been developed. Injecting at least two currents and measuring the corresponding images of Bz (we assume that the measured component of magnetic flux density is Bz) from multiple slices of the subject, it has been shown that conductivity images can be reconstructed using the harmonic Bz algorithm (Oh et al., 2003). This algorithm is based on the relation between ∇2 B and the conductivity distribution σ, thus requiring computation of ∇;2 B . Since twice differentiations of noisy images of Bz tend to amplify the noise, the harmonic Bz algorithm is sensitive to the measurement noise. Park et al (Park et al., 2004a, 2004b ) proposed the gradient Bz decomposition algorithm and the variational gradient Bz algorithm, using only one component of magnetic flux density measurement to reconstruct object conductivity image. In this algorithm Bz is differentiated only once, which represents a more robust feature against noise as compared with the harmonic Bz algorithm. However, in computer simulations, some undesirable side effects are observed which affect the accuracy of reconstructed images. Birgül et al (Birgül et al., 2003b) reported a MREIT phantom experiment using a two-dimensional (2D) reconstruction algorithm, which is based on the sensitivity matrix relation between conductivity and one component of magnetic flux distribution. İder and Onart (İder and Onart, 2004) reported a new MREIT algorithm using Bz to reconstruct 3D conductivity distribution of the object. In this method, the imaging problem is formulated as the solution of a non-linear matrix equation which is solved iteratively to reconstruct conductivity. Since this method needs to compute the inverse of a large matrix, substantial computational effort is needed in order to obtain high accuracy and spatial resolution in imaging electrical impedance. Recently, a RBF-MREIT algorithm was reported to estimate conductivity values of a 3D head using only one component of magnetic flux density Bz (Gao et al., 2005). In the RBF-MREIT algorithm, the radial basis function network and simplex method are used to reconstruct conductivity values in a 3D object. While promising simulation results have been obtained using the RBF MREIT algorithm, the training of artificial neural network is time consuming.
In the present study, we have developed a new conductivity imaging algorithm: RSM-MREIT algorithm, in which Response Surface Methodology (RSM) has been first incorporated in MREIT technique. The RSM-MREIT algorithm estimates conductivity values in a 3D object using only one component of measured magnetic flux density and therefore solves the aforementioned rotation problem effectively. The RSM-MREIT algorithm optimizes the conductivity distribution through minimizing the errors between the measured and calculated magnetic flux density.
In EEG/MEG source localization and imaging, piece-wise homogeneous head volume-conductor models, in which homogeneous and isotropic layers are used for the brain, skull and scalp are widely used (He, 2005), are widely adopted. In such head models, we only need to know the geometry and the ratio of the brain, the skull and the scalp. The detailed geometry information can be easily obtained through a MRI scanner (He et al., 1987). There are many different reports for the conductivities ratio, including 1:1/80:1 (Rush and Driscoll, 1969), 1:1/15:1 (Oostendorp et al., 2000), and 1/25:1 (Lai et al., 2005). Clearly, there is need to develop a conductivity imaging technique that can obtain the conductivity ratio accurately and noninvasively. In the present study, computer simulation studies were conducted to evaluate the performance of the proposed RSM-MREIT algorithm in estimating conductivity values of a 3-D human head.
II. Methods
Overview of RSM-MREIT
According to the approach of RSM-MREIT, a human subject lies in a MRI system and a low frequency current is injected into the subject’s head through a pair(s) of scalp electrodes. Then one component of induced magnetic flux density can be measured by the MRI system according to the principles of MRCDI technique. Using the information of the injected current and the measured component of magnetic flux density, the proposed RSM-MREIT technique can reconstruct the important conductivity values of compartments of the head.
One merit of RSM-MREIT is that a MRI system can not only measure induced magnetic flux density but also the geometry information of human head. This makes the proposed RSM-MREIT appealing since it can be easily incorporated in EEG/MEG source localization. Using the geometry information provided by MRI, we can define the regions of distinct conductivity (He, 2005). The main advantage of using these constraints is that the number of parameters to be estimated is reduced considerably. When, for instance, the head is assumed to consist of 3 regions of different conductivity, the scalp, the skull and the brain, only 3 parameters have to be estimated (He et al., 1999; He et al., 2002).
A bipolar rectangular current as described in Fig 1 (Joy et al., 1989) (I=4mA, Tc=50ms, f = 1/Tc = 20Hz) is injected into human head through a pair(s) of scalp electrodes. Then one component of the induced magnetic flux density can be measured by a MRI scanner. The direction of this component is parallel to the main magnetic field of MRI system. Theoretically speaking, the direction of measured component magnetic flux density can be arbitrary. In the present study, for the convenience of MRI measurement, we assume that the z-axis is parallel to the direction of the main magnetic field of MRI scanner and the measured magnetic flux density is . In the present simulation study, the “measured” is simulated as follows. Given the target value of human head conductivity distribution, through solving the forward problem, we can get the target magnetic flux density on the z direction. Gaussian white noise (GWN) is then added to the z-component of forward-calculated magnetic flux density to simulate noise-contaminated measurement.
Fig. 1.
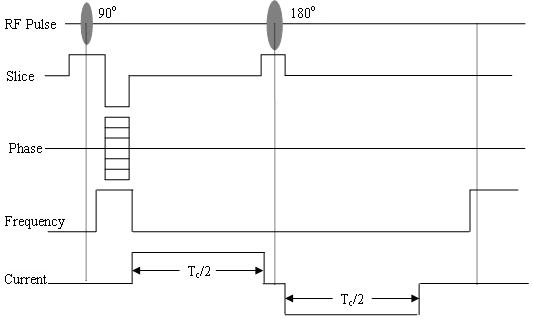
Rectangular bipolar current used in MREIT.
An initial guess of the conductivity values is made to start the inverse procedure (normally set at the middle of the preset region). Through solving the forward problem, every initial guess of conductivity distribution can get one Bz . An objective function that assesses the dissimilarity between the and Bz can be calculated. By minimizing this objective function, the optimal conductivity distribution can be estimated. The Response Surface Methodology (RSM) and Simplex method are used to solve the inverse problem.
Forward problem
Computation of the magnetic flux density distribution for a known conductivity distribution and boundary conditions is defined as the forward problem. Let Ω be a bounded and electrically conductive domain in R3 with boundary Γ. The electrical conductivity σ with the domain is assumed to be positive. The electrical potential distribution Φ obeys Laplace’s equation and Neumann boundary conditions as follows:
| (1) |
where n is the unit outward normal vector and Jinj is the injected current density which is non-zero only on the current injection electrodes. The current density distribution can then derived from the following equation
| (2) |
The magnetic flux density B, due to J, is given by the Biot-Savart integral
| (3) |
where r and r′ are field and source vectors defined in Ω, μ0 is the magnetic permeability of the free space.
Analytical solutions for complex conductivity distributions are not available for the Neumann boundary value problem (NBVP) given by equation (1). In the present study, the Finite Element Method (FEM) (Silvester and Ferrari, 1996) is used to solve the above problem and the conductivity is assumed to be constant within each element. In the calculation of magnetic flux density, in order to avoid the singularity where r = r′, we treat B(r) as node variables and use the value of J (r′) at the center of each finite element in equation (5) (Lee et al., 2003).
In order to evaluate the numerical accuracy of the FEM procedure, comparison with analytical solutions in a simple geometry object was made. For uniform conductivity distribution in a cylinder with 1cm radius and 10cm high, a current I is injected into this cylinder through two surface electrodes attached on the two circular surface of the cylinder. One magnetic flux density is analytically calculated and another is numerically calculated with the FEM procedure. The correlation coefficient between the two magnetic flux densities is 0.9668 and the relative error between them is 8.03%. This comparison result indicates the suitability and accuracy of the FEM procedure to solve the potential field forward problem.
Inverse problem
Given “measured” and injection current, the calculation of inner conductivity distribution is called the inverse problem or the image reconstruction of MREIT. In the present study, we used RSM to solve the inverse problem.
As mentioned above, we can construct a function that represents the dissimilarity between Bz and as function of conductivity distribution. The true relationship between the conductivity and the dissimilarity is complex and nonlinear. We constructed this function from sampled input-output pairs to represent the true relationship between the input and the output of the system, as illustrated in figure 2. In the present study, the conductivities of each compartment of human head are set to be the input parameters. e.g. If the human head is assumed to consist of 3 regions of different conductivities, the scalp, skull and brain, a three components vector σ = [σscalp, σskull, σbrain] can be considered as the input parameter. The objective function that reflects the dissimilarity between the simulated measurement and calculated Bz is set to be the output of the system. The objective function is defined as:
Fig. 2.
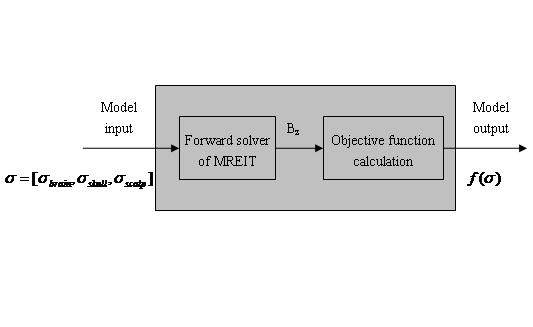
Schematic diagram of the black-box optimal problem for head conductivity reconstruction.
| (4) |
where and are the correlation coefficient (CC) and relative error (RE) between Bz and as described in (5) and (6):
| (5) |
| (6) |
Bz is the z-component of the magnetic flux density inside the head when the conductivity distribution equals to σ = [σscalp, σskull, σbrain]. Clearly, the conductivity parameter can be estimated when the objective function f(σ) is minimized.
For the function construction and function optimization, we used the Response Surface Methodology (RSM) algorithm. RSM is a collection of statistical and mathematical techniques useful for optimizing simulation models (Myers and Montgomery, 1995). In RSM, the parameters of the simulation model are usually called factors, whereas the output is called the response of the simulation model.
This algorithm is based on the approximation of the objective function by a low order polynomial on a small sub-region of the domain. The coefficients of the polynomial are estimated by Ordinary Least Squares (OLS) applied to a number of sampling input-output pairs of the simulation model in the small sub-region of the domain. To this end, the objective function is evaluated in an arrangement of points referred to as a simulation design. Based on the fitted polynomial, the local best point is derived, which is used as a current estimator of the optimum and as the center point of a new region of interest (Fu, 1994), where again the objective function is approximated by a low order polynomial.
Our RSM-MREIT algorithm comprises two phases. In the first phase, the response surface function is approximated by first-order polynomials, until a polynomial is fitted that shows significant lack-of-fit, or until there is no sign of improved response anymore. In the second phase, the objective function is approximated by a second-order polynomial (Fu, 1994) and the final optimum point is derived. The framework of our RSM algorithm is depicted in Figure 3.
Fig. 3.
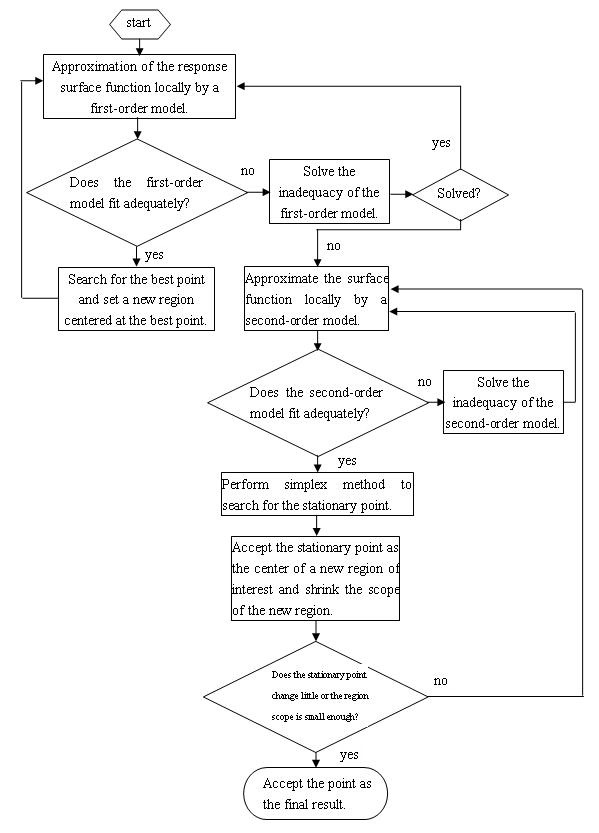
Schematic diagram of response surface methodology.
In each iteration n , n ≥ 1, we consider a small subregion of the domain, which is called the region of interest and is given by a k-dimensional rectangle
| (7) |
This region can be described by a center point
| (8) |
and step sizes
| (9) |
The first-order and second-order model used in the present study can be described by Eqs (10) and (11):
| (10) |
| (11) |
In order to increase the numerical accuracy in estimating the regression coefficients, we coded the factors into −1 and 1 (Youn and Choi, 2004), which gave the coded variables xi, i = 1,...,k :
| (12) |
and the coded first-order and second-order models are:
| (13) |
| (14) |
In the searching of the optimal point, we used the Simplex Method [27].
Simulation protocol
In the present simulation study, two head models were used to conduct the simulations. One is a three-spheres head model and another is a 3-layer realistic-geometry head model. The three-sphere concentric head model is commonly used in neural source localization, in which the brain, skull and scalp were modeled as concentric spheres with isotropic nature (for review, see (He, 2004, 2005). The conductivity ratio between the scalp, skull and brain with the brain is set to be 1, 1/25, and 1, respectively (Lai et al., 2005). The radii for the 3 spheres are set to 8.7, 9.2, and 10 cm, respectively (He et al., 2001). Figure 4 shows the finite element mesh used for the simulations. It includes 20,255 nodes and 14,380 triangular elements.
Fig. 4.

The finite element mesh of the three-spheres head model.
The realistic-geometry head model used in the present simulation study was constructed from MRI data of a human subject, and has three compartments - the brain, skull and scalp. The conductivity values for the scalp, skull and brain are set to be 1, 1/25, and 1, respectively (Lai et al., 2005). For the sake of simplicity, we normalized all conductivity values with reference to the brain conductivity. Using the images of the inner and outer contour of the skull and the outer contour of the head, the boundary element model of the head is constructed (Fig. 5). Then the finite element model of the head can be constructed through finite element meshing. Figure 6 depicts the finite element model of the realistic-geometry head model, which contains 57,041 quadratic tetrahedral elements and 78,893 nodes, respectively.
Fig. 5.
The realistic-geometry boundary element model for three compartments human head.
Fig. 6.
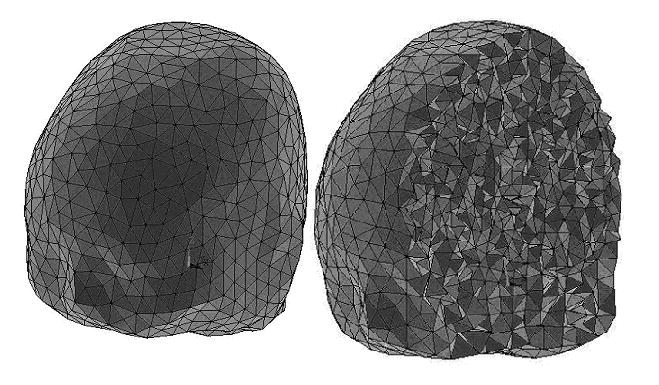
The realistic-geometry finite element head model.
As mentioned above, a bipolar rectangular current (see(Joy et al., 1989), Fig 1]; I=4mA, Tc=50ms, f = 1/Tc=20 Hz) was applied to the head model through a pair of electrodes (1cm2 each) (Joy et al., 1999). In order to test whether the current injections will influent the estimation results and how it does, we used several current injections for the two head models. For the spherical head model, we used three current injections, as depicted in figure 7. In the electrode configuration EL_A1, the angle between the two electrodes is 90° and the electrode configuration EL-A2, the angle is 30°. For the three configurations of current injection, the is depicted in figure 8. For the realistic-geometry head model, simulations were conducted using the two electrode configurations EL_O and EL_A1. For EL_O, one electrode is placed on the forehead and the other is on the occipital region of the scalp. For EL_A1, two electrodes are placed on the vertex of the head adjacently. The distributions are shown in figure 9.
Fig. 7.
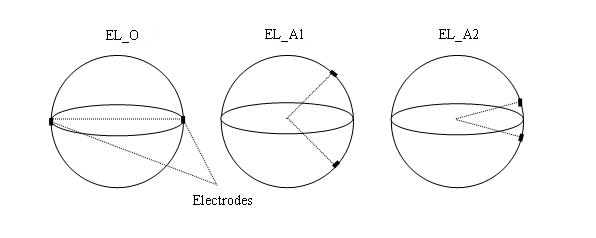
Configurations of current injections for the spherical head model.
Fig. 8.

An example of the calculated Bz for the three current injections in the spherical head model.
Fig. 9.
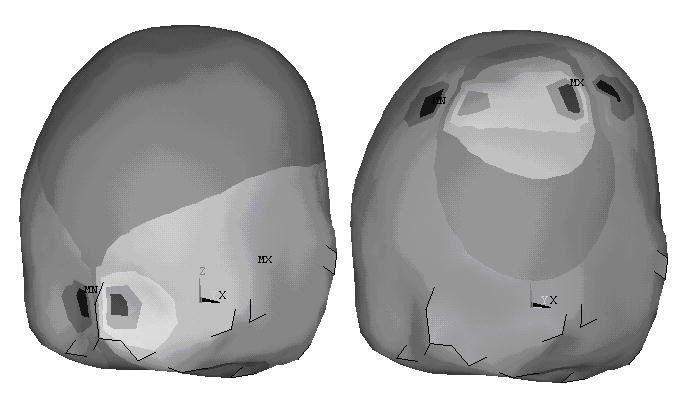
An example of the calculated Bz for the two current injections in the realistic-geometry head model.
Two numerical simulations were conducted on the two head models: single-variable simulation and three-variable simulation. In the single-variable simulation, only the skull-to-brain conductivity ratio is unknown (Lai et al., 2005). The input parameter was a scalar. The domain was set to be [1,1/ 50]. In the three-variables simulation, all the three compartments’ conductivities are unknown and the input parameter is a vector σ = [σbrain, σskull, σscalp]. The domain can be described by a three-dimensional rectangle, [10,1/10]×[1,1/ 50]×[10,1/10].
In order to test the effect of noise to the proposed algorithm, various levels of GWN were added to the target magnetic flux density to simulate the noise-contaminated “measured” . According to the noise analysis of CDI, the standard deviation of noise sB in the “measured” Bz is given by (Scott et al., 1992)
| (15) |
where γ=26.75×107radT−1s−1 is the gyromagnetic ratio of the hydrogen, Tc is the duration of injection current pulse, and SNR is the signal-to-noise ratio of the MR magnitude image. With Tc=50ms, when the SNR=80, 60, 40, 20 and 15, we obtain sB=2.9356×10−9T, 3.9142×10−9T, 5.8713×10−9T, 1.1742×10−8T, and 1.5657×10−8T, respectively.
In order to assess the clinical applicability of the present technique, the effects of electrode position uncertainty were also evaluated. GWN of 5mm was added to the current injection electrode positions to simulate the electrode position uncertainty in this phase of the simulation study.
III. Results
Simulation results in the three-spheres head model
Table 1 shows the estimation results for single-variable simulation, in which the unknown is the brain-to-skull conductivity ratio. When the SNR of MR magnitude image is 15, the estimated brain-to-skull conductivity ratio is 26.7290±1.8318 and the RE between the target and estimated skull conductivity is 0.0856±0.0407. The definition of RE is the same as Eq (6) except that Bz should be replaced by σ. These results suggest that the proposed algorithms can well estimate the brain-to-skull conductivity ratio.
Table 1.
Single-variable simulation results in the three-sphere head model.
| SNR | Estimated conductivity ratio | Relative Error |
|---|---|---|
| Infinite | 25.0002±0.0000 | 0.0005±0.0000 |
| 80 | 25.0133±0.5764 | 0.0180±0.0147 |
| 60 | 24.9972±0.6758 | 0.0232±0.0143 |
| 40 | 25.0698±1.3618 | 0.0435±0.0355 |
| 20 | 25.8506±1.9717 | 0.0701±0.0568 |
| 15 | 26.7290±1.8318 | 0.0856±0.0407 |
The performance of the RSM-MREIT algorithm was also tested by the estimation of three compartment conductivities of the human head - the brain, skull and scalp. The factor is a three component vector σ = [σbrain, σskull, σscalp]. This situation is more complex than the single-variable simulation due to the increased number of unknowns to be estimated. The estimation results for the three-variable simulation are depicted in figure 10. In figure 10 we can see that the biggest RE occurs at the brain compartment (when the SNR is 15, the RE for the brain is 10.05%.) and with the increase of noise level, the RE increased monotonously. This phenomenon suggests that the estimation of brain’s conductivity is more challenging because the brain is located deepest in the head.
Fig. 10.
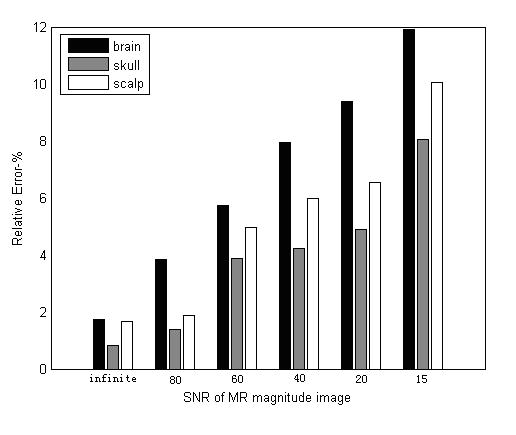
Relative error (RE) of conductivity estimation for all the three compartments of the three-spheres head model.
Simulation results in the realistic geometry head model
Both single-variable and three-variable simulations were conducted in the realistic-geometry head model. Table 2 lists the RE of the single-variable and three-variable simulation results for the realistic-geometry head model. In the single-variable simulation, the maximum RE is 0.0748±0.0095, and in the three-variable simulation, the maximum RE is 0.0878±0.0879. These simulation results suggest that the RSM-MREIT algorithm work well in the realistic-geometry head model.
Table 2.
Single variable and three variables simulation results for realistic-geometry head model
| SNR | RE | |
|---|---|---|
| Single variable simulation | Three variables simulation | |
| Infinite | 0.0008±0.0000 | 0.0412±0.0000 |
| 80 | 0.0181±0.0112 | 0.0508±0.0233 |
| 60 | 0.0263±0.0014 | 0.0536±0.0326 |
| 40 | 0.0384±0.0026 | 0.0744±0.0363 |
| 20 | 0.0684±0.0033 | 0.0829±0.0738 |
| 15 | 0.0748±0.0095 | 0.0878±0.0879 |
Influence of current injection
Fig. 11 depicts the estimation results for the three situations of current injection in the 3-spheres head model. The RE for the configuration EL_A2 is the biggest and the RE for the configuration EL_O is the smallest. This may be because when the current is injected oppositely, the amount of currents entering the brain compartment is the biggest. Figure 12 depicts the RE for two current injection configurations in the realistic-geometry head model. Note that similar results were obtained as in the spherical head model, shown in figure 11.
Fig. 11.
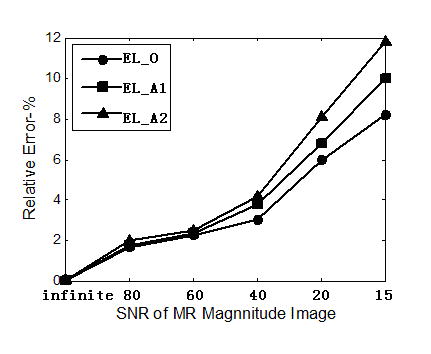
RE of conductivity estimation for the three current injections of the three-spheres head model.
Fig. 12.
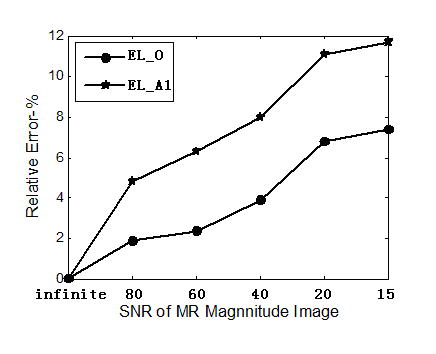
RE of conductivity estimation for the two current injections of the realistic-geometry head model.
Influence of number of current injections
Figure 13 depicts the estimation results for different numbers of current injections for the 3-spheres head model with the single-variable simulation protocol. The one, two and three current injections used one, two and three pairs of electrodes placed oppositely in the x-axis alone, the x-axis and y-axis, as well as the x-axis, y-axis, and z-axis. Note that the RE decreased when the number of current injections increased. However, this simulation suggests that such improvement is not significant – RE=9% for one current injection vs. RE=6% for two current injections.
Fig. 13.
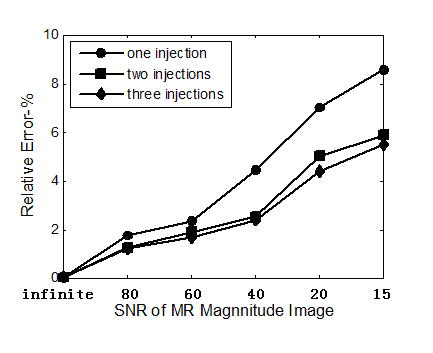
Influence of current injection number on the conductivity estimation for the spherical head model.
Effects of Electrode Position Uncertainties
In order to evaluate the effects of electrode position uncertainty on the accuracy of the present algorithm, GWN of 5mm was added to the positions of current injection electrodes when conducting the single-variable simulations on the three-sphere head model. When the SNR of MR magnitude image is 15, the RE is 0.0869±0.0468. This simulation result suggests that the present MREIT algorithm is robust against the electrode position uncertainty. Considering that MRI measurements will be made within the scanner, 5mm noise level is considered to be reasonable.
IV. Discussion
In the present study, we have developed a new electrical impedance imaging algorithm, RSM-MREIT algorithm. This new algorithm uses only one component of measured magnetic flux density to reconstruct subject conductivity image and solves the rotating problem existing in MREIT. The merits of the proposed RSM-MREIT algorithm as applied to estimation of conductivity values of head compartments are demonstrated in two computer simulations using the three-spheres head model and the three-shell realistic-geometry head model.
In the single-variable simulations, the brain-to-skull conductivity ratio is considered as the unknown. The accurate estimation of the brain-to-skull conductivity ratio using a noninvasive means is of importance for improving the accuracy of brain source imaging, since a large variation among reported data in the literature exist (Lai et al., 2005; Rush and Driscoll, 1969; Oostendorp et al., 2000). When the SNR of added GWN is 15, the RE between the target and estimated brain-to-skull conductivity ratio is 0.0856±0.0407 for the 3-spheres head model and 0.0748±0.0095 for the realistic-geometry head model, respectively. Compared with the variation in the reported skull-to-brain conductivity ratio (Lai et al., 2005; Rush and Driscoll, 1969; Oostendorp et al., 2000) which range from 1/80 to 1/15, the present estimation of this important parameter is quite robust with RE being less than 9%. This result suggests that the proposed RSM-MREIT can provide a good estimation of the brain-to-skull conductivity ratio for the 3-shell head model which is widely used in the field of brain source imaging and localization (He, 2004, 2005).
In the three-variable simulations, all the three compartments’ conductivities are unknown. The present simulation results gave REs less than 12% for both the 3-spheres head model and realistic-geometry head model, while the realistic-geometry head model showed smaller estimation error. Considering the variation of the conductivity values of the brain, skull and scalp (Lai et al., 2005; Rush and Driscoll, 1969; Oostendorp et al., 2000), this simulation result suggests that the proposed method may be used to estimate the conductivity values of the brain, skull and scalp in the popular 3-shell head models, which are widely used in brain source imaging and localization (He, 2004, 2005).
It can be noticed that with the increase of the number of unknowns, the estimation error increased as well. This phenomenon hints that the proposed RSM-MREIT may not be suitable to reconstruct continuous distribution of head conductivity. Development of other MREIT algorithms may be needed in order to deal with the continuous conductivity estimation.
The influence of current injection on the estimation results are assessed on both the head models. For the 3-spheres head model, three current injections, one opposite and two adjacent, were used. For the realistic-geometry head model, two current injections, one opposite and one adjacent, were used. The simulation results on both head models indicate that the opposite configuration of current injection gives better results. This may be because that opposite injection can enable much more currents entering into the brain.
It is shown by computer simulation that the present RSM-MREIT only needs one current injection. In order to make clear that whether more current injections will improve the estimation results, two and three currents were injected on both the head models. The simulation results indicate that more current injection can improve the estimation results but the degree of improvement is not significant. Compared with other algorithms reported in the literature (Kwon et al., 2002) which require two current injections, the one-current-injection feature seems to be one of the unique characteristics of the present RSM-MREIT algorithm.
In the present simulation study, a current of 4mA was injected into the human head. A current of 5mA is thought to be the upper safe limit for human being (IEC Criteria – see reference list) and the upper limit of injection current is different for different human tissue. While the present 4mA current is within the safety limit, further efforts shall be needed to reduce the magnitude of injecting current by means of using higher field MRI scanner (thus higher SNR), developing denoising techniques, and using bigger voxels.
Previous MREIT algorithms which use only Bz data to reconstruct conductivity images, such as the harmonic Bz algorithm (Oh et al., 2003), the variational gradient Bz algorithm (Park et al., 2004b), the gradient Bz decomposition algorithm (Park et al., 2004a). are all based on the fundamental equations of ∇·B = 0 and ∇× B = μ0 J. A drawback of such algorithm is that they are sensitive to noise. Also reported are the sensitivity matrix algorithm (Birgül et al., 2003) and the algebraic reconstruction algorithm (İder and Onart, 2004), in which only Bz data are used to reconstruct conductivity images. The sensitivity matrix algorithm uses sensitivity matrix to reconstruct the relative conductivity distribution images, then it is scaled using the peripheral voltage measurements to obtain the absolute conductivity distribution. In the algebraic algorithm, the imaging problem is formulated as the solution of a non-linear matrix equation which is solved iteratively to reconstruct conductivity distribution. Both algorithms transform the inverse problem of image reconstruction into the solution of algebraic equation. The accuracy and spatial resolution of the reconstructed image depends on the size of voxel used. While the accuracy can be improved by increasing the number of element (or decreasing the size of voxel), the computational loads are also increased accordingly.
The proposed RSM-MREIT algorithm treats the relation between the conductivity σ and the magnetic flux density Bz as a “black-box”, thus avoiding the complex mathematical analysis. The proposed algorithm uses low order polynomials to construct the function relationship between the conductivity σ and magnetic flux density Bz, then uses the Simplex method to find the optimal conductivity.
Note that a constraint is needed in order to obtain the absolute conductivity values. In the present study, we searched the solution in a preset region, which is known from prior research, which includes the true conductivity value. This a priori information serves as a constraint and allowed us to obtain the absolute conductivity values.
In summary, we have developed a new 3-D conductivity reconstruction algorithm - RSM-MREIT algorithm. This proposed algorithm uses only one component of the induced magnetic flux density to reconstruct subject conductivity distribution without rotating subject inside the MRI scanner. Moreover, this algorithm does not need any electrode voltage measurement, which is important in experimental and clinical applications. The feasibility of estimating conductivity values of the brain, skull and scalp using the proposed algorithm has been tested by computer simulation on both a three-concentric-spheres head model and a realistic-geometry piecewise homogeneous head model. The promising simulation results demonstrate that the present algorithm can reconstruct important conductivity values of the human head with good accuracy, and is robust against noise. The present study suggests the RSM-MREIT technique merits further investigations and may become an important alternative for imaging electrical impedance of human body.
Acknowledgments
The authors are grateful to Jin Li and Yuan Yao for technical assistance. This work was supported in part by NSF BES-0218736, NSF BES-0411898, and NIH R01 EB00178.
References
- Birgül Ö, Eyüboglu BM, İder YZ. Current constrained voltage scaled reconstruction (CCVSR) algorithm for MR-EIT and its performance with different probing current patterns. Phys Med Biol. 2003a;48:653–671. doi: 10.1088/0031-9155/48/5/307. [DOI] [PubMed] [Google Scholar]
- Birgül Ö, Eyüboglu BM, İder YZ. Experimental results for 2D magnetic resonance electrical impedance tomography (MR-EIT) using magnetic flux density in one direction. Phys Med Biol. 2003b;48:3485–3504. doi: 10.1088/0031-9155/48/21/003. [DOI] [PubMed] [Google Scholar]
- Eyüboğlu BM, Birgül Ö, İder YZ. Dual modality system for high-resolution true conductivity imaging. XIth Int Conf. Electrical Bioimpedance (ICEBI); Oslo, Norway. 2001. pp. 409–413. [Google Scholar]
- Eyüboğlu BM, Reddy R, Leigh JS. Imaging electrical current density using nuclear magnetic resonance. ELEKTRIK. 1998;6:201–214. [Google Scholar]
- Fu MC. Optimization via simulation: a review. Annals of Operations Research. 1994;53:199–247. [Google Scholar]
- Gao N, Zhu SA, He B. Estimation of electrical conductivity distribution within the human head from magnetic flux density measurement. Phys Med Biol. 2005;50:2675–2687. doi: 10.1088/0031-9155/50/11/016. [DOI] [PubMed] [Google Scholar]
- He B, editor. Modeling and Imaging of Bioelectrical Activity: Principles and Applications. Kluwer Academic/Plenum Publishers; 2004. [Google Scholar]
- He B, editor. Neural Engineering. Kluwer Academic/Plenum Publishers; 2005. [Google Scholar]
- He B, Lian J, Spencer KM, Dien J, Donchin E. A Cortical Potential Imaging Analysis of the P300 and Novelty P3 Components. Human Brain Mapping. 2001;12:120–130. doi: 10.1002/1097-0193(200102)12:2<120::AID-HBM1009>3.0.CO;2-V. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electric dipole tracing in the brain by means of the boundary element method and its solution accuracy IEEE Trans. Biomed Eng. 1987;34:406–414. doi: 10.1109/tbme.1987.326056. [DOI] [PubMed] [Google Scholar]
- He B, Wang Y, Wu D. Estimating Cortical Potentials from Scalp EEG’s in a Realistically Shaped Inhomogeneous Head Model By Means of the Boundary Element Method. IEEE Transactions on Biomedical Engineering. 1999;46:1264–1268. doi: 10.1109/10.790505. [DOI] [PubMed] [Google Scholar]
- He B, Zhang Z, Lian J, Sasaki H, Wu S, Towle VL. Boundary Element Method Based Cortical Potential Imaging of Somatosensory Evoked Potentials Using Subjects' Magnetic Resonance Images. NeuroImage. 2002;16:564–576. doi: 10.1006/nimg.2002.1127. [DOI] [PubMed] [Google Scholar]
- IEC Criteria. http://europa.eu.int/comm/enterprise/newapproach/standardization/harmstds/reflist.html.
- İder YZ, Muftuler LT. Measurement of AC Magnetic Field Distribution Using Magnetic Resonance Imaging. IEEE Transactions on Medical Imaging. 1997;16(5):617–622. doi: 10.1109/42.640752. [DOI] [PubMed] [Google Scholar]
- İder YZ, Onart S. Algebraic reconstruction for 3D magnetic resonance-electrical impedance tomography (MREIT) using one component of magnetic flux density. Physiol Meas. 2004;25:281–294. doi: 10.1088/0967-3334/25/1/032. [DOI] [PubMed] [Google Scholar]
- Joy MLG, Lebedev VP, Gati JS. Imaging of Current Density and Current Pathways in Rabbit Brain During Transcranial Electrostimulation. IEEE Transactions on Biomedical Engineering. 1999;46(9):1139–1149. doi: 10.1109/10.784146. [DOI] [PubMed] [Google Scholar]
- Joy M, Scott G, Henkelman M. In vivo detection of applied electric currents by magnetic resonance imaging. Magnetic Resonance Imaging. 1989;7(1):89–94. doi: 10.1016/0730-725x(89)90328-7. [DOI] [PubMed] [Google Scholar]
- Khang HS, Lee BI, Oh SH, Woo EJ, Lee SY, Cho MH, Kwon O, Yoon JR, Seo JK. J-Substitution algorithm in magnetic resonance electrical impedance tomography (MREIT) phantom experiments for static resistivity images. IEEE Trans Med Imaging. 2002;21:695–702. doi: 10.1109/TMI.2002.800604. [DOI] [PubMed] [Google Scholar]
- Kim S, Kwon O, Seo JK, Yoon JR. On a nonlinear partial differential equation arising in magnetic resonance electrical impedance tomography. SIAM J Math Anal. 2002;34:511–526. [Google Scholar]
- Kwon O, Woo EJ, Yoon JR, Seo JK. Magnetic Resonance Electrical Impedance Tomography (MREIT): Simulation Study of J-Substitution Algorithm. IEEE Trans Biomed Eng. 2002;49(2):160–167. doi: 10.1109/10.979355. [DOI] [PubMed] [Google Scholar]
- Lai Y, van Drongelen W, Ding L, Hecox KE, Towle VL, Frim DM, He B. In vivo human skull conductivity estimation from simultaneous extra- and intra-cranial electrical potential recordings. Clinical Neurophysiology. 2005;116(2):456–65. doi: 10.1016/j.clinph.2004.08.017. [DOI] [PubMed] [Google Scholar]
- Lee BI, Oh SH, Woo EJ, Lee SY, Cho MH, Kwon O, Seo JK, Lee JY, Baek WS. Three-Dimensional Forward solver and its performance analysis in magnetic resonance electrical impedance tomography(MREIT) using recessed electrodes. Phys Med Biol. 2003;48:1971–1986. doi: 10.1088/0031-9155/48/13/309. [DOI] [PubMed] [Google Scholar]
- Metheral P, Barber DC, Smallwood RH, Brown BH. Three dimensional electrical impedance tomography. Nature. 1996;380:509–512. doi: 10.1038/380509a0. [DOI] [PubMed] [Google Scholar]
- Myers RH, Montgomery DC. Response surface methodology: process and product optimization using designed experiments. Newyork: John Wiley & Sons; 1995. [Google Scholar]
- Oh SH, Lee BI, Woo EJ, Lee SY, Cho MH, Kwon O, Seo JK. Conductivity and current density image reconstruction using harmonic Bz algorithm in magnetic resonance electrical impedance tomography. Phys Med Biol. 2003;48:3101–3116. doi: 10.1088/0031-9155/48/19/001. [DOI] [PubMed] [Google Scholar]
- Oostendorp TF, Delbeke J, Stegeman DF. The Conductivity of the Human Skull: Results of In Vivo and In Vitro Measurements. IEEE Trans Biomed Eng. 2000;47(11):1487–1492. doi: 10.1109/TBME.2000.880100. [DOI] [PubMed] [Google Scholar]
- Park C, Kwon O, Woo EJ, Seo JK. Electrical Conductivity Imaging Using GradientBz Decomposition Algorithm in magnetic Resonance Electrical Impedance Tomography (MREIT) IEEE Trans Med Imag. 2004a;23:388–394. doi: 10.1109/tmi.2004.824228. [DOI] [PubMed] [Google Scholar]
- Park C, Park EJ, Woo EJ, Kwon O, Seo JK. Static conductivity imaging using variational gradient Bz algorithm in magnetic resonance electrical impedance tomography. Physiol Meas. 2004b;25:257–269. doi: 10.1088/0967-3334/25/1/030. [DOI] [PubMed] [Google Scholar]
- Rush S, Driscoll DA. EEG electrode sensitivity – an application of reciprocity. IEEE Trans Biomed Eng. 1969;16:15–22. doi: 10.1109/tbme.1969.4502598. [DOI] [PubMed] [Google Scholar]
- Saulnier GJ, Blue RS, Newelll JC, Isaacson D, Edic PM. Electrical Impedance Tomography. IEEE Signal Processing Magazine. 2001:31–43. [Google Scholar]
- Scott GC, Joy ML, Armstrong RL, Henkelman RM. Sensitivity of Magnetic-Resonance Current-Density Imaging. Journal of Magnetic Resonance. 1992;97:235–254. [Google Scholar]
- Silvester PP, Ferrari RL. Finite Element for Electrical Engineers. Cambridge: Cambride University Press; 1996. [Google Scholar]
- Walters FH, Parker LR, Morgan SL, Deming SN. Sequential Simplex Optimization. CRC Press; Boca Raton, Florida: 1991. [Google Scholar]
- Woo EJ, Lee SY, Mun CW. Impedance tomography using internal current density distribution measured by nuclear magnetic resonance. SPIE. 1994;2299:377–385. [Google Scholar]
- Youn BD, Choi KK. A new response surface methodology for reliability-based design optimization. Computer and Structures. 2004;82:241–256. [Google Scholar]
- Zhang N. MSc Thesis University of Toronto. 1992. Electrical impedance tomography based on current density imaging. [Google Scholar]


