A Matched Crossover Design for Clinical Trials

Abstract

Two design principles are used frequently in clinical trials: 1) A subject is "matched" or "paired" with a similar subject to reduce the chance that other variables obscure the primary comparison of interest. 2) A subject serves as his/her own control by "crossing over" from one treatment to another during the course of an experiment. There are situations in which it may be advantageous to use the two design principles –crossing over and matching –simultaneously. That is, it may be advantageous to conduct a "paired crossover design," in which each subject, while paired with a similar subject, crosses over and receives each experimental treatment. In this paper, we describe two clinical trials conducted by the National Heart, Lung and Blood Institute’s Asthma Clinical Research Network that used a paired 2 × 2 crossover design. The Beta Adrenergic Response by GEnotype (BARGE) Study compared the effects of regular use of inhaled albuterol on mildly asthmatic patients with different genotypes at the 16th position of the beta-agonist receptor gene. The Smoking Modulates Outcomes of Glucocorticoid (SMOG) Therapy in Asthma Study evaluated the hypothesis that smoking reduces the response to inhaled corticosteroids. For such paired crossover designs, the primary parameter of interest is typically the treatment-by-pairing interaction term. In evaluating the relative efficiency of the paired 2 × 2 crossover design to two independent crossover designs with respect to this interaction term, we show that the paired 2 × 2 crossover design is more efficient if the correlations between the paired members on the same treatments are greater than their correlations on different treatments. This condition should hold in most circumstances, and therefore the paired crossover design deserves serious consideration for any clinical trial in which the crossing over and matching of subjects is deemed simultaneously beneficial.

Introduction

It is widely accepted that randomization is an effective method of reducing any bias that might occur when assigning subjects to treatments in comparative clinical trials. When appropriately implemented, randomization guarantees that the assignment of treatments to subjects will be based on chance alone rather than on the hopes of the investigator or the prognosis of the subjects. It is for this reason that randomization is the preferred method of assigning treatments when clinical trials concern comparing two or more interventions.

Unfortunately, randomization is not always a practical nor ethical method of assigning a subject to a comparison group. For obvious reasons, for example, we cannot assign subjects to smoke or not smoke in an attempt to assess the effect of smoking on lung function. In such situations, we can rely instead on another widely accepted method of reducing bias, namely the method of matching.

The method of matching involves pairing a subject from one comparison group with a subject having the same values of the matching variable(s) in the other comparison group(s). The matching variables are chosen for their potential association with the primary response variable. For example, consider the aforementioned situation in which one wants to compare the lung function of smokers and non-smokers. Another variable that may be associated with lung function is amount of weekly aerobic exercise. Therefore, one might consider matching a smoker who exercises five times a week with a non-smoker who exercises five times a week. Similarly, a smoker who exercises only once a week might be matched with a non-smoker who exercises only once a week. After matching, we would expect the groups to be similar in all relevant aspects except with respect to the comparison of interest, i.e., smoking versus non-smoking.

Matching is typically used in comparative observational studies, in which subjects cannot be randomly allocated to the desired comparison groups. For these studies, subjects are either self-selected into identifiable groups (e.g., smokers and non-smokers, seat-belt wearers and not) or subjects have fixed, pre-determined characteristics that dictate their group membership (e.g., males and females, old and young). The primary advantage of matching is that biases due to baseline group differences are minimized, thereby reducing the variability, and increasing the precision, of the group comparisons. Experiments employing the method of matching are called matched pair designs [1].

A crossover design [2,3,4] is a design that uses a special kind of matching, namely a subject serves as his or her own match. The simplest crossover design, which involves comparing treatments A and B, is known as “the AB:BA crossover” or “the 2 × 2 crossover.” For this design, subjects are randomized to one of the two treatment sequences –either AB or BA. Subjects randomized to the AB sequence receive treatment A first, then “cross over” and receive treatment B, while subjects randomized to the BA sequence receive treatment B first, then “cross over” and receive treatment A. A treatment-free “wash out” period is typically inserted between the two active treatment periods when the treatments are pharmaceutical products. Because subjects cross over and thereby serve as their own match, the comparison between treatments A and B is typically purer in that differences between subjects are removed from the comparison. That is, crossover designs typically lead to more efficient treatment comparisons, since treatments are compared “within subjects.”

There are situations in which it may be advantageous to use all three design principles –randomization, matching, and crossing over –simultaneously. That is, it may be advantageous to conduct a “paired crossover design,” in which each subject, while paired with a similar subject, is randomized to an experimental treatment and then crossed over to receive a second experimental treatment. The matching is incorporated into the randomized crossover trial for the sole purpose of increasing the precision of estimators. Our review of the literature failed to find any instances in which a paired crossover design was used. However, the National Heart, Lung and Blood Institute’s Asthma Clinical Research Network [5] has since completed two clinical trials that used the design, is using it in an ongoing third trial, and is considering using the design for some of its subsequent trials. In this paper, we present the design, cite the two examples of its use, and discuss its relative efficiency.

Asthma Clinical Research Network

The Asthma Clinical Research Network (ACRN), of which one of the authors (V. Chinchilli) is a member, was established in 1993 by the National Heart, Lung and Blood Institute (NHLBI). The primary mission of this multicenter research consortium is to conduct well-designed clinical trials for rapid evaluation of new and existing asthma therapies and to disseminate its findings to the health care community. Between 1993 and 2003, when ACRN consisted of six clinical centers and one data coordinating center, the consortium completed 11 clinical trials, two of which are described herein. Since then, the NHLBI re-awarded the ACRN for another five years with eight clinical centers and one data coordinating center to continue pursuing the same mission. More background information about the ACRN can be found at its website (www.acrn.org).

Two Studies

As previously mentioned, the Asthma Clinical Research Network used a paired crossover design in two different study protocols, namely the Beta Adrenergic Response by GEnotype (BARGE) Study [6] and the Smoking Modulates Outcomes of Glucocorticoid (SMOG) Therapy in Asthma Study [7]. Both studies, and their results, have been described elsewhere. Here, we just introduce the objectives and designs of each of the two studies.

Beta Adrenergic Response by GEnotype (BARGE) Study

The most common treatment for patients with mild to moderate asthma has been scheduled daily use of inhaled albuterol (two puffs, four times a day). Retrospective analyses of previously published clinical trials on the long-term use of albuterol, however, suggested that such a treatment might yield adverse events in patients with certain genotypes. Specifically, it has been hypothesized that regular use of inhaled albuterol has a detrimental effect on the lung function of patients with the Arg/Arg genotype at the 16^th position of the beta-agonist receptor gene, but not in those with the Gly/Gly genotype at the same position. As a result, the Asthma Clinical Research Network set out to design a clinical trial in which the aforementioned hypothesis could be tested unequivocally.

The resulting study, the Beta Adrenergic Response by GEnotype (BARGE) Study, focused on comparing the regular use of inhaled albuterol (A) to placebo (P) in patients with the B16-Arg/Arg (R) genotype and in patients with the B16-Gly/Gly (G) genotype. The primary research question concerned whether or not the treatment effects differed for the two genotypes. That is, the primary hypothesis concerned inference about whether the parameter:

$$\gamma =({\mu }_{RA}-{\mu }_{RP})-({\mu }_{GA}-{\mu }_{GP})$$

is 0, where μ_kl is the population mean lung function of patients of genotype k on treatment l.

To get the most efficient comparison of the treatments within each genotype (μ_kA − μ_kP), a 2 × 2 (AP:PA) crossover design was used within each genotype k. Because a subject’s genotype is a pre-determined characteristic, subjects could not be randomly allocated to genotypic group. Therefore, to minimize confounding caused by potential differences in the baseline lung function of the two genotypic groups, each subject of genotype R was matched to a subject of genotype G with similar baseline lung function. The matched subjects were randomly assigned to the same sequence of the crossover design, and an eight-week washout period was placed between the two treatment periods (Figure 1). At the conclusion of the BARGE Study, each pair of subjects j of sequence i yielded the quadrivariate response Y_ij = (Y_ijRA, Y_ijRP, Y_ijGA, Y_ijGP), a vector containing the subjects’changes in lung function.

Figure 1.

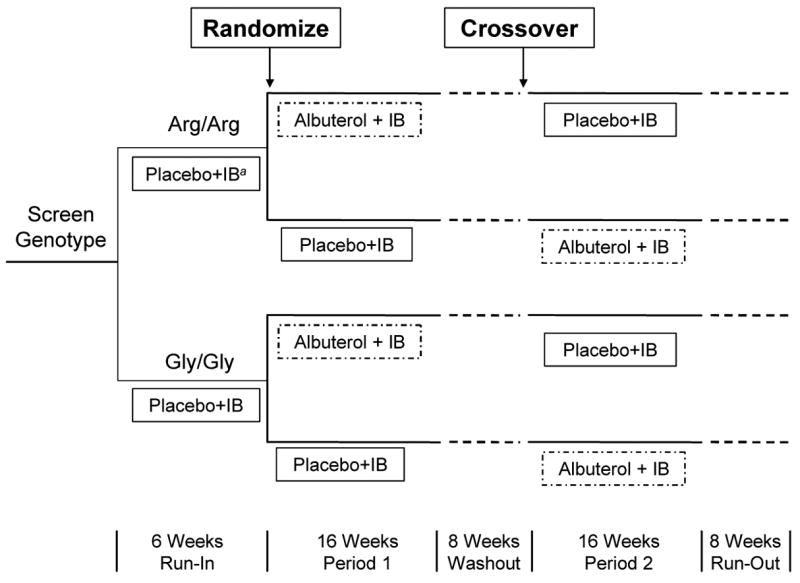
Design of the Beta-Adrenergic Response by Genotype (BARGE) Study

^aIB denotes ipratropium bromide, a rescue medication permitted during the study.

Smoking Modulates Outcomes of Glucocorticoid (SMOG) Therapy in Asthma Study

Despite the logical expectation that people with asthma would avoid exposure to cigarette smoke, studies suggest that approximately 30% of asthmatic individuals actively smoke [7], a prevalence equivalent to that of the population at large. Until recently, however, there has been little information regarding the effect of cigarette smoking on the response to asthma therapy, because most studies of asthma therapy have excluded subjects who smoke. The Asthma Clinical Research Network therefore specifically set out to design a clinical trial to evaluate the hypothesis that smoking reduces the response to inhaled corticosteroids.

The resulting study, the Smoking Modulates Outcomes of Glucocorticoid (SMOG) Therapy in Asthma Study, focused on comparing treatment with an inhaled corticosteroid (C) to a leukotriene receptor antagonist (L). A paired 2 × 2 crossover design was used in which a smoker (S) and non-smoker (N) were matched if they were from the same clinical center, of the same gender and had the same baseline lung function. The matched subjects were randomly assigned to the same sequence of the crossover design, and a six-week washout period was placed between the two treatment periods (Figure 2). At the conclusion of the SMOG Study, each pair of subjects j of sequence i yielded the quadrivariate response Y_ij = (Y_ijSC, Y_ijSL, Y_ijNC, Y_ijNL), a vector containing the subjects’changes in lung function. The primary research question concerned whether or not the treatment effects differed for smokers and nonsmokers. That is, the primary hypothesis concerned inference about whether the parameter:

Figure 2.

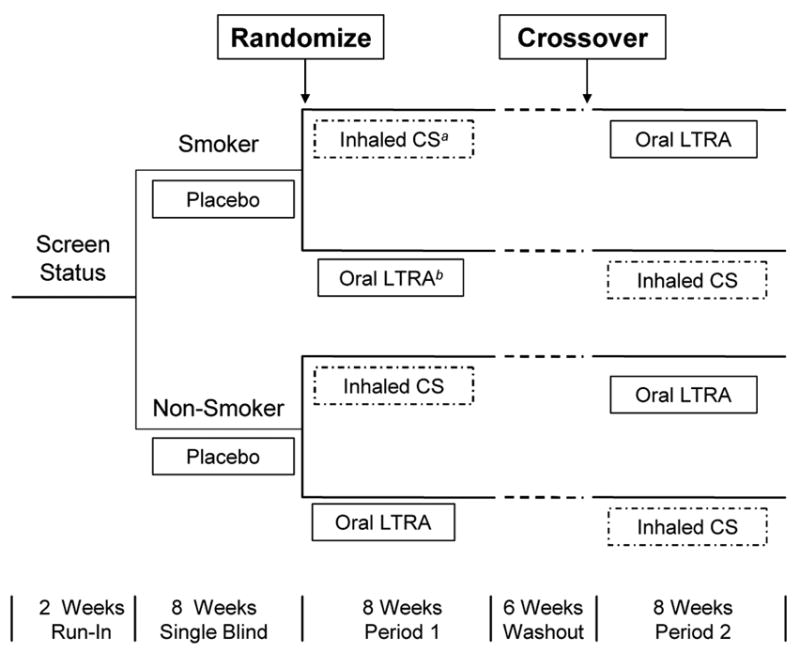
Design of the Smoking Modulates Outcomes of Glucocorticoid (SMOG) Therapy Study.

^aCS denotes corticosteroids.

^bLTRA denotes leukotriene receptor antagonist.

$$\gamma =({\mu }_{SC}-{\mu }_{SL})-({\mu }_{NC}-{\mu }_{NL})$$

is 0, where μ_kl is the population mean lung function of patients of smoking status k on treatment l.

Methods

Having described the two ACRN studies in which a paired 2 × 2 crossover design was utilized, we now briefly address methods for analyzing the data arising from such a design. We assume each subject contributes one response per period. The response may truly be a single post-treatment, outcome measure, such as forced expiratory volume in one second (“FEV₁”) in an asthma trial. Alternatively, and perhaps more commonly, the response could be a summary of multiple, repeated outcome measures, such as the change in response from pre- to post-treatment or the area under a dose-response curve (“AUC”) in a bioequivalence trial.

We propose a statistical model, present possible parameters of interest, and evaluate the relative efficiency of the design. Notationally, we refer to the two types of subjects who are matched as 1 and 2, and we label the treatments as A and B.

A Statistical Model

In formulating a statistical model for the paired 2 × 2 crossover design, we must address how to handle “treatment carryover.”In an AB sequence, a subject receives treatment A in the first period and treatment B in the second period. In this case, the “A carryover”(λ_A) is the component of the response in the second period due to the lasting effect of treatment A from the first period. Likewise, in a BA sequence, the “B carryover”( λ_B) is the component of the response in the second period due to the lasting effect of treatment B from the first period. In a 2 × 2 crossover, if the magnitude of the A carryover differs from that of the B carryover (λ_A ≠ λ_B), it is not possible to estimate the primary quantity of interest –the true treatment effect μ_A − μ_B.

There are two situations in which it is possible to estimate the true treatment effect: 1) if the carryover effects are the same for each treatment (λ_A = λ_B); or 2) if the time periods between the treatment periods, i.e., the washout periods, are designed to be lengthy enough to render both carryover effects negligible (λ_A = λ_B = 0). The BARGE and SMOG Studies both involved a substantial washout period with the intent of eliminating any carryover effects. We therefore proceed in formulating a model assuming the second situation holds. In general, if unequal carryover effects are suspected to exist, then a design more complex than the 2 × 2 crossover is needed.

As is often the case, we define a model that supposes each response is a function of some mean parameters (e.g., the treatments and the sequence in which they are taken), some random effects (e.g. the trial subjects), and some unexplained random error:

$$\text{response\hspace{0.17em}}Y=\text{mean\hspace{0.17em}parameters}+\text{random\hspace{0.17em}effects}+\text{random\hspace{0.17em}error}\text{.}$$

In statistical notation, we define such a general linear mixed-effects model [8] for the paired 2 × 2 crossover design with nonexistent carryover effects as:

$${\mathbf{Y}}_{ij}={\mathbf{X}}_{ij}\mathit{\beta }+{\mathbf{Z}}_{ij}{\mathbf{U}}_{ij}+{\mathit{\epsilon }}_{ij}$$

where:

• Y_ij = (Y_ij1A, Y_ij1B, Y_ij2A, Y_ij2B)′ is the response vector containing the outcome measures for the two subjects comprising pair j (1, 2, . . ., n_i) of sequence i (1 = AB, 2 = BA)

• X_ij is a 4 × 8 fixed-effects design matrix

• β = (μ_1A, μ_1B, μ_2A, μ_2B, ρ₁, ρ₂, ν₁, ν₂)′ is a fixed-effects parameter vector containing four type-by-treatment means (μ_1A, μ_1B, μ_2A, μ_2B), two period effects (ρ₁, ρ₂), and two sequence effects (ν₁, ν₂)

• Z_ij is a 4 × 4 random-effects design matrix

• U_ij = (U_ij1A, U_ij1B, U_ij2A, U_ij2B)′ is a random pair effect, and

• ε_ij = (ε_ij1A, ε_ij1B, ε_ij2A, ε_ij2B)′ is a random error term.

The mean of the responses derives directly from the X_ijβ portion of the model, while the variance of the responses derives directly from the Z_ijU_ij and ε_ij portions of the model.

Mean of the responses

Our proposed model for the mean of the responses arising from a paired 2 × 2 crossover design is a straightforward extension of the model commonly assumed for the mean of the responses arising from a basic 2 × 2 crossover design. That is, we assume that the mean of the response in any cell of the paired 2 × 2 crossover design is a function of the subject type and treatment (μ_kl), as well as the period (ρ_k) and sequence (ν_l) in which the treatments are taken. More specifically, we propose parameterizing the mean of the responses as:

Type	Sequence	Period 1	Period 2
1	AB	μ1A + ρ1 + ν1	μ1B − ρ1 + ν1
1	BA	μ1B + ρ1 − ν1	μ1A − ρ1 − ν1
2	AB	μ2A + ρ2 + ν2	μ2B − ρ2 + ν2
2	BA	μ2B + ρ2 − ν2	μ2A − ρ2 − ν2

Variance of the responses

Traditionally, the variance matrix for a crossover design is assumed to be compound symmetric. That is, the variance of the responses arising from one treatment is assumed to equal the variances of the responses arising from other treatments. And, the covariances between the responses of the subjects when on different treatments are also assumed to be equal. By virtue of the assumptions we make about the random components Z_ij, U_ij and ε_ij in our proposed model, the structure of our variance matrix is completely flexible.

Specifically, we assume that Z_ij is a 4 × 4 identity matrix and that the random error terms U_ij and ε_ij are independent and normally distributed. Like the approach of others [9–12], we allow the random pair effect U_ij to vary according to type k and treatment l. In doing so, we model the maximum number of variance components permitted for the paired 2 × 2 crossover design. That is, the variance of the response Y_ij:

$$\left[\begin{array}{cccc}{\sigma }_{1A,1A}& {\sigma }_{1A,1B}& {\sigma }_{1A,2A}& {\sigma }_{1A,2B}\\ {\sigma }_{1A,1B}& {\sigma }_{1B,1B}& {\sigma }_{1B,2A}& {\sigma }_{1B,2B}\\ {\sigma }_{1A,2A}& {\sigma }_{1B,2A}& {\sigma }_{2A,2A}& {\sigma }_{2A,2B}\\ {\sigma }_{1A,2B}& {\sigma }_{1B,2B}& {\sigma }_{2A,2B}& {\sigma }_{2B,2B}\end{array}\right]$$

is much more flexible than the compound symmetric structure traditionally assumed.

The data

As our model suggests, we assume the data are balanced (the occasions of measurement are the same for all subjects) and complete (measurements are available at each planned occasion for each subject). We can relax the completeness assumption, however, and instead just assume that the data are missing at random (the probability of response depends on the observed data but not the missing data) [13]. In either case, our formulated statistical model can be fit and inference conducted on the parameters of interest using the MIXED procedure in SAS 9.1.

Parameters of Interest

When conducting a paired 2 × 2 crossover experiment, researchers are most likely interested in answering one of the following three research questions:

• For type 1 subjects, what is the difference in the mean of the responses for the subjects when on treatment A and treatment B?

• For type 2 subjects, what is the difference in the mean of the responses for the subjects when on treatment A and treatment B?

• Does the effect of the treatments for type 1 subjects differ from the effect of the treatments for type 2 subjects?

The first two questions can be answered by estimating the quantities μ_1A − μ_1B and μ_2A − μ_2B; respectively. If researchers are merely interested in answering the first two questions, the paired 2 × 2 crossover design offers no real advantage. The researchers would be better off just conducting two independent 2 × 2 crossover experiments. On the other hand, if researchers are interested in determining if the treatment effects differ for each subject type, then they are interested in determining whether or not the quantity (μ_1A − μ_1B) − (μ_2A − μ_2B) is 0. In this case, the paired 2 × 2 crossover design affords a real advantage with respect to efficiency, which is illustrated in the next section.

Efficiency With Respect to the Parameter γ₃

The type of scientific questions posed by the BARGE and SMOG Studies concerned inference about the quantity (μ_1A − μ_1B) − (μ_2A − μ_2B). For the sake of simplicity, in this section, we’ll refer to this interaction effect as γ. Although primary interest concerned γ, the ACRN researchers might have instead considered conducting two independent 2 × 2 crossover designs rather than a paired 2 × 2 crossover design. The cost of doing so would likely have been increased variability in the responses and hence a less precise estimate of γ. In order to quantify the extent to which the variability of the responses arising from two independent 2 × 2 crossover designs is greater than that from a paired 2 × 2 crossover design, we investigate the relative efficiency of the paired 2 × 2 crossover design to two independent 2 × 2 crossover designs.

We define the relative efficiency of the paired 2 × 2 crossover design to a clinical trial of two independent 2 × 2 crossover designs as:

$$R{E}_{P,I}=\frac{Va{r}_I(\widehat{\gamma })}{Va{r}_P(\widehat{\gamma })}$$ (1)

where Var_I (γ̂) denotes the variance of the maximum likelihood estimator γ̂ under the independent 2 × 2 crossover model, and Var_P (γ̂) denotes the variance of the maximum likelihood estimator γ̂ under the paired 2 × 2 crossover model. Defined as such, relative efficiencies greater than one suggest that estimates of γ arising from two independent crossovers would be less precise than those from a paired crossover. Conversely, relative efficiencies less than one suggest that estimates of γ arising from two independent crossovers would be more precise than those from a paired crossover.

Now, under the paired 2 × 2 crossover model with random pair effects, it can be shown in a complete data situation that Var_P (γ̂) is proportional to:

$$\begin{array}{l}{\sigma }_{1A,1A}+{\sigma }_{1B,1B}+{\sigma }_{2A,2A}+{\sigma }_{2B,2B}-2{\sigma }_{1A,1B}-2{\sigma }_{2A,2B}\\ -2{\sigma }_{1A,2A}+2{\sigma }_{1A,2B}+2{\sigma }_{1B,2A}-2{\sigma }_{1B,2B}.\end{array}$$ (2)

And if we assume Var (Y_ij) ; the variance of the response vector, under the two independent 2 × 2 crossover model is:

$$\left[\begin{array}{cccc}{\sigma }_{1A,1A}& {\sigma }_{1A,1B}& 0& 0\\ {\sigma }_{1A,1B}& {\sigma }_{1B,1B}& 0& 0\\ 0& 0& {\sigma }_{2A,2A}& {\sigma }_{2B,2B}\\ 0& 0& {\sigma }_{2A,2B}& {\sigma }_{2B,2B}\end{array}\right]$$

then it can be shown in a complete data situation that Var_I (γ̂) is proportional to:

$${\sigma }_{1A,1A}+{\sigma }_{1B,1B}+{\sigma }_{2A,2A}+{\sigma }_{2B,2B}-2{\sigma }_{1A,1B}-2{\sigma }_{2A,2B}.$$ (3)

Inserting (2) and (3) into the relative efficiency formula defined in (1), we can calculate the relative efficiency of the paired 2 × 2 crossover to two independent 2 × 2 crossovers. Table 1 contains the calculated relative efficiencies, RE_P,I, assuming i) each of the variances (σ_1A,1A, σ_1B,1B, σ_2A,2A and σ_2B,2B) equal 1.0; ii) the correlations within a subject (σ_1A,1B and σ_2A,2B) are 0.5; iii) σ_1A,2A = σ_1B,2B and iv) σ_1A,2B = σ_1B,2A. For the examples we considered in Table 1, the relative efficiency exceeds 1.0 and in a few cases is much larger than 1.0. Therefore, we conclude that the paired 2 × 2 crossover design is more efficient than the unpaired design for reasonable values of the variance-covariance parameters.

Table 1.

Relative efficiency of the paired 2 × 2 crossover design.

σ1A,2A	σ1A,2B	REP,I	σ1A,2A	σ1A,2B	REP,I
0	0	1.00	0.40	0	5.00
0.1	0	1.25	0.40	0.1	2.50
0.1	0.1	1.00	0.40	0.2	1.67
0.2	0	1.67	0.40	0.3	1.25
0.2	0.1	1.25	0.40	0.4	1.00
0.2	0.2	1.00	0.50	0.1	5.00
0.3	0	2.50	0.50	0.2	2.50
0.3	0.1	1.67	0.50	0.3	1.67
0.3	0.2	1.25	0.50	0.4	1.25
0.3	0.3	1.00	0.50	0.5	1.00

In general, the paired 2 × 2 crossover design is more efficient than the unpaired design if:

$${\sigma }_{1A,2A}+{\sigma }_{1B,2B}>{\sigma }_{1A,2B}+{\sigma }_{1B,2A}.$$

In other words, the paired 2 × 2 crossover design is more efficient if the correlations between the paired members on the same treatments are greater than their correlations on different treatments. Intuitively, we would expect this condition to hold in most circumstances and therefore would highly recommend the paired crossover design for answering the types of scientific questions posed by the BARGE and SMOG Studies.

Discussion

While we have made the case for using a paired 2 × 2 crossover design in certain situations, there is a trade-off to consider when it comes to recruiting subjects. Under reasonable assumptions, as described in the previous section, the paired 2 × 2 crossover design does require fewer subjects than the design with two independent crossovers because it yields a smaller variance expression for the estimated type-by-treatment interaction. However, because of the pairing that must take place, the recruited subjects must meet more stringent criteria. As a result, clinical researchers will find themselves having to screen more patients in order to achieve their recruitment goals. Even then, recruitment levels may still lag behind.

Case in point, for the BARGE Study, each patient with the Arg/Arg genotype was supposed to be matched to a patient with the Gly/Gly genotype from the same clinical center and having similar lung function (as defined by a forced expiratory volume in one second within 10% of predicted). Subjects having the Gly/Gly genotype are more prevalent than subjects having the Arg/Arg genotype –of the 338 patients initially screened, 158 had an ineligible genotype, 125 had the Gly/Gly genotype and 55 had the Arg/Arg genotype. Many of the Gly/Gly subjects who met the BARGE eligibility criteria either waited a long period of time to get matched, or they never got matched, to eligible Arg/Arg subjects. As a result, the matching criteria were relaxed by opening up recruitment to the entire research network. That is, if a suitable match could not be found at a center within four weeks of establishing genotypic eligibility, the pool of potential matching patients was extended to the entire network. Even so, matches were never found for 41 subjects having the Gly/Gly genotype. A similar situation was encountered in the SMOG trial in which many of the non-smoking subjects who met the SMOG eligibility either waited a long period of time to get matched, or they never got matched, to eligible smoking subjects. These examples demonstrate the additional effort that may need to take place when conducting a matched crossover design.

Notwithstanding the aforementioned drawback, the paired crossover design is a design that deserves consideration in any clinical trial in which the crossing over and matching of subjects is deemed simultaneously beneficial. Although we presented here a specific form of the design –in which there were two treatments, two types to be matched, and one response per period –the matched crossover design can be easily extended to other situations in which there are more than two treatments, more than two types to be matched, and repeated measurements and/or multiple covariates in the same period (unpublished dissertation, Laura J. Simon). In fact, the BARGE trial consisted of repeated measurements within each treatment period and was analyzed accordingly [6].