The Impact of Dose on Parotid Salivary Recovery in Head and Neck Cancer Patients Treated with Radiation Therapy

Abstract

Purpose

A common side effect experienced by head and neck cancer patients after radiotherapy (RT) is impairment of the parotid glands’ ability to produce saliva. Our purpose is to investigate the relationship between radiation dose and saliva changes in the two years following treatment.

Methods and Materials

The study population includes 142 patients treated with conformal or intensity modulated radiotherapy. Saliva flow rates from 266 parotid glands are measured before and 1, 3, 6, 12, 18 and 24 months after treatment. Measurements are collected separately from each gland under both stimulated and unstimulated conditions. Bayesian nonlinear hierarchical models were developed and fit to the data.

Results

Parotids receiving higher radiation produce less saliva. The largest reduction is at 1–3 months after RT followed by gradual recovery. When mean doses are lower (e.g. <25Gy), the model-predicted average stimulated saliva recovers to pre-treatment levels at 12 months and exceeds it at 18 and 24 months. For higher doses (e.g. >30Gy), the stimulated saliva does not return to original levels after two years. Without stimulation, at 24 months, the predicted saliva is 86% of pre-treatment levels for 25Gy and <31% for >40Gy. We do not find evidence to support that the over-production of stimulated saliva at 18 and 24 months after low dose in one parotid gland is due to low saliva production from the other parotid gland.

Conclusions

Saliva production is impacted significantly by radiation, but with doses <25–30Gy, recovery is substantial and returns to pre-treatment levels two years after RT.

INTRODUCTION

Head and neck cancer patients are frequently treated with radiation therapy (RT) in combination with other treatments such as surgery and chemotherapy. However, the exposure to radiation can cause damage to parotid glands and impair their ability to produce saliva. The loss of salivary output is a major complication as it leads to dry mouth (xerostomia) and oral discomfort for patients after radiotherapy (1). It causes difficulty in chewing, swallowing, food-tasting and does harm to dental health. In some patients the reduction in saliva output is transient and in others it can persist for a year or longer. Therefore, treatment strategies that lead to long-term adequate saliva output are of vital clinical importance to the patient.

Conventional treatment planning generally requires high radiation dosage to both parotid glands and hence often leads to severely reduced salivary flow. Thus attempts to minimize the radiation dosage to these normal tissues in order to diminish this side effect have been necessary. Three-dimensional (3D) conformal and multisegmental intensity-modulated radiotherapy treatment planning makes it possible to reduce the dose to the parotid. Yet, at the same time, the technique gives adequate dosage to the tumors and lymph nodes (2–8). A common treatment strategy is to allow high doses to the ipsilateral parotid gland while delivering as small doses as possible to the contralateral gland. This strategy should ensure that the patient at least has some saliva production. It is also plausible that the patient’s saliva production from the contralateral gland will over-compensate if the saliva production from the ipsilateral gland is very low; a hypothesis we will investigate in this report.

The mechanisms by which radiation damages the cells in the parotid and by which this leads to reduced saliva output, is obviously complex and beyond the scope of this paper. Similarly, how damage in the parotid may be repaired over time and saliva production recovered is also complicated. This suggests the need to examine the whole time course of saliva measurements in order to properly assess the impact of the radiation.

Previous publications from our own data and from other institutions have demonstrated a clear impact of dose on saliva production rates after treatment (9–10). Besides University of Michigan, other centers have collected and analyzed similar data; these include datasets from Netherlands (11), from Washington University at St. Louis (12), from Helsinksi University Central Hospital in Finland and from University Hospital Gasthuisberg in Belgium (13, 14). These studies differ from the current one in a number of aspects, including methods for measuring saliva and the length of follow-up period. Also more patients are included in the current study. Our focus will be on using state-of-the-art statistical methods to use the available data to the maximum efficiency and give accurate quantitative information about the effect of radiation on saliva flow rates. Previous analyses sometimes dichotomize the saliva flow rate into a binary variable, whereas we utilize the full range of the measurements to make efficient use of the data.

The purpose of our study is to accurately examine the functional relationship between radiation dosage and the rates of functional recovery in parotid glands over the course of two years after radiotherapy. We prospectively followed the patients and investigated the functional alternations in the parotid glands in the course of two years. We use a sophisticated statistical model and a Bayesian estimation scheme. The model allows for a dose-response relationship that can vary with follow-up time. The model also accounts for the correlation among saliva flow rates of the same parotid glands over time and captures the excess of zero saliva output in our data. Besides the relationship between radiation dose and salivary flow rates, we also examine the hypothesis that the contralateral side may compensate for the loss of saliva secretion functionality on the ipsilateral side.

METHODS AND MATERIALS

PATIENT POPULATION

The study population includes 142 head and neck cancer patients who received conformal or intensity modulated therapy at the University of Michigan from 1994 to 2003. Informed consent forms approved by the Institutional Review Board of the University of Michigan are signed by all patients. These patients were treated with radiotherapy primarily or in combination with other types of treatment such as surgery or chemotherapy before irradiation. These data are an updated version of data that have been described previously (6). Previous analyses showed that neither chemotherapy or pre-RT surgery, nor type of medications received impacts saliva flow rates, thus these are not considered (6). All patients have data available on radiation dose to the parotid, and at least one saliva flow rate measurement. It is a prospective study and patients were followed for up to two years after RT.

RADIATION TREATMENT PLANNING

Three-dimensional conformal or intensity modulated radiotherapy allows customized radiation beam arrangement and more accurate delivery of specific radiation dosage to tumor cells according to each patient’s tumor location and the disease severity. The detailed University of Michigan planning system has been described previously (2–6, 15). The goal of the treatment planning is generally to give the contralateral parotid gland a low dose of radiation, to minimize the damage, while still allowing sufficient radiation to the tumor cells. The treatment scheme delivers radiation in small fractions; 1.8–2.0Gy per fraction to the tumor, one fraction per day, five fractions per week. The total dose prescribed to the tumor is about 60–75Gy. The computed tomography-based radiation therapy records give accurate 3D dose distributions in each parotid gland and the dose distribution is summarized by dose-volume histogram (DVH) (16). In our analysis, the mean radiation dose to each gland was calculated from the DVH.

SALIVA MEASUREMENTS

Salivary flow rates are measured before RT and 1, 3, 6, 12, 18 and 24 months after RT. Patients are measured separately on both ipsilateral and contralateral parotid glands using Carlson-Crittenden cups. Patients are not allowed to drink or eat for at least 90 minutes before the saliva collection and all the samples are collected in the morning to reduce diurnal variations in the saliva output. For each parotid gland of each patient, unstimulated and stimulated parotid saliva was collected. Stimulation of saliva flow was obtained by applying 2% citric acid on the dorsolateral surfaces of the tongue. Saliva samples were collected in small plastic containers. The flow rates are calculated as described previously (6) and the units of the flow rate are milliliters per minute.

STATISTICAL METHODS

We develop a Bayesian nonlinear hierarchical regression model for the saliva data. Since saliva output from the same parotid gland tends to be similar over time relative to that from other glands, we account for the possible correlations among saliva output of the same parotid with this model. Preliminary analyses suggested that there is little correlation between the flow rates on the ipsilateral and contralateral sides for the same person, so this potential correlation is not included in the model. Since saliva output under stimulated conditions is very different from that under unstimulated conditions, we modeled responses from stimulated and unstimulated conditions separately. An initial postulate is that saliva flow rates have a Poisson distribution, which would require integer counts. Thus we transformed the units of saliva flow rates by multiplying it by a factor of 150 and then round them up to be integers, which becomes our outcome of interest. When the radiation dosage is very high, for example, greater than 45 Gy, a majority of the patients did not produce saliva even after one or two years of recovery. The excess of zero saliva output can likely cause overdispersion, hence, we assumed an overdispersed Poisson distribution, also called a negative binomial distribution, for the transformed count data.

Let Y_ij be saliva output at time j for parotid i. When j = 0, it represents baseline before the treatment and j = 1,2,3,4,5 and 6 represent 1, 3, 6, 12, 18 and 24 months after the treatment respectively. Let d*_i be the average dose for parotid i. Let d_ij represents the average radiation dose for parotid gland i at time j. Thus d_i0 =0 and d_ij =d*_i for j>0. Y_ij follows the negative binomial distribution with mean μ_ij which can be parameterized as:

$$pr(Y_{ij}=y_{ij})=\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}{\left(\frac{1}{\beta +1}\right)}^{y_{ij}},y_{ij}=0,1,2,\dots$$

We model the outcome through the mean parameter μ_ij with a linear spline model and log link,

$$log({\mu }_{ij})={\alpha }_0+{\alpha }_{1j}{d}_{ij}+{\alpha }_2{(d_{ij}-25)}^{+}+{\alpha }_3{(d_{ij}-45)}^{+}+{\theta }_i$$ (i)

In this model, (d_ij −25)⁺ represents the difference between radiation dose and 25 if the dose is greater than 25, otherwise, the quantity equals 0, similarly for (d_ij −45)⁺; exp(α₀) is the transformed baseline saliva flow rate; αij represents the dose effect on saliva at time point j when dose is less than 25Gy; α₂ and α₃ denote the additional linear dose effect beyond 25Gy and 45Gy, respectively. This linear spline model allows for a continuous and different effect of dose at each time point. The parameters α₂ and α₃ were initially also allowed to depend on time j, but this did not improve the fit to the data.

The term θ_i is a random effect assumed to follow a normal distribution with mean 0 and variance ${\sigma }_{\theta }^2$ which allows each parotid to have its own initial level. By using θ₁, we capture the correlation among the saliva flow rates over time for the same parotid. The negative binomial distribution has mean of μ_ij and variance of ${\mu }_{ij}\left(\frac{\beta +1}{\beta }\right)$; the factor $\left(\frac{\beta +1}{\beta }\right)$ is the overdispersion factor relative to the Poisson distribution to capture the excess zero saliva flow rates in our data. A Bayesian estimation method was used to estimate the model parameters; the details are given in the Appendix.

We extend our model to evaluate the compensation hypothesis; that is, higher than expected saliva flow rate from one parotid, if the other parotid had very low flow rate. This was achieved by the following modification:

$$log({\mu }_{ij})={\alpha }_0+{\alpha }_{1j}{d}_{ij}+{\alpha }_2{(d_{ij}-25)}^{+}+{\alpha }_3{(d_{ij}-45)}^{+}+{\alpha }_{4}I(Y_{i^{\prime }j}\le C)I(j>0)+{\theta }_i$$ (ii)

where Y_i'j is the saliva flow rate from the parotid in the opposite cheek from that labeled as i and C denotes the cut-off value. I (Y_i'j ≤ C) equals to 1 if Y_i,j is less than or equal to C; otherwise, it equals 0. I (j > 0) is an indicator variable with value of 0 for the baseline measurement and 1 for other time points. The coefficient α₄ being positive would suggest overcompensation. A cut-off value of C=1 is used for stimulated data and about 1% of the baseline transformed saliva counts are less than or equal to 1. The cut-off for the unstimulated condition is C=0, which accounts for 3% of the baseline counts. A total of twenty people have occurrences of saliva measurements for one parotid but missing measurements for the opposite parotid at that time point. Besides excluding these observed but unpaired saliva measurements from the model, we performed two sensitivity analyses in which we assumed either that all the missing measurements were less than the cut-off or all were greater than the cut-off. The results from these sensitivity analyses were similar to those from the analyses that excluded these patients, so we present only results from these later analyses.

RESULTS

Patient Characteristics

Characteristics of the 142 patients are shown in Table 1. There are 30 patients treated unilaterally and 112 treated bilaterally. Patients treated unilaterally received high radiation dose on their ipsilateral sides and very scattered radiation dose on their contralateral sides. 124 patients have dose and at least one saliva flow measurement for both parotids, while the other 18 have both data only for one parotid.

Table 1.

Patient and Tumor Characteristics

Total Patient Number	142
Males	75.4%
Age, median(minimum, maximum)	56(25,83)
Surgery pre RT	67%
Chemotherapy	28%
Tumor Sites
Oral Cavity	20%
Oropharynx	57%
Larynx	19%
Other	4%

Radiation Dosage

The median of the mean radiation dose received by the 269 parotids is 28.6 Gy with an interquartile range of 18.7–55.4 Gy.

Salivary Flow Rates

The number of parotid glands with saliva flow rates measured at baseline, 1, 3, 6, 12, 18 and 24 months are 252, 183, 182, 169, 143, 96 and 84 respectively. Most of the attrition is due to patients' reluctance to continue the study procedure and a small fraction is due to disease progression. We assessed the potential bias due to drop out and found that there is no significant difference in radiation dosage received or baseline saliva flow rates between patients who do not have saliva data and those who do, at one year and at two years.

Irradiation Effect on Saliva Outcome

Figure 1 shows the stimulated saliva flow rates at each measured time plotted against the mean radiation dose received. The figure shows a dose response relationship between saliva production and average dose. Most parotids that receive a dose of greater than 40Gy produce zero or very little saliva in the first year after radiation. There is a clear increase in saliva flow as the follow-up time increases. This is particularly evident for parotids that received doses of less than 30Gy. Also some of the parotids that received higher doses did increase their saliva flow rate with increasing follow-up time. For some parotids that received less than 25Gy, it appears that the 18 and 24 month values can be higher than the pre-treatment values. Figure 2 shows the relationship between radiation dose and the amount of saliva produced under unstimulated conditions. The saliva flow rates under unstimulated conditions are much less than under stimulated conditions. There is a similar pattern to that in Figure 1. There is a dose response relationship and some evidence of recovery with time, except at the highest doses; however the recovery does not return the saliva flow rates to their pre-treatment values.

Figure 1.

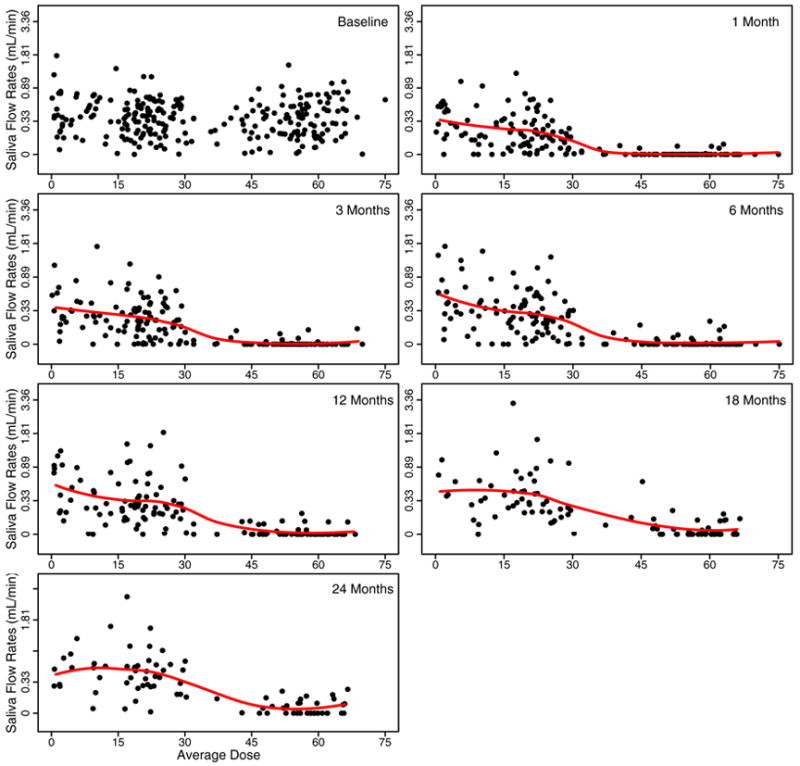
Stimulated saliva flow rates versus mean radiation dose at baseline and 1, 3, 6, 12, 18, 24 months after the completion of RT. The flow rates are plotted on a log(flow rates + 1) transformed scale for each gland. The solid line is the LOESS smoothing line describing the relationship between flow rates and mean doses.

Figure 2.

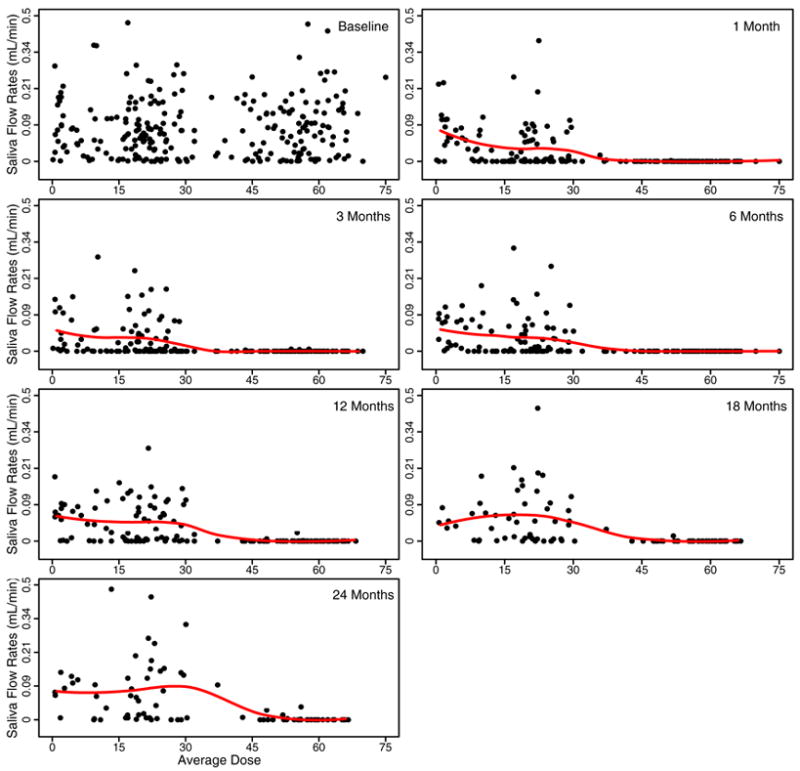
Unstimulated saliva flow rates versus mean radiation dose at baseline and 1, 3, 6, 12, 18, 24 months after the completion of RT. The flow rates are plotted on a log(flow rates + 1) transformed scale for each gland. The solid line is the LOESS smoothing line describing the relationship between flow rates and mean doses.

Statistical Model Fit to Stimulated Data

Table 2 lists the parameter estimates and their 95% credible intervals from fitting the negative bionomial model to the data. The effect of radiation is the largest at one month after radiation, indicated by the largest negative coefficient at one month after RT. The coefficients becoming less negative from one month to 24 months shows a gradual recovery in the parotid gland’s ability to produce saliva. For glands receiving dose d_ij < 25 Gy, the model predicted mean saliva rate equals exp(3.97–0.025* d_ij ) at one month, exp(3.97 + .00008* d_ij ) at 12 months and exp(3.97 + 0.014* d_ij ) at 24 months after RT, respectively. Thus, the predicted average saliva production is reduced by less than 50% at one month after RT if dose is less than 25 Gy. By 12 months after RT, the average saliva production achieves complete recovery and by 24 months, the parotid glands are able to produce more saliva than that at baseline. The coefficient of (d_ij -25)⁺ is negative and its 95% credible interval does not include zero, which implies significant additional radiation damage, beyond the linear projection, with dose greater than 25Gy. In other word, the rate of reduction in saliva flow becomes much larger when the radiation dose is greater than 25Gy. For glands receiving doses between 25Gy to 45Gy, the predicted mean saliva flow rates are exp(6.97–0.145* d_ij ) at one month and exp(6.97–0.106* d_ij ) at 24 months after RT. When radiation dosage is above 45 Gy, the significant positive coefficient indicates the rate of reduction decreases as the dose received approaches a very high level. Our data shows that for parotids receiving doses of greater than 45Gy, the extent of the saliva reduction approaches a maximum and many parotids produce zero saliva output. The easier way to understand the results from this model is through a graph to visualize the relationship between radiation dose and salivary recovery. The model-predicted saliva mean trajectory is described in Figure 3. It shows a complete recovery of saliva flow by the end of two years after radiotherapy if the radiation dosage is less than 30 Gy. When the dose received is larger, for example, 40 Gy, recovery continues during the course of two years; however, the extent of recovery is small relative to the saliva production at baseline. As most of the ipsilateral sides received more than 45 Gy, complete recovery happens mostly on the contralateral sides.

Table 2.

Posterior Means of Parameter Estimates of Model Specified in Equation (i) for Stimulated Saliva Flow Rates and Their 95% Equal Tailed Bayesian Credible Intervals (CI)

Time	Parameter	Posterior Mean	(95% CI)
Baseline	α0	3.97	(3.87, 4.07)
Dose (1 Month)	α11	−0.025	(−0.034, −0.018)
Dose (3 Months)	α12	−0.019	(−0.026, −0.012)
Dose (6 Months)	α13	−0.0094	(−0.016, −0.0021)
Dose (12 Months)	α14	0.00008	(−0.0072, 0.0074)
Dose (18 Months)	α15	0.0096	(0.0022, 0.017)
Dose (24 Months)	α16	0.014	(0.0063, 0.022)
†(Dose - 25)+	α2	−0.12	(−0.15, −0.099)
† (Dose - 45)+	α3	0.070	(0.018, 0.12)

^†(Dose - 25)⁺ represents the difference between radiation dose and 25 if the dose is greater than 25Gy, otherwise, the quantity equals 0. (Dose - 45)⁺ is similarly defined.

Figure 3.

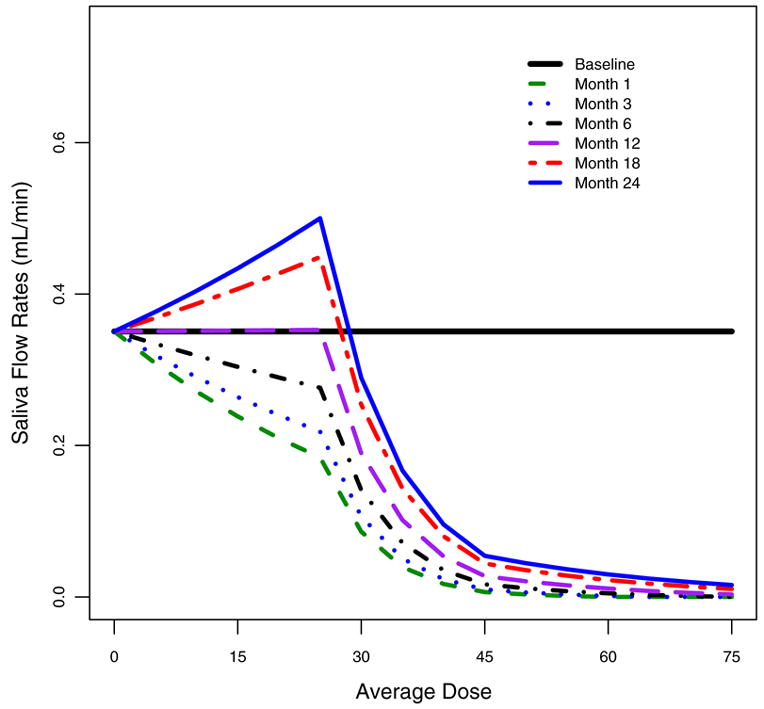
Mean stimulated saliva counts predicted by the estimated model specified in equation (i) for baseline and 1, 3, 6, 12, 18, 24 months after RT.

Statistical Model fit to Unstimulated Data

Similarly, we model the mean saliva output under no stimulated conditions assuming a negative binomial distribution. The parameter estimates are given in Table 3. The model-predicted saliva output is plotted in Figure 4. It shows that the recovery appears to be much slower compared to stimulated conditions. The recovery begins only about 12 months after radiotherapy. After two years, the salivary function has recovered to less than 86% of that at baseline when the radiation dosage is less than 25Gy and less than 31% when dosage is greater 40Gy. In general, when radiation dosage is higher than 30Gy, the damage is substantially larger and the recovery rate appears to be much slower.

Table 3.

Posterior Means of Parameter Estimates of Model Specified in Equation (i) for Unstimulated Saliva Flow Rates and Their 95% Equal Tailed Bayesian Credible Intervals (CI).

Time	Parameter	Posterior Mean	(95% CI )
Baseline	α0	2.44	(2.261, 2.40)
Dose (1 Month)	α11	−0.0447	(−0.0625, −0.0491)
Dose (3 Months)	α12	−0.0499	(−0.0688, −0.0544)
Dose (6 Months)	α13	−0.0499	(−0.0701, −0.0544)
Dose (12 Months)	α14	−0.0262	(−0.0415, −0.0302)
Dose (18 Months)	α15	−0.0229	(−0.0396, −0.0272)
Dose (24 Months)	α16	−0.00633	(−0.0226, −0.0107)
† (Dose - 25)+	α2	−0.0609	(−0.108, −0.0741)
† (Dose - 45)+	α3	−0.0734	(−0.205, −0.110)

^†(Dose - 25)⁺ represents the difference between radiation dose and 25 if the dose is greater than 25Gy, otherwise, the quantity equals 0. (Dose - 45)⁺ is similarly defined.

Figure 4.

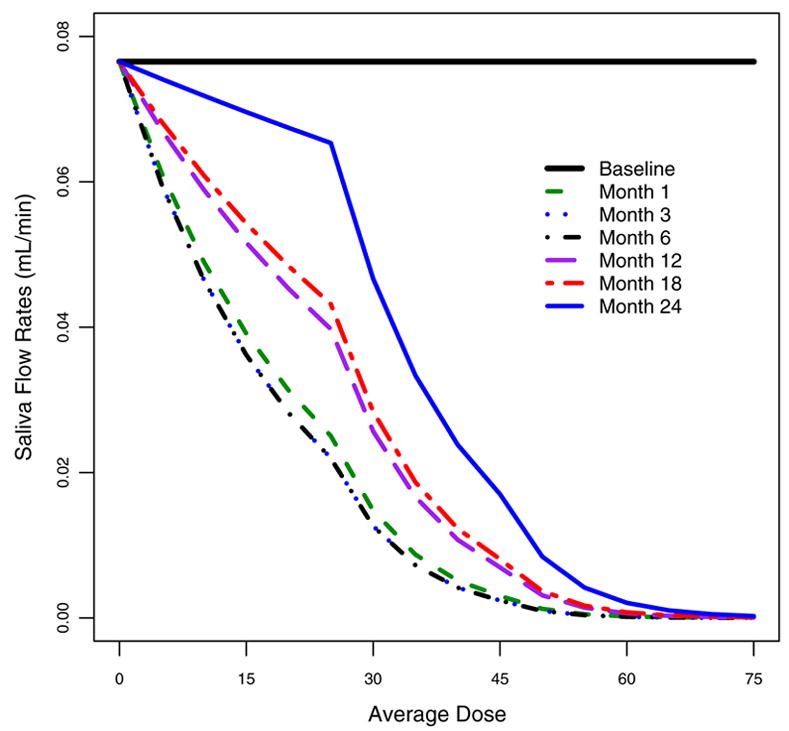
Mean unstimulated saliva counts predicted by the estimated model specified in equation (i) for baseline and 1, 3, 6, 12, 18, 24 months after RT.

As well as the predicted mean values presented in Figures 3 and 4, the models can also give whole distributions of likely saliva measurements. These are illustrated in Figure 5. This graph illustrates the heterogeneity in saliva flow rates between patients. The plots show the predicted saliva flow distributions at 18 months for a patient who receives a mean dose of 0Gy (pre-treatment), 20Gy, 30Gy and 40Gy. With or without stimulation, there is a considerable spread of possible saliva values, particularly at 20Gy, but much less spread at 40Gy. Under stimulation, the spread at 20Gy is slightly larger and slightly shifted to the right relative to that at 0Gy, indicating parotid glands likely generating more saliva at 18 months after RT than that before RT. However, no such phenomenon is observed under the unstimulated condition.

Figure 5.

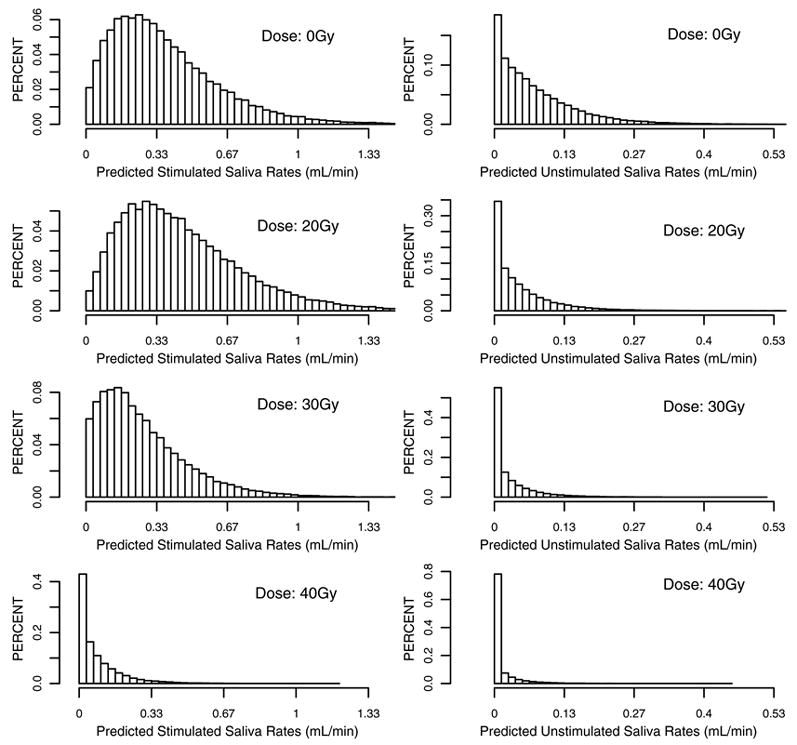
Distribution of saliva flow rates with and without stimulation at 18 months after radiation therapy when the mean radiation dose is 0, 20, 30, and 40Gy, respectively,

The extended negative binomial model in (ii) allows for us to evaluate the possible overcompensation effect in one parotid gland due to very low saliva flow rates from the patient’s other parotid gland. It is fit to both stimulated and unstimulated data. The extra coefficients are insignificant in both cases, indicating a lack of compensation from the opposite parotid, i.e. for stimulated saliva flow rates: α₄ =−0.051, 95%CI: (−0.16, 0.056); and for unstimulated saliva flow rates: α₄ =−0.11, 95%CI: (−0.28, 0.058). These results provide no evidence that the parotid with more functionality is producing more saliva in order to compensate for very low productivity from the other more impaired side.

DISCUSSION

In this paper we examined the radiation damage to the parotid glands and their functional recovery over the course of two years after radiation therapy. The amount of radiation exposure plays a central role in this process. A dose response is observed with the higher the radiation dose received the higher the extent of damage from radiation to parotid glands. The relationship between radiation dose and the reduction in saliva output is not linear. It appears that there is a significant increase in the extent of damage when radiation dose is greater than about 25Gy. When the radiation dose is above 45Gy approximately, the damage seems to reach a maximum with most parotid glands producing negligible saliva. The saliva reduction is the largest in the first month after radiotherapy followed by a gradual recovery. By the end of two years, most of the parotid glands receiving less than 30Gy have completely recovered their functionality in producing secretions under stimulated condition. Although we observe a very slow but gradual recovery for some parotid glands that received more than 45Gy, most of them can only produce very small or negligible amount of saliva two years after RT.

Most of the parotid glands that received less than 30Gy can generate more stimulated saliva output two years after RT than that before RT. The reason for this is not clear, but it does not appear to be associated with the saliva flow from the opposite parotid being very low. A similar phenomenon of overshoot in recovery following low doses is observed in radiation to the jejunum in animal experiments (17). In those experiments the number of cells per crypts after low doses of radiation is on average higher than in unirradiated animals. The theory is that a low dose of irradiation is not enough to kill all the cells in the stem cell compartment, but is sufficient to damage the compartment; the compartment then reacts by regenerating itself. However, the mechanism for regeneration overshoots. Whether such a similar phenomenon is plausible for the parotid cannot be assessed from our data.

The unstimulated saliva flow rates are significantly lower than the stimulated flow rates. They also show a dose response relationship. However the process of recovery does not start until at least 12 months after radiation and the flow rates do not return to the original pre treatment levels even after 24 months.

Our results show that the recovery process for the parotid glands to generate saliva is different between stimulated conditions and unstimulated conditions. Perhaps this results from the different biological mechanisms under the two conditions. For example, during resting conditions without stimulation, the submandibular glands secrete more saliva than the parotid glands; however, under stimulating condition, the main contributors for producing saliva are the parotid glands (7). Although this indicates the biological process can be different under the two conditions, it does not explain the difference in the recovery. Another hypothesis is that mechanisms that cause the parotid to respond to stimulation and produce more saliva are only minimally impacted by radiation doses below 25Gy. These and other possible factors may contribute to the difference between the stimulated and unstimulated recovery. However the full explanation of the differences cannot be deduced from the data in this paper.

The fact that there is recovery of the saliva flow rate over time has been noted by us and other authors (11, 18–21,29). Whether there are different mechanisms at play for the early (1–3 months) and the late (12–24 months) damage has been studied in in-vivo experiments (22, 23). Zeilstra (23) suggests that the early loss in function is due to compromised functioning of the acini, whereas the late effects are due to death of the normally proliferating cells. Vissink (24) concludes that early changes are due to irradiation damage to membrane structures, whereas late changes are dependent on repopulation of surviving stem cells. Stephens suggests that serous acini are the target cells and that interphase death is also important in early phase death, whereas late atrophy is a consequence of early injury rather than being due to damage to the vasculature. Thus the differences we see between early and late effects do have a rationale from these in-vivo studies, and the suggestion that the late damage is a consequence of early damage would be consistent with the sharp drop off in saliva production and minimal recovery for doses over 40Gy.

In this paper we have summarized the dose DVH to the parotid by its mean. There is a large literature on normal tissue complication models (NTCP) which includes different ways to summarize DVH’s (25, 26, 27). Others have investigated whether there are summaries of the DVH more strongly associated with saliva flow rates. For example, power law NTCP models have been used (6) and the optimal percentile of the DVH has been considered (28). By summarizing the dose by the mean we are implicitly ignoring the spatial aspects of the dose distribution, thus effectively assuming that the parotid is homogeneous. Other factors that may play a role in impacting the saliva production are fractionation effects; in particular we might expect a different effect of fraction size for the early and late responses. The statistical model we have presented can be extended to allow for these additional features, although larger sample sizes may be needed to get reliable information about these effects.

Our study uses an updated version of the data presented by Eisbruch et al (6). The number of patients increased from 88 to 142, the number of parotids increased from 152 to 266 and the maximum follow-up time is two years instead of one year. Eisbruch et al (6) examined the possible threshold values where saliva flow reduced to zero after radiotherapy and used a different statistical approach. They found that the best value for a threshold was 26Gy for stimulated saliva and 24Gy for unstimulated saliva. At doses higher than these thresholds there was very little saliva production and no significant recovery over time. At doses below the threshold they found a model which described the data that showed recovery over time and no relationship with dose. In a later paper by Eisbruch et al (29), they showed further recovery of the saliva flow rate after one year. In the current paper, we focus on modeling the relationship between saliva production and its recovery and radiation dosage received. There are some differences in the assumed model between our work and that shown in Eisbruch et al (6), for example, we assume that the dose-response relationship is continuous, rather than assuming that an absolute threshold exists. We chose a two knot spline to give a flexible, yet continuous curve for the dose-response relationship. We placed the knots at 25Gy and 45Gy, because they were well spaced interior doses and preliminary analysis suggested there may be noticeable changes in the effect of radiation at around these doses. In the model we also allow the salivary recovery as a smooth function of radiation dose received. We assume that the saliva production is roughly the same as the baseline at different time point when the radiation dose is zero and should only differ slightly from the baseline values when the radiation dose is very small. Because of the larger sample size, the longer follow-up and different statistical approach, we are able to examine some other features of the data. For example, rather than an absolute threshold in the dose response, we found a steep decline in the saliva production in the range 25Gy to 35Gy. We were also able to detect a modest but incomplete recovery of saliva flow rates at doses in the range 25Gy to 40Gy. For example, when patients receive 38Gy radiation doses, based on the fitted model, the stimulated saliva flow rates increase from 7% one month after RT to 35% of the baseline two years later.

One feature of this paper is the sophisticated statistical modeling. The hierarchical non-linear regression model we develop for these data enables us to capture the relationship between saliva and radiation dosage and the recovery of saliva over time. This model cannot be fit using standard software, it was fit using a Bayesian estimation method with code written specifically to fit this model to these data. It will also be possible to generalize and extend this analysis to accommondate a more complex framework. Using such a model, we can more efficiently use the data by making reasonable distributional assumptions. In our analysis, we assume a negative binomial distribution for the rounded saliva flow rates and introduce a random effect, this random effect allows each parotid to have a generally higher or lower than expected saliva flow rate, and can accommodate the excess of zero saliva flow rates after high doses of radiation. We can use these models to predict the extent of radiation damage on parotid glands in terms of their ability to produce saliva. The results of the model can be graphically represented, as in figures 3, 4 and 5. These figures are designed to help the physician and the patient in planning the dose to each parotid and in understanding the extent to which it may recover over time.

Appendix

The prior distributions of all regression parameters, α₀ , α₁, α₂ , α₃ , were assumed to be normal distributions N(0, 1000). We specify an informative prior Gamma (4, 4) for β so that β is around 1. The prior distribution for the variance parameter ${\sigma }_{\theta }^2$ is inverse Gamma (2.001, 2) so that it has a very large variance. Then the joint posterior density of all parameters f (ϕ| data) is proportional to

$$\left\{\prod _i\left[\prod _j\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}{\left(\frac{1}{\beta +1}\right)}^{y_{ij}}\right]\pi ({\theta }_i)\right\}\pi ({\alpha }_0)\prod _{j=1}^6\pi ({\alpha }_{1j})\pi ({\alpha }_2)\pi ({\alpha }_3)\pi ({\sigma }_{\theta }^2)\pi (\beta )$$

where, π(α₀), π(α_1j), π(α₂), π(α₃), π( ${\sigma }_{\theta }^2$) and π(β) and are prior distributions for those parameters. The estimates for the above model are obtained using a Markov Chain Monte Carlo (MCMC) procedure. This is an iterative procedure in which each parameter is drawn in turn from its conditional distribution given the remaining parameters and the data. Upon convergence we have draws from the posterior distribution, which are then used for inference. The conditional distributions for each of the parameters are given below.

Sample ${\sigma }_{\theta }^2$ from inverse gamma $(\frac{n}{2}+\phi ,\frac{\sum {\theta }_i^2+2\omega }{2})$

Sample θ_i ’s from $f({\theta }_i\mid .)\propto {\displaystyle \prod _j}\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}\frac{e^{-{\theta }_i^2/(2\times {\sigma }_{\theta }^2)}}{{\sigma }_{\theta }}$

Sample α₀ from $f({\alpha }_0\mid .)\propto {\displaystyle \prod _i}\left[{\displaystyle \prod _j}\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}\right]e^{-{\alpha }_0^2/(2\times 10000)}$

Sample α_1j from $f({\alpha }_{1j}\mid .)\propto {\displaystyle \prod _j}\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}{e}^{-{\alpha }_{1j}^2/(2\times 10000)}$

Sample α₂ from $f({\alpha }_2\mid .)\propto {\displaystyle \prod _i}\left[{\displaystyle \prod _j}\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}\right]e^{-{\alpha }_2^2/(2\times 10000)}$

Sample α₂ from $f({\alpha }_3\mid .)\propto {\displaystyle \prod _i}\left[{\displaystyle \prod _j}\left(\begin{array}{c}{y}_{ij}+\beta {\mu }_{ij}-1\\ y_{ij}\end{array}\right){\left(\frac{\beta }{\beta +1}\right)}^{\beta {\mu }_{ij}}\right]e^{-{\alpha }_3^2/(2\times 10000)}$

A C program was developed to fit the MCMC. We assessed the convergence using trace plots starting from different initial values. After 250,000 iterations of burn-in period, we saved every 100^th iteration and collected a total of 2,500 simulation draws. We can obtain the mean, median, credible intervals and other summary statistics of interest from these draws of the posterior distributions of the model parameters. Posterior predictive checks are used to assess the fit of the model (30). In this method, data are simulated from the fitted model and summary statistics from the original data are compared with those from the fitted data.