Stepped versus continuous rotatory motors at the molecular scale

Abstract

Nature invented molecular rotatory devices such as the flagellar motor and ATP synthase. Photoselection techniques have been frequently used to detect the rotational random walk of proteins but only rarely for the rotational drift of subunits in proteins. Pertinent theories predict an oscillatory behavior of the polarization anisotropy, r, for unidirectional rotational drift, as opposed to a monotonic relaxation of r for bidirectional random walk. The underlying assumption of an angular continuum is questionable for intersubunit rotation in proteins. We developed a theory for stepped rotatory devices. It predicts the damped oscillation of r under unidirectional drift. Damping increases with decreasing number of steps. For only three steps a quasi-monotonic relaxation of r is predicted for both random walk and drift. In photoselection experiments with active F-ATPase we observed the relaxation of r when a spectroscopic probe was attached to the central γ-subunit. This behavior is compatible with the expectation for a three-stepped rotatory device.

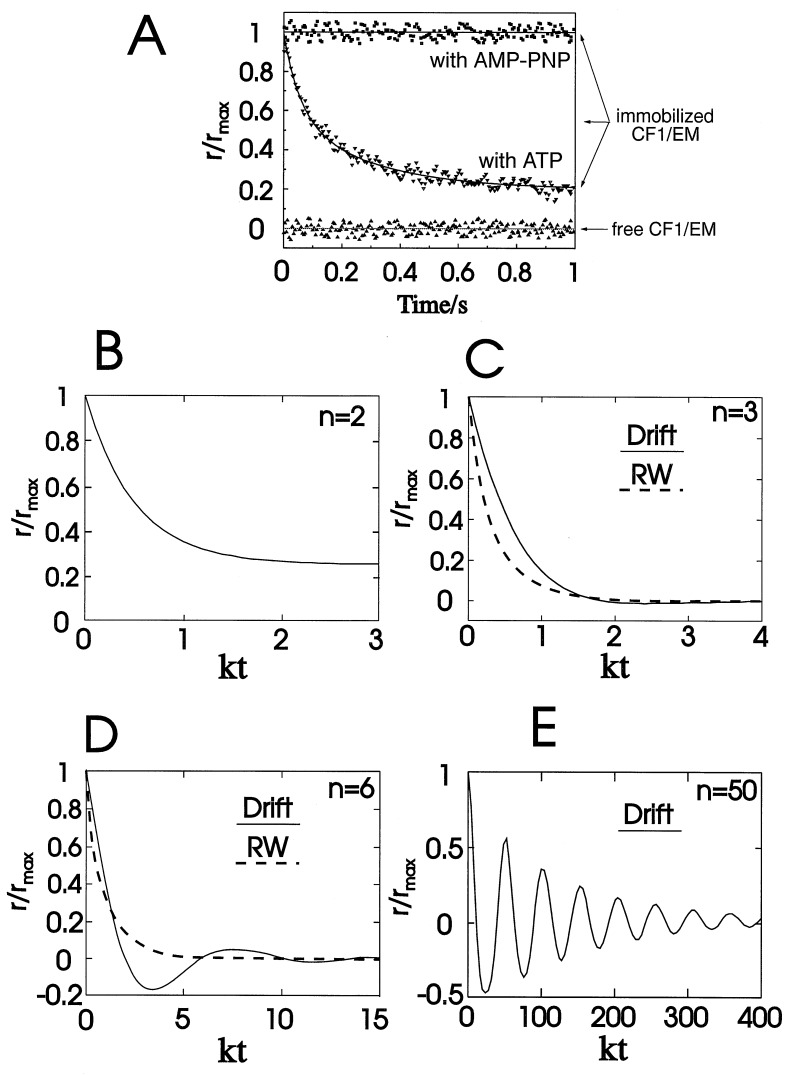
In the flagellar motor and in ATP synthase (F-ATPase) protein subunits rotate against each other. The rotation of bacterial flagellae has been detected in the light microscope by the rotation of the cell body after tethering of the flagellae to a solid support (1). The detection of rotatory motion in objects of smaller size like subunits in ATP-synthase or the load-free flagellar motor requires less macroscopic techniques. Recently, we detected and time resolved the activity-linked intersubunit rotation in F-ATPase by PARAP (polarized absorption recovery after photobleaching) (2). This spectroscopic technique applies to a large ensemble of molecules and is based on orientational photoselection. Rotational motion causes a transient of the polarization anisotropy, r (see Eq. 1). In these studies we observed a monotonic relaxation of the polarization anisotropy of a probe which was attached to γ-subunit of this enzyme. It occurred in about 100 ms, which conformed with the turnover time of the enzyme under the given experimental conditions (see Fig. 4A for data and Fig. 3 for the enzyme structure).

Figure 4.

Evolution of r/r_max as a function of time after a laser flash at t = 0 for stepped, uniaxially rotating devices (see text). (A) Experimentally observed (2). (B–E) Theoretical (this work). The inclination angle θ is set as 54.7° (magic angle). (A) Observed transients of r of γ-labeled, immobilized F-ATPase in the inactive (horizontal trace) and active state (monotonic decay). (B) Number of steps: n = 2. Rotational drift is undistinguishable from rotational random walk. (C) n = 3 (solid line, drift; broken line, random walk). Rotational drift is practically undistinguishable from rotational random walk. (D) n = 6 (solid line, drift; broken line, random walk). Rotational drift causes damped oscillation of r. (E) n = 50 (drift only). Rotational drift causes damped oscillation of r.

Figure 3.

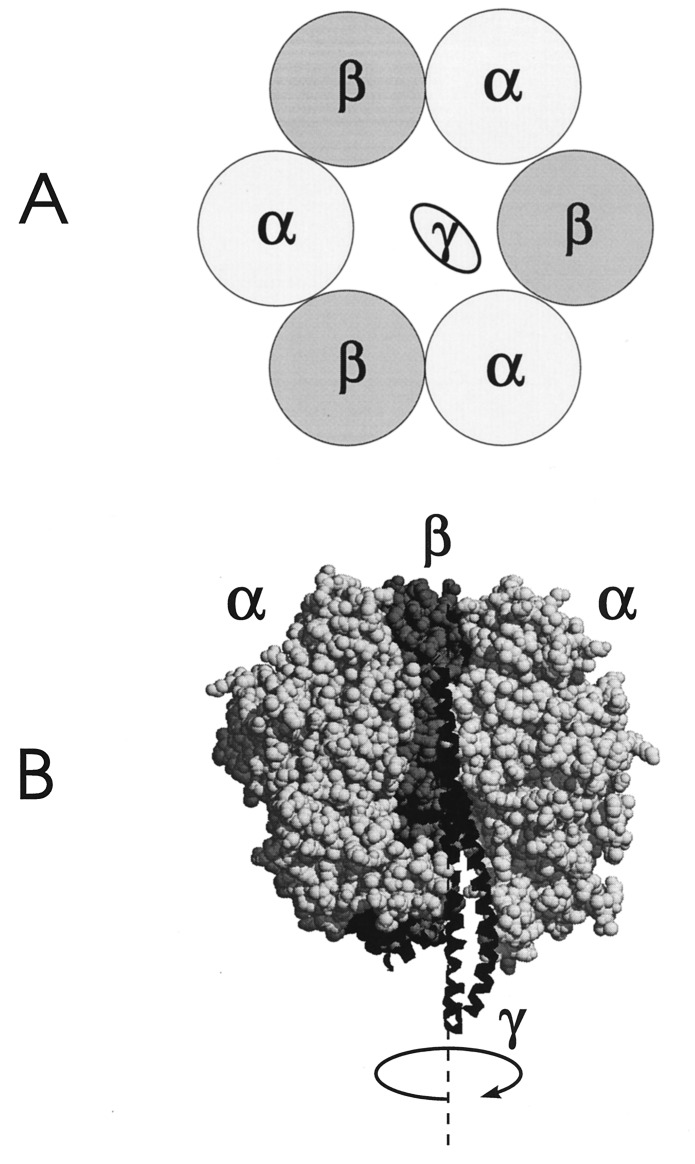
(A) Schematic view of the arrangement of subunits α, β and γ of F-ATPase. The three α- and three β-subunits alternate to form a hexagon with the rotatory γ-subunit in its center. (B) Partial structure of mitochondrial F₁ (8) with the front region removed to expose the γ-subunit shown (as a ribbon).

Does the transient behavior of r allow to discriminate between rotational random walk which is bidirectional from rotational drift under a driving force which is unidirectional? For a true rotatory motor—i.e., for drift without superimposed random walk—one expects an oscillatory transient of the r-parameter, and for rotatory random walk a monotonic decay. Theories for rotatory random walk and drift have been published by various authors (3–7). A theory by Hoshikawa and Asai (7) supports the above-mentioned expectation. Applying their equation 23 to a situation where the stator of a molecular rotatory motor is immobilized and a spectroscopic probe is attached to the rotor, an undamped oscillation of r is predicted. Their approach, however, is based on Fick’s phenomenological equation for diffusion in a continuous angular space. Considering the flagellar motor and even more so the atomic structure of F-ATPase (8) (see Fig. 3), this assumption may be questionable. In this article we developed a theory for noncontinuous rotatory devices—i.e., for molecular stepping motors.

Photoselection and the Anisotropy Parameter r

When photoselection experiments are carried out in absorption, two beams of linearly polarized light impinge at right angles on a sample containing an originally isotropic ensemble of chromophore molecules. The exciting flash of light causes absorption transients, ΔA, which are recorded by the continuous measuring beam. Because of its nonsaturating energy, the exciting flash photoselects an oriented subset of chromophores. Accordingly, the magnitude of absorption transients differs depending on whether the E-vector of the interrogating beam is polarized in parallel (ΔA_∥) or perpendicularly (ΔA_⊥) to the one of the exciting flash.

Data are usually interpreted in terms of the polarization anisotropy parameter r(t) (9):

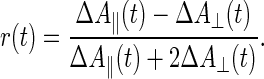1

The evolution in time of the anisotropy parameter, r(t), reflects the rotational motion of the chromophores. If an ensemble of chromophores is heterogeneous with respect to its rotatory properties, the resulting behavior of r is additive with weight factors which are proportional to the relative number of molecules in a given subset x_i:

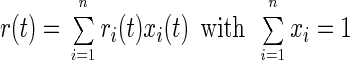2

Eq. 2 is a consequence of the additivity of absorbance, ΔA_tot = ∑ ΔA_i.

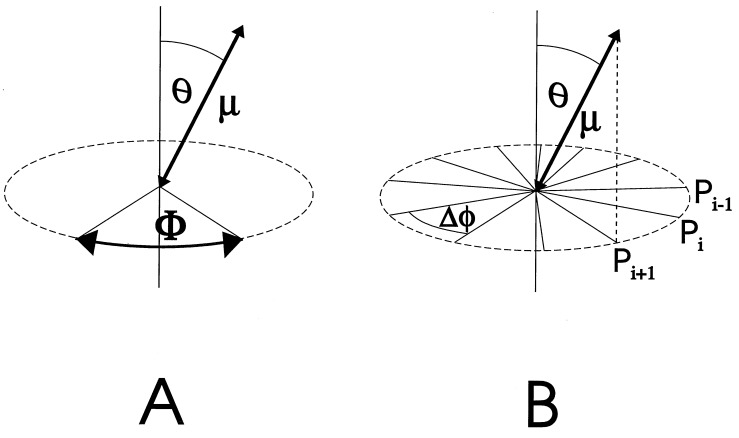
In this work, we examine the intersubunit rotation in a large ensemble of proteins that are fixed in space. The angular distribution of the proteins is isotropic. We consider a situation in which a single chromophore is attached to one particular subunit that rotates relative to the immobilized protein body. We assume only a single axis of rotation. The transition moment μ of the chromophore be inclined at an angle θ to the fixed axis of rotation (Fig. 1). The angular coordinate of rotation is the angle φ.

Figure 1.

Schematic drawing of a uniaxially rotating device with a covalently attached chromophore (transition moment μ), which is inclined at an angle θ toward the axis of rotation. (A) Continuous device: every position in the angular domain Φ can be occupied. (B) Stepped device: only discrete angular positions P_i(φ_i) are accessible; they are symmetrically arranged on a circle (Δφ = φ_i+φ − φ_i).

Rotational Random Walk and Rotational Drift in a Continuum

A rotatory device at the molecular scale undergoes Brownian rotational diffusion in response to very frequent (10¹³ s⁻¹) collisions with neighboring molecules (water, lipids, or protein residues). The kinetic energy of rotation is rapidly thermalized, and the average stop-distance is of subatomar length (10). The rotational diffusion is usually treated by a continuum approach as given by Fick’s equations. If there is a net driving force for rotational motion (e.g., protonmotive force in flagellae and ATP-synthase) rotational drift is superimposed on the rotational random walk. This adds a harmonic component to the rotational relaxation. Theories on the uniaxial rotational diffusion and drift in a continuum have been laid out by various authors (4, 7, 11–13).

Unrestricted rotational random walk causes the monotonic decay of the polarization anisotropy, r, by two exponentials down to a steady level, r(t → ∞), which depends on the inclination angle θ (4, 11, 12).

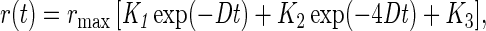3

with K₁ = 3sin² θ cos² θ, K₂ = 0.75sin⁴ θ, K₃ = 0.25(3cos² θ − 1)², and ∑_i=1³ K_i = 1.

D denotes the rotational diffusion coefficient and r_max the initial value at time zero after the exciting flash of light. For a chromophores with a nondegenerate transition, r_max = 0.4. If the transition is degenerate, r_max is smaller than 0.4 (see ref. 14 for heme a₃).

The steady level that is reached after infinite time,

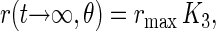4

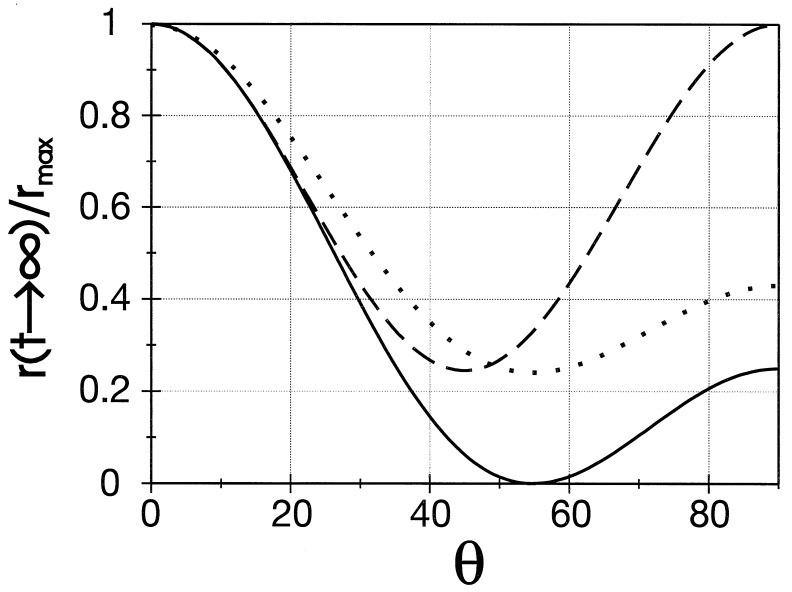
depends on the inclination angle θ. It is 100% of r_max (no decay) if θ = 0° and, for example, it is zero for θ = 54,7° (magic angle). This dependence is illustrated by the solid curve (A) in Fig. 2.

Figure 2.

The relative magnitude of the polarization anisotropy after infinite time, r(t → ∞)/r_max, as a function of the inclination angle θ. Solid line, unrestricted rotational random walk in a continuous angular space or in discrete angular space with C_n-symmetry (n ≥ 3). Broken line, stepped rotor with only two steps, φ₁ = 0° and φ₂ = 180° (C₂-symmetry). Dotted line, stepped rotor with only two steps, φ₁ = 0° and φ₂ = 120° (S₂-symmetry)

If the motion is restricted to an angular domain Φ (see Fig. 1A), the anisotropy parameter decays by an infinite series of exponentials and its steady value also depends on the width of the angular domain Φ as worked out by Wahl (13):

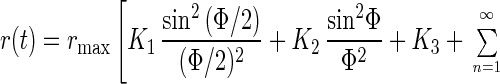5

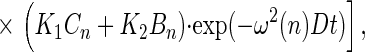with ω(n) = nπ/l. For K_1,2,3 see above and for the coefficients B_n and C_n see ref. 13.

The steady level is given by

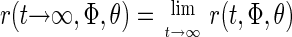6

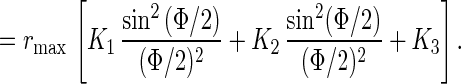The above considerations hold for random (i.e., bidirectional) walk. The superimposition of rotational random walk and drift has been treated by Hoshikawa and Asai (7). Depending on the ratio between the angular velocity of the drift, Ω, and the rotational diffusion coefficient, D, they calculate a more or less damped oscillation of the r-parameter. Drift alone causes undamped, harmonic oscillation of r.

Random Walk and Drift in a Stepped Rotational Device

The assumption of a continuous rotatory motion in proteins may be unrealistic. Fig. 3 shows the partial atomic structure of F-ATPase (8) as an example. Fig. 3A is a schematic drawing of the hexagon made up from three α- and three β-subunits. The rotatory γ-subunit is positioned in its center. Fig. 3B shows the side view with a front portion of the large subunits removed to expose γ within the middle. Although the enzyme reveals an approximate C₆-symmetry structurally, its functional symmetry is less, in the time average probably C₃, since it contains three catalytic sites that are mainly positioned on the β-subunits at the interface with the α-subunits. Inspection of Fig. 3 suggests that the angular probability distribution of γ-subunit after infinite time may not be continuous as assumed in the above cited theoretical work, but rather granular (as implied by the symmetry of this enzyme). It is conceptionally more appealing to consider the rotational motion of γ in terms of transitions from position A to B to C to … and finally cycling back to A to B, etc.

Master Equations

We consider uniaxial, rotational devices with n positions P_i(φ_i) (see Fig. 1B) that are equivalent and equidistantly distributed over a circle (C_n-symmetry):

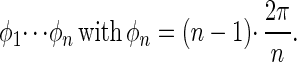7

We assume that the residence time at any of these n-positions is much larger than the one at any interstitial position. This conforms with the design of a stepping motor. We denote by x_i the probability to find elements of a large ensemble of stepping motors in position i (i = 1, 2 … , n). Accordingly

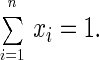8

There are two extreme cases of rotational motion, namely drift and random walk.

Drift.

The position of a device changes only in one direction—i.e., from P_i to P_i+1—but not in the reverse direction. In common terms of chemical kinetics this is equivalent to a situation where the back-reaction can be neglected under dominance of forward directed driving force—i.e., far from the thermodynamic equilibrium.

The master equation for clockwise rotational drift is

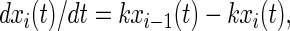9

wherein k denotes the rate constant of a transition from position i − 1 to i. In terms of chemical kinetics we assume (pseudo-)first-order reactions. It is implicitly assumed in Eq. 9 that the ensemble behaves ergodically, or in biochemical terms, that the enzyme preparation is homogenous.

We use one and the same transition probability for all transitions because of the assumed equivalence of the n positions and the presupposition that the transitions are mutually independent from each other.

Random Walk.

Transitions from P_i to P_i+1 and from P_i to P_i-1 are allowed with equal probability. The master equation for random walk is:

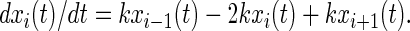10

In both cases and for each molecule the jumps from one position to the next are randomly distributed in time, although obeying to the same statistical distribution. A very large ensemble of molecules justifies the approximation of the random jump intervals by their ensemble average, as expressed by one and the same rate constant k.

Defining the state vector of the probability distribution

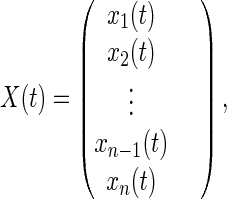11

the evolution in time of this state vector is given as

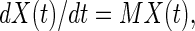12

wherein M is the matrix representing the respective master equation (Eqs. 9 and 10). For clockwise drift:

13

And in the case of random walk:

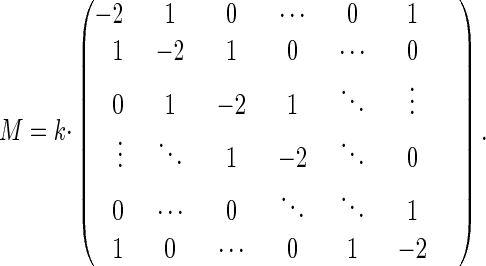14

The solution of the respective master equation (Eq. 12) is given by

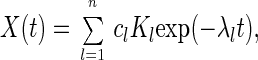15

with

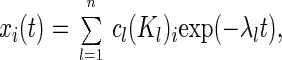wherein λ_l denotes the eigenvalues and K_l the eigenvectors of the respective matrix M. The eigenvalues λ_l result from the equation

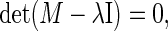16

and the eigenvectors K_l are given by

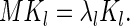17

Using the initial conditions x_i(t = 0) one calculates the constant coefficients c_l.

The solutions to Eq. 12 can be obtained by standard procedures. We obtained analytical solutions for n = 2 and 3 and numerical solutions of Eqs. 16 and 17 for n > 3 by using the mathcad software. Specific sample solutions are discussed below.

Implications for Photoselection Experiments: Some Special Cases

In a photoselection experiment (as described above) the exciting, linearly polarized flash of light photoselects an oriented subset of chromophores. By arbitrary choice we asign the initial position of each rotor in this subset of devices, that was hit by the flash, as P₁(φ₁ = 0).

The initial distribution of excited molecules is then given by

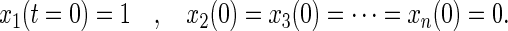18

With a nondegenerate chromophore the initial value of the polarization anisotropy is r(t = 0) = r_max = 0.4. A given subset of chromophores connected to devices that have moved into their respective new position P_i(φ_i) contributes a value to the anisotropy parameter, r(φ_i,θ), which depends on the angles φ_i and Θ. φ_i and Θ are defined in Fig. 1:

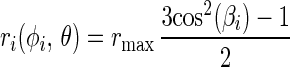19

with

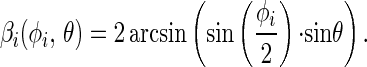According to Eq. 2, the overall anisotropy parameter of the ensemble, r(t), is the weighted sum of these contributions, namely

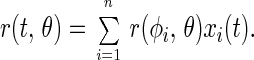20

In the following we discuss some special cases.

Two Positions (n = 2).

In the case of devices with only two positions P₁(φ₁ = 0°) and P₂(φ₂ = 180°) (C₂-symmetry) the matrices for rotational drift and random walk are identical, giving rise to the same redistribution behavior:

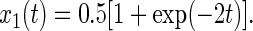21

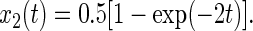22

The calculated transient of the polarization anisotropy, r, decays monotonically to a steady level as shown in Fig. 4B. The magnitude of this level is given by Eq. 23.

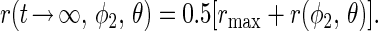23

Fig. 2 (broken line) shows the dependence of the relative magnitude of the steady level of r, r(t → ∞,φ₂,θ)/r_max, on the inclination angle θ. Its minimum value is 0.25.

If symmetry is reduced from C₂ to mirror symmetry S₂ (φ2 ≠ 180°) and if one assumes one and the same rate constant k for the transitions P₁ → P₂ and P₂ → P₁, the Matrix M is the same as for C₂-symmetry. As a consequence, Eqs. 21–23 are still valid. Fig. 2 (dotted line) shows r(t → ∞,φ₂,θ)/r_max as function of the inclination angle θ (with φ₂ arbitrarily set as 120°). Its minimum value is 0.25 for any angle φ₂.

Rotational Drift.

If there are more than two positions, the eigenvalues of M are complex numbers in the case of rotational drift. Accordingly, x_i(t) and r(t) reveal damped oscillations (see Eq. 15).

For three positions (n = 3) one finds the following complex eigenvalues of M:

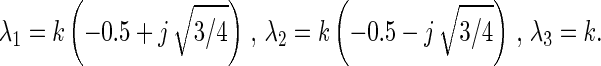24

The constant coefficients are:

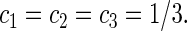25

The master equation for rotational drift (Eq. 12) has the following solution:

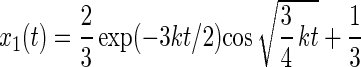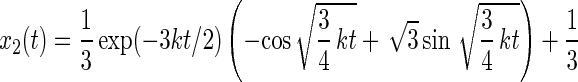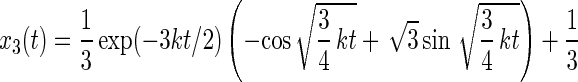26

The respective probabilities x_i are oscillatory and damped. The anisotropy parameter r(t) divided through its maximum value r_max is plotted in Fig. 4C. The damping almost fully hides the oscillation, so that the oscillation of r(t) in time is practically undetectable.

If there are more than three positions (n > 3), the damping becomes weaker and the harmonic behavior is the more pronounced the larger is n. Fig. 4 C and D show r(t)/r_max in the case of six and fifty symmetrically arranged positions. The lessened influence of dephasing is a consequence of the relative contraction of the angular distribution under the law of great numbers.

Rotational Random Walk.

In this case the eigenvalues of M are real numbers, there are no oscillating terms in x_i (t) and r(t). The anisotropy parameter decays monotonically. Fig. 4 B and C (broken lines) show r(t)/r_max for rotational random walk over three and six symmetrically arranged positions.

The steady levels of r after infinite time are the same for rotational drift and rotational random walk. For n ≥ 3 they are also the same for stepped and for continuous rotatory devices (see Eq. 4). The dependence of their relative steady level as function of the inclination angle θ is plotted in Fig. 2 by a solid line.

Summary and Discussion

Rotatory molecular motion is essential for the functioning of motor proteins, as kinesin/myosin and the flagellar motor, but also for ATP synthase, an enzyme that uses transmembrane protonmotive force to synthesize ATP. The (intact) flagellar motor has allowed the direct observation of its internal rotational motion due to the large size of the bacterial cell body (1). To detect the intersubunit rotation in more microscopic systems one has recurred to more indirect techniques [e.g., by measuring the vibrations of free hooks in the load-free flagellar motor (15)]. Aiming at the catalytic mechanism of F-ATPase we used a particular photoselection technique to resolve in real-time the rotational motion of one central subunit relative to the bulk of this enzyme (2). Published theories for a continuous rotatory device predict that the transient behavior of the polarization anisotropy (the r-parameter) allows to clearly dichotomize between rotatory random walk and unidirectional rotatory drift under driving force. Rotatory drift causes the oscillation of the polarization anisotropy whereas rotatory random walk causes its monotonic relaxation. Intersubunit rotation may be considered as quasi-continuous in the flagellar motor. Eight motor elements (16) and probably 120 proton binding sites [i.e., 1000 protons translocated per revolution (17)] are distributed over the perimeter of the flagellar disk (for reviews, see refs. 18–20). A fluctuation analysis revealed a minimum number of 400 steps per revolution (21). In F-ATPase, on the other hand, because of its about 10-fold smaller perimeter, the rotation is expected to be more granular.

In the present article we showed that if the number of steps is large, a stepped rotatory device behaves similarly as a continuous one, except for a (small) damping of the oscillations of the r-parameter (even under drift). If the number of steps is small, however, the dephasing of the transitions from one stepped position to the next is more severe. A three-stepped rotor is expected to show a quasi-monotonic relaxation of the r-parameter not only under rotatory random walk but even under strictly unidirectional drift.

We have observed the quasi-monotonic relaxation of the r-parameter in photoselection experiments with the active F-ATPase from chloroplasts (2). In these experiments the central γ-subunit has been labeled with a photobleachable dye (eosin-5-maleimide) and the enzyme body, (αβ)₃, immobilized on large globules of a cation exchange resin. The relaxation of the r-parameter in the time domain of several 10 ms has been observed if the enzyme was actively turning over, but not if the enzyme was inactivated. Data of this work (2) are reproduced in Fig. 4A. To avoid misconception, it is worth mentioning that the observed relaxation of r has been initiated by photolysis of the dye in the presence of ATP and while the enzyme was repetitively turning over before and after the photoselecting flash. Accordingly the relaxation is caused by the continuous operation of the enzyme and not by a single transient from one particular conformation into another one as might have happened in laser-flash experiments with caged-ATP, that has not been used in these experiments.

F-ATPase carries approximately C₆-symmetry structurally and C₃-symmetry functionally (see Fig. 3 and refs. 8 and 22). An alternating or rotatory mechanism of catalysis involving its highly cooperative nucleotide binding sites has been established by biochemical evidence (see ref. 23) and corroborated by electron microscopy (24), by x-ray crystal-structure analysis (8), and by the use of cleavable cross-linkers (25). Our results proved for the first time that γ-subunit was rotating in the time domain of the catalytic turnover and over a large angular range (>200°). But, did they discriminate rotational drift against rotational random walk?

According to the theory for stepping motors, the observed quasi-monotonic relaxation of the r-parameter in ref. 2 was to be interpreted in the following ways.

(i) If the number of reaction steps was greater than three the experimental result implied that γ-subunit was simply unlatched to carry out random rotational walk, once the enzyme was active. Even worse, it had to be assumed that the time course of this motion accidentally matched the one of the enzyme’s turnover. This interpretation seems rather far-fetched considering the pivotal role of γ-subunit both in ATP hydrolysis by isolated F1 and in the proton-driven ATP synthesis by the membrane-bound holoenzyme, FOF1 (for reviews, see refs. 26–28).

(ii) If F-ATPase behaved as a stepped device with only two accessible sites in C₂- or S₂-symmetry, the relaxation of r without any sign of oscillation was to be expected. This option, however, is incompatible with the observed relative magnitude of r in the steady-state that was 0.018 (2) and therewith significantly lower than the predicted minimum of 0.025 under these conditions (see Fig. 2).

(iii) If, on the other hand, F-ATPase behaved as a three-stepped motor, driven around by the force derived from ATP hydrolysis, the observed relaxation of the r-parameter (Fig. 4A) was compatible with such a motion (Fig. 4C). Still, the fascinating concept of F-ATPase as a three-stepped molecular motor cannot be proved by ensemble-spectroscopy above, as shown in this work. A discrimination between three-stepped random and drifting rotation can only be expected from spectroscopy on single molecules of F-ATPase.