Comparison of Velocity Profiles for Different Flow Chamber Designs Used in Studies of Microbial Adhesion to Surfaces

Abstract

Flow chambers are commonly used to study microbial adhesion to surfaces under environmentally relevant hydrodynamic conditions. The parallel plate flow chamber (PPFC) is the most common design, and mass transport occurs through slow convective diffusion. In this study, we analyzed four different PPFCs to determine whether the expected hydrodynamic conditions, which control both mass transport and detachment forces, are actually achieved. Furthermore, the different PPFCs were critically evaluated based on the size of the area where the velocity profile was established and constant with a range of flow rates, indicating that valid observations could be made. Velocity profiles in the different chambers were calculated by using a numerical simulation model based on the finite element method and were found to coincide with the profiles measured by particle image velocimetry. Environmentally relevant shear rates between 0 and 10,000 s⁻¹ could be measured over a sizeable proportion of the substratum surface for only two of the four PPFCs. Two models appeared to be flawed in the design of their inlets and outlets and allowed development of a stable velocity profile only for shear rates up to 0.5 and 500 s⁻¹. For these PPFCs the inlet and outlet were curved, and the modeled shear rates deviated from the calculated shear rates by up to 75%. We concluded that PPFCs used for studies of microbial adhesion to surfaces should be designed so that their inlets and outlets are in line with the flow channel. Alternatively, the channel length should be increased to allow a greater length for the establishment of the desired hydrodynamic conditions.

Microbial adhesion to surfaces is the onset of the development of a biofilm. Biofilm formation occurs on all surfaces exposed to an aqueous environment, such as an implanted biomaterial or tooth surface in the human body, rocks in rivers, pipelines in water works, or ship hulls. The rate of adhesion is determined by the number of microorganisms transported to the substratum surface by mass transport processes, like convection, diffusion, or sedimentation (18, 32). In relatively stagnant environments, such as the oral cavity or implanted biomaterial surfaces, convective mass transport (i.e., transport through liquid flow of suspended organisms) plays only a minor role, and sedimentation and diffusion are the main means of mass transport. However, on ship hulls, in rivers, or in water works, convective mass transport of suspended microorganisms is the major mechanism that controls the rate of microbial adhesion. Usually, increased fluid flow towards or parallel to a substratum surface results in faster adhesion of microorganisms due to higher mass transport, despite the presence of higher fluid shear stresses stimulating detachment (8). However, when fluid flow exceeds a critical limit, the resulting wall shear stresses may become high enough to prevent adhesion (21, 25). For instance, in aqueous solutions wall shear rates of 6,000 to 8,000 s⁻¹ were sufficient to prevent adhesion of Pseudomonas fluorescens to stainless steel, while wall shear rates of 12,000 s⁻¹ could remove attached cells. Furthermore, turbulent flow, as opposed to a laminar regime, is known to affect biofilm architecture (36, 38). Which flow regime is present in a situation under investigation is expressed by the Reynolds number (Re); Re values of >1,400 are frequently considered representative of turbulent flow.

Awareness of the importance of hydrodynamic conditions in microbial adhesion to surfaces has encouraged the design of different types of flow chambers by various research groups all over the world. All of the chambers have been designed to have a large surface on which the hydrodynamic conditions remain constant for a wide range of shear rates. In general, inlet and outlet conditions and flow chamber geometry dictate the length required for the flow to become stable and laminar (27). Thus, it is important that all designs are evaluated for establishment of the desired laminar flow conditions at the surface observed.

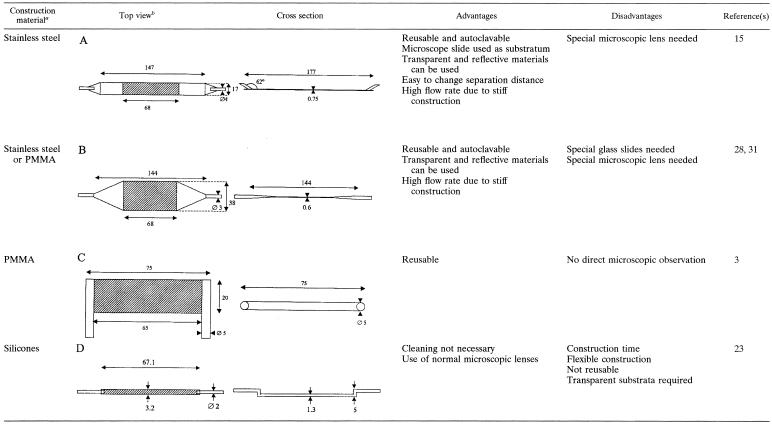
The parallel plate flow chamber (PPFC) is the design that is used most often (2, 4, 7, 11-13, 16, 17, 20, 24, 30, 34), evidently because it is conceptually simple. It can be used in combination with a broad range of materials, like glass, silicone rubber, and dental enamel; even metals can be studied when the appropriate microscopic technique is used (31). Table 1 summarizes the properties and use of four PPFCs that have been described in the literature on microbial adhesion to surfaces. For the different PPFCs shown in Table 1, there are clear differences in the essential dimensions and the design of the inlet and the outlet. Smooth transitions between the different parts of the chamber characterize flow chambers A (15) and B (28), in contrast to flow chambers C (3) and D (23), in which the transitions are more abrupt.

TABLE 1.

PPFCs (A to D) currently used to measure microbial adhesion to substrata, with critical sizes (in millimeters), advantages, disadvantages, and studies in which the chambers have been employed

^aPMMA, polymethylmethacrylate.

^bThe cross-hatched areas are the areas intended for observation.

Because of the increasing use of flow chambers in microbial adhesion research, it is important to critically evaluate the different PPFCs used in microbial adhesion studies in terms of the size of the area where the velocity profile is established with a range of flow rates, so that the chambers can be used to obtain valid observations.

MATERIALS AND METHODS

Flow chambers.

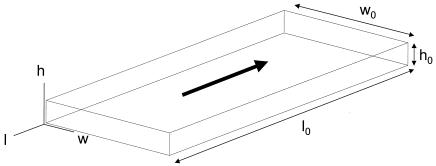
The four flow chambers which we evaluated are described in Table 1. In the analyses the critical sizes of the flow chambers are expressed as fractions of the length (l₀), width (w₀), and height (h₀), as shown in Fig. 1, which results in dimensionless distances. The Re for a PPFC is given by the following formula (6, 33):

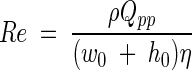(1)

where ρ is the fluid density (in kilograms per cubic meter), Q_pp is the volumetric flow rate (in cubic meters per second), w₀ is the width (in meters), h₀ is the distance between the parallel plates (in meters), and η is the absolute viscosity. For most aqueous fluids, including buffers, urine, and seawater and dilute suspensions of bacteria in these liquids, the absolute viscosity is around 1 × 10⁻³ kg m⁻¹ s⁻¹ at room temperature. Re values up to 1,400 represent a laminar velocity profile with a parabolic velocity profile over an imaginary line perpendicular to the plates.

FIG. 1.

Dimensions of the flow chambers (l₀, w₀, and h₀) and distances in the different directions (l, w, and h). The arrow indicates the direction of the fluid flow.

The hydrodynamic force exerted by the flow on an adhering organism is determined by the velocity profile near the wall. This force is proportional to the increase in fluid velocity from the surface (where the fluid velocity is zero), which is known as the shear rate (in seconds⁻¹). Shear rates can be calculated from velocity profiles determined either by particle image velocimetry or by numerical simulation by using

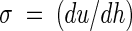(2)

where u is the velocity in the direction of the main flow (in meters per second) and h (in meters) is the height measured perpendicular to the substratum surface in a flow chamber. When laminar flow is well established, the theoretical shear rate in a PPFC at the bottom plate is given by the following formula (9):

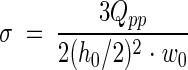(3)

The hydrodynamic force per unit of surface area exposed to a flow is defined as the shear stress (τ_w) (in newtons per square meter), which is obtained by multiplying the shear rate by the absolute viscosity of the fluid involved (19)

(4)

The shear stress should be constant over the area where adhesion is studied. By analyzing the velocity profile with relevant shear rates, this can be checked. The actual shear rates occurring in various environments where microbial adhesion occurs are hard to estimate reliably, but they are important in order to work under the most relevant conditions, as shown in Table 2, which provides a summary of environmental shear rates published previously. The area of the PPFC where a constant velocity profile is present for these ranges of shear rates represents the quality of a flow chamber.

TABLE 2.

Summary of environmental shear rates

Phenomenon	Shear rate (s−1)	Reference
Flow of a film over a vertical plate	0.1	5
Blinking of an eye	0.35	14
Fluid flow in the oral cavity	0.1−50	5
On teeth, while biting an apple	200	10
Urinary cathether	15	35
Channels within a biofilm	60−300	29
Ship in harbor	50	1
Ship navigating (turbulent flow)	125,000	1
Tumbling or pouring	10−100	5

Numerical simulation of velocity profiles by finite element modeling.

The inner geometry of each flow chamber shown in Table 1 was modeled by using the ANSYS-flotran finite element program (version 6.1; ANSYS Inc., Canonsburg, Pa.).

The boundary conditions for the simulation were a fluid velocity at the wall of 0 m s⁻¹ in all directions and atmospheric pressure at the outlet. The density of the fluid and the absolute viscosity of the fluid at 20°C were 9.98 × 10² kg m⁻³ and 1.0 × 10⁻³ kg m⁻¹ s⁻¹, respectively. Uniform inlet velocities were set at 10⁻⁴, 10⁻³, 10⁻², 10⁻¹, and 1.0 m s⁻¹ for each simulation, with the restriction that the Re did not exceed 1400, which ensured laminar flow conditions and shear rates that occur in the environment. Similar uniform inlet velocities, however, resulted in different flow rates for the flow chambers as the cross-sectional surfaces of the flow chambers differed greatly. The flow rates evaluated ranged from 3 × 10⁻⁴ to 25 ml s⁻¹. The simulations resulted in three-dimensional velocity profiles, which were used to determine the position in a flow chamber where the velocity profile became stable and thus was established. First, three perpendicular paths were drawn through the center of the PPFC in the direction of its length, width, and height, and the velocity profile in each direction was plotted. The velocity profile was assumed to be stable and to be established when the velocity changes for the length direction did not change more than 1% and the velocities in the height and width directions were less than 1% of the velocity in the length direction. The useful surface area of a PPFC is determined by the length, height, and width over which flow is stable and established.

Validation of numerical simulations by particle image velocimetry.

A Leica TCS SP2 confocal scanning laser microscope was used for particle image velocimetry. Fluorescent polystyrene microspheres (density at 20°C, 1.055 g cm⁻³; excitation wavelength, 580 nm; emission wavelength, 607 nm; diameter, 0.97 μm; Molecular Probes, Eugene, Oreg.) were suspended in demineralized water at a final concentration of 1 × 10⁷ microspheres per ml (22, 26, 29, 37). A flow chamber was positioned between two communicating vessels placed at different heights and containing the fluorescent particle suspension in order to create pulse-free flow by hydrostatic pressure. Fluid was recirculated with a roller pump between the vessels at the desired flow rate. Velocity patterns were obtained by capturing images over the height and width of the flow chamber by raising and lowering the motorized stage of the microscope and by moving the stage sideward at a fixed focal depth, respectively. Particles traveling across the microscope field of view appeared as dashed lines, and the velocity of a particle was calculated from the distance between the dashes and the time that it took to scan the number of frame lines crossed by the particle. The time that it took to scan one line was calculated from the scanning frequency of the confocal scanning laser microscope and was corrected for the difference in location on the scanning line where the particle crossed the line. Images of slowly moving particles were captured by using a ×40 objective at a scan frequency of 100 Hz, while images of faster particles were captured at a scan frequency of 400 Hz.

Velocity profiles were determined by using particle image velocimetry for flow chambers A and B at a flow rate of 0.050 ml s⁻¹ in order to validate the numerical simulation model. The numerical simulation model was considered to be valid when the shear rates for the bottom plates as calculated by the two methods deviated less than 1%.

RESULTS

Comparison of PPFC by numerical simulation of the flow.

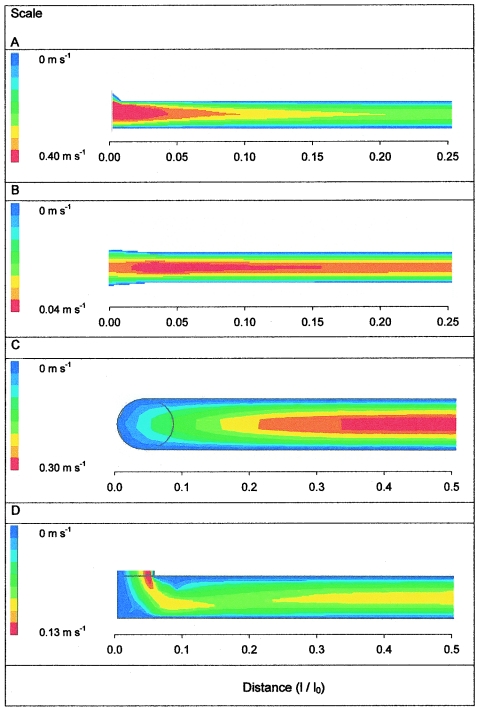
The velocity profiles in longitudinal cross sections of the channels of the PPFCs are shown in Fig. 2. In PPFC A (flow rate, 2.333 ml s⁻¹), the fluid velocity is highest at the transition between the inlet and the parallel plates, but it becomes stable at approximately 0.20(l/l₀ of the channel; i.e., the ratio of the actual distance from the inlet to the length of the channel), which is indicated by the constant width of the color distribution. In PPFC B (flow rate, 0.710 ml s⁻¹) there is also an area with high velocity at the transition to the parallel plates. For the flow rate used, a stable flow develops at approximately 0.20(l/l₀ of the channel). The example given for PPFC C (flow rate, 0.020 ml s⁻¹) involves the least-simulated low flow rate, but even in this case the perpendicularly positioned inlet causes a stagnant region opposite the inlet. As a result, there is stable flow only after the flow traverses approximately 0.40(l/l₀ of the channel). The inlet and outlet design of PPFC D (flow rate, 0.333 ml s⁻¹) also necessitates a change in flow direction. Consequently, the flow also stabilizes rather late in the channel (at approximately 0.45[l/l₀]).

FIG. 2.

Modeled velocity profiles in longitudinal cross section from the inlet to the center of each PPFC at different volumetric flow rates (2.333, 0.710, 0.020, and 0.333 ml s⁻¹ for flow chambers A, B, C, and D, respectively).

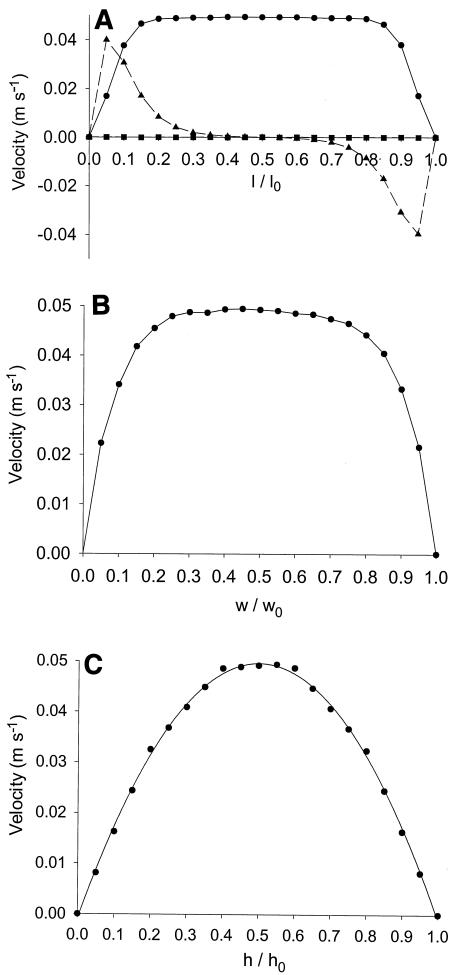
To determine more precisely the area over which flow is stable and established, we analyzed the velocity profile in the center of the PPFC as a function of the length, height, and width of the flow chamber. Examples of the graphs obtained are shown in Fig. 3 for PPFC C. For a relatively low flow rate (0.003 ml s⁻¹), there is no flow in the direction of the height over the length of the channel, while the fluid flow in the direction of the length is constant for a major percentage of the channel length (Fig. 3A). However, strong sideward velocities occur near the inlet and outlet, indicating that the flow is established only between 0.4(l/l₀) and 0.6(l/l₀). Figure 3B shows that at half height, the fluid velocity is constant, although it is slightly asymmetrical due to the inlet and outlet design, for a major part of the width of the channel, and there is a decrease in velocity only in the areas close to the side walls. Finally, Fig. 3C confirms that a parabolic Poisseuille flow develops over the height of the channel.

FIG. 3.

Flow velocities at a volumetric flow rate of 0.003 ml s⁻¹ in different directions, as determined from a numerical simulation for PPFC C as a function of the dimensionless length at the center of the flow chamber (0.5h₀ and 0.5w₀) (A), as a function of the dimensionless width at the center (0.5l₀ and 0.5h₀) (B), and as a function of the dimensionless height at the center (0.5l₀ and 0.5w₀) (C). Symbols: •, velocities in the direction of the channel (l); ▴, sideward (w) velocities; ▪, velocities in the direction of the height (h).

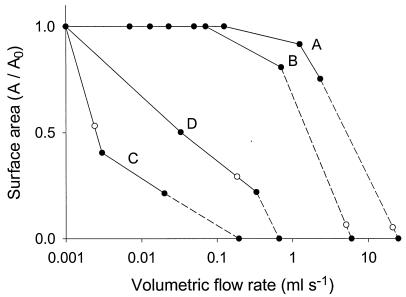
The velocity patterns as a function of length, height, and width for all flow chambers were analyzed further based on the useful surface area in order to compare the different designs. Figure 4 shows the surface areas (normalized to the maximal surface area obtained with the lowest simulated flow rate) at which a uniform flow is established and valid observations can be made by using the conditions described above. At this point it should be noted that the dimensions of the bottom plates of the various flow chambers differ by design (Table 1). PPFCs A and B perform well, and valid observations are feasible for almost the entire bottom plate of the flow chamber for inlet velocities corresponding to flow rates of up to 2.3 ml s⁻¹ (shear rate, 1,200 s⁻¹). PPFC B stops performing well at a slightly higher flow rate (6.0 ml s⁻¹, corresponding to a shear rate 2,700 s⁻¹) than PPFC A, breaking down at a flow rate of around 20.0 ml s⁻¹, corresponding to a shear rate of 10,000 s⁻¹. PPFCs C and D, in which both the inlet and the outlet are positioned perpendicularly, break down at considerably lower flow rates than PPFCs A and B; in particular, PPFC C breaks down rapidly at a flow rate of 0.2 ml s⁻¹.

FIG. 4.

Dimensionless surface areas (A/A₀) for which valid observations can be made as a function of the volumetric flow rate. Lines are drawn for clarity only and do not indicate any mathematical dependence. The open symbols indicate the flow rate for which an absolute surface area for valid observations of 1 cm² remains. A, B, C, and D refer to the flow chambers (see Table 1).

Shear rates.

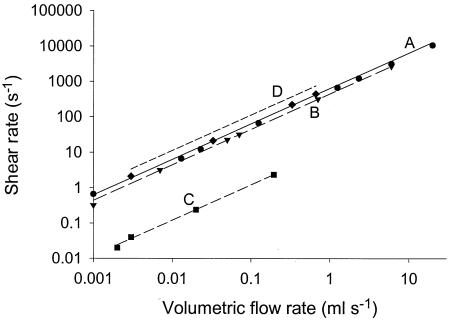
Figure 5 compares the modeled shear rates in the different PPFCs in the center as a function of the flow rate applied, together with the shear rates calculated from equation 4 for the range of flow rates yielding uniform flow in each chamber. The modeled shear rates deviated from the shear rates calculated from equation 3 for PPFCs A, B, and C (deviations up to 20%). For PPFC D the modeled shear rates deviated up to 75% from the calculated shear rates.

FIG. 5.

Modeled shear rates as a function of the volumetric flow rate for flow chambers A (•), B (▾), C (▪), and D (♦) up to the flow rate at which no uniform flow develops in the chambers. The lines indicate the shear rates calculated by using equation 4.

Validation of numerical simulations by particle image velocimetry.

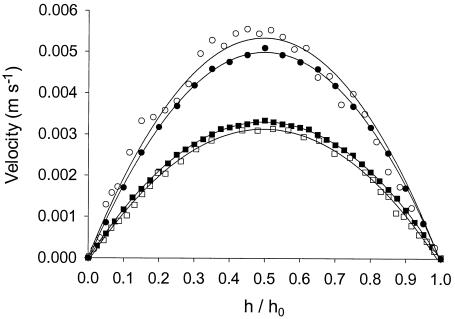
Figure 6 shows the fluid velocities in the center between the inlet and outlet for PPFCs A and B (Table 1) as a function of the dimensionless height (h/h₀) (i.e., the ratio of the actual distance from the plate to the height of the channel), as determined by particle image velocimetry and finite element analysis. Both the measured and modeled velocity patterns are parabolic (R² > 0.97), which is characteristic of laminar flow. The deviations between the measured and modeled patterns were minor (less than 5%). In flow chamber A, the maximum velocity calculated from the simulations at half height (0.5h₀) was lower than the velocity measured experimentally, whereas in flow chamber B, the velocities calculated from simulations were slightly higher than those measured by particle image velocimetry. The shear rates at the center of the bottom plate calculated from the measured and modeled velocity patterns were 28.6 and 26.9 s⁻¹, respectively, for PPFC A and 21.3 and 22.2 s⁻¹, respectively, for PPFC B. From this comparison, we concluded that finite element analysis yields valid estimates of the experimental velocity profiles.

FIG. 6.

Fluid velocities as a function of the dimensionless height (h/h₀) for flow chambers A (○ and •) and B (□ and ▪) at a volumetric flow rate of 0.050 ml s⁻¹, as measured by particle image velocimetry (open symbols) and as calculated with the simulation model (solid symbols). Fluid velocities are valid for the center of each flow chamber (i.e., the middle between the inlet and the outlet).

DISCUSSION

In this study, four PPFCs used for studies of microbial adhesion were analyzed on a theoretical basis. Numerical simulation and particle image velocimetry resulted in comparable velocity profiles, confirming the validity of the data obtained by numerical simulation. Due to design features of the different chambers, some of the designs appeared to be extremely limited by the range of flow rates over which a uniform flow developed, which is necessary for valid measurement over the bottom plate, where observations of microbial adhesion are usually made.

In the design of a flow chamber concessions have to be made quite frequently due to limitations in size, construction material, reuse and flexibility of the substratum, and eventually the cost of construction. However, the design appears to be crucial if a flow chamber is to be applicable over a wide range of flow rates. Two of the four designs were clearly flawed in the design of the inlet and outlet; because of this only small fractions of the bottom plates could be used for adhesion studies, and they could be used only over a limited flow range.

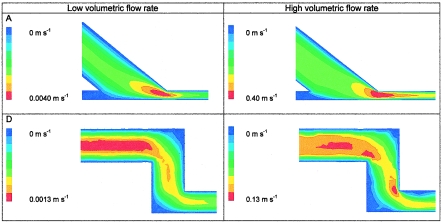
To indicate the importance of inlet design, Fig. 7 compares the flow in the inlet of PPFCs A and D at low flow rates, when both chambers perform well, and at the breakdown flow rate of each flow chamber. The gradual transition in PPFC A results in an area with high fluid velocity, which remains at the same position for high and low flow rates without affecting the establishment of flow in the observation area. At a low flow rate in PPFC D, which is characterized by an inlet with two bends with sharp edges, a Poisseuille flow develops close to the inlet, whereas at a slightly higher flow rate a clearly disturbed flow enters the chamber, as indicated by changing fluid velocities in the length direction (indicated by the irregular color distribution).

FIG. 7.

Inlet velocity profiles for PPFCs A and D for flow rates yielding uniform flow (left panels) and nonuniform flow (right panels) in each flow chamber. For the left panels low flow rates of 0.0013 ml s⁻¹ (PPFC A) and 0.003 ml s⁻¹(PPFC D) corresponded to shear rates of 6.6 and 2.1 s⁻¹, respectively. For the right panels high flow rates of 1.25 ml s⁻¹ (PPFC A) and 0.33 ml s⁻¹ (PPFC D) corresponded to shear rates of 659 and 219 s⁻¹, respectively.

Although in PPFC A the inlet and outlet are located under an angle, this design still allows the largest range of shear rates to be used due to the length of the channel. PPFCs A and B can be used for a wide range of the shear rates that occur in the environment (Table 2). These types of PPFCs have been used most frequently for studies of adhesion of medical strains on contact lenses, teeth, and catheter materials, but they allow workers to model situations with higher shear rates. Except for PPFC C, which is used to study biofilms in municipal sludge, in which the shear rate is limited to 2.4 s⁻¹, all of the PPFCs that were investigated could be used at flow rates relevant to the oral cavity or other systems with low to moderate shear rates (Table 2). For situations with higher shear rates, such as water works, urinary catheters, or ship hulls, design features of the flow chamber become increasingly important.

In conclusion, this study showed that the geometry is critical in the design of a PPFC. The design greatly affects the region of uniform flow and the subsequent observation of microbial adhesion. In combination with the length available for establishment of flow, the inlet geometry determines whether a flow chamber can be used as a valid model to study bacterial adhesion for the problem under investigation.