Lumped-Element Planar Strip Array (LPSA) for Parallel MRI

Abstract

The recently introduced planar strip array (PSA) can significantly reduce scan times in parallel MRI by enabling the utilization of a large number of RF strip detectors that are inherently decoupled, and are tuned by adjusting the strip length to integer multiples of a quarter-wavelength (λ/4) in the presence of a ground plane and dielectric substrate. In addition, the more explicit spatial information embedded in the phase of the signals from the strip array is advantageous (compared to loop arrays) for limiting aliasing artifacts in parallel MRI. However, losses in the detector as its natural resonance frequency approaches the Larmor frequency (where the wavelength is long at 1.5 T) may limit the signal-to-noise ratio (SNR) of the PSA. Moreover, the PSA’s inherent λ/4 structure severely limits our ability to adjust detector geometry to optimize the performance for a specific organ system, as is done with loop coils. In this study we replaced the dielectric substrate with discrete capacitors, which resulted in both SNR improvement and a tunable lumped-element PSA (LPSA) whose dimensions can be optimized within broad constraints, for a given region of interest (ROI) and MRI frequency. A detailed theoretical analysis of the LPSA is presented, including its equivalent circuit, electromagnetic fields, SNR, and g-factor maps for parallel MRI. Two different decoupling schemes for the LPSA are described. A four-element LPSA prototype was built to test the theory with quantitative measurements on images obtained with parallel and conventional acquisition schemes.

The strip array (1) has a number of advantages over conventional loop-resonator arrays (2) in high-field and parallel MRI. For instance, it allows a large number of non-adjacent elements to simultaneously receive MRI signals, with minimal coupling between elements (3). Compared with a loop array, the more explicit spatial information in the phase of the signals from a strip array makes parallel reconstruction less susceptible to aliasing artifacts. Also, it enables phased-array applications in open-geometry magnets, where conventional loop arrays are limited by field orientation. The basic element of a planar strip array (PSA) is a microstrip with both substrate and superstrate (the electrical length of which is either π/2 or π) terminated in either an open circuit or a short circuit (1). Its geometric length must be a quarter or half of the resonant wavelength λ of the electromagnetic (EM) field at the MRI frequency, or integer multiples thereof. Under these conditions, the array has the unique advantage that the PSA elements are intrinsically isolated from each other. However, at commonly used fields of 1.5T (63.87 MHz), λ is around 4.7 m (if the substrate is air), so a PSA with λ/4 and λ/2 would generally be too long.

The use of high-dielectric-constant substrates, instead of air, allows some reduction of λ to lengths practical for human imaging. However, the dielectric constant of a substrate is in general not easily varied, nor are there suitable materials available that possess a continuum of dielectric constants from which to choose. This limits our ability to arbitrarily adjust the PSA geometry in order to optimize its MRI performance in applications to a particular organ at a particular field strength. Nevertheless, the PSA elements are intrinsically isolated from one other, as long as their lengths are integer multiples of a quarter wavelength. Another disadvantage of the original PSA is that losses associated with the high-dielectric-constant substrate and large size of the distributed element can reduce the signal-to-noise ratio (SNR).

If instead of using a high-dielectric constant substrate to reduce the wavelength, one creates an artificial or “reduced-length” transmission line (RTL) (4) by deploying two or more discrete high-Q shunted capacitors along the strip, two advantages can be realized. First, the discrete capacitors reduce the electrical length of the PSA transmission line strips, and potentially enable the design of PSAs with much smaller geometric dimensions that can be adjusted for a given field strength. Second, the losses associated with the dielectric substrate and superstrate can be reduced, thereby increasing the SNR. Moreover, the geometric configuration can be adjusted to maximize the SNR for each specific application without being bound by the λ/4 criterion as applied to the physical strip length.

In this study we developed a lumped-element PSA (LPSA), employing RTLs for the array elements (5,6). In the LPSA, the electrical function of the substrate is replaced in part or substantially with two or more distributed shunt capacitors, yielding the equivalent electrical length of π/2 at 63.87 MHz with a much shorter strip length. At this frequency, an LPSA with a strip length of about 30 cm can be tuned with just two shunted 100 –200pF capacitors, while it can also be tuned with more uniformly distributed capacitors. A benefit of using only two capacitors in this situation (1.5T) is that the LPSA maintains a relatively homogeneous B₁ field while it is tuned to an electrical length of π/2. The interstrip decoupling mechanisms of the LPSA are different from those of the PSA. In the PSA, because of its quasi-transverse EM (TEM) field distribution, contributions from incident and reflected waves along a λ/4 strip cancel one another (1), so that the PSA is inherently decoupled. However, in the LPSA, at 1.5T the physical length of each strip can be much shorter than λ/4, and the condition of intrinsic decoupling is difficult to achieve.

In this study, we first apply a lumped-element circuit model to analyze the resonance condition and Q-factor of an RTL, and calculate its field and SNR. Second, interelement coupling, sensitivity profiles, and g-factor maps of the LPSA are evaluated in detail. Third, we describe two different schemes to isolate the RTL strips and substantially eliminate mutual coupling. In the past, shared (7) and interconnected (8) capacitors have been used to decouple loop MRI coils, as well as to couple transmission line sections (9), and in the first scheme we use interconnecting capacitors to decouple each nearest-neighbor pair. Low-input impedance preamplifiers are then deployed to decouple the remaining strips, as was implemented in the original phased array (2,10). The other scheme is to make the ratio of the strip spacing to the strip-to-ground distance large enough to achieve isolation (6). This approach limits the minimum separation between neighboring strips. Fourth, quantitative measurements of array characteristics and MRI experiments are used to demonstrate that the LPSA can produce high-quality in vivo MR images at 1.5 T with either phased-array or parallel data acquisition.

THEORY

RTL—The Basic Element of the LPSA

Whereas the basic detector element of the PSA is a transmission line resonator (1), the LPSA’s basic element can be viewed as an RTL resonator, in which the electrical length is achieved by combining a transmission line and shunt capacitors, as shown in Fig. 1a (a special case where only two capacitors are used). There is flexibility in adjusting the physical length, l, of the RTL. The RTL can initially be treated as a two-port network, which is commonly characterized by the “ABCD” matrix formalism that relates the input voltage and current, V₁ and I₁, to the output voltage and current, V₂ and I₂, via:

FIG. 1.

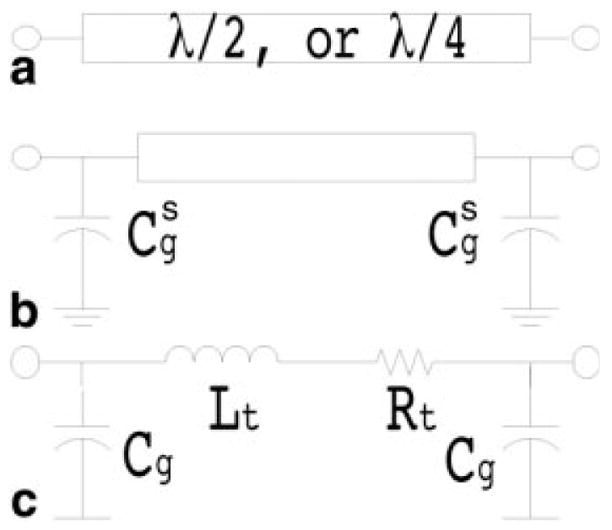
Schematics of a resonant transmission line (a), an RTL (b), and the equivalent circuit of the RTL (c).

$$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right].$$ [1]

If the two shunt capacitors at the ends of the line have value C_g^s, then the “ABCD” matrix for the RTL is

$$\begin{array}{r}\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left[\begin{array}{cc}1& 0\\ j\omega C_g^s& 1\end{array}\right]\left[\begin{array}{cc}cosh\gamma l& Z_{0}sinh\gamma l\\ sinh\gamma l/Z_0& cosh\gamma l\end{array}\right]\\ \times \left[\begin{array}{cc}1& 0\\ j\omega C_g^s& 1\end{array}\right],\end{array}$$ [2]

where ω is the angular frequency of the EM field, Z₀ is the characteristic impedance of the transmission line, and γ is known as the propagation constant (11). These last two are given by

$$Z_0=\sqrt{\frac{R^{\prime }+j\omega L^{\prime }}{G^{\prime }+j\omega C^{\prime }}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\gamma =\sqrt{(R^{\prime }+j\omega L^{\prime })(G^{\prime }+j\omega C^{\prime })}.$$ [3]

Here R′ is the series resistance per unit length of the transmission line, G′ is the shunt resistance per unit length, L′ is the series inductance per unit length, and C′ is the shunt capacitance per unit length. When the strip length is physically much less than one wavelength, cosh γl ≈ 1 and sinh γl ≈ γl. Then Eq. [2] becomes

$$\begin{array}{r}\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left[\begin{array}{cc}1& 0\\ j\omega C_g^s& 1\end{array}\right]\left[\begin{array}{cc}1& R_t+j\omega L_t\\ G_t+j\omega C_t& 1\end{array}\right]\\ \times \left[\begin{array}{cc}1& 0\\ j\omega C_g^s& 1\end{array}\right].\end{array}$$ [4]

If we assume that loading along the strip is uniform, then the series resistance, shunt resistance, series inductance, and shunt capacitance of the transmission line are R_t = R′l, G_t = G′l, L_t = L′l, and C_t = C′l, respectively.

The distance h between the strip and the ground has a significant effect on the field patterns of the RTL, especially for the electric field. When h is so small that the electric field lines are concentrated mostly between each strip and the ground plane, then the EM field of the RTL can be considered as quasi-TEM. But if h is relatively large (>5 mm), the electric field is oriented mostly along the strip (non-TEM). We consider only this second scenario, and avoid the first scenario and the other transition situations between these two scenarios. While the transmission line shunt capacitance, C_t, will decrease as h increases, its net effect may still be appreciable for choices of l and h, respectively, in a range of ~20 cm and ~1 cm (which is desirable for human studies), especially if a dielectric substrate is deployed to separate the strips from the ground plane (6). To simplify the analysis, we incorporate C_t into the lumped-element capacitance C_g, and neglect the shunt resistance (G_t ≈ 0). The RTL has a simple lumped LCR equivalent circuit as shown in Fig. 1c, where $C_g\sim C_g^s+C_t/2$ is the effective shunt capacitance, and R_t represents the net loss resistance. Eq. [3] becomes

$$\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left[\begin{array}{cc}1& 0\\ j\omega C_g& 1\end{array}\right]\left[\begin{array}{cc}1& R_t+j\omega L_t\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ j\omega C_g& 1\end{array}\right]$$ [5]

The admittance of the RTL can be derived from the ABCD matrix by letting the load at one port Z_L be infinity:

$$\begin{array}{l}Y=G_Y+j{B}_Y=\frac{C+D{Y}_L}{A+B{Y}_L}=\frac{C}{A}\\ =\frac{-{\omega }^2{R}_t{C}_g^2+j(2\omega C_g-{\omega }^3{L}_t{C}_g^2)}{1-{\omega }^2{L}_t{C}_g+j\omega R_t{C}_g}.\end{array}$$ [6]

Here G_Y is the conductance and B_Y is the susceptance, where

$$\begin{array}{l}{G}_Y=\frac{C_g^2{R}_t{\omega }^2}{1-2C_g{L}_t{\omega }^2+C_g^2{R}_t^2{\omega }^2+C_g^2{L}_t^2{\omega }^4}\\ B_Y=\frac{2C_g\omega +(-3C_g^2{L}_t+C_g^3{R}_t^2){\omega }^3+C_g^3{L}_t^2{\omega }^5}{1-2C_g{L}_t{\omega }^2+C_g^2{R}_t^2{\omega }^2+C_g^2{L}_t^2{\omega }^4}\end{array}$$ [7]

A low-frequency estimate of the inductance of the strip over the ground plane is (12,13):

$$L_t=\frac{{\mu }_{0}l}{\pi }\left[ln\frac{2l}{w}+\frac{1}{2}-ln\left(\frac{l}{2h}+\sqrt{1+\frac{l^2}{{(2h)}^2}}\right)+\sqrt{1+\frac{{(2h)}^2}{l^2}}-\frac{2h}{l}\right].$$ [8]

The resistance R_t is essentially the sum of the conductor losses and the sample losses.

Resonance Condition of the RTL

To calculate the resonance frequency of the RTL, one can set the susceptance B_Y = 0 in Eq. [7], and derive

$$\omega =\frac{1}{\sqrt{2}}\sqrt{\frac{3}{L_t{C}_g}-\frac{R_t^2}{L_t^2}\pm \frac{\sqrt{L_t^2-6L_t{C}_g{R}_t^2+C_g^2{R}_t^4}}{C_g{L}_t^2}}\approx {\sqrt{\frac{2}{L_t{C}_g}}\mid }_{R_t\approx 0}.$$ [9]

The impedance has a maximum value at resonance frequency ο in Eq. [9] only when the plus sign of the ± is chosen. If the minus sign is chosen, the admittance instead has a maximum value, a case that is not presently of interest.

The ω in Eq. [9] is not always a real number, which means that the RTL only resonates under certain conditions. To derive the resonance condition, one can let B = 0 in Eq. [7] and solve for C_g and L_t:

$$\begin{array}{l}{C}_g=\frac{3\omega L_t+\sqrt{{\omega }^2{L}_t^2-8R_t^2}}{2\omega (R_t^2+{\omega }^2{L}_t^2)}\\ L_t=\frac{3+\sqrt{1-4C_g^2{R}_t^2{\omega }^2}}{2C_g{\omega }^2}.\end{array}$$ [10]

To ensure that C_g and L_t remain real, the inductance of the strip and the equivalent capacitance of the shunt capacitors must satisfy the following conditions:

$$\begin{array}{l}{L}_t\ge \frac{2\sqrt{2}{R}_t}{\omega }\\ C_g\le \frac{1}{2\omega R_t}.\end{array}$$ [11]

For a given resonance frequency, the minimum inductance of the strip and maximum shunt capacitance are determined by the net sample and conductor resistance R_t. By combining L_t in Eqs. [8] and [11], one can estimate the minimum viable strip dimensions. Details of the calculation of R_t are given below.

Q Factor and Loading Factor of the RTL

The quality factor, Q, of the RTL, and the effect of a sample load, are measures of detector performance. The Q can be calculated from the admittance in Eq. [7]:

$$\begin{array}{l}{Q=\frac{{\omega }_r}{2G_Y}\frac{d{B}_Y}{d\omega }\mid }_{\omega ={\omega }_r}\\ =\frac{\begin{array}{l}2+(C_g^2{R}_t^2-5C_g{L}_t){\omega }^2+(5C_g^2{L}_t^2-5C_g^3{L}_t{R}_t^2\\ +C_g^4{R}_t^4){\omega }^4+(2C_g^4{L}_t^2{R}_t^2-3C_g^3{L}_t^3){\omega }^6+C_g^4{L}_t^4{\omega }^8\end{array}}{2C_g{R}_t\omega +(2C_g^3{R}_t^3-4C_g^2{L}_t{R}_t){\omega }^3+2C_g^3{L}_t^2{R}_t{\omega }^5}\end{array}$$ [12]

At the resonance frequency ο_r, C_g and L_t are interrelated via Eq. [10]. Substituting the expression for C_g from Eq. [10] into Eq. [12] yields the Q in terms of strip inductance L_t and the equivalent net loss resistance R_t in Fig. 1c:

$$Q=\frac{\begin{array}{l}-8R_t^6-20L_t^2{R}_t^4{\omega }^2+38L_t^4{R}_t^2{\omega }^4-4L_t^6{\omega }^6\\ +(4L_t{R}_t^4\omega +18L_t^3{R}_t^2{\omega }^3-4L_t^5{\omega }^5)\sqrt{{\omega }^2{L}_t^2-8R_t^2}\end{array}}{\begin{array}{l}14L_t{R}_t^5\omega +10L_t^3{R}_t^3{\omega }^3-4L_t^5{R}_t{\omega }^5+(2R_t^5\\ -2L_t^2{R}_t^3{\omega }^2-4L_t^4{R}_t{\omega }^4)\sqrt{{\omega }^2{L}_t^2-8R_t^2}\end{array}}$$ [13]

On the other hand, substituting the expression for L_t from Eq. [10] into Eq. [12] yields the Q in terms of C_g and R_t:

$$Q=\frac{2C_g{\omega }^2-7C_g^3{R}_t^2{\omega }^4+(2C_g{\omega }^2-C_g^3{R}_t^2{\omega }^4)\sqrt{1-4C_g^2{R}_t^2{\omega }^2}}{C_g^2{R}_t{\omega }^3(1+\sqrt{1-4C_g^2{R}_t^2{\omega }^2})}.$$ [14]

With the strip loaded with a sample, the value of the equivalent resistance R_t = R_L will differ from the unloaded value, R_t = R_U, leading to different loaded and unloaded Qs, Q_L and Q_U, respectively. The behavior of Eqs. [13] and [14] as a function of typical RTL equivalent impedances R_t, C_g, and L_t, and loading ratios R_L/R_U and Q_U/Q_L, are plotted in Fig. 2 at 64 MHz (parts a–d) and at 128 MHz (parts e–h). Despite the complexity of Eq. [13], Fig. 2a and e show that the relation between Q and L_t is almost linear with load resistance. Figure 2c and g show that larger values of C_g produce lower Qs. When R_L/R_U is 2 (1Ω/0.5Ω), 5 (5Ω/1Ω), or 10 (5Ω/0.5Ω), Fig. 2b, d, f, and h show that as L_t increases, or as C_g decreases, the loading factor Q_U/Q_L approaches R_L/R_U. However, when L_t is relatively small, or C_g is relatively large, an increase in sample load disproportionately reduces Q, so that Q_U/Q_L is much higher than R_L/R_U (Fig. 2b and h), where the electrical field loading on the capacitor becomes a considerable factor. To avoid this situation, it is preferable to increase L_t and reduce C_g.

FIG. 2.

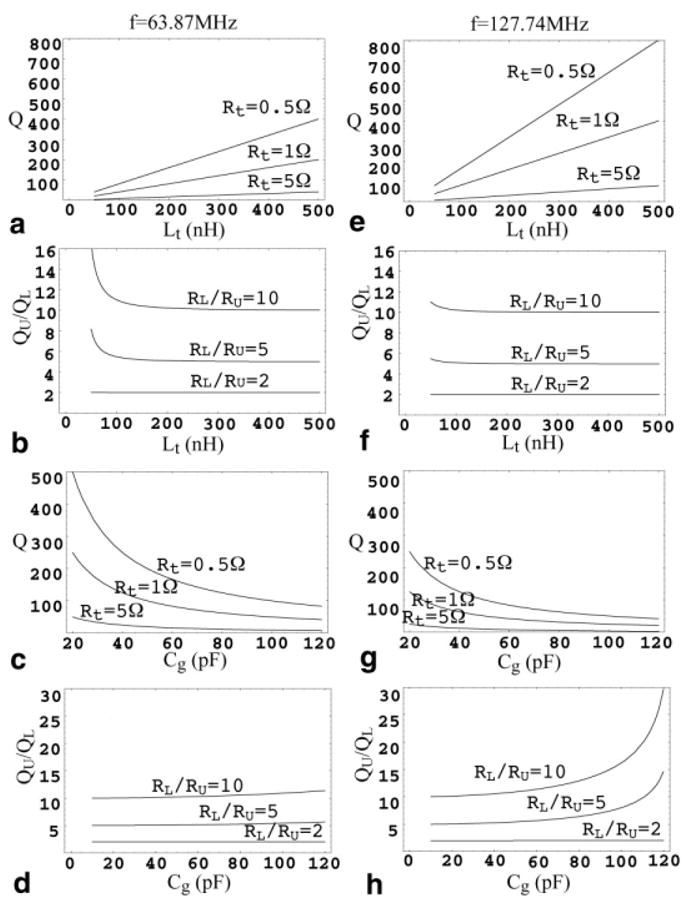
Dependence of quality factors, Q, on the loaded and unloaded RTL equivalent impedences calculated from Eqs. [13] and [14]. a: Quality factor Q of the RTL vs. L_t assuming different R_t values of 0.5Ω, 1Ω, and 5Ω at 1.5T. b: Ratio of unloaded to loaded quality factors, Q_U/Q_L vs. L_t assuming different ratios of unloaded to loaded R_t values, R_L/R_U at 1.5T. c: Q vs. various C_g and R_t values at 1.5 T. d: Q_U/Q_L vs. C_g and R_L/R_U at 1.5 T. e: Q vs. typical values of L_t and R_t at 3T. f: Q_U/Q_L vs. L_t and R_L/R_U at 3T. g: Q vs. C_g and R_t at 3T. h: Q_U/Q_L vs. C_g and R_L/R_U at 3T. At 1.5T, Q_U/Q_L is more sensitive to L_t variations; at 3T, Q_U/Q_L is more sensitive to C_g variations.

B Field and E Field

The RF magnetic and electric fields of an RTL with unit current can be derived from the vector potential. According to the reciprocity principle, they also represent the magnetic and electric fields detected by the RTL. The MR signal is proportional to the transverse component of the magnetic field, B₁. The MR noise is proportional to the square root of the noise resistance (14), which in turn can be determined from the integral of the square of the electric field (15) over the half space that extends from the ground plane of the RTL through the sample. Therefore, once the magnetic and electric fields of the RTL are known, the SNR can be evaluated.

To simplify the field calculations while preserving the characteristics of the RTL, we approximate the strip by a filament of length l along the z-direction of a Cartesian coordinate system (x, y, z) with the z-axis parallel to the static magnetic field B₀. The x- and y-axes are the horizontal and vertical directions, respectively. The filament has coordinates denoted by (x₀, y₀, z₀), and spans the region from z₀ = −l/2 to z₀ = l/2. The vector potential of the filament (16) is then

$$\begin{array}{l}\mathbf{A}=\frac{\mu }{4\pi }{\iiint }_{v=\mathit{current\_volume}}\frac{\mathbf{J}}{r}dv=\frac{\mu }{4\pi }{\int }_{-l/2}^{l/2}\frac{I}{r}d{z}_0\mathbf{z}\\ =\frac{\mu I}{4\pi }{\int }_{-l/2}^{l/2}\frac{d{z}_0}{\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z-z_0)}^2}}\mathbf{z}\\ =\frac{\mu I}{4\pi }ln\frac{l/2-z+\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z-l/2)}^2}}{-l/2-z+\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z+l/2)}^2}}\mathbf{z}.\end{array}$$ [15]

Here J is the current density, I is the current, r is the distance between (x₀, y₀, z₀) and an arbitrary spatial point (x, y, z), and μ is the permeability. The transverse magnetic field B₁ of the filament is

$${\mathbf{B}}_1=\nabla \times \mathbf{A}=B_{1x}\mathbf{x}+B_{1y}\mathbf{y}.$$ [16]

Let $r_{xy}^2={(x-x_0)}^2+{(y-y_0)}^2$. Then

$$\begin{array}{l}{B}_{1x}=\frac{\mu I}{4\pi }\frac{y-y_0}{r^2}\left(\frac{l/2+z}{\sqrt{r^2+{(z+l/2)}^2}}+\frac{l/2-z}{\sqrt{r^2+{(z-l/2)}^2}}\right)\\ B_{1y}=-\frac{\mu I}{4\pi }\frac{x-x_0}{r^2}\left(\frac{l/2+z}{\sqrt{r^2+{(z+l/2)}^2}}+\frac{l/2-z}{\sqrt{r^2+{(z-l/2)}^2}}\right)\end{array}$$ [17]

The electric field E of the filament can be derived from (17):

$$\begin{array}{l}\mathbf{E}=-\frac{\partial \mathbf{A}}{\partial t}=j\omega \mathbf{A}\\ =\frac{\omega \mu I}{4\pi }ln\frac{l/2-z+\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z-l/2)}^2}}{-l/2-z+\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z+l/2)}^2}}\mathbf{z}\end{array}$$ [18]

Note that this is the non-TEM case. As mentioned before, this only true when h is large enough.

When the conducting filament at y₀ = 0 is parallel to a conducting ground plane (zx), then, using the method of images (12), the magnetic field B₁ and electric field E₁ at (x, y, z) are given by:

$${\mathbf{B}}_1=\mathbf{B}(y_0=0)-\mathbf{B}(y_0=-2h)$$ [19]

$${\mathbf{E}}_1=\mathbf{E}(y_0=0)-\mathbf{E}(y_0=-2h).$$ [20]

Equations [19] and [20] give the analytic expressions for the magnetic and electric fields of the RTL. For example, for l = 30 cm and h = 2 cm, the horizontal (B_1x), vertical (B_1y), magnitude (|B₁|), and phase (∠B₁= atan[B_1y/B_1x]) components of B₁ in the z = 0 plane are illustrated in Fig. 3.

FIG. 3.

Axial view of the B₁ field in the z = 0 plane of a 30-cm-long RTL with h = 2 cm, and the x-axis horizontal. a and b: Contour plots of vector components B_x and B_y. c: Magnitude |B₁|. d: Arctan[B_1y/B_1x], which could translate into a phase of the received signal if a homogeneous B₁ transmitting field were supplied by an external coil. The contours span the ranges of (a) − 0.6 to + 0.7 μT, (b) ±0.7 μT, (c) +0.1 to 1.4 μT, and (d) ± π. Contour intervals are at one-eighth of the range. FOV = 40 cm × 20 cm.

SNR

The SNR of the RTL can be defined as (18):

$$\mathit{SNR}=\frac{j\omega \mu \mathbf{M}·{\mathbf{B}}_1}{\sqrt{4kT\mathrm{\Delta }f{\text{R}}_{\text{L}}}}=\frac{j\omega \mu (M_x{B}_{1x}+M_y{B}_{1y})}{\sqrt{4kT\mathrm{\Delta }f{\text{R}}_{\text{L}}}},$$ [21]

where M = M_xx + M_yy is the transverse magnetization, k is Boltzmann’s constant, T is the absolute temperature, and Δf is the receive bandwidth. Thus, for a given object, fixed T, and Δf, the SNR is determined by the ratio of $\mid {\mathbf{B}}_1\mid /\sqrt{R_L}$. The intrinsic SNR, which includes sample losses and excludes losses in the detector, is proportional to $\mid {\mathbf{B}}_1\mid /\sqrt{R_{L,S}}$, where R_L,S is the portion of R_L contributed by a sample with conductivity σ (19). We calculate R_L,S under conditions where Q_U/Q_L ≈ R_L/R_U (see the section entitled Q Factor and Loading Factor of the RTL), by numerical integration of (18):

$$R_{L,S}=\sigma {\int }_{V/2}{\mathbf{E}}_1^{2}dx\hspace{0.17em}dy\hspace{0.17em}dz,$$ [22]

and determine E₁ and B₁ from Eqs. [17]–[20].

Figure 4a shows R_L,S/σ vs. strip-to-ground distance h. Figures 4b and c show |B₁|, and the intrinsic $\text{SNR}\sim \mid {\mathbf{B}}_1\mid /\sqrt{R_{L,S}}$ vs. y at the z = 0 plane, with σ = 1 S/m. Although Fig. 4b demonstrates some |B₁| enhancement when h is increased, Fig. 4c shows that the intrinsic SNR scales inversely with h in the range of 1–5 cm, but becomes insensitive to h as depth increases. Thus, when h is above a certain value (non-TEM), increasing h may not provide an SNR gain for RTLs.

FIG. 4.

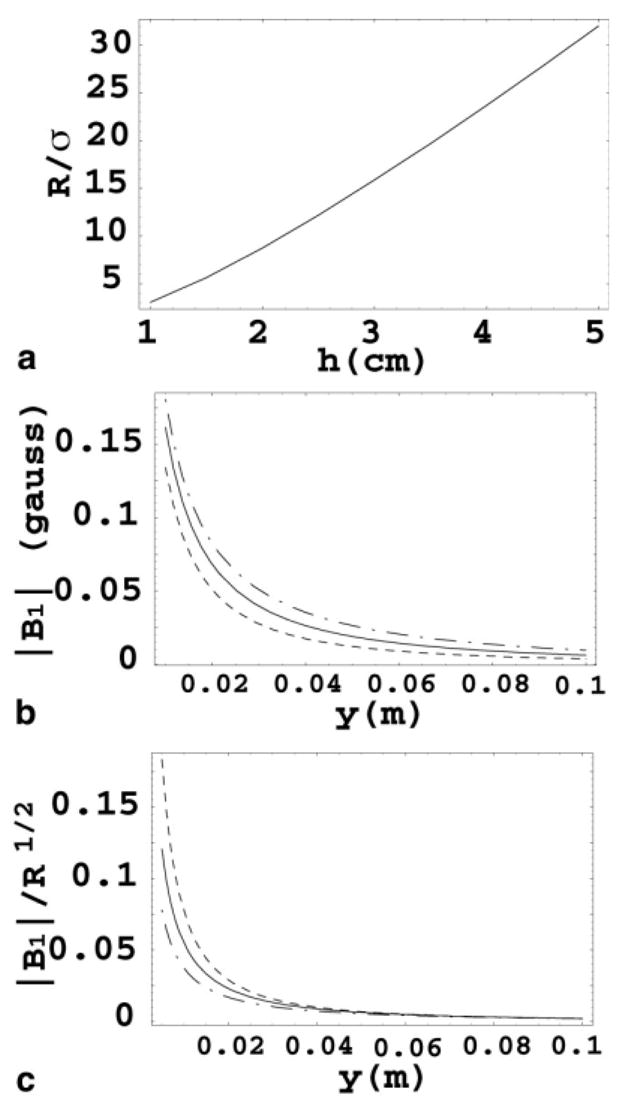
a: Ratio of noise resistance of the RTL to sample conductivity as a function of strip-to-ground distance h. b: Magnitude of B₁ of the RTL as a function of vertical depth y from the center of the strip. c: SNR of the RTL as a function of vertical depth y from the center of the strip. |B₁| and SNR exhibit quite different behaviors. Here the dashed, solid, and dash-dot lines correspond to h = 1 cm, 2 cm, and 4 cm, respectively.

Array Analysis

When a number of RTLs are laid side by side in parallel, both the SNR and the field patterns may be altered by mutual coupling between the RTLs if they are close enough. A general coupling analysis of a multiple-element system was outlined previously in Ref. 20. Here we only consider the special case where the mutual couplings are relatively weak, and the methods used in Ref. 2 to describe mutual couplings are valid. This is only sufficient when the number of elements of the LPSA is small.

Strip Coupling

The mutual coupling usually includes signal coupling and noise coupling, which can be quantitatively characterized by mutual inductance and mutual resistance, respectively. If two simple filaments are located at x₀ = 0 and x₀ = d, their mutual inductance can be analytically calculated from (12,13):

$$M(l,d)=\frac{{\mu }_{0}l}{2\pi }\left[ln\left(\frac{l}{d}+\sqrt{1+{\left(\frac{l}{d}\right)}^2}\right)-\sqrt{1+{\left(\frac{d}{l}\right)}^2}+\frac{d}{l}\right].$$ [23]

Here l is the filament length and d is the spacing between filaments. The mutual inductance between two neighboring RTLs, M_ij, can be calculated from Eq. [23] using the method of images. Assuming l² + d² ≫ 4h², where h is the strip-to-ground distance, we have

$$\begin{array}{l}{M}_{ij}=2M(l,d)-2M(l,\sqrt{d^2+4h^2})\\ \approx \frac{{\mu }_0}{\pi }\left(d-\sqrt{d^2+4h^2}+l\hspace{0.17em}ln\sqrt{1+\frac{4h^2}{d^2}}\right).\end{array}$$ [24]

Note that the relative values of h and d determine the mutual inductance. When 2h ≪d, the mutual inductance, and thus the mutual signal coupling, approach zero.

The mutual noise resistance (2) between an RTL at x₀ = 0 and one at x₀ = d is given by

$$R_m=\sigma {\int }_{V/2}{\mathbf{E}}_1(x_0=0)·{\mathbf{E}}_1(x_0=d)\hspace{0.17em}dV,$$ [25]

which can be numerically calculated with E₁ from Eq. [20].

The signal and noise coupling coefficients can also be calculated numerically from Ref. 2:

$$k_{ij}=\frac{M_{ij}}{\sqrt{L_{ii}{L}_{jj}}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}{\psi }_{ij}=\frac{R_{ij}}{\sqrt{R_{ii}{R}_{jj}}}.$$ [26]

Here M_ij, L_ii, L_jj, R_ij, R_ii, and R_ii can be calculated from Eqs. [8], [22], [24], and [25].

For example, consider a four-element LPSA. If the couplings are relatively weak, they can be characterized by a 4 × 4 signal coupling matrix K and a noise coupling matrix Ψ (2):

$$\begin{array}{l}\mathbf{K}=\left(\begin{array}{cccc}1& -k_{12}& -k_{13}& -k_{14}\\ -k_{12}& 1& -k_{23}& -k_{24}\\ -k_{13}& -k_{23}& 1& -k_{34}\\ -k_{14}& -k_{24}& -k_{34}& 1\end{array}\right),\\ \mathbf{\Psi }=\left(\begin{array}{cccc}1& {\psi }_{12}& {\psi }_{13}& {\psi }_{14}\\ {\psi }_{12}& 1& {\psi }_{23}& {\psi }_{24}\\ {\psi }_{13}& {\psi }_{23}& 1& {\psi }_{34}\\ {\psi }_{14}& {\psi }_{24}& {\psi }_{34}& 1\end{array}\right).\end{array}$$ [27]

If the mutual signal couplings are strong, then the diagonal terms are no longer unity and the matrices are more complex (20).

B₁ Profiles and g-Factor Maps for the LPSA

In the LPSA, the coupling of the magnetic field B₁ between strips is proportional to the coupling of the currents (20) in the strips. The coupling matrix for the currents can be simplified to K in Eq. [27], in the case where coupling is weak and there is no propagation of coupled currents among the RTLs (20). For a four-element LPSA, we describe the coupled and uncoupled magnetic fields, respectively, as

$${\widehat{\mathbf{B}}}_1^{\mathbf{C}}=\left(\begin{array}{c}{\mathbf{B}}_{1a}^{\mathbf{C}}\\ {\mathbf{B}}_{1b}^{\mathbf{C}}\\ {\mathbf{B}}_{1c}^{\mathbf{C}}\\ {\mathbf{B}}_{1d}^{\mathbf{C}}\end{array}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}{\widehat{\mathbf{B}}}_1=\left(\begin{array}{c}{\mathbf{B}}_{1a}\\ {\mathbf{B}}_{1b}\\ {\mathbf{B}}_{1c}\\ {\mathbf{B}}_{1d}\end{array}\right),$$ [28]

Then the B₁ profiles of the LPSA are related by

$${\widehat{\mathbf{B}}}_1^{\mathbf{C}}=\mathbf{K}{\widehat{\mathbf{B}}}_1.$$ [29]

For example, for a strip length l = 30 cm, width w = 1.27 cm, strip-to-ground distance h = 2 cm, and strip spacing d = 6 cm, the B₁ coupling matrix calculated from Eqs. [8], [24], and [27] for weakly coupled strips is:

$$\mathbf{K}=\left(\begin{array}{cccc}1& -0.0587& -0.0140& -0.0054\\ -0.0587& 1& -0.0587& -0.0140\\ -0.0140& -0.0587& 1& -0.0587\\ -0.0054& -0.0140& -0.0587& 1\end{array}\right)$$ [30]

Figure 5 shows the magnitude and phase components of the coupled magnetic field B₁ of the four-element LPSA calculated from Eqs. [19], [29], and [30]. Note that the field patterns of the outermost RTL differ from the inner ones: symmetry can be improved by adding an extra strip on each side as a “guard” (1).

FIG. 5.

Axial view of the B₁ field in the z = 0 plane of a weakly coupled four-element LPSA with l = 30 cm, h = 2 cm, width w = 1.27 cm, and strip spacing d = 6 cm. Parts a, c, e, and g are the amplitude of four channels, and b, d, f, and h are their corresponding arctan[B_1y/B_1x], which could translate into phase of the received signal in four channels if a homogeneous B₁ transmitting field were supplied by an external coil. Here the FOV is 20 cm × 20 cm with the x-axis horizontal. The contours span the ranges of (a–d) 0.16 –1.4 μT and (e– h) ±π. Contour intervals are at one-eighth of the range.

The g-factor map provides a quantitative measure of the performance of a phased array for parallel imaging applications (21,22). It is given by

$$g=\sqrt{{[{({\mathbf{S}}^H{\mathbf{\Psi }}^{-1}\mathbf{S})}^{-1}]}_{\rho ,\rho }{({\mathbf{S}}^H{\mathbf{\Psi }}^{-1}\mathbf{S})}_{\rho ,\rho }}.$$ [31]

Here S is the matrix of complex coil sensitivities of superimposed imaging areas from different coils (22). Table 1 shows the results of noise coupling calculations for three different combinations of h and d based on Eqs. [22], [25], and [26]. From Table 1, one can derive the noise coupling matrices from Eq. [27]:

Table 1.

Noise Resistance, Mutual Resistance and Noise Coupling Coefficients Calculations

h (cm)	d (cm)	R11/σ	R12/σ	R13/σ	R14/σ	Ψ12	Ψ13	Ψ14
2	6	8.755	6.02	3.834	2.712	0.69	0.44	0.31
2	10	8.755	4.222	2.329	1.394	0.48	0.27	0.16
1	6	3.06	1.631	0.999	0.697	0.53	0.33	0.23

$$\begin{array}{l}{\mathbf{\Psi }}_1(h=2cm,d=10cm)=\left(\begin{array}{cccc}1& 0.48& 0.27& 0.16\\ 0.48& 1& 0.48& 0.27\\ 0.27& 0.48& 1& 0.48\\ 0.16& 0.27& 0.48& 1\end{array}\right),\\ {\mathbf{\Psi }}_2(h=2cm,d=6cm)=\left(\begin{array}{cccc}1& 0.69& 0.44& 0.31\\ 0.69& 1& 0.69& 0.44\\ 0.44& 0.69& 1& 0.69\\ 0.31& 0.44& 0.69& 1\end{array}\right),\\ {\mathbf{\Psi }}_3(h=1cm,d=6cm)=\left(\begin{array}{cccc}1& 0.53& 0.33& 0.23\\ 0.53& 1& 0.53& 0.33\\ 0.33& 0.53& 1& 0.53\\ 0.23& 0.33& 0.53& 1\end{array}\right).\end{array}$$ [32]

Assuming that the signal from each RTL is isolated from the others, the axial-plane g-factor maps of Ψ₁, Ψ₂, and Ψ₃ at reduction factors of 2, 3, and 4 are shown in Fig. 6 for d = 6 and 10 cm and h = 1 and 2 cm. Overall, the figure shows little variation in g-factor performance for the different reduction factors. However, the larger the spacing d, the better the g-factor because the noise coupling is reduced. Also, g-factor performance deteriorates as h is reduced, because the spatial distinction between the B₁ fields generated by the different RTLs is less, even though the noise coupling is also reduced.

FIG. 6.

Axial view of the g-factor maps in the z = 0 plane for a four-element LPSA: for h = 2 cm, d = 10 cm, with a reduction factor of (a) 2, (b) 3, and (c) 4; for h = 2 cm, d = 6 cm, with a reduction factor of (d) 2, (e) 3, and (f) 4; for h = 1 cm, d = 6 cm, with a reduction factor of (g) 2, (h) 3, and (i) 4. The x-axis is horizontal, and scales (top right) indicate the g-value with contour intervals at one-tenth of the range.

Decoupling

Although an RTL can have the same electrical length as the λ/4 transmission line, the decoupling mechanisms for the PSA (1) do not necessarily hold. In particular, the intrinsic narrowband decoupling of the PSA may be lost if the length of the conductor strip in the RTL is much less than λ/4, and there is no standing wave to ensure that the coupling between the incident and reflected waves fully cancel. Here we describe two alternative decoupling schemes for the LPSA.

Interconnecting Capacitor Method

One way to decouple the LPSA is to place interconnecting capacitors between two RTLs at both ends of the strips to decouple nearest RTL pairs, which is analogous to the use of interconnected capacitive circuits to decouple multiple MRI loop detectors (8), and then use low-input impedance preamplifiers to decouple the remaining RTL pairs, as in the original NMR phased array (2). The coupling between two RTLs can be derived from even–odd mode theory (4). Here elements A and C in the ABCD matrix are A_e and C_e for the even mode, and A_o and C_o for the odd mode. For the even mode, where currents in the two RTLs are the same, A_e and C_e are derived from Eq. [6] by replacing L_t with L_t +M, where M is the mutual inductance.

$$\begin{array}{l}{A}_e=1-{\omega }^2(L_t+M)C_g+j\omega R_t{C}_g\\ C_e=-{\omega }^2{R}_t{C}_g^2+j(2\omega C_g-{\omega }^3(L_t+M)C_g^2)\end{array}$$ [33]

For the odd mode, where currents in the two RTLs have the same amplitude but opposite phase, A_o and C_o are obtained from Eq. [6] by replacing L_t with L_t– M and C_g with C_g+2C_c. Here C_c is the interconnecting capacitor.

$$\begin{array}{l}{A}_o=1-{\omega }^2(L_t-M)(C_g+2C_c)+j\omega R_t(C_g+2C_c)\\ C_e=-{\omega }^2{R}_t{(C_g+2C_c)}^2+j(2\omega (C_g+2C_c)-{\omega }^3(L-M){(C_g+2C_c)}^2)\end{array}$$ [34]

Then the even and odd reflection coefficients are

$${\mathrm{\Gamma }}_e=\frac{A_e-C_e{Z}_0}{A_e+C_e{Z}_0},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}{\mathrm{\Gamma }}_o=\frac{A_o-C_o{Z}_0}{A_o+C_o{Z}_0}.$$ [35]

Using Eq. [11] from Ref. 1, we find that the coupling k between two RTLs is

$$k_c=\frac{{\mathrm{\Gamma }}_e-{\mathrm{\Gamma }}_o}{2-{\mathrm{\Gamma }}_G({\mathrm{\Gamma }}_e+{\mathrm{\Gamma }}_o)}.$$ [36]

Here Γ_G is the reflection coefficient from the receiver at the input port of the RTL. To achieve decoupling, k_c = 0, one needs to solve the equation Γ_e – Γ_o = 0 to derive the decoupling capacitance:

$$C_c=(-b\pm \sqrt{b^2-4ac})/2a,$$ [37]

where

$$\begin{array}{l}a=2{\omega }^2(L_t-M)({\omega }^2{C}_g(L_t+M)-1)\\ b=2-2{\omega }^2{C}_g(L_t+M)+{\omega }^4{C}_g^2(L_t^2-M^2)\\ c=-{\omega }^2{C}_g^{2}M.\end{array}$$ [38]

Equation [37] gives the value of the interconnecting capacitor that will decouple an RTL pair.

This decoupling method works well when the number of array elements is relatively low. As the number of elements grows large, the array is more appropriately treated as an integrated system (20).

Broadband Decoupling

The LPSA, like the PSA, exhibits broadband decoupling (6); however, the decoupling criterion for the LPSA generally differs from that of the PSA when the EM fields on the LPSA do not have a TEM or quasi-TEM mode. The criterion for LPSA broadband decoupling can be derived from Eq. [24]: if d ≫ 2h, then d² + 4h² ≈ d², the mutual inductance approaches zero, and the LPSA is broadband-decoupled.

EXPERIMENTS

Because the MRI system on which we tested our method experimentally was limited to four channels (5,6), and our analysis example is a four-element LPSA, we constructed several four-element prototypes to test the SNR, the above decoupling schemes, and the in vivo MRI performance with both conventional and parallel sensitivity-encoded acquisitions.

Geometric Parameters of the LPSA: l, w, and h

The choice of geometric parameters for the LPSA affects its tuning. As shown by Eq. [8], the values of l, w, and h determine the inductance L_t of the RTL. At resonance, L_t and the shunt capacitance C_g are related by Eq. [9], and must satisfy Eqs. [10] and [11] for the RTL to resonate. The ratio of d and h determines the mutual inductance of an RTL pair, per Eq. [24]. Within this basic framework, the geometric parameters can be chosen to optimize the performance of the LPSA for a given application.

As an example, consider an LPSA designed for MRI of human muscle at 63.87 MHz (1.5 T). For muscle, σ = 0.86 S/m (23) ~ 1 S/m, as assumed for Fig. 4. From Eq. [22] and Fig. 4a, with h = 1–5 cm, R_t = 2.6–27.5Ω, assuming sample dominant noise. Equation [11] requires L_t > 18nH and C_g < 480pF when R_t= 2.6 Ω, and L_t > 194nH and C_g < 45pF for R_t = 27.5Ω at 63.87 MHz, with actual values given by Eq. [10]. Because increasing h reduces the maximum value of C_g, LPSAs with smaller h values are easier to tune.

Another consideration is the loading factor. As shown in Fig. 2, there is a minimum threshold inductance, L_m, beyond which the loading factor is substantially determined by the ratio of loaded and unloaded resistances. The dimensions of a strip should be chosen so that the strip inductance L > L_m. From Fig. 2b, if R_L/R_U = 2, L_m ≪ 50 nH for 1.5T. With R_U/R_L = 5, L_m is about 250 nH. With R_L/R_U = 10, L_m is about 300 nH. Thus, the smaller the loading factor, the smaller the value of L_m. Based on Eq. [8], for a 30-cm-long, 1.27-cm-wide strip with h = 2 cm, L = 302 nH. Figure 2b shows that this maintains L > L_m for a loading factor of up to about 10 at 1.5 T. At higher frequencies (e.g., 3T), L_m is smaller (see Fig. 2f) and h can be much less than 2 cm, provided that the transmission line shunt capacitance does not exceed the value of C_g needed to tune the strips, per the assumptions made for Eq. [5].

LPSA Prototype

An LPSA prototype was designed and built according to the above principles. Each RTL in the prototype had strip length l = 30 cm, strip width w = 1.27 cm, a strip-to-ground separation of h = 2 cm, and strip spacing d = 10 cm. Figure 7 shows the LPSA and its circuit diagram.

FIG. 7.

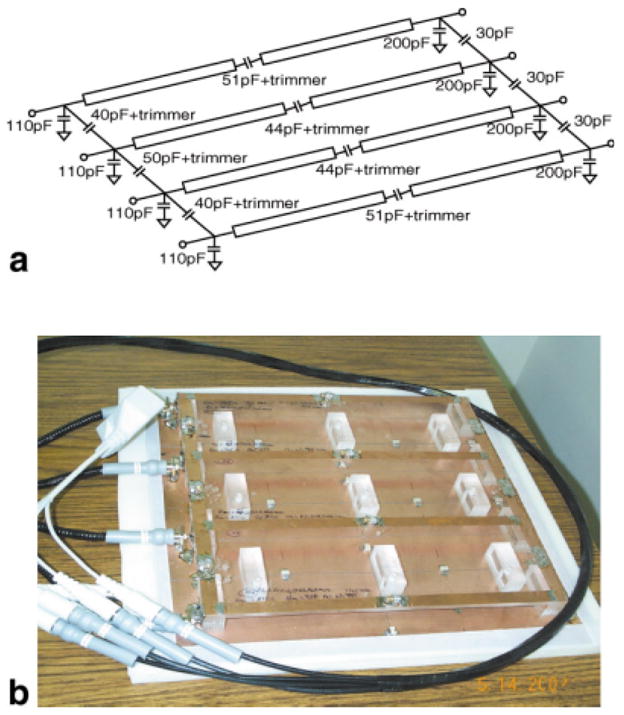
Schematic (a) and photo (b) of the prototype LPSA.

Each strip was separately tuned to the same frequency with the other strips open-circuited. Without any capacitors C_c connected between any nearest RTL pair, four resonant peaks are observed in the impedance spectrum due to the coupling between the strips, as shown in Fig. 8a. When the nearest RTL pairs are interconnected with capacitors C_c, the impedance spectrum of each RTL merges into a single peak, as seen in Fig. 8b. If channel 4 of the LPSA is shorted to simulate connection with a low-input-impedance preamplifier, the single peak remains, as seen in Fig. 8c. In Fig. 8c, Q_U ≈ 480 and Q_L ≈ 80 when loaded with a human chest, yielding a loading factor of 6. Every RTL was matched to 50Ω when loaded. The circuit’s S21 parameter curve of two RTLs is shown in Fig. 8d.

FIG. 8.

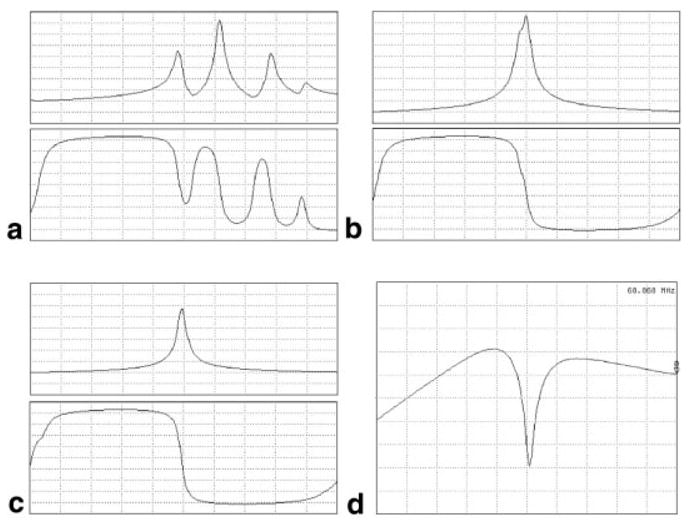
a: Impedance spectrum of a coupled four-element LPSA, as seen from the outside channel 1 (top spectrum, magnitude, 50Ω/div; bottom spectrum, phase, 20°/div). b: Spectrum with interconnecting capacitors for decoupling (magnitude, 5Ω/div at top; phase, 20°/div at bottom). c: Spectrum with interconnecting capacitors and channel 4 shorted (magnitude, 5Ω/div at top; phase, 20°/div at bottom) for decoupling. This is equivalent to a low-input impedance preamplifier. d: S21 for a nearest RTL pair. Dip is approximately −26 dB. The horizontal axes are frequency-centered on 63.87 MHz, with a span of 10 MHz.

If the ground plane of the LPSA is a solid conducting sheet, eddy currents induced by the gradients may affect image quality. To avoid this effect, the ground plane was segmented based on principles outlined in Ref. 12. The gap between two segments of conductors was 1 mm, and the gap spacing was 4.5 cm. The gaps were bridged with 2700 pF capacitors, which gave the ground plane an impedance of 0.9 Ω at 63.87 MHz and 5.9 kΩ at 10 kHz.

Experimental Results

The four-channel LPSA was connected to a four-channel GE LX CVi scanner (GE Medical Systems, Milwaukee, WI) for both conventional phased-array and parallel imaging. The array was laid flat with strips oriented parallel to the main field, producing optimum sensitivity encoding along the horizontal or x-axis. Figure 9 shows phantom and in vivo images obtained using the LPSA for conventional phased-array reconstruction. Figure 9a–d show images from each individual channel, and Fig. 9e shows the composite image from all four channels. The localization of signals in Fig. 9a–d demonstrates that every strip actively receives signals without significant coupling artifacts. Finally, Fig. 9f shows an axial image from the human knee.

FIG. 9.

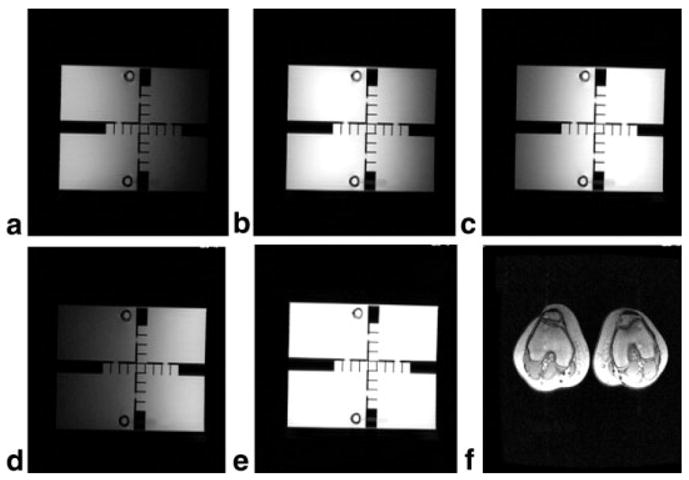
a–d: MR images acquired from each of the four different strips of the LPSA from a 27-cm-high, 20-cm-diameter phantom. e: Composite image produced using the root of the sum-of-the-squares method. Images were acquired with an FSE pulse sequence (echo train length (ETL) = 8, TE = 85 ms, TR = 2 s, NEX = 1, data-acquisition matrix 256 × 160, FOV = 36 cm). f: Composite phased-array axial image of the knees of a normal volunteer (TR = 150 ms, TE = 3.3 ms, NEX = 1, flip angle = 70, FOV = 48 cm, slice thickness = 7 mm, data matrix = 256 × 160, FOV = 48 cm).

Parallel Imaging With the LPSA

For parallel imaging, two different reconstruction schemes were used. One was GE’s implementation of the SENSE method (22), and the other was the general encoding matrix (GEM) method (21). For the SENSE reconstruction, in vivo T₁-weighted images of human legs were acquired with a fast gradient-echo pulse (fGRE) sequence, as shown in Fig. 10. These images in the coronal plane illustrate the uniformity of the strip’s sensitivity along the strip length, compared with the original PSA (1). Figure 10a is a conventional coronal image of the knees acquired in 25 s, while Fig. 10b was acquired with SENSE in 13 s with a reduction factor of 2.

FIG. 10.

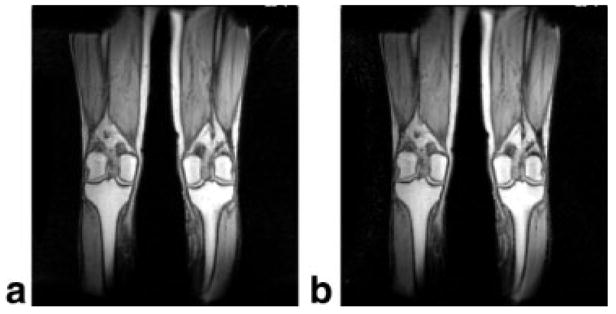
SENSE MRI of a normal volunteer acquired with four-element LPSA. a: Phased-array coronal image of a leg through the knees (TR = 150 ms, TE = 3.3 ms, NEX = 1, flip angle = 70, FOV = 48 cm, slice thickness = 7 mm, data matrix = 256 × 160, scan time = 25 s). b: Same section acquired with the same parameters, but for a reduction factor of 2 (scan time = 13 s).

With the four-channel LPSA, the GEM method yielded two-, three-, or fourfold scan-time reductions, as shown in Fig. 11. These images were reconstructed using a generalized encoding matrix with known k-space positions and measured coil sensitivities as described in Ref. 21. The matrix was inverted and multiplied by the raw signal data collected in all array elements to yield the accelerated images.

FIG. 11.

Images of the 27-cm-high, 20-cm-diameter phantom obtained with the GEM parallel reconstruction scheme. a: Fully gradient phase-encoded image. b–d: Images acquired with a reduction factor of 2 (b), 3 (c), and 4 (d). with a gradient-echo pulse sequence (TE = 6.7 msp, TR = 150 ms, flip angle = 30°, data acquisition matrix used to extract the sensitivity profile = 256 × 160, 256 × 256 points, NEX = 1, FOV = 34 cm, slice thickness = 5 mm). The coronal slice was 6 cm above the LPSA.

Comparison Between the RTL and a Circular Loop

Conventional MR phased arrays (2) typically use circular or rectangular loops as their basic elements. While it is presently unclear which specific loop and LPSA geometries can be meaningfully compared, given their inherently different sensitivities, the SNR for one element of the 30-cm prototype LPSA (with the other three elements open-circuit), and that of a GE single 15-cm-diameter circular loop, are shown as a function of depth in Fig. 12. In this case, the background noise levels from the strip and the loop are identical, with standard deviations (SDs) of 0.43 for both, and the net strip/coil lengths are roughly comparable. It is seen that the signal levels from the strip and the loop are also comparable overall, with the strip providing higher signal near the surface but lower signal at depths greater than ~3 cm for a profile through the mid-line (Fig. 12c), and signal levels at least as high as the loop at all depths, for a profile 4 cm away from the midline (Fig. 12d).

FIG. 12.

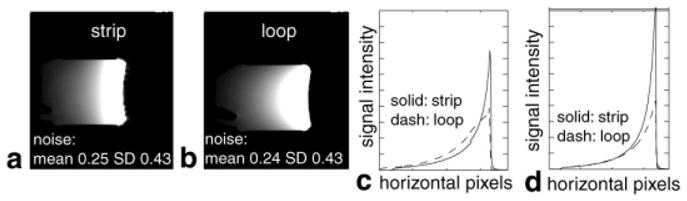
Comparison of a strip and a loop acquired from a phantom with the identical MRI sequence. a: Image acquired with one RTL (l = 30 cm, h = 2 cm). b: Image acquired with one circular loop (15-cm diameter). c and d: Profile comparisons of different rows in images a and b, respectively (horizontal scale is 1–256).

CONCLUSIONS

We have introduced a new type of MRI planar strip detector array, the LPSA, which can be tuned with lumped elements. The LPSA has an advantage over the original PSA in that its geometry is not limited by dielectric material and the wavelength therein, but can be arbitrarily adjusted within flexible guidelines that enable its performance to be optimized to suit a particular anatomy or region of interest (ROI) for a given MRI magnetic field strength. We have presented analytical expressions for the resonance conditions, Qs, magnetic field patterns, and SNR of the basic element of the LPSA—the RTL—along with criteria for choosing the geometric design and tuning elements that substantially eliminate coupling between the PSA elements. We analyzed the mutual coupling and g-factor maps of the LPSA, and fabricated a prototype LPSA according to the principles expounded. This LPSA demonstrated conventional phased-array MRI, as well as accelerated parallel sensitivity-encoded MRI of both phantoms and humans, with an underlying SNR of individual RTL elements comparable to that of a standard loop coil. These results affirm the potential of the LPSA as a useful, practical detector for multiple-channel MRI.

Although our strip arrays have been limited by our four-channel MRI system configuration (1,5), both the PSA and LPSA detector designs may provide important advantages over loops as the number of elements in the phased array increases to 8 or 16 or more channels. Increasing the number of elements in a conventional array comprised of loops increases the mutual coupling between loops, rendering them increasingly difficult to match, tune, and control (2,7,8). For strip arrays, mutual coupling problems may be minimized via intrinsic decoupling mechanisms in the case of the PSA (1), or by applying the design criteria for the LPSA discussed herein. In addition, for a given FOV, increasing the number of elements in a loop array for parallel sensitivity-encoded MRI eventually necessitates a reduction in loop size, and thus a reduction in the depth sensitivity of the entire detector. Strip arrays are not directly susceptible to this problem because the depth sensitivity does not depend on spacing between strips, although adequate decoupling must be maintained as the strips are positioned closer and closer together. Therefore, they have greater potential for packing more elements into a given FOV for the purposes of parallel imaging and/or retaining depth sensitivity, and thus represent a promising approach for massively parallel MRI (3).

The explicit phase relation between the LPSA and imaged objects can be used to simplify the parallel reconstruction, and the field orientation of the LPSA makes it a good candidate for open-field MRI. In addition, the naturally shielded structure of the LPSA may help prevent the severe coil losses often experienced at high fields.