Abstract
For pedigree-based quantitative trait loci (QTL) association analysis, a range of methods utilizing within-family variation such as transmission-disequilibrium test (TDT)-based methods have been developed. In scenarios where stratification is not a concern, methods exploiting between-family variation in addition to within-family variation, such as the measured genotype (MG) approach, have greater power. Application of MG methods can be computationally demanding (especially for large pedigrees), making genomewide scans practically infeasible. Here we suggest a novel approach for genomewide pedigree-based quantitative trait loci (QTL) association analysis: genomewide rapid association using mixed model and regression (GRAMMAR). The method first obtains residuals adjusted for family effects and subsequently analyzes the association between these residuals and genetic polymorphisms using rapid least-squares methods. At the final step, the selected polymorphisms may be followed up with the full measured genotype (MG) analysis. In a simulation study, we compared type 1 error, power, and operational characteristics of the proposed method with those of MG and TDT-based approaches. For moderately heritable (30%) traits in human pedigrees the power of the GRAMMAR and the MG approaches is similar and is much higher than that of TDT-based approaches. When using tabulated thresholds, the proposed method is less powerful than MG for very high heritabilities and pedigrees including large sibships like those observed in livestock pedigrees. However, there is little or no difference in empirical power of MG and the proposed method. In any scenario, GRAMMAR is much faster than MG and enables rapid analysis of hundreds of thousands of markers.
MAPPING genes responsible for variation in quantitative traits (QTs) relevant to human health and disease, such as blood pressure, glucose level, and body composition, is a valuable approach to disentangling complexity of common disorders (Rice et al. 2001; Blangero 2004). In this context, association mapping, also termed linkage-disequilibrium (LD) mapping has the potential to be more powerful for QTL detection and to map with higher resolution than classical linkage analysis. In recent years, remarkable methodological and technical progress has been achieved in the area of LD mapping. Much emphasis has been placed on LD mapping in unrelated cases and controls coming from the general population and LD mapping of binary and quantitative traits, using family data; see Forabosco et al. (2005) for review. For pedigree-based QTL association analysis, a range of methods and software that utilize information about transmission of alleles, such as the orthogonal test for within-family variation (quantitative trait transmission disequilibrium test, QTDT) (Abecasis et al. 2000) and the family-based association test (FBAT) (Lange et al. 2002; Horvath et al. 2004) have been developed. As these methods analyze within-family variation, or association between the trait and transmission of marker alleles, they are robust even when population stratification is present.
Population stratification may be expected to be present in general and recently admixed populations. At the same time, study populations that have been carefully selected using stringent ethnic origin criteria and study populations based on some special, genetically isolated populations are under minimal risk of stratification. Moreover, genetic stratification may be detected using molecular markers (Pritchard et al. 2000; Falush et al. 2003), and individuals that are likely to be genetic “outliers” may be excluded from further study, or analysis may be adjusted for population substructure.
When ethnic stratification can be ruled out, the measured genotype approach (Hopper and Mathews 1982; Boerwinkle et al. 1986; George and Elston 1987) or overall test of within- and between-family variation may serve as a powerful tool for QTL analysis (Havill et al. 2005; Lange et al. 2005). In this approach, a genetic polymorphism under study is included as a fixed effect or covariate in a mixed model that includes a polygenic component as a random effect and a likelihood ratio (when using maximum likelihood) or the Wald test [when using restricted maximum likelihood (REML)] is performed to assess significance of the effect of the polymorphism.
Unfortunately, when analyzed pedigrees are large, which is especially the case for genetically isolated populations (Newman et al. 2001; Bourgain and Genin 2005; Pardo et al. 2005), or for some ethnic subgroups (Charlesworth et al. 2005; Lehman et al. 2006), the computations required for the measured genotype approach may be very time consuming. This stems from the need to analyze a relatively complex mixed model for each of many markers to be tested. Even testing the effect of a single polymorphism may take from several minutes to hours and therefore genomewide association analysis takes significant computational resources and would be practically infeasible when run on a single computer. Moreover, even with small pedigrees, empirical techniques such as permutation analysis and bootstrapping cannot be applied to the data, as they do not have an exchangeable structure: permutation of trait values across the entire sample breaks both trait–marker and trait–pedigree (due to polygenes) relationships.
In this study we explore alternative approaches to pedigree-based QTL association analysis and we introduce a new, fast, and simple method (GRAMMAR) that can be applied using existing software and that will facilitate whole-genome high-density single-nucleotide polymorphism (SNP) scans. We compare the power, type 1 error, and operational characteristics of the new approach to those of the measured genotypes and TDT-based approaches.
MATERIALS AND METHODS
Proposed method:
The simplest test for the effect of a SNP or other marker that can be considered is a contrast of the means of alternative genotype classes in a linear model. Such an approach provides a very fast analysis, but in the context of data from a pedigree or a number of families it ignores the covariance between individuals that these relationships produce. Therefore, application of this method can lead to high levels of false positive associations. The use of a mixed analysis that models the polygenic relationships between individuals as a random component (and can include additional random components to allow for other features such as common family environmental effects) can resolve this problem. However, this modeling also greatly slows down the analysis. The basic idea of the proposed method is to perform a single polygenic analysis using the complete pedigree but ignoring marker data. Subsequently, we use residuals from this analysis, which are now adjusted for polygenic covariation and fixed effects, as a novel quantitative trait for association analyses with each of many markers using classical methods for unrelated individuals (“population-based design”).
In the initial step, the data are analyzed under the mixed model
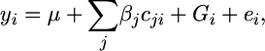 |
(1) |
where yi is the phenotype of the ith individual, cij is the value of the jth covariate or fixed effect for the individual i, βj is an estimate of the jth fixed effect or covariate, and Gi and ei are random additive polygenic and residual effects, respectively. The random effects are assumed to follow a multivariate normal distribution with mean zero. The variance for the polygenic effects is defined as Φ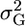 , where Φ is the relationship matrix and
, where Φ is the relationship matrix and 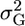 is the additive genetic variance due to polygenes. For the residual random effects, the variance is defined as
is the additive genetic variance due to polygenes. For the residual random effects, the variance is defined as 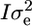 , where I is the identity matrix and
, where I is the identity matrix and 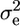 is the residual variance.
is the residual variance.
The residuals from this analysis are given by
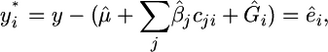 |
where 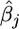 is the estimate of the jth fixed effect and
is the estimate of the jth fixed effect and 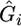 is the estimated contribution from the polygene (breeding value).
is the estimated contribution from the polygene (breeding value).
In the second step, these residuals are used as the dependent trait in a simple linear regression for each SNP,
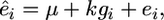 |
(2) |
where 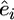 is the vector of residuals from (1), μ is the mean, g is the vector of genotypes at the marker under study, k is the marker genotype effect, and e is the vector of random residuals. We call this analytical approach GRAMMAR.
is the vector of residuals from (1), μ is the mean, g is the vector of genotypes at the marker under study, k is the marker genotype effect, and e is the vector of random residuals. We call this analytical approach GRAMMAR.
Subsequent to the GRAMMAR analysis, markers showing test statistics greater than some predefined threshold are selected for a final analysis using the measured genotype (MG) model:
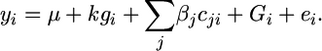 |
(3) |
The first step of the GRAMMAR approach, i.e., computation of residuals from a polygenic model (1), is relatively slow and takes from minutes to hours for very complex (tens of thousands of members) pedigrees. However, fitting model (2) can be performed at a rate of a few thousands of tests per second. The subsequent MG analysis is the most time consuming, as it requires reevaluation of a number of polymorphisms in complete model (3), each taking minutes to hours to run in complex pedigrees, although this step is applied to a limited number of markers.
Simulations:
Three pedigree structures were considered in our simulation study:
Three hundred thirty seven nuclear pedigrees (NP): The founders in each pedigree were assumed to be unrelated. Each pedigree had three phenotyped and genotyped siblings and thus a total of 1011 individuals were available for analysis. This sample simulates a family-based study as typically performed in the general population.
Erasmus Rucphen family (ERF) (1010 pheno- and genotyped individuals in a single large complex pedigree, including 9818 individuals in total): The pedigree spreads for 23 generations and includes thousands of loops. The phenotyped individuals are a part of the ERF study, performed in a young genetically isolated Dutch population (Pardo et al. 2005).
Idealized pig population (IPP): To test whether the method is applicable to larger full- and half-sib family sizes, as commonly encountered in livestock studies, we simulated 10 sires, each mated to 10 dams, 9 of which have 10 and 1 of which has 11 measured offspring. Thus, each sire has 101 half-sib offspring in families of 10 full-sibs. The total phenotyped population consists of 1010 individuals.
For each of these three pedigrees, we simulated genetic data under several models. The single-nucleotide polymorphism (SNP), which was analyzed for association, had a minor allele frequency of either 10 or 50%. For studying the type 1 error, this SNP was not involved in the control of the trait, while for studying the statistical power this SNP explained 1, 2, or 3% of the total trait variation and acted in an additive manner. The total heritability of the trait was set to 30, 50, or 80%; this heritability included the variation due to the QTL studied.
In addition, we simulated 7351 linked SNPs for the ERF pedigree, to assess performance and power of different methods in a large-scale analysis. These SNPs are part of the Affymetrix GeneChip Mapping 100,000 SNP set (Matsuzaki et al. 2004), covering chromosome 1. In our simulations, we used the genetic map and Caucasian allelic frequencies as provided by Affymetrix. The total length of the map was 273 cM. One of the SNPs, located at 108 cM, was chosen to explain 3% of the QTL variation in our simulations. The residual heritability was set to 27%. One hundred replicates were generated and analyzed.
ANALYSIS
The data were analyzed using six methods:
Disregarding family structure (DFS): The correlations between relatives were not accounted for; essentially, pedigree-based data were treated as a sample of unrelated individuals. Analysis under this model was performed using the “lm” procedure of the freely available R software, v. 2.1.1 (http://www.r-project.org). The linear model included the trait value as an outcome and SNP genotype as a covariate. The SNP was coded as the number of rare allele copies (0, 1, or 2) across all methods.
Measured genotype (MG): We used restricted maximum likelihood, as implemented in ASReml (Gilmour et al. 2002) software. The SNP to be tested was included as a covariate in a polygenic model (3); heritability and SNP effect were estimated jointly. The Wald test was used to assess significance of the SNP effect.
MG–fixed heritability (FH): MG–FH is similar to MG, with the exception that only the SNP effect was estimated, while heritability was fixed at the estimate obtained from analysis of trait and pedigree data. This method has the potential to speed up computations; as in genomewide analysis, heritability would be estimated only once and the fixed estimate used for analysis of all SNPs.
GRAMMAR: As described in materials and methods, residuals from a polygenic model were obtained using ASReml according to model (1); these residuals were used as an outcome variable for the lm procedure according to model (2) and similar to DFS analysis.
QTDT: As implemented in the QTDT (Abecasis et al. 2000) software, the orthogonal test for within-family association was used.
FBAT: As implemented in FBAT (Horvath et al. 2004; Lange et al. 2002) software, the “fbat” command with no further options was used.
For DFS and GRAMMAR we also derived empirical, permutation-based P-values. For every simulated data set, empirical P-values were obtained in the following manner: Sampling without replacement was performed 1000 times and analysis was repeated for every permuted set. The empirical P-value was defined as the proportion of times the statistics obtained on permuted sets were greater than or equal to the original statistics. For FBAT we derived permutation P-values using 10,000 replicates (the “hbat −p 10,000” command was used).
For studying the type 1 error, we generated and analyzed 1000 replicates for all pedigree structures and all scenarios. For studying the statistical power, we generated and analyzed 1000 replicates for the nuclear pedigrees and the IPP and 100 replicates for the ERF pedigree.
GRAMMAR followed by MG (GRAMMAR + MG) was implemented for the analysis of the 7351 SNPs on the ERF data. The power to achieve chromosome- and genomewide significance was estimated as the proportion of tests exceeding chi-square statistics of 20.22 (α = 0.05/7351) and 24.37 (α = 0.05/100,000). From the earlier simulations, we determined the lower boundary of the ratio between the noncentrality parameter (NCP) of the MG and that of the GRAMMAR. For the full MG reanalysis we selected the SNPs that generated test statistics greater than or equal to the genome- (chromosome)wide threshold, corrected for this deflation factor.
RESULTS
Table 1 shows the 95% quantile of the test statistics distribution and the type 1 error (obtained by comparison with tabulated thresholds corresponding to α = 0.05 and 0.01) for the evaluated methods. As expected, the MG approach had a type 1 error that was close to the prespecified α. The type 1 error of MG–FH was similar to that of the MG (results not shown). The 95% quantiles of the FBAT null distribution also followed 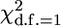 -distribution closely. The QTDT test was conservative when heritability was high (h2 ≥ 0.5, Table 1).
-distribution closely. The QTDT test was conservative when heritability was high (h2 ≥ 0.5, Table 1).
TABLE 1.
Ninety-five percent quantiles of the distribution of the test statistics and type 1 error of measured genotype (MG), GRAMMAR, disregarding-family-structure (DFS), QTDT, and FBAT analyses
| Type 1 error at given threshold
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pedigree:a | 95% quantile
|
χ2 ≥ 3.84 (α = 0.05)
|
χ2 ≥ 6.63 (α = 0.01)
|
||||||||||||
| h2b | MG | GRAMMAR | DFS | QTDT | FBAT | MG | GRAMMAR | DFS | QTDT | FBAT | MG | GRAMMAR | DFS | QTDT | FBAT |
| NP | |||||||||||||||
| 0.3 | 3.80 | 3.25 | 4.13 | 3.62 | 4.10 | 0.049 | 0.029 | 0.060 | 0.040 | 0.058 | 0.015 | 0.010 | 0.014 | 0.008 | 0.013 |
| 0.5 | 3.54 | 2.89 | 4.57 | 2.87 | 3.75 | 0.043 | 0.021 | 0.072 | 0.020 | 0.048 | 0.006 | 0.002 | 0.015 | 0.002 | 0.009 |
| 0.8 | 4.08 | 2.92 | 5.66 | 2.3 | 3.79 | 0.059 | 0.026 | 0.101 | 0.012 | 0.049 | 0.014 | 0.006 | 0.033 | 0.002 | 0.009 |
| ERF | |||||||||||||||
| 0.3 | 3.65 | 3.08 | 4.87 | 3.46 | 3.75 | 0.043 | 0.031 | 0.082 | 0.037 | 0.049 | 0.009 | 0.004 | 0.019 | 0.005 | 0.005 |
| 0.5 | 4.04 | 3.15 | 5.49 | 3.17 | 3.88 | 0.055 | 0.023 | 0.107 | 0.033 | 0.051 | 0.008 | 0.003 | 0.025 | 0.006 | 0.011 |
| 0.8 | 3.96 | 2.71 | 6.55 | 3.5 | 4.05 | 0.053 | 0.021 | 0.112 | 0.041 | 0.055 | 0.013 | 0.001 | 0.050 | 0.009 | 0.009 |
| IPP | |||||||||||||||
| 0.3 | 3.88 | 2.73 | 11.95 | 3.33 | —c | 0.053 | 0.019 | 0.264 | 0.035 | — | 0.012 | 0.003 | 0.149 | 0.008 | — |
| 0.5 | 4 | 2.58 | 18.41 | 2.84 | — | 0.055 | 0.012 | 0.385 | 0.028 | — | 0.011 | 0.004 | 0.242 | 0.005 | — |
| 0.8 | 3.8 | 2.27 | 23.92 | 2.43 | — | 0.050 | 0.012 | 0.421 | 0.019 | — | 0.012 | 0.000 | 0.302 | 0.000 | — |
Type 1 error significantly (P ≤ 0.05) inflated is underlined and conservative is in italics. Score test of deviation of proportion from a fixed value was used.
Pedigree studied. NP, 337 nuclear pedigrees; ERF, large human pedigree; IPP, idealized pig population.
Total heritability.
This structure is not analyzable with FBAT.
When analysis was performed without correction for family structure (DFS analysis), the 95% quantiles and the type 1 error were markedly inflated. The type 1 error was inflated more with higher heritabilities and larger full-sib family sizes and reached 42% for IPP at heritability of 80%. The GRAMMAR analysis exhibited the opposite behavior: It was conservative and this tendency was more pronounced for models with higher heritability and larger full-sib family sizes.
Marker allele frequency did not affect the type 1 error (results not shown). For methods where permutation could be performed (GRAMMAR, DFS, and FBAT) the empirical 95% quantiles obtained using permutation within each set of data were very similar to the tabulated asymptotic values. Hence empirical type 1 errors derived by comparison against these values were also very similar to those derived by comparison to the asymptotic values (supplemental Table 1 at http://www.genetics.org/supplemental/).
Table 2 shows power of different approaches to detect a QTL when using fixed thresholds following a 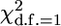 -distribution. It must be noted that, given the results of type 1 error analysis, the power of conservative methods (GRAMMAR and QTDT) is underestimated because the same fixed threshold is used across all methods.
-distribution. It must be noted that, given the results of type 1 error analysis, the power of conservative methods (GRAMMAR and QTDT) is underestimated because the same fixed threshold is used across all methods.
TABLE 2.
Mean χ2-statistics (M[χ2]) and proportion of results for which the test statistic was more than or equal to the tabular critical value for measured genotype (MG), GRAMMAR, QTDT, and FBAT analyses
| Proportion of simulations resulting in a χ2 ≥
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pedigree: |
M[χ2]
|
3.84 (α = 0.05)
|
6.63 (α = 0.01)
|
||||||||||
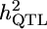 a a
|
h2 | MG | GRAMMAR | QTDT | FBAT | MG | GRAMMAR | QTDT | FBAT | MG | GRAMMAR | QTDT | FBAT |
| NP | |||||||||||||
| 0.3 | 10.28 | 8.86 | 4.21 | 4.76 | 0.84 | 0.80 | 0.45 | 0.50 | 0.67 | 0.06 | 0.21 | 0.27 | |
| 0.01 | 0.5 | 10.27 | 8.15 | 4.34 | 5.53 | 0.86 | 0.79 | 0.47 | 0.57 | 0.69 | 0.56 | 0.21 | 0.33 |
| 0.8 | 10.59 | 7.52 | 4.15 | 6.51 | 0.88 | 0.77 | 0.45 | 0.66 | 0.67 | 0.49 | 0.19 | 0.42 | |
| 0.3 | 19.9 | 17.12 | 7.95 | 8.61 | 0.99 | 0.99 | 0.77 | 0.80 | 0.96 | 0.93 | 0.54 | 0.59 | |
| 0.02 | 0.5 | 19.69 | 15.59 | 7.73 | 9.48 | 0.99 | 0.98 | 0.79 | 0.87 | 0.96 | 0.93 | 0.54 | 0.66 |
| 0.8 | 20.21 | 14.26 | 7.42 | 11.2 | 0.99 | 0.97 | 0.80 | 0.91 | 0.96 | 0.91 | 0.5 | 0.76 | |
| 0.3 | 29.52 | 25.23 | 11.2 | 11.83 | 1.00 | 1.00 | 0.91 | 0.94 | 1.00 | 0.99 | 0.76 | 0.80 | |
| 0.03 | 0.5 | 29.31 | 23.13 | 11.36 | 13.52 | 1.00 | 1.00 | 0.93 | 0.96 | 0.99 | 0.99 | 0.79 | 0.86 |
| 0.8 | 30.26 | 21.39 | 11.09 | 16.2 | 1.00 | 1.00 | 0.95 | 0.98 | 0.99 | 0.99 | 0.79 | 0.93 | |
| ERF | |||||||||||||
| 0.3 | 9.89 | 8.32 | 2.96 | 3.13 | 0.81 | 0.79 | 0.26 | 0.31 | 0.71 | 0.58 | 0.1 | 0.14 | |
| 0.01 | 0.5 | 9.86 | 7.70 | 3.44 | 3.63 | 0.83 | 0.75 | 0.34 | 0.40 | 0.68 | 0.52 | 0.18 | 0.19 |
| 0.8 | 10.35 | 7.14 | 2.71 | 3.18 | 0.83 | 0.73 | 0.23 | 0.28 | 0.65 | 0.46 | 0.11 | 0.16 | |
| 0.02 | 0.3 | 18.69 | 15.67 | 5.75 | 5.43 | 0.97 | 0.96 | 0.59 | 0.54 | 0.92 | 0.89 | 0.36 | 0.31 |
| 0.5 | 19.28 | 14.89 | 5.97 | 6.13 | 0.99 | 0.98 | 0.63 | 0.60 | 0.93 | 0.9 | 0.34 | 0.40 | |
| 0.8 | 20.87 | 14.4 | 6.01 | 6.83 | 0.99 | 0.99 | 0.62 | 0.69 | 0.98 | 0.92 | 0.40 | 0.47 | |
| IPP | |||||||||||||
| 0.3 | 8.39 | 5.57 | 5.41 | — | 0.76 | 0.60 | 0.55 | — | 0.55 | 0.33 | 0.32 | — | |
| 0.01 | 0.5 | 8.55 | 5.31 | 5.46 | — | 0.76 | 0.57 | 0.56 | — | 0.55 | 0.30 | 0.31 | — |
| 0.8 | 10.10 | 5.88 | 5.62 | — | 0.82 | 0.62 | 0.59 | — | 0.62 | 0.36 | 0.34 | — | |
| 0.3 | 16.01 | 10.65 | 10.30 | — | 0.94 | 0.88 | 0.83 | — | 0.86 | 0.73 | 0.66 | — | |
| 0.02 | 0.5 | 16.84 | 10.43 | 10.46 | — | 0.95 | 0.88 | 0.85 | — | 0.87 | 0.7 | 0.66 | — |
| 0.8 | 18.18 | 10.58 | 9.96 | — | 0.96 | 0.88 | 0.85 | — | 0.89 | 0.71 | 0.67 | — | |
Proportion of the trait variation, which is explained by the QTL.
Among methods that did not show inflated type 1 errors, MG was most powerful and MG–FH had very similar power (results not shown). The MG, MG–FH, and GRAMMAR approaches outperform TDT-based approaches under all scenarios studied. For example, MG, MG–FH, and GRAMMAR had ∼80% power to detect a QTL explaining 1% of variation at α = 0.05 in a sample of nuclear families while QTDT had 45–47% power and FBAT had 50–66% power with the same data (Table 2). For all methods, the power to detect QTL when SNP frequency was 0.5 did not differ notably from the situation when the frequency was 0.1.
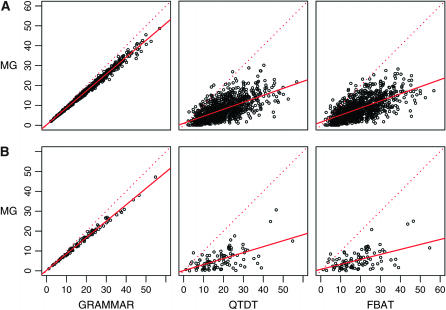
The power of MG also shows a weak, but consistent trend to increase with higher heritability. Relative to MG, GRAMMAR had lower power. Nonetheless, the GRAMMAR statistics show almost perfect (≥0.99) correlation with the MG statistics (Figure 1). Interestingly, for GRAMMAR the NCP was always lower than that from MG.
Figure 1.—
Scatterplot of the χ2-statistics coming from the measured-genotype (MG) approach vs. χ2-statistics coming from GRAMMAR, QTDT, and FBAT. The model assumes heritability of 0.28 and a QTL explaining 0.02 of the total variance. Results of analysis of data from 337 sib-trios (A) and ERF pedigree (B) are presented. The dotted line represents a slope of unity.
In Table 3, we show a more appropriate comparison of statistical power between different methods, taking account of their different null distributions. To compute the empirical power, we used the 95% quantile of the appropriate Monte Carlo-derived null distribution (i.e., analysis of data sets generated under the null hypothesis with polygenic effects but with no marker effect) as a significance threshold, rather than the tabulated 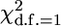 -value. The empirical distributions were computed for each combination of method and genetic model using 1000 simulations (Table 1). As expected, under these conditions that account for the bias in NCP, GRAMMAR had power that was very similar to that of the MG, while DFS was less powerful. Power of QTDT and FBAT was much lower than that of MG under these conditions, but power of QTDT became very similar to that of FBAT. These results demonstrate the power of the alternative analyses when compared to the appropriate null hypothesis distribution.
-value. The empirical distributions were computed for each combination of method and genetic model using 1000 simulations (Table 1). As expected, under these conditions that account for the bias in NCP, GRAMMAR had power that was very similar to that of the MG, while DFS was less powerful. Power of QTDT and FBAT was much lower than that of MG under these conditions, but power of QTDT became very similar to that of FBAT. These results demonstrate the power of the alternative analyses when compared to the appropriate null hypothesis distribution.
TABLE 3.
Empirical power for measured genotype (MG), GRAMMAR, disregarding-family-structure (DFS), QTDT, and FBAT analyses
| Pedigree: | Analysis method
|
|||||
|---|---|---|---|---|---|---|
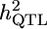 |
h2 | MG | GRAMMAR | DFS | QTDT | FBAT |
| NP | ||||||
| 0.01 | 0.3 | 0.85 | 0.85 | 0.84 | 0.47 | 0.48 |
| 0.5 | 0.87 | 0.87 | 0.82 | 0.57 | 0.59 | |
| 0.8 | 0.86 | 0.86 | 0.75 | 0.67 | 0.66 | |
| 0.02 | 0.3 | 0.99 | 0.99 | 0.99 | 0.78 | 0.78 |
| 0.5 | 0.99 | 0.99 | 0.99 | 0.88 | 0.87 | |
| 0.8 | 0.99 | 0.99 | 0.96 | 0.92 | 0.91 | |
| 0.03 | 0.3 | 1 | 1 | 1 | 0.92 | 0.92 |
| 0.5 | 1 | 1 | 1 | 0.96 | 0.96 | |
| 0.8 | 1 | 1 | 0.99 | 0.98 | 0.98 | |
| ERF | ||||||
| 0.01 | 0.3 | 0.82 | 0.81 | 0.83 | 0.31 | 0.32 |
| 0.5 | 0.80 | 0.80 | 0.75 | 0.42 | 0.40 | |
| 0.8 | 0.82 | 0.86 | 0.74 | 0.29 | 0.27 | |
| 0.02 | 0.3 | 0.97 | 0.98 | 0.95 | 0.64 | 0.54 |
| 0.5 | 0.99 | 0.99 | 0.99 | 0.67 | 0.60 | |
| 0.8 | 0.99 | 0.99 | 0.96 | 0.68 | 0.68 | |
| IPP | ||||||
| 0.01 | 0.3 | 0.76 | 0.73 | 0.42 | 0.61 | — |
| 0.5 | 0.74 | 0.73 | 0.28 | 0.67 | — | |
| 0.8 | 0.82 | 0.81 | 0.27 | 0.75 | — | |
| 0.02 | 0.3 | 0.94 | 0.95 | 0.69 | 0.86 | — |
| 0.5 | 0.95 | 0.94 | 0.53 | 0.91 | — | |
| 0.8 | 0.96 | 0.95 | 0.42 | 0.94 | — | |
In Table 4, we show the average of the allelic effect estimates resulting from three different analysis approaches (MG, GRAMMAR, and DFS). It can be seen that both MG and DFS methods estimate the allelic effect rather well in an unbiased manner. On the contrary, GRAMMAR analysis strongly underestimated the effect. From Table 4, it is also clear that, compared to MG, the DFS tends to underestimate the “true” (MG-derived) standard errors, which is a consequence of its ignoring the familial correlations. This explains why the DFS method has increased type 1 error.
TABLE 4.
Mean of the allelic effect estimates (± mean SE of the estimates) from measured genotype (MG), GRAMMAR, and disregarding-family-structure (DFS) analyses
| Pedigree: | Analysis method
|
||||
|---|---|---|---|---|---|
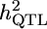 |
Simulated effect | h2 | MG | GRAMMAR | DFS |
| NP | |||||
| 0.01 | 0.3 | 0.234 ± 0.077 | 0.149 ± 0.053 | 0.235 ± 0.074 | |
| 0.236 | 0.5 | 0.237 ± 0.078 | 0.106 ± 0.039 | 0.236 ± 0.074 | |
| 0.8 | 0.238 ± 0.077 | 0.044 ± 0.017 | 0.236 ± 0.074 | ||
| 0.02 | 0.3 | 0.334 ± 0.077 | 0.213 ± 0.053 | 0.334 ± 0.074 | |
| 0.333 | 0.5 | 0.336 ± 0.078 | 0.149 ± 0.039 | 0.336 ± 0.074 | |
| 0.8 | 0.334 ± 0.077 | 0.062 ± 0.017 | 0.336 ± 0.074 | ||
| 0.03 | 0.3 | 0.408 ± 0.077 | 0.259 ± 0.053 | 0.409 ± 0.073 | |
| 0.408 | 0.5 | 0.411 ± 0.078 | 0.183 ± 0.039 | 0.411 ± 0.073 | |
| 0.8 | 0.411 ± 0.076 | 0.076 ± 0.017 | 0.412 ± 0.073 | ||
| ERF | |||||
| 0.01 | 0.3 | 0.236 ± 0.079 | 0.149 ± 0.054 | 0.239 ± 0.075 | |
| 0.236 | 0.5 | 0.237 ± 0.081 | 0.105 ± 0.041 | 0.240 ± 0.077 | |
| 0.8 | 0.234 ± 0.078 | 0.044 ± 0.018 | 0.247 ± 0.073 | ||
| 0.02 | 0.3 | 0.333 ± 0.082 | 0.209 ± 0.056 | 0.333 ± 0.077 | |
| 0.333 | 0.5 | 0.336 ± 0.079 | 0.150 ± 0.040 | 0.340 ± 0.074 | |
| 0.8 | 0.344 ± 0.078 | 0.068 ± 0.018 | 0.343 ± 0.075 | ||
| IPP | |||||
| 0.01 | 0.3 | 0.235 ± 0.089 | 0.125 ± 0.058 | 0.236 ± 0.071 | |
| 0.236 | 0.5 | 0.237 ± 0.088 | 0.093 ± 0.043 | 0.235 ± 0.067 | |
| 0.8 | 0.238 ± 0.082 | 0.044 ± 0.019 | 0.237 ± 0.060 | ||
| 0.02 | 0.3 | 0.334 ± 0.089 | 0.178 ± 0.058 | 0.332 ± 0.076 | |
| 0.333 | 0.5 | 0.335 ± 0.087 | 0.131 ± 0.043 | 0.335 ± 0.074 | |
| 0.8 | 0.329 ± 0.083 | 0.058 ± 0.019 | 0.325 ± 0.069 | ||
Finally, in Table 5 we show results of analysis of performance and power of different methods (QTDT, FBAT, DFS, and MG) in large-scale analysis using the ERF pedigree and also evaluate the complete strategy of GRAMMAR followed by MG proposed in materials and methods. This procedure involved chromosomewise GRAMMAR analysis first; then SNPs that passed a relaxed threshold of 14.14 (for chromosomewide significance analysis) and 17.04 (for genomewide) were selected to be followed up with MG. These thresholds were chosen on the basis of the observation that GRAMMAR test statistics would be up to 30% smaller than the “gold standard” MG statistics (Table 2). The power to achieve chromosome and genomewide significance was estimated as the proportion of tests exceeding chi-square statistics of 20.22 (α = 0.05/7351) and 24.37 (α = 0.05/100,000), respectively.
TABLE 5.
Results of analysis of 7351 SNPs located at chromosome 1, using 100 simulations on ERF pedigree
| Method | Time | RAM | Accuracy | PowerCHR1 | AccuracyCHR1 | PowerGW | AccuracyGW |
|---|---|---|---|---|---|---|---|
| MG | 76 daysa | 32 | — | 0.77b | — | 0.62b | — |
| GRAMMAR | 17 minc | 101 | 0.89 | 0.57 | 1.00 | 0.33 | 1.00 |
| GRAMMAR+MG | 40 mind | 101 | 0.87 | 0.75 | 0.97 | 0.55 | 1.00 |
| QTDT | 6 hr 20 min | 559 | 0.20 | 0.12 | 0.50 | 0.04 | 1.00 |
| FBAT | 20 min | 142 | 0.08 | 0.02 | 0 | 0 | — |
QTL explains 3% of total variation, residual heritability set to 27%. Time, time to complete single chromosomewide analysis; RAM, maximum amount of RAM memory (megabytes) required for analysis; Accuracy, proportion of simulations in which the maximum test statistic was observed at the position of the SNP controlling QT variation. PowerCHR1 [PowerGW]: proportion of simulations in which chromosomewise (α = 0.05/7351) [genomewise (α = 0.05/100000)] significance was achieved. AccuracyCHR1 (AccuracyGW): proportion of chromosomewide (genomewide) significant simulations for which the maximum test statistic was observed at the position of the SNP controlling QT variation.
Estimated assuming 15 min per MG analysis of a single marker.
Power is estimated assuming that expected NCP for MG is 27.5.
Fourteen min to estimate residuals and 3 min for analysis using R.
Fourteen min to estimate residuals, 3 min for analysis using R, and 23 min on average to reanalyze selected SNPs with MG.
Not surprisingly, the fastest method was our GRAMMAR approach, which required ∼17 min to complete analysis of chromosome 1 (most of the time being taken with the single analysis needed to preadjust the data); the estimated time to complete a full genome scan was 55 min. In a GRAMMAR + MG chromosomewide analysis the average number of SNPs that were taken forward for analysis with MG at the final step was 1.53; therefore average time to complete a GRAMMAR + MG analysis was ∼40 min. However, the time for this approach depends on the number of SNPs selected from GRAMMAR and varied from 17 min (no SNPs selected) to 1.5 hr (5 SNPs selected). FBAT required 20 min to analyze chromosome 1 (and thus ∼5 hr to complete a genomewide scan); QTDT was notably slower (>6 hr for chromosome 1 and an estimated 3.5 days to finish a genomewide scan). The time to finish a single SNP- measured genotype analysis was 15 min, and thus MG analysis of chromosome 1 would have required 76 days and the genomewide analysis time estimate is ∼2.5 years.
All programs used a reasonable amount of memory, with QTDT requiring a maximum amount of 559 MB. Because the time to perform complete chromosomewide analysis was prohibitively long for MG, we approximated the expected power of MG analytically. This power may serve as a gold standard in our comparisons. The QTDT and the FBAT demonstrated relatively low power for chromosomewise and genomewise analysis. The GRAMMAR approach had power that was lower than that expected of MG. However, the application of GRAMMAR + MG led to rather high power that was close to that estimated for MG. Also, GRAMMAR and the GRAMMAR + MG approaches proposed here outperformed other methods in location accuracy.
DISCUSSION
In this work, we suggested a novel approach (GRAMMAR) for genomewide pedigree-based association analysis. The method is based on obtaining residuals from a polygenic model followed by association analysis of these residuals with genetic polymorphisms using classical methods for unrelated individuals. One can then follow up selected polymorphisms with MG analysis as a final step. We compared type 1 error, power, and operational characteristics of the proposed methods with those of MG- and TDT-based approaches (FBAT and QTDT).
Our results indicate that the power of the MG approach is much higher than that of TDT-based approaches. Basically, when using the MG approach, the sample size may be reduced to half or even one-third of the sample required by a TDT-based approach to have the same power. This is in line with theoretical considerations (Hernández-Sánchez et al. 2003) and recent findings of Havill et al. (2005).
GRAMMAR followed by MG leads to a mild reduction of power when compared to MG, but substantially (hundreds and thousands of times) outperforms MG in terms of time required for analysis. Therefore we recommend future use of GRAMMAR + MG in genomewide pedigree-based QTL association analysis. At the final step, markers showing test statistics greater than some predefined threshold are selected for a final analysis using the MG model. The choice of this threshold represents a balance between computational time (the lower the threshold, the more markers are to be followed up) and power (the higher the threshold, the larger is the chance to miss a marker that would have been significant in the MG analysis). It is not clear a priori what threshold should be chosen. For the present study, we estimated the ratio between the NCP of MG and GRAMMAR and applied the same ratio to adjust the threshold for selecting the SNPs for the full MG reanalysis.
Interestingly, when applying thresholds that are obtained under simulation of the null distribution, the GRAMMAR approach has equivalent empirical power to MG and the final step is required only to reestimate the QTL effects. On the basis of this observation, a powerful approach to analysis of genomewide scans may be proposed. In this approach, we suggest the following procedure: (a) Simulate an unlinked trait with heritability reflecting the one of the trait of interest, (b) perform genomewide analysis of this unlinked trait, (c) save the minimal P-value, and (d) repeat a–c several hundred times. The resulting set of minimal P-values provides an empirical distribution from which the genomewide significance threshold may be obtained.
The GRAMMAR approach has some additional advantages. After fitting the polygenetic model in stage1, the residuals are free from familial correlations; therefore, the structure of the data becomes exchangeable. This means that permutation techniques may be applied to derive empirical measures of significance. In the analysis of data where adjacent SNPs are correlated due to linkage disequilibrium, thresholds set via permutation will account for these correlations and result in less stringent thresholds than those set by Bonferroni correction. Thus in practice, when very dense marker maps are used, the GRAMMAR approach may be more powerful than the MG approach where computational requirements dictate that the threshold is set by Bonferroni correction. Our experience shows that with the GRAMMAR approach, derivation of empirical genomewide significance based on 1000 permutations of a genomewide scan including 100,000 SNPs will require no more than a few hours if a fast implementation of a score test (see, e.g., Schaid et al. 2002; Aulchenko et al. 2007) is used.
Another attractive feature of the GRAMMAR procedure is that a range of new methods developed for a classical “unrelated individuals” design can be applied at stage 2 of the analysis. In recent years, much progress was made in the development of powerful methods and software that are robust to possible allelic heterogeneity through the utilization of haplotype clustering and population genetic coalescence modeling (Durrant et al. 2004; Zollner and Pritchard 2005). Although we show that application of the GRAMMAR approach leads to conservative results when using tabulated threshold values, the benefits of using more advanced modeling methods may outweigh this consideration.
Finally, the GRAMMAR approach was developed in the framework of genetically homogeneous populations. It may be possible to apply the principles of the approach more widely in association studies. Yu et al. (2006) recently proposed unified models for association studies where a fixed effect was fitted for population structure and a random effect for marker-based relatedness. It would be worthwhile to explore GRAMMAR approximations for these unified approaches.
We show that the GRAMMAR approach is conservative under the null hypothesis and becomes more so with increased familial correlations. When a pedigree includes large, closely related sibships (idealized pig population), the NCP from the GRAMMAR approach drops closely to that from TDT-based methods. Also, there is a tendency that more NCP is lost with the analysis of more heritable traits. Still, the GRAMMAR approach would be a method of choice for analysis of large human pedigrees such as ERF (with any heritability, NCP from GRAMMAR was at least twice as high as that from TDT-based methods). Moreover, the power of this method compares well to that of the MG approach when trait heritability is moderate (30%).
The power and type 1 error of the MG–FH approach were very similar to those of the complete MG. In the MG–FH approach, heritability is estimated only once, and the fixed estimate is used in the genomewide SNP analysis. This eliminates the necessity of joint estimation of heritability and the SNP effect at every step and speeds up the analysis. However, the throughput is increased by five to six times only, as one iteration is still required to estimate the SNP effect. Therefore, this approach will not be feasible for genomewide analyses in large pedigrees. However, this may be an interesting approach to the analysis of regional data on a few hundreds of SNPs. Moreover, implementation of this approach within the framework of the score test, which does not require estimation of the parameter tested, may provide a fast and powerful alternative to our GRAMMAR approach.
In Table 5, the power of the GRAMMAR approach to achieve genomewide significance was relatively low (33%). However, the pedigree used in simulations is part of a pedigree including ∼3000 members. With a complete pedigree of 3000 members the power to detect a SNP explaining 3% of variation is >95%, and the power to detect a SNP explaining 2% is >90%. With 10,000 individuals included in a GRAMMAR analysis one would obtain >80% power to detect a SNP explaining as little as 0.5% of a trait's variation at a genomewide P-value of 5%. Moreover, additional power is achieved by using GRAMMAR followed by MG. Nowadays, studies aimed at genomewide association analysis routinely collect thousands of study subjects and active collaboration and joint analysis of the data are becoming more and more common. In this context, the methods we propose here will have power to detect QTL explaining as little as 0.5–1% of trait variation.
To summarize, we developed a fast, simple, and powerful method for pedigree-based QTL association analysis. The method's power is close to that of the gold standard measured genotype approach and is much higher than the power of TDT-based approaches. Our method is much faster than the measured genotype approach and it makes possible the analysis of hundreds of thousands of markers in a genomewide pedigree-based QTL association analysis. It may allow the use of such computationally extensive techniques as permutation analysis to set significance thresholds and two-dimensional genomic scans for interactions (Marchini et al. 2005).
Acknowledgments
We thank C. M. van Duijn, L. Cardon, P. Visscher, I. White, and an anonymous reviewer for valuable discussion and suggestions. Y.S.A. was supported by the Netherlands Organization for Scientific Research (NWO R96-249, NWO-RFBR 047.016.009), the Center for Medical Systems Biology (CMSB), EUROpean Special Populations reseArch Network (EUROSPAN, European Framework Program 6), Stichting MS Research, and the Russian Foundation for Basic Research (RFBR). D.J.K. and C.S.H. acknowledge support from the Biotechnology and Biological Sciences Research Council (BBSRC) and the EC funded Integrated Project SABRE (EC contract number FOOD-CT-2006-01625).
References
- Abecasis, G. R., L. R. Cardon and W. O. Cookson, 2000. A general test of association for quantitative traits in nuclear families. Am. J. Hum. Genet. 66: 279–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aulchenko, Y. S., S. Ripke, A. Isaacs and C. M. van Duijn, 2007. GenABEL: an R library for genome-wide association analysis. Bioinformatics (in press). [DOI] [PubMed]
- Blangero, J., 2004. Localization and identification of human quantitative trait loci: king harvest has surely come. Curr. Opin. Genet. Dev. 14: 233–240. [DOI] [PubMed] [Google Scholar]
- Boerwinkle, E., R. Chakraborty and C. F. Sing, 1986. The use of measured genotype information in the analysis of quantitative phenotypes in man. I. Models and analytical methods. Ann. Hum. Genet. 50(Pt. 2): 181–194. [DOI] [PubMed] [Google Scholar]
- Bourgain, C., and E. Genin, 2005. Complex trait mapping in isolated populations: Are specific statistical methods required? Eur. J. Hum. Genet. 13: 698–706. [DOI] [PubMed] [Google Scholar]
- Charlesworth, J. C., T. D. Dyer, J. M. Stankovich, J. Blangero, D. A. Mackey et al., 2005. Linkage to 10q22 for maximum intraocular pressure and 1p32 for maximum cup-to-disc ratio in an extended primary open-angle glaucoma pedigree. Invest. Ophthalmol. Vis. Sci. 46: 3723–3729. [DOI] [PubMed] [Google Scholar]
- Durrant, C., K. T. Zondervan, L. R. Cardon, S. Hunt, P. Deloukas et al., 2004. Linkage disequilibrium mapping via cladistic analysis of single-nucleotide polymorphism haplotypes. Am. J. Hum. Genet. 75: 35–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush, D., M. Stephens and J. K. Pritchard, 2003. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forabosco, P., M. Falchi and M. Devoto, 2005. Statistical tools for linkage analysis and genetic association studies. Expert Rev. Mol. Diagn. 5: 781–796. [DOI] [PubMed] [Google Scholar]
- George, V. T., and R. C. Elston, 1987. Testing the association between polymorphic markers and quantitative traits in pedigrees. Genet. Epidemiol. 4: 193–201. [DOI] [PubMed] [Google Scholar]
- Gilmour, A. R., B. J. Gogel, B. R. Cullis, S. J. Welham and R. Thompson, 2002. ASReml User Guide Release 1.0. NSW Agriculture, Orange, Australia.
- Havill, L. M., T. D. Dyer, D. K. Richardson, M. C. Mahaney and J. Blangero, 2005. The quantitative trait linkage disequilibrium test: a more powerful alternative to the quantitative transmission disequilibrium test for use in the absence of population stratification. BMC Genet. 6(Suppl. 1): S91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernández-Sánchez, J., C. S. Haley and P. M. Visscher, 2003. Power of QTL detection using association tests with family controls. Eur. J. Hum. Genet. 11(11): 819–827. [DOI] [PubMed] [Google Scholar]
- Hopper, J. L., and J. D. Mathews, 1982. Extensions to multivariate normal models for pedigree analysis. Ann. Hum. Genet. 46(4): 373–383. [DOI] [PubMed] [Google Scholar]
- Horvath, S., X. Xu, S. L. Lake, E. K. Silverman, S. T. Weiss et al., 2004. Family-based tests for associating haplotypes with general phenotype data: application to asthma genetics. Genet. Epidemiol. 26: 61–69. [DOI] [PubMed] [Google Scholar]
- Lange, C., D. L. DeMeo and N. M. Laird, 2002. Power and design considerations for a general class of family-based association tests: quantitative traits. Am. J. Hum. Genet. 71: 1330–1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange, K., J. S. Sinsheimer and E. Sobel, 2005. Association testing with Mendel. Genet. Epidemiol. 29: 36–50. [DOI] [PubMed] [Google Scholar]
- Lehman, D. M., J. Hamlington, K. J. Hunt, R. J. Leach, R. Arya et al., 2006. A novel missense mutation in ADRB3 increases risk for type 2 diabetes in a Mexican American family. Diabetes Metab. Res. Rev. 22: 331–336. [DOI] [PubMed] [Google Scholar]
- Marchini, J., P. Donnelly and L. R. Cardon, 2005. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat. Genet. 37: 413–417. [DOI] [PubMed] [Google Scholar]
- Matsuzaki, H., S. Dong, H. Loi, X. Di, G. Liu et al., 2004. Genotyping over 100,000 SNPs on a pair of oligonucleotide arrays. Nat. Methods 1: 109–111. [DOI] [PubMed] [Google Scholar]
- Newman, D. L., M. Abney, M. S. McPeek, C. Ober and N. J. Cox, 2001. The importance of genealogy in determining genetic associations with complex traits. Am. J. Hum. Genet. 69: 1146–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo, L. M., I. MacKay, B. Oostra, C. M. van Duijn and Y. S. Aulchenko, 2005. The effect of genetic drift in a young genetically isolated population. Ann. Hum. Genet. 69: 288–295. [DOI] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. Inference of population structure using multilocus genotype data. Genetics 155: 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice, J. P., N. L. Saccone and E. Rasmussen, 2001. Definition of the phenotype. Adv. Genet. 42: 69–76. [DOI] [PubMed] [Google Scholar]
- Schaid, D. J., C. M. Rowland, D. E. Tines, R. M. Jacobson and G. A. Poland, 2002. Score tests for association between traits and haplotypes when linkage phase is ambiguous. Am. J. Hum. Genet. 70: 425–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, J., G. Pressoir, W. H. Briggs, B. I. Vroh, M. Yamasaki et al., 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38: 203–208. [DOI] [PubMed] [Google Scholar]
- Zollner, S., and J. K. Pritchard, 2005. Coalescent-based association mapping and fine mapping of complex trait loci. Genetics 169: 1071–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]