Multilevel Selection 3: Modeling the Effects of Interacting Individuals as a Function of Group Size

Abstract

Bijma et al. (2007a,b) presented a quantitative genetic theory of multilevel selection and showed how to estimate the relevant parameters using standard restricted maximum-likelihood (REML) methodology. Extending their results we develop a wider class of models that provide a more realistic framework for capturing the effects of interacting individuals. These models also make use of standard REML techniques and include the original model as a special case.

IN a recent issue of Genetics, Bijma et al. (2007a) introduced a quantitative genetic model of multilevel selection and showed how the parameters of this model could be estimated using existing software (Muir 2005; Bijma et al. 2007b). Taken together, these articles are an important advancement in the study of multilevel selection since they present a useful, and useable, framework for predicting a response to multilevel selection among interacting individuals with any degree of relatedness. Their work generalizes the classic quantitative genetic model, to include heritable environmental effects on phenotype that arise from social interactions among group members (so-called “associative effects”). These effects have major implications for our understanding of evolutionary responses to natural selection (Frank 1998) and for optimization of artificial selection regimes in the agricultural sciences (Muir 2005).

Bijma et al. (2007b) show that, if data are collected from individuals reared under constant group sizes, it is possible to correctly estimate genetic variance components attributable to both the direct (additive) effects and associative effects that contribute to heritable trait variation. However, these variance components cannot properly be interpreted without knowledge of the relationship between group size and associative effect. The authors avoid this difficulty by making the assumption that the effect an individual has on the phenotype of another member of the group (the associative effect) is independent of group size. The authors themselves admit that this assumption may not always be reasonable, and there are certainly many cases where such a relationship is known not to hold.

Using standard restricted maximum-likelihood (REML) random regression techniques we provide a powerful way to model the relationship between associative effects and group size while simultaneously estimating the relevant quantitative genetic parameters. By placing various restrictions on the random regression parameters we can recover a reparameterized version of Bijma's original model, but also an alternative model of the same complexity that we suggest is a more reasonable null model in many circumstances.

Following the example presented in the second article (Bijma et al. 2007b), imagine a population of layer hens that experience reduced lifespan due to pecking behavior. In this case longevity may be the focal trait of interest to a breeder, with associative effects arising from aggressive interactions (pecking) among members of a group (cage). In the model originally proposed, the number of times two random individuals within the group peck each other is independent of group size. Under this scenario the genetic variance in associative effect increases dramatically with group size even if between-group differences in pecking rates are small. This situation arises because the deviation of a focal individual's phenotype from the mean is the sum of these differences across the remaining group members. The logical endpoint of this model is that the genetic variance for the focal trait will be maximized at an infinite group size.

This conclusion stems from the expression for the total genetic variance under Bijma et al.'s model,

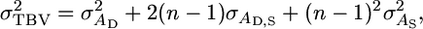(1)

where 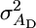is the usual additive genetic variance, 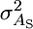is the variance in associative effects, and 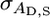is the covariance between these terms. n is group size, and as n gets large the total genetic variance is dominated by the variance in associative effects through the term (n − 1)². In matrix notation

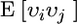(2)

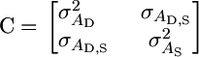(3)

However, if the number of times two individuals peck each other is independent of group size then this implies that the total amount of pecking performed by each individual must increase linearly with group size, so as to maintain a constant associative effect.

In our proposed model we use random regression to model associative effects as a polynomial function of reciprocal group size [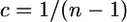]. To illustrate, a more realistic assumption for the current scenario would be that the total amount of pecking remains constant such that the influence of any two random individuals on each other diminishes linearly with group size. In this case the associative effect of each individual is modeled as a simple first-order function of reciprocal group size.

In general, if we model an individual's associative effect as a first-order function of reciprocal group size, we then estimate the genetic covariance matrix,

(4)

where 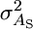is now the genetic variance in associative effects when c = 0 and 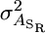is the genetic variance in slopes.

The expectation for the total genetic variance is now

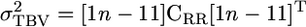(5)

and approximate standard errors can be obtained using the Delta method (Fischer et al. 2004). We can place various constraints on C_RR that capture specific types of model. For example,

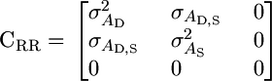(6)

recovers a reparameterized version of Bijma et al.'s original model. Alternately, the model where the influence of any two random individuals on each other diminishes linearly with group size can be captured by constraining the variation in intercepts to be zero:

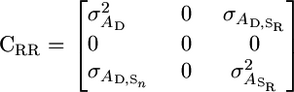(7)

In this model σ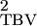 does not vary with group size and is equivalent to an alternative model suggested by Bijma et al. (2007a) for food sharing. By constraining some random regression parameters to be zero these models are identifiable even when group sizes do not vary. However, if group size does vary, then we can empirically test the assumptions of the underlying models using standard model selection criteria and try to model the underlying process more accurately using higher-order polynomials. By using reduced-rank methods (Kirkpatrick and Meyer 2004) it should be possible to describe the distribution of associative effects well using relatively few parameters. However, caution should still be exercised when extrapolating to group sizes outside the range of the data. Under these circumstances it may be better to consider methods with a stronger parametric ethos as more robust alternatives (Pletcher and Geyer 1999).