Using Quantitative Trait Loci Results to Discriminate Among Crosses on the Basis of Their Progeny Mean and Variance

Abstract

To develop inbred lines, parents are crossed to generate segregating populations from which superior inbred progeny are selected. The value of a particular cross thus depends on the expected performance of its best progeny, which we call the superior progeny value. Superior progeny value is a linear combination of the mean of the cross's progeny and their standard deviation. In this study we specify theory to predict a cross's progeny standard deviation from QTL results and explore analytically and by simulation the variance of that standard deviation under different genetic models. We then study the impact of different QTL analysis methods on the prediction accuracy of a cross's superior progeny value. We show that including all markers, rather than only markers with significant effects, improves the prediction. Methods that account for the uncertainty of the QTL analysis by integrating over the posterior distributions of effect estimates also produce better predictions than methods that retain only point estimates from the QTL analysis. The utility of including estimates of a cross's among-progeny standard deviation in the prediction increases with increasing heritability and marker density but decreasing genome size and QTL number. This utility is also higher if crosses are envisioned only among the best parents rather than among all parents. Nevertheless, we show that among crosses the variance of progeny means is generally much greater than the variance of progeny standard deviations, restricting the utility of estimates of progeny standard deviations to a relatively small parameter space.

IN inbred line development, parents are crossed to generate segregating populations from which superior inbred progeny are selected. The value of a particular cross depends on the performance of its best progeny rather than on its mean progeny performance. In a typical breeding program, far too many crosses are possible between elite candidate parents for exhaustive evaluation. For example, among 50 elite parents there are 1225 possible crosses. Even if it were feasible to evaluate a sufficient set of progeny from all those crosses, it is unlikely that that would be efficient. Rather, one would want to predict, among possible crosses, which ones are most likely to lead to superior inbred lines.

Schnell and Utz (1975) introduced the usefulness concept for line development. Their definition of the usefulness of the cross m was 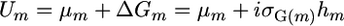, where μ_m is the population mean of homozygous lines that can be derived from cross m, 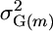is the genetic variance among these lines, h_m is the square root of the heritability, and i is the standardized selection intensity. Two other criteria for similar usefulness are the varietal ability (Wright 1974; Gallais 1979) and the probability of obtaining transgressive segregants (Jinks and Pooni 1976). Here, rather than focus on the genetic gain that might be obtained within a cross, we sought a simpler characterization that expresses which crosses would generate progeny with higher genotypic values. Given the focus on genotypic value, we ignored the heritability to obtain what we call the superior progeny value, 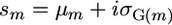. With this definition, s_m equates to U_m with a heritability of 1.

In traditional breeding based solely on phenotypic measurements, μ_m can be predicted from the breeding values of the two parents but the only information available relevant to predicting 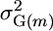is the coancestry between parents. Thus, assuming two possible crosses have identical μ_m, it is preferable to cross the parents with lower coancestries. After the advent of DNA markers, Van Berloo and Stam (1998) were the first to point out that marker information and quantitative trait loci (QTL) analysis could be used to identify complementary parents such that their progeny might segregate at more loci and show more extreme phenotypes. As in Van Berloo and Stam (1998), the breeding scenario investigated in this article involves first deriving recombinant inbred lines (RIL) from a cross between two parents and then selecting among possible RIL pairs ones to cross to generate maximal superior progeny value. Without attempting to estimate a cross's 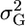, Van Berloo and Stam (1998) utilized a marker score computed from the flanking marker genotypes and weighted by QTL effects to discriminate among the crosses (Van Berloo and Stam 1998).

More recently, Bernardo et al. (2006) used QTL information to compute 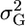to aid in the selection of crosses. In their computation, however, they assumed that the covariance between QTL effects could be ignored (Bernardo et al. 2006), which is equivalent to assuming that all QTL resided on different chromosomes. As the ability to detect QTL improves and the number of QTL known to segregate within a population increases, however, accounting for linked QTL will become more important. In a toy example, we contrast cross 1, [+ − +] × [− + −] with cross 2, [+ + −] × [− − +], where + and − represent increasing and decreasing alleles. The variance among progeny from cross 2 will be greater than that from cross 1 because cross 2 is more likely to generate progeny with [+ + +] and [− − −] genotypes that will have extreme phenotypic values. Thus, we need to account for recombination between QTL since two recombinations are required to generate those genotypes in cross 1, but only one recombination in cross 2.

The preceding discussion assumes previously estimated QTL positions and effects. The method used to obtain these estimates, however, has a large impact on the effectiveness of marker-assisted selection (MAS) (Hospital et al. 1997; Moreau et al. 1998). The primary problem of QTL analysis is that the number of independent variables is large relative to the number of observations. Two different approaches have been used to deal with this situation, variable selection and shrinkage estimation.

Stepwise regression (Jansen 1993; Jansen and Stam 1994; Kao et al. 1999) is one common procedure for variable selection in QTL analysis. A weakness of stepwise regression is that effects are included and removed from the model according to somewhat arbitrary statistical thresholds. Because many markers are tested in QTL mapping the process necessarily entails relatively high significance thresholds for marker inclusion in the model. A corollary is that included markers have inflated effect estimates (Beavis 1994; Xu 2003a; Schon et al. 2004). On the other hand, the relaxed significance levels generally used for choosing significant markers for MAS (Hospital et al. 1997; Johnson 2001; Bernardo et al. 2006) may lead to the inclusion of spurious markers. In the context relevant here of predicting a cross's mean and variance, both sorts of errors would be compounded.

New developments in shrinkage estimation seek to avoid variable selection by including all markers as predictors in the model and shrinking the allowed effect estimates toward zero, rather than choosing a “best” set among them. Ridge regression (Hoerl and Kennard 1970) is a classical example of shrinkage estimation in which the least-squares effect estimators 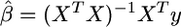are replaced by 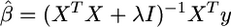(Whittaker et al. 2000). A high value for the parameter λ causes a penalty for large β, thereby avoiding inflated estimates. This approach has strong affinities with the estimation of β using random Bayesian models that assumed a prior distribution for .

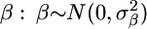A drawback of the ridge regression solution for including all markers is that all marker effects are equally penalized. To remove this constraint, Xu (2003b) proposed a hierarchical model that allowed for a different variance for each β_i (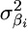), based on the random-model approach of Meuwissen et al. (2001). Xu (2003b) showed that the posterior distributions of all parameters could be readily estimated using Markov chain Monte Carlo. His method performed well for both real and simulated data sets, although important improvements to the model were proposed by Ter Braak et al. (2005). Because of the success of Xu's model in QTL detection and the value of similar models in MAS (Meuwissen et al. 2001), we have adopted this approach in our analyses.

As presented thus far and as implemented in previous studies (e.g., Bernardo et al. 2006), the prediction of superior progeny value is a multistep analysis process. QTL analysis is first performed using one of the methods described above and the resulting map positions and effect estimates are then used to compute cross means and variances. We find fault with this two-step process because it prevents the individual or cross selection process from accounting for errors inherent to the QTL analysis. If, on the contrary, the selection process could account for the full uncertainty of the QTL analysis, different individuals or crosses might be selected. Bayesian analysis should allow MAS to account for uncertainty by using the full posterior distributions of the estimates of QTL effects.

The objectives of this study were first to specify more completely the theory to predict the value of a cross on the basis of its superior progenies, second to determine analytically the potential utility of accounting for the variance among a cross's progeny in predicting superior progeny value, and third to evaluate through simulation the effectiveness of different statistical approaches to predict superior progeny value. In particular, we wanted to contrast approaches that included or did not include an estimate of progeny variance in the prediction of superior progeny value, approaches that performed marker selection as opposed to including all markers in the QTL analysis, and approaches that split the QTL analysis from superior progeny value estimation into two steps as opposed to integrating them in a single step.

THEORY

Predicting the superior progeny value of a cross:

As indicated above, for cross m, the superior progeny value s_m is 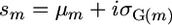, and predicting it requires predicting μ_m and σ_G(m) and defining a selection intensity, i. In what follows, we assume an additive model. Suppose there are L QTL affecting the phenotype in the whole population and L_m (L_m ≤ L) loci segregating in cross m. Then the expected progeny value is a function of the L QTL effects and their genetic variance is a function of the segregating L_m QTL effects,

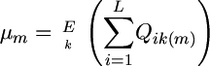(1)

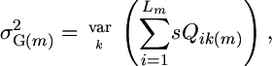(2)

where Q_ik(m) is a random variable representing the effect of QTL i in progeny k of cross m, and sQ_ik(m) is a random variable representing the effect of segregating QTL i in progeny k of cross m. Note that if the parents of a cross carry the same allele at the QTL, then the QTL will not segregate and Q_ik(m) will be a constant. Expanding Equation 2 gives

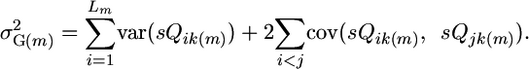(3)

To calculate the terms in Equation 3, suppose the segregating QTL i and j recombine with rate c_ij, the homozygous effects of QTL i are +α_i and −α_i, and those of QTL j are +α_j and −α_j. Table 1 lists the inbred progeny frequencies and genotypic values from a cross between a parent homozygous for the increasing allele at both loci and a parent homozygous for the decreasing allele at both loci (Bulmer 1985).

TABLE 1.

Inbred progeny frequencies and genotypic values from crossing a parent homozygous for the increasing allele with a parent homozygous for the decreasing allele at two loci

Genotype	Progeny frequency	Genotypic value
+ +	0.5/(1 + 2cij)	αi + αj
− +	cij/(1 + 2cij)	−αi + αj
+ −	cij/(1 + 2cij)	αi − αj
− −	0.5/(1 + 2cij)	−αi − αj

The loci recombine with frequency c_ij and inbred progeny are obtained by repeated generations of selfing.

Given these frequencies and genotypic values,

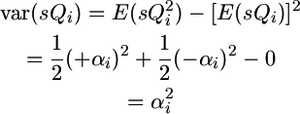(4)

and

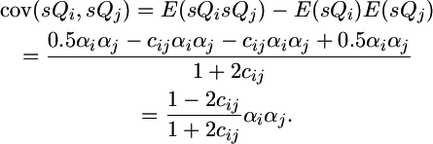(5)

Note that the covariance between QTL effects is positive in this case because the QTL were assumed in coupling in the parents crossed: one parent carried two increasing alleles while the other parent carried two decreasing alleles. To generalize across coupling and repulsion possibilities, the parameters +α_i and +α_j should be set to the QTL effects of one of the parents while −α_i and −α_j should be set to the QTL effects of the other parent. In this way, the α_iα_j term will be positive when QTL are in coupling and negative when they are in repulsion.

Substituting Equations 4 and 5 into Equation 3 gives

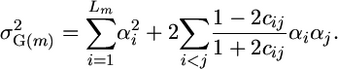Thus, predicting the genetic variance among inbred progeny of a cross between inbred parents requires estimates of homozygous QTL effects and of recombination frequencies between all pairs of QTL. Estimates of these parameters derive from the QTL analysis.

Utility of accounting for σ_G² in predicting superior progeny value:

The setup now is that two inbred lines that differ at L loci are crossed to generate a population of RIL. The objective then is to select pairs of RIL to cross to obtain maximal superior progeny value, s. We consider the variance of s and its origins. Given the definition 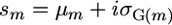and assuming that μ and σ_G have zero covariance, 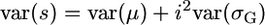. Thus, the influence of 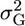on s depends on the variance of μ relative to that of σ_G, and we investigate the ratio t = var(σ_G)/var(μ). Assume that QTL allele frequencies are 0.5, as would happen in a population derived from a cross between two inbred lines. For a single locus, three types of cross are possible between RIL from this population (Table 2).

TABLE 2.

Three possible cross types and their frequencies assuming equal QTL allele frequencies

	Cross type
	[ + ] × [+ ]	[+] × [ − ]	[−] × [ − ]
Cross frequency	0.25	0.50	0.25
μ	+α	0	−α
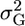	0	α2	0

The genotypic value of the homozygous increasing allele is +α and that of the decreasing allele is −α.

If only a single QTL affects the trait in the population, then 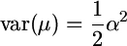and 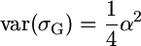, such that 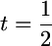. If L independent QTL affect the trait in the population, then , where Q_i is the mean effect conferred by locus i, and

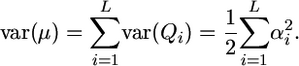(6)

For L independent loci, it is also simple to obtain 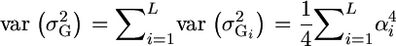. Unfortunately, what we need is 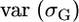. A first approach to obtain this variance is by the delta method (Lynch and Walsh 1998). Using first-order expansion, if 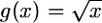, then 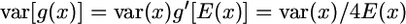. Setting 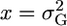, we have

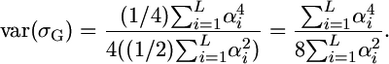(7)

Combining Equations 6 and 7 gives

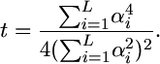(8)

If all of the L loci have equal effects α, then the expression simplifies to t = (4L)⁻¹. Consequently as the number of independent loci of equal effect increases, the ratio t tends to zero and the influence of the variance of σ_G among crosses on superior progeny value becomes negligible. If the L loci do not have equal effects, but, as is often assumed (Lande and Thompson 1990), their variances follow a geometric series such that 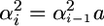, Equation 8 reduces to

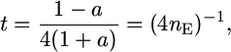(9)

where n_E is the effective number of QTL (Lande and Thompson 1990). Note that for L = 1, Equations 8 and 9 give t = . We know, however, from the simple analysis of Table 2 that for a single-locus trait, t = . The discrepancy arises from the linear approximation used in the delta method to obtain Equations 8 and 9.

An exact expression for t assuming loci of equal effect that are unlinked and biallelic with allele frequencies of 0.5 can be obtained as follows. From Table 2, we know that the probability that a given cross will segregate at a given locus is 0.5. Assuming as before L independent QTL segregating in the population, then the probability that a given cross will segregate at L_m loci follows the binomial distribution 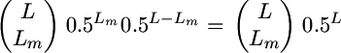. Given loci of equal effect, the genetic variance generated from L_m loci will be L_mα². Therefore, 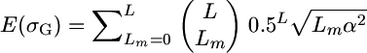and . We thus obtain

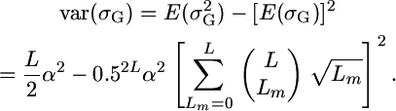(10)

Combining Equation 10 with Equation 6 gives

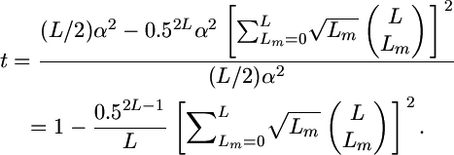(11)

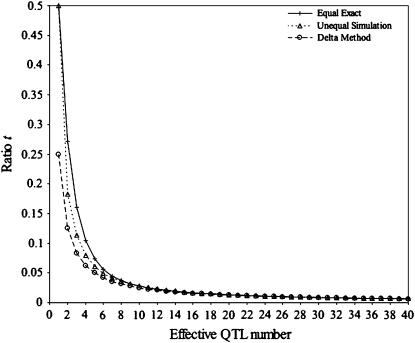
Substituting L = 1 in Equation 11 does indeed give t = . Regardless of the approximation used, if QTL are independent, computing the ratio t shows that the influence of the variance among progeny within crosses on superior progeny value rather quickly becomes small (Figure 1). For example, with six unlinked QTL of equal or unequal variance, t is close to 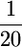. The simulations of Figure 1 involved the following. A RIL population of 200 single-seed-descent progeny derived from a cross between two inbred lines was generated. For a given effective QTL number n_E, the rate of geometric decay of the variance was calculated as a = (n_E − 1)/(n_E + 1), and the actual number of QTL simulated was twice n_E for n_E > 5 and 10 for n_E ≤ 5. In each simulation, the variances of μ and σ_G were calculated from 800 crosses chosen by randomly ordering the RIL into a loop and then crossing each RIL with the four neighbors to either side of it. The ratio t was obtained as 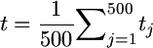from 500 replicate simulations.

Figure 1.—

Ratio t for independent QTL. Equal exact: the ratio t for QTL with equal variances derived analytically. Unequal simulation: the ratio t for QTL with geometrically distributed variances derived from simulation. Delta method: the ratio t for QTL with either equal or geometrically distributed variances derived from the delta method.

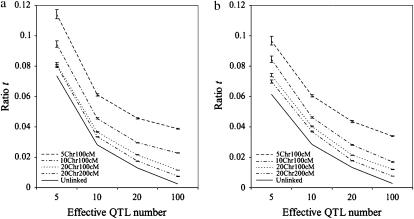
Because the simplifying assumption of independent loci rarely holds, we also assessed the impact of linkage on the ratio t through simulations similar to those for Figure 1. Instead of being independent, QTL were randomly populated on one of the four different genomes: 5 chromosomes of 100 cM each, 10 chromosomes of 100 cM each, 20 chromosomes of 100 cM each, and 20 chromosomes of 200 cM each. The QTL variances were either equal or followed a geometric series. For each QTL, increasing and decreasing alleles were also assigned to parents at random.

From these simulations, we see that the effect of having a smaller genome is akin to the effect of having fewer QTL: the smaller the genome, the higher the ratio t, and the more relevant the variance of σ_G will be in determining superior progeny value (Figure 2). Nevertheless, the influence of this variance diminishes rather quickly with increasing QTL number (Figure 2). For example, for the genome with 10 chromosomes of 100 cM each, 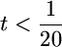for 10 QTL. In general, then, when QTL number is high, accounting for σ_G will be of limited value. This was the phenomenon that Bernardo et al. (2006) observed under the high QTL numbers that they simulated.

Figure 2.—

Ratio t for different genome sets. (a) Simulation results with equal QTL variances. (b) Simulation results with QTL variances following a geometric series. 5Chr100cM, 5 chromosomes of 100 cM each; 10Chr100cM, 10 chromosomes of 100 cM each; 20Chr100cM, 20 chromosomes of 100 cM each; 20Chr200cM, 20 chromosomes of 200 cM each; Unlinked, independent QTL.

SIMULATIONS

Genetic model:

The basic genetic model (model A) for the population was as follows:

• Genomes were of 10 chromosomes of 100 cM each and covered by markers every 10 cM.

• The genome was then populated with QTL at randomly chosen positions such that the effective QTL number n_E was 10. For each QTL, increasing and decreasing alleles were also assigned to parents at random. Thus coupling and repulsion linkages were generated at random. The QTL variances followed a geometric series (Lande and Thompson 1990).

• Genotypic values were calculated for 200 RIL progeny, and a normal deviate was added to the genotypic value to obtain phenotypic value assuming a heritability of 0.4.

A number of models that differed from the above in one parameter were tested, as follows:

• Model B: Markers spaced every 20 cM rather than every 10 cM.

• Model C: Heritability of 0.1 rather than 0.4.

• Model D: Heritability of 0.8 rather than 0.4.

• Model E: 5 rather than 10 effective QTL affected the trait.

• Model F: 20 rather than 10 effective QTL affected the trait.

• Model G: 20 rather than 10 chromosomes.

• Model H: Chromosomes of 200 rather than 100 cM.

Statistical analysis:

The phenotypic values and marker information of the simulated RIL population were submitted to genomewide Bayesian shrinkage analysis using the model proposed by Xu (2003b) and implemented in WinBUGS (Spiegelhalter et al. 2007). Two chains were run, and after 5000 burn-in iterations, 1000 MCMC samples were thinned from a total of 20,000 iterations. Each sample consisted of the predicted genetic effects associated with all markers covering the genome. These data were used to obtain estimators of the superior progeny. For each estimator involving the among-progeny variance, the estimator was calculated for selection intensities of 20, 15, 10, 5, 2, and 1%. Values of the standardized selection differential i corresponding to these intensities were calculated assuming progeny values were normally distributed. Six estimators were calculated as follows:

1. Full Bayesian treatment (denoted s_Full): For MCMC sample j the superior progeny value of a cross m was calculated as 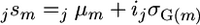using sampled genetic effects for all markers. The estimator s_Full was calculated as the mean sampled superior progeny value, .

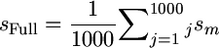2. All marker posterior average treatment (denoted s_All): Average marker effects were calculated across all MCMC samples. For example, for marker i, 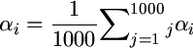. Parameters 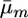and 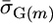for a cross m were then calculated from these mean marker effects and .

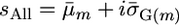3. All marker cross mean treatment (denoted μ_All): Here simply 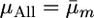from the s_All treatment.

4. Selected marker posterior average treatment (denoted s_Sel): Average marker effects were calculated as in s_All. Those markers that explained ≥2% of the total marker variance were retained and used to calculate the parameters 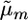and 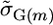for a cross m. Then, 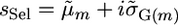. This treatment most closely resembles a typical two-step approach of running QTL analysis first and then using results of that analysis for MAS.

5. Selected marker cross mean treatment (denoted μ_Sel): Here, 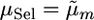from the s_Sel treatment.

6. Phenotypic selection (denoted μ_Phen): The simplest approach used was to take the average phenotype of two parents as the prediction of their superior progeny mean.

These estimators of s were calculated for 800 random crosses chosen as in the ratio study above. To assess the utility of an estimator, we correlated it to the true superior progeny value calculated from the known simulated QTL effects and positions. For a given cross, the “true s_m” was calculated by simulating 5000 inbred progeny that might derive from it. The genotypic values of the top 20, 15, 10, 5, 2, and 1% of these progeny were averaged and used as the true s_m for the corresponding selection intensity.

RESULTS

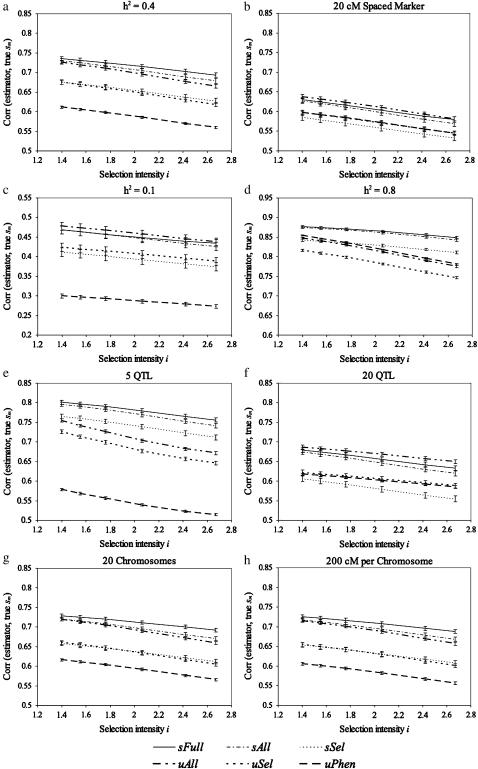
Under model A the accuracy of estimators was s_Full > s_All > μ_All > s_Sel > μ_Sel > μ_Phen across all selection intensities (Figure 3a). While the inclusion of all markers in the model was more important than the inclusion of the term accounting for among-progeny variance, this latter term increased in importance as the selection intensity among progeny increased. The ordering changed when markers were spaced every 20 cM rather than every 10 cM (Figure 3b). The inclusion of all markers in the model remained far better than selecting markers before estimating superior progeny value, but with sparse markers, using estimates of σ_G to predict s_m appeared to introduce more error than information. Note that all estimators, save μ_Phen that was not affected, were negatively affected by the decrease in marker density, although particularly those models incorporating the σ_G term suffered. The coarser marker grid presumably led to poorer estimation of the position of the QTL effects, which, in turn, affected estimates of σ_G. This result suggests that a marker spacing of 10 cM is minimal for this type of analysis and investigation of higher marker densities is warranted.

Figure 3.—

Correlations from random crosses between simulated values and different estimators. (a–h) The results under models A–H, respectively. Six selection intensity values, i = 1.40, 1.55, 1.76, 2.06, 2.42, and 2.67, correspond to selected fractions of 20, 15, 10, 5, 2, and 1%, respectively. Note that c and d have different y-axis scales.

Under low heritability (model C) the relative merit of the estimators involving markers was quite similar to that under sparse markers: including all markers in the model was again the most important step to take, while incorporating estimates of σ_G made prediction worse (Figure 3c). It is also noteworthy that under the low heritability, even though only one or two QTL were correctly identified (data not shown), the prediction from μ_All outperformed that from μ_Phen. Under high heritability (model D), in contrast, σ_G was well estimated and above a selection intensity of ∼10%, all estimators that incorporated it did better than estimators that did not (Figure 3d). Interestingly also, at this high heritability the phenotype was such a good guide to the underlying genotypic value that μ_Phen did better than μ_All. For higher heritability, an index that incorporates phenotypic and marker information should be used to predict the cross mean (Lande and Thompson 1990). Once the cross mean is optimally predicted in that way, including consideration of among-progeny variance might further prove valuable.

Given our previous analysis of the utility of including σ_G in the prediction of s_m, the impact of having few QTL (model E) or many QTL (model F) was not surprising. Under model E, estimators that included σ_G were favored (Figure 3e), whereas under model F they were penalized (Figure 3f). With few QTL, incorporating σ_G into the prediction had a greater beneficial effect than incorporating all markers (Figure 3e), contrary to the results found for the previous four models. In contrast, with many QTL, incorporating σ_G had a negative effect on prediction accuracy (Figure 3f). It may be that when more QTL are present, higher marker densities would be beneficial to tease them apart. In any event these simulations also make clear that with greater QTL numbers, less benefit should be expected from considering σ_G.

Finally, given the conditions of model A, overall genome size and the allocation of the genome to many smaller chromosomes (model G) or few larger chromosomes (model H) did not affect the ranking of estimators (Figure 3, a, g, and h). Results under the large genomes of models G and H resembled each other and the results under model A closely.

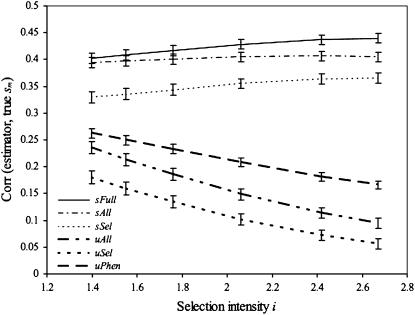
In the preceding simulation, we assessed the ability of the different estimators to discriminate between crosses among all progeny. In practice, breeders would not attempt crosses among all progeny but would consider only crosses among the best progeny (say, those with high values). To evaluate the effect of considering crosses among only high-value progeny, we computed the correlation between the true and estimated s_m in model A, using all 780 pairwise crosses among the 40 RIL (of 200) with the highest genetic values. In this case, incorporating σ_G into the prediction of s_m had an important beneficial effect that increased with the selection intensity (Figure 4). For randomly selected crosses, t = 0.04 (Figure 2b) but it increased to 0.21 for crosses among the best parents. Interestingly, for crosses among best parents, μ_Phen did better than either μ_All or μ_Sel (Figure 4), contrary to its behavior for crosses among all parents (Figure 3a).

Figure 4.—

Correlations, corresponding to model A, from the top 40 parent crosses between the simulation truth and different predictors.

DISCUSSION

Beyond results pertaining to specific genetic models, a number of results held across all the tested configurations. First, μ_All was always superior to μ_Sel, which means that avoiding model selection by including all markers in the final statistical model was always beneficial. This is consistent with other MAS studies (Lange and Whittaker 2001; Meuwissen et al. 2001), which indicate that a better estimate of breeding values is obtained by incorporating all markers in the molecular score. Second, s_Full always performed better than s_All (though often only slightly). Therefore, including the uncertainty of parameter estimation from QTL analysis appears always to be beneficial.

The fact that μ_All outperformed μ_Phen at low heritability where few QTL were correctly identified (Figure 3c) indicates that genomewide analysis models may capture at least a portion of the effects of QTL that they do not specifically identify. This phenomenon may have implications for how MAS statistical methods should deal with polygenic effects. These effects are typically included in models to account for loci of small effect that are not detected as QTL (Kennedy et al. 1992). If statistical models including all markers capture variance from loci with very small effect, the polygenic effect may no longer be necessary. Indeed, two examples of MAS simulation exist where excellent response was obtained without a polygenic effect (Meuwissen et al. 2001; Bernardo and Yu 2007). Whether this is a general phenomenon or whether further improvement might be obtained by inclusion of a polygenic effect remains to be explored.

Both dense marker spacing and high heritability increased the accuracy of σ_G estimation due to the increased accuracy of marker effect and position estimation. Overall, it appears therefore that error in the estimates of marker effects, whether due to low heritability, sparse markers, or possibly small population size, has a more negative effect on the accuracy of estimates of σ_G than of μ. This fact, along with the generally low ratio of var(σ_G) to var(μ), limits the parameter space wherein it may be valuable to account for σ_G in the estimation of superior progeny value. Field experiments from different crop species also indicated that the usefulness of a cross is mainly influenced by the midparent value (Gumber et al. 1999; Utz et al. 2001; Miedaner et al. 2006).

In our development, we assumed that μ and σ_G would have a covariance of zero. Intuitively, however, it seems unlikely that these parameters will be independent: two RIL that have similar extreme phenotypes (either high or low) may be fixed for the same alleles across a high fraction of loci. Thus, we predict that extreme high or low μ will be associated with lower values of σ_G. In the general case, this mechanism would not generate a covariance between μ and σ_G, but in the case where crosses are attempted only between high-phenotype RIL (e.g., Figure 4), the mechanism will probably generate a negative covariance between the two. Nevertheless, we believe that the ratio between var(μ) and var(σ_G) that we have investigated will still be the most relevant single parameter to judge the utility of accounting for σ_G in making predictions.

The effect of considering crosses among only high-value progeny was primarily to decrease var(μ), which in turn enhanced the importance of accounting for var(σ_G) in the estimation of superior progeny value. The increase in the ratio t by a factor of 5.25 (from 0.04 to 0.21) can be attributed almost entirely to a drop in var(μ): under truncation selection with an intensity of 20%, the variance of the selected tail will be smaller by a factor of 4.05 relative to the variance of the distribution as a whole (Falconer and Mackay 1997). The fact that t increased by more than that may indicate that truncation selection also increased var(σ_G), possibly because of negative linkage disequilibria among loci introduced by selection. The reason why μ_Phen better predicted s_m than either μ_All or μ_Sel under these conditions is unclear. It may be that estimates of genotypic value derived from markers decrease in accuracy as the genotypic value becomes more extreme. The phenotype, however, does not reflect the genotypic value less accurately at the extremes. We are not aware of previous reports of this phenomenon and if it indeed occurs it would warrant further investigation.

Another assumption that our setup forced was that allele frequencies in the initial population were 0.5. We briefly consider relaxing this assumption in the simplest way: if the favorable QTL allele frequency is p, the cross frequency row of Table 2 would become p², 2pq, and q². Some algebra shows that 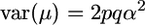whereas 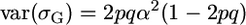such that, for one QTL, 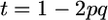. Thus, the ratio t is minimal for the case that we considered and, as p deviates from 0.5, t increases and accounting for σ_G may become more important.

While Van Berloo and Stam (1998) first presented the idea of using markers and QTL analysis to identify complementarity between parents, the simulations they presented did not directly assess whether using complementarity increased gain from selection relative to more standard MAS procedures. Bernardo et al. (2006) found that estimating and accounting for σ_G in marker-assisted recurrent selection generally did not lead to more rapid selection response (Table 2 of Bernardo et al. 2006). Thus, their result is not in agreement with ours (Figure 4). Several differences in simulation conditions will have reduced the utility of accounting for σ_G in Bernardo et al. (2006). First, their genome size (1746 cM) was greater and marker density (every 17 cM) was lower than that presented here. In three of four simulations, the number of individuals used in the QTL analysis (N = 100) was lower than that here, which would have reduced accuracy of QTL estimation. Our results suggest that this accuracy is more critical to estimating σ_G than to estimating cross means (see, for example, the effect of reduced heritability on the utility of σ_G, Figure 3). In addition, we simulated inbred lines while they simulated F₂ or S₀ lines, both of which provide less power and accuracy for QTL detection. Although they indicated that they generally detected ∼40 QTL on a genome of 10 chromosomes, they did not account for QTL linkage in the calculation of σ_G, which would in principle lead to error in its prediction. Most importantly, however, three of four of their simulation conditions involved either 40 or 100 QTL. With these high QTL numbers we show that the ratio t would be very small such that, even without errors in the QTL analysis, accounting for σ_G would be predicted to have low utility. There are nevertheless inconsistencies between their results and ours. For example, we would have predicted greater advantage to their “unequal fitness” methods (those that account for σ_G) in their genetic models with just 10 QTL. No trend in that sense was apparent. We also would have predicted greater advantage to the unequal fitness methods under high than low heritability. Again, no trend was apparent. We have no hypotheses to propose for the absence of these trends.

One aspect of MAS that we have emphasized here is the value of retaining information about the uncertainty of estimates from QTL analyses in the selection process. Indeed, the comparison of an estimator that did (s_Full) vs. did not (s_All) use the information showed that using it always improved the accuracy of estimates. Bayesian analysis, with its output of posterior distributions, facilitates the incorporation of uncertainty in analyses. Other studies on the value of crossing complementary parents have assumed that QTL information was known without error (Hospital et al. 2000; Servin et al. 2004). Hospital et al. (2000) used a recurrent selection framework in which the sole selection criterion depended on genotypes at markers flanking QTL. Complementation of QTL was introduced by measures to include parents carrying rare favorable QTL in the selected set. The study showed that the QTL complementation method was more efficient and robust than simple truncation selection on the marker score (Hospital et al. 2000). Servin et al. (2004) took this approach one step further by considering an exhaustive list of possible pedigrees that could be used to pyramid a specified number of QTL. Given known QTL positions, the number of progeny required to generate the needed recombinants with a given probability at each generation can be calculated. In this way the process identifies the pedigree that can pyramid the QTL in a specified number of generations while requiring the evaluation of a minimum number of progeny. An important innovation brought by Servin et al. (2004) is that they consider a selection strategy planned over several generations whereas other MAS strategies operate one generation at a time (e.g., Lande and Thompson 1990; Hospital et al. 2000; this study). The issue of optimal MAS considering an extended planning horizon was also addressed by Dekkers and Van Arendonk (1998), where the central issue was the appropriate weighting of QTL vs. phenotypic information.

While Hospital et al. (2000) and Servin et al. (2004) take a perspective that ignores the phenotype and is therefore quite different from the one adopted here, they also show that knowledge of marker segregation provides a benefit by allowing parents to be matched on a rational basis. The development of this “rational basis” has historically sought to tackle the problems of (1) how best to conduct the QTL analysis in view of the purpose of MAS (e.g., Bernardo and Yu 2007), (2) how best to account for both QTL and phenotypic (or polygenic) information (e.g., Lande and Thompson 1990), (3) how to optimize plans over a horizon of longer than one generation (e.g., Servin et al. 2004), and (4) how to allow for other than additive modes of gene action (e.g., Jannink 2007). To these we add the question of considering error in QTL estimation. Clearly there remains a large terrain to explore in the combination of these five dimensions as they interact with the genetic determination of the trait(s) of interest. In addition, MAS methods must harmonize with plant breeding practice. For example, plant breeders usually generate many families each of relatively small size. Combining information from multiple families has been shown to be a powerful approach for QTL mapping (Rebaï and Goffinet 1993; Muranty 1996; Xie et al. 1998; Xu 1998; Rebaï and Goffinet 2000; Blanc et al. 2006; Verhoeven et al. 2006). Extending genomewide MAS and the identification of complementary parents to this context should be valuable.