Age Specificity of Inbreeding Load in Drosophila melanogaster and Implications For the Evolution of Late-Life Mortality Plateaus

Abstract

Current evolutionary theories explain the origin of aging as a byproduct of the decline in the force of natural selection with age. These theories seem inconsistent with the well-documented occurrence of late-life mortality plateaus, since under traditional evolutionary models mortality rates should increase monotonically after sexual maturity. However, the equilibrium frequencies of deleterious alleles affecting late life are lower than predicted under traditional models, and thus evolutionary models can accommodate mortality plateaus if deleterious alleles are allowed to have effects spanning a range of neighboring age classes. Here we test the degree of age specificity of segregating alleles affecting fitness in Drosophila melanogaster. We assessed age specificity by measuring the homozygous fitness effects of segregating alleles across the adult life span and calculated genetic correlations of these effects across age classes. For both males and females, we found that allelic effects are age specific with effects extending over 1–2 weeks across all age classes, consistent with modified mutation-accumulation theory. These results indicate that a modified mutation-accumulation theory can both explain the origin of senescence and predict late-life mortality plateaus.

SENESCENCE is an age-related decline in individual performance and fitness that is a nearly universal feature of multicellular organisms (Finch 1990; Lithgow 1996). The evolutionary explanation for senescence is that natural selection is very efficient in eliminating genetic variants (alleles) that have detrimental effects early in life, but much less efficient at removing alleles with detrimental effects that are confined to late ages (Medawar 1952; Williams 1957; Hamilton 1966; Charlesworth 1994). Alleles with deleterious effects confined to late ages therefore accumulate in populations and so cause age-related increases in morbidity and mortality. Mathematically, the decline in the strength of selection with age is inevitable in age-structured populations, at least under biologically realistic scenarios for mammals, birds, insects, and other organisms with determinate growth (Charlesworth 1994; Vaupel et al. 2004). However, population genetic models of senescence depend on the assumption that populations harbor genetic variants (alleles) with deleterious effects that are confined to specific age classes. Specifically, the antagonistic pleiotropy (AP) model assumes that mutations contributing to senescence have pleiotropic effects that are beneficial at early ages but harmful at late ages. In contrast, the mutation-accumulation (MA) model assumes that mutations causing senescence have only harmful effects and that these effects are confined to late ages. Both versions of the general evolutionary model require age-specific effects of alleles, and both predict that the fertility and survival of individuals will decrease with advancing age (organisms will senesce).

Despite substantial empirical evidence supporting the evolutionary models (see recent reviews, e.g., Hughes and Reynolds 2005; Partridge and Gems 2006), the discovery of late-life mortality plateaus (Carey et al. 1992; Curtsinger et al. 1992), in which cohort mortality rates appear to plateau or even decrease at late ages, challenged the validity of evolutionary explanations of aging. Under traditional MA and AP models, the effects of age-specific alleles are confined to a single age class, and age-specific mortality should increase monotonically with advancing age (Charlesworth 1990; Curtsinger 1995; Pletcher and Curtsinger 1998; Baudisch 2005), producing a “wall of death” coincident with or slightly prior to (Steinsaltz et al. 2005) the cessation of reproduction. In contrast to this prediction, mortality appears to plateau at ∼20% per day in common and Mediterranean fruit flies (Carey et al. 1992; Curtsinger et al. 1992). Qualitatively similar results are found for yeast (Pohley 1987), nematodes (Brooks et al. 1994; Vaupel et al. 1998; Johnson et al. 2001), beetles (Tatar et al. 1993), and humans (Wilkin 1982).

Although traditional MA and AP theories do not predict mortality plateaus, subsequent studies have suggested that the phenomenon could result from the decline in the force of natural selection. Rose et al. (2002) and Rauser et al. (2006) reported that manipulating the age at which the force of natural selection reaches zero caused a coincident change in the timing of the onset of plateaus in late-life mortality and fecundity. Indeed, it has been proposed that both MA and AP processes can lead to mortality plateaus, if the assumption of strict age specificity is relaxed. Specifically, alleles with late-life effects may be under weak but nonzero selection because they affect a broad window of ages, thus overlapping with reproductive ages, or because they have some pleiotropic effects on prereproductive ages (Abrams and Ludwig 1995; Mueller and Rose 1996; Charlesworth and Partridge 1997; Pletcher and Curtsinger 1998; Wachter 1999; Charlesworth 2001; Steinsaltz et al. 2005).

Recently, Charlesworth (2001) presented a modified MA model in which mortality plateaus are predicted to occur at late ages if alleles affecting fitness do so for more than one age class (moderate age specificity). Under this model, late-life mortality plateaus were predicted whether deleterious alleles affected fitness during a “window” of just a few age classes or affected fitness cumulatively at all ages after a given age. Computer simulations testing this model of age specificity were consistent with existing data on late-life mortality (Charlesworth 2001).

Whether, on average, alleles affecting fitness show the strict age specificity assumed under the original MA theory, or are more moderately age specific as modeled by Charlesworth, can be assessed by measures of correlations of allelic effects across age classes (Charlesworth 2001). If the effects of most alleles are highly age specific, as assumed under traditional MA theory, we should observe low (or no) genetic correlations among age classes. If average allelic effects are moderately age specific, then adjacent ages will have higher genetic correlations than will nonadjacent ages; the correlations should fall off with time between age classes. Finally, it is possible that the majority of alleles affecting fitness are age independent, having highly correlated effects across the life span. Under this scenario, there is little scope for the evolution of senescence under current models.

To test whether or not evolutionary theory can explain mortality plateaus, we must examine evolutionarily relevant alleles: those affecting fitness. We used Drosophila melanogaster as a model system in an assay of the average age specificity of segregating alleles on chromosome III (cIII) sampled from a natural population in Raleigh, North Carolina. We first measured the age-specific inbreeding load due to cIII alleles derived from the Raleigh population. We then assessed genetic correlations in inbreeding load among age classes. Our results indicate that cIII alleles affecting fitness in this population are age specific on the scale of 1–2 weeks, consistent with MA theory and the Charlesworth (2001) model of moderately age-specific effects.

MATERIALS AND METHODS

Experimental organisms:

For this experiment we used nine cIII extraction lines created in the laboratory of T.F.C. Mackay at North Carolina State University. These lines were derived from a natural population in Raleigh, North Carolina. Chromosome III was extracted from each isofemale line and substituted into a common genetic background (the Samarkand inbred strain; De Luca et al. 2003) using balancer chromosomes and standard Drosophila crossing schemes (Greenspan 1997). Each isogenic line thus contained naturally occurring variation at cIII, which accounts for ∼40% of the genome; all lines were genetically identical at all other loci. Ebony flies used as competitors in the fitness assay were derived from a spontaneous mutation that arose in an inbred Ives population stock in 1990 (provided by D. Houle). The ebony mutation results in a dark body color and has since been introgressed into a large randomly mating Ives population to retain the body-color mutation while eliminating effects of inbreeding.

Fitness assays:

The modified MA model depends on the assumption of moderate age specificity of fitness effects of segregating alleles. We chose to use reproductive performance as a metric for measuring age-specific fitness effects, rather than mortality rates for several reasons. First, while Charlesworth's 2001 theory makes predictions about the pattern of mortality expected in late life, the mathematical model is based upon the correlated effects of any allele affecting fitness, not just those alleles whose effects are solely on viability or longevity (Charlesworth 2001). Second, measures of mortality rate suffer from being biased estimates whenever mortality is low relative to the inverse of sample size, yielding a downward bias in estimates of genetic variance in mortality for those age classes (Shaw et al. 1999). Alternately, measures of reproductive fitness do not suffer from the measurement bias inherent in age-specific mortality.

We also chose to use measures of inbreeding load rather than estimates of genetic variance in fitness measures (typically used for calculating genetic correlations). Estimates of genetic variance are often associated with large standard errors (Lynch and Walsh 1998), making it difficult to distinguish among different correlation patterns and thus to evaluate the age specificity of alleles. Calculations of inbreeding load are relatively precise and yield smaller standard errors than estimates of additive genetic variance. Additionally, inbreeding load itself has great relevance to fitness since, on average, segregating deleterious alleles have partially dominant effects (h = 0.2) (Simmons and Crow 1977; Hughes 1995; Caballero et al. 1997; Houle et al. 1997; Garcia-Dorado and Caballero 2000), and measures of inbreeding load will reflect the effects of alleles contributing to variation in fitness components in natural populations (Hughes 1995; Santos 1997; Kelly 2003). Inbreeding load is thus an excellent metric by which to determine the age specificity of alleles affecting fitness in model organisms and for studying the evolution of aging in general. Here we assume that patterns of correlations among ages for inbreeding load will be similar to patterns of correlation of the heterozygous effects of segregating alleles.

To calculate age-specific inbreeding load, we produced inbred and noninbred genotypes from a complete diallel cross of nine isogenic lines. Each diallel consisted of all possible crosses among each of the nine genotypes, using each line as both sire and dam (a complete diallel with reciprocals). We performed the diallel cross three times, in independent replicates using different parental flies in each replicate. Within each replicate, we produced the parents for the diallel by crossing 12 males and females of each isogenic line and supplied them with 10 ml of standard corn–soy media. We removed adults after 7 days and collected adult offspring 3 days later. These offspring were separated by sex within 4 hr of emergence and housed separately until 3–6 days posteclosion. To produce the 81 genotypes of the complete diallel, we crossed 25 males and females of the appropriate genotypes in 175-ml plastic bottles supplied with agar–molasses substrate and fresh yeast paste. After 2 days, three collections (sets) of 30 first-instar larvae were made from each laying bottle, all within a single 12-hr period. Each set of 30 larvae was housed in a separate vial until emergence. Adults were collected within 4 hr of emergence and housed separately by sex until 3 days postemergence.

To obtain the ebony competitor males and females for the fitness assays, we placed seven ebony males and seven ebony females in each vial with standard media and allowed them to mate and lay eggs for 7 days, at which time adults were discarded. Virgin ebony male and female offspring were collected from these vials within 4 hr of emergence and housed separately until 3 days of age, at which time they were used in a competitive mating assay with one of the 81 focal genotypes.

To calculate age-specific inbreeding load we assayed an aspect of fitness, male and female competitive reproductive success. Reproductive success was assayed separately for each of the three sets of flies per genotype produced within a given replicate of the diallel cross. For each genotype, all three sets of flies within a replicate shared the same parents. For each assay of age-specific male fitness, 3 virgin 3-day-old males of a given genotype were placed together in a vial with 3 male and 3 female 3-day-old virgin ebony flies. Flies were transferred to fresh vials without anesthesia every 7 days until all wild-type flies in a vial had died. At each transfer dead flies were removed and counted, and all ebony flies were replaced with virgin, 3-day-old ebony flies. To minimize any possible competition bias due to ebony source vial, these ebony flies were collected from many different source vials, mixed, and randomly assigned to experimental vials in which competitors were needed. We maintained levels of competition within each vial by adjusting the number of competitor flies for the number of remaining focal flies; for example, if 1 focal male died, leaving 2 live focal males, then 2 male ebony (competitor) flies and 2 ebony females were placed into the new vial with them. Each vial was retained for 10 days after flies were removed, and all emerging offspring were counted. Because the ebony mutation is a recessive body color mutation, the parentage of offspring from competitive trials was easily determined by body color. Age-specific male fitness was measured in two ways: (1) the total number of wild-type offspring produced from a single vial and (2) the average number of wild-type offspring produced per individual within a particular vial. Male fitness was measured for ∼730 adult males, producing a total of 212,992 offspring.

Female age-specific fitness was assayed in a similar manner, by placing 3, 3-day-old virgin females of a focal genotype together with 3 virgin ebony 3-day-old females and three virgin ebony 3-day-old males. Age-specific female fitness was measured as the total number of wild-type offspring produced from each vial and the average number of wild-type offspring produced per individual within a vial, as for males. Female fitness was measured for ∼730 adult females, producing a total of 192,991 offspring. All replicates of male and female assays were completed between June and October of 2003.

Inbreeding load:

For both male and female fitness assays, we calculated two measures of age-specific inbreeding load to reflect the age-specific deleterious effects of segregating alleles. First, we calculated a traditional measure of inbreeding load, standardized inbreeding depression (SID), which is the difference in fitness between inbred and noninbred individuals, standardized by the mean noninbred fitness (Hartl and Clark 1997). For each sex, we calculated SID at age x as SID_x = (w_o,x − w_i,x)/w_o,x, where w_o,x is the mean trait value at age x for all the heterozygous (outbred cIII) genotypes that had that particular inbred genotype as a parent, and w_i,x is the mean value of male or female competitive reproductive success at age x for an inbred cIII genotype (one of the nine genotypes produced by crossing males and females from the same cIII isogenic line). This standard measure of inbreeding load is valid assuming that factors affecting fitness are multiplicative on a linear scale. If independent factors affecting fitness are multiplicative on a log scale rather than a linear scale, then as outbred fitness decreases with age, age-specific inbreeding depression (ID) will be biased toward higher values at later ages (Snoke and Promislow 2003). Thus, we used an additional, unstandardized measure of load (ID), assuming multiplicative effects on a log scale, calculated simply as the difference in fitness between inbred and noninbred genotypes at each age: ID_x = (w_o,x − w_i,x) (e.g., Snoke and Promislow 2003; Moorad and Wade 2005).

In both male and female assays of competitive reproductive success, >70% of all genotypes were present for the first 4 weeks, after which less than half of the genotypes were represented. Therefore, we restricted our analysis to weeks 1–4 of the reproductive success data. Untransformed values of SID and ID are reported in the figures and tables; however, statistical tests were conducted on transformed values to meet the assumptions of statistical analysis by mixed linear models. To meet these assumptions, the values of w_o,x and w_i,x were transformed before statistical analysis by taking the square root, as appropriate for count data, and SID_x values were arcsine square-root transformed as appropriate for proportions (Zar 1999).

Statistical analysis:

Within each replicate, reproductive success was assayed separately for each of the three sets of flies per genotype produced within a given replicate of the diallel cross. For each genotype, all three sets of flies within a replicate shared the same parents. Therefore, we used a nested analysis with the three measures derived from each genotype within a replicate being nested within replicate (Ott and Longnecker 2001, p. 1016). We also included a random block term in the analysis to account for time-of-year effect that could have differed among replicates.

We used the Mixed Procedure (PROC MIXED) of SAS v.9 to conduct a repeated-measures mixed linear model analysis to test for changes in SID and ID with age and to determine the pattern of covariance and correlation of SID and ID across age classes (Littell et al. 2002). For both measures of inbreeding load, we fit the model 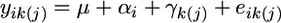, where y_ik(j) is SID (or ID) of genotype k at age i from replicate j, μ is the grand mean, α_i is the fixed effect of age i, γ_k(j) is the random effect associated with genotype k nested within replicate j, and e_ik(j) is the random error associated with the kth genotype from replicate j at at age i. SID or ID was treated as the repeated measure. There was no effect of experimental block (time of year the replicate was performed), nor were there effects of any interactions terms; thus they were not included in our final model.

A significant result for age as a continuous variable indicates a directional change (nonzero slope) in SID or ID with age. To determine the covariance and correlation of SID and ID across ages, we tested the different covariance structures described in Table 1. We used the finite-population corrected Akaike's information criterion (AICC) (Burnham and Anderson 1998) to determine the best-fitting covariance structure for the data. If alleles are age specific on the scale of <1 week (consistent with traditional MA theory), the data should best fit the independent covariance model. If alleles are moderately age specific, data will fit a model of maximum correlation for neighboring age classes and decreasing correlation with increasing distance in time. Models consistent with this pattern include the autoregressive, antedependence, Toeplitz, or unstructured covariance models. If alleles are age independent on average (pleiotropic across the life span), data will best fit either independent or compound symmetry models.

TABLE 1.

Distinctions among major covariance structures

Covariance structure	Description
Independent (In)	Assumes there are no correlations among age classes for the dependent variable.
Compound symmetry (Cs)	Assumes that measurements at each age are correlated to all other measurements to the same degree, e.g., there is only one correlation value for all pairs of age classes.
First-order autoregressive (Ar1)	Assumes that correlations are high for neighboring age classes and fall off as time between age classes increases.
	Correlations decrease as a specific, linear function of time between age classes until correlations reach zero.
	Assumes equal variances among ages.
	h option allows unequal variances (Ar1h).
First-order autoregressive with random effects (Ar1R)	Assumes that correlations will decrease by some linear function determined by the amount of time between the two ages being correlated. Incorporates the possibility that because repeated measures were taken on the same individuals over time, no two measurements are completely independent, regardless of the separation between them, and therefore correlations never reach zero.
	Assumes equal variances among ages.
	h option allows unequal variances (Ar1Rh).
Toeplitz (Toep)	Assumes decreasing correlation with time between ages.
	Does not require that these correlations decrease by a definable function.
	h option allows unequal variances (Toeph).
Unstructured (Un)	Assumes that each age class may have a unique correlation with any other age class.
	Allows for unequal variances, covariances among age classes.
	Running PROC MIXED using the unstructured covariance model allows viewing the raw covariance and correlation values for each pair of age classes, without assuming an underlying pattern of correlations.

If the data fit a model indicating moderate age specificity of alleles, the width of average allelic effects will be defined as the amount of time during which both covariances and correlations between age classes are significantly different from zero. Covariances of age-specific inbreeding load were considered significantly different from zero if maximum-likelihood-ratio tests produced chi-square statistics with P-values <0.05. To perform the maximum-likelihood-ratio tests, we first fit the full model while holding all covariance values constant at the values under the best-fit model. Next, we fit a reduced model setting the covariance of interest to zero. Finally, we calculated the difference between the −2 residual log-likelihood values and assigned the difference a P-value based upon a chi-square distribution with 1 d.f. Correlations across age classes were computed using the rcorr option in PROC MIXED. Correlations were considered to be significantly different from zero at α = 0.05 if the 95% confidence interval of correlation values did not overlap zero, where confidence intervals were determined by jackknife resampling (Efron 1979).

Differences between males and females in age-specific patterns of inbreeding load were tested using a maximum-likelihood framework and repeated-measures mixed linear models. We used the model 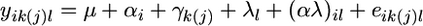, where y_ik(j)l is SID or ID of an individual of sex l in genotype k from replicate j at week i, μ is the grand mean of SID or ID, α_i is the fixed effect of age i, γ_k(j) is the random effect of genotype k nested within replicate j (subject term), λ_l is the fixed effect of sex l, αλ is the possible interaction between sex l and age i, and e_ik(j)l is the random error associated with sex l in the kth genotype from replicate j at age i. The effect of block was not significant; therefore, we did not include block in our final model. We performed this repeated measures analysis of variance using the best-fit covariance model as determined above. A significant result for the interaction among sex and age terms would indicate that the change in SID or ID with age depends upon sex.

RESULTS

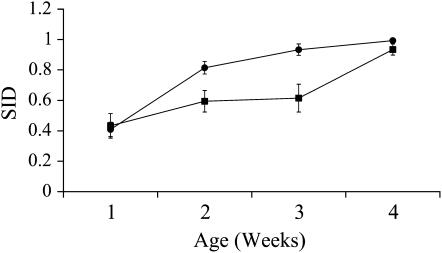
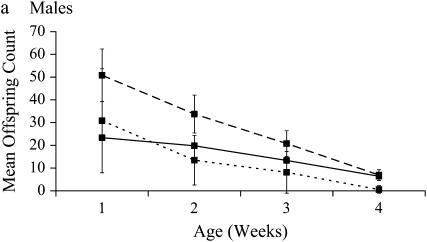
In this experiment, the mean adult life span for reproductive, noninbred males was 17.3 days and for females was 11.0 days (∼27.3 and 21.0 days from egg, respectively). Results using individual-level fitness produced the same best-fit covariance models and significant correlations among ages as did those using vial-level fitness (results not shown). Vial-level fitness measures were used to produce the following results. For both sexes, competitive reproductive success declined with age in both inbred and noninbred genotypes (Table 2). SID increased significantly with age for both males and females (Figure 1, Table 3). In contrast, ID declined significantly with age in both sexes, due to a dramatic decline with age in outbred fitness combined with an absorbing boundary of zero for inbred fitness (Figure 2, Table 3). There were no significant differences between the sexes for either measure of inbreeding load or for the change in SID with age. However, the change in ID with age is dependent upon sex, as indicated by a significant sex-by-age interaction (Table 4, Figure 2).

TABLE 2.

Mean competitive reproductive success by week

	Mean no. of offspring
Treatment group	Wk 1	Wk 2	Wk 3	Wk 4
Males, inbred crosses	30.6	14.0	14.8	3.5
Males, heterotypic crosses	51.1	34.8	27.4	14.7
Females, inbred crosses	37.7	4.2	0.9	0.2
Females, heterotypic crosses	65.5	18.2	6.9	2.3

Figure 1.—

Change in mean SID with age. Males are represented by squares, and females are represented by circles. Error bars are standard deviation from the mean.

TABLE 3.

Effect of age on inbreeding load

Data set	Covariance structure	Effect	Num. d.f.	Den d.f.	F value	Pr > F
Male SID	ar(1)	Age	1	91.9	40.36	<0.0001
Female SID	arh(1)	Age	1	43.1	353.30	<0.0001
Male ID	arh(1)	Age	1	46.7	14.23	0.0005
Female ID	arh(1)	Age	1	45.4	131.88	<0.0001

Num., numerator; Den., denominator.

Figure 2.—

Change in mean ID with age. Dashed lines represent heterozygous reproductive success, dotted lines indicate homozygous reproductive success, and the solid line indicates ID. Error bars are standard deviation from the mean.

TABLE 4.

Test for age-by-sex interaction

Metric of inbreeding load	Covariance structure	Effect	Num. d.f.	Den d.f.	F value	Pr > F
SID	arh(1)	Age	1	58.5	162.41	<.0001
		Sex	1	54.2	0.02	0.89
		Age by sex	1	63.4	1.60	0.21
ID	arh(1)	Age	1	69.7	92.97	<.0001
		Sex	1	58.6	0.17	0.68
		Age by sex	1	66.5	4.45	0.04

Num., numerator; Den., denominator.

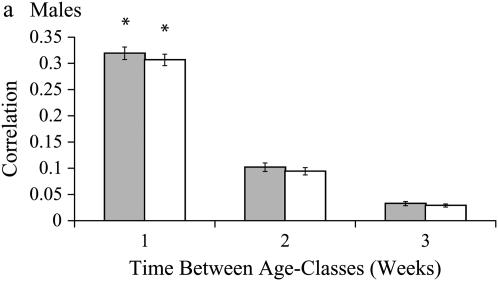
Covariances in inbreeding load across age classes are reported for both sexes in Table 5. For males, age-specific SID was best described by the first-order autoregressive covariance model (Table 6, Ar1); that is, genetic correlations among neighboring age classes are the maximum present correlations and decrease by a linear function as time between age classes increases. Age-specific ID was also best described by a first-order autoregressive model, but with unequal variances in ID across age classes (Table 6, Arh1). Best-fit covariance structures for both SID and ID indicate that alleles affecting inbreeding load in males have moderate age specificity, with small but significant correlations between age classes 1 week apart. Correlations for age classes separated by ≥2 weeks tend toward zero as the time between classes increases (Figure 3a).

TABLE 5.

Age-specific variances and covariances in inbreeding load

	Age classes compared (wk x, wk y)
Data set	1, 1	1, 2	1, 3	1, 4	2, 2	2, 3	2, 4	3, 3	3, 4	4, 4
Male SID	0.22*	0.07*	0.02	0.01	0.22*	0.07	0.02	0.22*	0.07	0.22*
Female SID	0.05*	0.03	0.01	0.001	0.17*	0.05*	0.004	0.21*	0.02	0.02*
Male ID	4.46*	1.12*	0.31	0.03	3.01*	0.84	0.08	2.50*	0.24	0.24*
Female ID	2.32*	0.39	0.05	0.004	0.86*	0.11*	0.01	0.20*	0.01	0.01*

Variances and covariances in inbreeding load are shown as calculated by repeated measures analysis of variance (SAS) using the best-fit covariance structure. Covariances are listed under the age classes being compared; e.g., “1, 1” is the variance of week 1, while 1, 2 is the covariance in inbreeding load between weeks 1 and 2. Asterisks indicate that a value is significantly different from zero at α = 0.05.

TABLE 6.

Corrected Akaike information criterion scores for likely covariance structures

	Covariance structure
Data set	In	Cs	Ar(1)	Arh(1)	Ar(1)R	Arh(1)R	Toep	Toeph	Un
Male SID	142.8	137.4	136.2a	139.1	138.2	141.3	140.6	——b	146.4
Female SID	73.2	73.0	70.8	44.5a	70.5	46.4	73.4	48.4	53.1
Male ID	382.6	378.2	376.4	342.8a	378.4	342.8	381.9	——b	351.3
Female ID	271.0	269.3	269.3	167.8a	271.2	169.2	275.1	170.5	175.9

^aBest-fit covariance structure.

^bAnalysis stopped because of too many likelihood evaluations.

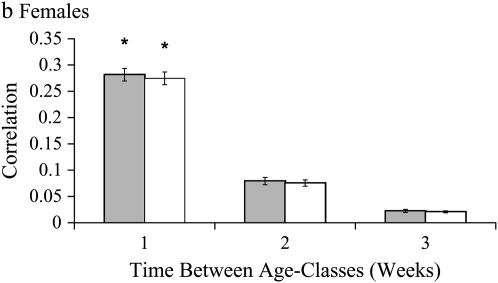
Figure 3.—

Correlations in inbreeding load among age classes. Each bar represents the correlation between two age classes; e.g., the first bar is the correlation in inbreeding load for age classes 1 week apart. Shaded bars represent correlations among age classes using SID values. Open bars represent correlations among age classes using ID values. Error bars are the standard deviation of the jackknifed data set.

For females, age-specific patterns of both SID and ID best fit the autoregressive 1 covariance model allowing for heterogeneity of variances among ages (Table 6). As in males, there are significant positive correlations for age classes 1 week apart, with decreasing correlations for age classes >1 week apart (Table 5, Figure 3b). These patterns indicate that segregating alleles have a window of significant deleterious effects spanning at least 1, but <2 weeks.

DISCUSSION

We have shown that alleles affecting inbreeding load have effects that are significantly positively correlated over 40% of mean life span for males and 64% of mean life span for females. Average allelic effects are apparently neither pleiotropic for the entire life span nor extremely age specific in the style of traditional MA theory. These data are therefore most consistent with modified MA theory assuming a moderate age specificity of allelic effects.

If the alleles affecting inbreeding depression are strictly deleterious in nature, then the inbreeding load should be inversely related to the sensitivity of fitness with age: inbreeding load should increase with cohort age (Charlesworth and Hughes 1996). We found that SID increased dramatically with age in both sexes (Figure 1), as has been shown in other experiments (Hughes et al. 2002; Snoke and Promislow 2003). Snoke and Promislow (2003) also showed an increase in ID with age. In contrast, ID values in this experiment decreased significantly with age. In this case, it is likely that the decrease in ID with age is due to a decrease in both inbred and outbred fitness, combined with an absorbing boundary of zero for inbred fitness: of competition vials that produced offspring at 14 days, 40% of inbred male competition vials produced zero wild-type offspring, and 59% of inbred female competition vials produced zero wild type (these vials did produce ebony flies). Results on the direction of change in inbreeding load with age should be interpreted with caution: the validity of the prediction could be sensitive to violation of its underlying assumptions. One assumption implicit in the prediction that inbreeding load should increase with age is that the effects of alleles are independent across ages. Our data show that the effects of alleles are not completely independent among neighboring age classes. Future work is necessary to determine how these developments in our understanding of the nature of alleles contributing to inbreeding load do or do not change predictions concerning the trajectory of ID with age.

Our results indicate that female ID decreases faster than does male ID with age (Table 3, Figure 2). Alleles affecting male and female fitness traits need not be the same. Indeed, there is considerable evidence for sex-specific allelic effects from quantitative trait locus (QTL) experiments investigating life span and age-specific survival in D. melanogaster (Nuzhdin et al. 1997, 2005; Leips and Mackay 2000; but see Vieira et al. 2000; Reiwitch and Nuzhdin 2002) and sex-specific effects of inbreeding in general (Saccheri et al. 2005). Even alleles affecting fitness similarly in both sexes could have different temporal patterns of age specificity in males and females (Nuzhdin et al. 2005) or different magnitudes of effects in the sexes (e.g., Clancy et al. 2001; Flurkey et al. 2002; Holzenberger et al. 2003; Kapahi et al. 2004). Despite evidence for ubiquitous sex specificity of allelic effects, our results indicate that alleles determining inbreeding depression have similar duration of effect in both sexes: ∼1 week (Figure 3).

Previous mutation-accumulation and quantitative genetic experiments have been used to estimate genetic correlations in fitness components among ages. One previous study (Tatar et al. 1996) measured the age specificity of naturally segregating alleles affecting female fecundity in a population of laboratory-adapted D. melanogaster. In that study, additive genetic correlations in age-specific fecundity at 3 days of age (the earliest age class measured) and later ages were not significantly different from zero. Correlations among all other age classes were significantly positive. The focus of the Tatar et al. study was to determine the general sign of correlations across ages; although the study showed that correlations were generally positive for most age comparisons, statistical tests comparing additive genetic correlations for neighboring vs. distant age classes were not presented.

In a study of D. melanogaster homozygous lines that had been accumulating spontaneous mutations for 47 generations, Pletcher et al. (1998, 1999) found that mutations affecting both male and female mortality at generation 19 were significantly positively correlated across age classes separated by 1–3 weeks: 26–78% of average adult life span. In that experiment, correlations across ages were also calculated at generations 10 and 47 of mutation accumulation, but large estimates of standard errors made statistical significance unclear.

Life-span QTL identified in a cross between lines selected for divergent longevity had significantly positively correlated effects across ages separated by 7–35 days (61–100% of mean adult life span; Curtsinger and Khazaeli 2002). Leips et al. (2006) identified QTL affecting fecundity at 1 week of age, but not at 4 weeks of age, with no genetic correlation in fecundity between the two ages, while the genetic variance among homozygous lines increased with age.

Overall, these studies indicate that new mutations (Pletcher et al. 1999) and segregating alleles (this study; Curtsinger and Khazaeli 2002; Leips et al. 2006) have moderately age-specific effects, on average. All estimates, except for those derived from the QTL study, reflect the average correlations of allelic effects across particular chromosomes, or whole genomes. Our findings do not rule out a small to moderate number of alleles that act in an antagonistically pleiotropic manner. There is no a priori expectation that MA and AP are mutually exclusive; in fact, there is a substantial body of evidence for antagonistic pleiotropy among fitness traits in D. melanogaster (e.g., Chippindale et al. 1994; Rose et al. 2002; Leips et al. 2006).

Although we have shown that alleles affecting fitness are consistent with a modified MA model and are moderately age specific on average, further investigations are needed to determine what types of age specificity are common for these alleles. The Charlesworth (2001) modified MA model covers a continuum of alleles with moderately age-specific effects. On one end of the continuum, alleles may have a window of age-specific effects such that there are an age of onset and an age at which the effects are no longer seen. At the other end of the continuum, alleles may have “cumulative” effects: an age of onset and pleiotropic effects throughout the rest of the life span. These effects could remain the same for each remaining age class, or the effects could worsen with age, e.g., Alzheimer's disease. It is not possible to distinguish what proportion of the alleles that we detected have typical window-style vs. cumulative effects (or something in between) using our data. Although considerable variation in age specificity may exist, the empirical results support theoretical models that predict mortality plateaus when the assumptions of strict age specificity are relaxed.

In conclusion, we have shown a moderate age specificity of allelic effects on inbreeding depression. We provide evidence that the evolutionary theory of late life, based on the decline in the efficacy of natural selection with age, explains—indeed, predicts—mortality plateaus. This conclusion is consistent with studies in which the timing of the decline in the force of natural selection was altered and the timing of mortality and fecundity plateaus changed in the predicted direction (Rose et al. 2002; Rauser et al. 2006). Our results do not imply that selection on moderately age-specific alleles is the only or even the predominant cause of observed mortality plateaus. For example, nongenetic heterogeneity among individuals in a population can lead to mortality plateaus for purely demographic reasons (Vaupel et al. 1979; Service 2000), as can age-related changes in individual behavior (Kowald and Kirkwood 1993; Sgro and Partridge 1999) or in environmental conditions (Nusbaum et al. 1993; Robine and Ritchie 1993; Khazaeli et al. 1996; Partridge 1997). Resolution of the question of whether mortality plateaus are mainly an evolved characteristic of populations or are a statistical consequence of demographic variation will require experiments that manipulate both potential causes and possible interactions between them.