Skip to main content
PMC home page
British Journal of Pharmacology logoLink to British Journal of Pharmacology
. 2007 Apr 30;151(5):713–720. doi: 10.1038/sj.bjp.0707258

Influence of biophase distribution and P-glycoprotein interaction on pharmacokinetic-pharmacodynamic modelling of the effects of morphine on the EEG

D Groenendaal 1,4, J Freijer 2, D de Mik 1, M R Bouw 3, M Danhof 1,2, E C M de Lange 1,*
PMCID: PMC2013992  PMID: 17471181

Abstract

Background and purpose:

The aim was to investigate the influence of biophase distribution including P-glycoprotein (Pgp) function on the pharmacokinetic-pharmacodynamic correlations of morphine's actions in rat brain.

Experimental approach:

Male rats received a 10-min infusion of morphine as 4 mg kg−1, combined with a continuous infusion of the Pgp inhibitor GF120918 or vehicle, 10 or 40 mg kg−1. EEG signals were recorded continuously and blood samples were collected.

Key results:

Profound hysteresis was observed between morphine blood concentrations and effects on the EEG. Only the termination of the EEG effect was influenced by GF120918. Biophase distribution was best described with an extended catenary biophase distribution model, with a sequential transfer and effect compartment. The rate constant for transport through the transfer compartment (k1e) was 0.038 min−1, being unaffected by GF120918. In contrast, the rate constant for the loss from the effect compartment (keo) decreased 60% after GF120918. The EEG effect was directly related to concentrations in the effect compartment using the sigmoidal Emax model. The values of the pharmacodynamic parameters E0, Emax, EC50 and Hill factor were 45.0 μV, 44.5 μV, 451 ng ml−1 and 2.3, respectively.

Conclusions and implications:

The effects of GF120918 on the distribution kinetics of morphine in the effect compartment were consistent with the distribution in brain extracellular fluid (ECF) as estimated by intracerebral microdialysis. However, the time-course of morphine concentrations at the site of action in the brain, as deduced from the biophase model, is distinctly different from the brain ECF concentrations.

Keywords: morphine, P-glycoprotein, population pharmacokinetic-pharmacodynamic modelling, biophase distribution, EEG

Introduction

Mechanism-based pharmacokinetic–pharmacodynamic (PK–PD) models for the central action of opioids contain expressions for (a) blood PK, (b) biophase distribution, which is mainly determined by blood–brain barrier (BBB) transport, (c) receptor interaction kinetics and (d) signal transduction (Danhof et al., 2005). Especially for morphine, biophase distribution is an important determinant of the onset and duration of the effect because of its hydrophilic nature and the interaction with the efflux transporter P-glycoprotein (Pgp). Research on the influence of biophase distribution on morphine PK–PD relationships has so far primarily focused on rather empirical biophase distribution models. Bouw et al. (2000) have proposed a single biophase compartment model to account for the delay of the anti-nociceptive effect of morphine relative to corresponding plasma concentrations. Transport across the BBB accounted for 84% of the observed hysteresis. For morphine, a limited number of studies have focused on the role of active transport mechanisms at the BBB. Specifically, it has been shown that after oral pretreatment with the specific Pgp inhibitor GF120918, the anti-nociceptive effect of morphine was prolonged due to its prolonged half-life in the brain, presumably resulting from inhibition of Pgp as an active efflux mechanism (Letrent et al., 1998, 1999). Moreover, the role of transporters other than Pgp efflux at the BBB on brain distribution of morphine has been indicated by interaction studies with probenecid (Tunblad et al., 2003).

Recently, the brain distribution of morphine has been characterized in greater detail with intracerebral microdialysis (MD) (Groenendaal et al., 2007, companion paper). Brain distribution was nonlinear and was successfully described by a complex brain distribution model with specific expressions for (1) passive diffusion, (2) active saturable influx and (3) active efflux, which could in part be inhibited by GF120918. Against this background, it is of considerable interest to characterize, in a mechanistic manner, the biophase distribution kinetics of morphine in a PK–PD investigation.

Detailed characterization of the biophase distribution kinetics requires the availability of high-density PD data. In this respect, quantitative analysis of drug effects on the electroencephalogram (EEG) yields attractive biomarkers, which are continuous, sensitive and reproducible (Dingemanse et al., 1988). Quantitative EEG parameters have been widely used as a PD end point in preclinical and clinical investigations on the PK–PD correlations of a variety of central nervous system (CNS) active drugs. The synthetic opioid alfentanil, which is frequently used in anaesthesia produces a progressive slowing of the EEG with a pre-dominant increase in the delta frequency band (0.5–4.5 Hz) of the EEG power spectrum in both animals (Young and Khazan, 1984; Wauquier et al., 1988; Mandema and Wada, 1995; Cox et al., 1997) and humans (Wauquier et al., 1984; Young and Khazan, 1984; Scott et al., 1985). The increase in the delta frequency band of the EEG has been widely used as a biomarker in numerous studies on the PK–PD correlations of synthetic opioids. In preclinical studies, an increase in the delta frequency band of the EEG reflected μ-opioid receptor activation (Cox et al., 1997, 1998, 1999). Moreover, in clinical studies, this biomarker has been validated as a surrogate marker for depth of anaesthesia (Scott et al., 1985, 1991; Lemmens et al., 1995; Egan et al., 1996).

The aim of the present study was to investigate the influence of biophase distribution and Pgp interaction at the BBB on the PK–PD relationships of morphine and to compare the time course of the predicted effect-site concentrations with the time course of the brain extracellular fluid (ECF) concentrations as determined by intracerebral MD.

Methods

The PKs in blood and PDs were investigated in two sets of experiments, the classic EEG experiments and the EEG-MD experiments. The details of the EEG-MD experiments have been described previously (Groenendaal et al., 2007, companion paper).

Surgical procedures

Details of the anaesthetic and surgical procedures have been described previously (Groenendaal et al., 2007, companion paper). For the EEG experiments, seven cortical electrodes were stereotaxically implanted into the skull of rats 10 days before the start of the experiments as described before (Cox et al., 1997). Briefly, the electrodes were placed at the locations 11 mm anterior and 2.5 mm lateral (Fl and Fr), 3 mm anterior and 3.5 mm lateral (Cl and Cr) and 3 mm posterior and 2.5 mm lateral (Ol and Or) to lambda. A reference electrode was placed on lambda. Stainless-steel screws were used as electrodes and connected to a miniature connector. For the EEG-MD experiments, the rats were chronically instrumented with four EEG electrodes at the Fl, Cl, Ol and reference position and with a CMA/12 guide cannula with a dummy probe placed in the striatum of the right brain hemisphere (anterior–posterior: +0.5 mm, lateral: +2.7 mm with bregma as reference and ventral: −3.5 mm ventral to the skull).

Experimental procedures

All experimental procedures were identical for both the EEG groups and the EEG-MD groups, as described previously (Groenendaal et al., 2007, companion paper). The EEG signal was continuously monitored via bipolar EEG leads on the left hemisphere (Cl–Ol) using a Nihon-Kohden AB-621G Bioelectric Amplifier (Hoekloos BV, Amsterdam, The Netherlands) and concurrently digitized at a rate of 256 Hz using a CED 1401plus interface (CED, Cambridge, UK). The digitized signal was transferred into a Pentium III computer and stored on hard disk for offline analysis. For each 5 s epoch, quantitative EEG parameters were obtained offline by fast Fourier transformation with a user-defined script within the software package Spike2 for Windows, version 3.18 (CED, Cambridge, UK). Changes in the amplitudes in the δ-frequency band of the EEG (0.5–4.5 Hz) averaged over 1 min time intervals were used as a PD end point. Further reduction of the EEG data was performed by averaging the signals over predetermined time intervals using a user-defined script within the software package Matlab, version 6.1 (The Mathworks Inc., Gouda, The Netherlands). The size of the intervals was dependent on the different periods of the experiment. The intervals were 3 min for baseline, 3 min between start of infusion (time=0) and 75 min, 5 min between 75 and 200 min after start of infusion and 10 min between 200 and 360 min after start of the infusion. These intervals were chosen on the basis of visual inspection of the 1 min datafile.

Blood samples were analysed for morphine, GF120918 and midazolam as described previously (Groenendaal et al., 2005).

The selection of the biophase distribution model

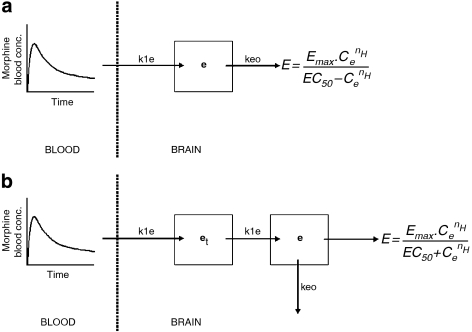
A profound delay in the EEG effect (hysteresis) of morphine was observed. The hysteresis was characterized on the basis of two biophase distribution models: (a) the one-compartment biophase distribution model, also known as the effect-compartment model and (b) the extended catenary biophase distribution model (Figure 1).

Figure 1.

Figure 1

Open in a new tab

A schematic overview of the one-compartment distribution model (a) and the extended-catenary biophase distribution model (b) to describe the biophase kinetics of morphine. The blood PKs were described with a three-compartment model and used as input function for morphine in the brain. The one-compartment distribution model consists of one effect compartment (e), whereas the biophase distribution model consists of two sequential compartments, the transfer (et) and the effect (e) compartment. The concentrations in the effect compartment were related to the EEG effect on the basis of the sigmoidal Emax model. In the figure, k1e represents the rate constant for transport through the transfer compartment, keo represents the rate constant for loss from the effect compartment and is influenced by GF120918 and Emax represent the intrinsic activity and EC50 represents the potency.

One-compartment biophase distribution model

Hysteresis is often characterized on the basis of the one-compartment biophase distribution model. With this model the assumption is made that the rate of onset and offset of the drug effect is governed by the rate of drug distribution to the hypothetical ‘effect-site' (Sheiner et al., 1979). This effect compartment is then linked to the blood concentrations with the rate constant k1e and the rate constant for drug loss keo. The rate of change of the drug concentration in the effect compartment can then be expressed by the equation where Cb represents the blood concentration and Ce represents the effect-site concentration. Under the assumption that in equilibrium the effect-site concentration equals the blood concentration, this equation can be simplified to

This model describes a symmetrical biophase. In contrast, when k1e is not equal to keo, the biophase is considered to be asymmetrical. Both models were investigated.

Extended catenary biophase distribution model

The extended catenary biophase distribution model consists of two sequential compartments, a transfer (et) and an effect (e) compartment which was based on the ‘tank-in-series' models described by Upton et al. (2000) and provides a simple method for accounting for dispersion of drug in transit through the brain. The rate of change of the concentrations in the effect compartments can then be described as follows: where Cet and Ce describe the concentrations in the transfer and effect-compartment, respectively. The concentrations in the effect-compartment were then linked to the pharmacological effect. Both the symmetrical (k1e=keo) and the asymmetrical (k1e≠keo) biophase models were investigated.

PK–PD analysis of the EEG effect

For the development of the structural PK–PD model for the EEG effect of morphine, the PREDPP subroutine ADVAN6 was used, which is a general nonlinear model that uses a numerical solution of the differential equations.

After hysteresis minimization, the individual concentration–effect relationships were fitted to the sigmoidal Emax model: where E0 is the no-drug response, Emax is the intrinsic activity, EC50 is the potency and nH is the slope factor.

In the experiments described here, two experimental approaches were used, the EEG method and the EEG-MD method. Since the removal of three EEG electrodes and the subsequent implantation of a MD probe could possibly result in a change in baseline EEG, a covariate was included in the analysis to validate the EEG-MD method. The following equation was used where Pi is the individual value of model parameter and θ1 and θ2 are the parameter values obtained with METHOD=1 for EEG-MD and METHOD=0 for EEG.

The influence of co-infusion of GF120918 on the biophase distribution rate constants was tested with the following equation where Pi is the individual value of model parameter and θ3 and θ4 are the parameter estimate and Pgp inhibition value and GF120918 is a factor, set to 1 if GF120918 is co-infused and set to 0 is vehicle is co-infused.

Inter-animal variability on E0 and Emax was described with a proportional variability model according to equation: with where Pi is the individual value of the model parameter P, Ptyp is the typical value (population value) of parameter P in the population, and ηi is inter-animal random variable. The assumption was made that all other parameters were log-normal distributed with mean zero and variance ω2.

The inter-animal variability on all other parameters was described with an exponential error model according to the equation with

Inter-animal variability was investigated for each parameter and was fixed to zero when the MVOF did not improve. Correlations between the inter-animal variability of the various parameters were graphically explored. In addition, correlations between the PD parameters and dose and between the PD parameters and the co-infusion of GF120918 were also investigated graphically.

The residual error, which accounts for unexplained errors (such as measurement and experimental errors) in the EEG measurements, was best described with a proportional error model according to the equation where Cobs,ij is the jth observation of the ith individual, Cpred,ij is the predicted concentration and ɛij is a realization from the normally distributed residual random variable with mean zero and variance σ2

Data analysis

The details of the general modelling procedures have been described previously (Groenendaal et al., 2007, companion paper). The EEG effects of morphine were analysed using nonlinear mixed effect modelling as implemented in the NONMEM software version V, level 1.1 (Beal and Sheiner, 1999). Population analysis was undertaken using the first-order conditional estimation method (FOCE interaction). Individual PK parameter estimates were used as input for the PD models. Individual blood concentrations were calculated at the times of the EEG measurements.

Results

PDs and hysteresis

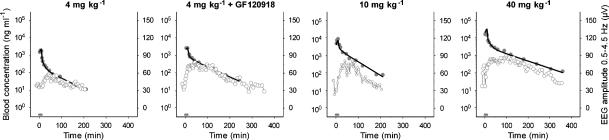
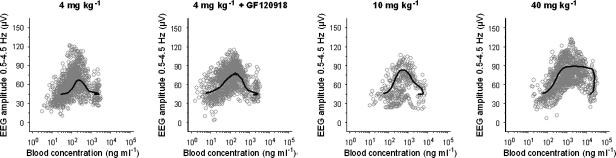
After the start of the morphine infusion, a gradual increase in the EEG effect, expressed as the absolute amplitude in the 0.5–4.5 Hz frequency range, was observed. The maximal effect was 60 μV and was observed around 20 min after the end of the morphine infusion. The duration of the effect (from the start of the infusion until the return to baseline values) was around 180 min following the infusion of 4 and 10 mg kg−1 morphine whereas after a dose of 4 mg kg−1 combined with GF120918, or 40 mg kg−1 morphine alone, the duration of the effect was around 360 min. In Figure 2, the PKs and the PDs of a typical rat of each experimental group are shown. It was found that the derived blood concentration–EEG effect relationships showed profound hysteresis for all experimental groups (Figure 3), which was counterclockwise.

Figure 2.

Figure 2

Open in a new tab

PKs and PDs of a typical rat after administration of the opioids. Observed blood concentrations (grey dots), individual predicted blood concentrations (black line) and observed EEG effect (grey open dots) are depicted for each dose group. The grey bar indicates the infusion time.

Figure 3.

Figure 3

Open in a new tab

PK–PD relationship after administration of morphine. Observed (grey dots) and population predictions (black line) are depicted for each dose group. A clear counterclockwise hysteresis loop was observed for all morphine doses.

The selection of the biophase distribution model

To describe the observed hysteresis, two biophase distribution models were proposed: (1) the one-compartment distribution model and (2) the extended catenary biophase distribution model. First, the biophase distribution kinetics was fitted according to the one-compartment biophase distribution model. Both the symmetrical and asymmetrical effect compartment models was tested. With the symmetrical (k1e=keo) biophase distribution no results were obtained (minimization terminated), whereas with the asymmetrical (k1e≠keo) effect compartment model no precise estimates could be obtained and bias was observed between the observed and predicted values. Therefore, the extended catenary biophase distribution model was proposed, consisting of two sequential compartments; a transfer and an effect compartment. Both the symmetrical and asymmetrical model was used. The asymmetrical model resulted in the lowest objective function, 24671 (k1e≠keo) versus 24936 (k1e=keo) and precise estimates of the parameters of the biophase distribution kinetics were obtained (Table 1). The value of the rate constant for transport through the transfer compartment (k1e) was unaffected by the co-administration of GF120918. The population predictions of blood and biophase concentration–time profiles are shown in Figure 4. The best fit was obtained when the influence of GF120918 was described with a Pgp inhibition factor that influences the keo. This Pgp inhibition factor was estimated at a value indicating that in the presence of GF120918, the keo was decreased by 64%. The inter-animal variability (ω2) on keo was estimated with an exponential error model. The inter-animal variability could not be estimated for the other parameters and were therefore fixed to zero.

Table 1.

Population pharmacokinetic parameter estimates of the biophase distribution of morphine obtained with the extended catenary biophase distribution model

Parameter Estimate CV% LLCI–ULCI
Structural model
k1e (min−1) 0.0378 8.4 0.0315–0.0441
       
keo (min−1)
 −GF120918 0.0426 10.0 0.0342–0.0510
 +GF120918a 0.0152    
Pgp inhibition factor −0.644 −7.3 −0.736–−0.552
       
Interindividual variability
 ω2 keo 0.237 20.2 0.143–0.331
       
Open in a new tab

Abbreviations: CV%, coefficient of variation; k1e, rate constant for transport to the effect-site; keo, rate constant for the loss from the effect-site; LLCI, lower limit of confidence interval; ULCI, upper limit of confidence interval.

a

keo(+GF120918)=keo(−GF120918)·(1+Pgp inhibition factor).

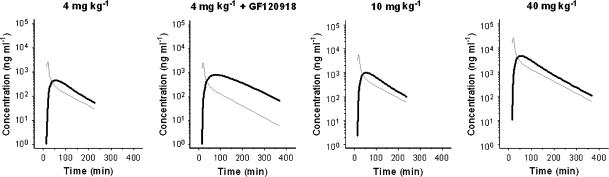
Figure 4.

Figure 4

Open in a new tab

Population predicted blood and biophase concentration–time profiles of morphine obtained with the extended catenary biophase distribution model. The grey lines represent the blood concentration–time profiles and the black lines represent the biophase concentration–time profiles.

PK–PD analysis of the EEG effect

The individual predicted biophase concentrations were related to the EEG effect on the basis of the sigmoidal Emax PD model. As the EEG and EEG-MD experiments were performed in parallel, covariate analysis was included to investigate the influence of the MD probe on the PD parameters. Since no differences were observed in E0 and Emax values between the EEG and the EEG-MD group, a single parameter value was estimated. Morphine PK–PD relationships were accurately described as shown in Figure 5 and Table 2. Co-infusion of GF120918 did not influence the PD parameters. Inter-animal variability (ω2) was estimated with a proportional error model for E0 and Emax. Inter-animal variability could not be estimated for the other parameters and were therefore fixed to zero. Graphical analysis showed that no significant correlations were observed between the estimates of the PD parameters and dose and between PD parameter estimates and co-infusion of GF120918.

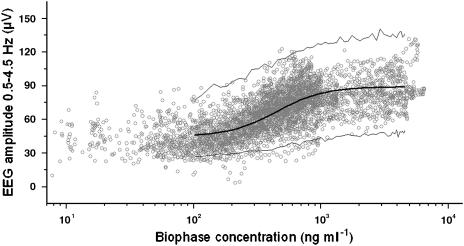
Figure 5.

Figure 5

Open in a new tab

PK–PD relationships of the opioids after hysteresis minimization with the extended catenary biophase distribution model. Observed (grey dots), population predicted (solid line) and 2.5 and 97.5% quantiles (dotted lines) are depicted versus the predicted biophase concentration as shown in Figure 4. The PK–PD relationship was obtained using the extended catenary biophase distribution model to describe the distribution to the effect-site and the sigmoidal Emax model to relate the biophase concentrations to the EEG effect.

Table 2.

Population pharmacodynamic parameter estimates of morphine EEG effect obtained with the sigmoidal Emax model after hysteresis minimisation with the extended catenary biophase distribution model

Parameter Estimate CV% LLCI–ULCI
Structural model
 E0 (μV) 44.6 2.3 42.6–46.6
 Emax (μV) 44.5 8.0 37.5–51.5
 EC50 (ng ml−1) 451 17.3 298–604
 nH 2.32 10.4 1.85–2.79
       
Interindividual variability
 ω2 kE0 0.034 17.8 0.022–0.045
 ω2 kEmax 0.121 24.1 0.064–0.178
       
Residual variability
 Proportional error 0.027 7.6 0.023–0.031
Open in a new tab

Abbreviations: CV%, coefficient of variation; E0, no-drug response; Emax, intrinsic activity; EC50, measure of potency; nH, slope factor; LLCI, lower limit of confidence interval; ULCI, upper limit of confidence interval.

Discussion

Biophase distribution can be defined as the distribution processes between the blood and the effect-site. The aim of the present study was to investigate the influence of biophase distribution and Pgp interaction at the BBB on the PK–PD relationships of morphine and to compare the time course of the predicted effect-site concentrations with the time course of the brain ECF concentrations as determined by intracerebral MD.

So far the PK–PD investigations of morphine have focussed on the anti-nociceptive effects (Letrent et al., 1998; Bouw et al., 2000). In these studies, the hysteresis has been described with the standard symmetrical effect compartment model consisting of a single effect compartment, where k1e is equal to keo. In these models, a wide difference in keo values (hysteresis) was observed; the keo values were 0.228 and 0.022 min−1, for the doses of 1 mg kg−1 and 10 or 40 mg kg−1, respectively. This difference may be explained by the different dose used (1 mg kg−1 versus 10 or 40 mg kg−1), the difference in infusion speed (bolus versus 10 min infusion) and the differences in experimental set-up to measure the anti-nociceptive effect (hot-lamp tail-flick latency assay versus electrical stimulation vocalization method). With anti-nociceptive effect measurements, only a limited number of data points can be obtained, which may limit a detailed PK–PD analysis.

Morphine induces both analgesia and sedation. Changes in EEG are often used as a measure to reflect the depth of sedation or anaesthesia (Stanski, 1992). As EEG effect measurements have the advantage of being continuous, sensitive, objective and reproducible, EEG has been used in this study to investigate the influence of biophase distribution on the PK–PD relationship of morphine. Between rats, only very small differences were observed in baseline (E0) values, indicating the robustness of the EEG model. The method, either EEG or EEG-MD, had no influence on the E0 and Emax.

A profound counter clockwise hysteresis was observed for the concentration–effect relationships of each group, which may result from the formation of metabolites that influence the effect of morphine. In rats, only the metabolite M3G is formed in significant amounts. Since the affinity of M3G for the μ-opioid receptor is much lower compared to morphine (Bartlett and Smith, 1995; Loser et al., 1996; de Jong et al., 2005), it was concluded that the influence of M3G on the observed hysteresis could be neglected. Therefore, M3G was not quantitated in the present study. The hysteresis of the EEG effects of morphine was characterized on the basis of two biophase distribution models: (a) the one-compartment biophase distribution model, also known as the effect-compartment model and (b) the extended catenary biophase distribution model. The biophase distribution kinetics could neither be described with the symmetrical nor the asymmetrical one-compartment biophase distribution model, indicating that the biophase distribution process of the EEG effect included multiple distribution processes. Therefore, the extended catenary biophase distribution model was developed. This model consists of two sequential biophase compartments; the transfer and the effect compartment. The extended catenary biophase distribution model is based on a ‘tank-in-series' model as proposed by Upton et al. (2000). This model provides a simple method for accounting for dispersion of drug in the transit through the brain (Upton et al., 1999). The concentrations in the effect compartment were related to the EEG effects, defined by the rate constant for transport through the transfer compartment (k1e) and for loss from the effect compartment (keo). These rate constants are distinctly different since only the keo could be influenced by co-infusion of the specific and potent Pgp inhibitor GF120918.

The biophase distribution observed for morphine is more complex than those of other opioids. For alfentanil, the biophase distribution was too fast to be identified, while for fentanyl and sufentanil, the hysteresis could be described with simple keo values of 0.32 and 0.17 min−1, for fentanyl and sufentanil, respectively (Cox et al., 1998). These observations confirm that application of morphine as an anaesthetic is more difficult compared to fentanyl-like opioids.

The PD parameters of the EEG effects of morphine could be accurately described with the sigmoidal Emax model. All EEG experiments were performed in the presence of a steady-state infusion of midazolam to prevent opioid-induced seizure activity. Since a constant midazolam concentration was present in all treatment groups, the comparison of the biophase distribution and EEG effect is still valid. In addition, midazolam is a weak Pgp inhibitor, but is not transported by Pgp (Mahar Doan et al., 2002) and therefore the influence of midazolam could be neglected.

The next step was to correlate the biophase distribution kinetics with the previously investigated brain ECF distribution PKs (Groenendaal et al., 2007, companion paper). To describe the brain ECF distribution kinetics, a nonlinear transport model was proposed consisting of one brain compartment with distinction between passive diffusion, active linear efflux which is partly mediated by Pgp and active saturable influx by a yet unknown transport mechanism. In contrast, the extended catenary biophase distribution model consists of two sequential compartments. There were no indications for nonlinearity in the biophase distribution kinetics of morphine. The difference between the models indicates that transport into the brain ECF is distinctly different from transport to the effect site. Transport into the brain ECF is dependent on both passive diffusion and active saturable influx, whereas for biophase distribution the transport to the effect site is a linear process. The effects of GF120918 on the distribution kinetics of morphine in the effect compartments were consistent with recent observations on the distribution in brain ECF (Groenendaal et al., 2007, companion paper). When comparing the concentration–time profiles in brain ECF and biophase, it was noted that they were distinctly different (Figure 6). The concentration in brain ECF peaked early, whereas the maximum biophase concentration showed a profound delay. In addition, at the low dose of morphine, a ‘plateau' was observed in brain ECF whereas in the biophase concentrations, a clear decline over time was observed. These observations indicate that the brain ECF cannot be used to explain the hysteresis. This is in contrast with the observation by Bouw et al. (2000) where 85% of the observed hysteresis for the anti-nociceptive effect could be explained by distribution into the brain ECF. In addition, Bouw et al. (2000) did not identify the active uptake of morphine in the brain ECF. This indicates that the site of action for the anti-nociceptive effects is distinctly different from that for the EEG effect.

Figure 6.

Figure 6

Open in a new tab

Comparison of the population predicted biophase concentration–time profiles (black lines) and the population predicted brain ECF fluid concentration–time profiles (grey lines) as obtained previously (see Groenendaal et al., 2007, companion paper). The time-course of the biophase concentrations differs substantially from the time course of the brain ECF concentrations indicating that biophase equilibration is slower than transport into the brain ECF.

A discrepancy between the predicted effect-site concentration and the measured CNS time course has also been observed for the EEG effects of amobarbital, where the amobarbital effect-site concentrations did not reflect the measured cerebrospinal fluid concentrations (Mandema et al., 1991). In addition, Chenel et al. (2004) showed that the extensive time delay between EEG effect and plasma concentrations of norfloxacin, best described with an effect-compartment model, could not be explained by slow distribution to the biophase. For norfloxacin the brain ECF concentrations peaked very early, whereas the EEG effect was delayed, which was also seen for morphine. For norfloxacin, the brain ECF profiles were parallel to the plasma profiles, whereas for morphine a nonlinearity was observed at the low dose (4 mg kg−1). Chenel et al. (2004) showed that the keo did not decrease when the ECF data were included in the PK–PD analysis, whereas for morphine the brain ECF and EEG effects could not be analysed simultaneously.

In conclusion, the biophase distribution kinetics of morphine was adequately described with the extended catenary biophase distribution model. Comparison with the previously developed nonlinear distribution model for morphine distribution into the brain showed that the time course of morphine at the site of action in the brain is distinctly different from the brain ECF concentrations as estimated by intracerebral MD.

Acknowledgments

We gratefully acknowledge the technical assistance of MCM Blom-Roosemalen, SM Bos-van Maastricht and P Looijmans. The supply of GF120918 by GlaxoSmithKline in the United Kingdom is highly appreciated. These investigations were financially supported by GlaxoSmithKline in the United Kingdom.

Abbreviations

CNS

central nervous system

ECF

extracellular fluid

MD

microdialysis

PD

pharmacodynamics

Pgp

P-glycoprotein

PK

pharmacokinetics

Conflict of interest

The authors state no conflict of interest.

References

  1. Bartlett SE, Smith MT. The apparent affinity of morphine-3-glucuronide at mu1-opioid receptors results from morphine contamination: demonstration using HPLC and radioligand binding. Life Sci. 1995;57:609–615. doi: 10.1016/0024-3205(95)00311-s. [DOI] [PubMed] [Google Scholar]
  2. Beal SL, Sheiner LB. NONMEM Users Guide. San Francisco: CA; 1999. [Google Scholar]
  3. Bouw MR, Gardmark M, Hammarlund-Udenaes M. Pharmacokinetic-pharmacodynamic modelling of morphine transport across the blood–brain barrier as a cause of the antinociceptive effect delay in rats – a microdialysis study. Pharm Res. 2000;17:1220–1227. doi: 10.1023/a:1026414713509. [DOI] [PubMed] [Google Scholar]
  4. Chenel M, Marchand S, Dupuis A, Lamarche I, Paquereau J, Pariat C, et al. Simultaneous central nervous system distribution and pharmacokinetic-pharmacodynamic modelling of the electroencephalogram effect of norfloxacin administered at a convulsant dose in rats. Br J Pharmacol. 2004;142:323–330. doi: 10.1038/sj.bjp.0705748. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cox EH, Kerbusch T, van der Graaf PH, Danhof M. Pharmacokinetic-pharmacodynamic modeling of the electroencephalogram effect of synthetic opioids in the rat: correlation with the interaction at the mu-opioid receptor. J Pharmacol Exp Ther. 1998;284:1095–1103. [PubMed] [Google Scholar]
  6. Cox EH, Langemeijer MW, Gubbens-Stibbe JM, Muir KT, Danhof M. The comparative pharmacodynamics of remifentanil and its metabolite, GR90291, in a rat electroencephalographic model. Anesthesiology. 1999;90:535–544. doi: 10.1097/00000542-199902000-00030. [DOI] [PubMed] [Google Scholar]
  7. Cox EH, Van Hemert JG, Tukker EJ, Danhof M. Pharmacokinetic-pharmacodynamic modelling of the EEG effect of alfentanil in rats. J Pharmacol Toxicol Methods. 1997;38:99–108. doi: 10.1016/s1056-8719(97)00065-8. [DOI] [PubMed] [Google Scholar]
  8. Danhof M, Alvan G, Dahl SG, Kuhlmann J, Paintaud G. Mechanism-based pharmacokinetic-pharmacodynamic modeling-a new classification of biomarkers. Pharm Res. 2005;22:1432–1437. doi: 10.1007/s11095-005-5882-3. [DOI] [PubMed] [Google Scholar]
  9. de Jong LA, Kramer K, Kroeze MP, Bischoff R, Uges DR, Franke JP. Development and validation of a radioreceptor assay for the determination of morphine and its active metabolites in serum. J Pharm Biomed Anal. 2005;39:964–971. doi: 10.1016/j.jpba.2005.04.049. [DOI] [PubMed] [Google Scholar]
  10. Dingemanse J, Sollie FA, Breimer DD, Danhof M. Pharmacokinetic modeling of the anticonvulsant response of oxazepam in rats using the pentylenetetrazol threshold concentration as pharmacodynamic measure. J Pharmacokinet Biopharm. 1988;16:203–228. doi: 10.1007/BF01062261. [DOI] [PubMed] [Google Scholar]
  11. Egan TD, Minto CF, Hermann DJ, Barr J, Muir KT, Shafer SL. Remifentanil versus alfentanil: comparative pharmacokinetics and pharmacodynamics in healthy adult male volunteers. Anesthesiology. 1996;84:821–833. doi: 10.1097/00000542-199604000-00009. [DOI] [PubMed] [Google Scholar]
  12. Groenendaal D, Blom-Roosemalen MC, Danhof M, Lange EC. High-performance liquid chromatography of nalbuphine, butorphanol and morphine in blood and brain microdialysate samples: application to pharmacokinetic/pharmacodynamic studies in rats. J Chromatogr B Analyt Technol Biomed Life Sci. 2005;822:230–237. doi: 10.1016/j.jchromb.2005.06.008. [DOI] [PubMed] [Google Scholar]
  13. Groenendaal D, Freijer J, de Mik D, Bouw MR, Danhof M, Lange EC.Population pharmacokinetic modelling of non-linear brain distribution of morphine: influence of active saturable influx and P-glycoprotein mediated efflux Br J Pharmacol 2007151701–712.this issue [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lemmens HJ, Egan TD, Fiset P, Stanski DR. Pharmacokinetic/dynamic assessment in drug development: application to the investigational opioid mirfentanil. Anesth Analg. 1995;80:1206–1211. doi: 10.1097/00000539-199506000-00024. [DOI] [PubMed] [Google Scholar]
  15. Letrent SP, Pollack GM, Brouwer KR, Brouwer KL. Effect of GF120918, a potent P-glycoprotein inhibitor, on morphine pharmacokinetics and pharmacodynamics in the rat. Pharm Res. 1998;15:599–605. doi: 10.1023/a:1011938112599. [DOI] [PubMed] [Google Scholar]
  16. Letrent SP, Pollack GM, Brouwer KR, Brouwer KL. Effects of a potent and specific P-glycoprotein inhibitor on the blood–brain barrier distribution and antinociceptive effect of morphine in the rat. Drug Metab Dispos. 1999;27:827–834. [PubMed] [Google Scholar]
  17. Loser SV, Meyer J, Freudenthaler S, Sattler M, Desel C, Meineke I, et al. Morphine-6-O-beta-D-glucuronide but not morphine-3-O-beta-D-glucuronide binds to mu-, delta- and kappa-specific opioid binding sites in cerebral membranes. Naunyn Schmiedebergs Arch Pharmacol. 1996;354:192–197. doi: 10.1007/BF00178720. [DOI] [PubMed] [Google Scholar]
  18. Mahar Doan KM, Humphreys JE, Webster LO, Wring SA, Shampine LJ, Serabjit-Singh CJ, et al. Passive permeability and P-glycoprotein-mediated efflux differentiate central nervous system (CNS) and non-CNS marketed drugs. J Pharmacol Exp Ther. 2002;303:1029–1037. doi: 10.1124/jpet.102.039255. [DOI] [PubMed] [Google Scholar]
  19. Mandema JW, Veng-Pedersen P, Danhof M. Estimation of amobarbital plasma-effect site equilibration kinetics. Relevance of polyexponential conductance functions. J Pharmacokinet Biopharm. 1991;19:617–634. doi: 10.1007/BF01080870. [DOI] [PubMed] [Google Scholar]
  20. Mandema JW, Wada DR. Pharmacodynamic model for acute tolerance development to the electroencephalographic effects of alfentanil in the rat. J Pharmacol Exp Ther. 1995;275:1185–1194. [PubMed] [Google Scholar]
  21. Scott JC, Cooke JE, Stanski DR. Electroencephalographic quantitation of opioid effect: comparative pharmacodynamics of fentanyl and sufentanil. Anesthesiology. 1991;74:34–42. doi: 10.1097/00000542-199101000-00007. [DOI] [PubMed] [Google Scholar]
  22. Scott JC, Ponganis KV, Stanski DR. EEG quantitation of narcotic effect: the comparative pharmacodynamics of fentanyl and alfentanil. Anesthesiology. 1985;62:234–241. doi: 10.1097/00000542-198503000-00005. [DOI] [PubMed] [Google Scholar]
  23. Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther. 1979;25:358–371. doi: 10.1002/cpt1979253358. [DOI] [PubMed] [Google Scholar]
  24. Stanski DR. Pharmacodynamic modeling of anesthetic EEG drug effects. Annu Rev Pharmacol Toxicol. 1992;32:423–447. doi: 10.1146/annurev.pa.32.040192.002231. [DOI] [PubMed] [Google Scholar]
  25. Tunblad K, Jonsson EN, Hammarlund-Udenaes M. Morphine blood–brain barrier transport is influenced by probenecid co-administration. Pharm Res. 2003;20:618–623. doi: 10.1023/a:1023250900462. [DOI] [PubMed] [Google Scholar]
  26. Upton RN, Huang YF, Mather LE, Doolette DJ. The relationship between the myocardial kinetics of meperidine and its effect on myocardial contractility: model-independent analysis and optimal regional model. J Pharmacol Exp Ther. 1999;290:694–701. [PubMed] [Google Scholar]
  27. Upton RN, Ludbrook GL, Grant C, Doolette DJ. The effect of altered cerebral blood flow on the cerebral kinetics of thiopental and propofol in sheep. Anesthesiology. 2000;93:1085–1094. doi: 10.1097/00000542-200010000-00033. [DOI] [PubMed] [Google Scholar]
  28. Wauquier A, Bovill JG, Sebel PS. Electroencephalographic effects of fentanyl-, sufentanil- and alfentanil anaesthesia in man. Neuropsychobiology. 1984;11:203–206. doi: 10.1159/000118078. [DOI] [PubMed] [Google Scholar]
  29. Wauquier A, De Ryck M, Van den Broeck W, Van Loon J, Melis W, Janssen P. Relationships between quantitative EEG measures and pharmacodynamics of alfentanil in dogs. Electroencephalogr Clin Neurophysiol. 1988;69:550–560. doi: 10.1016/0013-4694(88)90167-8. [DOI] [PubMed] [Google Scholar]
  30. Young GA, Khazan N. Differential neuropharmacological effects of mu, kappa and sigma opioid agonists on cortical EEG power spectra in the rat. Stereospecificity and naloxone antagonism. Neuropharmacology. 1984;23:1161–1165. doi: 10.1016/0028-3908(84)90233-8. [DOI] [PubMed] [Google Scholar]

Articles from British Journal of Pharmacology are provided here courtesy of The British Pharmacological Society

RESOURCES