Abstract
Aims
We compared the relationships between the plasma concentrations (C) of perindoprilat, active metabolite of the angiotensin I-converting enzyme inhibitor (ACEI) perindopril, and the effects (E) induced on plasma converting enzyme activity (PCEA) and brachial vascular resistance (BVR) in healthy volunteers (HV) and in congestive heart failure (CHF) patients after single oral doses of perindopril.
Methods
Six HV received three doses of perindopril (4, 8, 16 mg) in a placebo-controlled, randomized, double-blind, crossover study whereas 10 CHF patients received one dose (4 mg) in an open study. Each variable was determined before and 6–12 times after drug intake. E (% variations from baseline) were individually related to C (ng ml−1) by the Hill model E=Emax.Cγ/(CE50γ + Cγ). When data showed a hysteresis loop, an effect compartment was used.
Results
(means±s.d.) In HV, relationships between C and E were direct whereas in CHF patients, they showed hysteresis loops with optimal ke0 values of 0.13 ± 0.16 and 0.13 ± 0.07 h−1 for PCEA and BVR, respectively. For PCEA, with Emax set to −100%, CE50 = 1.87 ± 0.60 and 1.36 ± 1.33 ng ml−1 (P = 0.34) and γ= 0.90 ± 0.13 and 1.11 ± 0.47 (P = 0.23) in HV and CHF patients, respectively. For BVR, Emax=−41 ± 14% and −60 ± 7% (P = 0.02), CE50 = 4.95 ± 2.62 and 1.38 ± 0.85 ng ml−1 (P = 0.02), and γ= 2.25 ± 1.54 and 3.06 ± 1.37 (P = 0.32) in HV and CHF patients, respectively.
Conclusions
Whereas concentration-effect relationships were similar in HV and CHF patients for PCEA blockade, they strongly differed for regional haemodynamics. This result probably expresses the different involvements, in HV and CHF patients, of angiotensinergic and nonangiotensinergic mechanisms in the haemodynamic effects of ACEIs.
Keywords: concentration-effect relationship, congestive heart failure patients, effect compartment, haemodynamics, healthy volunteers, perindopril, PK-PD modelling, sigmoid model
Introduction
It is now well established that pharmacokinetic–pharmacodynamic (PK-PD) modelling constitutes a meaningful tool to determine the optimal dosage and the best mode of administration of a new drug [1, 2]. In cardiovascular pharmacology, this approach has been used for a long time, especially during the development of vasodilators (e.g. α-adrenoceptor antagonists, angiotensin I-converting enzyme inhibitors, calcium channel blockers, potassium channel openers…) not only in hypertensives [3–5], but also in normotensive healthy volunteers (HV) [6–8]. It appeared then that HV provided valuable data to predict the response of hypertensives [9, 10]. This approach has also been used in congestive heart failure (CHF) patients [11, 12], but far less frequently, and comparison of pharmacodynamic parameters between HV and CHF patients has never been performed.
Angiotensin I-converting enzyme inhibitors (ACEIs) represent a class of drugs for which such comparisons could be of interest since they have been demonstrated to affect haemodynamics mainly through angiotensinergic effects in CHF patients [13] and nonangiotensinergic effects in HV [14]. Among ACEIs, perindopril is a mono-acid mono-ester prodrug which is hydrolysed in vivo into an active diacid metabolite, perindoprilat [15]. A few years ago, we have studied its pharmacodynamics both in HV [16] and in CHF patients [17]. Since we had simultaneously investigated its pharmacokinetics, the main objective of the present study has been to establish the relationships between perindoprilat plasma concentrations and its biological and regional haemodynamic effects, both in HV and in CHF patients, in order to assess the consequences of the above-mentioned difference between the two types of subjects on the pharmacodynamic parameters.
Methods
Experimental protocol
The experimental protocols of the two studies have been reported previously [16, 17]. Therefore, we will just recall their main features. Both protocols had been approved by our hospital Ethics Committee and all subjects had given written informed consent to participate.
Experimental designs
The first study was performed in our Clinical Pharmacology Unit in six healthy male volunteers (means ±s.d. 25 ± 3 years, 63 ± 7 kg, 174 ± 6 cm) who received, at weekly intervals, single oral administrations of perindopril 4, 8 and 16 mg. The study was placebo-controlled, randomized, double-blind, crossover, and performed according to a latin square design. The second study was performed in the Intensive Care Unit of our hospital in 10 chronic CHF patients (7 males/3 females, 64 ± 8 years, 65 ± 11 kg, 166 ± 12 cm) in NYHA functional class III (five patients) or IV (five patients). This was an open study. Etiology of CHF was ischaemic in seven patients and idiopathic in the other three. About 2 weeks before inclusion, all patients had been hospitalized in the Intensive Care Unit for an acute pulmonary oedema unrelated to acute myocardial infarction. At inclusion, the patients had to be in stable haemodynamic and functional conditions (without cardiotonics and/or vasodilators and with fixed doses of diuretics and a controlled sodium intake of 2 g daily) for at least 6 days. Diuretics were withheld 24 h before investigation.
Pharmacodynamic variables
The following haemodynamic as well as biological variables were investigated at rest, in the recumbent position, before and repeatedly during the 24 h after drug intake. Investigations were performed at least at 1, 2, 3, 4, 6, 8, 10 and 24 h in HV and at 1, 2.5, 4, 6, 8 and 24 h in CHF patients.
Systolic and diastolic arterial pressures (SAP, DAP, mmHg) were measured using an automatic monitor connected to a brachial cuff sphygmomanometer in HV and directly through an intra-arterial catheter placed in the radial artery in CHF patients. Mean arterial pressure (MAP, mmHg) was calculated as MAP = (1/3) SAP + (2/3) DAP. Brachial artery flow (BAF, ml min−1) was measured with a bidimensional pulsed Doppler system (Echovar Doppler pulsé 8 MHz, Alvar Electronics, Montreuil, France) as previously described and validated [18]. Brachial vascular resistance (BVR, mmHg.s ml−1) was calculated as BVR = MAPx60/BAF. Pulmonary capillary wedge pressure (PCWP, mmHg) was measured (in CHF patients only) with a triple lumen Swan-Ganz catheter (Baxter Healthcare Corp., Edwards Division, model 93 A-131–7F, Santa Ana, Ca, USA) introduced into the jugular vein. Plasma converting enzyme activity (PCEA, nmol ml−1 min−1) was determined by spectrophotometry [19]. For this variable, additional determinations were performed at 12 and 48 h in HV and at 2, 3, 10, 12, 48 and 72 h in CHF patients.
Plasma concentrations of the parent drug and of its metabolite
Perindopril and perindoprilat plasma concentrations (ng ml−1) were determined from venous blood samples by radioimmunoassay as previously described [20]. Measurements were performed before and 0.5, 1, 1.5, 2, 2.5, 3, 4, 6, 8, 10, 12, 16, 20, 24, 48 and 72 h after drug intake in HV. In CHF patients, the same schedule was used except that the two samples drawn at 16 and 20 h were replaced by a single one drawn at 18 h. The detection limit of the assay was 0.4 ng ml−1 for both perindopril and perindoprilat.
PK study
Perindopril and perindoprilat PK parameters were determined in each individual subject. Peak concentration (Cmax, ng ml−1) and time to peak concentration (tmax, h) were determined from the observed data. Area under the concentrations vs time curve between 0 and 72 h (AUC(0,72 h), ng ml−1 h) and mean residence time (MRT, h) were determined accordingly using the trapezoidal rule. Terminal elimination half-life (t1/2,z, h) was estimated using log-linear regression.
PK-PD modelling
The PK-PD modelling was performed, in each individual subject, with a software developed in our laboratory [21, 22]. This software has four important features. Firstly, when the concentrations and effects of a drug are studied in the same subject after a single administration of several doses, it allows to determine the concentration-effect relationship for that subject using the data of all doses simultaneously [22, 23]. Secondly, when the concentration-effect relationship displays an anticlockwise hysteresis loop, it allows to use an effect compartment [24], but the estimation of the first order rate constant ke0 which governs the kinetics of the drug in the effect compartment is performed with non parametric kinetic and dynamic models [25]. As compared with the semiparametric approach [26], this non parametric approach does not require the predetermination of a pharmacokinetic model to estimate ke0: plasma concentrations at any given time are calculated by linear interpolation between the concentrations observed at the two measurement times bracketing this time; effect compartment concentrations at any given time are calculated by numerical integration of the differential equation which governs the kinetics of the drug in the effect compartment [25]. Thirdly, the optimal value of ke0 can be obtained by using either a one-dimensional minimization algorithm (golden section search or parabolic interpolation) implemented in the program [27], or, in case of difficulties of convergence, a step by step procedure driven by the user under the graphic control of the reduction of the hysteresis [12, 23]. Fourthly, when several doses of a drug are studied in the same subject and when the concentration-effect relationships display anticlockwise hysteresis loops, the software allows to estimate an optimal value of ke0 either for each dose separately or for all doses simultaneously [23, 28].
The PK-PD modelling included one or two successive steps depending upon the type of the relationship (direct or indirect) between perindoprilat plasma concentrations and effects. When the concentration-effect relationship did not display a hysteresis loop (direct relationship), modelling was performed by using perindoprilat plasma concentrations and observed effects. When the concentration-effect relationship displayed a hysteresis loop (indirect relationship), an effect compartment was used. After determination of the optimal value of ke0, modelling was performed by using the concentrations of perindoprilat computed in the effect compartment and the observed effects.
The PK-PD modelling was performed between perindoprilat concentrations and the following drug effects: percent variations from baseline values for PCEA and BVR and absolute values for BAF and PCWP. In each case, the sigmoid pharmacodynamic model was used. The general form of the model is E = [Emax.Cγ/(CE50γ + Cγ)] + E0, where E is the predicted effect, C the concentration of perindoprilat, Emax the maximum theoretical effect, CE50 the concentration of perindoprilat which induces an effect of 50% of Emax, γ the Hill coefficient, and E0 the baseline value of the variable of effect (i.e. the value without drug). A non linear regression was performed using a non weighed least squares criterion. In HV, the model was fitted to the data of the three doses simultaneously. The two main parameters of the model (Emax and CE50) were estimated simultaneously using four multidimensional minimization algorithms (downhill simplex, direction set, conjugate gradient and variable metric) implemented in the program [27], the two others (γ and E0) being constrained to fixed values [23]. For the effects expressed as percent variations from baseline values (PCEA and BVR), this procedure was only applied to estimate γ, E0 being set to 0, whereas for the effects expressed as absolute values (BAF and PCWP), the procedure was applied to estimate both γ and E0. In the first case, the least squares criterion was computed for all the values of γ in the range [0.5, 5.0] with a step of 0.5. In the second case, the least squares criterion was computed for all the possible pairs (γ, E0), γ being defined in the range [0.5, 5.0] with a step of 0.5 and E0 being defined as the 10 values bracketing the observed basal value with a step of 1 unit. In each case, the goodness of fit was assessed from the visual distribution of residuals. When several sets of parameters allowed to satisfactorily describe experimental data, the choice of the best set was performed based upon the value of the objective function and of the determination coefficient (r2).
Statistical presentation of results and analyses
For each subject, results of the PK-PD modelling were expressed as point-estimates with asymptotic s.d. derived from the variance-covariance matrix estimated at the optimum (these s.d. correspond to standard errors). For the whole population, the distribution of each PK and (estimated or fixed) PD parameter was expressed as the mean with a s.d. computed from individual point-estimates. Statistical analyses were performed with the BMDP statistical software (Los Angeles, Ca, USA). The distributions of PK parameters were compared in HV between the three doses using repeated measures anova (program 2 V). The distributions of PK (after 4 mg) and of PD parameters were compared between HV and CHF patients using Student's t-test (program 3D).
Results
PK study (Table 1)
Table 1.
Pharmacokinetic parameters of perindopril and perindoprilat in healthy volunteers (HV) and in congestive heart failure (CHF) patients. Data are means±s.d.
| Cmax (ng ml−1) | tmax (h) | AUC (0,72 h) (ng ml−1 h) | MRT (h) | t1/2,z (h) | |
|---|---|---|---|---|---|
| Perindopril | |||||
| HV 4 mg | 87 ± 32 | 0.8 ± 0.3 | 136 ± 33 | 1.9 ± 0.4 | 1.0 ± 0.2 |
| HV 8 mg | 181 ± 66 | 1.4 ± 0.5 | 313 ± 147 | 2.1 ± 0.5 | 0.9 ± 0.2 |
| HV 16 mg | 248 ± 97 | 1.3 ± 0.8 | 449 ± 111 | 2.3 ± 0.6 | 1.0 ± 0.2 |
| CHF 4 mg | 113 ± 40 | 1.9 ± 1.2 | 544 ± 337 | 6.9 ± 2.9 | 4.6 ± 1.9 |
| P value [1] | 0.0083 | 0.1259 | 0.0009 | 0.5115 | 0.3707 |
| P value [2] | 0.2036 | 0.0224 | 0.0040 | 0.0003 | 0.0002 |
| Perindoprilat | |||||
| HV 4 mg | 5 ± 2 | 4.3 ± 2.9 | 92 ± 30 | 58.9 ± 19.4 | 43.8 ± 13.2 |
| HV 8 mg | 12 ± 6 | 7.0 ± 2.8 | 156 ± 41 | 51.4 ± 9.8 | 44.4 ± 8.1 |
| HV 16 mg | 31 ± 18 | 3.6 ± 1.4 | 305 ± 98 | 30.9 ± 17.5 | 40.1 ± 18.9 |
| CHF 4 mg | 16 ± 8 | 2.9 ± 2.0 | 109 ± 85 | 6.1 ± 1.9 | 3.5 ± 1.7 |
| P value [1] | 0.0017 | 0.1206 | 0.0005 | 0.0306 | 0.8967 |
| P value [2] | 0.0023 | 0.2705 | 0.6668 | 0.0011 | 0.0006 |
Cmax: peak concentration, tmax: time to peak concentration, AUC(0,72 h): area under the concentrations vs time curve between 0 and 72 h, MRT: mean residence time, t1/2,z: terminal elimination half-life. The P values correspond to comparisons between HV groups (repeated measures anova) [1] and between HV 4 mg and CHF 4 mg groups (Student's t-test) [2].
Perindopril
Cmax was observed between 0.8 and 1.4 h (the differences between doses being not significant) in HV whereas it was observed significantly later, at 1.9 h, in CHF patients. In HV, Cmax was not totally proportional to the dose, the concentration obtained after 16 mg being far below an expected value of 360 ng ml−1 (if we consider the mean values obtained after 4 and 8 mg). In CHF patients, Cmax reached about 110 ng ml−1, this concentration being not significantly different from the one obtained in HV after 4 mg. In HV, AUC(0,72 h) was not totally proportional to the dose either, the area obtained after 16 mg being far below an expected value of about 600 ng ml−1 h. In CHF patients, AUC(0,72 h) reached about 550 ng ml−1 h, this value being significantly greater than that obtained in HV after 4 mg. In fact, this value was also greater than those obtained in HV after 8 and even 16 mg. Finally, in HV, MRT and t1/2,z were between 1.9 and 2.3 h and 0.9 and 1.0 h, respectively (the differences between doses being not significant). In CHF patients, these parameters were significantly and strongly increased at 6.9 and 4.6 h, respectively.
Perindoprilat
For the active metabolite, the results of the PK study did not include the CHF patient 9 because this patient had only one perindoprilat detectable level during the 72 h following perindopril administration (0.4 ng ml−1 at 2.5 h). Cmax was observed between 3.6 and 7.0 h in HV whereas it was observed at 2.9 h in CHF patients (the differences between doses in HV and between HV and CHF patients after 4 mg being not significant). In HV, Cmax was not totally proportional to the dose, the concentration obtained after 16 mg being greater than an expected value comprised between 20 and 24 ng ml−1 (if we always consider the mean values obtained after 4 and 8 mg). In CHF patients, Cmax reached 16 ng ml−1, this concentration being significantly greater (by more than 3 fold) than that obtained in HV after 4 mg. In HV, AUC(0,72 h) was roughly proportional to the dose. In CHF patients, AUC(0,72 h) was not significantly different from that obtained in HV after 4 mg. Finally, in HV, MRT and t½,z were, respectively, between 30.9 and 58.9 h (depending upon the dose) and 40.1 and 44.4 h (the differences between doses being not significant). In CHF patients, these parameters were significantly and strongly decreased at 6.1 and 3.5 h, respectively.
PK-PD modelling
PK-PD modelling was performed in each subject except CHF patient 9 because of the above-mentioned lack of data of perindoprilat concentrations.
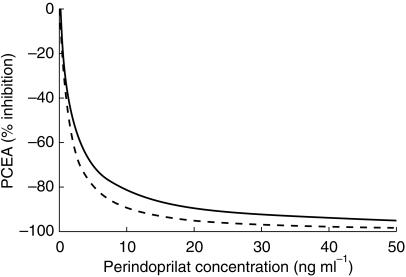
PK-PD model for PCEA (Table 2) For PCEA, the modelling was successful in all subjects. The maximum theoretical effect corresponding to a complete blockade of enzyme activity, Emax was set to −100%. CE50 was 1.87 ± 0.60 and 1.36 ± 1.33 ng ml−1 (P = 0.3424) and γ was 0.90 ± 0.13 and 1.11 ± 0.47 (P = 0.2302) in HV and in CHF patients, respectively. Figure 1 illustrates these results. Observed concentration-effect relationships were always direct in HV but they showed major hysteresis loops in CHF patients. When using an effect compartment, estimated ke0 was 0.13 ± 0.16 h−1, the mean value corresponding to a half-life of 5 h and 20 min
Table 2.
Pharmacodynamic parameters of the relationship between perindoprilat concentrations and effects on plasma converting enzyme activity in healthy volunteers (HV) and in congestive heart failure (CHF) patients.
| Subject number | CE50 (ng ml−1) | Asymptotic s.d. CE50 (ng ml−1) | γ | ke0 (h−1) | r2 |
|---|---|---|---|---|---|
| HV | |||||
| 1 | 1.91 | 0.25 | 1.00 | NH | 0.7019 |
| 2 | 1.82 | 0.14 | 1.00 | NH | 0.8353 |
| 3 | 2.32 | 0.19 | 1.00 | NH | 0.8492 |
| 4 | 2.28 | 0.28 | 0.80 | NH | 0.7093 |
| 5 | 2.15 | 0.26 | 0.90 | NH | 0.5890 |
| 6 | 0.71 | 0.10 | 0.70 | NH | 0.7887 |
| Mean±s.d. | 1.87 ± 0.60 | 0.90 ± 0.13 | |||
| CHF patients | |||||
| 1 | 0.41 | 0.06 | 0.75 | 0.06 | 0.8800 |
| 2 | 0.86 | 0.08 | 1.50 | 0.05 | 0.8730 |
| 3 | 2.41 | 0.24 | 1.50 | 0.55 | 0.8935 |
| 4 | 0.45 | 0.06 | 0.75 | 0.20 | 0.8723 |
| 5 | 4.16 | 0.32 | 1.00 | 0.06 | 0.7470 |
| 6 | 0.51 | 0.08 | 1.00 | 0.06 | 0.9157 |
| 7 | 0.33 | 0.07 | 1.00 | 0.07 | 0.8550 |
| 8 | 0.73 | 0.13 | 0.50 | 0.08 | 0.8716 |
| 10 | 2.41 | 0.15 | 2.00 | 0.04 | 0.7840 |
| Mean±s.d. | 1.36 ± 1.33 | 1.11 ± 0.47 | 0.13 ± 0.16 | ||
| P value | 0.3424 | 0.2302 | |||
CE50: concentration of perindoprilat which induces an effect of 50% of maximum theoretical effect, γ: Hill coefficient, ke0: first order rate constant which governs the kinetics of the drug in the effect compartment, r2: determination coefficient. NH: no hysteresis. Maximum theoretical effect (Emax) and baseline value of the variable of effect (E0) set to −100% and 0, respectively. The P values correspond to comparisons between HV and CHF patients groups (Student's t-test). In HV: model fitted to the data of the three doses simultaneously.
Figure 1.
Perindoprilat plasma converting enzyme activity (PCEA) blockade concentration-effect relationship in healthy volunteers (HV, solid line) and in congestive heart failure (CHF, dotted line) patients. The models have the following parameters: Emax=−100%, CE50 = 1.87 ng ml−1, γ= 0.90, and E0 = 0 in HV, and Emax=−100%, CE50 = 1.36 ng ml−1, γ=1.11, and E0 = 0 in CHF patients.
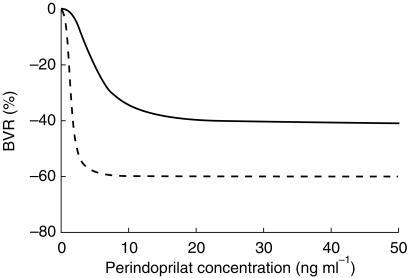
PK-PD model for BVR (Table 3) and BAF For both variables, the modelling was successful in all subjects but one (CHF patient 1, because of a complete lack of relationship between perindoprilat concentrations and regional haemodynamic effects without hysteresis phenomenon). For BVR, Emax was −41 ± 14 and −60 ± 7% (P = 0.0196), CE50 was 4.95 ± 2.62 and 1.38 ± 0.85 ng ml−1 (P = 0.0195) and γ was 2.25 ± 1.54 and 3.06 ± 1.37 (P = 0.3187) in HV and in CHF patients, respectively. Figure 2 illustrates these results. For BAF, the results of the modelling were quite similar (except for Emax) and therefore individual data are not shown. Emax was 36 ± 18 and 36 ± 17 ml min−1 (P = 0.9823), CE50 was 4.97 ± 2.45 and 2.08 ± 1.23 ng ml−1 (P = 0.0129), γ was 3.42 ± 1.63 and 3.69 ± 1.31 (P = 0.7352) and E0 was 72 ± 3 and 26 ± 6 ml min−1 (P < 0.0001) in HV and in CHF patients, respectively. For both variables, observed concentration-effect relationships were always direct in HV, but they showed major hysteresis loops in all CHF patients but one (CHF patient 6). When using an effect compartment, estimated ke0 were 0.13 ± 0.07 and 0.16 ± 0.10 h−1 for BVR and BAF, respectively.
Table 3.
Pharmacodynamic parameters of the relationship between perindoprilat concentrations and effects on brachial vascular resistance in healthy volunteers (HV) and in congestive heart failure (CHF) patients.
| Subject number | Emax (%) | Asymptotic s.d. Emax (%) | CE50 (ng ml−1) | Asymptotic s.d. CE50 (ng ml−1) | γ | ke0 (h−1) | r2 |
|---|---|---|---|---|---|---|---|
| HV | |||||||
| 1 | −37 | 3.63 | 2.39 | 0.52 | 2.00 | NH | 0.2069 |
| 2 | −44 | 5.30 | 5.81 | 1.02 | 3.00 | NH | 0.5685 |
| 3 | −23 | 2.15 | 1.87 | 0.26 | 5.00 | NH | 0.3610 |
| 4 | −60 | 11.74 | 6.93 | 2.88 | 1.00 | NH | 0.5416 |
| 5 | −30 | 4.70 | 4.11 | 1.19 | 1.50 | NH | 0.3509 |
| 6 | −54 | 9.10 | 8.56 | 3.17 | 1.00 | NH | 0.5276 |
| Mean±s.d. | −41 ± 14 | 4.95 ± 2.62 | 2.25 ± 1.54 | ||||
| CHF patients | |||||||
| 2 | −61 | 4.08 | 1.02 | 0.18 | 2.00 | 0.07 | 0.8611 |
| 3 | −61 | 0.60 | 1.31 | 0.02 | 4.50 | 0.15 | 0.9959 |
| 4 | −63 | 9.25 | 1.72 | 0.18 | 4.00 | 0.23 | 0.7768 |
| 5 | −62 | 21.17 | 0.72 | 0.51 | 1.00 | 0.03 | 0.6665 |
| 6 | −55 | 3.03 | 1.40 | 0.64 | 3.00 | NH | 0.7959 |
| 7 | −68 | 2.24 | 0.12 | 0.03 | 5.00 | 0.19 | 0.9234 |
| 8 | −47 | 0.81 | 3.00 | 0.15 | 2.00 | 0.17 | 0.9905 |
| 10 | −66 | 6.41 | 1.76 | 0.22 | 3.00 | 0.07 | 0.7796 |
| Mean±s.d. | −60 ± 7 | 1.38 ± 0.85 | 3.06 ± 1.37 | 0.13 ± 0.07 | |||
| P value | 0.0196 | 0.0195 | 0.3187 | ||||
Emax: maximum theoretical effect, CE50: concentration of perindoprilat which induces an effect of 50% of Emax, γ: Hill coefficient, ke0: first order rate constant which governs the kinetics of the drug in the effect compartment, r2: determination coefficient. NH: no hysteresis. Baseline value of the variable of effect (E0) set to 0. The P values correspond to comparisons between HV and CHF patients groups (Student's t-test). In HV: model fitted to the data of the three doses simultaneously.
Figure 2.
Perindoprilat brachial vascular resistance (BVR) decrease concentration-effect relationship in healthy volunteers (HV, solid line) and in congestive heart failure (CHF, dotted line) patients. The models have the following parameters: Emax=−41%, CE50 = 4.95 ng ml−1, γ= 2.25, and E0 = 0 in HV, and Emax=−60%, CE50 = 1.38 ng ml−1, γ= 3.06, and E0 = 0 in CHF patients.
PK-PD model for PCWP
(Table 4) For PCWP, the modelling was successful in all subjects but one (CHF patient 1 for the same reason as for BVR and BAF). Emax was −11 ± 4 mmHg, CE50 was 1.54 ± 1.50 ng ml−1, γ was 3.63 ± 1.51 and E0 was 24 ± 3 mmHg. As for PCEA, observed concentration-effect relationships showed major hysteresis loops in all CHF patients. When using an effect compartment, estimated ke0 was 0.11 ± 0.05 h−1.
Table 4.
Pharmacodynamic parameters of the relationship between perindoprilat concentrations and effects on pulmonary capillary wedge pressure in congestive heart failure patients.
| Subject number | Emax (mmHg) | Asymptotic s.d. Emax (mmHg) | CE50 (ng ml−1) | Asymptotic s.d. CE50 (ng ml−1) | γ | ke0 (h−1) | r2 |
|---|---|---|---|---|---|---|---|
| 2 | −12 | 0.25 | 1.84 | 0.07 | 3.00 | 0.11 | 0.9855 |
| 3 | −19 | 0.34 | 0.28 | 0.03 | 2.00 | 0.16 | 0.9711 |
| 4 | −10 | 0.83 | 0.77 | 0.09 | 4.00 | 0.10 | 0.8380 |
| 5 | −8 | 0.40 | 0.21 | 0.03 | 4.00 | 0.07 | 0.7742 |
| 6 | −10 | 1.27 | 3.82 | 0.61 | 5.00 | 0.08 | 0.8124 |
| 7 | −11 | 0.78 | 0.16 | 0.07 | 5.00 | 0.20 | 0.6239 |
| 8 | −15 | 2.63 | 3.68 | 1.63 | 1.00 | 0.06 | 0.8030 |
| 10 | −4 | 0.54 | 1.56 | 0.20 | 5.00 | 0.09 | 0.5492 |
| Mean±s.d. | −11 ± 4 | 1.54 ± 1.50 | 3.63 ± 1.51 | 0.11 ± 0.05 |
Emax: maximum theoretical effect, CE50: concentration of perindoprilat which induces an effect of 50% of Emax, γ: Hill coefficient, ke0: first order rate constant which governs the kinetics of the drug in the effect compartment, r2: determination coefficient. Baseline value of the variable of effect (E0) equal to 24 ± 3 mmHg.
Discussion
We have compared the PK parameters of perindopril and perindoprilat and the PD parameters of perindoprilat for biological and regional haemodynamic effects in HV and in CHF patients after single oral administrations of perindopril.
PK study
The parent drug and its metabolite displayed quite different kinetics in HV and in CHF patients and the kinetics of both compounds, following the administration of perindopril 4 mg, were also quite different between HV and CHF patients.
In CHF patients, the parent drug was more slowly absorbed (tmax at approximately 2 h vs 1 h) and more slowly metabolized (MRT and t½,z of about 7 and 4.5 h, respectively, vs 2 and 1 h, respectively) than in HV. The slowing down of the absorption of perindopril in CHF patients probably results from the strong decrease in hepatosplanchnic blood flow observed in these patients [17, 29]. Nevertheless, the combination of the effects of illness on absorption and metabolism resulted in no significant change in Cmax, as compared with HV. The AUC(0,72 h) of perindopril was strongly increased in CHF patients. Since the absolute bioavailability of the drug ranges between 66 and 95% [15] and even if one postulates a complete absorption in CHF patients, it can be concluded that the clearance of the parent drug was greatly decreased in these patients. This alteration, which can also partly result from the strong decrease of the hepatosplanchnic blood flow observed in these patients [17, 29], can explain the above-mentioned increases of MRT and t½,z. For the metabolite, the MRT and t½,z values (approximately 6.0 and 3.5 h, respectively) were strongly reduced as compared to corresponding values in HV (approximately 45 and 42 h, respectively). Since, in CHF patients, these two parameters tended to be below those computed for the parent drug, it can be hypothesized that the elimination of the metabolite was rate-limited by its formation and that the calculated t½,z corresponds in fact to the formation half-life of the metabolite (flip-flop phenomenon) [29]. In this context, that the Cmax and AUC(0,72 h) values of the metabolite in CHF patients were either greater (for the former) or at least as great (for the latter) than or as those observed in HV allows to hypothesize that the elimination half-life of the metabolite was, in CHF patients, at least as long as in HV.
PK-PD modelling
As expected, and although displaying similar relationships for PCEA blockade, HV and CHF patients show rather different relationships for regional haemodynamics.
The parameters of the perindoprilat PCEA blockade concentration-effect relationship were not significantly different between HV and CHF patients leading to almost identical relationships (Figure 1). Our CE50 and γ-values (1.87 ng ml−1 and 0.90 in HV and 1.36 ng ml−1 and 1.11 in CHF patients) were very similar to those reported in HV not only for perindoprilat (1.6 ng ml−1 and 0.8) [30], but also for other ACEIs like lisinopril (1.4 ng ml−1 and 0.6) [22] and zabiciprilat (2.2 ng ml−1 and 1.0) [31]. They seem to be a little below those reported in CHF patients for spiraprilat (3.9 ng ml−1 and 2.4) [12].
The CE50s of the perindoprilat haemodynamic concentration-effect relationships were significantly decreased in CHF patients as compared to HV (−72 and −58% for BVR and BAF, respectively). In addition, the Emax of the relationship on BVR was strongly increased in CHF patients thus resulting in very different relationships (Figure 2). Given the fact that the blood pressure profile during the daytime period (period of the haemodynamic investigation) did not vary under placebo in healthy volunteers [16] and most likely also in CHF patients (as demonstrated in a placebo-controlled study performed under the same conditions in this type of patients [32]), our findings strongly suggest that the vascular response to perindopril was enhanced in CHF patients. These modifications of the pharmacodynamics of perindoprilat, together with the modifications of the pharmacokinetics of both perindopril and perindoprilat discussed above, clearly explain why the dose of 4 mg was sufficient to induce maximal haemodynamic effects in CHF patients.
The CE50s of perindoprilat for haemodynamic variables displayed a great homogeneity within each group. Moreover, in HV, the CE50s of perindoprilat for haemodynamic effects (about 5 ng ml−1 for both BVR and BAF) were greater (by 2.5 fold) than that found for PCEA blockade. Similar findings have already been reported with lisinopril in HV [22]. They probably express that, in HV, saturation of tissue converting enzyme occurs for concentrations larger than those necessary for PCEA blockade, thus inducing further effects for greater concentrations. In CHF patients, in whom there is a strong stimulation of the renin-angiotensin-aldosterone system, a similar phenomenon does not seem to exist, the CE50s of perindoprilat for haemodynamic effects (about 1.4 ng ml−1 for both BVR and PCWP) being completely similar to that found for PCEA blockade.
Finally, whichever the variable considered, perindoprilat concentration-effect relationships displayed major hysteresis loops in CHF patients whereas they were always direct in HV. Moreover, within CHF patients, ke0 values displayed a great homogeneity. We have no explanation for the fact that no hysteresis loop was observed in HV. Indeed, hysteresis phenomenons have already been reported with perindoprilat in HV [30]. Since we observed such phenomena in CHF patients in whom the pharmacokinetics of perindopril and perindoprilat were delayed as compared with those observed in HV, it is unlikely that the lack of delay between the kinetics of perindoprilat and the kinetics of effects in HV could result from a limiting absorption step, as described for lisinopril [22]. Anyhow, in contrast with previous observations with zabiciprilat [31], these hysteresis phenomena probably correspond to true delays between the kinetics of perindoprilat and the kinetics of PCEA blockade since they induced in turn very similar phenomenons for each haemodynamic effect.
In conclusion, as expected, HV and CHF patients show major differences after perindopril administration not only in terms of pharmacokinetics but also in terms of haemodynamic pharmacodynamics. Since concentration-effect relationships for PCEA blockade were similar in the two groups of subjects, this result probably expresses the different involvements, in HV and CHF patients, of angiotensinergic and nonangiotensinergic mechanisms in the haemodynamic effects of ACEIs.
References
- 1.Kroboth PD, Schmith VD, Smith RB. Pharmacodynamic modelling. Application to new drug development. Clin Pharmacokinet. 1991;20:91–98. doi: 10.2165/00003088-199120020-00001. [DOI] [PubMed] [Google Scholar]
- 2.Peck CC, Barr WH, Benet LZ, et al. Opportunities for integration of pharmacokinetics, pharmacodynamics, and toxicokinetics in rational drug development. Clin Pharmacol Ther. 1992;51:465–473. doi: 10.1038/clpt.1992.47. [DOI] [PubMed] [Google Scholar]
- 3.Elliott HL, Donnelly R, Meredith PA, Reid JL. Predictability of antihypertensive responsiveness and α-adrenoceptor antagonism during prazosin treatment. Clin Pharmacol Ther. 1989;46:576–583. doi: 10.1038/clpt.1989.188. [DOI] [PubMed] [Google Scholar]
- 4.Donnelly R, Meredith PA, Elliott HL, Reid JL. Kinetic-dynamic relations and individual responses to enalapril. Hypertension. 1990;15:301–309. doi: 10.1161/01.hyp.15.3.301. [DOI] [PubMed] [Google Scholar]
- 5.Donnelly R, Meredith PA, Miller SHK, Howie CA, Elliott HL. Pharmacodynamic modeling of the antihypertensive response to amlodipine. Clin Pharmacol Ther. 1993;54:303–310. doi: 10.1038/clpt.1993.151. [DOI] [PubMed] [Google Scholar]
- 6.Meredith PA, Kelman AW, Elliott HL, Reid JL. Pharmacokinetic and pharmacodynamic modelling of trimazosin and its major metabolite. J Pharmacokinet Biopharm. 1983;11:323–335. doi: 10.1007/BF01058953. [DOI] [PubMed] [Google Scholar]
- 7.Kleinbloesem CH, Van Brummelen P, Van de Linde JA, Voogd PJ, Breimer DD. Nifedipine: kinetics and dynamics in healthy subjects. Clin Pharmacol Ther. 1984;35:742–749. doi: 10.1038/clpt.1984.105. [DOI] [PubMed] [Google Scholar]
- 8.Francis RJ, Brown AN, Kler L, et al. Pharmacokinetics of the converting enzyme inhibitor cilazapril in normal volunteers and the relationship to enzyme inhibition: development of a mathematical model. J Cardiovasc Pharmacol. 1987;9:32–38. [PubMed] [Google Scholar]
- 9.Thuillez C, Leroy JP, Loueslati H, Bellissant E, Giudicelli JF. Débits cardiaque et régionaux non invasifs chez le volontaire sain. Intérêt prédictif. Arch Mal Coeur. 1989;82:1275–1279. [PubMed] [Google Scholar]
- 10.Meredith PA, Elliott HL, Donnelly R, Reid JL. Dose–response clarification in early drug development. J Hypertens. 1991;9(Suppl6):S356–S357. [PubMed] [Google Scholar]
- 11.Dunselman PHJM, Edgar B, Scaf AHJ, et al. Plasma concentration-effect relationship of felodipine intravenously in patients with congestive heart failure. J Cardiovasc Pharmacol. 1989;14:438–443. doi: 10.1097/00005344-198909000-00013. [DOI] [PubMed] [Google Scholar]
- 12.Bellissant E, Chau NP, Thuillez C, Gerbeau C, Richard C, Giudicelli JF. Pharmacokinetic-pharmacodynamic model relating spiraprilat plasma concentrations to systemic and regional hemodynamic effects in congestive heart failure. J Cardiovasc Pharmacol. 1997;30:253–260. doi: 10.1097/00005344-199708000-00016. [DOI] [PubMed] [Google Scholar]
- 13.Kiowski W, Beermann J, Rickenbacher P, et al. Angiotensinergic versus nonangiotensinergic hemodynamic effects of converting enzyme inhibition in patients with chronic heart failure. Assessment by acute renin and converting enzyme inhibition. Circulation. 1994;90:2748–2756. doi: 10.1161/01.cir.90.6.2748. [DOI] [PubMed] [Google Scholar]
- 14.Kiowski W, Linder L, Kleinbloesem C, van Brummelen P, Bühler FR. Blood pressure control by the renin-angiotensin system in normotensive subjects. Assessment by angiotensin converting enzyme and renin inhibition. Circulation. 1992;85:1–8. doi: 10.1161/01.cir.85.1.1. [DOI] [PubMed] [Google Scholar]
- 15.Todd PA, Perindopril Fitton A. A review of its pharmacological properties and therapeutic use in cardiovascular disorders. Drugs. 1991;42:90–114. doi: 10.2165/00003495-199142010-00006. [DOI] [PubMed] [Google Scholar]
- 16.Richer C, Thuillez C, Giudicelli JF. Perindopril, converting enzyme blockade, and peripheral arterial hemodynamics in the healthy volunteer. J Cardiovasc Pharmacol. 1987;9:94–102. [PubMed] [Google Scholar]
- 17.Thuillez C, Richard C, Loueslati H, Auzepy P, Giudicelli JF. Systemic and regional hemodynamic effects of perindopril in congestive heart failure. J Cardiovasc Pharmacol. 1990;15:527–535. doi: 10.1097/00005344-199004000-00002. [DOI] [PubMed] [Google Scholar]
- 18.Safar ME, Peronneau PA, Levenson JA, Toto-Moukouo JA, Simon AC. Pulsed Doppler: diameter, blood flow velocity and volumic flow of the brachial artery in sustained essential hypertension. Circulation. 1981;63:393–400. doi: 10.1161/01.cir.63.2.393. [DOI] [PubMed] [Google Scholar]
- 19.Cushman DW, Cheung HS. Spectrophotometric assay and properties of the angiotensin-converting enzyme of rabbit lung. Biochem Pharmacol. 1971;20:1637–1648. doi: 10.1016/0006-2952(71)90292-9. [DOI] [PubMed] [Google Scholar]
- 20.Doucet L, De Veyrac B, Delaage M, Cailla H, Bernheim C, Devissaguet M. Radioimmunoassay of a new angiotensin-converting enzyme inhibitor (perindopril) in human plasma and urine: advantages of coupling anion-exchange column chromatography with radioimmunoassay. J Pharm Sci. 1990;79:741–745. doi: 10.1002/jps.2600790817. [DOI] [PubMed] [Google Scholar]
- 21.Bellissant E, Chau NP, Giudicelli JF. A computer program for kinetic-dynamic modeling in non steady-state experiments (Abstract) Clin Pharmacol Ther. 1996;59:147. [Google Scholar]
- 22.Bellissant E, Chau NP, Giudicelli JF. Pharmacokinetic-pharmacodynamic model relating lisinopril plasma concentrations to regional hemodynamic effects in healthy volunteers. J Cardiovasc Pharmacol. 1996;28:470–478. doi: 10.1097/00005344-199609000-00018. [DOI] [PubMed] [Google Scholar]
- 23.Bellissant E, Sébille V, Paintaud G. Methodological issues in pharmacokinetic-pharmacodynamic modelling. Clin Pharmacokinet. 1998;35:151–166. doi: 10.2165/00003088-199835020-00004. [DOI] [PubMed] [Google Scholar]
- 24.Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther. 1979;25:358–371. doi: 10.1002/cpt1979253358. [DOI] [PubMed] [Google Scholar]
- 25.Unadkat JD, Bartha F, Sheiner LB. Simultaneous modeling of pharmacokinetics and pharmacodynamics with nonparametric kinetic and dynamic models. Clin Pharmacol Ther. 1986;40:86–93. doi: 10.1038/clpt.1986.143. [DOI] [PubMed] [Google Scholar]
- 26.Fuseau E, Sheiner LB. Simultaneous modeling of pharmacokinetics and pharmacodynamics with a nonparametric pharmacodynamic model. Clin Pharmacol Ther. 1984;35:733–741. doi: 10.1038/clpt.1984.104. [DOI] [PubMed] [Google Scholar]
- 27.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical RecipesThe Art of Scientific Computing. Cambridge: Cambridge University Press; 1986. [Google Scholar]
- 28.Bellissant E, Giudicelli JF. Pharmacokinetic-pharmacodynamic model for fantofarone cardiac and brachial haemodynamic effects in healthy volunteers. Br J Clin Pharmacol. 1999;48:801–810. doi: 10.1046/j.1365-2125.1999.00091.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rowland M, Tozer TN. Concepts and applications. 2. Philadelphia: Lea & Febiger; 1989. Clinical pharmacokinetics. [Google Scholar]
- 30.Lees KR, Kelman AW, Reid JL. Effect of repeated dosing on concentration-effect relationships with the angiotensin converting enzyme inhibitor, perindopril (Abstract) Br J Clin Pharmacol. 1986;22:234P. [Google Scholar]
- 31.Bellissant E, Giudicelli JF. Pharmacokinetic-pharmacodynamic model relating zabiciprilat plasma concentrations to brachial and femoral haemodynamic effects in normotensive volunteers. Br J Clin Pharmacol. 1998;46:383–393. doi: 10.1046/j.1365-2125.1998.00786.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Annane D, Bellissant E, Pussard E, et al. Placebo-controlled, randomized, double-blind study of intravenous enalaprilat efficacy and safety in acute cardiogenic pulmonary edema. Circulation. 1996;94:1316–1324. doi: 10.1161/01.cir.94.6.1316. [DOI] [PubMed] [Google Scholar]