Learning from previous responses in phase I dose-escalation studies

Abstract

Dose escalation in phase I studies is generally performed on the basis of clinical experience and judgement. In this paper some of the statistical approaches that have been proposed for the formalization of the procedure are described. Apart from the use of the Continual Reassessment Method in oncology studies, such formal methods have received little implementation. The purpose of presenting them here is to promote their further exploration and appropriate implementation. Certain limitations are discussed, which will be best overcome by collaboration between clinical pharmacologists and statisticians.

Introduction

This is the last in a series of three papers on the use of interim analyses in clinical trials. In this series we have stepped backwards through the drug development process, starting with phase III [1] where sequential methods are now well established, followed by phase II [2] where interim analyses are becoming more formalized. This paper concerns phase I first-in-man studies, for which approaches are most naturally sequential and least formalized.

Phase III is the final and definitive stage of clinical drug development, and phase III trials are designed to establish the existence of drug efficacy with very little chance of error, and to quantify accurately its magnitude. The well-known statistical tools of significance testing, estimation and confidence intervals are appropriate for this purpose. But statistics includes other methods, more suited to the smaller scale world of phase II and phase I, for making decisions about the continuation of projects and about which actions to take next. Methods of decision theory have already been mentioned in this series in the context of phase II, and they are even more suitable for phase I.

Formal statistical methods for phase I trials have mostly been developed for oncology. In that context, the need for efficient and ethical trial design is particularly acute, and the stark nature of the adverse effects of treatment allows the application of simple statistical methods. Because most existing procedures have been developed within cancer treatment centres, these will inevitably be the focus of this paper. However, they should be seen as an illustration of what can be achieved, and are intended to stimulate the development of similar, but possibly more complex, approaches in other therapeutic areas. An example of application to healthy volunteer studies will be given.

Background

First-in-man studies generally share certain characteristics. A series of ascending dosing levels are identified in advance, with the lowest apparently very safe, as far as extrapolation from animal data can determine. A group of subjects (known as a cohort) is treated concurrently, and each member may receive just one dose, or else a dose in each of a series of consecutive treatment periods. Data from each cohort, or from each period within a cohort, are collected and assessed prior to choosing the next set of doses for administration. The objective is to escalate doses up a predetermined series until a dose level or range of dose levels is identified that is suitable for use in later trials. In all cases it is essential that the dose(s) chosen for further investigation be considered acceptably safe, and in certain cases therapeutic effect is also a consideration.

It can be seen that procedures used are inherently sequential. Data are collected and analysed, and then conclusions are drawn and decisions made about whether to continue the study, and if so which doses to administer next. This is a statistical procedure. However, in many cases the nature of this statistical procedure is not formalized: no equations are used and no probabilistic models are fitted. Instead, ‘clinical judgement’ is used to make sense of what has been observed and to determine what will happen next. Regardless of how it is described, this process of ‘data in–decision out’ should be subjected to evaluation and assessment according to statistical criteria.

The objective of phase I is to deliver the most promising treatments (in terms of safety and potential benefit) through to later clinical research phases without undue delay or expenditure, while treating the phase I subjects safely and respectfully. No formal statistical procedure can take full account of the quantity and complexity of the observations made on each subject. The statistical procedure indicates the optimal action based on a single primary response from each subject; often this is just a record of whether a certain adverse event occurred, YES or NO. Thus, statistical procedures are intended to be used as guidance and not as rigid rules: the recommendations might not be implemented if clinical judgement of the more complete picture indicates otherwise. An advantage of the newer procedures described in this paper is that they can learn from the responses of all subjects, whether or not they were dosed according to ‘the rules’. The flexible application of statistical procedures is appropriate in phase I, which is far removed from the formality and prespecification of phase III. Drugs going forward from phase I will have to pass through those more rigid procedures prior to being accepted.

Conventional approaches

The characteristics shared by first-in-man studies were described above. Within those common characteristics lies a diversity of procedures, governed mainly by the severity of the condition for which the treatment is intended. For many compounds it is anticipated that adverse events will be few, and phase I subjects will be healthy volunteers. Adverse events will be noted if they occur, but the principal observations of interest will be pharmacokinetic and pharmacodynamic endpoints. It will be of interest to monitor the former, as a precautionary measure, in order to ensure that plasma concentrations do not rise too high. Pharmacodynamic measures may also be monitored in order to avoid precursors of adverse events, and possibly to identify evidence of the intended physiological effect which has the potential to benefit patients. The healthy study volunteers may themselves be given more than one dose in separate sessions with intervening wash-out periods.

At the other end of the severity spectrum, oncology drugs will receive first human administration in late stage volunteer patients for whom other treatments have failed. Toxicity is usually anticipated, its risk being regarded as a necessary price to pay for the chance of benefit. Usually, the principal response of interest will be occurrence of toxicity, often graded on a four-point scale. A dose will be sought which is as large as possible while having an acceptable risk of toxicity. Sometimes, indications of benefit will also be available, although these may not be observed within the study duration. In the setting of oncology, each subject will normally receive only one study dose on one occasion.

Clinical pharmacologists seek a safe dose for future clinical trials. In phase I oncology studies, this is often interpreted as being the highest dose associated with no adverse outcomes, and is referred to as the ‘maximum tolerated dose’. However, the value of such a maximum tolerated dose depends in part on the sample size used in the trial, as the more subjects tested, the lower it is likely to be. In order to make progress with statistical formulation of the problem, it is necessary to move beyond the fiction of a perfectly safe dose, and to accept that the objective is to identify a dose which is ‘safe enough’. For statistical purposes a population characteristic must be sought, rather than a quantity calculated from the sample. Such a value might be the ‘toxic dose 20’ (TD₂₀), which is the dose for which the probability of toxicity is 0.20. Often the maximum tolerated dose identified in conventional procedures has a population risk of around this magnitude.

Conventional procedures tend to have formal rules concerning escalation following adverse events. A standard approach used in oncology, known as the ‘3 + 3’ design, is described by Carter [3] and Carter et al. [4], and is reviewed by Edler [5]. It proceeds as follows: starting at the lowest dose, cohorts of size three are treated and assessed. If no toxicity is observed, then the next cohort is treated at the next higher dose. Escalation continues in this way until toxicity is seen within a cohort. If toxicity is seen in two or three patients in the cohort, then the trial is terminated. If only one patient experiences the toxicity, then the dose is repeated for the next cohort: no further toxicity leads to resumption of dose-escalation, otherwise the trial is terminated. The dose below the highest administered is then declared the maximum tolerated dose. In a healthy volunteer scheme, described by Patterson et al. [6], the trial starts with a cohort of four subjects, three treated at the lowest dose and one on placebo. The same cohort participates in three more treatment periods, each individual receiving placebo (blindly) on one occasion, and otherwise receiving the first three doses of the series in ascending order. The next cohort is dosed in the same pattern, starting with repetition of the third dose. The scheme is illustrated in Figure 1, and is followed until excessive plasma concentrations are observed.

Figure 1.

A conventional dose-escalation scheme for healthy volunteer studies: arrangements for the first two cohorts.

The one formal statistical procedure that has already won a place in the conduct of phase I studies is the Continual Reassessment Method (CRM), introduced by O'Quigley et al. [7]. It was originally devised for dose-escalation in oncology, but it could be equally appropriate for application in other serious diseases. The original paper envisages a study in which volunteer patients are treated one at a time, in order to detect the TD₂₀, that is the dose associated with a probability 0.20 of toxicity. The response from each patient treated in the procedure consists of the binary record of ‘toxicity’ or ‘no toxicity’, where the definition of this dichotomy is left to the investigator. For example, ‘any toxicity of grade 2 or above’ might be chosen to be the more complete definition of a ‘toxicity’. It is supposed that the volunteer patient's best interest is served by administering a dose as close as possible to the TD₂₀: more would be too toxic, but less would carry too little chance of benefit.

Before beginning the study, investigators have to provide what they feel to be the most likely value of the probability of toxicity for each of the series of available doses. Although these pretrial guesses may well be quite inaccurate, they do offer initial guidance for the selection of doses. The first patient or cohort of patients is treated at the dose considered to be the best, that is the dose for which the probability of toxicity is closest to 0.20. Having observed whether toxicity has occurred, the most likely value of the probability of toxicity for each dose is recalculated, using the Bayesian method of statistics. The second patient or cohort of patients now receives the dose for which the probability of toxicity is now closest to 0.20. The procedure continues in this way until it settles on a single dose.

The CRM homes in on a single dose very quickly, and it is actually the dose closest to the TD₂₀ with high probability. This is quantified in simulations presented by O'Quigley et al. [7], and more extensively by O'Quigley & Shen [8]. As each case studied is different, it is not easy to summarize these tables. Here we consider only the results in the latter paper for the original (1990) CRM and for sample sizes of 25. The entries in Tables 3 and 4 of O'Quigley & Shen are wrongly labelled ‘% of recommendation’ in the legends, but correctly described as ‘percentages of in-trial allocation’ in the text. They show that, in the various situations simulated, between 28% and 54% of all subjects were allocated the dose closest to the TD₂₀, while fewer than 10% were allocated a dose equal to or exceeding the TD₅₀. Tables 1 and 2 show that between 40% and 73% of all simulated runs correctly identified the TD₂₀, while no more than 1% of runs actually recommended a dose equal to or exceeding the TD₅₀. O'Quigley & Shen do not include a systematic comparison with the 3 + 3 design, although direct comparisons in single runs indicate considerable advantages. An example of the CRM is given in Figure 2, where it is contrasted with the dose-escalation actually conducted, which was a rather loose interpretation of the 3 + 3 design.

Figure 2.

Ferry et al. [24] used conventional methodology to explore the relationship between the risk of renal toxicity (WHO grade 2 or above) and the dose of quercetin in patients with solid tumours at various sites. Doses of 60, 120, 200, 300, 420, 630, 945, 1400 and 1700 mg m⁻² were available, and the results are represented in (a). Each square represents a subject, plotted against dose and cohort number. Open squares represent subjects suffering no toxicity and solid squares those with toxicity. The method described in ‘Background’ has been applied, with some flexibility. Escalation was rather slow, with 18 subjects observed before toxicity was seen. In (b), the effect of retrospectively applying the CRM to these data is explored. It is imagined that, prior to starting the study, the probabilities of toxicity at each of the doses were 0.03, 0.05, 0.1, 0.02, 0.3, 0.4, 0.5, 0.65 and 0.75. The CRM proceeds by applying the dose currently believed to be the closest to the TD₂₀, to the next cohort of subjects, thus the first cohort receives the fourth dose: 300. The observation of no toxicity at this dose leads to a reassessment, with the conclusion that the sixth dose, 630, is closest to the TD₂₀. In this reconstruction, the data from the real cohorts treated at the recommended dose have been used as far as possible: circles represent ‘made up’ data. The imaginary procedure is terminated once the chosen dose has stabilised at 630. The figure demonstrates what is simultaneously the strength and weakness of the procedure. It jumps immediately to the dose 300, and then proceeds quickly to the doses 630 and 945. The latter doses were chosen by the conventional procedure as closest to the TD₂₀, but the CRM reaches them quickly by exposing early cohorts to high and potentially dangerous doses. The modified versions of the CRM cited in ‘Conventional approaches’ seek a compromise between the conventional approach and the CRM: the original CRM is shown here in order to dramatise the contrast between the approaches.

The predicted toxicity probabilities given by the CRM for doses that are not close to the TD₂₀ are generally inaccurate, but accuracy across the range of doses is not an objective of the method. It has one purpose alone – to find the TD₂₀ – and it achieves this with remarkable efficiency.

Since the appearance of the first paper describing the CRM, the procedure has been the focus of much interest and debate. Concern has been expressed about the objective of treating each subject with the dose believed at the time to be closest to the TD₂₀. Early in the study, when little is known about the nature of potential toxic reactions, the concern is not just about occurrence of a toxic reaction but also about its nature. Too high a dose may lead to severe or even lethal consequences, and so it is felt to be more appropriate to move cautiously upwards towards the TD₂₀, and to avoid erring too much on the high side. Authors such as Faries [9], Korn et al. [10] and Goodman et al. [11] have suggested modifications such as starting at the lowest dose, never skipping a dose during the escalation, and always choosing the highest dose below that which is currently believed to be the TD₂₀. With these modifications the CRM has been widely implemented. O'Quigley & Shen [8] have also suggested important modifications to the CRM, using a two stage procedure in which dose-escalation starts at the lowest dose and proceeds conventionally until the first toxicity is observed. Then the CRM is applied, but in a modified form which does not use the Bayesian method to update probabilities. O'Quigley [12] addresses many of these criticisms, and provides an up-to-date review of the methodology.

Bayesian decision procedures

Bayesian decision theory supplies a general framework for making decisions under uncertainty which can be applied in many scientific and business fields. The subject area is clearly introduced in the classic text by Lindley [13], and more recently in a book by Smith [14]. In order to use the approach, a model for the data to be observed must be specified, and prior opinion concerning unknown parameters of the model must be expressed. The decision to be made is which dose to administer to each subject in the next cohort, and this is to be done in a way that maximizes a predefined ‘gain function’ describing the gain made under every combination of parameter values and action.

The original CRM is a Bayesian decision procedure, although a specific form of prior opinion is imposed, rather than being elicited from investigators. The modified forms of CRM depart from pure Bayesian principles by imposing constraints on the actions allowed, and the method advocated by O'Quigley & Shen [8] abandons the Bayesian approach altogether.

The application of Bayesian decision theory to dose-finding has long been of interest to mathematical statisticians; Eichhorn & Zacks [15, 16] describe theory for the case in which patient responses are quantitative. Gatsonis and Greenhouse [17], Whitehead & Brunier [18], Whitehead [19], Whitehead & Williamson [20] and Babb et al. [21] have all considered the use of Bayesian decision theory to achieve the same goal as sought by the CRM. In each case, a simple model, which depends on two unknown parameters, is assumed to describe the way in which the risk of toxicity increases with dose. The elicitation and representation of prior information is considered, and its modification in the light of accumulating data described. Gatsonis & Greenhouse [17] show how the formal representation of opinion can be used to inform the choice of doses, whilst Whitehead and colleagues identify doses that will (according to specific criteria) optimize the outcome of the next subject or else maximize information gained about a parameter such as the TD₂₀.

Amongst the criteria considered by Whitehead & Williamson [20] is ‘the patient gain’, in which subjects are to be allocated doses as close to the TD₂₀ as possible: this is the same objective as the CRM. Figure 3 of Whitehead and Williamson presents the success of the Bayesian method in fulfilling that objective. Across the five situations investigated for sample sizes of 30, between 28% and 48% of all subjects were allocated the dose closest to the TD₂₀, while up to 6% received a dose in excess of the TD₅₀. These figures are similar to those achieved by the CRM (see Conventional approaches in this paper), but it must be emphasized that the sample sizes and detailed scenarios of the two sets of simulations differ. Whitehead & Williamson do not report percentages of correct recommendations, but instead display the accuracy of the final estimated TD₂₀.

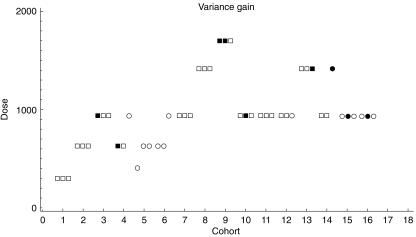
Figure 3.

This represents the application of a Bayesian decision procedure to the data of Ferry et al. [24] which also features in Figure 2. Once more each square represents a subject, plotted against dose and cohort number. Open squares represent subjects suffering no toxicity and solid squares those with toxicity. The criterion adopted was that each dose should be applied in order to maximise the information about the TD₂₀ learned from the cohort treated. This example was run long enough to provide sufficient data for illustration; in practice a stopping rule could be applied based on the precision with which the TD₂₀ is estimated. The criterion used in this example is known as the variance gain, and it does not include any constraint relating to the safety of the patient. Whilst such a procedure would clearly be unethical for implementation in cancer studies, there are two reasons for including it here. First, it emphasises the difference between this particular Bayesian decision procedure approach and the others. In particular, preference is for a wide range of doses to be tried, and members of the same cohort can be offered different doses. Second, while inappropriate for cancer studies, the method may be acceptable in milder conditions where the adverse events are irritating but volunteer subjects are willing to tolerate them for the advancement of science. Once the extremes of procedures are understood, investigators can work with statisticians to develop suitable compromises between them.

Figure 2 shows an example of a Bayesian decision procedure seeking to maximize information about the TD₂₀. Babb et al. [21] impose a safety constraint on a Bayesian decision procedure, thereby addressing the same concerns as are met through the modifications of the CRM.

Patterson et al. [6] and Whitehead et al. [22] describe an application to healthy volunteer studies of the type described in Background. Here a quantitative pharmacokinetic response such as log area-under-the-curve is related to log-dose through a linear regression model. As each subject is to be observed more than once, appropriate allowance has to be made for the correlation between each subject's responses. Prior information is elicited from investigators in a way that reflects their clinical opinion. The actions available consist of the dose combinations to administer to the current cohort of subjects in the current treatment period. Gain functions reflecting the increase in precision of regression coefficients can be used. The procedure learns from past observations on previous cohorts and from past observations on current patients. Thus, the dose for each subject will be individualized. A safety constraint, that the probability of AUC exceeding some limiting value should be controlled, is imposed.

The Bayesian methods described in this section are of recent origin, and have yet to be widely implemented in practice. When they are, it will be necessary to develop and modify them in order to meet practical needs. Indeed, it is likely that greatest success will follow from carefully tailoring the methods to individual trials. Practical problems will include departures from treatment schedules, the influence of baseline prognostic factors, delays in learning of response values and the need to model responses which are neither binary nor normally distributed. Such modifications should not be difficult conceptually, but will take time to develop and to incorporate into software. The case of bivariate responses, reflecting both toxicity and benefit, is also important. Thall & Russell [23] discuss this situation, and further approaches are currently being developed. Despite such generalizations, it has to be conceded that formal methods for dose-escalation will remain guidelines to support rather than to replace clinical decision making.

Discussion

Of the three phases of clinical research, interim analyses and sequential methodology are most used and least formalized in phase I. Any statistical procedure developed for use in phase I has to be sequential, for that is how data are collected and investigations are conducted. The purpose of this paper is to describe the range of statistical methods that are available and to promote the benefits that they might bring. It is necessary to emphasize that statistical methodology has more to offer than the rigid hypothesis testing and estimation procedures that are appropriate in the final analysis of a phase III trial.

Application of the new methods described in this paper will require informed clinical input in order to work, and sympathetic and patient consideration as they are first assessed retrospectively on old data sets in order to identify and remove undesirable features. Bayesian methods require formal specification of prior opinion, and it will take some experience to learn how to do this effectively. At first, runs with fictitious or simulated data will allow the consequences of various choices to be seen. If and when a satisfactory choice has been made, the procedure will make consistent and logical dose-escalations for any situation occurring in practice. With experience, users will learn to vary these preliminary settings, in order to allow escalation to be quicker or more cautious in particular trials.

One important topic has been neglected in this account, and that is the issue of stopping rules. Simple rules can be imposed: stop when a set number of subjects has been observed; stop when the recommended dose ceases to vary appreciably; stop when the Bayesian estimate of the appropriate dose becomes sufficiently accurate. Such rules will be suitable for a start. Once specific procedures for general use emerge, then a more formal evaluation of what rules are optimal can be made.

It has been the intention of this series of papers to promote the proper and appropriate use of interim analyses in all phases of clinical research. The authors believe that, if done wisely, this will contribute substantially to the goal of speeding up and making more efficient the process of clinical drug development. Meeting this goal depends most of all on effective collaboration between clinicians and statisticians in implementation of these procedures.