Skip to main content
PMC home page
British Journal of Clinical Pharmacology logoLink to British Journal of Clinical Pharmacology
. 1999 Jul;48(1):43–52. doi: 10.1046/j.1365-2125.1999.00974.x

Population pharmacokinetics of methadone in opiate users: characterization of time-dependent changes

Amin Rostami-Hodjegan 1, Kim Wolff 2,*, Alastair W M Hay 2, Duncan Raistrick 3, Robert Calvert 4, Geoffrey T Tucker 1
PMCID: PMC2014882  PMID: 10383559

Abstract

Aims

Although methadone is widely used to treat opiate dependence, guidelines for its dosage are poorly defined. There is increasing evidence to suggest that a strategy based on plasma drug monitoring may be useful to detect non-compliance. Therefore, we have developed a population-based pharmacokinetic (POP-PK) model that characterises adaptive changes in methadone kinetics.

Methods

Sparse plasma rac-methadone concentrations measured in 35 opiate-users were assessed using the P-Pharm software. The final structural model comprised a biexponential function with first-order input and allowance for time-dependent change in both clearance (CL) and initial volume of distribution (V). Values of these parameters were allowed to increase or decrease exponentially to an asymptotic value.

Results

Increase in individual values of CL and increase or decrease in individual values of V with time was observed in applying the model to the experimental data.

Conclusions

A time-dependent increase in the clearance of methadone is consistent with auto-induction of CYP3A4, the enzyme responsible for much of the metabolism of the drug. The changes in V with time might reflect both up- and down-regulation of α1-acid glycoprotein, the major plasma binding site for methadone. By accounting for adaptive kinetic changes, the POP-PK model provides an improved basis for forecasting plasma methadone concentrations to predict and adjust dosage of the drug and to monitor compliance in opiate-users on maintenance treatment.

Keywords: methadone, CYP3A4, enzyme induction, population kinetics, compliance

Introduction

Although methadone is widely used to treat opiate dependence in the US, Australia and much of Europe, guidelines for its optimal dosage are poorly defined. However, there is increasing evidence to suggest that a strategy based upon the monitoring of plasma drug concentrations may be useful in this respect [1–6]. This is reinforced by a better understanding of the influence of incomplete compliance with dosage [1, 7], the effects of supplementation of dosage with illicit methadone [7], the role of variable metabolism of the drug and metabolic interactions [5, 8–10], and of adaptive changes in its kinetics[4, 11–13].

We have previously used the population model approach in an attempt to define the single-dose kinetics of methadone in opiate users by augmenting the more limited data (0–27 h sampling) obtainable from such individuals with a richer data set from normal subjects (0–57 h sampling) [14]. Although it was possible to demonstrate that the kinetics of methadone were different in the two groups of subjects, the study indicated that an accurate description of the time-course of plasma drug concentrations in opiate-users would require an extended sampling period and data from both single and continuous dosage. Thus, the current investigation extends our single-dose study in opiate users (0–27 h) to include data obtained after multiple doses (0–37 days). The population kinetic analysis now combines single dose (17 subjects) and steady-state (19 subjects) data together with regularly measured trough plasma methadone concentrations (7 subjects), and accommodates adaptive changes in kinetics during the course of treatment. Hence, this refined model provides a more accurate basis for population-based forecasting methods to predict and adjust the dosage of methadone in opiate users on maintenance treatment.

Methods

Subjects and protocols

A total of 35 opiate users was studied after monitoring for signs of opiate withdrawal using the Symptom Severity Assessment (SSA) chart [15], and before commencing methadone maintenance treatment. They were grouped according to three different protocols (G1, G2 and G3) and combinations thereof. Demographic characteristics and a brief description of each protocol are given in table 1. The mean initial daily dose of rac-methadone HCl was 39±16 s.d. mg (range 5–80 mg), given as Drug Tariff Formula (DTF) mixture; the mean final maintenance dose was 40±17 s.d. mg (range 5–80 mg). In protocols G1 and G2 oral intake of the drug was witnessed daily in the morning. A week’s supply of methadone was dispensed to the subjects in protocol G3. They were instructed to take one dose every morning, rinsing the container and swallowing the residue. One subject reported that, on one occasion, he took two doses together and missed the next day’s dose. Another subject indicated that he divided the daily dose, taking half in the morning and half in the afternoon. It was assumed that the other subjects adhered to the daily dosage regimen.

Table 1.

Demographic characteristics of subjects and description of protocols.

graphic file with name bcp0048-0043-t1.jpg

Open in a new tab

In protocol G1 6–10 plasma drug concentrations were measured up to 27 h after a single dose of methadone in 17 subjects. One to two 24 h concentration-time profiles (4–37 samples) were measured during days 6–37 of multiple dosing in 19 subjects in protocol G2. Of these individuals, eight were also included in G1 since they provided first dose profiles as well as data at steady-state.

Protocol G3 was designed to overcome shortcomings noted during the analysis of the G1 data set with respect to evaluation of the terminal elimination half-life [14] which in turn could prevent full characterisation of methadone accumulation. Trough plasma drug concentrations were measured daily from day 2 to days 18–30 of treatment. Plasma concentrations of α1-acid glycoprotein were measured in serial trough samples from all G3 patients.

A total of 501 plasma concentration measurements, combined from all of the protocols, was used in the POP-PK analysis.

Sample collection

Pre-dose and trough blood samples were drawn by venepuncture; a butterfly cannula was placed in a forearm vein to obtain samples during more intensive study periods (Protocols G1 and G2). All samples (10ml) were collected in heparinised Monovette collection tubes (Sarsted, Leicester UK). After centrifugation of the blood for 5 min (1000 g) the plasma was transferred to polypropylene tubes and stored at −20°C until assay. Pre-dose urine samples (20 ml) were also collected on every visit for routine drug screening purposes and their pH was measured.

Analytical methods

Plasma (2 ml) was assayed for methadone by liquid chromatography as described previously [14]. The between- and within-day coefficient of variation of the assay at a methadone concentration of 100 ng ml−1 (and 5 ng ml−1) were 9.5% and 3.5% (9.8% and 7.2%), respectively (n = 10). Urine samples were screened for common drugs of abuse including opiates, cocaine, cannabinoids, benzodiazepines and amphetamines using an automated enzyme immunoassay (EMIT, Syva, Berkshire UK). Plasma concentrations of α1-acid glycoprotein were measured using an antibody reaction and nephelometry (Behring Diagnostics, Frankfurt). The reference range was 0.5–1.2 g l−1 of α1-acid glycoprotein and the CV of the assay was 15% at a concentration of 0.77 g l−1.

Data analysis

As there were insufficient measurements in each subject to obtain estimates of individual PK parameters for methadone by classical analysis, the population approach was applied using the P-Pharm software package (Version 1.4, SIMED, Creteil, France) run on a PC with a Pentium-90 processor. The algorithm in P-Pharm is Bayesian in nature and is described as being of the two-stage expectation-maximisation (EM) type [16] that was introduced for analysing incomplete data in the late 1970s [17]. Nevertheless, some consider the P-Pharm algorithm to be more like the iterative two-stage procedure proposed by Prévost [18].

The time-course of plasma methadone was described by a bi-exponential disposition function with first-order input since we had previously reported that this was superior to a structural model incorporating mono-exponential disposition [14]. The population model was the same as that described in our previous report [14] except that a log-normal rather than a normal distribution was assumed for all population pharmacokinetic parameters. The Kolmogorov-Smirnov test (embedded in P-Pharm) rejected normal distribution of the same parameters with the present data set. Parameter estimates for individual subjects were obtained by the maximum a posteriori probability (MAP) Bayesian fitting procedure within P-Pharm. In all analyses oral clearance (CL/F), central volume of distribution (V/F), the transfer rate constants between central and peripheral compartments (k12, k21), the apparent absorption rate constant (ka) and the absorption lag time (tlag) were considered as primary parameters. Thus, a population geometric mean value and an estimate of its variability were obtained for each parameter. The terminal elimination half-life (t1/2,z) was considered as a secondary parameter. In this case, different population values could be calculated depending upon the approach used [14]. Here, we report only the approximate estimates of half-life and its variance obtained using individual values of kinetic parameters determined by the MAP Bayesian fitting procedure. Age, sex, weight, methadone dose and urine pH were investigated as covariates for CL (initial and steady-state) and V (initial and steady-state).

The data from each protocol were analysed both separately and grouped. Pharmacokinetic parameters derived from the steady-state data (19 G2 subjects—excluding data from the first dose—plus 7 G3 subjects—excluding data prior to 120 h) were compared with those estimated from first dose (17 G1 subjects) using the Z-test.

For those individuals in whom it was possible to define values of kinetic parameters by the MAP Bayesian fitting after their first dose of methadone and at steady-state (the eight subjects overlapping G1 and G2 protocols), a paired t-test was used to compare parameters. In addition, superimposition of predicted and observed profiles (steady-state from first dose and vice versa) was examined in these subjects. Finally, all data (35 subjects) were analysed together.

To investigate time-dependency in the values of pharmacokinetic parameters, the pooled data (G1+G2+G3) were re-analysed after splitting them according to the time that blood sampling occurred after the first methadone dose. Therefore, the data from the 35 subjects were treated as if they effectively represented 58 subjects. Time bin (TB) was introduced as a new covariate, taking one of three values in each effective subject (I = 0–120 h; II = 120–300 h; III≥300 h). The statistical significance of adding this co-variate was investigated using stepwise multiple regression, as implemented in P-Pharm, and an appropriate F value (α = 0.05).

Having detected time-dependency using TB as a covariate, the phenomenon was then incorporated into the structural model. Thus, auto-induction of metabolism was accommodated by allowing the initial value of clearance (CL(0)) to increase mono-exponentially to an asymptotic value (CL(ss)), as described by Levy et al. [19] (Equation 1, where kI is an induction rate constant).

graphic file with name bcp0048-0043-m1.jpg (1)

Although Equation 1 defines an induction process, in practice, the value of CL could also decrease since CL(ss) was allowed to take values greater or less than CL(0). Absolute values of systemic clearance (CL) are indeterminant from oral data alone since systemic availability (F) is also a variable. Therefore, in order to implement Equation 1, the value of F was arbitrarily set to 1 (experimentally determined values range from 0.79 to 0.95 [11, 20], and clearance was reported as the hybrid term CL/F.

However, it was still possible to assess relative change in CL under the assumption of constant F. Since the systemic clearance of methadone is reported to be much lower than hepatic blood flow [11, 20], any time-dependent change in F was considered likely to have relatively little effect on plasma drug concentrations compared with a similar change in systemic clearance. Thus, for a low extraction drug such as methadone [21] a large change in first-pass metabolism would be reflected in a much smaller change in systemic availability. Nevertheless, in the absence of data to allow characterisation of the drug elimination rate (i.e. when only single trough concentrations are available) any change in CL would have the same effects as F, but in the opposite direction. Change in CL and F are distinguishable only when multiple samples are taken (as in protocol G2) since a change in CL will influence the elimination rate but a change in F will not. Therefore, time-dependent change in F as an alternative to and in addition to that in CL was investigated using a function analogous to Equation 1. Similarly, the influence of a time-dependent change in V was assessed, alone and in combination with changes in CL and F. The values of the rate constants defining the changes in CL, V and F with time were allowed to vary independently.

Results

Model building

First-dose (G1) vs steady-state (G2+G3) data

The population mean value of CL/F was significantly lower (P<0.05) in subjects at the start of methadone treatment (G1) than in those at steady state (G2+G3). This change in clearance was also confirmed by an increase (P<0.0001) in the a posteriori estimate of this parameter from first dose to steady-state in the eight subjects included in both G1 and G2 protocols. In addition, these subjects showed mean decreases in V/F (P<0.03) and ka (P<0.02) and a decrease in terminal elimination half-life (P<0.0001). Accordingly, their full multiple dose plasma drug concentration-time profiles were not super-imposable whether predicted from the initial first dose or from steady-state data (Figure 1).

Figure 1.

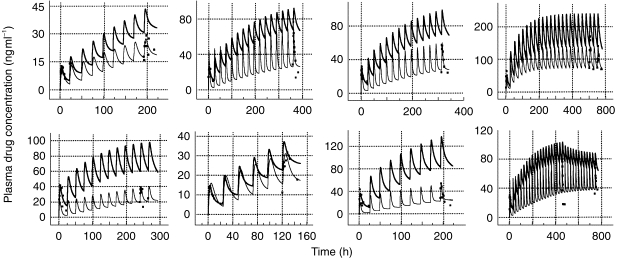
Figure 1

Open in a new tab

Predictions of plasma methadone concentrations during continuous drug administration from single dose (thicker line) or late dose (thinner line) data. Experimental data are normalised for a dose of 10 mg methadone HCl and indicated by ▪.

Pooled data (G1+G2+G3)

Ignoring any time dependent changes, the overall mean population values were 8.79 l h−1 (147 ml min−1) for CL/F and 153 l for V/F; the estimate of the mean terminal elimination half-life was 35 h. Covariate analysis indicated that CL/F was inversely related to urine pH (Equation 2), although it explained only 27% of the variance:

graphic file with name bcp0048-0043-m2.jpg (2)

Female opiate users had higher values of V/F and this parameter was directly related to weight. Sex and weight (Equation 3) together explained 33% of the variance in V/F:

graphic file with name bcp0048-0043-m3.jpg (3)

Time as a covariate

The covariate designated TB (i.e. time bin I =0–120 h; II =120–300 h; III≥300 h) was found to be a significant determinant of CL (P<0.007; coefficient of TB = 1.06). Thus, assuming that all other parameters remained constant, CL increased by 1.06 l h−1 for each successive time category (I–III). This trend for a time-dependent increase in CL was also apparent on visual inspection of pooled data (not shown), despite the fact that the time categories included different subjects. Profiles in those individuals with data in 2–3 of the time categories show this change more clearly (Figure 2).

Figure 2.

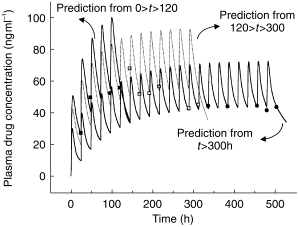
Figure 2

Open in a new tab

Model fits (lines) to plasma methadone concentrations (data points) in a representative individual according to the time bin (TB) used (▪ TB I = 0–120 h; □ TB II = 120–300 h; • TB III≥300 h). Experimental data are normalised for a daily dose of 10 mg methadone HCl.

The final model

Incorporation of adaptive kinetics into the population model

Addition of the parameters CL(ss) and kI, defining auto-induction of methadone metabolism, to the original model improved its ability to predict the experimental data, as indicated by maximum likelihood (-LL) and the Akaike Information Criterion (AIC) [22] (table 2). The residual sum of squares was reduced from 2.825×104 to 2.445×104 (P=0.02, F test).

Table 2.

Maximum likelihood (LL) and AIC values for various models used to describe the kinetics of methadone.*

graphic file with name bcp0048-0043-t2.jpg

Open in a new tab

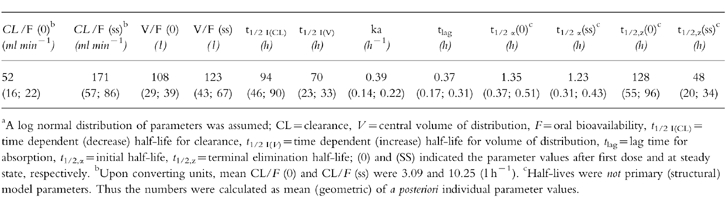
The revised model was considerably better at fitting plasma drug concentrations in those individuals with both single dose and steady-state profiles, predicting the trend for trough concentrations to increase and then decrease with time to a steady value during constant daily dosing (Figure 3). Nevertheless, the fits to some individual data were still not satisfactory with respect to capturing the degree of oscillation of the plasma drug concentration at steady state (figure 4b). A greater swing between maximum and minimum plasma drug concentrations at steady-state than predicted from single dose data is indicative of a decrease in distribution volume. Alternative models incorporating time-dependence in V without change in CL and time-dependence in F with and without change in CL and/or V were investigated but produced inferior fits to those obtained using a time-dependent clearance. However, incorporation of time-dependence in both CL and V (constant F) not only improved the general fit significantly (table 2), but described the larger than expected swings seen in some of the steady-state data (figure 4c). Addition of a lag time for induction did not produce any further improvement (table 2). Thus, the final model incorporated adaptive changes in both the clearance and the distribution of methadone. The residual sum of squares was reduced from 2.445×104 to 1.768×104 (P = 0.01, F test) by using this model. Values of the PK parameters for the model are reported in table 3. The changes in CL and V commenced immediately after the first exposure to the drug and were characterised by different and highly variable half-lives ( population geometric mean 120 h (range 34–600 h) for CL change and population geometric mean 65 h (range 51–86 h) for V change).

Figure 3.

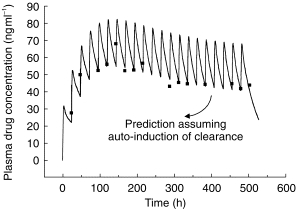
Figure 3

Open in a new tab

Fit (line) of model incorporating time-dependent clearance to plasma methadone concentrations (▪) in a representative subject. Experimental data are from the same subject as shown in Figure 2.

Figure 4.

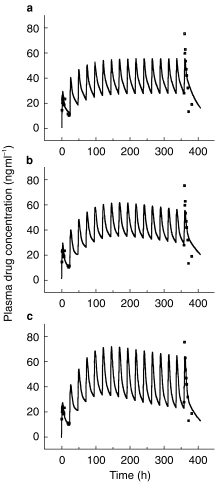
Figure 4

Open in a new tab

Model fits to the same individual data set: (a) simple two compartment model, (b) as (a) but with time-dependent clearance, and (c) as (a) but with time-dependent clearance and volume of distribution (experimental data are normalised for a daily dose of 10 mg methadone HCl).

Table 3.

Values of population pharmacokinetic parameters (mean (±s.d.) describing the time-dependent kinetics of methadone.a

graphic file with name bcp0048-0043-t3.jpg

Open in a new tab

Our model of time dependency assumed that the magnitude of changes in time variant parameters (such as CL) were the same regardless of the concentration of methadone. To test whether subjects on higher doses of methadone showed greater induction, the individual dose of methadone was investigated as a covariate for changes in clearance and volume of distribution. Despite the wide ranges of doses among the subjects, no relationship with the magnitude of induction was detected. In contrast to the time-invariant model, none of the covariates (weight, sex, pH, dose) influenced variation in CL or V significantly.

A comparison of individual changes in CL/F, V/F and t1/2,z with values obtained from analysis of the data using the model that assumed no time dependency are shown in Figure 5. The average increase in CL/F from the first dose of methadone to steady state was about 3.5 fold whereas, the average increase in V/F was only about 1.1 fold. Some subjects (as discussed previously) showed a marked decrease in V with time. These various changes were accompanied by a decrease in the mean terminal elimination half-life from 128 h to 48 h.

Figure 5.

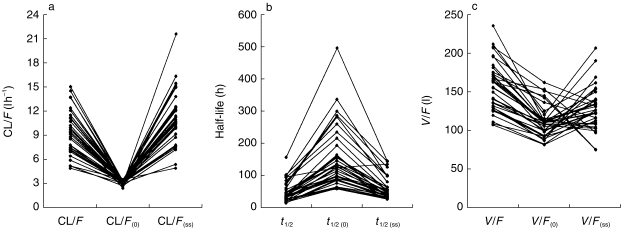
Figure 5

Open in a new tab

Individual estimates of (a) oral clearance, (b) terminal elimination half-life, and (c) volume of distribution obtained using a simple two compartment model (no time dependency in any PK parameter) and on incorporating time-dependence in clearance and distribution ((0) signifies first dose value; (ss) signifies values at steady state).

The mean value of plasma α1-acid glycoprotein concentration measured in the subjects of protocol G3 did not change significantly over time, although individuals showed both decreases and increases from the normal range (0.5–1.2 g l−1) (Figure 6).

Figure 6.

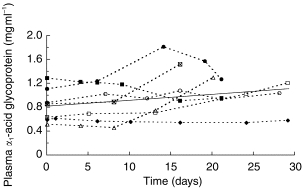
Figure 6

Open in a new tab

Plasma α1-acid glycoprotein concentrations in subjects taking part in protocol G3. Solid line indicates the best regression fit (r2 = 0.054; P=0.17).

Discussion

It has been suggested previously that the kinetics of methadone undergo adaptive changes during repeated administration of the drug. These changes have been variously attributed to an increase in clearance [4, 11–13] or volume of distribution, or to a decrease in systemic availability [11]. We have confirmed a time-dependence in the kinetics of methadone and have described it quantitatively with a kinetic model incorporating progressive changes in clearance and distribution of the drug. The mechanisms of these changes are unknown. However, since the metabolism of methadone has been shown in vitro to be mediated largely by CYP3A4 [8, 9, 23], an inducible enzyme, auto-induction of metabolism may be responsible for the increase in CL with time. Marked increases in the maintenance dosage requirements for methadone in patients receiving rifampicin, a known inducer of CYP3A4, have been documented [24, 25].

A time-dependent decrease in the plasma concentrations of carbamazepine during continuous dosage is well-documented and this compound is also a substrate for CYP3A4 [26]. Thus, a model incorporating enzyme turnover [27] to account for the auto-induction of carbamazepine [28] was used to describe our methadone data. The model has been applied previously to account for both hetero- and auto-induction with respect to several drugs using classical pharmacokinetic analysis [19, 27, 29–31]. Hussain & Posner [32] have also used a similar approach in a population kinetic analysis of lamotrigine, which appears to induce its own glucuronidation to a small extent [33]. In the analysis of Hussain & Posner [32], the data were not stratified by time bin as an intermediate step in model building since their subjects had a wide variation in exposure to lamotrigine over time. Hence, exposure time from the start of therapy was examined as a covariate affecting clearance.

Drugs inducing the same enzyme should exhibit the same induction half-life since the induction half-life is related to turn-over of the enzyme. However, the time to reach the final steady-state of drug concentrations depends on the relative values of the rate constants for enzyme turnover and for elimination of the inducer [34]. Our mean value of 94 h (range 62–205 h) for the auto-induction half-life of methadone compares with similar values reported for the auto-induction of carbamazepine (mean value 106 h; range 53–282 h [19]), the induction of clonazepam (mean value 72 h; range 20–146 h, [29]) and ethosuximide (range 85–806 h [27]) by carbamazepine, and the induction of nortriptyline (mean value 140 h; range 48–284 h, [31]) by pentobarbitone. Data for the auto-induction of ifosfamide and cyclophosfamide, also substrates of CYP3A4, indicate shorter mean induction half-lives (9–10 h; range 2–158 h) [30]. In part, the differences between induction half-lives for the various substrates and their wide individual variation could reflect the influence of co-induction of other cytochromes P450 with different turnover times. Methadone, for example, is metabolised by both CYP3A4 and, to a lesser extent, CYP1A2 [8]. Application of a model incorporating differential rates of induction would require a bi-exponential function analogous to Equation 1 and more intensive plasma sampling during the induction phase.

Most of the pharmacological effects of rac-methadone seem to reside in the R-isomer [35, 36]. Differences in the kinetics of the isomers have been reported, albeit with some disagreement as to their magnitude and direction [4, 36–40]. However, since CYP3A4 is the main enzyme responsible for the metabolism of both isomers [23], it is unlikely that their metabolism undergoes a differential degree of induction. Indeed, Eap et al. [23], despite observing wide inter-individual variation of R/S ratios, did not show any significant change in the intra-individual plasma R/S methadone concentration ratio during continuous treatment with the racemate.

The changes in V with time supported by our final kinetic model are more difficult to account for than the increase in clearance. One hypotheses in this regard relates to changes in plasma protein binding. It has been shown that inducers of CYP3A4 such as phenobarbitone and rifampicin are also capable of up-regulating the production of α1-acid glycoprotein and hence increasing the plasma binding of basic drugs [41, 42]. Since methadone appears to induce CYP3A4 and it is highly bound to α1-acid glycoprotein [43], its administration could cause a time-dependent decrease in its own volume of distribution. A time-dependent decrease in V in 12 of our subjects was consistent with this phenomenon. On the other hand, a mechanism whereby plasma binding might decrease, causing the volume of distribution of methadone to increase with time, as indicated in some of our other subjects, can also be postulated. Thus, heroin addicts who show objective signs of opiate withdrawal tend to have elevated plasma levels of α1-acid glycoprotein and increased ex vivo plasma binding of methadone compared with normal subjects [44]. Similarly, increased plasma binding of methadone has been observed in rats with withdrawal effects immediately after chronic heroin administration [45]. Hence, it may be postulated that substitution of heroin with methadone and suppression of opiate withdrawal symptoms is accompanied by a decrease in the level of α1-acid glycoprotein and of methadone binding. Thus, the net effect of an increase in plasma drug binding, due to induction of the protein, and a decrease, due to alleviation of stressful withdrawal symptoms, on the direction of any change in the volume of distribution of methadone may be difficult to predict in individual subjects. This would be consistent with the lower mean increase in V/F (1.1 fold) compared with the mean increase in CL/F (3.5 fold) observed in our subjects (Figure 5), and the failure to find any consistent alteration of α1-acid glycoprotein levels in the seven subjects in whom the protein was monitored (Figure 6). Another complication with respect to interpreting changes in V is a gradual alteration in the body composition of opiate users during therapy with methadone due to improvement in overall health[46].

There has been considerable difficulty in assigning a value to the terminal elimination half-life of methadone owing to model mis-specification and the use of limited sampling times [14]. The present analysis suggests another reason arising from the time-dependence of CL and V . Time-dependence in these determinants may either work together to maintain the value of the half-life or, if they are not co-regulated, to increase or decrease it. This is in agreement with early observations of Kreek et al. [24] showing that while rifampicin increased the oral clearance of methadone, this was not always accompanied by a decrease in its elimination half-life. However, in most of our subjects we observed a marked decrease in t1/2,z with time (Figure 5).

In conclusion, we have developed a population based pharmacokinetic model for methadone in opiate users on maintenance treatment that takes account of adaptive changes in the fate of the drug. Further refinements that need exploration include allowance for individual differences in plasma drug binding [44, 47–49] and stereoselectivity in the kinetics of methadone enantiomers [4, 40]. Nevertheless, it is anticipated that the present model will be useful in association with plasma drug concentration monitoring and Bayesian forecasting to optimise methadone dosage, to detect incomplete compliance and illicit methadone ingestion, and to rationalise methadone detoxification regimens using opioid antagonists.

Acknowledgments

The assistance of Jean Higginson, Department of Clinical Pathology and Immunology, Leeds General Infirmary in assaying α1-acid glycoprotein is gratefully acknowledged. We also thank Roberto Gomeni and Philip Michon for their help in implementing the time-dependency model in P-Pharm.

References

  • 1.Wolff K, Hay AWM. Plasma methadone monitoring with methadone maintenance treatment. Drug Alcohol Dependence. 1994;36:69–71. doi: 10.1016/0376-8716(94)90012-4. [DOI] [PubMed] [Google Scholar]
  • 2.Nilsson MI, Gronbladh L, Wilderlov E, Anggard E. Pharmacokinetics of methadone in methadone maintenance treatment: Characterisation of therapeutic failures. Eur J Clin Pharmacol. 1983;25:497–501. doi: 10.1007/BF00542117. [DOI] [PubMed] [Google Scholar]
  • 3.Loimer N, Schmid R. The use of plasma levels to optimise methadone maintenance treatment. Drug Alcohol Dependence. 1992;30:241–246. doi: 10.1016/0376-8716(92)90058-k. [DOI] [PubMed] [Google Scholar]
  • 4.Eap CB, Finkbeiner T, Gastpar M, Scherbaum N, Powell K, Baumann P. Replacement of (R)-methadone by a double dose of (R, S)-methadone in addicts: Inter-individual variability of the (R)/(S) ratios and evidence of adaptive changes in methadone pharmacokinetics. Eur J Clin Pharmacol. 1996;50:385–389. doi: 10.1007/s002280050128. [DOI] [PubMed] [Google Scholar]
  • 5.De Vos JW, Ufkes JGR, Van Brussel GHA, Van Den Brink W. Craving despite extremely high methadone dose. Drug Alcohol Dependence. 1996;40:181–184. doi: 10.1016/0376-8716(95)01207-9. [DOI] [PubMed] [Google Scholar]
  • 6.Menelaou A, Dyer KR, White JM, Somogyi AA, Foster DJR, Bochner F. Methadone disposition and plasma concentration-effect relationships in a methadone maintenance program. Proc Austral Soc Exp Pharmacol Toxicol. 1995;2:112. [Google Scholar]
  • 7.Wolff K, Hay A, Raistrick D, Calvert R, Feely M. Measuring compliance in methadone maintenance patients: Use of a pharmacologic indicator to ‘estimate’ methadone plasma levels. Clin Pharmacol Ther. 1991;50:199–207. doi: 10.1038/clpt.1991.125. [DOI] [PubMed] [Google Scholar]
  • 8.Iribane C, Berthou F, Baird S, et al. Involvement of cytochrome P450 3A4 enzyme in the N-demethylation of methadone in human liver microsomes. Chem Res Toxicol. 1996;9:365–373. doi: 10.1021/tx950116m. [DOI] [PubMed] [Google Scholar]
  • 9.Moody DE, Alburges ME, Parker RJ, Collins JM, Strong JM. The involvement of cytochrome P450 3A4 in the N-demethylation of L-α-acetylmethadol (LAAM), norlaam, and methadone. Drug Metab Dispos. 1997;25:1347–1353. [PubMed] [Google Scholar]
  • 10.Schall U, Pries E, Katta T, Kloppel A, Gastpar M. Pharmacokinetic and pharmacodynamic interactions in outpatient maintenance therapy of intravenous heroin users with levomethadone. Addiction Biol. 1996;1:105–113. doi: 10.1080/1355621961000124736. [DOI] [PubMed] [Google Scholar]
  • 11.Nilsson MI, Anggard E, Holmstrand J, Gunne LM. Pharmacokinetics of methadone during maintenance treatment: Adaptive changes during the inductive phase. Eur J Clin Pharmacol. 1982;22:343–349. doi: 10.1007/BF00548404. [DOI] [PubMed] [Google Scholar]
  • 12.Verebely K, Volavka J, Mulé S, Resnick R. Methadone in man: pharmacokinetic and excretion studies in acute and chronic treatment. Clin Pharmacol Ther. 1975;18:180–190. doi: 10.1002/cpt1975182180. [DOI] [PubMed] [Google Scholar]
  • 13.Anggard E, Gunne LM, Holmstrand J, McMahon RE, Sandberg CG, Sullivan HR. Disposition of methadone in methadone maintenance. Clin Pharmacol Ther. 1975;17:258–266. doi: 10.1002/cpt1975173258. [DOI] [PubMed] [Google Scholar]
  • 14.Wolff K, Rostami-Hodjegan A, Shires S, et al. The pharmacokinetics of methadone in healthy volunteers and opiate users. Br J Clin Pharmacol. 1997;44:385–392. doi: 10.1046/j.1365-2125.1997.t01-1-00591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Leeds Addiction Unit and Northern Regional Drugs and Alcohol Service, Newcastle. Opioid Symptom Severity Assessment (SSA) Chart. 1991 [Google Scholar]
  • 16.Mentré F, Gomeni G. A two step iterative algorithm for estimation in nonlinear mixed effect models with an evaluation in population pharmacokinetics. J Biopharm Stat. 1995;5:141–158. doi: 10.1080/10543409508835104. [DOI] [PubMed] [Google Scholar]
  • 17.Dampster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J Roy Stat Soc B. 1977;39:1–38. [Google Scholar]
  • 18.Bennet JE, Wakefield JC. A comparison of the Bayesian population method with two other methods as implemented in commercially available software. J Pharmacokinet Biopharm. 1996;24:403–432. doi: 10.1007/BF02353520. [DOI] [PubMed] [Google Scholar]
  • 19.Levy RH, Pitlick WH, Troupin AS, Green JR. Pharmacokinetic interactions of chronic drug treatment in epilepsy: carbamazepine. In: Benet L, editor. In The Effects of Disease State on Drug Pharmacokinetics. Washington DC: Academy of Pharmaceutical Sciences; 1976. pp. 87–95. [Google Scholar]
  • 20.Meresaar U, Nilsson MI, Holmstrand J, Anggard E. Single dose pharmacokinetics and bioavailability of methadone in man studied with a stable isotope method. Eur J Clin Pharmacol. 1981;20:473–478. doi: 10.1007/BF00542102. [DOI] [PubMed] [Google Scholar]
  • 21.Inturrisi CE, Colburn WA. Pharmacokinetics of methadone. In: Foley KM, Inturrisi CE, editors. In Advances in Pain Research and Therapy. New York: Raven Press; 1986. pp. 191–199. [Google Scholar]
  • 22.Yamaoka K, Nakagawa T, Uno T. Application of Akaike’s information criteria (AIC) in the evaluation of linear pharmacokinetic equations. J Pharmacokin Biopharm. 1976;6:165–165. doi: 10.1007/BF01117450. [DOI] [PubMed] [Google Scholar]
  • 23.Eap CB, Bertschy G, Powell K, Baumann P. Fluvoxamine and fluoxetine do not interact in the same way with the metabolism of the enantiomers of methadone. J Clin Psychopharmacol. 1997;17:113–117. doi: 10.1097/00004714-199704000-00010. [DOI] [PubMed] [Google Scholar]
  • 24.Kreek MJ, Garfield JW, Gutjahr CL, Giusti LM. Rifampicin-induced methadone withdrawal. N Engl J Med. 1976;294:1104–1106. doi: 10.1056/NEJM197605132942008. [DOI] [PubMed] [Google Scholar]
  • 25.Raistrick D, Hay A, Wolff K. Methadone maintenance and tuberculosis treatment. Br Med J. 1996;313:925–926. doi: 10.1136/bmj.313.7062.925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Kerr BM, Thummel KE, Wurden CJ, et al. Human liver carbamazepine metabolism- role of CYP3A4 and CYP2C8 in 10,11-epoxide formation. Biochem Pharmacol. 1994;47:1969–1979. doi: 10.1016/0006-2952(94)90071-x. [DOI] [PubMed] [Google Scholar]
  • 27.Levy RH. Time-dependent pharmacokinetics. In: Rowland M, Tucker GT, editors. In Pharmacokinetics: Theory and Methodology. Oxford: Pergamon Press; 1986. pp. 115–130. [Google Scholar]
  • 28.Pitlick WH, Levy RH, Troupin AS, Green JR. Pharmacokinetic model to describe self-induced decreases in steady state concentrations of carbamazepine. J Pharm Sci. 1976;65:462–463. doi: 10.1002/jps.2600650344. [DOI] [PubMed] [Google Scholar]
  • 29.Lai AA, Levy RH, Cutler RE. Time-course of interaction between carbamazepine and clonazepam in normal man. Clin Pharmacol Ther. 1978;24:316–323. doi: 10.1002/cpt1978243316. [DOI] [PubMed] [Google Scholar]
  • 30.Boddy AV, Cole M, Pearson ADJ, Idle JR. The kinetics of the auto-induction of ifosfamide metabolism during continuous infusion. Cancer Chemother Pharmacol. 1995;36:53–60. doi: 10.1007/BF00685732. [DOI] [PubMed] [Google Scholar]
  • 31.Von Bahr C, Steiner E, Koike Y, Gabrielsson J. Time course of enzyme induction in humans: effects of pentobarbital on nortriptyline metabolism. Clin Pharmacol Ther. 1998;64:18–26. doi: 10.1016/S0009-9236(98)90018-2. [DOI] [PubMed] [Google Scholar]
  • 32.Hussein Z, Posner J. Population pharmacokinetics of lamotrigine monotherapy in patients with epilepsy: Retrospective analysis of routine monitoring data. Br J Clin Pharmacol. 1997;43:457–466. doi: 10.1046/j.1365-2125.1997.00594.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Ramsay RE, Pellock JM, Garnett WR. Pharmacokinetics and safety of lamotrigine (Lamictal) in patients with epilepsy. Epilepsy Res. 1991;10:191–200. doi: 10.1016/0920-1211(91)90012-5. [DOI] [PubMed] [Google Scholar]
  • 34.Abramson FP. Kinetic models of induction: I. Persistence of the inducing substance. J Pharm Sci. 1986;75:223–228. doi: 10.1002/jps.2600750302. [DOI] [PubMed] [Google Scholar]
  • 35.Scherabaum N, Finkbeiner T, Leifert K, Gastpar LM. The efficacy of l-methadone and racemic methadone in substitution treatment for opiate addicts- a double-blind comparison. Pharmacopsychiat. 1996;29:212–215. doi: 10.1055/s-2007-979573. [DOI] [PubMed] [Google Scholar]
  • 36.Olsen GD, Wendel HA, Livermore JD, Leger RM, Lynn RK, Gerber N. Clinical effect and pharmacokinetics of racemic methadone and its optical isomers. Clin Pharmacol Ther. 1977;21:147–157. doi: 10.1002/cpt1977212147. [DOI] [PubMed] [Google Scholar]
  • 37.Lanz M, Thormann W. Characterisation of the stereoselective metabolism of methadone and its primary metabolite via cyclodextrin capillary electrophoretic determination of their enantiomers. Electrophoresis. 1996;17:1945–1949. doi: 10.1002/elps.1150171223. [DOI] [PubMed] [Google Scholar]
  • 38.Nakamura K, Hachey DL, Kreek MJ, Irving CS, Klein PD. Quantitation of methadone enantiomers in humans using stable isotope-labeled [2H3]-, [2H5]-, and [2H8]-methadone. J Pharm Sci. 1982;71:40–43. doi: 10.1002/jps.2600710110. [DOI] [PubMed] [Google Scholar]
  • 39.Kreek MJ, Hachey DL, Klein PD. Stereoselective disposition of methadone in man. Life Sci. 1979;24:925–932. doi: 10.1016/0024-3205(79)90343-6. [DOI] [PubMed] [Google Scholar]
  • 40.Kristensen K, Blemmer T, Angelo HR, et al. Stereoselective pharmacokinetics of methadone in chronic pain patients. Ther Drug Monit. 1996;18:221–227. doi: 10.1097/00007691-199606000-00001. [DOI] [PubMed] [Google Scholar]
  • 41.Bai SA, Abramson FP. Interactions of phenobarbital with propranolol in the dog: Plasma protein binding. J Clin Pharmacol. 1982;222:589–594. [PubMed] [Google Scholar]
  • 42.Abramson FP, Lutz MP. The kinetics of induction by rifampicin of α1-acid glycoprotein and antipyrine clearance in the dog. Drug Metab Dispos. 1986;14:46–51. [PubMed] [Google Scholar]
  • 43.Olsen GD. Methadone binding to human plasma proteins. Clin Pharmacol Ther. 1974;14:338–343. doi: 10.1002/cpt1973143338. [DOI] [PubMed] [Google Scholar]
  • 44.Calvo R, Aguirre C, Trodniz IF, Lopz , Garrido MJ. Proc VI World Congress on Clinical Pharmacogy and Therapeutics. Argentina: Buenos Aires; 1996. Alpha α1-acid glycoprotein and serum protein binding of methadone in heroin addicts during withdrawal; pp. 174–174. [Google Scholar]
  • 45.Garrido MJ, Jiminez R, Gomez E, Calvo R. Influence of plasma-protein binding on the analgesic effect of methadone in rats with spontaneous withdrawal. J Pharm Pharmacol. 1996;48:281–284. doi: 10.1111/j.2042-7158.1996.tb05917.x. [DOI] [PubMed] [Google Scholar]
  • 46.Ball JC, Lange WR, Myers CP, Friedman SR. Reducing the risk of AIDS through methadone maintenance treatment. J Health Soc Behav. 1988;29:214–226. [PubMed] [Google Scholar]
  • 47.Romach MK, Piafski KM, Abel JG, Khow V, Sellers EM. Methadone binding to orosomucoid (α1-acid glycoprotein): determinant of free fraction in plasma. Clin Pharmacol Ther. 1981;29:211–217. doi: 10.1038/clpt.1981.34. [DOI] [PubMed] [Google Scholar]
  • 48.Eap CB, Cuendet C, Baumann P. Binding of d-methadone, l-methadone, and dl-methadone to proteins in plasma of healthy volunteers: Role of the variants of α1-acid glycoprotein. Clin Pharmacol Ther. 1990;47:338–346. doi: 10.1038/clpt.1990.37. [DOI] [PubMed] [Google Scholar]
  • 49.Wilkins JN, Ashofteh A, Setoda D, Wheatley WS, Huigen H, Ling W. Ultrafiltration using the amicon MPS-1 for assessing methadone plasma protein binding. Ther Drug Monitor. 1997;19:83–87. doi: 10.1097/00007691-199702000-00015. [DOI] [PubMed] [Google Scholar]

Articles from British Journal of Clinical Pharmacology are provided here courtesy of British Pharmacological Society

RESOURCES