Early mortality surge in protein-deprived females causes reversal of sex differential of life expectancy in Mediterranean fruit flies

Abstract

Experiments based on over 400,000 medflies revealed that females maintained on a normal diet (sucrose plus protein) have a higher life expectancy than males maintained on a normal diet, with a difference of 1.30 ± 0.27 days in favor of females. However, this sex differential reverses under protein deprivation, with a difference of 2.24 ± 0.18 days in favor of males. The reversal of the male–female life expectancy differential is caused by a sustained surge in early female mortality under protein deprivation that is tied to egg-laying and physiological processes. In contrast, male mortality and life expectancy are only mildly affected by protein deprivation. The surge in early mortality for female medfly cohorts is an instance of a vulnerable period. These vulnerable periods are linked with patterns in hazard rates.

Life expectancy or average lifespan of individuals is an important quantitative characteristic for comparing the survival and thus frailty of cohorts subjected to various genetic and/or environmental influences. Genetic factors play an important role in determining life expectancy, as exemplified by the well-known sex differential in life expectancy (1–4). Although life expectancy is an overall measure of longevity, the specific dynamics of mortality and the aging process are reflected by the hazard rate or force of mortality.

We report the results of an experiment concerning the survival of cohorts of male and female Mediterranean fruit flies (Ceratitis capitata) under a full sugar-plus-protein diet and under protein deprivation (sugar only). The motive for this study was our interest in determining why hazard rates in female medflies began to level off at an earlier age and at a lower level than hazard rates in male medflies. These mortality patterns were observed in several recent studies involving a total of more than 1.2 million medflies (5), all of which were protein-deprived. We initiated the current investigation to see whether this phenomenon was due to protein deprivation and whether protein deprivation has a sex-dependent effect on life expectancy and hazard rates.

MATERIALS AND METHODS

We investigated these issues by maintaining large cohorts of medflies at the Moscamed medfly mass-rearing facility located in Metapa, Chiapas, Mexico. Technical details on fruit fly mass rearing are as described in ref. 6. Adult flies were maintained under the following environmental conditions: 12-h/12-h light/dark cycle, 24.0°C (±2°C), and 65% relative humidity (±9%). Medflies were kept on one of two dietary regimes: (i) a sugar-plus-protein diet in which flies were provided with sucrose and a protein source; and (ii) a protein-free diet in which flies were provided with a diet consisting only of sucrose (protein-deprived). A total of 416,289 medflies (about equally divided between males and females) were maintained in 66 aluminum cages, 15 × 60 × 90 cm, each containing about 6,000 medflies, males and females grouped together. Thirty-three cages were assigned to the sugar-plus-protein diet and the other 33 cages to the protein-free diet. Diets were assigned alternately as new cages became available for the experiment. The protein-plus-sugar diet consisted of a mixture of three parts sucrose and one part yeast hydrolysate (ICN); we note that yeast hydrolysate also contains vitamins and trace elements in addition to protein. Each day dead flies were removed and counted and their sex was determined. Statistical curve estimation methods were used to obtain hazard rate estimates from the observed life tables. The statistical methods are described in Appendix.

RESULTS

Reversal of Life Expectancy Sex Differential.

Our first finding was that life expectancy is reduced in both male and female medflies if they are deprived of protein. This reduction is much greater in females (26.7%) than in males (5.9%), and this male–female asymmetry in the amount of reduction leads to a reversal of the female advantage in life expectancy. Whereas under the sugar-plus-protein diet, female life expectancy exceeds male life expectancy by 1.30 ± 0.27 days (x̄ ± SEM) SEM = s/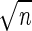, under protein deprivation, female life expectancy is shorter than male life expectancy by 2.24 ± 0.18 days (Table 1). This finding was statistically significant (P < 10⁻³; see Appendix Appendix A).

Table 1.

Life expectancies at eclosion in days for male and female medflies

Diet	No. of cohorts	Life expectancy, males	Life expectancy, females	Difference female–male
Sugar plus protein	33	15.2 ± 2.4	16.5 ± 2.5	1.30 ± .81
Sugar only (protein-deprived)	33	14.3 ± 2.1	12.1 ± 1.8	−2.24 ± .28
Difference sugar-plusprotein minus sugar only		0.84 ± .56	4.4 ± .53

Reported are samples means ± SEM. Medflies are maintained on either protein-deprived or sugar-plus-protein diets. Total number of flies is 416,289. The change in the difference of female minus male life expectancies from the sugar-plus-protein diet to the protein-deprived diet demonstrates the reversal of the life expectancy sex differential (P < 10⁻³). Life expectancies for males do not differ significantly between sugar-plus-protein and sugar-only groups (P = 0.14), whereas for females they differ significantly (P < 10⁻³). 

This is the first study that we are aware of to establish a reversal of the male–female life expectancy differential under dietary manipulation. This reversal of the male–female life expectancy differential demonstrates that this differential is subject to influences exerted by external factors and may be reversed under environmental change. Dietary effects on longevity have recently been studied by many authors (7–10).

Hazard Rates and Early Surge in Mortality.

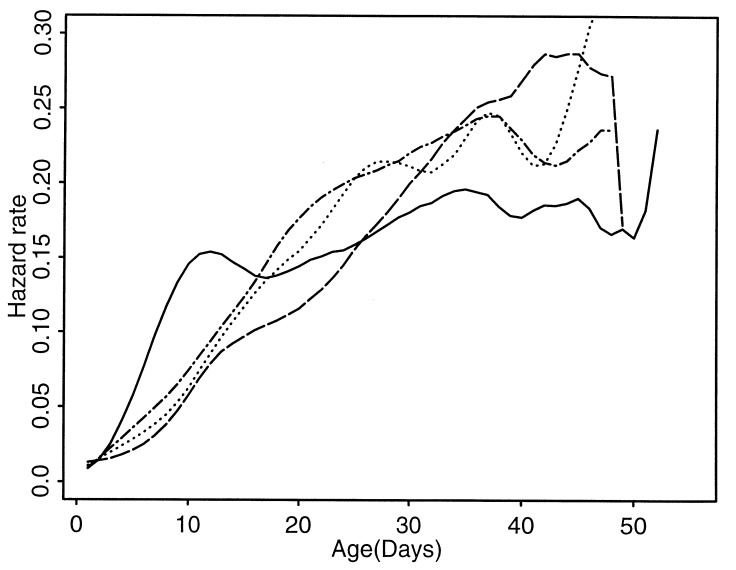
To assess the dynamics underlying the reversal of the sex differential in life expectancy, we obtained hazard rate estimates for the following four groups of medflies (Fig. 1; see Appendix Appendix B): (i) females, protein-deprived; (ii) females, sugar-plus-protein diet; (iii) males, protein-deprived; (iv) males, sugar-plus-protein diet. Our second major finding is that female mortality is strongly influenced by diet. The female protein-deprived group shows a strong peak of size 0.17 at day 12 in the hazard rate, and this peak in the hazard rate is absent in the female sugar-plus-protein group. The peak in hazard rates for protein-deprived females corresponds to a surge in early mortality, which emerges as the cause of the reversal of the sex differential in life expectancies under protein deprivation. After day 25 the hazard rates of the two female groups cross.

Figure 1.

Estimated hazard rates for four groups of medflies: females, protein-deprived (solid); females, sugar-plus-protein diet (dashed); males, protein-deprived (dash-dot); males, sugar-plus-protein diet (dotted). Each curve is based on an initial number of more than 100,000 individuals. Time is in days on the x axis.

In contrast, for male medflies protein deprivation leads to a uniform slight increase in the hazard rate with only minor shape changes. Until about day 11, the hazard rate of the female sugar-plus-protein group stays close to the hazard rates of the two male groups. But it is considerably lower at days 20–30, which helps to explain the higher female life expectancy for the sugar-plus-protein groups. After day 30, the hazard rate of sugar-plus-protein females joins and perhaps exceeds that of males. Early on, the female protein-deprived group has by far the highest hazard rate of all groups until day 15, when its hazard rate crosses the hazard rates of the other groups and finally flattens out at older ages, being substantially below that of all other groups.

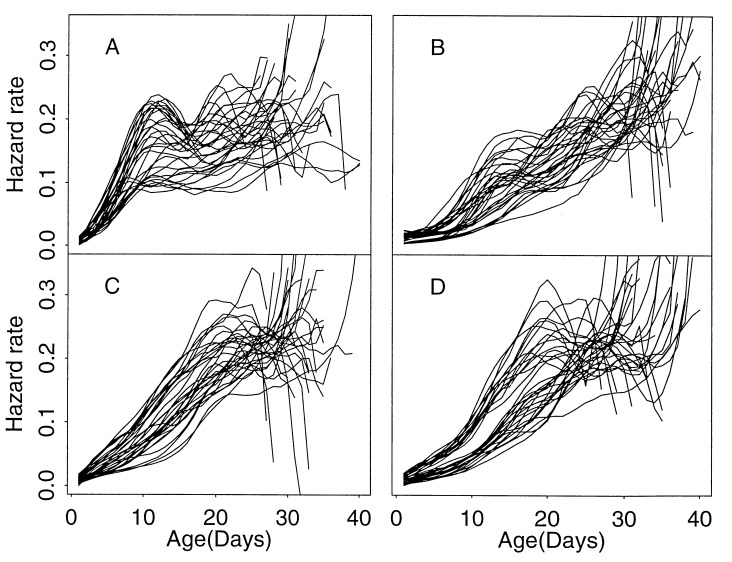
Estimated hazard rates for all 132 cohorts of medflies studied in this experiment are presented in Fig. 2 for each of the four groups. The early surge of mortality with a strongly expressed peak in the hazard rate is found to occur in all 33 female protein-deprived cohorts without exception, providing strong evidence for the consistency of this feature.

Figure 2.

Estimated hazard rates obtained separately for each of 132 cohorts of medflies. Each cohort contains approximately 3000 medflies. Each panel consists of 33 estimated hazard functions for the female protein-deprived group (A), the female sugar-plus-protein group (B), the male protein-deprived group (C), and the male sugar-plus-protein group (D). Time is in days on the x axis.

Peaks in mortality curves with later timing are found for the cohorts belonging to the other three groups as well. Average timing, peak size, and spread of these mortality peaks are similar for the two male groups, which have late peaks and therefore relatively high peak levels of hazard rate with substantial spread in timing and size. The female groups have much earlier and less variable peaks, with the female protein-deprived group having the earliest peak locations with relatively large sizes. The values for mean peak locations ± SEM in days/mean peak amplitudes ± SEM were: for the female sugar-plus-protein group, 16.73 ± 0.31/0.1253 ± 0.0094; for the female protein-deprived group, 11.52 ± 0.31/0.1663 ± 0.0086; for the male sugar-plus-protein group, 21.91 ± 0.86/0.2092 ± 0.0114; for the male protein-deprived group, 21.18 ± 0.71/0.2017 ± 0.0089. The differences between the sugar-plus-protein and protein-deprived groups were significant for females both for peak location and amplitude (P < 0.01) and not significant for males (P > 0.5).

Vulnerable Periods.

We infer from Fig. 1 the existence of vulnerable periods during which the hazard rates surge, with associated higher risk and decreased chance of survival. The major example is the early surge in mortality for protein-deprived females. It is remarkable to what extent this surge in mortality is confined to a strictly limited time period, as is seen in Fig. 2A. Other, less expressed vulnerable periods seem to occur for both male groups around day 38 and for the protein-deprived female group around day 35, corresponding to discernible peaks in the hazard rates (see Figs. 1 and 2).

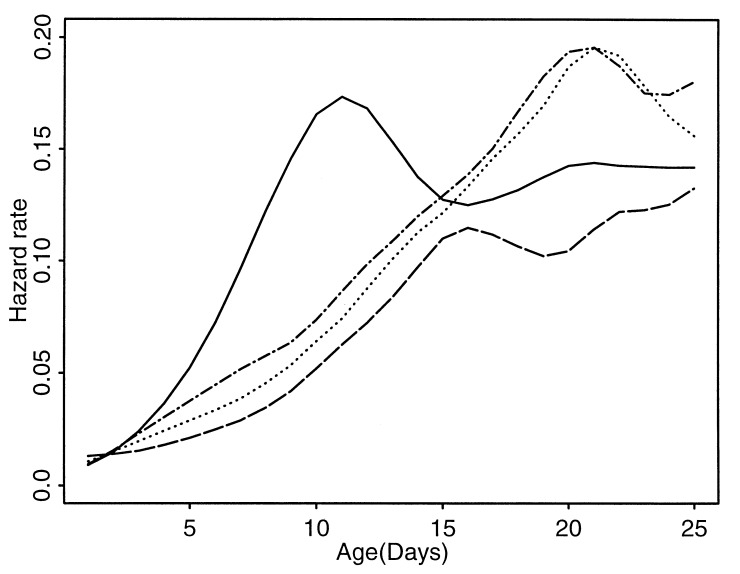
A more detailed study of early mortality for the different groups can be based on peak-aligned hazard rate estimates (Fig. 3; see Appendix Appendix C). Focusing on the first 25 days, the pronounced early mortality surge at day 11 for the female protein-deprived group under peak alignment corresponds in size and width almost to a late surge in male mortality observed at day 21. All hazard rate trajectories are close together at day 15. Before this junction, the female protein-deprived group stands out, as these medflies go through a major vulnerable period. After it, the female hazard rate trajectories continue to differ, whereas the male trajectories continue to stay close together.

Figure 3.

Peak-aligned estimated hazard rates from 0 to 25 days. Hazard rates are shown separately for the four groups: females, protein-deprived (solid); females, sugar-plus-protein diet (dashed); males, protein-deprived (dash-dot); males, sugar-plus-protein diet (dotted). Each curve is based on an initial number of more than 100,000 individuals. Time is in days on the x axis.

DISCUSSION

These analyses demonstrate that the normally present female advantage in life expectancy is mainly caused by a markedly lower female hazard rate compared with the male hazard rate in the age range 20–30 days. The reversal of the sex differential in life expectancies is caused by the early surge in female mortality under protein deprivation, which is so strong that the later decline in the hazard rate cannot make up for the resulting loss in life expectancy. In contrast, male hazard rate trajectories are considerably less affected by protein deprivation.

The early surge in female mortality under protein deprivation may be due to the weakening effect caused by the transfer of proteins and other essential nutrients required for egg production that would otherwise be used for maintenance and repair. This finding is consistent with the hypothesis that the early surge in mortality of protein-deprived females is a consequence of stress induced by attempting to produce eggs under conditions that are not commensurate with both reproduction and maintenance (see ref. 11, p. 165). Our findings thus point to a vulnerable period with specific nutritional demands for females during reproduction, and a resulting surge in mortality if these specific demands are not met. Before day 15, protein deprivation has a major differential effect only for females, but after day 15, an overriding sex differential predominates, although a lingering diet effect remains for females.

Three lines of evidence support the hypothesis that nutritional demands caused by the activation of the reproductive system for individual females are the underlying reason for the early vulnerable period and corresponding surge in mortality in protein-deprived females. (i) High rates of mating and egg production in female medflies are observed during the first 7 to 10 days (12–15). It is likely that the reproductive system of females is “programmed” to begin egg production and maturation shortly after eclosion. If no protein is available, then adults must draw on larval reserves. (ii) This early surge is not observed in protein-deprived females when they are subjected to ionizing radiation (16). The likely reason for this is that the radiation renders females sterile and, therefore, unable to produce and mature eggs. (iii) Male cohorts did not exhibit this pattern irrespective of diet. We note that sucrose-fed females of a related species, the apple maggot fly (Rhagoletis pomonella), were able to produce a few eggs (17). This was likely due to the transfer of protein and vitamins from immature stages to the adult.

The finding of decreased hazard rates at older ages in protein-deprived compared with protein-fed females could be due to: (i) demographic selection (18), or (ii) deactivation of the reproductive system after the initial vulnerable period when females attempted to produce eggs from protein reserves acquired in the larval stage. Thus, females with access to an external protein source continue to lay eggs, which is costly and leads to higher hazard rates, whereas females without access shut down reproduction, conserve energy, and reduce risk.

CONCLUSION

Using advanced statistical curve estimation methods, we found and analyzed an early surge in mortality for protein-deprived female medflies. This surge in early mortality was shown to cause a reversal of the life expectancy sex differential. This points to a vulnerable period in the life cycle of female medflies that is narrowly confined in time and corresponds to the time of reproduction and egg-laying.

The results presented here provide evidence that changes at the level of the individual account for changes observed in hazard rates for cohorts of individuals. Such changes at the individual level can account for the observed leveling off of hazard rates at older ages in fruit flies (4, 19). Other explanations for this leveling off based on density effects (20), demographic selection and heterogeneity (18, 21), or epigenetic stratification (22) do not have to be invoked.

STATISTICAL METHODS

In this appendix we describe a statistical test for the null hypothesis that there is no reversal in the life expectancy sex differential (Appendix Appendix A). We then provide more details regarding the curve estimation techniques that we developed for estimating hazard rates from life table data (Appendix Appendix B). The peak alignment technique used in Fig. 3 is explained in Appendix Appendix C. We conclude with a brief review in Appendix Appendix D of the auxiliary smoothing technique that is used for hazard rate estimation in Appendices Appendix B and Appendix C.

Appendix Appendix A: A Test for the Reversal of the Life Expectancy Sex Differential.

In testing for change in the male–female life expectancy relation, the null hypothesis was {female life expectancy ≤ male life expectancy for the sugar-plus-protein group, or female life expectancy ≥ male life expectancy for the protein-deprived group. The alternative hypothesis was female life expectancy > male life expectancy for the sugar-plus-protein group, and female life expectancy < male life expectancy} for the protein-deprived group. The alternative hypothesis is seen to describe the reversal of the female advantage in life expectancy under protein deprivation, and the null hypothesis corresponds to nonreversal. Because female and male medflies share the same cages, we determined differences of life expectancies (female minus male) for each cage. These differences were found to be reasonably Gaussian. Pairing the 33 cages of protein-deprived medflies with the 33 cages of protein-plus-sugar medflies yielded a bivariate normal sample of size 33 with zero correlation coefficient. It is then straightforward to obtain confidence ellipsoids of any desired confidence level for the bivariate population mean (see ref. 23, p. 188). The null hypothesis was rejected at the level α = 10⁻³ by constructing the corresponding confidence ellipsoid at the 99.99% confidence level. This confidence ellipsoid was found to be entirely contained in the second quadrant of the Cartesian plane, defined by negative x and positive y coordinates, implying that the differences of life expectancies (female–male) are negative for protein-deprived and positive for protein-plus-sugar medflies.

Appendix Appendix B: Estimating Hazard Rates.

We developed a transformation plus smoothing technique to estimate the hazard rate

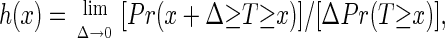where Pr denotes probability (compare also ref. 24). The hazard rate estimates are shown in Figs. 2 and 3. The starting point are the life table data (d_j, n_j), j ≥ 1, where d_j is the number of recorded deaths on day j, and n_j is the number of medflies at risk at the beginning of day j. One problem that needs special attention is the discretization bias. This bias occurs when one attempts to make the transition from discrete probabilities, which correspond to the life table data with Δ = 1 day, to the hazard rate h(x), which corresponds to a limit as Δ → 0. Attenuation of this discretization bias can be achieved by the transformation h̃_j = −log(1 − d_j/n_j), j = 1, 2, … .. The hazard rate estimate at age x is then ĥ(x) = S(x, b, (t_j, h̃_j, n_j)_{j=1, … , n}), using a smoother S, which is described in Appendix Appendix D. This is interpreted as smoothing the scatterplot (t_j, h̃_j), j = 1, … , n, using the case weights W_j = n_j. [For nonparametric hazard rate estimation in the case of exact (nonaccumulated) data, see refs. 25 and 26].

Appendix Appendix C: Peak-Aligned Averaging. The aim of this technique is to avoid biases associated with averaging peaks across cohorts. Such averaged peaks tend to “flatten out” because of the heterogeneity (variability) in the timing of the peaks for individual cohorts. Assume that the hazard rate of the jth cohort has a peak at location θ_j. To estimate θ_j, the first step is to estimate the hazard rate for the jth cohort, j = 1, … , N, using the method described in Appendix Appendix B. Next, the location θ̂_j of the peak of the estimated hazard rate is obtained. This provides an estimate of the cohort peak location θ_j. The estimated average peak location for all cohorts is obtained by averaging all individual cohort peak locations:

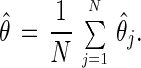Scaled alignment of the hazard rates of individual cohorts to the average peak location θ̂ is then achieved by transforming the time coordinate t for each of the N cohorts as follows: use the transformed time t′_j = (tθ̂)/θ̂_j for the data of the jth cohort. This time-scale transformation maps all individual peak locations θ̂_j to θ̂. After transforming the time scale (originally in days) separately for each cohort, the method of Appendix Appendix B is used again to obtain the final peak-aligned hazard rate estimates.

Appendix Appendix D: Smoothing with Locally Weighted Least Squares.

The estimation of hazard rates in Appendices Appendix B and Appendix C requires the smoothing of scatterplot data. A variety of statistical smoothing techniques such as locally weighted least squares, kernels, and splines are available for this purpose (27). The locally weighted least squares method (28–30) is particularly well suited for this purpose because it permits inclusion of case weights in a straightforward way. Given scatterplot data (X_j, Y_j)_{j=1, … , n} and associated case weights W_j, the basic assumptions are: (i) E(Y_j|X_j = x) = f(x) with a smooth function f, and (ii) var(Y_j|X_j = x) is finite. Then a consistent curve estimate of f(x) using locally weighted least squares is:

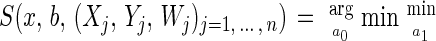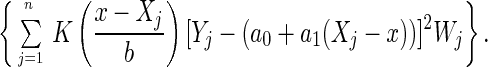Here, b is the bandwidth of the smoother, and K is a nonnegative kernel function. This estimate fits local linear lines by weighted least squares to the data falling into a window [x − b, x + b] around the point x where the estimate is desired. We chose the kernel function K(x) = (1 − x²), |x| ≤ 1, K(x) = 0, |x| > 1, which was shown to be optimal in the mean square error sense (29). The bandwidth b = 4 days was found to be very close to the cross-validation bandwidth (31) and was chosen throughout for our smoothing applications. For smoothing a hazard function, we choose X_j = j (in days), Y_j = h̃_j (see Appendix Appendix B), and W_j = n_j, j = 1, … , n.