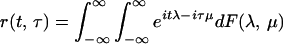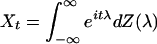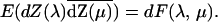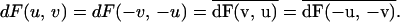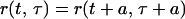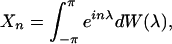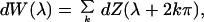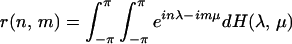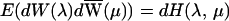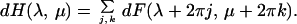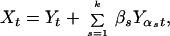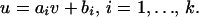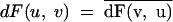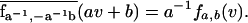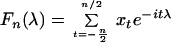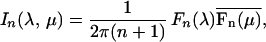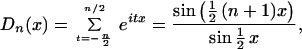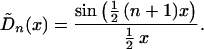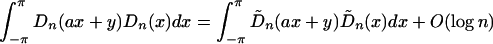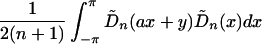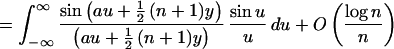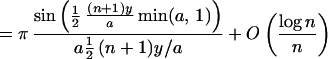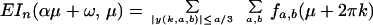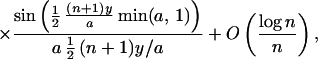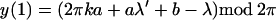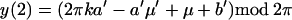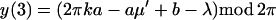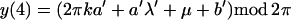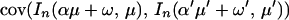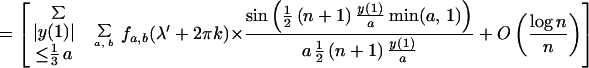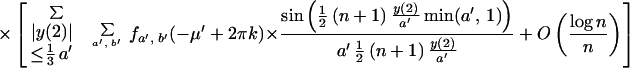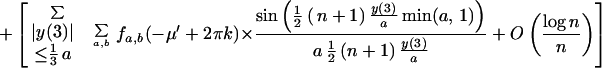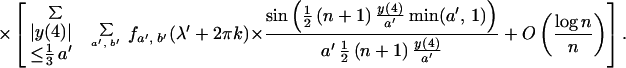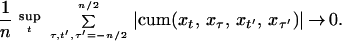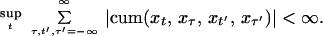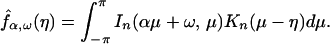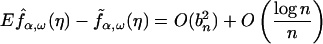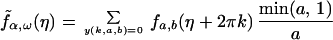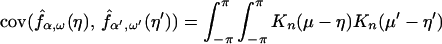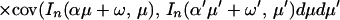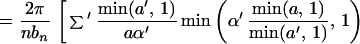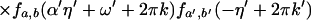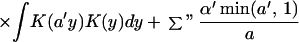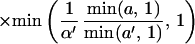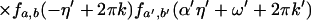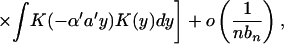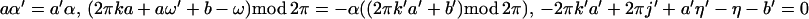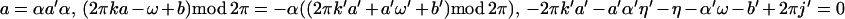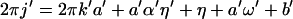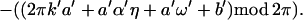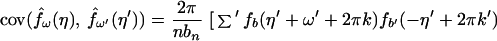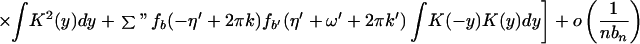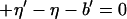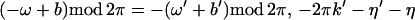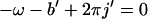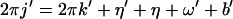Abstract
Harmonizable processes with spectral mass concentrated on a number
of straight lines are considered. The asymptotic behavior of the bias
and covariance of a number of spectral estimates is described. The
results generalize those obtained for periodic and almost periodic
processes.
Keywords: nonstationarity, spectral estimation, asymptotic bias
and covariance
Let {Xt} be a continuous time parameter
harmonizable process continuous in mean square, −∞ < t
< ∞, with EXt ≡ 0. By this we mean
that the covariance function r(t, τ) =
E(Xt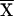 τ) has a Fourier
representation
τ) has a Fourier
representation
with F(λ, μ) a function of bounded
variation. This implies that Xt itself
has a Fourier representation in mean square
in terms of a random function Z(λ) with
If the process Xt is real-valued,
In the case of a weakly stationary process r(t, τ)
= r(t − τ, 0) and all the spectral mass is located on the
diagonal line λ = μ. If the process is periodic with
for some period a or almost periodic the
spectral mass is located on a finite or countable number of lines in
the (λ, μ) plane with slope one. If the process is discretely
observed Xn, n = 0, ±1,
±2, … there is an analogous representation
with
The folding of F(λ, μ) to obtain H(λ,
μ) is referred to as aliasing.
There is an enormous literature concerned with spectral estimation in
the case of stationary processes (1). Recently efforts have been made
to obtain analogous results on spectral estimation for periodic and
almost periodic processes (2–7). It is well known that one generally
does not have consistent estimates of spectral mass for a harmonizable
process when the function F (or H) is absolutely
continuous with a spectral density function f, dF(λ, μ) =
f(λ, μ)dλdμ, with f(λ, μ) ≠ 0 on a set of
positive two-dimensional Lebesgue measure, and one is sampling from the
process X−n, … , Xn and
n → ∞. A simple example is given by
X0 normal with mean zero and variance one and
Xk ≡ 0 with probability one for k
≠ 0. It is clear that consistency of spectral estimates in the
case of stationary and periodic processes is due to the fact that the
spectral mass is concentrated on lines that in these cases happen to be
of slope one. We shall consider spectral estimation for harmonizable
processes when the spectrum is concentrated on a finite (or possibly
countable) number of lines. For convenience the slope of the lines will
be assumed to be positive, though the modification for negative slopes
is clear. A simple example of a harmonizable process with spectral mass
on lines is given by
where Yt is stationary and
βs and αs are real
and positive numbers, respectively. The object is to give some insight
into an interesting class of nonstationary processes.
Assume that Xt is a harmonizable real-valued
process as already specified with
A1. All its spectral mass on a finite number of lines with
positive slope
A2. The spectral mass on the line u =
aiv + bi is given by a continuously
differentiable spectral density
fai,bi(v) if
ai ≤ 1. Notice that the real-valued property
implies that if u = av + b is a line of spectral
mass, then so are the lines u = av − b and
u = a−1v ± a−1b. If
there are lines of nonzero spectral mass, the diagonal λ = μ must
be one of them with positive spectral mass. The condition
implies if u = av + b
is a line of nonzero spectral mass, then so is u =
a−1(v − b) with
A3. The spectral densities
fai,bi(v) and their
derivatives are bounded in absolute value by a function h(v)
that is a monotonic decreasing function of |v| that
decreases to zero as |v| → ∞ and that is
integrable as a function of v.
As already remarked, aliasing or folding of the spectral
mass occurs when the process is discretely sampled at times
n = … , − 1, 0, 1, … rather than
continuously. The following simple remark indicates how a process with
line spectra may differ from a stationary or almost periodic process in
terms of aliasing. The aliasing in the case of a harmonizable process
has a more complicated character.
Proposition 1. Let Xt be a continuous time parameter process continuous in
mean square satisfying conditions A1–A3. Assume that the
lines of spectral support have spectral density nonzero at all points
v, |v| > s for some s > 0. The process discretely
observed Xn then has a countably dense set of lines of
support in [−π, π]2 if and
only if one of the lines of spectral support of Xt has
irrational slope a.
The Periodogram
We shall consider spectral estimation for the discretely observed
process Xn. The estimates will be obtained by
smoothing a version of the periodogram. Before dealing with the
spectral estimates, approximations for the mean and covariances of the
periodogram are obtained. Let
be the finite Fourier transform of the data
x−n/2, … , xn/2. The
periodogram
and it is to be understood that |λ|, |μ| ≤ π with
−π identified with π so that in effect one is dealing with the
torus in (λ, μ). Set
These expressions are versions of the Dirichlet kernel adapted to
(−π, π] and (−∞, ∞). The following result is useful in
obtaining the expressions for the mean and covariance of the
periodogram.
Lemma 1. If a > 0, |y| < π,
and
if |y| ≤ a/3, while if
|y| ≥ a/3 the expression is itself of order
log n/n.
Whenever we refer to an expression ω = z mod 2π it
is understood that −π < ω ≤ π. Let {u} be the
integer ℓ such that −1/2 < u − ℓ ≤
1/2. Our version of z mod 2π is then z
mod 2π = z − {z/(2π)}2π. In the following
an approximation is given for EIn(αμ + ω,
μ) with the condition imposed that α > 0 and −π < αμ
+ ω, μ ≤ π. Let y = y(k, a, b) = (2πka +
(a − α)μ + b − ω) mod 2π.
Theorem 1. The mean
where in the sum it is understood that the k are integers
and the pairs (a, b) correspond to the lines u =
av + b in the spectrum of the continuous time parameter process
Xt that one is observing at integer t.
In the following result an approximation is given for the
cov(In(αμ + ω, μ), In(α′μ′ +
ω′, μ′)). Here
with λ = αμ + ω, λ′ = α′μ′ + ω′, −π < λ,
λ′, μ, μ′ ≤ π. Also (a, b), (a′, b′) correspond to
lines in the spectrum of the continuous time parameter process
Xt that one is observing at integer
times.
Theorem 2. The covariance in the case of a normal process Xt is
Corollary 1. The result of Theorem 2 holds with an additional error term
O(1/n) for a nongaussian harmonizable process with finite
fourth-order moments if the fourth-order cumulants satisfy
This will be the case if
Spectral Estimates
We consider an estimate
f̂α,ω(η) of
f̃α,ω(η) obtained by
smoothing the periodogram. Let K(η) be a nonnegative
bounded weight function of finite support with ∫ K(η)dy
= 1. The weight function Kn(η) =
bn−1 K(bn−1η) with
bn ↓ 0 as n → ∞ and
nbn → ∞. The weight functions
Kn should be considered as functions on the
circle (−π, π] with −π identified with π. The estimate
Proposition 2. If A2 is strengthened so that the spectral densities
fai,bi(ν) are assumed
to be twice continuously differentiable and K is symmetric, then
where
as n → ∞.
The asymptotic behavior of covariances is described in the
following result.
Theorem 3. Let Xt be a continuous time parameter harmonizable process
continuous in mean square satisfying assumptions A1–A3 and
16. Then
where the first sum Σ′ is over a, a′, b, b′, k,
k′ such that
with 2πj′ = 2πk′a′ + b′ − ((2πk′a′ +
b′)mod 2π), while the second sum Σ" is over
a, a′, b, b′, k, k′ such that
with
In the almost periodic case we have the following corollary.
Corollary 2. If the assumptions of Theorem 3 are satisfied with
Xt almost periodic
where the first sum is over b, b′, k, k′ such
that
with 2πj′ = 2πk′ + b′ − ((b′)mod 2π)
while the second sum is over b, b′, k, k′ with
with
On heuristic grounds one would expect to be able to estimate a
spectral density localized on a piecewise smooth curve in the plane.
Acknowledgments
This research is partly supported by Office of Naval Research Grant
N00014-92-J-1086.
References
-
1.Yaglom A M. Correlation Theory of Stationary and Related Random Functions. New York: Springer; 1986. , Vols. I and II. [Google Scholar]
-
2.Dandawate A, Giannakis G. IEEE Trans Inf Theory. 1994;40:67–84. [Google Scholar]
-
3.Gardner W, Franks L. IEEE Trans Inf Theory. 1975;21:4–14. [Google Scholar]
-
4.Hurd H. IEEE Trans Inf Theory. 1989;35:350–359. [Google Scholar]
-
5.Hurd H, Gerr N. J Time Ser Anal. 1991;12:337–350. [Google Scholar]
-
6.Leskow J, Weron A. Stat Prob Lett. 1992;15:299–304. [Google Scholar]
-
7.Leskow J. Stochastic Processes Appl. 1994;52:351–360. [Google Scholar]
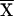 τ) has a Fourier
representation
τ) has a Fourier
representation