Cosmological implications of a large complete quasar sample

Abstract

Objective and reproducible determinations of the probabilistic significance levels of the deviations between theoretical cosmological prediction and direct model-independent observation are made for the Large Bright Quasar Sample [Foltz, C., Chaffee, F. H., Hewett, P. C., MacAlpine, G. M., Turnshek, D. A., et al. (1987) Astron. J. 94, 1423–1460]. The Expanding Universe model as represented by the Friedman–Lemaitre cosmology with parameters q_o = 0, Λ = 0 denoted as C1 and chronometric cosmology (no relevant adjustable parameters) denoted as C2 are the cosmologies considered. The mean and the dispersion of the apparent magnitudes and the slope of the apparent magnitude–redshift relation are the directly observed statistics predicted. The C1 predictions of these cosmology-independent quantities are deviant by as much as 11σ from direct observation; none of the C2 predictions deviate by >2σ. The C1 deviations may be reconciled with theory by the hypothesis of quasar “evolution,” which, however, appears incapable of being substantiated through direct observation. The excellent quantitative agreement of the C1 deviations with those predicted by C2 without adjustable parameters for the results of analysis predicated on C1 indicates that the evolution hypothesis may well be a theoretical artifact.

Since soon after being discovered by Schmidt (1), quasars have appeared as extremely varied and strange objects within the frame of the expanding universe theory of the redshift, which is represented by the conventional Friedman model. In addition to their extraordinary intrinsic brightness, ranging up to 5000× that of the Milky Way, and their paucity at the high redshifts where they would be expected to be most plentiful, their intrinsic luminosity distribution appeared extremely wide. (See, for example, ref. 2 and references within.) The quasar observations have been reconciled with the Friedman theory by assuming “evolution” in intrinsic luminosity and/or space density. This evolution has been fit more or less directly to the observations and has had little sustained predictive power.

In contrast, the chronometric cosmology proposed by Segal (3) immediately explained the apparent, remarkable, intrinsic brightness of quasars and their paucity at higher redshifts, notwithstanding its vulnerability in principle arising from its lack of adjustable parameters such as the q_o and Λ of Friedman–Lemaitre cosmology. Rigorous statistical analysis of complete optical quasar samples, such as the Bright Quasar Sample of Schmidt and Green (4), indicated that quasars had a quite narrow distribution of luminosities within the frame of chronometric cosmology (5). This has been confirmed for similar complete samples in the x-ray and radio bands (6, 7), as well as in large eclectic samples, for example (8).

Well defined, reliably complete samples, such as are required for rigorous statistical analysis, have, however, been quite small. Thus, the Bright Quasar sample of Schmidt and Green included only 114 quasars and had an average limiting magnitude somewhat fainter than 16. At a uniform limiting magnitude of 18.41, the Large Bright Quasar Sample (9) includes 683 quasars. This provides a basis for a quite stringent test of the chronometric analysis of quasars and the scientific role of the evolution hypothesis. Because quasars are observed at redshifts more than a thousand times those of the paper of Hubble (10) that led theorists to the expanding universe model (notwithstanding Hubble’s skepticism and that of the discoverer of the redshift, V. M. Slipher), they necessarily play an essential role in any objective consideration of the nature of the redshift.

Statistical Procedure.

To estimate a luminosity distribution function and compare the theoretical predictions derived from it with observation, a nonparametric form of the method of maximum likelihood is used (11). For each cosmology, the range of absolute magnitudes is divided into equally sized bins in which the luminosity function appears, within the accuracy of measurement, as substantially constant. For equitability, the range of absolute magnitudes that varies with the redshift (i.e., is subject to so-called Malmquist bias) is divided into 10 bins in each cosmology in the present analysis. Bins of the same size are used also for the remaining (brighter) part of the absolute magnitude range in which the luminosity function may properly be estimated naively (i.e., with disregard for the observational magnitude cutoff). The values of the luminosity function in each bin (i.e., the heights of corresponding histogram rectangles) then are determined by the method of maximum likelihood.

The validity of this method depends only on the completeness of the sample in flux and not necessarily in redshift because no assumption with regard to the spatial distribution is required, unlike most earlier methods for the estimation of the luminosity function from complete sample observations. Having estimated the luminosity function for a given cosmology, its predictions for directly observable quantities are determined uniquely. Among major cosmology-independent such quantities are the mean and dispersion of the apparent magnitudes and the slope of the regression of apparent magnitude on log redshift.

We applied this method to Friedman–Lemaitre cosmology as represented by the values q_o = 0 = Λ. These values are proposed in much recent literature, and the results are insensitive to their values in the range generally regarded as empirically tenable. We apply the identical method to chronometric cosmology, which has no adjustable presently relevant cosmological parameters.

We denote these two cosmologies as C1 and C2, respectively. We thank C. Foltz (University of Arizona) for electronic transmission of the data used here, which is described in ref. 1. This sample is confined to the redshift range 0.2 ≤ z ≤ 3.4 and includes 683 quasars of magnitude ≤18.41, the limiting apparent magnitude of the sample as a whole. The data were used without adjustments of any type, apart from corrections to the spectral index of −0.5 estimated for quasars by Richstone and Schmidt (12), corrections that are, in any event, quite small.

Predictions were made here by Monte Carlo analysis. Objects were drawn at random from the estimated luminosity function and placed successively at each observed redshift, subject to the limiting apparent magnitude. The observable quantities within the frame of the given cosmology then were computed for this random sample. The average of the results obtained from 100 such random samples and the dispersion in these results are given in Table 1. For comparative cosmological purposes, it is convenient throughout this paper to define the “absolute magnitude” as the apparent magnitude at the fixed redshift 1 rather than at a fixed distance, as it has been defined traditionally; this definition serves also to bypass the unsettled issue of the cosmic distance scale.

Table 1.

Observed and predicted statistics for full sample

Statistic	Observed value	Friedman (C1) prediction	Chronometric (C2) prediction	Errors, SD
				C1	C2
〈m〉	17.94	17.67 ± 0.025	17.91 ± 0.016	11.0	2.1
sm	0.40	0.71 ± 0.032	0.40 ± 0.014	9.6	0.1
β	0.26	0.62 ± 0.087	0.24 ± 0.054	4.0	0.4
〈M1〉	17.86	17.58 ± 0.025	17.82 ± 0.016	11.0	2.1
σ1	1.71	1.71 ± 0.020	1.72 ± 0.015	0.2	0.5
ρ1	−0.97	−0.92 ± 0.0078	−0.97 ± 0.0020	7.4	0.5
〈M2〉	18.03	17.75 ± 0.025	17.99 ± 0.016	11.0	2.1
σ2	0.43	0.69 ± 0.029	0.43 ± 0.014	8.9	0.1
ρ2	−0.34	−0.07 ± 0.038	−0.37 ± 0.039	7.4	0.6

In the order in which they appear in Table 1, the quantities predicted are as follows, where the subscript “1” refers to Friedman cosmology and “2” refers to chronometric cosmology: (i) the mean apparent magnitude, 〈m〉; (ii) the SD of the apparent magnitudes, s_m; (iii) the slope of the regression of apparent magnitude on log redshift, β; (iv and vii) the mean absolute magnitudes 〈M₁〉 and 〈M₂〉; (v and viii) the SDs of the absolute magnitudes σ₁ and σ₂; and (vi and ix) the correlations of absolute magnitude with log redshift, ρ₁ and ρ₂.

All of the chronometric predictions are accurate within ≈2σ. In contrast, relatively few of the Friedman predictions appear consistent with observations, and their deviations range up to 11σ. The correctness of the Friedman estimate for σ₁ is largely an automatic result of the statistical context and typically is found for any reasonable cosmology. The Friedman prediction for the correlation of its absolute magnitude with log redshift is deviant by >7σ, but the chronometric prediction for this quantity (the correlation of the Friedman absolute magnitude with log redshift) is notably accurate. This is simply explicable in the chronometric frame by the domination of the observed correlation by the nonstochastic difference between the constant-luminosity predictions of the two cosmologies as a function of redshift.

Relatedly, luminosity “evolution” equal to the fixed function of redshift representing the difference between the nonevolutionary chronometric and Friedman constant-luminosity predictions will result in Friedman predictions identical to those of chronometric cosmology and thereby in agreement with observation. Because the same could be done for any other cosmology, this provides no nontrivial statistical support for the validity of the Friedman model. The applicability of luminosity evolution to quasars is not ruled out, but, in the absence of an observationally falsifiable procedure for its substantiation, its rigorous scientific status appears questionable.

No less to the point, chronometric theory fully explains the incorrect predictions of the Friedman model for the cosmology-independent quantities 〈m〉, s_m, and β without introducing ancillary parameters or appealing to an unverifiable hypothesis. The predictions of chronometric theory for the results of analysis predicated on the nonevolutionary Friedman model are derived from the prediction of the former for the luminosity function of the latter. This prediction is achieved by a variant of the Monte Carlo procedure indicated, in which the Friedman luminosity function is determined in each of 100 random samples constructed assuming chronometric cosmology by the nonparametric maximum likelihood procedure described above. The average of these 100 luminosity functions is then the chronometric estimate for the Friedman luminosity function. Table 2 is derived from this luminosity function by drawings of 100 random samples placed at the observed redshifts in accordance with Friedman cosmology, in each of which the same statistics as above were computed and averaged. The SDs of the prediction errors (shown in the fourth column) are the square roots of the sums of the squares of the SDs in the second and third columns. In no case does the error of the chronometric prediction differ significantly from zero.

Table 2.

The actual and chronometric-predicted results of analysis predicated on Friedman cosmology

Statistic	C1 prediction using C1-estimated C1 luminosity function	C1 prediction using C2-estimated C1 luminosity function	Error
〈m〉	17.67 ± 0.025	17.61 ± 0.025	0.06 ± 0.04
sm	0.71 ± 0.032	0.72 ± 0.034	0.04 ± 0.05
β	0.62 ± 0.087	0.70 ± 0.098	0.08 ± 0.13
〈M1〉	17.58 ± 0.025	17.53 ± 0.025	0.06 ± 0.04
σ1	1.71 ± 0.020	1.70 ± 0.023	0.01 ± 0.03
ρ1	−0.92 ± 0.0078	−0.90 ± 0.0092	0.01 ± 0.01
〈M2〉	17.75 ± 0.025	17.80 ± 0.025	0.06 ± 0.04
σ2	0.69 ± 0.029	0.72 ± 0.030	0.03 ± 0.04
ρ2	−0.07 ± 0.038	−0.03 ± 0.040	0.04 ± 0.06

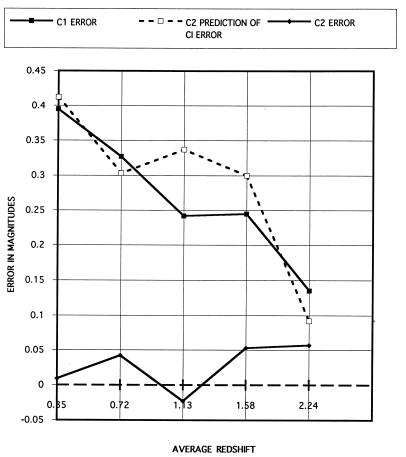
The redshift-dependent implications of the narrow width of the chronometric luminosity function are clarified by Fig. 1, which shows the average prediction errors for the mean apparent magnitude in each of five disjoint redshift bins containing equal numbers of quasars, plotted at the geometric mean of their redshifts. The C1 errors are conspicuous and substantial as predicted by C2 for the results of analysis predicated on C1 whereas the C2 errors appear as possible statistical fluctuations.

Figure 1.

Prediction errors for the mean apparent magnitude in five redshift bins in the Large Bright Quasar Sample to its overall limiting magnitude of 18.41.

The subsample of 436 quasars in the higher redshift range 0.8 ≤ z ≤ 3.4, in which evolution would be expected to be most pronounced, was tested in the same way as a further check. The results are shown in Table 3 and sustain the indications from the full sample.

Table 3.

Observed and predicted statistics for the high-redshift subsample (0.8 ≤ z ≤ 3.4)

Statistic	Observed value	C1 prediction	C2 prediction	Errors, SD
				C1	C2
〈m〉	17.99	17.83 ± 0.024	17.97 ± 0.016	6.3	1.0
sm	0.35	0.53 ± 0.028	0.35 ± 0.016	6.3	0.1
β	0.33	0.84 ± 0.16	0.75 ± 0.13	3.1	2.0
〈M1〉	16.82	16.67 ± 0.024	16.81 ± 0.017	6.3	1.0
σ1	0.95	0.96 ± 0.022	0.99 ± 0.018	0.5	2.0
ρ1	−0.93	−0.84 ± 0.016	−0.93 ± 0.0056	5.5	0.7
〈M2〉	17.93	17.78 ± 0.024	17.91 ± 0.016	6.3	1.0
σ2	0.35	0.52 ± 0.027	0.35 ± 0.016	6.2	0.1
ρ2	0.038	0.17 ± 0.043	−0.07 ± 0.051	3.0	2.0

Tests of Spatial Uniformity.

The analysis above has required no assumption as to the spatial distribution of quasars and reaches no conclusion in this regard. The relative paucity of quasars at large redshifts in the frame of Friedman cosmology has, however, occasioned many studies confirming its statistically significant overestimates of quasar numbers at high redshifts. (See, for example, refs. 13 and 14). These studies provided indications in the direction of number (or density) evolution, which appear relatively natural in the frame of C1.

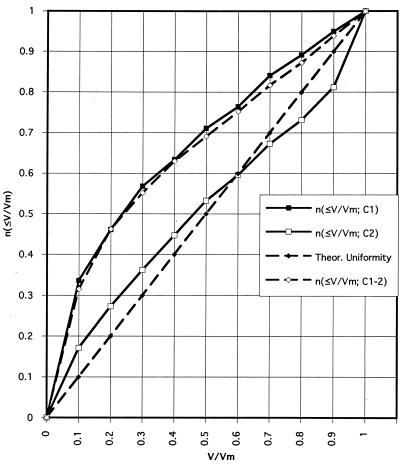
The high-redshift subsample of the preceding paragraph provides a considerably larger sample than those treated earlier in this connection. The results of the Schmidt V/V_m test for spatial uniformity in the Friedman and chronometric cosmologies, as well as the prediction of the latter cosmology for the results of analysis predicated on the former, are shown in Fig. 2. The results confirm the apparent need for number (or density) evolution shown by earlier studies in the frame of Friedman cosmology but show also that chronometric cosmology explains quantitatively, without evolution or adjustable parameters, the deviations from spatial uniformity implied by Friedman cosmology. The same Monte Carlo procedure as earlier was used to treat the spatial distribution question, except that the redshifts of the 100 simulated samples constructed were chosen at random according to theoretical spatial uniformity in the frame of whichever cosmology was tested.

Figure 2.

Spatial uniformity (V/V_m) tests at high redshifts (0.8 ≤ z ≤ 3.4).

Possible Statistical Refinements.

The results above appear insensitive to equitable changes in the binning procedure. As smaller bins, corresponding to more adjustable parameters, are used, the fit is improved for both cosmologies, but the C1 deviations remain statistically significant and coincident with the predictions of C2 for the results of analysis predicated on C1. The use of the same data both to estimate the luminosity functions and to test their predictions of observed quantities may affect statistical significance levels to an extent dependent on the number of parameters estimated compared with sample size. The fits of both cosmologies are likely to be better than they would be if independent samples were used for these two purposes. The effect has the potential in principle to decrease the deviations of prediction from observation for both cosmologies.

However, only 10 nontrivial parameters are estimated in the analysis of a sample of 700 objects, which normally would be expected to have only a marginal effect. That this is the case can be tested by analyses of randomly selected half-samples, in which one-half is used to estimate the luminosity functions whereas the other half is used to compare prediction based on the luminosity function estimated from the other half-sample with observation. Table 4 summarizes the results of this analysis for the basic cosmology-independent quantities and the correlation of the Friedman absolute magnitude with log z. As might be expected from the reduction in sample size by a factor of 2, the C1 deviations are reduced somewhat, but they remain statistically significant by ≈7σ and again are quantitatively as predicted by C2. The C2 deviations remain at an acceptable level.

Table 4.

Predictions for a random half-sample based on the luminosity functions of the complementary half-sample

Statistic	〈m〉	sm	β	ρ1
Observed value	17.93	0.43	0.29	−0.97
C1 prediction	17.67 ± 0.04	0.71 ± 0.05	0.55 ± 0.13	−0.92 ± 0.01
C1 prediction	17.91 ± 0.02	0.39 ± 0.02	0.30 ± 0.08	−0.97 ± 0.003
Errors, SD,
C1	−7.2	6.1	1.9	4.7
C2	−0.7	−1.9	0.1	0.6
Errors for C1, physical units	−0.26	0.28	0.25	0.05
Errors for C2 predictions of C1 results	−0.28 ± 0.05	0.29 ± 0.06	0.43 ± 0.19	0.05 ± 0.2

CONCLUSION

The hypothesis of quasar evolution appears flawed from a methodological, scientific standpoint, whether expressed as Occam’s razor or as Popper’s criterion for science. In addition to its lack of clear and objective observational falsifiability, the deviations of the predictions of nonevolutionary Friedman cosmology from observation are quantitatively coincident with those otherwise predicted by a rational alternative without the intervention of any adjustable parameters. C2 dispersion of quasars in apparent magnitude is only approximately one-fourth of that in C1 in the present sample and of the order of that of putative “standard candles” at lower redshifts. From the standpoint of C2, quasars appear, therefore, as extremely valuable probes of the cosmos.

An interesting qualitative test of evolution is the comparison of the spectra of high- and low-redshift quasars. Schneider, Schmidt, and Gunn (15), in a study of 10 quasars at very high redshifts (z > 4), report that “the most striking conclusion to be drawn from these spectra is that, to first order, there is nothing that distinguishes them from quasars of lower redshift” (15). This similarity between the spectra of high- and low-redshift quasars would not be expected in strongly evolutionary Friedman cosmology but is consistent, rather, with expectation in chronometric cosmology.