Second-order correction to the Bigeleisen–Mayer equation due to the nuclear field shift

Abstract

The nuclear field shift affects the electronic, rotational, and vibrational energies of polyatomic molecules. The theory of the shifts in molecular spectra has been studied by Schlembach and Tiemann [Schlembach, J. & Tiemann, E. (1982) Chem. Phys. 68, 21]; measurements of the electronic and rotational shifts of the diatomic halides of Pb and Tl have been made by Tiemann et al. [Tiemann, E., Knöckel, H. & Schlembach, J. (1982) Ber. Bunsenges. Phys. Chem. 86, 821]. These authors have estimated the relative shifts in the harmonic frequencies of these compounds due to the nuclear field shift to be of the order of 10⁻⁶. I have used this estimate of the relative shift in vibrational frequency to calculate the correction to the harmonic oscillator approximation to the isotopic reduced partition-function ratio ²⁰⁸Pb³²S/²⁰⁷Pb³²S. The correction is 0.3% of the harmonic oscillator value at 300 K. In the absence of compelling evidence to the contrary, it suffices to calculate the nuclear field effect on the total isotopic partition-function ratio from its shift of the electronic zero point energy and the unperturbed molecular vibration.

Recent experiments have shown that chemical equilibrium isotope-exchange separation factors are not necessarily a linear function of the atomic mass differences of the isotopomers (1–8). The most extensive experiments are those of Fujii et al. (5–8), which involve the exchanges of the isotopes ²³²U, ²³³U, ²³⁴U, ²³⁶U, and ²³⁸U between an aqueous phase and an anion-exchange resin. The aqueous phase is principally U(IV); the resin phase is principally U(VI), hydrated or complexed uranyl ion. In each of these exchange reactions the heavy isotope concentrates in the aqueous phase, that is U(IV). The nonlinearity and the fact that the heavy isotope concentrates in the U(IV) species arise from the shift in the minimum of the electronic potential energy due to the different nuclear sizes and shapes of the isotopomers. This is known as the nuclear field shift. A quantitative calculation of this effect (9) is in excellent agreement with experiment.

The calculation is based on the addition of a term due to the nuclear field shift to the Bigeleisen–Mayer equation for the logarithm of the isotopic separation factor and the reduced partition-function ratio. Analogous to the Bigeleisen–Mayer function, ℓn(s/s′)f₀, we define ℓn(s/s′)f_ns as the nuclear field shift correction and ℓn(s/s′)f_T as the total reduced partition-function ratio corrected for the nuclear field shift.

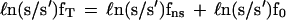1

The nuclear field shift correction is simply,

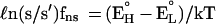2

where (E_H^° − E_L^°) is the difference in the ground state electronic energy.

The Bigeleisen–Mayer equation is based on the Born–Oppenheimer approximation and uses an isotope-independent potential energy; it also assumes simple harmonic vibrations. Because the vibrational force constants are the second derivatives of the electronic energy with respect to the mutual distances between atoms, a correction needs to be applied to ℓn(s′/s′)f₀ for the nuclear field shift. The formal theory of the nuclear field shift on the equilibrium force constant of a diatomic molecule has been given by Schlembach and Tiemann (10). From the theory and their data on the electronic and rotational spectra of diatomic Pb chalcogenides and Tl halides, Tiemann et al. (11) estimated the relative vibrational frequency shifts in these compounds resulting from the nuclear field shifts to be of the order of 10⁻⁶. I now show that a relative frequency shift of this order of magnitude is a negligible, second-order correction to ℓn(s/s′)f₀.

In my study of the nonlinearity of the isotope separation factor, I found it convenient to use the first finite polynomial approximation to ℓn(s/s′)f₀ because this utilizes the isotopomer masses directly.

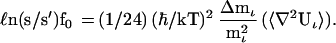3

For the present purpose it is more convenient to use the Bigeleisen–Mayer free energy function, G(u_ι), for the calculation of the correction to ℓn(s/s′)f₀. We write

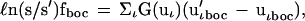4

where u_ιboc = hν_ιboc/kT and ν_ιboc is the vibrational frequency corrected for the nuclear field shift and G(u) = 1/2 − 1/u + (e^u − 1)⁻¹). To calculate (ν′_ιboc − ν_ιboc) we set the nuclear field shift correction in the heavy isotope equal to zero. Then,

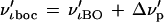5

where ν′_ιBO is the Born–Oppenhemier frequency and Δν′_p is the perturbation due to the nuclear field shift. In Table 1 I summarize the results of the calculation of ℓn(s/s′)f_boc for (²⁰⁷Pb³²S/²⁰⁸Pb³²S). The correction to ℓn(s/s′)f₀ due to the nuclear field shift is estimated to be 0.3% of the value of ℓn(s/s′)f₀. It is a second-order correction. This estimate of the effect of the nuclear field shift on the vibrational frequency suggests that the correction to the Bigeleisen–Mayer equation due to the nuclear field shift can be limited to the ground-state energy correction alone, Eq. 1.

Table 1.

Correction to the isotopic vibrational partition-function ratio of ²⁰⁸Pb³²S/²⁰⁷Pb³²S due to the nuclear field shift

208Pb32S
νe = 428.14 cm−1 G(uι) = 0.15996
δνe(207Pb − 208Pb) = 0.1379 cm−1
Δνp = 4.28 × 10−4 cm−1 (est.)
ℓn(s/s′)f0(300 K) = 0.15996 × (6.61 × 10−4)
ℓn(s/s′)fboc − ℓn(s/s′)f0 = 0.15996 × (2.05 × 10−6).