Engineering analysis of biological variables: An example of blood pressure over 1 day

Abstract

Almost all variables in biology are nonstationarily stochastic. For these variables, the conventional tools leave us a feeling that some valuable information is thrown away and that a complex phenomenon is presented imprecisely. Here, we apply recent advances initially made in the study of ocean waves to study the blood pressure waves in the lung. We note first that, in a long wave train, the handling of the local mean is of predominant importance. It is shown that a signal can be described by a sum of a series of intrinsic mode functions, each of which has zero local mean at all times. The process of deriving this series is called the “empirical mode decomposition method.” Conventionally, Fourier analysis represents the data by sine and cosine functions, but no instantaneous frequency can be defined. In the new way, the data are represented by intrinsic mode functions, to which Hilbert transform can be used. Titchmarsh [Titchmarsh, E. C. (1948) Introduction to the Theory of Fourier Integrals (Oxford Univ. Press, Oxford)] has shown that a signal and i times its Hilbert transform together define a complex variable. From that complex variable, the instantaneous frequency, instantaneous amplitude, Hilbert spectrum, and marginal Hilbert spectrum have been defined. In addition, the Gumbel extreme-value statistics are applied. We present all of these features of the blood pressure records here for the reader to see how they look. In the future, we have to learn how these features change with disease or interventions.

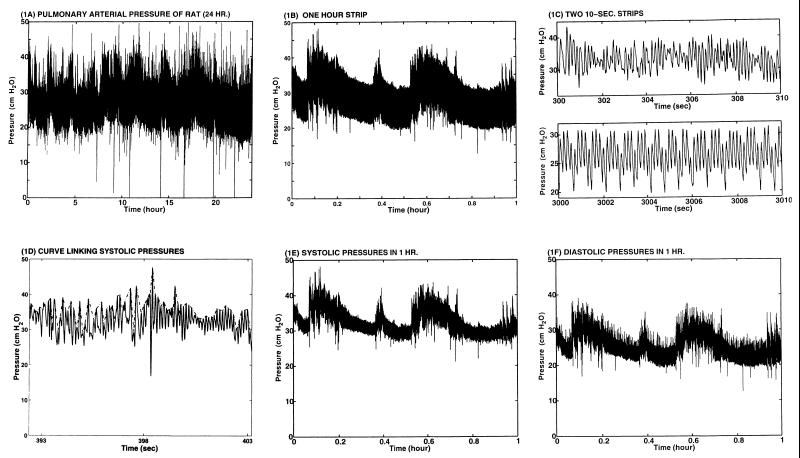
We recorded the blood pressure in the pulmonary arterial trunk (between the pulmonic valve and the bifurcation point of the right and left pulmonary arteries). The recording was done continuously with an implanted catheter as a part of a research plan to study the remodeling of the three layers of vascular tissues of the arterial wall in response to changes of stresses in the tissues (1–6). Pulmonary arteries were chosen as an object of tissue engineering research because blood pressure in pulmonary arteries can be changed quickly and noninvasively by changing the oxygen concentration in the gas that the animal breathes. Blood pressure is a major parameter related to the stress distribution in the blood vessel wall. The present article is focused on the analysis of the blood pressure records of a normal rat breathing normal atmosphere at sea level. Fig. 1A shows a record over a 24-h period. Fig. 1 B and C show segments recorded at an expanded time scale. It is seen that the amplitude and frequency are variable. The changes are nonstationary, and definitions are needed to know what the heart rate, the mean blood pressure, and the amplitude of pressure oscillations are. Our objective is to see how these quantities can be characterized mathematically.

Figure 1.

Blood pressure in pulmonary arterial trunk of the rat (rat code: 12099701). (A) Twenty four-hour strip, from 12/9/97 1118 h to 12/10/97 1118 h. (B) One-hour strip 12/9 1118 to 1218 h. (C) Two 10-s strips. (D) A short section illustrating a curve linking systolic peaks. (E) Systolic peaks in 1 h. (F) Diastolic peaks in 1 h.

MATERIALS AND EXPERIMENTAL METHODS

For the purpose of long term recording of blood pressure, a catheter must be implanted into an artery. The Riva–Rocci cuff inflation method of blood pressure measurement based on Korotkoff sounds cannot provide the desired data. We studied adult male Sprague–Dawley rats under a protocol approved by the University of California, San Diego Committee on Animal Research. Rats purchased from Harlan–Sprague–Dawley were given 3–7 days to acclimatize to their housing. Housing temperature was controlled (70°F/72°F) and a 12:12 h light–dark cycle was imposed at 0600 and 1800 h. They had continuous access to standard rat chow (Harlan–Sprague–Dawley) and tap water.

During the implantation of the pressure probe, the rat must be anesthetized. Halothane causes liver injury (7), and Nembutal affects blood pressure (8). We found that isoflurane (1-chloro-2, 2, 2-trifluoroethyl difluoromethyl ether) gas (9) anesthetizes rats quickly and without untoward effect. We installed in a fume hood an isoflurane delivery system, which consisted of a compressed air line and an isoflurane vaporizing, cooling, and delivery apparatus. The compressed air line (4 mm i.d.) was divided into two branches: one to the animal, the other to the isoflurane delivery apparatus consisting of a Pyrex bottle (Fisher Scientific) as a vaporizing chamber. Air flow bubbled through the liquid isoflurane and was controlled by a Nupro valve (6.35 mm i.d.) (Fisher Scientific) and adjusted for the desired depth of anesthesia according to the animal’s respiratory rate and reflexes to touching. The isoflurane–air mixture was cooled in 250-ml Pyrex flask suspended in an ice bath to prevent condensation in the tubing, which, in one branch, goes to an anesthesia induction chamber (a transparent vacuum desiccator, 4330 ml, Fisher Scientific) for quick initial anesthetization and in another branch goes to a nose cone for continuous operation. The anesthetized rat was placed on a water-filled, temperature-controlled pad (American Pharmaseal, Valencia, CA) with its nose loosely positioned within the nose cone.

Instrumented Rat.

Sterile technique was used to catheterize the pulmonary artery of an anesthetized rat with a Micro-Renathane implantation tubing (MRE 025, 0.305 mm i.d., 0.635 mm o.d.; Braintree Scientific) with the aid of a trocar-like Introducer. The MRE 025 catheter, 20 cm long, was marked with permanent ink 7, 9, and 14 cm from the distal tip (the tip inserted into the artery). The Introducer, 7 cm long, was a PE-90 tubing (0.86 mm i.d., 1.27 mm o.d.). Its distal part (1 cm) was bent 30° from the axis, the tip was carefully blunted to avoid any cutting edges, and its surface was marked with permanent ink 4, 5, and 7 cm from the distal tip. The mark at 7 cm was made to indicate the direction of the distal tip of the Introducer.

The proximal end of the Introducer was first connected to a Statham (Hato Rey, PR) P23ID pressure transducer with a Silastic tubing (Dow-Corning). While observing the pressure tracings on a Soltec 8K21 polygraph (Soltec, Sun Valley, CA), we very gently inserted the Introducer into the jugular vein and advanced through the right atrium to the right ventricle. The location of the tip of the Introducer can be recognized by the signature of the pressure trace. After the Introducer was placed in the right ventricle, the tubing that was connected to the pressure transducer was replaced by the MRE 025 catheter, which was passed inside the Introducer. The proximal end of the MRE 025 catheter was connected to a 40-cm long Silastic tubing (1.016 mm i.d., 2.159 mm o.d.) attached to the Statham pressure transducer. By gentle advancement of the catheter within the Introducer, we cannulated the pulmonary artery, with its tip position verified by the typical arterial pressure signature. Then the Introducer was slipped out over the catheter and removed. The catheter then was secured in the jugular vein with sutures, tunneled s.c. to the back of the neck, and protected with a jacket-swivel system, which allowed the rat to move freely but did not allow scratching or biting of the catheter.

Continuous Measurement of Pulmonary Arterial Pressure in a Conscious and Unrestrained Rat.

The free-moving rat then was placed in a standard-sized cage and moved to a quiet room that was maintained at ≈70° and illuminated by fluorescent lighting from 0600 to 1800 h. The tubing leading from the animal to the swivel was protected by a lightweight, highly compliant open spiral Latex shield and was connected to an infusion pump and a Statham P23ID transducer through a “T” tube. The catheter was irrigated continuously with heparinized saline (20 units/ml saline) at a rate of 0.6 ml/h pumped by a RAZEL Syringe Pump (Model A-99, RAZEL Scientific Instruments, Stamford, CN).

Pressure data were collected continuously by a computer while the pressure waveform was recorded on an Astro-Med recorder (Model MT8500, Astro-Med, West Warwick, RI). The analog-to-digital conversion was accomplished by a data translation board (DT31-EZ, Data Translation, Marlboro, MA). The pressure waveform was sampled 100 points/s each minute over a 24-h period.

Data Analysis Methodology.

The well known Fourier spectral analysis works well for strictly periodic or stationary random functions of time. To deal with nonperiodic or nonstationary functions, a number of methods have been introduced, such as the Spectrogram (10), the Wavelet analysis (11–14), the Wigner–Ville distribution (15, 16), the Evolutionary Spectrum (17), the Modal Analysis (18), and some others, all designed to modify the global representation of the Fourier analysis. They all failed in one way or another as discussed by Huang et al. (19, 20). For the present analysis, we use a new method proposed by Huang et al. (20), namely, the “empirical mode decomposition method,” which is explained below.

We adopted the spacing of the extrema as the time scale. A sifting process was proposed to decompose any given set of data into a set of intrinsic mode functions (IMF), which are defined as any function that fulfills the following conditions: (i) in the whole data set, the number of extrema and the number of zero-crossings must either equal or differ at most by one and (ii) at any time, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.

How to derive an intrinsic mode function from a set of data, X(t)? Answer: by computing the envelopes and subtracting the mean. To compute, one first identifies the successive extrema of X(t), then the local maxima are connected by a cubic spine as the upper envelope, and all of the local minima are similarly connected as the lower envelope. The mean of these envelopes is a function of time and is designated as m₁(t). The difference between the data X(t) and the mean m₁(t) is computed and is designated as the first component h₁(t):

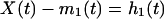1

This h₁(t) is almost an IMF, except that some error might be introduced by the curve fitting process. To make sure, we treat h₁(t) as a new set of data, determine its upper and lower envelopes, and compute their new mean m₁₁(t). The difference, h₁ − m₁₁ = h₁₁, is designated as h₁₁(t). This h₁₁(t) again is treated as new data, and the process is repeated a number of times until it converges. The convergent result is designated by the C₁(t). C₁(t) is the first intrinsic mode function of the data set X(t). It has zero local mean. Now, subtract C₁(t) from the data X(t) and call the difference “the first residue” R₁(t)

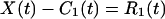2

The residue R₁(t) is analyzed as new data by the same method. The new mean is found, and the difference of R₁(t) minus its mean converges to a function of time, C₂(t), which is the second intrinsic mode function of the data X(t). It also has zero local mean. The process can be continued until either the residue or the intrinsic mode becomes less than a predetermined value of no substantial consequence or the residue becomes a constant or a monotonic function from which no more IMF can be extracted. If the process takes n steps, then we have

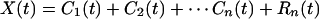3

Now that the residue R_n is understood clearly, we will drop it from further consideration. All C₁^… C_n have zero mean. We now perform a Hilbert transformation defined by Eq. 4 on every term in Eq. 3. The Hilbert Transform of X(t) is designated as Y(t):

4

Here the integral is defined in the sense of Cauchy principal value. Hilbert has shown (21) that X(t) and Y(t) enjoy a reciprocal relationship as shown in Eq. 4, and the complex variable Z(t) = X(t) + iY(t) is an analytic function of t. Write Z(t) in polar coordinates as

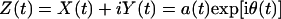5

6

Huang et al. (19) defined the instantaneous frequency ω(t) as the derivative of θ(t) with respect to time t:

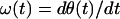7

and justified it in several ways. If ω(t) is introduced into Eq. 5, then Z(t) can be expressed as a function of the amplitude a_j and frequency ω_j of the IMFs:

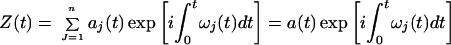8

The vanishing of the local means of C₁^… C_n is very important because a_j(t), θ_j(t) are sensitive to the local means. For example, if X(t) = sin t, then Y(t) = cos t, and Z(t) = sin t + icos t. But if X(t) = sin t + α + icos t, then Y(t) = cos t still, and Z(t) = sin t + α + icos t. Thus, you see that a(t) and θ(t) are very much a function of α. So it is nice to have α = 0.

The three variables a, ω, and t are related by Eq. 8 as a surface in three dimensions and can be drawn as contour map on the planes of (ω,t), (a,t), or (a,ω). Any one of these projections may be called a Hilbert Spectrum. The amplitude as a function of ω, t is called the Hilbert Amplitude Spectrum, H(ω,t). We also can define the Marginal Hilbert spectrum h(ω) as a function of frequency

9

which offers a measure of total amplitude (or energy) contribution from each frequency value. It represents the cumulated amplitude over the entire data span in a probabilistic sense.

Watching the animal while its pulmonary blood pressure was recorded, we noticed that that high systolic peaks usually were associated with animal motion: raising an arm or leg, reaching for food or drink, etc. Naturally we ask: What is the highest systolic peak in a given period? Gumbel (22) has shown that, for an unlimited variate obeying a statistical distribution of the exponential type, the probability that the largest value in a sample of size n be equal to or less than a certain value x is given by the Gumbel extreme-value distribution:

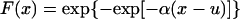10

in which α and u are parameters depending on n. The parameter u is the mode and is the most probable value of x. The inverse of the parameter α is a measure of dispersion, called the Gumbel slope. The function T(x) = [1 − F(x)]⁻¹ is called the returned period and is the number of observations required such that, on the average, there is one observation equaling or exceeding x. Practical calculation is made simple by using charts given in ref. 23. Methods to compute the confidence limits are given in refs. 21–23.

RESULTS

Five healthy rats, weighing 360.2 ± 6.7 g, were used in this study. They were active after surgery. Average time lapse between the end of operation and the start of data collection was 43 min.

Fig. 1A shows a 24-h record of blood pressure of a normal rat measured in the pulmonary arterial trunk. Fig. 1B shows a 1-h strip. Fig. 1C shows two random 10-s strips, one more “regular” than the other. Fig. 1D shows how an envelop linking the systolic pressure was drawn in a 10-s strip. Fig. 1 E and F are the systolic peaks and diastolic troughs for the 1-h record shown in Fig. 1B, obtained by connecting the successive peaks and successive valleys, respectively.

Fig. 2A shows the Fourier spectrum for the 1-h data given in Fig. 1B, from which we easily can identify the spectral peaks at 1.5, 6.5, and 13 Hz. The 6.5-Hz peak represents the heartbeats, and the 13-Hz peak represents its harmonics. The 1.5-Hz peak probably is related to respiration, but we are not certain. The Fourier spectra for the two 10-s sections given in Fig. 1C are presented in Fig. 2B in respective upper and lower panels. The result of the 1-min window Fourier analysis for a 1-h data is given in Fig. 2C. In Fig. 2C, the locations of the highest peaks of the Fourier spectra in every 1-min window are plotted on the time–frequency plane. A perspective view of the windowed 1-h and 10-h Fourier results are given in Fig. 2 D and E to show the variation of the amplitudes of the signals. Finally, a comparison of the Fourier (dotted line) and the Marginal Hilbert (solid line) spectra defined by Eq. 9 are given in Fig. 2F for a typical irregular 10-s section (Fig. 1C, upper panel).

Figure 2.

Fourier Spectrum (FS) of rat pulmonary blood pressure recording. (A) FS of the first hour data shown in Fig. 1B. (B) FS of two 10-s strips shown in Fig. 1C. (C) FS of the first hour data. A plot of the locations (time and frequency) of the highest peaks of the FS in every 1-min window. (D) FS, first hour. Plot of the amplitude of the spectrum as a function of the frequency in every 1-min window on the time–frequency plane in linear scales. (E) FS, first 10 h. Similar to D but with an enlarged time span. (F) Fourier (dotted line) and Marginal Hilbert (solid line) spectra of the first 10-s strip shown in Fig. 1C, Upper.

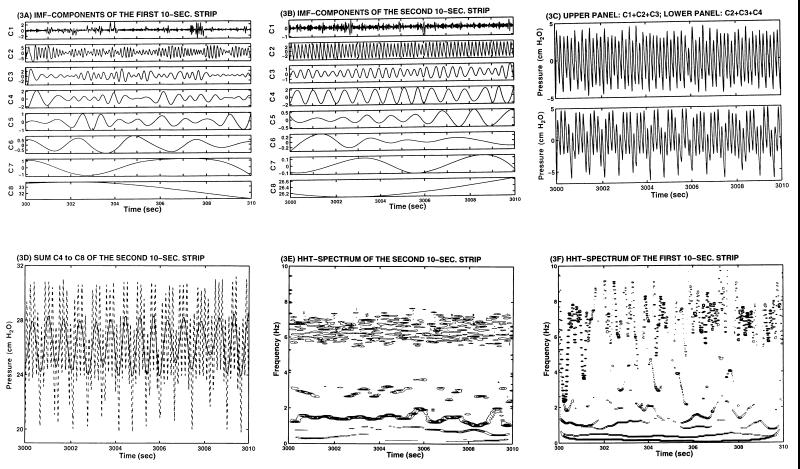
The results of the empirical mode decomposition method are illustrated by sifting the two 10-s records shown in Fig. 1C. The resulting IMF components are given in Fig. 3A and B for the upper and lower panels of Fig. 1C, respectively. The residual IMF R₈ is constant in both cases. In Fig. 3B, the IMF components have very different amplitudes; the most energetic ones are C2, C3, and C4. The amplitude and the periodicity of these three main components maintain very near their respective constant levels. Their sum offers a strikingly faithful representation of the signal variation as shown by comparing the lower panels of Figs. 3C and 1C. The only difference is the reference level at ≈26 cm H₂O given by C8. If one plots the sum of IMF components C4–C8 (solid line), one will recover the slow variation of the pressure signal (dotted line) as shown in Fig. 3D and the lower panel of Fig. 1C. The IMF components for the wave in the upper panel of Fig. 1C are given in Fig. 3A. Large variation in both amplitudes and periodicity are seen. The Hilbert Transforms of these IMF components give the Hilbert spectrum shown in Fig. 3E for the record in lower panel of Fig. 1C, showing that the most prominent energy bands are centered at 6.5, 3, and 1.5 Hz. These intra-wave frequency modulations as discussed by Huang et al. (20) are indications of nonlinear dynamics. Fig. 3F shows the Hilbert spectrum corresponding to Fig. 3A and the upper panel of Fig. 1C. The wide fluctuations of the frequency values make any visual mean estimation impossible. The Hilbert spectrum can be integrated to give the marginal Hilbert spectrum as given in Fig. 2F. Here, we can see the prominent spectral peaks at 7 and 1.3 Hz. Comparison of the marginal Hilbert spectrum with the Fourier spectrum indicates that their mean peaks do line up. However, the Hilbert spectrum clearly depicts the fluctuation of the frequency with time, whereas the Fourier spectrum gives the distribution of energy over frequencies without allowing the frequency of oscillation to be variable in the whole period of the time window. The basic difference between the spectral plots of Fig. 2C and Fig. 3 D and E lies in the stationarity hypothesis. Fig. 2C, the Fourier spectrum, assumes stationary oscillation. Fig. 3 D and E, the Hilbert spectra, are valid for nonstationary oscillations.

Figure 3.

The IMF and Hilbert Spectrum (HHT) of the blood pressure data. (A) IMF of the first 10-s strip of data shown in Fig. 1C, Upper. (B) IMF of the second 10-s strip shown in Fig. 1C, Lower. (C) Upper: sum C1+C2+C3; Lower: sum C2+C3+C4 of the second 10-s strip. (D) Sum C4–C8 of the second 10-s strip of data, IMF in B, is shown by the solid line, which reveals the slow variation of the blood pressure. The full signal, which is shown in the lower panel of Fig. 1C, is replotted here by the dotted line. (E) HHT spectrum of the second 10-sc strip. (F) HHT spectrum of the first 10-s strip. The residual R₈ in both cases are zero.

The statistical analysis of the extreme values of the mean blood pressure is illustrated in Fig. 4. The raw data are given in Fig. 4A. Because of the high fluctuation of the blood pressure values, any running mean would be misleading for there is no proper time scale to define the mean. To overcome this difficulty, we resorted to a method of envelope-mean. The procedure is to construct the envelopes for the systolic peaks and diastolic troughs as discussed before. Because of the nature of the data, even after one envelope smoothing, the smoothed systolic and diastolic pressure values still seemed to overlap over this time scale. So, we took the envelope of the envelope and repeated the procedure six times. Even after this smoothing, the results were still highly variable, as shown in Fig. 4B for the mean value in 24 h. For a 1-h section, the mean, systolic, and diastolic pressure values given in Fig. 4C are separable.

Figure 4.

(A) Oscillation of the mean blood pressure from 12/9/97 1118 to 12/10/97 1118 h (rat code: 12099701). (B) Oscillation of the mean blood pressure (smoothed by method explained in text). (C) The oscillation of the mean, systolic, and diastolic pressure in one hour (12/9/97 1118 to 1218 h). (D) The Gumbel extreme value statistics of the maximum systolic blood pressure in successive 10-min periods from 12/12/97 1050 to 2150 h plotted against a reduced variate that is related to cumulative probability on a Gumbel distribution paper. (E) The Gumbel extreme value statistics of a data set of the largest systolic pressure in successive 1-min periods. (F) The return period for any assumed extreme values of systolic pressure, based on the Gumbel statistical distribution of the extreme systolic pressure recording taken on 12/12/97 1050 to 2150 h.

To predict the maximum expected systolic pressure within a given time duration, we collected data on the largest systolic pressure in every 10-min segment of record. The set of extreme values is tested against the Gumbel distribution by plotting the probability on a Gumbel probability paper (ref. 23 and see refs. 21 and 22 for detailed methods). The results are given in Fig. 4D. The solid line is the fitted Gumbel distribution curve. The dotted lines are the confidence interval. Fig. 4E gives the corresponding results based on the largest systolic pressure in successive 1-min sections. From the Gumbel slope (1/α in Eq. 10), we obtained the return period for any assumed extreme systolic blood pressure as shown in Fig. 4F.

It is not the purpose of this article to explain the fluctuations of the blood pressure in a normal animal but to recognize the features of blood pressure records. The method described here does offer a more comprehensive view of the blood pressure fluctuation than the classical Fourier analysis. In more comprehensive experiments on determining the effects of hypoxia, tissue remodeling, and diseases, it would be interesting to see how the Fourier spectrum, Hilbert spectrum, intrinsic mode functions, and Gumbel extreme-value statistics would change. The applicability of this type of analysis to biology and medicine is evident.

ABBREVIATION

IMF

intrinsic mode function