An MEG-based Brain-Computer Interface (BCI)

Abstract

Brain-Computer Interfaces (BCIs) allow for communicating intentions by mere brain activity, not involving muscles. Thus, BCIs may offer patients who have lost all voluntary muscle control the only possible way to communicate. Many recent studies have demonstrated that BCIs based on electroencephalography (EEG) can allow healthy and severely paralyzed individuals to communicate. While this approach is safe and inexpensive, communication is slow. Magnetoencephalography (MEG) provides signals with higher spatiotemporal resolution than EEG, and could thus be used to explore whether these improved signal properties translate into increased BCI communication speed. In this study, we investigated the utility of an MEG-based BCI that uses voluntary amplitude modulation of sensorimotor μ and β rhythms. To increase the signal-to-noise ratio, we present a simple spatial filtering method that takes the geometric properties of signal propagation in MEG into account, and we present methods that can process artifacts specifically encountered in an MEG-based BCI. Exemplarily, six participants were successfully trained to communicate binary decisions by imagery of limb movements using a feedback paradigm. Participants achieved significant μ-rhythm self control within 32 minutes of feedback training. For a subgroup of three participants, we localized the origin of the amplitude modulated signal to the motor cortex. Our results suggest that an MEG-based BCI is feasible and efficient in terms of user training.

1 Introduction

Brain Computer Interfaces (BCIs) are communication devices that allow for communicating intentions by mere brain activity, not involving muscles (Wolpaw et al., 2002).

BCIs are of great importance for patients with diseases or traumatic injuries that lead to loss of voluntary muscle control, and to severe or total motor paralysis. Without muscle control, patients are cut off from communicating their needs and feelings to their environment (locked-in syndrome). The locked-in state may result from degenerative diseases such as amyotrophic lateral sclerosis, cerebral palsy, muscular dystrophy, multiple sclerosis, or from traumata such as brainstem stroke, brain or spinal cord injury. Some of these conditions impair the neural pathways that control muscles while others impair the muscles themselves.

BCIs may be classified according to the kind of brain signal they use for communication. BCIs are mainly based on electrophysiological signal acquisition methods, such as electro-encephalography (EEG), electrocorticography (ECoG) and recordings from individual neurons inside the brain. In recent years there has also been growing interest in BCIs based on imaging methods such as functional magnetic resonance imaging (fMRI) (Weiskopf et al., 2003) or near infrared spectroscopy (NIRS) (Coyle et al., 2004).

One type of brain-computer interface utilizes amplitude modulation of the μ-rhythm. This EEG component is typically found over sensorimotor cortex with a base frequency of 10–12 Hz. Its arc-shaped wave form implies a strong first harmonic in the β band at 20–24 Hz. μ-rhythm amplitude is decreased during planning, execution, or mere imagination of limb movements (desynchronization of the μ-rhythm) (Gastaut, 1952; Pfurtscheller, 1999; McFarland et al., 2000).

With a typical μ-rhythm based BCI, participants learn to control these rhythms in a real-time neurofeedback setting. Rhythm amplitude is extracted from brain signals over select locations and then translated into movement of a cursor on a screen. Initially, participants are prompted to control the cursor by imagination of limb movements. Aided by visual feedback, participants typically achieve voluntary rhythm modulation over time, and in those regions of the motor cortex that are associated with the respective limbs. Such a system allows for the communication of the user’s intent using simple cursor control, word processing, etc.

EEG-based μ-rhythm BCIs have proven their feasibility with healthy participants and with severely paralyzed patients (Pfurtscheller et al., 2000, 2003; Wolpaw et al., 2000; Kübler et al., 2005). While these systems can accurately communicate the user’s intent, they require extensive user training over many weeks or months. Furthermore, EEG data in the order of a few seconds are needed to reliably extract a single binary decision (Wolpaw et al., 2002). Other signal acquisition techniques such as electro-corticography (ECoG) (Leuthardt et al., 2004), or magneto-encephalography (MEG), may reduce training time, or increase reliability of a BCI. When compared to EEG, MEG supports a larger number of sensors, providing more spatial information (Bradshaw et al., 2001), and can detect information in the frequency range above 40 Hz (Kaiser et al., 2005) which is not present in EEG recordings. These considerations encourage exploration of MEG-based BCIs.

In this paper, we present a μ-rhythm based BCI using MEG for brain signal data acquisition. For MEG, the presence of the μ-rhythm is well-known (Salmelin et al., 1997), but the feasibility of an MEG-based μ-rhythm BCI is not immediately obvious. Despite the close relationship between EEG and MEG, characteristic differences in spatial signal propagation from source to sensors require approaches to data analysis and to spatial filtering different from EEG-based BCIs. At the same time, suitable methods are not readily available because common MEG data analysis methods are focused on source localization of stimulus-induced evoked responses, steady state responses, or identification of stationary sources (Salmelin and Hari, 1994; Liljeström et al., 2005), rather than on extraction of BCI signals. Additionally, different kinds of artifacts occur for EEG and MEG, which implies the need for artifact processing methods that are specific for each.

Data from six healthy participants illustrate the viability of our approach, and that training time and accuracy are comparable to what is common for EEG based BCIs.

While there have been in-depth investigations into the spatial origin of stationary brain rhyhtms (Liljeströom et al., 2005), the modulated μ-rhythm which is exploited by BCIs has not been subject to localization studies. Combined EEG and fMRI studies have been proposed, but remain difficult due to scanner artifacts difficult to deal with in the on-line case. MEG, on the other hand, suggests itself for source localization applications, because source-to-sensor signal propagation of magnetic fields is less influenced by the unknown physical properties of the skull than is the case with EEG (Hämäläinen et al., 1993). We show that data obtained during BCI operation can be used to localize, with high spatial precision, the origin of the μ-rhythm used for cursor control, and demonstrate exemplary localization for three of the six participants.

2 Materials and Methods

2.1 Participants

Six healthy adult volunteers participated in the study (five male, one female, mean ± SD age 30.0 ± 6.4), all being naïve to BCI operation. The study was approved by the ethics committee of the University of Tübingen Medical Faculty, and all participants gave informed consent.

2.2 Experimental Setting

Participants were seated upright, watching a 20 × 15 cm area on a screen located at an eye distance of 1.2 m, resulting in a maximum visual angle of 6° from the central direction.

Recordings were performed in sessions lasting about 1 h each. In an initial session (screening), no feedback was provided; instead, participants were asked to perform actual repetitive hand and feet movements, followed by corresponding imagery (left hand vs. right hand, both hands vs. both feet). The task was indicated by cues that appeared on the screen for 4 s, with 2 s intervals between the cues.

Data from this session comprised 20 trials with actual movement for each condition, and 30 trials of imagery for each condition. These data were used to determine parameters for the subsequent feedback sessions, in which participants learned self-control of their μ-rhythm amplitude. For training sessions, participants were instructed to try hand vs. feet movement imagination, or imagined hand movement vs. rest, whichever strategy produced the largest changes in their brain signals.

After each of those sessions, data were analyzed and on-line parameters were adapted as described in section 2.6.

Training sessions comprised 16 runs lasting 2 minutes each. Each run was followed by a short break of 10 to 20 seconds. Every 6 runs, there was a resting period of about 5 minutes.

2.3 MEG Recordings

MEG was recorded in a magnetically shielded room using a whole-head system (CTF Inc., Vancouver, Canada) comprising 151 first-order gradiometers distributed with an average distance between sensors of 2.5 cm. Data were sampled at a rate of 625 Hz with an anti-aliasing filter at 208 Hz. Head position was recorded continuously using localization coils that were fixed at the nasion and at the preauricular points, forming a head-relative coordinate system. The coils were driven with sinusoidal currents of 156 1/4 Hz, 125 Hz, and 104 1/6 Hz (1/4, 1/5, and 1/6 of the sampling frequency), generating a strong signal (1 pT, ca. 50 times the amplitude of brain signals), far above the brain signal’s frequency range of interest (10-40 Hz), thus avoiding distortions inside that range of interest. From the coil signals present in the recordings, it was possible to compute the head’s relative position and orientation off-line using narrowband filtering and least-squares fitting of each coil’s amplitude distribution to a magnetic dipole forward model. This was done as part of the source localization procedure described in section 2.7, and to control for head movement artifacts off-line as described in section 2.8.2.

2.4 Real-time Feedback

In intervals of 70.4 ms, blocks of 44 samples were transmitted from the MEG to a real-time feedback system attached via a network interface. The real-time feedback system was implemented using the BCI2000 general-purpose BCI system (Schalk et al., 2004). MEG data acquisition hardware was connected to a standard PC running a Linux operating system via a SCSI interface. Data acquisition and hardware control was done through a proprietary software (Acquire, CTF Inc.) running on the Linux machine. To allow real-time data access, CTF’s Acquire program writes raw digitized MEG data into a shared memory area in constant-sized blocks, immediately after digitization. On this machine, a second program was running that acted as a relay to BCI2000 via a TCP/IP-based socket interface. This second program, which was specifically written for this purpose, implements a widely used protocol defined for the Neuroscan SCAN server (Compumedics, El Paso, TX, USA). Thus, it was possible to use an existing BCI2000 component (i.e., the Neuroscan client) for data acquisition.

On arrival of each block of data, the feedback system computed and updated a cursor position representing the time course of μ or β bandpower amplitude observed at a subset of MEG sensors. Sensors and bandpower frequencies were chosen individually for each participant as described in section 2.6.

During feedback, the cursor moved from left to right at a constant rate, beginning its movement at the center of the feedback area’s left margin; μ or β bandpower determined its vertical speed such that the cursor’s final position at the right margin represented the trial mean of μ-rhythm activity quantified as described in section 2.5. The participant’s task was to move the cursor into a pre-defined half of the right margin indicated by a red bar (“target”). Feedback was provided in discrete trials lasting 6.7 s each (fig. 1). A trial consisted of

Fig. 1. Elements of a feedback trial.

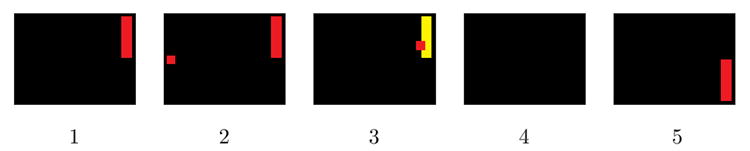
A trial consisted of (1) a 1 s period in which the target indicated the required response but no cursor was visible, (2) a 4.2 s feedback period with cursor movement, (3) a 1.5 s period during which the target was highlighted to indicate successful performance, or remained neutral in case of a miss, (4) an inter-trial interval of 0.5 s, followed by another trial (5).

• a 1 s period in which the target indicated the required response but no cursor was visible;

• a 4.2 s feedback period during which the cursor moved from left to right at a constant rate, and up or down depending on the participant’s μ-rhythm amplitude;

• a 1.5 s period during which the target turned yellow to provide feedback about successful performance, or kept its red color if the participant’s response did not meet the task requirement.

Between trials, there was an interval of 0.5 s.

2.5 Real-time Signal Processing

Each block of 44 samples, i.e., the most recent 70.4 ms of data, was analyzed by an autoregressive (AR) spectral estimation method (Burg Maximum Entropy Method, Marple (1987)), and the amplitude (square root of power) in a 3 Hz-wide frequency band was determined from the AR coefficients. The band was selected as described below in section 2.6. Vertical cursor speed υ_y was then a linear function of this amplitude S:

$${\upsilon }_y=b(S-a),$$

where the intercept a and the gain b was adapted dynamically to optimize the participant’s control over cursor movement (McFarland et al., 1997a). Considering cursor movement and subsequently hitting one out of two targets as a linear binary classification, it follows from the optimal linear classification rule (Rencher, 1998) that optimum control is achieved if a equals the mean of the two class means:

$$a=\frac{1}{2}({\overline{S}}_{\mathrm{top}}+{\overline{S}}_{\mathrm{bottom}}).$$

An adaptive on-line estimate of the class means ${\overline{S}}_{\mathrm{top}}$ and ${\overline{S}}_{\mathrm{bottom}}$ was calculated as the average of S over the 3 most recent trials for the respective target. To achieve an appropriate magnitude of cursor movement, b was chosen such that for a signal value equaling a class mean, the cursor hit the center of the associated target:

$$\frac{1}{b}\propto ({\overline{S}}_{\mathrm{top}}-{\overline{S}}_{\mathrm{bottom}}).$$

2.6 Spatial and Temporal Filtering

For the initial training session, spatial and temporal filter parameters were chosen according to the analysis results of the initial screening session. Between training sessions, these parameters were again adapted if suggested by the previous session’s analysis.

Off-line analysis of screening and training sessions comprised computation of topographical and spectral maps of determination coefficients (squared correlation values). These maps indicate, for each sensor and each frequency band, the amount of amplitude variance accounted for by the task condition, i.e., imagination of movement vs. rest (fig. 2 and 3). For off-line processing, we used the Welch method to compute spectrograms rather than the AR method used in the on-line case (625 samples, or 1 s, window size, no overlap, rectangular window).

Fig. 2.

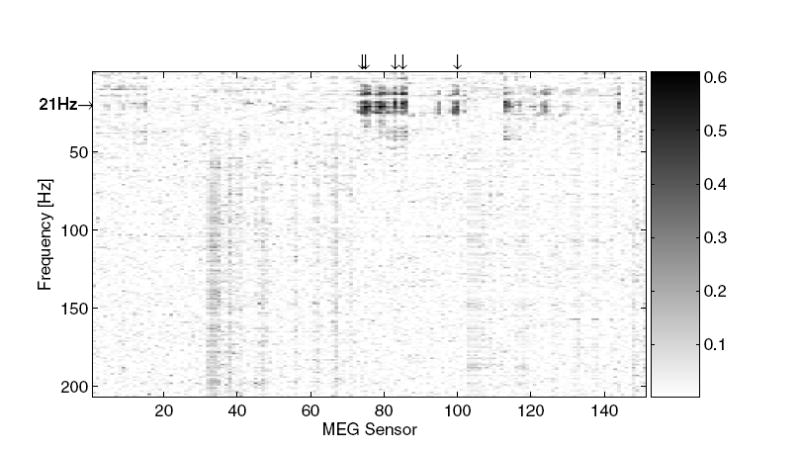
Spectral map of determination coefficients computed from three runs (54 trials) selected from participant A’s second training session. Arrows on the top indicate sensors used to compute the feedback signal, and an arrow on the left indicates the frequency entering into fig. 3.

Fig. 3.

Topographical maps of determination coefficients (r² values) (a) and amplitude differences (b) for the data from fig. 2 between 21 and 22 Hz. (All topographies are viewed from the top.)

For on-line feedback, we chose a single frequency band within the μ (9-15 Hz) or β (18-30 Hz) range that displayed the largest correlation with the target position. As a spatial filter, sensors with the highest correlation values were linearly combined with weights of +1 or −1 depending on the relative orientation of the magnetic field lines at the respective sensor locations (into or out of the skull).

This spatial filtering method was designed as an analogy to Laplacian filtering used for EEG signals. Due to the propagation properties of EEG signals, Laplacian filtering provides a global linear filter that results in signals which are more “localized” than the original signals – localized in the sense that transformed channels contain less signals from remote locations than the un-filtered signals. Thus, Laplacian filtering is a simple linear filter that improves signal-to-noise ratio for BCI purposes (McFarland et al., 1997b). In the case of MEG, individual sensors still record linear mixtures of source signals. However, due to the more intricate geometry of magnetic fields vs. electric fields, it is not possible to find a general spatial filter that improves signal-to-noise ratio in analogy to Laplacian filtering; rather, position and orientation of the sources of interest must be taken into account. Magnetic field lines form circles around a source current located inside the skull, thus each field line that leaves the skull at one location will enter it at a different location distant from the first one. This results in a bipolar pattern for dipole sources (fig. 3 and 4). Knowing the pattern associated with a source of interest, it is possible to improve signal-to-noise ratio by a simple linear combination of sensors located inside the pattern’s two areas associated with maximum field amplitude, using +1 and −1 as weights according to the relative orientation of the magnetic field.

Fig. 4.

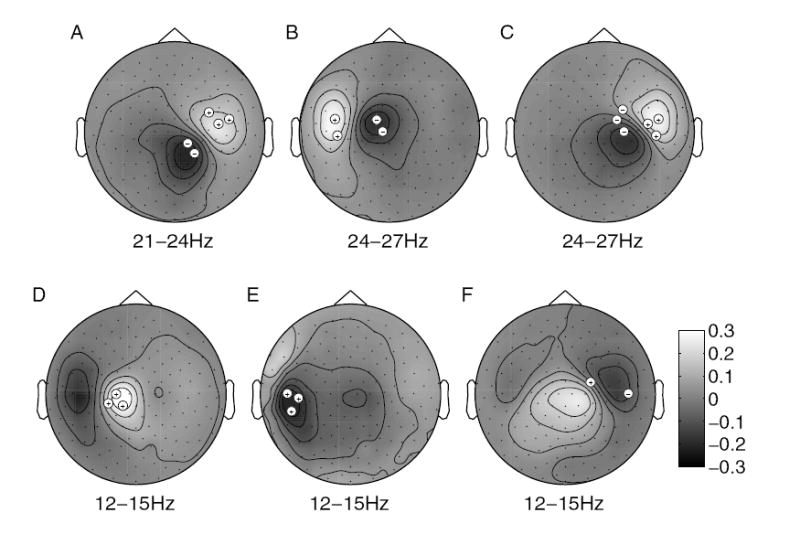
PDA extracted principal components of amplitude differences (as exemplified by fig. 3) for all participants. A–D and F clearly resemble single current dipole fields, E is less distinct. Computation was based on the participants’ 3 to 4 most successful training runs (54 to 72 trials). Dots indicate sensors, lines are isocontours of normalized field strength (actual field strength is indicated in fig. 7). Markers indicate which sensors enter into cursor feedback, and the signs of their respective weights in spatial filtering. (All topographies are viewed from the top.)

To determine the spatial distribution of the modulated magnetic field, a principal component analysis (PCA) related technique was used which we call “Phase Decorrelation Analysis” (PDA). This technique was designed to linearly decompose the signal difference between the two conditions – imagined movements vs. rest, or upper vs. lower target – into orthogonal components by using amplitude and phase relations between sensors as described in )app. A. This method allowed to extract a dominant modulated source from a background of less pronounced modulation and noise.

As an example, fig. 4 A shows the main component extracted from the difference topography depicted in fig. 3, and illustrates how much information is gained over the amplitude difference when phase information is taken into account by the PDA method.

Finally, as a criterion for the number of sensors chosen, we used the decay of determination coefficients, avoiding the use of sensors with neighbors for which the determination coefficient dropped below 80% of its maximum value. This criterion was chosen to minimize the spatial filter’s sensitivity to the participant’s absolute head position while still benefitting from a larger number of sensors in cases where determination coefficients were high over a relatively large area (for an illustration, compare fig. 3 a with the actual sensor locations chosen in fig. 4 A).

2.7 Source Localization

Unlike electrical potentials measured by EEG, magnetic fields that originate from the brain are not distorted by the dominating spherically symmetric part of the distribution of conductivity inside the skull (Hämäläinen et al., 1993). Thus, for a given magnetic field distribution measured by a sensor array, source localization is possible using an inverse fitting procedure without knowledge of the conductivity distribution.

As discussed in app. A, the spatial weights of a PDA component may be interpreted in a way similar to the interpretation of source-to-sensor-space transformations derived by blind source-separation algorithms (Cardoso and Soloumiac, 1993). In this interpretation, a certain source’s spatial source-to-sensor weights may be identified with the field of that source at a certain point in time, up to a multiplicative constant. Thus, these weights may be used as a field distribution input to a dipole fitting procedure.

For the localization of source dipoles (fig. 6), the PDA component with the largest absolute eigenvalue was used as input to a least-squares current dipole fitting procedure (Equivalent Current Dipole (ECD) fitting using a homogenous spherical head model, software by CTF Inc., Vancouver, Canada). To transform the resulting MEG-based dipole location into the coordinate system of a participant’s MRI scan, the positions of the head localization coils were determined relative to MEG sensor positions. Then, these were identified with the corresponding positions (fiducial points at the nasion, and the preauricular points) as visible in the participant’s MRI scan. As a measure for errors, pairwise distances were computed between coil positions in the MEG coordinate system, and compared to pairwise distances between the fiducial points in the MRI coordinate system, and found to be below 4 mm. This error is on the same order as that typically achieved for applying localization coils to a participant’s head. For the ECD fit itself, spatial accuracy has been found to be in the order of below 4 mm in realistic simulations for a single dipole and noise up to 20 dB (Jerbi et al., 2004). These two errors combine to give a total localization error of less than 5.6 mm.

Fig. 6.

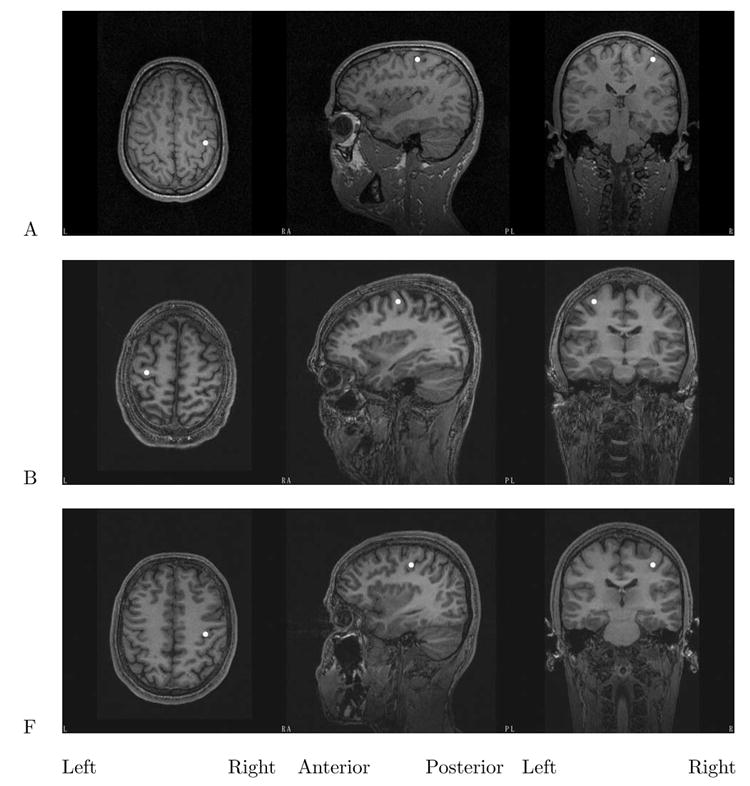
Locations of μ-rhythm sources obtained by Equivalent Current Dipole (ECD) fitting of PDA components displayed in fig. 4, plotted into MRI scans of participants A, B, and F. ECD fitting errors were 2.3%, 1.9%, and 5.2% (normalized least-squares).

2.8 Artifact Control

2.8.1 Muscular Artifacts

Electromyographic (EMG) activity originating from facial and neck muscles is reflected in large amplitude signals over wide frequency ranges. Because EMG signals can extend into μ and β bands, it could be possible for a participant to control the feedback cursor by muscle tension and relaxation. These artifacts are readily identified by their broad-banded spectrum, imposing a vertically dominant structure that extends to high frequencies on a feature map (fig. 8), while modulation of brain rhythms with their line spectra displays a dominantly horizontal line structure in a feature map (fig. 2).

Fig. 8.

Determination coefficients (r² values) over channels and frequencies from 72 trials of participant C showing contamination with task-related myographic activity. Dark horizontal lines indicate spatially distributed task correlation for cortical signals at distinct frequency bands, dark vertical lines indicate broad-banded task correlation for myographic signals. In this example, task-correlated myographic activity does not extend to the sensors and frequencies used for actual cursor control (as in fig. 2.7, these are indicated by arrows).

2.8.2 Head Movements

Head movements alter the distance from sources to sensors as well as their relative orientation. In the case of a physiological current dipole, the magnetic field component measured by MEG sensors strongly depends on source-sensor distance (∝ r⁻³), thus amplitude modulation at the sensors used for cursor movement may be achieved by head movements.

To control for head movements, localization coils were used as described in section 2.3. These coils define a head-relative coordinate system which was used for off-line detection of task-related head motion. Thereby, task-related translations were obtained by linearly correlating the three spatial coordinates of the head-centered coordinate system’s origin with the task condition variable (± cases corresponding to the two task conditions):

$${\overrightarrow{r}}_{\pm }=\pm \frac{1}{2}\mathrm{\Delta }\overrightarrow{r}+{\overrightarrow{r}}_0.$$ (1)

Task-related rotations and scaling transformations were obtained by forming a 3×3-matrix from the coordinate system’s three basis vectors, taking its matrix logarithm, and linearly correlating it with the task condition variable:

$${[{\overrightarrow{e}}_1,{\overrightarrow{e}}_2,{\overrightarrow{e}}_3]}_{\pm }=e^{\pm \frac{1}{2}\mathrm{\Delta }M}{e}^{M_0}.$$ (2)

For each participant session, linear regression resulted in an intercept $\{{\overrightarrow{r}}_0,M_0\}$ representing an average head position, and a slope $\{\mathrm{\Delta }\overrightarrow{r},\mathrm{\Delta }M\}$ that represented task-related movements. More precisely, task-related rotation around an average axis was available in form of the anti-symmetric part of ΔM, with the largest imaginary part of its eigenvalues representing the rotation angle (“task” columns in tab. 1).

Table 1.

Intra-session head motion. For the head-centered coordinate system derived from dipole-fit inferred coil locations, the following values are reported: In the “total” columns, standard deviations from its mean position and orientation, in terms of translatory and rotational movement. In the “task” columns, amount of task-related movement, with associated descriptive p-values in the “p” columns if significant (<0.05). In the two rightmost columns, brain signal modulation during training sessions is given in terms of relative amplitude modulation ΔA/A₀. In the “actual” column: Relative amplitude modulation after spatial and spectral filtering as done on-line. In the “simulated” column: Estimated amount of modulation caused by task-related movements. Index 0 denotes the initial session (without feedback). For participant F’s second training session, no localization data was available. Please refer to the text for further details (sec. 2.8.2).

Participant Session		Localized Coil Positions						Brain Signal Modulation
		Translation (mm)			Rotation (degrees)
		total	task	p	total	task	p	simulated	actual
A	0	1.30	0.05	<0.05	1.74	0.06
	1	1.49	0.08	<0.001	1.87	0.04	<0.04	0.003	0.140
	2	1.20	0.10	<0.001	2.66	0.05	<0.002	0.003	0.129
B	0	3.88	0.07		8.46	0.14
	1	4.47	0.21	<0.001	8.32	0.42	<0.001	0.002	0.035
	2	8.87	0.24	<0.001	8.90	0.21	<0.001	0.016	0.068
	3	5.44	0.18	<0.001	6.66	0.13	<0.001	0.007	0.083
C	0	6.59	0.09		4.83	0.17	<0.02
	1	1.58	0.03	<0.006	2.82	0.06	<0.001	0.001	0.103
	2	2.46	0.07	<0.005	2.46	0.06	<0.05	0.006	0.077
D	0	1.68	0.03		4.13	0.04
	1	2.38	0.02		2.94	0.02		0.001	0.040
	2	2.03	0.03	<0.001	2.83	0.04		0.002	0.125
E	0	6.41	0.30	<0.04	7.60	0.25	<0.02
	1	7.40	0.03		4.74	0.07		0.000	0.017
	2	2.00	0.03	<0.04	2.65	0.01		0.000	0.035
F	0	2.15	0.08	<0.004	1.64	0.06	<0.008
	1	2.63	0.01		2.39	0.00		0.003	0.015

In addition, for each head position sample, the linear transformation relative to the session’s average head coordinate system was computed. From these data, the standard deviation of the translation vector and the rotation angle were determined (“total” columns in tab. 1).

Analogously, the linear transformation connecting average head positions of subsequent sessions were used to infer the amount of re-positioning error between a participant’s sessions (tab. 2). Here, a re-scaling of the head-centered coordinate system may occur in addition to translations and rotations, due to errors when placing localization coils to the fiducial points. This rescaling is represented by the symmetric part of ΔM, and quantified by that symmetric part’s largest eigenvalue. In tab. 2, we give the scaling error in terms of length change for a fiducial point’s position vector in the participant’s head-centered coordinate system.

Table 2.

Inter-session head motion (re-positioning error). For each pair of subsequent sessions, the amount of translatory and rotational movement, and scaling is reported that corresponds to the transformation of one session’s head-centered coordinate system into the next session’s one. Unlike translatory and rotational movement, scaling only depends on the error in reproducing fiducial points, i.e. when placing localization coils to the head. Index 0 denotes the initial session (without feedback). For participant F’s second training session, no localization data was available. Please refer to the text for further details (sec. 2.8.2).

Participant Session		Translation (mm)	Rotation (degrees)	Scaling (mm)
A	0–1	1.30	8.0	0.23
	1–2	2.99	12.6	0.78
B	0–1	5.63	5.84	0.33
	1–2	10.9	3.27	1.57
	2–3	6.90	4.66	1.46
C	0–1	5.70	4.54	0.93
	1–2	4.62	2.37	0.49
D	0–1	6.10	8.62	0.16
	1–2	4.68	5.89	0.51
E	0–1	5.76	8.11	0.94
	1–2	10.4	2.31	0.05
F	0–1	5.01	2.25	0.32

During feedback training, participants may have followed the feedback cursor with their eyes and, in synchrony, with their heads. To evaluate the influence of these movements on our results, we considered relative modulation of brain signals, which is defined as the ratio of amplitude difference between task conditions, and mean amplitude. From a linear regression of brain signal amplitude on the task condition variable, one obtains (again, ± cases corresponding to the two task conditions):

$$A_{\pm }=\pm \frac{1}{2}\mathrm{\Delta }A+A_0,$$

with a relative modulation of ΔA/A₀.

For each training session, we computed the brain signal’s relative modulation after spatial and spectral filtering as it was done on-line (“actual” column in tab. 1). To assess whether this modulation could be due to systematic head movements, we simulated the influence of the observed task-related movements on the signal of a realistic dipole source. In detail, we determined realistic source dipole parameters for each participant by fitting a single Equivalent Current Dipole model to the data displayed in fig. 4. Then, for each session, the resulting dipole’s position and orientation were subjected to the transformations corresponding to the + and − cases of eq. 1 and 2. The corresponding field distribution was computed for each case, and a relative modulation was determined for the signal resulting from spatial filtering (“simulated” column in tab. 1). Comparing the simulated effect of head movements to the actually observed modulation of brain signals, we find that actual modulation is consistently greater than what might be induced by head motion. This result is inconsistent with the hypothesis that cursor control was primarily governed by head motion (sec. 3.4).

2.8.3 Hand/feet movements

Generally, actual hand or feet movements defy the sense of a BCI which, by definition, does not rely on external muscles for transmitting information. Investigations of covert hand movements during the use of an EEG-based μ-rhythm BCI used forearm EMG recordings to correlate muscular with μ-rhythm activity. These investigations show that covert movements were not involved (Vaughan et al., 1998; Wolpaw and McFarland, 2004).

Actual hand or feet movements do not directly cause artifacts but may be necessary to produce the signal that controls the cursor. To account for this possibility, we monitored participants using a video camera. Additionally, participants were instructed that they were welcome to use hand movements if that improved their control, but they should report usage of hand movements to the instructor. None of the participants displayed or reported actual hand movements.

3 Results and Discussion

In this study, we developed methods suited for an MEG-based μ-rhythm BCI, and validated these methods by successfully training six healthy participants in the use of this BCI.

3.1 Behavioral Results

Learning curves for all participants are presented in fig. 5. To reduce statistical noise, accuracies were smoothed over three runs, so each accuracy value is computed from 3 * 18 = 54 trials. At 54 binary trials, an accuracy of 63% or better is statistically significant at the p < 0.05 level. We thus considered accuracies at or above 63% as significant cursor control. In fig. 5, this significance level is indicated by a dashed line.

Fig. 5.

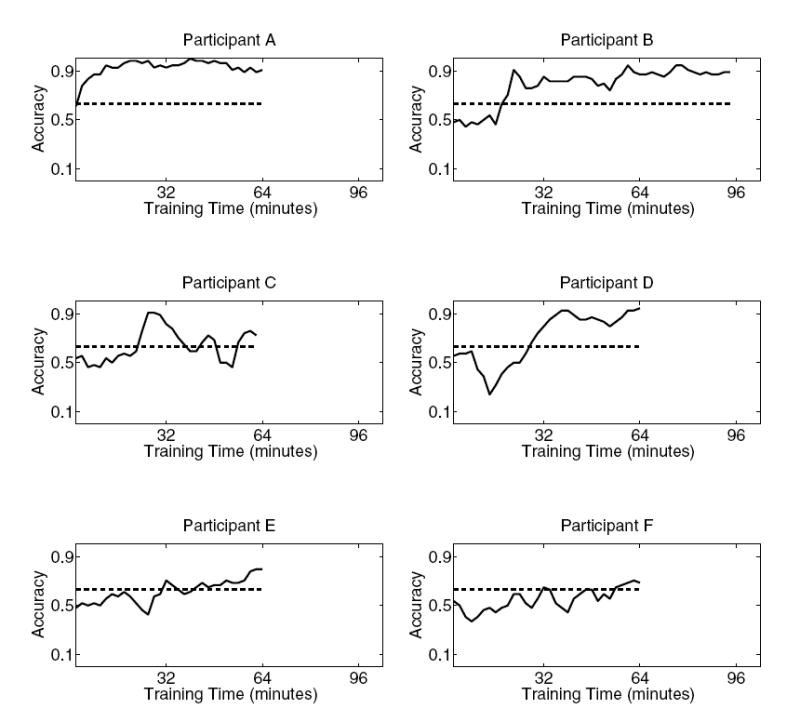
Time courses of accuracies (correct responses per total number of trials) for all participants, smoothed over three runs of 2 min each, corresponding to 54 trials. The dashed line indicates the p < 0.05 significance level. For all participants, two training sessions were performed, except for B who participated in three training sessions. With participant E, we conducted four additional runs within the last session.

Four participants (A–D) achieved reliable cursor control (accuracy ≥ 90%), three of them within the first training session, i.e., within 32 minutes of feedback training. All participants achieved significant cursor control during the second training session, i.e., within less than 64 minutes of feedback training. Participant C ascribed the considerable drop in performance in the second training session to a lack of concentration. Three participants (B–E) reported to control the cursor using movement imagery of both hands vs. rest; participant A reported imagery of his left hand vs. rest.

3.2 Sensorimotor Rhythm Properties

For all participants, typical difference and r² spectra are given in fig. 7, with a base frequency in the μ range, and a first harmonic in the β band.

Fig. 7.

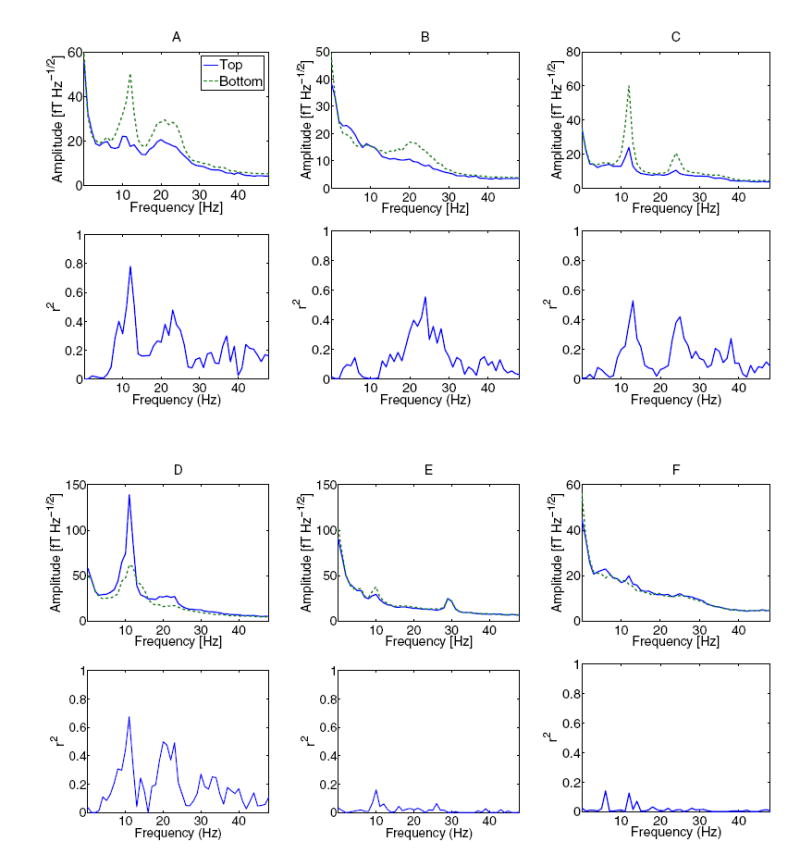
Averaged amplitude spectra for top target and bottom target conditions, and determination coefficients (r² values) computed from the 5 most successful runs (90 trials) selected from each participant’s best training session. Prior to computing the spectra, spatial filtering was applied as indicated by the sensors and weights in fig. 4. The curves show the amount of amplitude modulation that is present in the μ-rhythm at its base frequency around 10 Hz and/or its first harmonic around 20 Hz.

Using the PDA method, we were able to identify the signal of the main amplitude modulated source – the source of the sensorimotor rhythm – from data recorded on a grid of sensors, and isolate its projection weights. These weights, along with the sensor positions and frequency bands used for cursor feedback, are indicated in fig. 4. As explained in detail in sec. 2.6, the bipolar patterns observed are consistent with field distributions of localized currents, which is also what is expected for single sources with small spatial extent.

Participant E’s low performance was accompanied by a diffuse spatial pattern of amplitude modulation (fig. 4 E). Here, the insensitivity of MEG to radially oriented dipole sources may have resulted in a low signal-to-noise ratio. For participant F, performance was low despite a clear pattern of amplitude modulation emerged from the analysis (fig. 4 F), suggesting a difficulty in learning rather than a technical problem.

Feeding spatial weight distributions from fig. 4 into an ECD fitting procedure, we performed spatial localization for participants A, B, and F. Results have a spatial accuracy better than 5.6 mm (sec. 2.7) and show the origin of the modulated brain signal (sensorimotor rhythm) in the precentral gyrus (participants B and F), suggesting a motor character; for participant A, it cannot be decided within the accuracy available whether the source is located in the precentral or postcentral gyrus, i.e. whether the modulating activation is sensory or motor.

3.3 Spatial Filtering

In the present investigation, we developed an MEG equivalent to the Laplacian filtering approach commonly used with EEG. Our results suggest that this approach is viable despite its simplicity. An important aspect is the spatial filter’s sensitivity to the participant’s absolute head position. This is illustrated by fig. 4, which shows the extracted spatial pattern of source-sensor projection weights together with the sensor positions used in spatial filtering. As described in sec. 2.6, the spatial filter was always based on the analysis of the participant’s previous session. For participants A, C, and F, it is clearly visible that absolute head positions differed so much between sessions that the derived sensors were no more optimal. Still, our robust spatial filtering method allowed for reasonable and even high accuracies in the first two cases (the pattern in fig. 4 C was computed from this participant’s first training session with a final accuracy of > 85%), but could not deal with the change in head position that occurred for participant F.

In our setup, it was not possible to perform head localization on-line in real time. This made reproduction of the participant’s absolute head position across sessions a problematic task. Our results show that, without the possibility of interactively adjusting the participant’s head to a pre-defined position, the reproduction error was of the same magnitude as the spacing between MEG sensors (tab. 2). These results further suggest that more sophisticated approaches to spatial filtering such as Beamforming (Gross and Ioannides, 1999), Independent Component Analysis (ICA) (Cardoso and Soloumiac, 1993), or Common Spatial Patterns (CSP) (Koles, 1991) do not provide an immediate advantage when applied to an MEG BCI unless it becomes possible to adjust the participant’s head position on-line, because they will tend to overfit in the presence of head positioning errors. A recent cross-validation study of ICA and CSP based spatial filtering of MEG data in a BCI context (Hill et al., in press) supports this view by displaying poor generalization of these methods for MEG data, as opposed to their good performance in EEG-based BCIs.

3.4 Myographic and Head Movement Artifacts

Myographic artifacts, as well as head movements, are a possible source of signal modulation that should be carefully controlled for and monitored in BCI experiments. Despite their importance, these artifacts have not been considered by previous studies dealing with MEG-based BCIs (Lal et al., 2005; Kauhanen et al., 2006; Georgopoulos et al., 2005).

While weakly task-correlated myographic activity if often present in the recordings (fig. 2.7), only one of our participants (C) displayed muscular artifacts with a task correlation comparable to that of the brain signal. At the same time, this participant’s data reveal μ-rhythm control that does not overlap spatially with task-correlated myographic signals as illustrated by fig. 8. There, horizontal lines indicate task correlation for cortical signals at distinct frequency bands, and vertical lines indicate broad-banded task correlation typical for myographic signals. At the same time, the spatial source pattern (fig. 4) reflects a dipolar source rather than a spatially extent source as would be the case for a muscle located on the skull. Thus, even where contamination with myographic activity was present, cursor control was based on cortical signals. Still, these signals might be dependent on the concurrent presence of myographic activity, i.e. their modulation might reflect brain activity used to control the muscles generating the myographic signals that are visible in the analysis. With long-term BCI training, careful topographical and spectral analyses and proper instruction of participants such contamination has been shown to disappear over time (McFarland et al., 2005).

To control the influence of head movements on the modulation of brain signals, we introduced the use of head localization coils for continuous monitoring of the head position. Usually, head localization is done prior to and after an MEG recording to assess the amount of head movements that may have occurred during the measurements (e.g., Kaiser et al. (2005)). Driving those coils continuously as described in sec. 2.3 will record a continuous trace of head position with the brain signals, such as to allow for off-line analysis of head movements. Due to movements of the head when a participant follows the cursor with the eyes, there exists a significant correlation between head position and task condition for all participants (tab. 1). However, using the approach described in sec. 2.8.2 and comparing movement-induced relative amplitude modulation to the actually observed brain signals (rightmost columns in tab. 1), we find that movement-induced brain signal modulation as a main mechanism of cursor control can be ruled out for all participants.

Another class of artifacts present in MEG recordings is caused by static magnetic fields originating from ferromagnetic particles contaminating skin, oral cavity, lungs, or stomach of a participant, in combination with movement of these parts of the body. In the present study, this type of artifacts was present with participant E, whose signal spectrum (fig. 7 E) displays a marked increase at frequencies below 5 Hz when compared to the other participants’ spectra. These artifacts do not modulate or produce magnetic field oscillations in the frequency range relevant to the present study but need to be controlled if low-frequency signals are used for signal classification as it is the case in a recent off-line MEG BCI study involving decoding of hand movements (Georgopoulos et al., 2005).

3.5 Immediate Feedback

A first MEG-based BCI system was recently described by Lal et al. (2005), and shares hardware and data acquisition with the system presented here. As in the present investigation, the system of Lal et al. uses AR-computed spectral features of brain signals recorded over a period of a few seconds for binary classification. Unlike the present system, their system does not provide continuous feedback of brain signal features but displays the classification result (“feedback of results”) with a delay of 3 s. For self-regulation of brain states, it has been shown for EEG that timely feedback is important to facilitate learning (Mulholland et al., 1979; Rockstroh et al., 1990), so we implemented a feedback system with minimal delay. In the paper of Lal et al., no classification rates or other data are given that allow a judgement of on-line performance or learning rates. Their error rates for off-line classification are comparable to error rates in the second session of the present investigation as given in tab. 3; although there is a trend in favor of the present investigation, error rates do not differ significantly (Mann-Whitney U Test, descriptive p < 0.15). Thus, it appears that their Machine Learning (ML) approach does not provide a marked advantage in terms of classification performance.

Table 3.

Binary on-line classification errors during training sessions. For all participants except B, two training sessions were performed. Each session comprised 288 trials; correspondingly, an error below 44.8% implies significant control at the p < 0.05 level.

Session	A	B	C	D	E	F
1	6.9%	34.7%	35.1%	45.8%	44.4%	49.0%
2	5.9%	16.3%	35.9%	11.5%	30.9%	40.3%
3		10.7%

Furthermore, Lal et al. applied ML methods to MEG signals rather than introducing methods individually suited to MEG. In their study, they did not employ spatial filtering but processed data from all MEG channels in parallel, followed by an automatic selection of channels, and did not consider artifacts such as head movements or EMG as possible sources of signal modulation.

3.6 Comparison to EEG

Without specifically designed studies, it is difficult to isolate the role of a single factor such as data acquisition, signal processing, or participant instruction when comparing the results of different types of BCIs. Generally, the number of participants in BCI studies is low, and it cannot be assumed that they constitute a representative sample. To assess the performance of the present MEG-based BCI in relation to what may be considered “common” for EEG, we refer to Guger et al. (2003) who conducted a field study where participants learnt to operate two variants of a state-of-the-art sensorimotor rhythm BCI. They provide histogram data of on-line classification accuracies for 94 participants. After 20-30 minutes of training, their investigation found that on-line classification accuracy over 40 trials was distributed as displayed in fig. 9. For a comparison with our own results, we used the accuracies achieved during the last 40 trials of our participants’ first training sessions, i.e. after 30 minutes of training. While 4 of our 6 participants performed better than what was median performance in the reference study, there was no significant difference between the two distributions (Mann-Whitney U Test, descriptive p < 0.62).

Fig. 9.

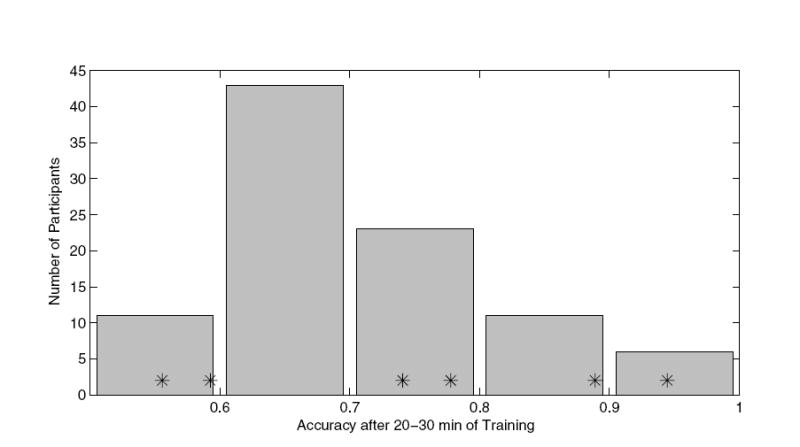
Histogram of typical EEG on-line classification accuracies over 40 trials after 20-30 minutes training time (data from Guger et al. (2003), tab. II, sum of session counts computed from third and fifth column). Accuracies from the last 40 trials of our participants’ first training sessions (i.e., our participants’ accuracies after 30 minutes of training) are indicated by asterisks. Significant control at the p < 0.05 level corresponds to an accuracy of 65%.

4 Conclusion

In the present study, we demonstrate an MEG-based BCI that provides continuous visual feedback of μ rhythm amplitude in real time. All of the 6 participants achieved significant μ rhythm self control in the course of feedback training.

In our experimental data, spectral properties of the amplitude modulated signal agree well with what is reported for EEG (Kübler et al., 2005) and ECoG (Leuthardt et al., 2004), and its origin is shown to be spatially located in the motor cortex for 3 out of 6 participants. Unlike prior investigations into the spatial origin of brain rhythms, we were able to exploit BCI on-line performance as an indicator to choose a subset of data best suited for localization analysis, and we could use a priori-information about the sources’ amplitude modulation in the localization procedure. This allowed us to approximately extract single-dipole spatial patterns using a simple, parameter-free method (PDA), and to arrive at results comparable to investigations that use considerably more complex analysis methods (Liljeström et al., 2005).

Albeit the number of participants is limited and the performance of some participants is low, learning curves increase most expressedly during the first and the beginning of the second session of feedback, corresponding to a training duration of 30 to 40 minutes. In the present study, the performance of our MEG-based BCI is similar to what has been reported for a state-of-the-art EEG-based μ-rhythm BCI with a large number of participants (Guger et al., 2003). At the same time, we think that our MEG-based BCI bears the potential for improvement well beyond what has been demonstrated here. In our system, reproduction of a participant’s head position was only possible up to a relatively large error, on the order of one MEG sensor distance. We believe that a solution to this problem will substantially improve the accuracy of feedback and classification, and even allow for the use of more advanced spatial filtering methods. Finally, MEG-based cursor feedback may be less affected by noise than its EEG-based counterpart, resulting in a more consistent feedback experience for the participant, and thus fast learning of μ-rhythm control comparable to what has been reported for ECoG (Leuthardt et al., 2004).

A Phase Decorrelation Analysis

The present “phase decorrelation” approach aims at separating amplitude modulated signals emitted by a small number of incoherent sources at a single frequency. Computational steps are

• (1)computing complex covariance matrices for each of two conditions (labels),
• (2)taking the difference of these two covariance matrices,
• (3)diagonalizing the resulting Hermitian complex-valued covariance difference, resulting in positive and negative eigenvalues and associated complex-valued eigenvectors.

This method applies to cases where a signal is represented as a time series of complex amplitudes, e.g. single Fourier coefficients computed over a moving window, or, similarly, the analytic signal of a band-pass filtered signal as constructed using a Hilbert transform. As for principal component analysis (PCA), resulting components will be orthogonal in sensor space. This limits applicability to cases with only a single modulated source, or a number of modulated sources with little or no overlap in sensor space.

For a justification of the method as outlined above, we consider N sources emitting signals s_k with a common frequency ω, such that

$$s_k=c_k{e}^{i\omega t},k\in \{1\dots N\},$$

where

$$c_k=A_k{e}^{i\varphi k},A_k\in [0,\infty [,{\varphi }_{\kappa }\in [0,2\pi [,$$

denotes a complex amplitude representing a single sample of source k’s activity during some time interval with real amplitude A_k and phase φ_k. Modeling incoherent sources, we require that the phases φ_k, φ_j for two distinct sources k, j be statistically independent. Additionally, we require that the φ_k be statistically independent of the A_k and follow a uniform random distribution over the interval [0, 2π[.

Then the complex signal covariance matrix in source space, as defined by

$$S_{\mathit{jk}}=\langle c_j{c}_k^{\ast }\rangle$$

will be diagonal, reducing to

$$S_{\mathit{jk}}=\langle A_j{A}_k{e}^{i({\varphi }_j-{\varphi }_k)}\rangle =\langle A_j{A}_k\rangle \langle e^{i({\varphi }_j-{\varphi }_k)}\rangle =\langle A_j^2\rangle {\delta }_{jk}.$$

Now, considering two conditions with associated amplitudes A_1k and A_2k, and grouping samples according to those conditions, we introduce a covariance matrix difference

$$S_{\mathrm{\Delta }jk}=\langle c_{1j}{c}_{1k}^{\ast }\rangle -\langle c_{2j}{c}_{2k}^{\ast }\rangle$$

which, under the above conditions, evaluates to

$$S_{\mathrm{\Delta }jk}=(\langle A_{1k}^2\rangle -\langle A_{2k}^2\rangle ){\delta }_{jk}=:{\mathrm{\Delta }}_{12k}{\delta }_{jk}.$$

For a linear law of signal propagation, and a set of M sensors measuring signals emitted by the N sources, the measured signal ${s\prime }_{\alpha }$ will be

$${s\prime }_{\alpha }=\sum _{k=1}^N{s}_k{a}_{k\alpha }+n_{\alpha },\alpha \in \{1\dots M\},$$

with complex amplitudes

$${c\prime }_{\alpha }=\sum _{k=1}^N{c}_k{a}_{k\alpha }+\stackrel{\sim }{c_{\alpha }},$$

where n_a denotes additive noise with zero mean complex amplitudes $\stackrel{\sim }{c_{\alpha }}$ which need not be spatiotemporally uncorrelated. a is a signal propagation matrix representing a linear transformation from source space into sensor space. In case of infinite propagation speed, no phase shift will be introduced by the propagation matrix, i.e. a will be real-valued.

For any covariance matrix S in source space, the associated covariance S′ in sensor space is

$${s\prime }_{\alpha \beta }=\langle {c\prime }_{\alpha }{c\prime }_{\beta }^{\ast }\rangle =\sum _{j,k=1}^N\langle c_j{c}_k^{\ast }\rangle a_{ja}{a}_{k\beta }^{\ast }+\langle {\stackrel{\sim }{c}}_a{\stackrel{\sim }{c}}_{\beta }^{\ast }\rangle =\sum _{j,k=1}^N{S}_{jk}{a}_{ja}{a}_{k\beta }^{\ast }+S_{\mathrm{noise}\alpha \beta }.$$

In case of the covariance difference as introduced above, noise terms will cancel out, and the difference matrix will appear in sensor space as

$${s\prime }_{\mathrm{\Delta }\alpha \beta }=\sum _{k=1}^N{\mathrm{\Delta }}_{{12}_k{a}_{k\alpha }{a}_{k\beta }^{\ast }.}$$

For real-valued a, ${S\prime }_{\mathrm{\Delta }}$ will be real-valued as well.

Writing ${S\prime }_{\mathrm{\Delta }}$ in terms of its eigenvalues λ_k and associated eigenvectors v_kα, we obtain

$$\sum _{k=1}^N{\mathrm{\lambda }}_k{V}_{k\alpha }{V}_{k\beta }^{\ast }={S\prime }_{\mathrm{\Delta }\alpha \beta }=\sum _{k=1}^N{\mathrm{\Delta }}_{{12}_k{a}_{k\alpha }{a}_{k\beta }^{\ast }.}$$

In case of a single dominating source, or for two sources with opposite modulation (i.e. opposite sign of associated eigenvalues), the expansion of ${S\prime }_{\mathrm{\Delta }}$ will be unambiguous outside its null (noise) space, and we can read off that the source-to-signal projection vectors a_k will be proportional to the eigenvectors v_k. Similarly, for a number of sources, if it is known a priori that the projection vectors may be considered orthogonal, and if the λ_k are pairwise distinct with respect to noise level, then the expansion will be unambiguous, and the non-nullspace eigenvectors v_k may be identified with the normalized projection vectors.

In such cases, the hermitian conjugate v^† of v provides a de-mixing matrix, separating the sensor signal into N modulated source signals, and into an (M − N)-dimensional noise subspace.