On Calderón’s conjecture for the bilinear Hilbert transform

Abstract

We show that the bilinear Hilbert transform defined by

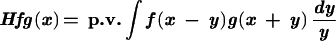maps L^p × L^q into L^rfor 1 < p, q ≤ ∞, 1/p + 1/q = 1/r, and 2/3 < r < ∞.

Section 1. Introduction

We continue the investigation begun in ref. 1 concerning the bilinear Hilbert transform defined by

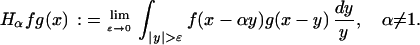This singular integration is initially defined only for certain functions f and g, for instance those in the Schwartz class on ℝ. But H_α can be extended to a bounded operator on certain L^p classes, as ref. 1 showed. We extend the theory of that paper with this result:

Theorem 1.1. For any α ≠ 1, H_α extends to a bounded operator on L^p₁ × L^p₂ into L^p₃, provided 1 < p₁, p₂ ≤ ∞, 1/p₃ = 1/p₁ + 1/p₂, and 2/3 < p₃ < ∞.

A special instance of this theorem was conjectured by A. P. Calderón in connection with ref. 2, namely L² × L^∞ into L² or, by duality, L² × L² into L¹. A special feature of the result is that the index p₃ for the image space need only be bigger than 2/3. We do not know that this is necessary for the theorem, although it is necessary for our proof.

The proof refines the method in ref. 1, with a more effective organization of the elements of the proof and an extension of certain almost orthogonality results in that paper to L^p functions for 1 < p < 2.

Section 2. The Model Sums

As in ref. 1, the essence of the matter concerns an analysis of a analogue of H_α that is more suited to the methods we employ. In particular, we utilize combinatorial features of the space–frequency plane.

Let D be a dyadic grid in ℝ. Call I × ω ∈ D × D a tile if |I|⋅|ω| = 1. The interval ω is a union of four dyadic subintervals of equal length, ω₁, ω₂, ω₃, and ω₄, which we list in ascending order. Thus, ξ_i < ξ_j for all 1 ≤ i < j ≤ 4 and ξ_j ∈ ω_j. We adopt the notation t = I_t × ω_t and t_j = I_t × ω_tj for j = 1, 2, 3. Fix a Schwartz function φ with φ̂ supported on [−1/8, 1/8]. Set for all tiles t, and j = 1, 2, 3,

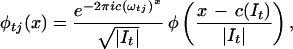where c(J) denotes the center of the interval J.

Then our model of the bilinear Hilbert transform is any of the following sums

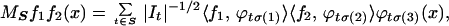in which S is a finite subset of S_all, the set of all tiles and σ : {1, 2, 3} → {1, 2, 3} is any one-to-one map. Including this map σ emphasizes the symmetry of these model sums under duality. We comment that the sum above makes sense only a priori for finite sums. We provide estimates for M_S that are independent of the number of elements in S, and hence the sum can be extended to S_all. It is in this sense that several statements below should be interpreted.

The analogue of Theorem 1.1 is

Theorem 2.1. For any choice of σ, M_Sall extends to a bounded operator on L^p₁ × L^p₂ into L^p₃, provided the indices p_i are as in the previous theorem.

Indeed, our proof supplies the additional information that the sum over tiles t is unconditionally convergent. And for this to hold an example shows that the inequality p₃ ≥ 2/3 is necessary.

We shall take the prior result from ref. 1 for granted, namely that M_Sall is a bounded operator on L^p₁ × L^p₂ → L^p₃ provided 2 < p₁, p₂, p₃/(p₃ − 1) < ∞. Then, taking duality and interpolation into account, one can see that it suffices to prove Theorem 2.1 in the case that 1 < p₁, p₂ < 2 and 2/3 < p₃ < 1. This we shall do, assuming that the map σ : {1, 2, 3} → {1, 2, 3} is the identity.

Indeed, this last case follows from a more precise statement that fully exploits the symmetry in the definition of the model sums.

Lemma 2.2. Let 1 < p₁, p₂, p₃ < 2 satisfy 1 < 1/p₁ + 1/p₂ + 1/p₃ < 2. Let f_i ∈ L^p_i be of norm one and let

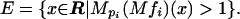Then for an absolute constant C

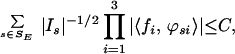where S_E = {s ∈ S_all | I_s ⊄ E}, Mf denotes the Hardy–Littlewood maximal function, and M_rf = (M|f|^r)^1/r.

Let us indicate how this proves Theorem 2.1 for 1 < p₁, p₂ < 2 and 1 < 1/p₁ + 1/p₂ < 3/2. There is a simple reduction. By linearity and scaling invariance, the inequality

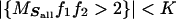holding for all ∥f₁∥_p1 = ∥f₂∥_p2 = 1 will prove that M_Sall maps into the appropriate weak L^p₃ space. Then Marcinceiwcz interpolation proves the theorem.

Fix f₁ and f₂ of norms one in their respective L^p_i spaces. We use the set

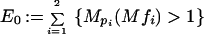to split up S_all and the set whose measure we are to estimate. Let S_in := {s ∈ S_all | I_s ⊂ E₀}, S_out := S_all − S_in, and define E_in := {M_Sinf₁f₂ > 1} and similarly E_out := {M_Soutf₁f₂ > 1}. It suffices to bound the measures of these last two sets by constants.

The essential term, |E_out|, is controlled by Lemma 2.2. Indeed, we may assume that |E_out| > 1, for otherwise there is nothing to prove. Then choose p₃ with 1 < 1/p₁ + 1/p₂ + 1/p₃ < 2 and we take the third function to be the indicator of E_out, normalized in L^p₃; that is, we take f₃(x) := |E_out|^−1/p₃ χ_Eout(x). Observe that this function is strictly less than one. Therefore, Lemma 2.2 gives us the desired result,

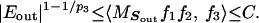The estimate of E_in begins by defining

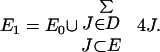This set has measure |E₁| ≤ 5|E₀| ≤ C′, and we shall not estimate M_Sin on this set. And off of this set we have

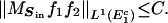This inequality is, however, of a routine nature, and so we do not supply a proof of it here. This finishes the discussion of the proof of Theorem 2.1 from Lemma 2.2.

Section 3. The Combinatorics of Lemma 2.2

We devote ourselves to the proof of Lemma 2.2, beginning with issues related to the combinatorics of the collection S_E, and concluding with the issues related to almost orthogonality. View the functions f_i as fixed and set

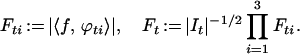There is a partial order on tiles given by t < t′ if I_t ⊂ I_t′, ω_t ⊃ ω_t′. By splitting the collection of tiles into two we can assume that if s <≠ t then 4|I_s| ≤ |I_t|.

Call a collection of tiles T a tree with top q if t < q for all t ∈ T. For 1 ≤ i ≤ 4, call T an i-tree if in addition to T being a tree with top q, ω_ti ∩ ω_q for all t ∈ T. In this case, observe that for s <≠ t <≠ q in the tree, we must have ω_si ⊃ ω_t ⊃ ω_ti ⊃ ω_q. Thus, for j ≠ i the intervals {ω_tj | t ∈ T} not only are disjoint but are lacunary. And indeed, the Littlewood–Paley Theory applies to the collection of functions {ϕ_tj | t ∈ T}.

There are comparisons to maximal functions. Observe that for a single tile we have

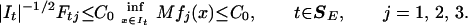3.1

The last inequality follows from the definition of S_E.

At a deeper level, we have the following for a tree. For an i-tree T ⊂ S_E with top q and j ≠ i, observe that the Littlewood–Paley inequalities imply

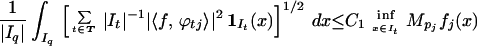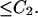This inequality hold for each subtree of T, whence we conclude that the dyadic bounded mean oscillation (BMO) norm of the integrand above is at most C₂. The BMO structure then gives us the formally stronger assertion that

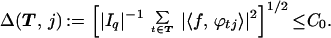3.2

The square functions Δ(T, j) are relevant here, due to the following estimate valid for an i-tree T. By Cauchy–Schwartz,

3.3

We summarize the combinatorics of S_E in the following decomposition. Set n₀ = 2 log₂ C₀, the constant C₀ appearing in the previous two paragraphs. The collection S_E is a union of subcollections S_ni for i = 1, 2, 3 and n ≥ n₀ so that

3.4

for all j-trees T ⊂ S_ni, j ≠ j′. Furthermore, denote by S^*_ni those elements of S_ni that are maximal with respect to the partial order ‘<’. The critical property is

3.5

where 0 < η < 2 − Σ 1/p_i.

Once this decomposition is established, the proof of Lemma 2.2 is easily accomplished. For each n ≥ n₀ and i = 1, 2, 3, the collection S_ni is a union of trees T_q with tops q ∈ S^*_ni. Each tree is a union of four trees to which the estimate 3.3 applies. Hence, the properties of S_ni imply that

But, by the choice of η and the requirements on the p_i, the exponent on n is negative. And so this estimate has a finite sum over n ≥ n₀.

We turn to the task of achieving this decomposition of S_E. It is inductive and best done by defining some auxiliary collections. Assume that the S_mi are defined for all m < n and all 1 ≤ i ≤ 3, in such a way that for S^r = S∖(∪_m<n ∪_iS_mi) we have

3.6

and for any i-tree T ⊂ S^r, Δ(T, j) ≤ 2^{−n/p′_j+2}, for j ≠ i.

The collections S_ni will be a union of four subcollections denoted S_nij for 1 ≤ j ≤ 4. We define S^*_n11 to be the set of maximal tiles q with |I_q|^−1/2|〈f₁, φ_q1〉| ≥ 2^{−n/p′₁−1}, and take S_n11 to consist of all tiles t so that t1 < q for some q ∈ S^*_n11. These tiles are removed from S^r, and then S_nii is defined similarly for i = 2, 3. After the deletion of the tiles D₀ = ∪_i=1³ S_nii, we have |〈f_i, φ_ti〉| ≤ 2^{−n/p′_i−1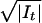} for all tiles t ∈ S^r′ = S^r∖D₀. In the subsequent section we will prove that

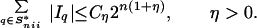3.7

We now concentrate on 1-trees T ⊂ S^r′ for which Δ(T, 2) is suitably large. This collection of trees we denote as S_n12, and its construction has a particular purpose. Namely, the trees we construct should consist of nearly orthogonal functions, a notion that we encode in the purely combinatorial terms of assertion 3.8.

Consider tiles q such that there is a 1-tree T_q ⊂ S^r′ with top q so that Δ(T, 2) ≥ 2^{−n/p′₂+1}. We take T_q to be the maximal 1-tree with this property. Let q(1) be such a top, which is maximal with respect to <, and in addition sup{ξ | ξ ∈ ω_q} is maximal. Remove the tiles T_q(1), and repeat this procedure to define T_q(2) and so on. S_n12 is then ∪_ℓT_q(ℓ) and S^*_n12 = {q(ℓ) | ℓ ≥ 1}. Observe that for any 1-tree T ⊂ S^r′∖S_n12, we have Δ(T, 2) ≤ 2^{−n/p′₂+1}. These procedures are repeated inductively to define the S_nij for all n, i, j. However, in the case of i > j, we choose the top q to be maximal first with respect to ‘<’ and then with respect to inf{ξ | ξ ∈ ω_q}. In the subsequent section we will prove that the collections S^*_nij also satisfy inequality 3.7.

The particulars of the construction of S_nij lead to this combinatorial fact, which for specificity we state in the case of S_n12. For q ∈ S^*_n12, denote by T_q^r the 1-tree T_q defined above, less those tiles in it that are minimal in the partial order ‘<’. Set S_n12^r = ∪_q∈S^*n12T_q^r. Then

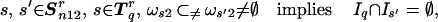3.8

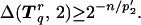3.9

The first assertion is a condition concerning the disjointness of the trees in the space–frequency plane that will be a sufficient condition for orthogonality in the subsequent section.

Suppose that condition 3.8 is not true. Thus I_q ∩ I_s′ ≠ ∅ and hence I_s′ ⊂ I_q. Yet s′ ∈ T_q′^r for some q′ and there is an s" ∈ T_q′ with s" < s′. Hence ω_q ⊂ ω_s′2 ⊂ ω_s"1 as T_q′ is a 1-tree. But ω_q′ ⊂ ω_s′1 so that sup{ξ | ξ ∈ ω_q} > sup_ξ′{ξ′ ∈ ω_q′}. Hence we have violated the construction of these 1-trees. The second condition, 3.9, follows immediately from the observation that for any t ∈ S_n12 and q ∈ S^*_n12, we have 4|I_t|^−1/2|〈f₂, ϕ_t2〉| ≤ Δ(T_q, 2).

Section 4. Counting the Number of Trees

We prove inequality 3.5 first in the case of S := S_nii. The properties that we use are that the tiles in S are disjoint and |I_t|^−1/2|〈f_i, ϕ_ti〉| ≥ b for b := 2^−n/p′_i. The proof requires several devices.

Step 1. We set N_S′(x) := Σ_t∈S′χ_It(x). We are to estimate the L¹ norm of N_S, but it is an integer-valued function, so it suffices to prove a weak type 1 + ɛ estimate for some ɛ > 0. That is, we prove

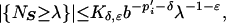4.1

for certain arbitrarily small δ, ɛ > 0. Fix such a λ ≥ 1. Because the intervals I_q are dyadic, there is a subcollection S′ ⊂ S so that {N_S ≥ λ} = {N_S′ = λ} and ∥N_S′∥_∞ = λ. We work with the collection S′.

Step 2. For A > 1 to be specified we can write S′ = S^♭ ∪ ∪_m=1^A10 S_m for which the tiles in each S_m are widely separated in the space variable, namely

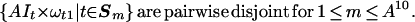While S^♭ is small in that

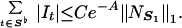For a proof of this inequality see the separation lemma of ref. 3. It is then clear that

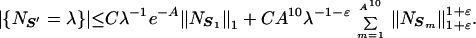We will show that for appropriate A and 0 < ɛ, δ to be chosen, but arbitrarily small, that we have a uniform estimate on the 1 + ɛ norm of the counting functions of the S_m. Namely,

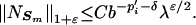4.2

This will prove inequality 4.1.

Step 3. Orthogonality decisively enters the argument. As a consequence of the orthogonality lemmas of ref. 1, we have for any g ∈ L² the inequality

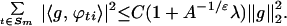On the other hand, the following is trivially bounded by the maximal function,

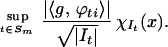Hence it maps L^p into itself for all p > 1. Interpolation with the better L² bound then provides the bound below for all 1 < p < 2 and δ > 0.

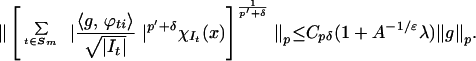This estimate can be localized, yielding a better inequality for our purposes. For a dyadic interval J set S_m,J := {t ∈ S_m | I_t ⊂ J}. Then

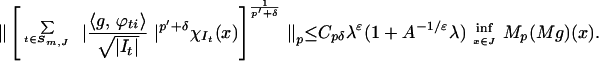This last inequality holds for all p and g. We specialize to the case of f_i and p = p_i. Moreover, we have the information supplied from the exclusion of tiles t with I_t ⊂ E. Thus,

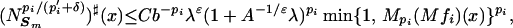where g^♯ denotes the sharp maximal function. This inequality proves inequality 4.2 by raising to the r = (p′_i + 2δ)/p_i power, integrating and using ∥g∥_r ≤ C_r∥g^♯∥_r.

Finally, there is the case of providing the counting function estimate for S_nij for i ≠ j. But we have taken care to construct trees that are disjoint in the sense of condition 3.8 and so they too satisfy an orthogonality principle; see Lemma 3 of ref. 1. The argument is then much like the one just presented.