Periodic Modulation of Motor-Unit Activity in Extrinsic Hand Muscles During Multidigit Grasping

Abstract

We recently examined the extent to which motor units of digit flexor muscles receive common input during multidigit grasping. This task elicited moderate to strong motor-unit synchrony (common input strength, CIS) across muscles (flexor digitorum profundus, FDP, and flexor pollicis longus, FPL) and across FDP muscle compartments, although the strength of this common input was not uniform across digit pairs. To further characterize the neural mechanisms underlying the control of multidigit grasping, we analyzed the relationship between firing of single motor units from these hand muscles in the frequency domain by computing coherence. We report three primary findings. First, in contrast to what has been reported in intrinsic hand muscles, motor units belonging to different muscles and muscle compartments of extrinsic digit flexors exhibited significant coherence in the 0- to 5- and 5- to 10-Hz frequency ranges and much weaker coherence in the higher 10–20 Hz range (maximum 0.0025 and 0.0008, respectively, pooled across all FDP compartment pairs). Second, the strength and incidence of coherence differed considerably across digit pairs. Third, contrary to what has been reported in the literature, across-muscle coherence can be stronger and more prevalent than within-muscle coherence, as FPL–FDP2 (thumb-index digit pair) exhibited the strongest and most prevalent coherence in our data (0.010 and 43% at 3 Hz, respectively). The heterogeneous organization of common input to these muscles and muscle compartments is discussed in relation to the functional role of individual digit pairs in the coordination of multiple digit forces in grasping.

INTRODUCTION

Holding an object against gravity using multiple digits requires fine coordination of forces and moments (Baud-Bovy and Soechting 2002; Flanagan et al. 1999; Rearick et al. 2003; Shim et al. 2003; Zatsiorsky and Latash 2004; Zatsiorsky et al. 2002, 2003). While the temporal and spatial coordination of multiple forces has been studied in detail (see Schieber and Santello 2004 for review), the underlying neural mechanisms have not been studied to the same extent and are not well understood. It has been suggested that synchrony of motor units belonging to different hand muscles might play a significant role in the temporal coordination of finger forces during multidigit grasping (Rearick and Santello 2002; Rearick et al. 2003; Santello and Fuglevand 2004). Therefore we recently used a time domain measure, the common input strength (CIS) (Nordstrom et al. 1992), to quantify the extent to which synchrony occurs in motor units across different muscle compartments of the flexor digitorum profundus (FDP) and across muscles, i.e., FDP and flexor pollicis longus (FPL), during multidigit grasping (Winges and Santello 2004). We found moderate to strong motor-unit synchrony that was heterogeneously distributed across these muscles and muscle compartments.

Strong motor-unit synchrony, measured in the time domain, is considered to be the result of branched presynaptic input to the motoneurons originating from a common source (Farmer et al. 1993; Sears and Stagg 1976; Semmler et al. 2002). Motor-unit coherence, a frequency domain measure of the correlation of motor-unit activity, complements the information obtained from time domain measures (Hamm et al. 2001; Semmler et al. 2002) as it reflects the frequency content of the common synaptic input (Farmer et al. 1993; Halliday 2000; Rosenberg et al. 1998). In fact, significant motor-unit coherence has been observed in the absence of motor-unit synchrony, suggesting that different mechanisms may underlie these two measures of correlated motor-unit activity (Semmler et al. 2003). It has also been suggested that the correlated firing of motor units, as measured by coherence, might be a mechanism by which the central nervous system reduces the number of independent degrees of freedom to be controlled (e.g., motor units, forces) (Farmer 1998; Semmler et al. 2004).

To further examine the mechanisms underlying the coordination of motor-unit activity during grasping, we analyzed the activity of the same motor-unit pairs as in our previous study (Winges and Santello 2004) in the frequency domain to assess the existence of a common periodic input across muscles (FPL-FDP) and across FDP compartments and the relative contribution of periodic and nonperiodic common input to each muscle/muscle compartment pair. Although motor-unit coherence has been reported for a variety of tasks (Farmer et al. 1993; Iyer et al. 1994; Kakuda et al. 1999; Marsden et al. 1999; Semmler et al. 2002) and a limited number of muscles (Farmer et al. 1993; Halliday et al. 1999; Kakuda et al. 1999; Marsden et al. 1999), most studies of motor-unit coherence have focused on coherence occurring between motor units belonging to the same muscle, intrinsic hand muscles (e.g., primarily in 1st dorsal interosseus) and during force production tasks under visual or auditory feedback. Hence, an additional objective of the present study was to extend the application of coherence analysis to motor units of different extrinsic digit flexor muscles and to a natural grasping task. Preliminary accounts of these results have been published as an abstract (Johnston et al. 2004).

METHODS

Experimental task

A total of six subjects (4 males and 2 females; mean age: 29 yr, range: 21–37 yr) took part in the experiments. The experimental procedures were approved by the Institutional Review Board at Arizona State University and were in accordance with the declaration of Helsinki. All subjects gave their informed consent prior to each recording session.

The experimental data analyzed for this manuscript were the same as those reported in our previous study examining motor-unit synchrony in the time domain (Winges and Santello 2004). However, different treatments of the data are reported here. Subjects sat in an adjustable dental chair with their right arm in a semi-pronated position and resting comfortably on a flat platform surface. Subjects were asked to grasp, lift, and hold the grip manipulandum (Fig. 1; weight: 0.250 kg) at a height of ∼5 cm from the support surface for a minimum period of 3 min, after which the subject replaced the object on the platform. Note that force and electromyographic (EMG) data were recorded during the hold period only. Before object lift, the distal pad of each digit was placed on individual sensors the vertical position of which was adjusted for each subject to allow a comfortable grip of the device (Fig. 1). After object lift, the experimenter placed a soft support (a rolled towel) under the forearm and proximal to the ulnar styloid to prevent fatigue of the elbow flexor muscles (see Winges and Santello 2004).

FIG. 1.

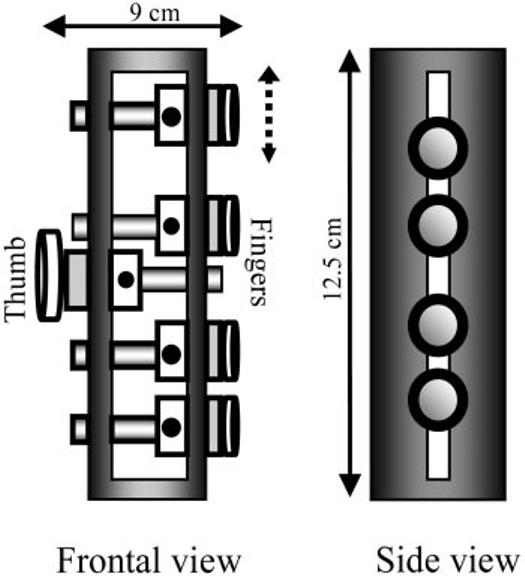
Grip device. The frontal and side views of the device used to measure normal forces and horizontal torques is shown.

To allow physiological variability in forces and motor-unit firing rates during object hold, no explicit instructions or feedback were given with respect to the amount of forces to apply or the motor-unit firing rate to maintain. The only task requirement was to exert sufficient forces at the fingertips to prevent object slip while maintaining the object aligned with the vertical throughout the trial. We gave rest periods of minimum 5 min between trials to ensure that subjects were fully rested before starting a new trial. Further details concerning the experimental methods can be obtained from Winges and Santello (2004).

Force and EMG recording

The diameter of the contact surface of the force/torque sensors for the fingers and the thumb was 17 and 25 mm, respectively. The center of the thumb sensor was aligned approximately mid-point between the sensors of the middle and ring fingers (Fig. 1). Analysis of normal forces and horizontal torques has been presented in Winges and Santello (2004) and will not be reported here.

Motor-unit potentials were recorded with tungsten microelectrodes inserted into FDP and FPL (Frederick Haer, Bowdoinham, ME; 1–5 μm tip diameter, 5–10 μm uninsulated length, 50-mm shaft length; 250-μm shaft diameter, ∼200 kΩ impedance at 1,000 Hz after insertion). One surface electrode (10-mm diam gold-plated silver disc, Model F-E5GH, Grass Instruments; West Warwick, RI) was placed on the radial styloid to serve as a reference for each intramuscular electrode. Two microelectrodes were inserted to record the activity of separate motor units in either two digit compartments of FDP (FDP2, FDP3, FDP4 or FDP5; index, middle, ring or little finger, respectively) or one digit compartment of FDP and FPL (see Winges and Santello 2004).

Once both electrodes were in place, we verified proper microelectrode placement using weak electrical stimulation (100–150 μA, 1-ms duration, 1 Hz; S48 Stimulator, Grass Instruments). The depth and/or angle of insertion of the microelectrode were adjusted until an isolated movement of the distal phalange indicated that the microelectrode was in the target muscle or muscle compartment. After this procedure, subjects performed isometric contractions at each digit to confirm that the microelectrode detected only the electrical activity of the target muscle or muscle compartment (i.e., that no EMG cross-talk occurred). Electrodes were then connected to differential amplifiers and the intramuscular EMG signals were amplified (×1,000), band-pass filtered (0.3–3 kHz; Grass Instruments) and displayed on oscilloscopes (see Winges and Santello 2004).

Before each new trial, the needle electrodes were slightly repositioned until a new motor unit could be detected in at least one channel. The procedures described in the preceding text to assess EMG cross-talk were then repeated as were the electrical stimulation procedures if necessary. Within one experimental session we recorded single motor-unit activity from 3–10 pairs of motor units.

Data acquisition and analysis

A 16-channel 12-bit A/D converter board (E-Series DAQ 6023E; National Instruments, Austin, TX) was used to acquire the EMG data with a sampling frequency of 20 kHz. Custom software (LabVIEW 6.1, National Instruments) was used to acquire, display and store the EMG data. Individual motor units were discriminated from each channel (Fig. 2, A and B) using an algorithm that developed templates based on amplitude and temporal characteristics of the action potential (Spike2, Cambridge Electronic Design, Cambridge, UK). Figure 2C shows the action potentials for both discriminated motor units in Fig. 2B. Motor-unit discharges characterized by very short (<20 ms) interspike intervals (ISI) were classified as false-positive errors (see Fig. 2D, top) and eliminated from analysis (see Winges and Santello 2004).

FIG. 2.

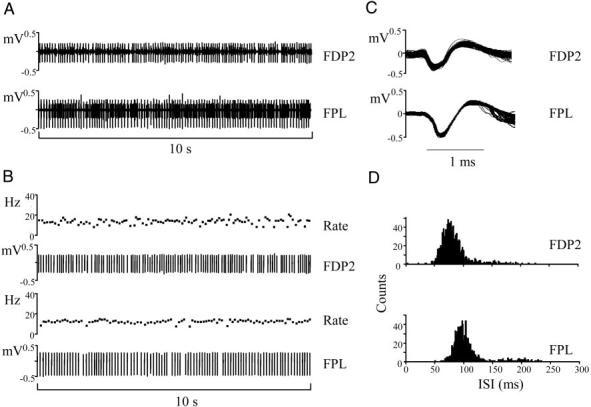
Motor-unit activity during object hold. A: raw electromyographic (EMG) data from the index finger compartment of FDP (FDP2; top) and a thumb flexor (FPL; bottom). B: motor units discriminated from each raw EMG trace and their respective instantaneous firing rates (bottom and top, respectively). C: the action potentials of the discriminated motor units (1347 and 1144 from FDP2 and FPL EMG records, respectively). D: the interspike interval (ISI) distributions of each motor unit. The data shown in A and B are from a smaller recording period than the entire duration of the object hold trial (∼4 min). All traces are from the same subject (subject 3).

After elimination of false-positive errors, the entire ISI distribution was used to calculate the mean (μ), standard deviation (SD), and coefficient of variation (CV) of motor-unit firing rate. To calculate the mean firing rate for each motor unit, we first determined the instantaneous firing rates by computing the inverse of individual ISIs. Mean firing rate was then computed by averaging the instantaneous firing rates. For each motor unit, CV of firing rate was calculated as SD/μ. The geometric mean and geometric CV of firing rate were computed for each motor-unit pair. The geometric mean of firing rate and CV of firing rate of motor units 1 and 2 was computed as (μ₁ · μ₂)^1/2 and (CV₁ · CV₂) , respectively (see Winges and Santello 2004).

After the discrimination of individual motor units, the motor-unit data were down-sampled to 200 Hz by binning the data into 5-ms segments and assigning a value of 1 if that segment contained a discharge and a 0 if it did not (Semmler et al. 2003). The mean offset of each motor-unit spike train was removed by subtracting the mean of each 1-s segment from the data set (Warner 1998). We then performed coherence analysis on individual motor-unit pairs to determine their linear dependence in the frequency domain. Similar to the coefficient of determination in linear statistics, the value of coherence at a given frequency is bounded between 0 and 1, where 1 indicates a perfect linear relationship and 0 indicates no linear relationship at that frequency.

CORRELATED MOTOR-UNIT ACTIVITY IN THE TIME AND FREQUENCY DOMAINS

Figure 3, A-C, shows examples of time and frequency domain approaches to quantify the correlation between pairs of concurrently active motor units. In time domain measures of motor-unit synchrony such as CIS (Nordstrom et al. 1992), a “reference” and “test” EMG channel are defined (arbitrarily) and a cross-correlogram between the two motor units is computed over ±100 ms from the discharge of the reference unit (Fig. 3, A-C, middle). A cumulative sum (cusum); (Ellaway 1978) (Fig. 3, A-C, top) is computed to determine the existence of a peak in the cross-correlogram. The peak is defined by the area between the 10th to 90th percentiles (Fig. 3, A-C, dotted vertical lines) of the largest inflection in the cusum within ±20 ms (Fig. 3, A-C,) of the reference unit firing (Keen and Fuglevand 2004; Schmied et al. 1993). If a peak cannot be defined within this region, a region of 11-ms duration, centered at time 0, is used for the assessment of the strength of motor-unit synchrony for that motor-unit pair (Semmler et al. 1997). The CIS index is computed as the ratio of the total counts in the peak minus the counts due to chance (Fig. 3, A-C, middle, horizontal lines), i.e., the mean number of counts per bin occurring within –100 to –40 and 40–100 ms normalized by trial duration. The value of the CIS index represents the number of synchronous discharges in excess of chance per second for a given motor-unit pair. The CIS values computed in our previous study (Winges and Santello 2004) have been used here to assess the relationship between CIS and coherence strength (see following text). The CIS computed on the data shown in Fig. 3, A-C, revealed weak, moderate and strong motor-unit synchrony (CIS = 0.18, 0.47, and 0.79, respectively).

FIG. 3.

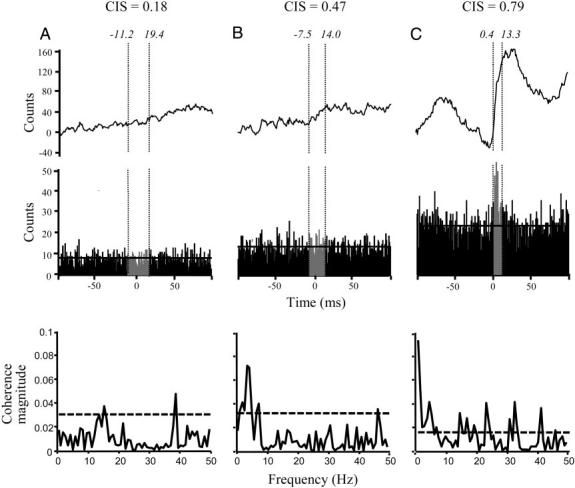
Comparison of time and frequency domain analysis. A--C, middle: the cross-correlograms computed on motor-unit pairs from FPL–FDP3, FPL–FDP2, and FDP4–FDP5 (subjects 5, 3, and 4, respectively). The CIS values are given as well as the peak start and end times (in italics). Top: the cumulative sum (cusum) of the counts in each cross-correlogram used to define the peak region. Vertical dotted lines delineate the peak duration. Bottom: the coherence between the same motor-unit pairs used to compute the cross-correlograms above. The values on the y axis are the magnitude of the motor-unit coherence across the frequency range of interest (x axis; bin width = 0.78 Hz). Horizontal dotted line indicates the 95% confidence limit above which the magnitude of the coherence is defined as statistically significant.

Peaks and troughs that occur at consistent time intervals in the cross-correlogram are indicative of periodicities of correlated firing of a motor-unit pair (Farmer et al. 1997; Moore et al. 1970; Perkel 1970) and are not quantified by time domain measures. The existence of such periodicities, however, can be quantified by frequency domain measures such as coherence. Motor-unit coherence at a given frequency indicates correlated rhythmic activity of the two motor units and reflects the influence of a common periodic input to their motoneuronal pools. Each of the bottom panels in Fig. 3, A-C, illustrates the coherence calculated from the same motor-unit pairs used to calculate the cross-correlogram in the middle panel.

COHERENCE MAGNITUDE

We computed coherence between motor-unit pairs for each trial using the cross-spectrum f_xy and auto-spectra f_xx, f_yy estimated from 1.28 s of nonoverlapping segments of data (i.e., 256 point windows) (Semmler et al. 2003). This resulted in a bin resolution of 0.78 Hz. The coherence estimate, R_xy, was determined from the combined spectra

$$\mid R_{\mathrm{xy}}\left(\lambda \right){\mid }^2=\mid f_{\mathrm{xy}}\left(\lambda \right){\mid }^2∕\left(f_{\mathrm{xx}}\left(\lambda \right)f_{\mathrm{yy}}\left(\lambda \right)\right),$$ (1)

where λ is the frequency at which coherence is calculated.

The significance of the coherence estimate was computed using the test provided by Rosenberg et al. (1989). The confidence limit for zero coherence at the α = 0.05 and for the number of disjoint segments, L (i.e., total trial duration/data segment duration) is given by

$$\mathrm{sig}\left(\alpha \right)=1-{(1-\alpha )}^{1∕(L-1)}$$ (2)

The hypothesis of noncorrelated activity at each frequency is rejected if the estimated coherence at that frequency exceeds the value given by Eq. 2.

RELATIONSHIP BETWEEN COHERENCE MAGNITUDE AND MOTOR-UNIT FIRING PARAMETERS

We found that the magnitude of significant coherence differed across muscle/muscle compartment pairs (Fig. 5). Therefore we used linear regression analysis to assess the extent to which differences in the number of motor-unit action potentials within each trial, the geometric mean, and the geometric CV of motor-unit firing rates might have affected the heterogeneous distribution of coherence magnitudes across digit pairs. These variables were regressed against maximum coherence (defined in the following text). With regard to the first variable, the ISIs were used to determine the total number of discriminated action potentials per trial for each motor unit. The average number of motor-unit action potentials was then computed for each motor-unit pair to obtain a single variable for the regression analysis versus maximum coherence.

FIG. 5.

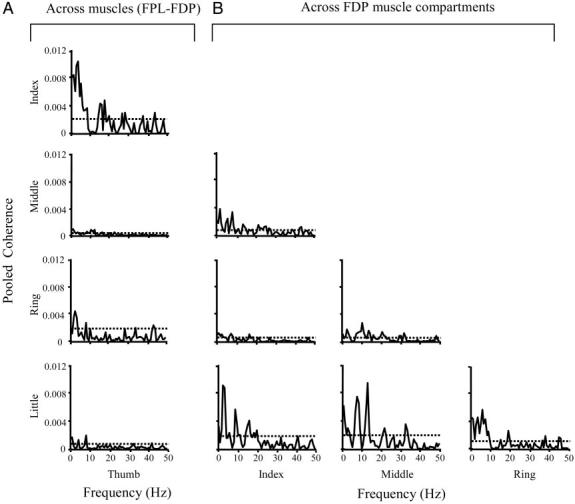
Pooled coherence from individual digit pair combinations. Plots in A and B show pooled coherence computed on motor units from FPL–FDP compartment and from FDP compartment combinations, respectively. ⋯ , the 95% confidence limit.

Maximum coherence was determined by finding the largest coherence magnitude within the frequency range of interest and then subtracting the coherence magnitude at the 95% significance level (see Eq. 2), i.e., the coherence value denoted by a horizontal dashed line in Fig. 3, bottom. The resulting maximum coherence value represents the maximum coherence above significance level within a given frequency range. If the largest coherence magnitude within a given frequency range did not reach significance (i.e., was below the coherence magnitude indicated by the dashed lines in Fig. 3), the maximum coherence was assigned a value of 0.

Significant coherence between motor units of intrinsic hand muscles is most commonly found within 1- to 12- and 16- to 32-Hz frequency ranges (Farmer et al. 1993; Marsden et al. 1999; Semmler et al. 2002). As most of our data were characterized by coherence peaks in the low-frequency range (i.e., within 0–10 Hz; Fig. 5), we computed maximum coherence within three frequency ranges: 0–5, 5–10, and 10–20 Hz (the actual ranges given the frequency bin resolution of 0.78 was: 0.78–4.69, 5.47–9.38, and 10.16–19.53 Hz, respectively).

INCIDENCE OF COHERENCE

Each 0.78-Hz bin was assigned a 1 if the coherence estimate exceeded the confidence limit and 0 otherwise. These values were then combined across trials and subjects and divided by the total number of trials to create a frequency distribution histogram of the percentage of trials characterized by significant coherence (Farmer et al. 1993; Halliday et al. 1999; Semmler et al. 2002). To assess possible differences in the incidence of coherence across muscles and muscle compartments, frequency distribution histograms were computed for motor-unit pairs from FPL–FDP compartment combinations, across FDP compartment combinations, and each of the 10 across-muscle/muscle compartment combinations.

POOLED COHERENCE

We also computed pooled coherence (Amjad et al. 1997) to determine the strength of coherence across the entire data set, i.e., across trials and subjects. Pooled coherence can be considered as a weighted average of individual coherence estimates and is calculated by

$$\frac{\mid {\displaystyle \sum _{i=1}^k}{f}_{\mathrm{xy}}\left(\lambda \right)L_i{\mid }^2}{\left({\displaystyle \sum _{i=1}^k}{f}_{\mathrm{xx}}\left(\lambda \right)L_i\right)\left({\displaystyle \sum _{i=1}^{\mathrm{k}}}{f}_{\mathrm{yy}}\left(\lambda \right)L_i\right)}$$ (3)

where i is the trial number, k is the total number of trials used to compute the average, and L_i is the number of disjoint segments used in the spectra calculations for trial i. To assess possible differences across muscles and muscle compartments, pooled coherence was computed for all motor-unit pairs from FPL–FDP compartment combinations, across FDP compartment combinations, and each of the 10 across-muscle/muscle compartment combinations.

STATISTICAL ANALYSIS ON POOLED COHERENCE

The “difference of coherence test” (Amjad et al. 1997; Rosenberg et al. 1989) was performed on pooled coherence to determine the frequencies at which significant differences between muscle/muscle compartment pairs occurred. The test consists of normalizing each pooled coherence estimate by computing the arc hyperbolic tangent transformation (Fisher Transform) of coherency R_xy, i.e., the square root of the coherence estimate (Amjad et al. 1997). This transform, tanh⁻¹|R_xy|, acts to normalize the variance of the coherence estimates, which is necessary due to the limited range of possible coherence values (i.e., 0 to 1) (Mima and Hallett 1999). With this transformation, the difference between the pooled coherence estimates, tanh⁻¹|R_mn(λ)| − tanh⁻¹|R_op(λ)|, is approximately normally distributed allowing for computation of confidence intervals to test for significant differences between the two. The hypothesis of equal coherences is rejected for any frequency at which the difference value falls outside the confidence interval (i.e., dotted lines, Fig. 4C). This test of difference was computed between across-muscle (FPL–FDP) and across FDP compartment pooled coherences and the pooled coherences for each pair of the 10 individual digit pair combinations. To illustrate the magnitude of significant differences of pooled coherence across digit pairs, we computed the area outside each confidence level of the test of difference plots within 0- to 5-, 5- to 10-, and 10- to 20-Hz ranges. These values were then plotted in matrix format (Fig. 6).

FIG. 4.

Incidence and pooled coherence. A and B: the incidence of significant coherence and pooled coherence, respectively, for all motor-unit pairs from across FDP compartment and FPL–FDP compartment combinations (left and right, respectively). ⋯ , the 95% confidence level. C: the difference between the Fisher transformed pooled coherencies of B, left and right (across FDP compartments and across FPL-FDP, respectively). Values falling outside the 95% confidence interval (⋯) indicate a significant difference between the 2 pooled coherencies at that frequency.

FIG. 6.

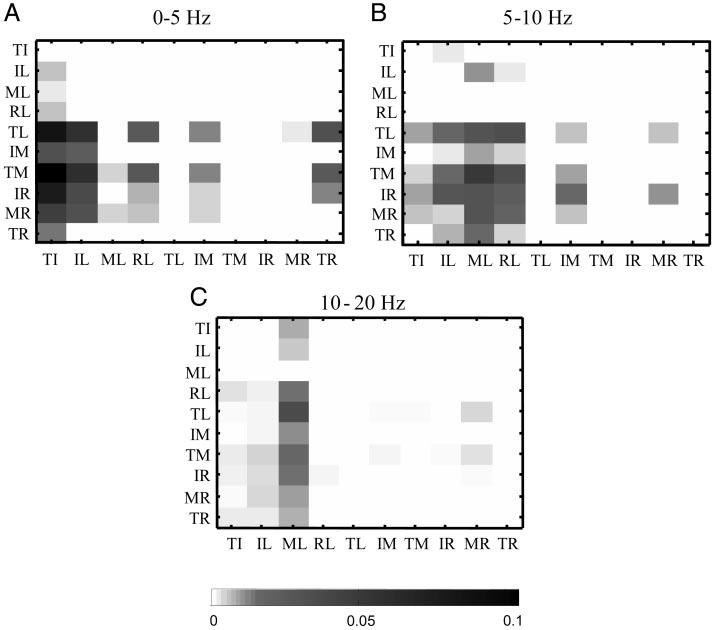
Significant differences in pooled coherence for all digit pair comparisons. A–C: the magnitude of the significant differences between digit pairs from within 0–5, 5–10, and 10 –20 Hz, respectively. The magnitudes of significant difference were quantified as the area outside the confidence intervals of the difference plot (e.g., Fig. 4C). White and black indicate no difference and maximum difference, respectively (0 and 0.1 on the grayscale bar). Note that the darker squares indicate that the pooled coherence from the digit pairs on the horizontal axis are greater than those computed from the digit pairs on the vertical axis. Index, middle, ring, little fingers and the thumb are denoted I, M, R, L, and T, respectively.

RELATIONSHIP BETWEEN MOTOR-UNIT SYNCHRONY AND COHERENCE MAGNITUDE

Strong motor-unit synchrony in the time domain has been interpreted as motor-unit pairs receiving branched presynaptic input (Farmer et al. 1993; Kirkwood 1979; Sears and Stagg 1976). Common periodic input would be revealed by significant motor-unit coherence (Farmer et al. 1993; Semmler et al. 2002, 2004). It follows that if common input is delivered through branched pre-synaptic pathways and is characterized by periodicities, the preceding time and frequency domain measures would be correlated. Conversely, a lack of correlation between these two measures would suggest that common inputs are delivered through independent pathways. Therefore linear regression analysis was used to assess the extent to which the CIS (computed for our previous study) (see Winges and Santello 2004) correlated with maximum coherence within 0–5, 5–10 and 10–20 Hz frequency ranges. Linear regression analysis was computed for motor-unit pairs from each muscle/muscle compartment pair.

The relationship between motor-unit synchrony and coherence is influenced by the duration of the cross-correlogram peak (Semmler et al. 2004). Narrow peak durations are indicative of direct common input to the motoneurons, whereas broader peak durations are considered reflective of indirect common input, i.e., common input with one or more interposed neurons (Semmler et al. 2004). We separated our motor-unit pairs into those characterized by peak durations ≤11 ms (18 motor-unit pairs) and >11 ms (189 motor-unit pairs). We chose a cut-off value of 11 ms for consistency with previous studies of human motor units (e.g., Semmler et al. 2004; but see following text). Thirty motor-unit pairs exhibited no peak in the cross-correlogram, and peak durations could not be determined. Therefore these motor-unit pairs were excluded, resulting in a total of 207 motor-unit pairs for the linear regression analysis between motor-unit synchrony and coherence for these two data sets. Note that our algorithm to determine peak duration is different from that used by other studies (e.g., visual inspection of cusum inflection) (Nordstrom et al. 1992; Reilly et al. 2004; Semmler et al. 2004). Specifically, we defined the peak duration of the cross-correlogram as the time between the 10th and 90th percentile of the inflection of the cusum within ±20 ms from the reference unit (Keen and Fuglevand 2004; Schmied et al. 1993). Using this algorithm was also preferred for the sake of consistency with our previous study (Winges and Santello 2004). The significance level of P < 0.05 was used for all statistical analyses.

RESULTS

Motor-unit activity

Figure 2A shows a typical record of EMG activity from the index finger compartment of the FDP (FDP2) and a thumb flexor muscle (FPL) during object hold. Single motor units were reliably discriminated off-line from the EMG recordings of each muscle (Fig. 2B). We were able to discriminate a total of 315 motor units, resulting in the analysis of 98 motor-unit pairs across FPL–FDP muscles and 139 motor-unit pairs across FDP compartments for a total of 237 motor-unit pairs (see Table 1).

TABLE 1.

Motor-unit firing parameters

Across Muscles (FPL-FDP)					Across FDP Muscle Compartments
Digit pair	FPL-FDP2	FPL-FDP3	FPL-FDP4	FPL-FDP5	FDP2-FDP3	FDP2-FDP4	FDP2-FDP5	FDP3-FDP4	FDP3-FDP5	FDP4-FDP5
n	16	46	11	25	26	31	13	36	14	19
No. of action potentials	1210 ± 238	1758 ± 525	1990 ± 639	1705 ± 443	1915 ± 558	1985 ± 516	1728 ± 478	1559 ± 407	1483 ± 501	1794 ± 536
GM firing rate, Hz	11.41 ± 1.34	10.45 ± 1.18	11.31 ± 0.63	10.12 ± 1.24	10.91 ± 1.01	10.69 ± 0.84	11.58 ± 1.09	10.64 ± 1.76	11.51 ± 1.13	11.08 ± 1.04
GM coefficient of variation, %	28 ± 9	25 ± 6	26 ± 7	27 ± 5	23 ± 4	23 ± 4	21 ± 5	28 ± 10	25 ± 7	26 ± 13

Values are means ± SD. FPL, flexor pollicis longus; FDP, flexor digitorum profundus; GM, geometric mean.

Motor units were tonically active during object hold and had fairly stable firing rates (Fig. 2B; tonic activity was a requirement of our data collection protocol, see methods). The mean ± SD of the number of action potentials recorded from all motor units was 1,728 ± 528. The mean number of action potentials and the average geometric mean and CV of firing rate for each pair of muscles/muscle compartments are also listed in Table 1.

Normal forces exerted by each digit (not shown) were relatively constant throughout the task, and the distribution of thumb and finger normal forces was similar to those reported by previous studies on multidigit grasping with heavier objects (i.e., >1 kg) (Rearick and Santello 2002; Santello and Soechting 2000), i.e., finger forces were progressively smaller from the index to the little finger (for more details on force analysis, see Winges and Santello 2004).

Incidence of significant coherence

Figure 4A shows the distributions of significant coherence plotted as the proportion of trials characterized by coherence at or above the 95% significance level across the entire frequency range of interest (1–50 Hz).

We found similar distributions across frequencies for both the across-muscles and across-muscle compartment combinations, with the greatest incidence of significant coherence occurring within the lower frequency ranges (i.e., 0–10 Hz). With regard to coherence computed across FDP compartments (Fig. 4A, left), motor-unit activity was also significantly correlated within the range from 10 to 50 Hz, although not as consistently as for the lower frequency ranges. Specifically, a large percentage of the significant coherence from motor units belonging to FDP compartment pairs occurred within 0–5, 6–12, and 13–19 Hz (a total of 58% of the total frequency distribution), with the largest incidence at ∼1 Hz (22%). The largest incidence of significant coherence from across-muscle motor units (Fig. 4A, right) also occurred between 0 and 10 Hz (31% of the total frequency distribution) with the greatest incidence of 16% at 2 and 4 Hz. The incidence of significant coherence across FDP compartments, particularly in the 0- to 10-Hz frequency range, was greater than that found in motor units across-muscles (38 vs. 31% of total frequency distribution).

Closer examination of the incidence of significant motor-unit coherence across-muscles and muscle compartments revealed a large variation in the extent to which significant coherence occurred across digit pairs. The greatest incidence of across-muscle coherence occurred in motor units from FPL-FDP2 (thumb-index digit pair) within the 0-to 5-Hz frequency range. For this digit pair, the highest consistency of significant coherence was at 3 Hz (7/16, 43% of all trials), with a large percentage of occurrences in the 0- to 10-Hz frequency range (43% of the entire frequency spectrum). In contrast, the incidence of significant coherence computed on FPL-FDP3, FDP4, and FDP5 (thumb-middle, ring, and little digit pairs, respectively) was low (less than ∼20%) and uniformly distributed across the entire frequency spectrum.

Significant coherence of motor-unit pairs from FDP compartments was also found more consistently at low than high frequencies. This was particularly evident for coherence computed on motor units from FDP5 (little finger) and each of the other FDP compartments, i.e., FDP2 (index finger, 5/13; maximum of 38% at 10 Hz), FDP3 (middle finger, 5/14; 36% at 3 Hz), and FDP4 (ring finger, 6/19, 32% at 8 Hz). Other FDP compartment pairs also exhibited some peaks in the frequency distribution of significant coherence (i.e., FDP3–FDP4, middle-ring finger pair) but not to the same extent as finger pairs involving the little finger.

Strength of individual trial and pooled coherence

Individual motor-unit pairs exhibited significant coherence with peak magnitudes that ranged from 0.03 to 0.22 primarily within 0–10 Hz. Although the measure of coherence quantifies the strength of correlated activity in a given motor-unit pair, pooled coherence is a measure of average correlation as it quantifies the extent of coupling between many motor-unit pairs (see methods). Therefore significant pooled coherence suggests the existence of common periodic input to the population of motor-unit pairs studied. Figure 4B shows the pooled coherence computed from motor units belonging to FDP compartment and FPL-FDP compartment pairs (left and right, respectively).

The greatest magnitudes of pooled coherence occurred in the 0- to 10-Hz frequency range and, to a smaller extent, within 15–25 Hz. The strongest pooled coherence across muscles (Fig. 4B, right) was found at 1, 8, and 16 Hz (0.0017, 0.0007, and 0.0005, respectively). Significant pooled coherence across muscle compartments of the FDP was also strongest at low frequencies with peaks at 2 and 8 Hz (0.0025 and 0.0016, respectively; Fig. 4B, left), with a smaller peak (0.0008) at 21 Hz. Even though both across-muscle and across-muscle compartment coherence were characterized by a stronger magnitude at low frequencies (within 0–10 Hz), the difference of coherence test (see methods) revealed a significantly larger coherence across-FDP compartments than across-muscles at 2, 7, 13, and 21 Hz (P < 0.05; Fig. 4C).

To explore possible differences across digit pairs, we computed pooled coherence on motor units from FPL and FDP compartments associated with each of the 10 digit pair combinations (Fig. 5).

We found large differences in the strength of pooled coherence across digit pairs. The strongest across-muscle pooled coherence occurred in motor units from FPL–FDP2 (thumb-index digit pair; 0.010 at 3 Hz). Weaker pooled coherence was observed for the remaining FPL–FDP compartment pairs (Fig. 5A). With regard to pooled coherence computed on motor units from FDP compartments (Fig. 5B), FDP2–FDP5, FDP3–FDP5, and FDP4–FDP5 (index-little, middle-little, and ring-little finger pairs, respectively) were characterized by the strongest coherence (0.009 at 2 Hz, 0.009 at 13 Hz, and 0.006 at 5 Hz, respectively). All other finger pair combinations exhibited weaker, although in some cases still significant, coherence (Fig. 5B).

Figure 6 shows the magnitudes of the significant differences (test of difference; see methods) for all pooled coherence comparisons (n = 45) across the 10 digit pairs. The grayscale represents the magnitude of the significant difference, i.e., the darker the square, the larger the significant difference, for frequencies ranging from 0–5, 5–10, and 10 –20 Hz (Fig. 6, A-C, respectively).

Three observations can be made from Fig. 6. First, most of the significant differences in the pooled coherence among digit pairs occurred at low frequencies (i.e., 0–10 Hz, A and B). In fact, it appears that the number and magnitudes of significant differences in pooled coherence decrease with increasing frequency, i.e., dark squares become fewer and lighter from A to C. Second, most of the significant differences are found when comparing the thumb-index digit pair (TI) and the finger pairs involving the little finger (i.e., IL, ML and RL; Fig. 6, A-C) with the other digit pairs. This indicates that pooled coherence of motor units from FPL-FDP2 (thumb-index digit pair) and FDP combinations involving the FDP5 (little finger) were stronger than that found for the remaining digit pairs. Last, the coherence magnitude of the middle-little finger pair was significantly greater than all other digit-pair combinations in the highest frequency range (Fig. 6C).

Relationship between maximum coherence and motor-unit firing parameters

We performed linear regression analysis to assess the extent to which differences in motor-unit firing rate parameters (mean firing rate and within-trial firing rate variability) and number of action potentials across muscle/muscle compartment pairs might have contributed to differences in maximum pooled coherence (see methods; Fig. 5). We found statistically significant, but weak correlations between the 1) geometric mean of firing rates and 10- to 20-Hz maximum coherence (r² = 0.062, P < 0.001),2) geometric mean of the CV of firing rate and 0–5 Hz maximum coherence (r² = 0.016, P = 0.05), and 3) average number of action potentials and maximum coherence in the 0- to 5- and 5- to 10-Hz frequency ranges (r² = 0.024, P < 0.05 and r² = 0.021, P < 0.05, respectively). All other correlations were nonsignificant. These weak coefficients of determination suggest that the differences in maximum coherence across digit pairs (Fig. 5) could not be accounted for by differences in the average number of discriminated action potentials or the mean and variability of firing rates of motor-unit pairs.

Strength of motor-unit synchrony and coherence for each digit pair combination

The strength of motor-unit synchrony and coherence can both provide insights into the underlying structure of the common input received by a given motor-unit pair (see methods). To graphically illustrate the strength of common and periodic inputs to individual muscle/muscle compartment pairs, the mean motor-unit synchrony (CIS) and pooled coherence within the three frequency ranges of interest were plotted in Fig. 7. Thumb-index and index-little fingers (TI and IL, respectively; Fig. 7A) exhibited moderate to strong motor-unit synchrony (CIS = 0.49 and 0.39, respectively) and strong 0- to 5-Hz pooled coherence (0.01 and 0.009, respectively). In contrast, thumb-middle and thumb-little (TM and TL, respectively; Fig. 7A) exhibited weak motor-unit synchrony (CIS <0.3) and weak 0- to 5-Hz pooled coherence (<0.003). The remainder of the digit pairs fell within this continuum from weak to strong motor-unit synchrony and weak to strong 0- to 5-Hz coherence, indicating more moderate levels of nonperiodic and low frequency periodic common inputs, respectively. As the coherence frequency increases (Fig. 7, B and C), the range of coherence strengths becomes narrower (i.e., coherence becomes weaker in general). However, the clustering of digit pairs observed in Fig. 7A is preserved within the continuum from weak to strong motor-unit synchrony and coherence, with one notable exception. The middle-little finger pair which exhibited moderate to strong motor-unit synchrony (CIS = 0.48), exhibited its largest mean pooled coherence within 10–20 Hz (0.0093; Fig. 7C).

FIG. 7.

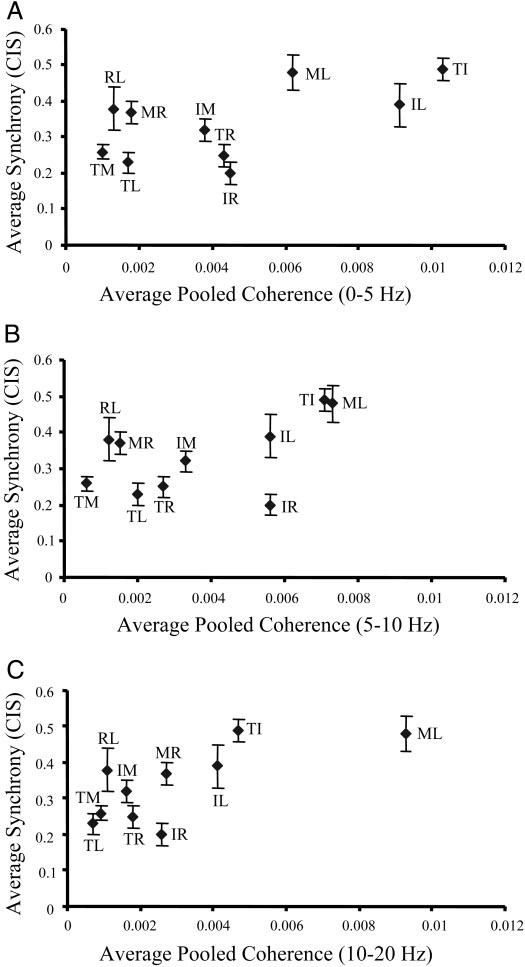
Strength of motor unit synchrony and coherence. Each data point represents the average motor unit synchrony (CIS; vertical axis) and pooled coherence averaged within 0–5 Hz (A), 5–10 Hz (B), and 10–20 Hz (C) frequency ranges (horizontal axis) for each of the 10 digit pair combinations. Vertical error bars indicate the SD of the mean CIS values. For graphical clarity, SD of the mean coherence was omitted. Digits labeled as in Fig. 6.

Correlation between motor-unit synchrony and maximum coherence

Note that the data shown in Fig. 7 were plotted to provide a qualitative summary of the overall distribution of both periodic and nonperiodic common inputs to individual muscle/muscle compartment pairs. Specifically, the data shown in Fig. 7 cannot be used to assess a relationship between CIS and coherence within a given digit pair. This relationship was assessed by linear regression analysis on CIS and the maximum coherence within 0–5, 5–10, and 10–20 Hz across the motor units for each muscle/muscle compartment pair (see methods; Table 2). We found significant linear correlations in 5 of the 10 digit pair combinations. The significant r² values were generally weak, ranging from 0.141 to 0.405, and the statistical significance was weakest when correlating CIS with the highest frequency range (10–20 Hz).

TABLE 2.

Coefficient of determination (r²) values for linear correlations between motor-unit coherence and synchrony (CIS) for each digit pair combination

	TI	IM	IR	IL	TM	MR	ML	TR	RL	TL
0–5 Hz	0.219	0.327**	0.038	0.357	0.010	0.141*	0.073	0.137	0.005	0.155*
5–10 Hz	0.059	0.281**	0.003	0.140	0.013	0.385***	0.023	0.045	0.113	0.044
10–20 Hz	0.280*	0.163*	0.035	0.044	0.063	0.072	0.405*	0.022	0.196	0.092

Maximum coherence was determined for 0- to 5-, 5- to 10-, and 10- to 20-Hz frequency ranges. I, M, R, L, and T indicate index, middle, ring, little fingers, and thumb, respectively. Asterisks indicate significant correlations:

^*P < 0.05

^**P < 0.01

^***P < 0.001

We found that 9% (18/207) of the motor-unit pairs were characterized by peak durations ≤11 ms (average: 7.3 ms, range: 2 –11 ms; each digit pair was represented in this data set with the exception of the ring-thumb pair) and 91% (187/207) of the motor-unit pairs exhibited peak durations >11 ms (average: 21.3 ms; range: 11.2 –38.6 ms) (see Winges and Santello 2004 for more details). We found significant correlations between CIS and 5- to 10- and 10- to 20-Hz maximum coherence in the data characterized by peak durations ≤11 ms (r² = 0.408, P < 0.01 and r² = 0.566, P < 0.001, respectively). For the data set characterized by broad peak durations, we found significant, but much weaker correlations between CIS and 0- to 5-, 5- to 10-, and 10- to 20-Hz maximum coherence (r² = 0.06, P = 0.001, r² = 0.152, P < 0.001, and r² = 0.076, P < 0.001, respectively).

DISCUSSION

The present study is the first attempt to examine the common periodic input across extrinsic digit flexors during a natural task requiring fine spatial and temporal coordination of multiple forces, i.e., multidigit grasping. Our analysis revealed three primary findings. First, in contrast to what has been reported in intrinsic hand muscles, motor units belonging to different muscles and muscle compartments of the extrinsic digit flexors exhibited significant coherence in the low-frequency ranges (0–5 and 5–10 Hz) and much weaker coherence in the higher 10- to 20-Hz range. Second, the strength and incidence of coherence differed considerably across digit pairs, indicating that common periodic input to these muscles was not uniformly distributed. Analysis of both motor-unit synchrony (CIS index) and coherence further confirmed a heterogeneous organization of the pathways by which common inputs are delivered to the muscles and muscle compartments controlling individual digit pairs. Third, contrary to what has been reported in the literature, across-muscle coherence can be stronger and more prevalent than within-muscle coherence, as FPL-FDP2 (thumb-index digit pair) exhibited the strongest and most prevalent coherence in our data.

Strength, incidence and frequency content of common periodic input to motor units

During our grasping task, individual motor-unit pairs exhibited significant coherence with maximum magnitudes that ranged from 0.03 to 0.22, which is comparable to that of previous research¹ (Farmer et al. 1993; Semmler et al. 2002). Coherence of such magnitudes can be indicative of both periodic and nonperiodic common inputs. However, nonperiodic common input produces motor unit coherence with a broad frequency range, i.e., 1–50 Hz (Halliday 2000; see also Taylor and Enoka 2004a), whereas the significant coherence peaks observed in the present study were very narrow and often not wider than 2 Hz. Therefore the coherence exhibited by our individual motor-unit pairs is likely to have arisen from common periodic input (Halliday 2000; Taylor and Enoka 2004a).

Despite these results from individual motor-unit pairs, the strength of pooled coherence was very weak (e.g., FPL–FDP compartment, 0.0017; FDP compartment, 0.0025) and lower than the values reported by Halliday et al. (1999), i.e., 0.04 for a similar number of motor-unit pairs (n = 106) from within the extensor digitorum communis (EDC) during a postural finger task. Contributing to our weaker pooled coherence was the fewer incidences of significant coherence, i.e., our maximum incidence was 43% (FPL–FDP2; thumb-index digit pair) compared with what has been reported in other studies (Farmer et al. 1993; 77%; Halliday et al. 1999; 60%; Kakuda et al. 1999; 83%; Semmler et al. 2002; 91%).

Differences between our data and that of the previous literature are also evident in the predominant frequencies of coherence observed. Significant motor-unit coherence is often observed within 1- to 12- and 16- to 32-Hz frequency bands (Farmer et al. 1993; Halliday et al. 1999; Marsden et al. 1999; Semmler et al. 2002). However, we observed significant peaks of coherence in the 0- to 5- and 5- to 10-Hz frequency ranges with a much weaker coherence in the higher frequency range of 10–20 Hz.

The differences observed in the present study and those reported in the literature may primarily be due to the analysis of motor units belonging to the same muscle (i.e., within-muscle coherence) versus those from different muscles or muscle compartments (i.e., across-muscle/muscle compartment coherence), intrinsic versus extrinsic hand muscles and/or the differences in task requirements, e.g., force production under visual and/or auditory feedback versus object hold against gravity. Each of these factors is discussed separately in the following text.

WITHIN- VERSUS ACROSS-MUSCLE MOTOR-UNIT COHERENCE

While most research has examined coherence in motor units from within the same muscle (e.g., Halliday et al. 1999; Kakuda et al. 1999; Kilner et al. 2002; Semmler et al. 2002), Farmer et al. (1993) examined the incidence of coherence in motor units obtained from within the first dorsal interosseus (1DI) as well as across the 1DI and second dorsal interosseus muscles. These authors observed a significant reduction in the incidence of coherence when the coherence was computed on motor units across- versus within-muscles (54 vs. 77%, respectively). This suggests that common periodic input might be more prevalent in motor units belonging to the same muscle than to different muscles.

Our results support this notion as coherence was stronger and more prevalent between motor units from different compartments of the same muscle (i.e., FDP compartments) than those from two separate muscles (i.e., FPL and FDP; see Fig. 4, A and B). Thus it appears that common periodic modulation is greater for motoneurons within a single pool innervating different muscle compartments of the same muscle (i.e., FDP) than for motoneuron pools or sub-pools innervating separate muscles (i.e., FDP and FPL). However, further analysis revealed that the difference between within- and across-muscle coherence is not obligatory as the strongest common periodic modulation occurred in motor units obtained from different muscles (i.e., FPL-FDP2, thumb-index digit pair; see Fig. 5).

While examination of motor units within versus across muscles may account for differences in the strength and prevalence of coherence, it does not appear to influence the frequency content of motor-unit coherence (see Figs. 1 and 2) (Farmer et al. 1993). Therefore other factors must be contributing to the weaker high-frequency coherence observed in our data.

EFFECT OF TASK

We used a task characterized by behavioral consequences (i.e., prevent the object from slipping) and imposed no constraints such as auditory or visual feedback of forces and/or motor-unit firing rate as has been done in previous motor-unit coherence studies (Farmer et al. 1993; Kakuda et al. 1999; Kilner et al. 2002; Marsden et al. 1999; Semmler et al. 2002). Attentional demands of the task can affect the strength of common input to motor units (Schmied et al. 2000). Therefore the different attentional demands required to prevent object slip versus maintaining a constant motor-unit firing rate or visual tracking of force might have contributed to the preceding differences in motor-unit coherence between our results and those reported in the literature.

Task dependencies have also been observed in the frequency of motor-unit coherence. It has been suggested that the functional significance of the higher frequency range (16–32 Hz) observed in motor-unit coherence provides a “binding” mechanism (see Gray 1994) by which task-related groups of neurons are efficiently activated (Farmer 1998; McAuley and Marsden 2000). Coherence peaks within this frequency range are observed during postural tasks (Halliday et al. 1999; Semmler et al. 2002) and steady contractions (Baker et al. 1999; Kilner et al. 2002) and are stronger when interacting with objects of greater compliance (Kilner et al. 2002) but weaker during slow wrist movements (Kakuda et al. 1999) and ramp changes in force magnitude (Baker et al. 1999; Kilner et al. 2002). Furthermore, the strength of motor-unit coherence in this frequency range is smallest in subjects with training in fine motor-skills compared with untrained and strength-trained subjects (Semmler et al. 2004). Given that supraspinal activity is believed to be essential for this frequency range of coherence (see following text), Semmler et al. (2004) interpreted the above finding as a reduction in the oscillatory supraspinal descending command to allow for a more independent control of a greater number of degrees of freedom (e.g., motor units) in tasks requiring fine-motor skills.

The task dependencies of the low-frequency component of motor-unit coherence are not as well understood. For instance, the strength of coherence in the 6- to 12-Hz frequency range—unlike the high-frequency range (see preceding text)—does not appear to be affected by the degree of object compliance during grasping (Kilner et al. 2002). However, stronger 1- to 10-Hz coherence magnitudes were observed in the 1DI in strength trained compared with untrained and skill trained subjects when performing isometric contractions. Furthermore, Kakuda et al. (1999) observed an increase in the magnitude of 6- to 12-Hz coherence in motor units from the extensor carpi radialis (ECR) during slow wrist movements when compared with position holding. In contrast, Semmler et al. (2002) found stronger coherence for position holding and lengthening muscle contractions versus shortening contractions in the 2- to 12-Hz frequency range. It has also been suggested that tasks using visual tracking may produce 2- to 3-Hz oscillations in movements and contribute to periodic modulation of motor-unit discharge times at this frequency (Kakuda et al. 1999). Yet, this frequency of motor-unit coherence (i.e., ∼3 Hz) was also observed in the current study (e.g., FPL–FDP2, thumb-index digit pair; see Fig. 5) even though no visual tracking was required, suggesting that other factors contribute to the motor-unit coherence within this low-frequency range.

INTRINSIC VERSUS EXTRINSIC HAND MUSCLE MOTOR-UNIT COHERENCE

Motor-unit coherence within both 1–12 and 16–32 Hz is preserved in deafferented patients, but the higher frequency band is abolished in stroke patients (Farmer et al. 1993). This suggests that afferent activity is not necessary for the generation of coherence in either frequency band (however, see Kilner et al. 2004), but supraspinal activity is necessary for motor-unit coherence to occur within the 16- to 32-Hz frequency range. Stronger and more prevalent coherence in the higher frequency range has been observed in motor-unit pairs obtained from the distal 1DI compared with those from more proximal muscles (biceps brachii, Farmer et al. 1993; paraspinals, Marsden et al. 1999; ECR, Kakuda et al. 1999). Farmer et al. (1993) suggested that it is the greater activation of direct corticomotoneuronal projections to distal compared with proximal muscles that accounts for the differences observed in the higher frequency range in these muscles. This is consistent with the stronger and more prevalent direct corticomotoneuronal projections found in the intrinsic compared with extrinsic hand muscles in monkeys (Buys et al. 1986; Lemon 1993) and in humans (Palmer and Ashby 1992). Therefore the weaker high-frequency coherence exhibited by our population of motor-unit pairs may result from fewer corticomotoneuronal projections to the extrinsic hand muscles.

The significant low frequency coherence observed in our population of motor-unit pairs was weaker and less prevalent than that observed in other extrinsic muscles, e.g., the ECR muscle (43 compared with 83%) (Kakuda et al. 1999). Therefore while differences between intrinsic and extrinsic hand muscles may account for the weaker high-frequency coherence, it does not entirely account for the weaker and less-prevalent low-frequency coherence observed in the present study. It is possible, however, that the difference in the coherence between the extrinsic digit flexors and the ECR reflects their different functional roles (i.e., digit flexion versus wrist extension).

Mechanisms contributing to low-frequency motor-unit coherence

Spinal mechanisms are considered a possible means by which motor-unit coherence is generated at frequencies within 6–12 Hz (Kakuda et al. 1999) that may account for this range of frequencies observed in the present data (see Fig. 5). Elble and Randall (1976) suggested that Renshaw recurrent inhibition feedback loops may cause a 10-Hz modulation of motor-unit activity. Modeling studies have revealed that inhibitory interneurons can influence the strength and frequency of oscillations in cortical networks (Pauluis et al. 1999) as well as the strength of motor-unit coherence (Taylor and Enoka 2004a,b). Furthermore, inhibition interacts with intrinsic properties of motoneurons producing different effects on the correlation of motor-unit activity (Taylor and Enoka 2004a,b). Last, it has been suggested that the coherence of frequencies <4 Hz, as observed in our data, could be sustained by oscillations in both transcortical and spinal reflex loops (Kakuda et al. 1999) and may minimize the need for cortical control of motor-unit recruitment (De Luca and Erim 1994).

Structure of common input

Linear correlation between CIS and coherence has been interpreted as reflective of common periodic input to the motoneurons through branched presynaptic pathways (see methods) (Farmer et al. 1993; Semmler et al. 2002). Semmler et al. (2004) suggested that this analysis should take into account the peak durations of the cross-correlogram as narrow and broad peak durations are indicative of direct and indirect common input to the motoneurons, respectively (Semmler et al. 2004). Therefore significant linear correlations between coherence and synchrony of motor-unit pairs with narrow or broad peak durations may reflect common periodic input that is delivered either through direct or indirect branched pathways, respectively.

We found a significant linear correlation between CIS and coherence in the 5- to 10- and 10- to 20-Hz range for the 9% (18/207) of motor-unit pairs with narrow cross-correlogram peak durations (≤11 ms). This suggests that for these motor-unit pairs, the higher frequency periodicity delivered through direct branched input was consistently observed in the output of the motor-unit pairs. On the other hand, much weaker relationships between synchrony and coherence were observed for the 91% of motor-unit pairs with broad peak durations (>11 ms), suggesting a less consistent transmission of the input periodicities to the output of the motor-unit pairs. This predominance of indirect branched pathways in our population of motor-unit pairs may also account for the relatively weak coherence observed in our data (Taylor and Enoka 2004a). The results of the linear regression analysis within each digit pair (Table 2) coupled with the strength of both CIS and coherence (Fig. 7) revealed a heterogeneous distribution of periodic and nonperiodic inputs to the extrinsic hand muscles. It appears that these common inputs were delivered through different combinations of indirect and direct branched presynaptic as well as independent pathways.

Note, however, that our interpretation of the existence or absence of linear correlation between motor-unit synchrony and coherence should be interpreted with caution. Interpreting the lack of correlation between motor-unit synchrony and coherence as indicative of the existence of independent pathways relies heavily on the assumption that the interaction between periodic and branched common input does not vary within each trial. However, it is also possible that these processes may be independently modulated within a given trial. In such cases, motor-unit synchrony and coherence might not be linearly related even though common input with a variable extent of periodicity is delivered through the same branched pathway.

Moreover, our data revealed limited ranges for both coherence and CIS values, i.e., 0–0.21 and 0–0.86, respectively. Evaluating the linear relationship between two variables over such a limited range might not be sufficient to assess the existence or lack of linear relationships. The range of CIS values that have been correlated with coherence in the literature tend to be larger (i.e., 0 to ∼2.5) (Semmler et al. 2004) and this could be due to the fact that these values were computed from within, rather than across, muscles.

Functional significance of neural common input

The heterogeneous organization of common input across muscle/muscle compartment pairs controlling individual digit pairs may reflect differences in their functional roles in the control of multidigit grasping. For example, in our task the thumb and index finger pair produces the largest force among all digit pairs (Winges and Santello 2004). Furthermore, index and little fingers are responsible for the control of moments more so than fingers that are more collinear with the thumb, i.e., middle and ring fingers. Therefore these differences might account—to some extent—for the stronger common input (both periodic and nonperiodic) observed in the thumb-index digit pair and in all the finger combinations involving the little finger.

It is also possible that the stronger common input found in these digit pairs might reflect the degree to which they are concurrently active during a broad range of common manipulative behaviors. For instance, the thumb is opposed to the index finger more often than it is with the other fingers (i.e., in both precision and power grips). Similarly, when a grasp includes the little finger, it is rarely opposed to the thumb in isolation as it inevitably includes the other fingers as well. We could therefore speculate that long-term and/or preferential usage of specific digit pairs might lead to different degrees of neural common input as has been suggested for force and fine motor skill training (Semmler et al. 2004).

The behavioral consequences of common input to motor units are not well understood. To address this issue, a recent motor-unit simulation was conducted to put into perspective the functional meaning of common input of variable strengths (Santello and Fuglevand 2004). The results of this simulation indicated that a CIS value of 0.3, indicative of moderate synchrony across two muscles, was sufficient to constrain the temporal relationships between grip forces. This suggests that common input might be a mechanism contributing to force coordination during grasping (Winges and Santello 2004). However, the functional role of periodic and nonperiodic input has not been formally tested and is currently under investigation.

Conclusions

Our results revealed a heterogeneous distribution of common input characterized by various degrees of periodicity, primarily in the low-frequency range, to motoneurons inner-vating different muscles/muscle compartments of the extrinsic digit flexors. The frequency content, structure, and organization of this common input may reflect the different roles played by individual digit pairs in the control of grasping. However, further investigation is needed to characterize the task dependencies and functional role of common input during manipulative behaviors.