Choreography for nucleosomes: the conformational freedom of the nucleosomal filament and its limitations

Abstract

Eukaryotic DNA is organized into nucleosomes by coiling around core particles of histones, forming a nucleosomal filament. The significance for the conformation of the filament of the DNA entry/exit angle (α) at the nucleosome, the angle of rotation (β) of nucleosomes around their interconnecting DNA (linker DNA) and the length of the linker DNA, has been studied by means of wire models with straight linkers. It is shown that variations in α and β endow the filament with an outstanding conformational freedom when α is increased beyond 60–90°, owing to the ability of the filament to change between forward right-handed and backward left-handed coiling. A wealth of different helical and looped conformations are formed in response to repeated β sequences, and helical conformations are shown to be able to contract to a high density and to associate pairwise into different types of double fibers. Filaments with random β sequences are characterized by relatively stable loop clusters connected by segments of higher flexibility. Displacement of core particles along the DNA in such fibers, combined with limited twisting of the linkers, can generate the β sequence necessary for compaction into a regular helix, thus providing a model for heterochromatinization.

INTRODUCTION

DNA in the cell nucleus is organized in nucleosomes by repetitive coiling ∼1.8 times around core particles consisting of two copies of each of four different core histones (H2A, H2B, H3 and H4). In higher eukaryotes a fifth histone, H1, is bound to the majority of the nucleosomes, bridging the DNA at the entry and exit of its coiling around the core particle. On average, one nucleosome is present for every 160–240 bp of DNA [the nucleosomal repeat length (NRL)]. The structure of the nucleosome is known in detail (1), and several models have been proposed for folding of the nucleosomal filaments into fibers with a diameter of ∼30 nm (2), which have been observed by electron microscopy. These models are based on experimental evidence obtained by a number of different techniques, using nuclear preparations, isolated chromatin and reconstituted oligonucleosomes. One of the main differences between the models is whether the DNA, which connects the nucleosomes (linker DNA), is straight or bent. Studies of chromatin in isolated nuclei have provided evidence for an organization of the filament into globular assemblies of nucleosomes (supranucleosomes or superbeads) (3) as well as for interdigitation of 30 nm fibers (4,5). Supranucleosomes have been proposed to be caused by dislocations in a cross-linker helical structure (6), but no models have been developed to explain the geometry of double fibers.

The conformational freedom of the nucleosomal filament, i.e. the number of different conformations it can attain, is limited by collisions between the nucleosomes, and is in first instance determined by the basic geometry of the filament, which is therefore of importance for the structure and function of the chromatin in the cell. One function concerns its role in transcription and transcriptional regulation, in which its dynamic nature (7) and structural plasticity (8) must play an important role. Another function concerns the putative architectural role of the chromatin in the nucleus, of which not so much is known. A long-standing question is to which extent the chromatin is a self-organizing polymer and to which extent it is being organized by other structures in the nucleus (9,10). It is not known whether the basic geometry of the filament by itself makes possible the formation of stable fiber associations.

Provided that the linker DNA is straight—and there is evidence to suggest that this is so in the cell (11)—conformational variations of the filament are mainly determined by two angles: the change in direction of the DNA every time it coils around a core particle and the angle between the flat faces of consecutive nucleosomes around their interconnecting linker DNA. This angle is often referred to as the rotational angle, because the positions of the core particles in the filament follow the right-handed rotation of the DNA double helix and therefore vary with the linker length. The conformational changes caused by variations in these two angles have been studied by computer models (12–14), but existing models do not take into account the full consequences of the size of the directional change of the DNA at the nucleosome, the asymmetry of rotation around the linker DNA and the conformational limitations imposed by the linker length. The present study shows that these parameters are of major importance for the conformational freedom of the filament, and explores the possible conformations by means of physical models. It provides a survey of different conformations of the nucleosomal filament and how they are related to each other, as well as to existing models of the chromatin fiber. It is shown that repeated or periodic variations in β sequence give rise to different types of helical and looped conformations and that helical conformations are able to associate pairwise as a zip, to form double helices, intercalate and contract to a high density. Finally, the irregular conformation of a filament with a random β sequence is described as well as how it can be converted into a regular helix by chromatin remodeling and limited twisting of the linkers. Although physical models are static and do not account for the linker flexibility, they might be useful in studies of chromatin ultrastructure and serve as reference models for the analysis of transmission electron microscopic images.

MATERIALS AND METHODS

Models of the nucleosomal filament were built in the scale 1.25 × 10⁶:1 using a plastic-coated copper wire with a mean diameter of 2.5 mm. Filaments were folded into pentagonal star- and polygon fibers at β = 0° using a metal block perforated by five displaceable parallel cylindrical metal rods of 8.5 mm in diameter, placed in the corners of a regular pentagon with a center-to-center distance of 21 mm. These dimensions correspond to a NRL of 86 mm (196 bp) and 98 mm (205 bp) for the star- and the polygon fiber, respectively. The fibers were subsequently modified by hand. In the star fiber, the orientation of the linkers of every single nucleosome was first adjusted, using η₁ = 9°. The nucleosomes were then rotated around the linker DNA in steps of β = 36° corresponding to ∼10 bp/coil of the DNA. This was done by orienting the dinucleosomes with their connecting linker in the viewing direction, defining β as the angle between the exiting or the entering coils of the nucleosomal DNA. In the polygon fiber, the orientation of the terminal linkers of the dinucleosomes was adjusted after rotation of the nucleosomes, using η₂ = 10°. A number of videos of the models shown on Figures 3–6 are presented at: http://icmm.ku.dk/ansat/personsider/mogens_engelhardt/choreography/

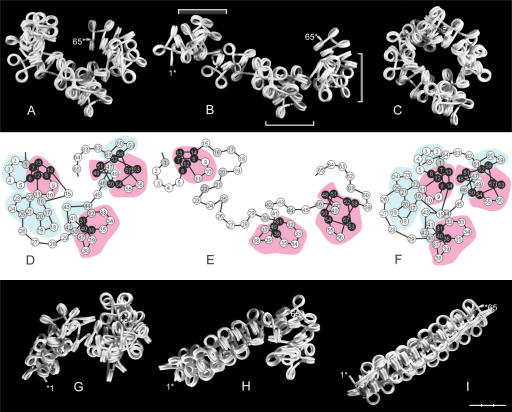
Figure 3.

Selected conformations of star and polygon fibers with repeated β sequences. (A) A star fiber with β sequence (11)_n showing collisions between every fifth nucleosome. (B–I) Polygon fibers. (B and C) (22)_n, (C) in a compact form as seen from the side and from the end. (D) A coil formed by (44)_n. (E and F) A polygon fiber with the approximate β sequence (222)_n, as shown in side-on view from two angles differing by 90° (E), and in a more compact form (F). (G–I) The fiber (1111)_n as seen in side view from two angles and from the end (G). One and the same nucleosome is marked by an asterisk. (H) Model of the fiber in (G, F) with partially overlapping hexanucleosomal loops. The first four nucleosomes (•1•1•1•1) in each repeat are painted in same color in the sequence red, green, blue, yellow and red (top to bottom) and numbered 1–4. (I) A loop formed by β sequence (3333)_n. α = 36 and 108° in the star- and polygon fibers, respectively, except in (E, F) where α = 90°. Bar = 30 nm.

Figure 4.

Swivel-linkers and compaction of a polygon fiber (α = 108°). (A) A fiber with β sequence (033033)_n, in which β(0)-swivel-linkers (arrows) connect trinucleosomes, which alternate between left- (•3•3•) and right-handed (•3•3•) orientation. (B–H) Compaction of a fiber (B) with β sequence (333)_n in which (3)-swivel-linkers (arrows) are separating right-handed trinucleosomes (•3•3•), two of which are numbered 1–3 and 4–6. The fiber is compacted by decreasing α at the terminals of the swivel-linker (C) and in the trinucleosomes (D). (E) Axial view of the compacted fiber showing the superposition of linkers of two consecutive trinucleosomes. (F) Compact fiber as viewed from the side. Nucleosomes with an orientation close to the fiber axis (blue arrows) are stacking edge-to-edge and nucleosomes perpendicular to the fiber axis (red arrows) have the potential to interact with nucleosomes in the same orientation in a neighboring fiber by interdigitation. (G) Interdigitation of two compact fibers as seen from the end and from the side. (H). Packing of three sheets (red, green, yellow), each consisting of three interdigitated fibers, as seen from the end. Rectangles delineate the cross-section area used for density calculation. Bar = 30 nm.

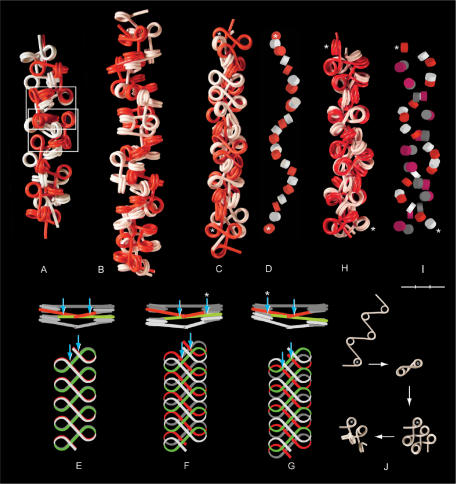
Figure 5.

Four types of chromatin double fibers formed by polygon fibers (red and white). (A) Two filaments with β sequence (333)_n and α = 108° (as shown in Figure 4B) align and interlock like a zip, in which nucleosomes in one fiber fit spatially into the space provided by a swivel-linker between two trinucleosomes in the other fiber (framed). (B) Two fibers with closed, negative linker configuration, β sequence (3033)_n, α = 108°, coil right-handed around each other forming a double helix. The swivel-linkers are parallel to the axis of the fiber, with alternating positions of the red and the white filament on the outside of the fiber. (C) Two fibers coil left-handed around each other by intercalation of every second nucleosome, α varying between 85 and 120° and β between 72 and 160°. (D) The positions of the intercalated core particles in the fiber in (C). (E–G) Two nucleosomal filaments with β(5) (180°) placed one on top of the other. (E) Nucleosomes stacking face-to-face with every second linker (red and green) touching each other at two crossover points (arrows), which are symmetrically positioned relative to the midpoint of the linker. (F and G) Parallel staggering of the ribbons along the fiber axis causes one crossover to be displaced toward the middle of the linker and the other toward the nucleosomal DNA of every second nucleosome, which is located at one edge of the ribbon (arrows). (H and I) A left-handed double helix formed by two filaments with alternating negative and positive linker configuration folded from a filament with open linker configuration; ∼90° < α < ∼108°; ∼β(+3). (I) The positions of the core particles in (H) with negative (red and white) and positive linker configuration (mauve and gray). (J) Folding of a nucleosomal filament leading to the conformation in (H). The first nucleosome is marked by an asterisk. Asterisks in (C, D, H, I) indicate the first and the last nucleosome in a sequence of intercalated nucleosomes. Bar = 30 nm (A–I).

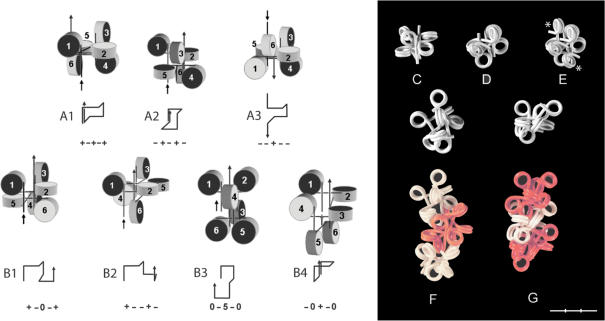
Figure 6.

Loops of hexa- and octanucleosomes with different β combinations. (A and B) Hexanucleosomal loops formed by β = 0°, ±90° and 180° (0, +, −, 5). Arrows indicate the direction of the filament from nucleosome No. 1→6. The flat faces of the core particles nearest to the entering linkers are dark while the faces nearest to the exiting linkers are light. The line diagrams show the orientation of the five linkers in each loop. (A1–3) Closed loops; (B1–4) locked loops. (C and D) Hexanucleosomes; (23131) (C); (41414) (D). (E) A nucleosome is added to each terminal linker of the loop in (D) (asterisks). (F and G) Loops of six plus two nucleosomes as shown singly and in series of three. (F) A trimer, 1(13132)2, connected by β(2); (G) A trimer, 3(33123)5, connected by β(5). Values of β are approximate. α = 90°. Bar = 30 nm (C–G).

RESULTS

Basic parameters

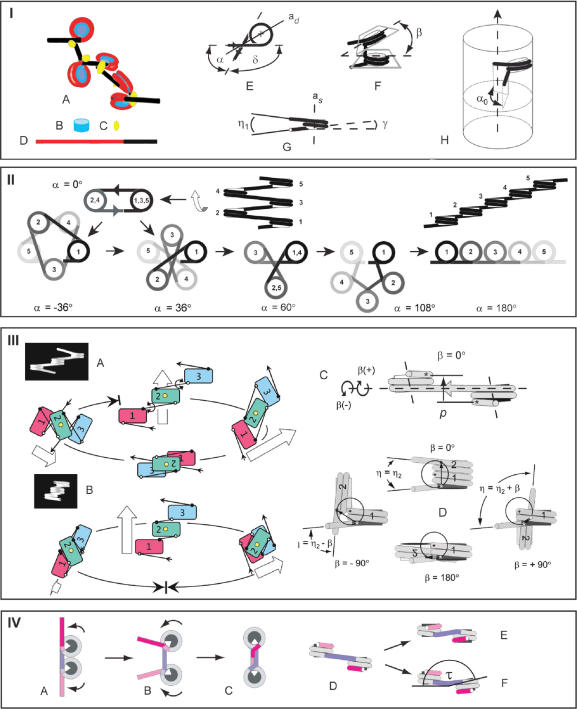
The conformation of a nucleosomal filament with straight linkers is determined by a number of geometric parameters, which are shortly introduced in the following (Figure 1-I). The two most important parameters are the angle (α) between the entering and exiting linkers of the nucleosome, caused by the change in the direction of the linker DNA (δ = 180°−α) and the angle (β) between the flat faces of consecutive nucleosomes. According to the X-ray crystal structure of the nucleosome, the ends of the 146 bp of nucleosomal DNA are separated by ∼75° (1) corresponding to a default value of α = 105°. The size of α is sensitive to binding of one molecule of linker histone (H1) (15,16), while β varies with the length of the interconnecting linker. When α and β are constant the filament forms a regular fiber within a cylindrical space, with an axial symmetry determined by α (for β = 0°) or the projection of α (α₀) into a plane perpendicular to the fiber axis (for β ≠ 0°). Because of the slope of the DNA [γ = 4.5° (13)] due to its coiling around the core particle, the two linkers diverge (negative conformation) by an angle (η₁), as defined by their projections into a plane of symmetry formed by the dyad axis and the symmetry axis of the nucleosome. If the linkers are bent so that their projections into this plane cross each other, they are said to be in a positive conformation. Linkers have also been proposed to be able to approach each other as a result of an allosteric change of the nucleosome (nucleosome gaping) in which the coils of the DNA are separated like a local opening of a spring (17). In the following, the significance of α and β for the conformation the nucleosomal filament will be demonstrated, assuming the linker DNA to be straight, entering and exiting the nucleosomes as tangents to their circular surface.

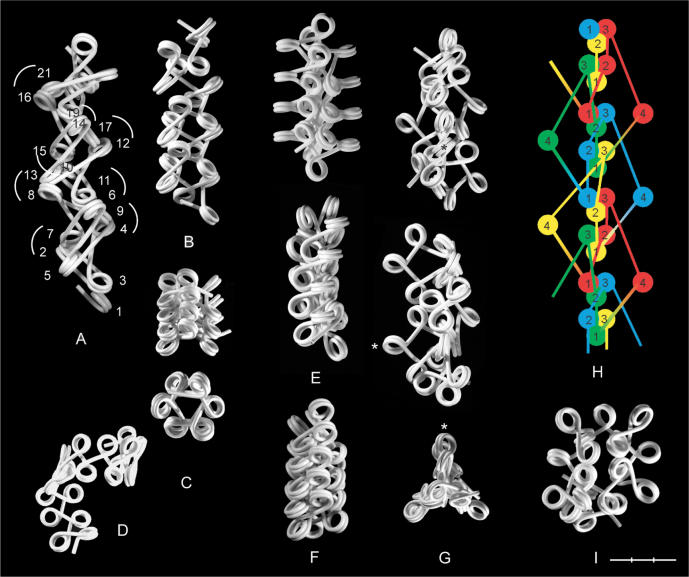
Figure 1.

Basic structure and folding of the nucleosomal filament. Panel I: (A) A nucleosomal filament with five nucleosomes. (B) Core particle. (C) Histone H1, (D) A nucleosomal repeat length (NRL) of 200 bp consisting of 146 bp of nucleosomal DNA (red) plus 54 bp of linker DNA (black). (E) The angle (α) between the entering and exiting linkers, the change in direction of the linkers (δ = 180°−α) and the dyad axis (a_d). (F) The rotational angle (β) between the flat faces of the nucleosomes. (G) The slope of the DNA (γ) and the angle (η₁) between the projection of the linkers into a plane through the axis of symmetry of the nucleosome (a_s) and the dyad axis, bisecting α. (H) The projection (α₀) of α in a chromatin fiber into a plane perpendicular to the fiber axis. Panel II: Unfolding the nucleosomal filament from α = 0° to α = 180°. Panel III: The effect of β on the direction and coiling of the filament. Rotation of the terminal nucleosomes of a trinucleosome of a polygon fiber (A) and a star fiber (B). The trinucleosomes are oriented with the dyad axis of the central nucleosome (yellow) in the viewing direction. Arrows indicate the direction of the filament from nucleosome No. 1→3. (C) Side-on view of a dinucleosomes showing the pitch (p) of the dinucleosomes, as defined by the height difference between the entry and exit sites of the terminal linkers in a plane perpendicular to the interconnecting linker. (D) Dinucleosomes oriented with the interconnecting linker in the viewing direction and nucleosome no. 1 in front. Clockwise and counter clockwise rotations are indicated by (+) and (−) and the pitch of the dinucleosomes is indicated by arrows. White and black asterisks indicate the entry and exit sites of the terminal linkers. Panel IV: Possible effects of binding of histone H1 on the geometry of the dinucleosome, as shown for NRL = 200 bp. (A and B) The entry and exit sites of the linkers on the nucleosomes approach each other, corresponding to two full coils of DNA around the core particles, while the size of α is decreased below 180° by bending of the linkers close to their entry/exit sites, causing the nucleosomes to rotate away from each other (arrows). (C) Rotation of the nucleosomes until α = 0°, forming a stem conformation, which occupies 25–30 bp of the linker. (D–F) Bending of the linker may introduce a twist angle (τ) between the flat faces of the nucleosomes. 146 bp nucleosomal DNA (gray); 54 bp connecting linker DNA (blue). The angle (75°) between the terminals of the 146 bp nucleosomal DNA is shown by the white sectors on the core particles.

The effect of α on the axial symmetry: star fibers and polygon fibers

The conformation of the filament is determined by the size of α when β = 0° (Figure 1-II). At α = 0° the direction of the DNA is changing 180° (δ) at each nucleosome, placing every second nucleosome on top of each other as two columns parallel to the fiber axis, like the edges of a ribbon. The filament unfolds when α is increased, forming a linear string of nucleosomes at α = 180°, and α can be increased either by directing the linkers toward each other (closed conformation) or away from each other (open conformation). A filament with linkers in the closed conformation uncoils clockwise with a concomitant decrease in the distance between the nucleosomes, as more of the linker DNA becomes associated with the core particles. Conversely, a filament with linkers in the open conformation uncoils counter-clockwise, increasing the distance between the nucleosomes as the terminals of the nucleosomal DNA are peeled off the core particles. Thus, at α = 180° the DNA coils twice around the core particles when linkers are in the closed conformation, but only once if linkers are in the open conformation. The effective linker length, i.e. the fraction of the NRL, which is available for keeping distance between the nucleosomes, thus depends on the size of α and the conformation of the linkers (open or closed). In the following, only the geometry of filaments with negatively closed linkers will be considered, if not stated otherwise.

During uncoiling of the filament the two stacks of every second nucleosome rotate in opposite direction of the filament, arranging themselves in stacks parallel to the fiber axis at every value of α < 60° that equals the angle of a regular star, and at every value of α ⩾ 60°, which equals the angle of a regular polygon. With reference to this difference in symmetry fibers will be called star fibers for α < 60° and polygon fibers for α ⩾ 60° (compare Figure 1-II, α = 36 and 108°).

The helical symmetry of fibers formed by 0° < α < 180° is characterized by the number of 360° coils of the nucleosomes at the fiber periphery (in other words: how many nucleosomes it takes to traverse the fiber periphery 360°), as defined by the helical twist of the nucleosomes (coils/nucleosome). As one nucleosome is placed at the periphery of the fiber for every turn (δ) of the linkers, the fibers are also characterized by the number of turns of the linkers, i.e. how many times the linkers have to turn 360° to place all the nucleosomes in a coil (turns/coil). Star and polygon fibers of the same axial symmetry have the same number of coils/nucleosome, but differ in the number of turns/coil. Thus, while filaments with α = 36° (δ = 144°) and α = 108° (δ = 72°) both have 1/5 coil/nucleosome, the former has two turns/coil (5 × 144° = 2 × 360°) and the latter has only one (5 × 72° = 360°).

The effect of β on the conformation of the filament

The rotational angle (β) between the flat faces of consecutive nucleosomes varies with the length of the interconnecting linker because the position of the core particle is fixed relative to the minor and major grooves of the nucleosomal DNA. Insertion or deletion of base pairs in the linker therefore makes the nucleosome follow the right-handed helix of the linker DNA, rotating clockwise [β(+)] or counter-clockwise [β(−)], respectively, in steps corresponding to the twist angle between the base pairs.

The number of sterically allowed values of β depends on whether or not every second nucleosome is able to pass each other side-by-side at β = 180° (Figure 1-III). When this is possible, the conformation of the filament is changed by clockwise rotation from a helix at β = 0° to a ribbon at β = 180° with a concomitant 90° change in direction, because the pitch (p) of the dinucleosomes is reduced to zero. The conformation at β = 180° is possible only for combinations of α and linker lengths, which allow for alignment of every second nucleosome side-by-side, requiring a NRL of at least ∼224 bp for α = 60° and 200 bp for α = ∼85°. Clockwise rotation of the nucleosomes beyond 180° makes the filament coil left-handed in the opposite direction, but a full 360° rotation is not possible because of the change from left- to right-handed coiling, except for filaments shorter than a single coil (Figure 1-IIIA). The size of β at which the change between right- and left-handed coiling takes place depends on α and the linker length. A star fiber with α = 36° and a NRL of 200 bp will only be able of right-handed coiling (Figure 1-IIIB).

Conformations of filaments caused by homogeneous variations in β

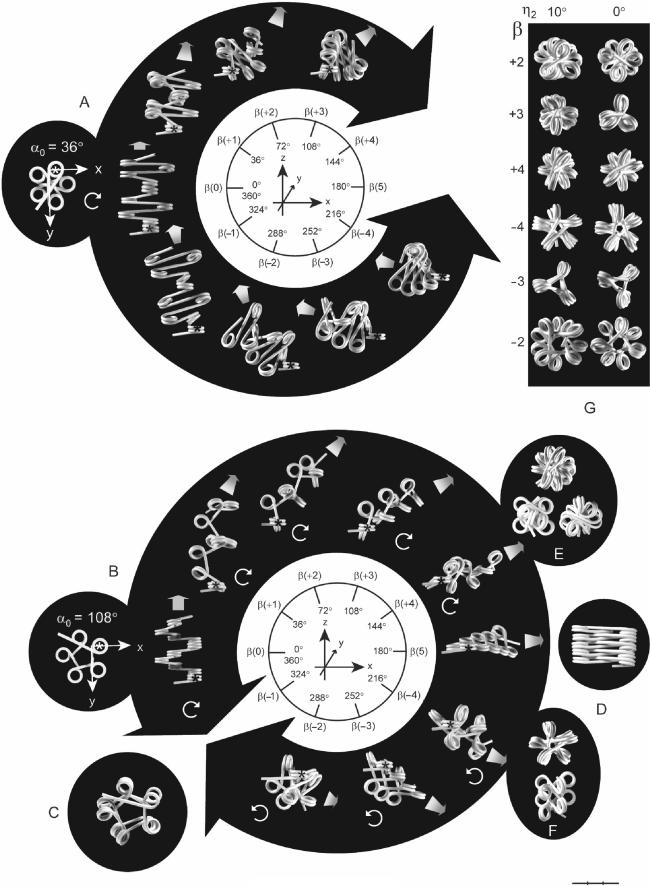
The conformational changes of the filament induced by rotation of the nucleosomes were studied by wire models, prefolded into pentagonal star fiber and polygon fibers at β = 0°, followed by rotation of the nucleosomes in steps of 36° (Figure 2). In the following, rotations are denoted according to the number of steps from β(±1) to β(±4) (+ for 0° < β < 180° and-for 180° < β < 360°) and β(0) and β(5) for 0 and 180°, respectively.

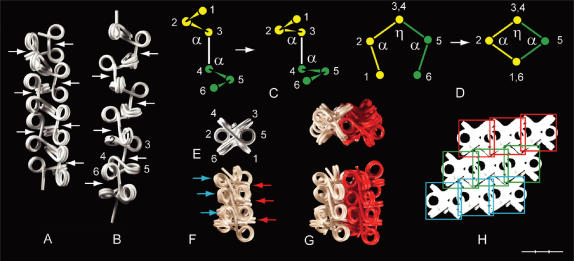
Figure 2.

The influence of β on the conformation of a star fiber (A) and a polygon fiber (B) with pentagonal axial symmetry (α = 36 and 108°, respectively). Each fiber contains 10 nucleosomes. The first nucleosome in each fiber is indicated by an asterisk. The nucleosomal repeat length [205 bp (A) and 196 bp (B)] is kept independent of β, which is varied in steps of 36°, corresponding to ∼10 bp/turn of the DNA, and numbered according to the number of increments of 36°. Large, black arrowheads point towards values of β that are not allowed for sterical reasons. Circular, white arrows indicate the coiling direction. The fibers in A and B are oriented with the connecting linker of the first dinucleosome in the viewing direction (y-axis). As the shifting directions of the fibers do not follow the plane of the paper, as indicated by the thick fibers in gray scale, except for β = 0°, their true length cannot be inferred from the figure. (C) Polygon fiber with NRL 210 bp at β(−1). (D) Stacking of nucleosomes at β(5) into two columns with alternating positive and negative linker orientations by reducing the size of α. The fiber in (D) has NRL = 230 bp and α = ∼36°. (E and F) Compressed polygon fibers formed by reducing the size of α. (E) β(+4) is shown from the end (top) and from the side as seen from two different angles. (F) β(−4) seen from the end (top) and from the side. (G) Axial symmetries of the polygon fiber as a function of β at η₂ = 10 and 0°. Bar = 30 nm.

The star fiber (α = 36°) is unable to attain conformations between ∼β(+3) and ∼β(−4), as this requires a NRL of at least ∼275 bp (Figure 2A). Conformations of a star fiber with linker lengths that are sufficiently long to allow the nucleosomes to pass each other at β(5) have been studied by a computer model (12). In the polygon fiber rotation beyond 180° is allowed because of the larger value of α, causing a shift from right- to left-handed coiling (Figure 2B). At β(5) the polygon fiber has the form of a ribbon with α₀ = η₁ because the direction of the ribbon is perpendicular to the coiling of the DNA around the core particles. The ribbon is therefore not planar but coils right-handed. (For η₁ = 2γ = 9°, the ribbon will have 1/20 coil/nucleosome and 9.5 turns/coil). As β gets near to 360° the polygon fiber approaches the so-called interdigitated model of the chromatin fiber, in which every fifth nucleosome stacks upon each other, forming five left-handed coils of stacked nucleosomes (18) (except for the linkers not being bent in the present model). A NRL > 200 bp is required for the conformation at β(−1), as shown for two coils of the filament in Figure 2C.

Provided that the linkers are long enough, α can be decreased in the polygon fiber at β(5) to generate a ribbon of stacked nucleosomes in which the orientation of the linkers alternates between positive and negative conformation (Figure 2D). This type of ribbon can be wrapped on the surface of a cylinder to form a fiber in which linker DNA zigzags up and down the helical axis, and such conformations have been described by two models as the twisted ribbon (19) and the helical ribbon (20), which are derived from filaments having an open and closed linker configuration at β(5), respectively (data not shown).

The axial symmetry of the fiber is changed when |β| is increased from 0° due to the decreasing size of α₀. The axial symmetry of a polygon fiber is thus changed into that of a star fiber at α₀ < 60°. If, furthermore, the size of α is reduced, this will cause the fiber to become more compressed. The pentagonal polygon fiber can thus be compressed at β(+3) into the triple helix model (21), named after its three left-hand rotating columns of every third nucleosome (data not shown). At β(+4) α can be reduced to ∼80°, accompanied by intercalation of the every second nucleosome and a slight rotation, until the linkers are aligned side-by-side in the interior of the fiber (Figure 2E). This is an example of the double-helical crossed linker model (6), which has recently been found to correspond to the crystal structure of the tetranucleosome (22). Much less compaction is possible at β(−4) (Figure 2F).

Asymmetries of clockwise and counter-clockwise rotations

The asymmetry of clockwise and counter-clockwise rotations can be seen by considering a dinucleosome with a defined direction of the DNA from nucleosome no. 1 to no. 2, in which nucleosome no. 2 is rotated either clockwise or counter-clockwise around the interconnecting linker from β = 0° to 180° (Figure 1-IIIC, D). In both cases the pitch (p) of the dinucleosomes is reduced to zero. However, as the entry and exit sites of the terminal linkers are not diametrically positioned relative to the axis of rotation at β = 0° the changes in p are different for clockwise and counter-clockwise rotation. Thus, by clockwise rotation p goes through a slightly negative minimum, and by counter-clockwise rotation, p increases to a maximum before reaching zero at β = 180° (Figure 1-IIID). For the same value of |β| the axial symmetry of nucleosomal filaments therefore differ for β(+) and β(−), the former being more compact than the latter, which has a larger diameter with a hole in the middle (Figure 2G).

Another asymmetry of clockwise and counter-clockwise rotation is due to variations in the angle (η) between the terminal linkers of the dinucleosomes, as defined by their projections into a plane perpendicular to the interconnecting linker (Figure 1-IIID). As the two linkers are not parallel to each other at β = 0°, but diverge by a small angle (η₂), ∣η∣ will be larger for clockwise rotations (η₂ + β) than for counter-clockwise rotations (η₂ − β) of the same size. The difference in η is greatest for small values of β as seen from the difference in axial symmetry of fibers with η₂ = 10 and 0° (Figure 2G).

Variations in α and linker conformation caused by binding of linker histone H1

The wire models could only be made with straight linkers leaving the nucleosomes as tangents to their curved surface, because bent linkers cannot be folded with any precision. As the linkers in the nucleosomal filament are in fact bent as a result of the binding of histone H1, this represents a major simplification of the geometry. Thus, the size of α is to a large extent determined by binding of H1, which bridges the linkers close to their entry/exit sites and inhibits their fluctuation (16). This makes the entry and exit sites approach each other, so that the DNA makes two full coils around the core particle (as for α = 180°, see Figure 1-IVA), thereby decreasing the effective linker length. However, binding of H1 stabilizes α at a value below 180° by bending of the linkers close to their entry/exit sites, causing the nucleosomes to rotate away from each other around the linker entry/exit sites (Figure 1-IVB). A conformation of the linkers at α = 0° has been reported, in which the two linker DNA segments are juxtaposed ∼8 nm from the nucleosome center and remain apposed for 3–5 nm before diverging, forming a so-called stem motive (23–25) (Figure 1-IVC). As the stem takes up 25–30 bp of the linker, a NRL of more than ∼200 bp is required to accommodate a stem at each nucleosome plus an additional linker DNA segment between the stems to provide a pitch of the dinucleosome ≠ 0° and to make α > 0° at the entry/exit of the stem. Bending of the linkers at their entry/exit sites by binding of H1 may also change the slope of the linker DNA, reducing the pitch of the dinucleosomes (Figure 1-IVD and E). Moreover, bent linkers may introduce a tilt angle between the flat faces of the core particles (Figure 1-IVF).

Although the wire models do not reflect the path of the linker as affected by histone H1 they can, by minor adjustments of NRL, η₁ and η₂, imitate changes in the distance between the nucleosomes that may be caused by effects of linker histone binding on the effective linker length and on the pitch of the dinucleosomes.

Regular fibers with repeated variations in β: helices and loops

Repeated β sequences along the nucleosomal filament give rise to a large number of different conformations, some of which are described below using the following nomenclature: Values of β are numbered according to the convention in Figure 2, β(−1) − β(−4) being underlined and in italics. β Angles without specified values are indicated only by (+) and (−) and nucleosomes are indicated by a dot, when convenient. A fiber with alternating positive and negative values of β can thus be written as (+−)_n or (•+•−)_n•. Star- and polygon fibers have been folded with α = 36 and 108°, respectively, unless stated otherwise.

Star fibers retain the axial symmetry of a star fiber for all sterically allowed combinations of β(+) and β(−) and little variation in β is allowed owing to the small value of α. Thus, even in a filament with as little variation in β as (11)_n every fifth nucleosome is touching each other (Figure 3A).

Regular helices are formed by polygon fibers with alternating β(+)- and β(−)-linkers, which make the filament shift repeatedly between forward and backward direction. Fibers with β sequence (22)_n and (33)_n can be compacted into short tubes by very small changes in α and β (Figure 3B and C), while the coiled ribbon at (44)_n cannot be compacted (Figure 3D). Another type of helix, which can be circumscribed by an ellipsoid cylinder, is formed by the triple repeat (222)_n (approximate values). This fiber can be slightly condensed by minor adjustments of the size of η₁ (Figure 3E and F).

The shift between forward and backward direction in the polygon fiber, caused by β(+) and β(−), leads to a different type of fiber when the sign of β is changed at every second linker, as shown in Figure 3G. The occurrence of β(−) linkers in the repeated β sequence (1111)_n thus causes the filament to change direction at every second nucleosome, forming a fiber with a 3-fold axial symmetry and partially overlapping loops of six nucleosomes (•1•1•1•1•1•) (numbered 1-2-3-4-1-2 in Figure 3H). Only a single nucleosome in each loop (No. 4) protrudes from the central axis, which consists of groups of three nucleosomes, formed by contacts between one nucleosome from each of three consecutive loops. These nucleosome triplets are located very close to each other and may form dimers. Another conformation, caused by the same periodical shift between β(+) and β(−), but with larger values of β, (3333)_n, consists of large loops of ∼20 nucleosomes (Figure 3I).

Swivel-linkers and fiber compaction

Linkers with an orientation close to that of the fiber axis have the potential of functioning as a swivel between intermittent coils. In the presence of such ‘swivel-linkers’ coiling of the intermittent nucleosome sequences becomes independent of each other, making possible a shift between right- and left-handed coiling, such as (033033)_n (Figure 4A) and (03030303)_n (data not shown). In some cases, the presence of swivel-linkers makes possible a reduction of α without rotation of the fiber. This is shown by the sequence (333)_n in which the (3)-linker functions as a swivel-linker, connecting two right-handed trinucleosomes (•3•3•), forming a coil of 6 nucleosomes spanning a little more than 360° (because η of the swivel-linker is larger than 108°) (Figure 4B). Reduction of α at the terminals of the swivel-linker makes the trinucleosomes approach each other, and reduction of α in the trinucleosomes to ∼72° makes them close like a pair of pincers (Figure 4C and D). As a result of these changes every second linker becomes super positioned (Figure 4E), allowing for compaction of the fiber (Figure 4F).

The compaction is limited by collision of nucleosomes connected by every second swivel-linker, which stack edge-to-edge in an orientation close to that of the fiber axis (blue arrows in Figure 4F). The fiber therefore has ∼6 nucleosomes per 11 nm. If the volume of the fiber is calculated as a cylinder with a diameter equal to two times the radius of gyration (32 nm), this corresponds to a density of 0.15 g DNA/ml, which is not different from the density of the solenoid model (26). However, the cross-section area is more closely circumscribed by a rectangle of ∼28 × 26 nm, corresponding to a density of 0.18 g DNA/ml. These values are within the range of densities calculated from metaphase chromosomes in a variety of organisms (26). The compact fibers can associate by interdigitation between nucleosomes, which are oriented perpendicular to the fiber axis (red arrows in Figure 4F) forming sheets, which can be packed into a slightly higher density (Figure 4G and H).

Pairwise association of polygon fibers: zip and double helices

Separation of coils in a fiber by swivel-linkers makes space for interactions with other fibers. Two fibers with the sequence (333)_n can align side-by-side and interlock like a zip, in which nucleosomes in each fiber fit spatially into a pocket of five to six nucleosomes (•3•3•3•3•3•) in the other fiber (Figure 5A). The minimum size of α required for the formation of this type of double fiber is between 108° and 90°.

In a fiber with β sequence (3033)_n, (3) swivel-linkers separate right-handed coils of four nucleosomes (•3•0•3•), providing sufficient space for the formation of a double helix in which swivel-linkers in one filament is alternately located on the inside and outside of swivel-linkers in the other filament (Figure 5B). This type of double fiber can be compressed to ∼70% of its original size by reducing α to ∼90°.

Double fibers can also be formed by intercalation of every second nucleosome in filaments with irregular β sequences. This type of double fiber can be considered to be derived from the inter fiber contacts between two filaments at β(5), in which every second linker is exposed on each of the flat faces. If two such ribbons are placed one on top of the other with the nucleosomes being stacked, every linker in one ribbon has two symmetrically positioned crossover points with two linkers in the other ribbon (Figure 5E). If the two ribbons are staggered in parallel with the axes of the ribbons, the linkers slide along each other, one crossover moving toward the middle of the linker, the other moving toward the terminal region of the nucleosomal DNA. The nucleosomal DNA of every second nucleosome in one filament will thus have a crossover point with the same region at every second nucleosome in the other filament (Figure 5F–G). Rotation of the nucleosomes counterclockwise from β(5) makes the two filaments coil left-handed around each other, maintaining the crossovers by intercalation.

The ability to form double fibers by intercalation (Figure 5C,D) is not limited to filaments with closed, negative configuration. In Figure 5H and I is shown an example of a left-handed double helix with α varying between ∼90° and ∼108°, and ∼β(+3). This type of double fiber is formed by filaments with alternating positive and negative linker configurations, which are folded from filaments with an open linker configuration at β(5) (Figure 5J).

Looping of polygon fibers with periodic variations in β

The ability of the filament to form longitudinal loops of six nucleosomes (five linkers) with the β sequence (1111)_n (Figure 3G and H) raised the question of whether loops could be formed by other pentameric series of β. This was addressed by folding of loops with six nucleosomes (α = 90°), using β = 0°, +90°, 180° and −90°, followed by adjusting the β values to integers of 36°. Many models of such loops could only be folded from filaments with β(5), and β values different from β(5) often had to be introduced in a specific folding sequence to avoid collisions between the nucleosomes. The loops could be classified according to their opening in response to a linear stretch of the filament, into closed loops, which could be opened after a slight displacement of the terminal nucleosomes, and locked loops, which could only be opened after rotation of the terminal nucleosomes (Figure 6A and B).

The loops were relatively independent of the actual β values and could exist in several different conformations after adjusting β to integers of 36°. Thus, the closed loop (+−+−+), which is shown on Figure 6C with the β sequence (23131), underwent no major changes in compaction when the β values were changed corresponding to a stepwise increase in linker length up to 10 bp (data not shown). Many of the loops could not be serially connected as the terminal linkers were located too close to each other or to neighboring nucleosomes to provide sufficient space, and an extra nucleosome therefore had to be added to each terminal linker (compare Figure 6D and E). Some of these octanucleosomes had highly compact conformations with crossed linkers and linkers and nucleosomes touching each other, as in the fibers shown in Figure 6F and G). Thus, in the octamers in Figure 6G, 6 of the 7 linkers are either crossing another linker or touching a nucleosome.

Fibers consisting of such structural motives of octanucleosomes were highly stable and stretch resistant with little flexibility, except at the interconnecting linkers. The β sequence of this type of fibers was thus periodic, being divided into segments of six or eight β angles within which the β sequence could vary independently. No folding sequence appeared to exist for models of such octanucleosomal structures, which were made by first folding the hexanucleosomal loop and then rolling on a nucleosome on each of the terminal linkers.

Characteristics of polygon fiber conformations with random β sequences

Random variations in β give rise to irregular conformations which depend on the mean β value, the degree of deviation from the mean value as well as the actual β sequence. NRLs for a large number of different organisms and cell types have been shown to be quantized by integral multiples of ∼10 bp, corresponding to integral multiples of helical turns of linker DNA, with experimentally determined SDs of ∼2–4 bp (27). It therefore seemed to be most relevant to explore conformations of polygon fibers with β varying up to β(±3) around a mean value of β(0). Such fibers could not be folded with high precision, and were therefore made in triplicate in order to account for minor inaccuracies, which will inevitably affect the mutual orientation of nearby nucleosomes.

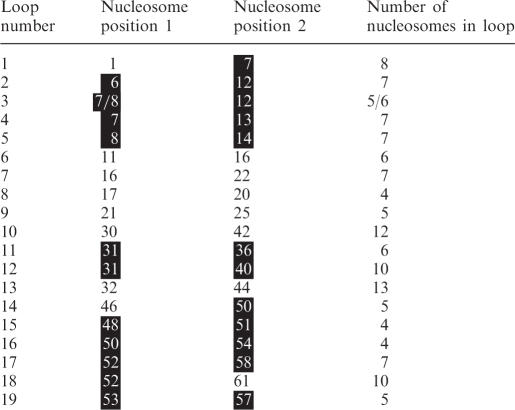
Figure 7 shows a model of a polygon fiber consisting of 65 nucleosomes (α = 90°) with the β sequence shown in Figure 8. Analysis of three models of this fiber showed the presence of clustered loops of 4–13 nucleosomes (Table 1). One class consisted of loops formed by nucleosomes, which tended to stay in touch in all three models (black in Figure 7D-F). In the model in Figure 7, these nucleosomes were even not separated by a mild stretch of the fiber, thus forming relatively stable domains. A second class consisted of loops formed by nucleosomes, which were more unstably associated (gray in Figure 7D-F), being separated by even a mild stretch of the fiber and showing a more variable mutual localization in the three models. Both types of clusters were connected by more flexible segments of the filament with nucleosomes, which were generally not in touch with other nucleosomes (white in Figure 7D-F). Because of a high flexibility mainly in these regions, the fiber easily formed loops by contacts between nucleosomes at the ends of the fiber. The loop shown in Figure 7C was stabilized by nucleosome No. 65 fitting into a pocket formed by the first five nucleosomes of the filament, analogous to the zip-motive of the double fiber shown in Figure 5A.

Figure 7.

Polygon fiber of 65 nucleosomes (α = 90°) with a random β sequence (shown in Figure 8). (A) Relaxed fiber. (B) Stretched fiber. (C) Loop formation by interaction of nucleosome No. 1–5 with nucleosome No. 65. Stable loop clustering is indicated by brackets. (D–F) Nucleosome interactions in (A, B, C). Clusters of stable and flexible loops are shown in red and blue regions, respectively, and nucleosomes with relative stable and variable mutual positions are black and gray, respectively. (G–I) Compaction of nucleosome No. 1–20 (G), 1–40 (H) and 1–65 (I) after chromatin remodeling and twisting of the linkers to form β sequence (333)_n, as shown in Figure 8. Bar = 30 nm.

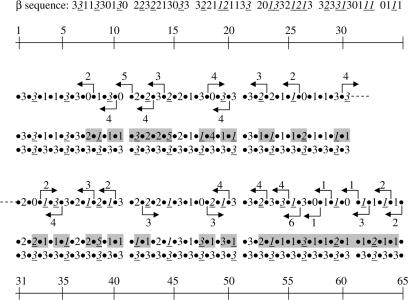
Figure 8.

β sequences of the polygon fiber shown in Figure 7. The original sequence was remodeled by moving nucleosomes the number of base pairs indicated in the directions shown by the arrows. The resulting β sequence is shown in the second row, the changed β values being indicated by a gray background. The third row shows the β sequence (333)_n after twisting of the linkers within the twist constraints.

Table 1.

Loops of a filament with random variation in β^*

*The loops are for the filament shown in Figure 7A–F.

Nucleosomes in relatively stable clusters are marked with a black background.

Given the irregular conformation of fibers with random variation in β, it was finally asked whether such fibers could be transformed into more regular fibers, especially the type of fiber (333)_n, which can be compacted to a high density (Figure 4F). Two properties of the filament made this possible. First, the displacement of core particles along the DNA changes the two flanking β values in opposite direction by the same amount. Secondly, twist constraints of the linkers are negligible for variations of β corresponding to maximally ±2 bp (28). In Figure 7G–I and Figure 8 it is shown how the fiber can be changed by displacements of core particles to generate a β sequence which, by twisting of the linkers maximally ±2 × 36°, can attain the β sequence (333)_n, which can be compacted. Changing the conformation in this way step-by-step from one end of the filament to the other provides a simple model for the spread of heterochromatin. As (333)_n is also the sequence required for formation of one type of double fiber (Figure 5A), combinations of core particle displacements (chromatin remodeling) and limited linker twisting may thus provide the β sequences necessary for stable inter fiber associations.

DISCUSSION

A major result of the present study is the demonstration of the significance of α for the conformational freedom of the nucleosomal filament. When α is smaller than 60° the filament thus remains a helix with little space for variations in the β sequence, while larger values of α provide it with a freedom to attain conformations, which are not dependent on a helical symmetry, by allowing for an increased variation in β sequence. The size of α in chromatin is not known with certainty, but α has been shown by cryo-EM imaging of native chromatin fibers (24,29) to decrease from 85 to 35° when the salt concentration is increased. These relatively small DNA entry–exit angles have been suggested to be caused by the stem motive, which has not been observed by scanning force microscopy (SFM). Studies by SFM of chromatin fibers fixed at low ionic strength have yielded average values of α of 100 ± 40° in the presence and 130 ± 40° in the absence of linker histones (15), and unfixed mononucleosomes at 10 mM MgCl₂ showed two maxima of α at around 80 and 136° in the absence of H1 and one maximum at 85–88° in the presence of H1 (16) (mean values differed slightly for samples scanned in air and liquid). These large values of α thus correspond to a polygon fiber geometry.

An important property of the polygon fiber is the length expansion at 0° < β < 180° (in contrast to the star fiber, which contracts) and the more than 90° change in direction at β > 180°. These properties are essential for creation of swivel-linkers and for transformation of helical coils into loops by reversing the pitch of the filament. Swivel-linkers can make space for close contacts between two fibers by separating two coils in a filament, thereby forming a pocket of 5–6 nucleosomes in which a nucleosome from another filament can bind. Tandem repeats of the β sequences of such pockets allow for the side-by-side association of two fibers like a zip, and the separation of helical coils by swivel-linkers can also provide space for the formation of double helices. It is tempting to speculate that tandem repeated DNA sequences, which often contain regularly positioned nucleosomes, might be stabilized and compacted by such types of fiber interactions.

Another type of double fiber, which does not involve regularly spaced nucleosomes, is represented by the left-handed coiling of two polygon fibers around each other by intercalation of every second nucleosome (Figure 5C). The positions of close contacts between the intercalated nucleosomes in this type of fiber appear to fit well with the positions of alternating asymmetric protection of nucleosomes in isolated nuclei against digestion by DNase I (30), which were shown to give rise to a dinucleosomal DNA repeat pattern (31–34). However, this type of double fiber may not provide the high degree of protection of the linkers, as inferred from analysis of the cleavage pattern, which was explained as a result of intercalation of nucleosomes in helical crosslinker model with linkers being buried in the interior of the fiber (35). Although the interdigitated model may not be able to fully explain these observations, the polygon fiber geometry has the potential to provide the chromatin with architectural properties by facilitating the formation of double fibers, thus enabling the filaments to form 3D networks.

A special property of the helical conformation formed by β sequence (333)_n is the ability to compact to a high density by a decrease in α, followed by interdigitation. The extent of compaction (∼6 nucleosomes/11 nm), as well as the radius of gyration (32 nm), agrees with results of neutron scattering and scanning electron microscopy of isolated chromatin at elevated ionic strength (36), but the volume of the fiber is smaller because the cross-section area is smaller, and the shape of the fiber allows for interdigitation into sheets, which can be packed to a density corresponding to metaphase chromosomes. This high density is so far only exceeded by two other models in which the compaction was caused by bending of the linkers (18) and by nucleosome gaping (17,37).

Energy analyses have indicated that the balance between repulsion among linker DNA and internucleosome interactions determines the salt-dependent condensation of the nucleosomal filament (38), and positively charged core histone N-terminal tails are important in this process by mediating favorable internucleosomal interactions and screening DNA repulsion (39). Compaction of the fiber would seem to require a high degree of charge neutralization, as linker DNA and nucleosomal DNA are brought very close to each other, while face-to-face internucleosomal interactions are only involved in interdigitation of the fibers and in apposition of layers of interdigitated fibers.

Since a regular spacing of nucleosomes is rare, it is noteworthy that repeated β sequences required for double fiber formation and compaction can also be formed by fibers with a random distribution of β values after displacement of nucleosomes and limited twisting of the linkers. This supports speculations that the nucleosome repositioning activity of chromatin remodeling factors may provide the chromatin fiber with dynamic properties at the supra-nucleosomal level (40). It furthermore shows that variations in β may not only be caused by differences in linker length but also by twisting of the linker. There is therefore no unambiguous correlation between β and linker length. In addition, linkers of the same length can differ slightly in their β values owing to sequence-dependent variations in the helical twist angle of base pairs in the linker DNA.

An important consequence of the polygon fiber geometry is the ability of the filament to form loops in response to variations in β. Closed and locked loops formed by periodic variations in β(0), β(+), β(5) and β(−) remained compact at many different combinations of β values, and the flexibility of the filament was caused only by the interconnecting linkers. The fact that some of these types of loops required the addition of one nucleosome at each terminal linker to provide space for being serially connected is reminiscent of the supranucleosomal organization of the chromatin. The size of supranucleosomes isolated by nuclease digestion thus varies from a minimum of 6 or 8 nucleosomes up to 40 nucleosomes (3). Filaments with random variations in β sequence also seem to be able to attain a supranucleosomal organization by the formation of relatively stable loop clusters separated by more flexible segments.

It is generally recognized that the nucleosome filament is highly dynamic owing to limited twisting of the linkers within the twist constraints and a rapid exchange between free and bound histone H1 (41). The major significance of static models may well be to show conformations that have the potential to be stabilized, either by double fiber formation, by the presence of closed and locked loops, or by cross linking of nucleosomes by nuclear proteins (42). The stability of loop clusters in filaments with a random distribution of β may thus be increased by cross-linking of nearby nucleosomes.

In light of the importance of α, β and the linker length for the conformation of the nucleosomal filament, what is then the role of these parameters for the organization of chromatin in the nucleus? A discussion of this question has to take into account that the geometry of the linker can be affected by bending. Stretches of poly(dAdT) are often bent and have an increased likelihood of being present in linkers (43) and linkers may also bend as a result of binding of H1. Moreover, theoretical calculations do not exclude that electrostatic interactions with core histone tail domains (44) can bend the linker DNA, despite the known large persistence length of the DNA (45). Mesoscopic computer models have indeed shown that when chromatin fiber models include real DNA flexibility and charge, then the internucleosome interactions overcome the pre-designed linker DNA geometry and result in establishing new nucleosome chain configurations. However, the internucleosomal interactions appeared to be relatively weak and probably insufficient to maintain highly bent linker DNA (39).

Bending and twisting of linker DNA may be the result of aggregation of nucleosomes (28), which have a propensity to aggregate at high concentration and in high salt, and the sequence of aggregation of newly synthesized nucleosomes to their nearest neighbors, might in fact function as a folding path for nucleosomal filaments in the nucleus. The potential importance of a folding path is seen from models of fibers consisting of hexanucleosomal loops, some of which needed an extra nucleosome at the terminals to give space for being serially connected. Such sequences of eight nucleosomes could not be folded from preformed filaments and are therefore unlikely to be generated from pre-existing filaments as a result of a thermodynamic equilibrium.

The narrow distribution of NRLs in every cell type and organism around a single mean value suggests that there is a range of preferred β values in the chromatin. NRLs for a large number of different organisms and cell types have been shown to be quantized by integral multiples of ∼10 bp, corresponding to integral multiples of helical turns of linker DNA (27), suggesting that preferred β values might be the same for these organisms. However, as the NRL can be changed experimentally by up to 15 bp without fatal effects (46,47), it seems that chromatin higher order structure can accommodate to a wide range of β values. This is in fact the case for the closed and locked hexanucleosomal looping of the filament, which depends more on the distribution of (+)- and (−)-linkers than on the actual values of β(+) and β(−). While looping appears to be an inherent property of the filament, occurring even as a result of a stochastic distribution of linker lengths, the location, conformation and length of the loops depend on the actual β sequence. This suggests that for a supranucleosomal organization of the chromatin, changes in linker lengths have a modulating effect on the conformation of the filament, leaving some loops unaltered, changing the conformation of others, destroying some loops and creating new ones, thus leaving the principal structure of the fiber roughly unaltered and within the same average dimensions.

The models predict that this will be different for conformations, which are more dependent on a specific β sequence, as expected for regular fibers and for some types of double fibers with repeated β sequences. Since these types of fibers have a potential architectural role in the large-scale organization of the chromatin, changes in β within these segments of the filaments might have fatal effects. An invariable placement of nucleosomes in these regions may therefore be more important than in others. Maintenance of the higher order organization of the genome might thus depend on the existence of series of ‘architectural’ nucleosomes located in invariable positions. Such nucleosomes might possibly belong to the most firmly bound nucleosomes whose positions are encoded by the DNA (48).