Denoising based on Time-Shift PCA

Abstract

We present an algorithm for removing environmental noise from neurophysiological recordings such as magnetoencephalography (MEG). Noise fields measured by reference magnetometers are optimally filtered and subtracted from brain channels. The filters (one per reference/brain sensor pair) are obtained by delaying the reference signals, orthogonalizing them to obtain a basis, projecting the brain sensors onto the noise-derived basis, and removing the projections to obtain clean data. Simulations with synthetic data suggest that distortion of brain signals is minimal. The method surpasses previous methods by synthesizing, for each reference/brain sensor pair, a filter that compensates for convolutive mismatches between sensors. The method enhances the value of data recorded in health and scientific applications by suppressing harmful noise, and reduces the need for deleterious spatial or spectral filtering. It should be applicable to a wider range of physiological recording techniques, such as EEG, local field potentials, etc.

I Introduction

Magnetoencephalography (MEG) measures magnetic fields produced by brain activity using sensors placed outside the skull. The fields to be measured are extremely small, several orders of magnitude below fields from unavoidable sources such as electric power lines, ventilators, elevators, or vehicles. Environmental noise is combatted by a combination of magnetic and electromagnetic shielding, active noise field cancellation, the use of gradiometers, spectral and spatial filtering, averaging responses to repeated stimulus presentations, and various other signal-processing methods to reduce noise. MEG signals may also be contaminated by sensor noise arising in the quantum devices or associated electronics, and physiological noise from physiological activity other than of interest (a category that is study- or application-dependent). We focus on environmental noise, but our approach is complementary with techniques that deal with the other two types of noise.

Shielding, the primary method for noise reduction, involves placing the system and subject within a chamber lined with layers of aluminium and mu-metal. In a recent proposition, head and sensors are surrounded by a superconducting shield bathed in liquid helium (Volegov et al., 2004). Active shielding has also been proposed (Platzek et al., 1999). However, the cost and bulk of shielding is an obstacle to widespread deployment of MEG in scientific and health applications (Okada et al., 2006; Papanicolaou, 2005). New applications such as brain-machine interfaces (BMI), and advances in MEG technology (e.g. the non-cryogenic system of Xia et al., 2006) make the perspective of systems without shield attractive. For an existing system better shielding may not be an option. A signal-processing alternative to reduce the level of noise is thus welcome.

A second measure is the use of gradiometer sensors, implemented in hardware or synthesized in software from magnetometer arrays (Vrba, 2000; Baillet et al., 2001)). There are 9 components to the magnetic field gradient (three spatial derivatives of each of the three spatial components), but typical systems sample only a few: radial gradiometers measure the radial derivative of the radial component, and planar gradiometers one or two of its tangential gradients. Brain sources produce fields with large gradients at nearby sensors, whereas most environmental sources are distant and produce a relatively homogenous field, that the gradiometer discounts. Gradiometers are also more sensitive to shallow than deep brain sources. This property may be useful in some cases, but there is no flexibility to tune or disable it without compromising environmental noise rejection. Sensor geometry could more easily be optimized for brain sensitivity if environmental noise were taken care of by other means.

A third approach is spectral filtering. Environmental noise is typically dominated by slowly varying fields from elevators, vehicles, etc., and by power line components at 60 Hz (or 50 Hz outside the US) and multiples, that may be attenuated by hardware filters before analog-to-digital conversion. A typical protocol involves a combination of a highpass filter (e.g. 0.1 or 1 Hz) and a notch filter at 60 Hz, in addition to the mandatory antialiasing low-pass filter. Further filtering may be applied in software. Spectral filtering has two serious drawbacks. First, recordings are blind to eventual brain activity within the frequency bands that are rejected. Second, features of the time-course of activity are “smeared” over an interval equal to the duration of the impulse response, which is on the order of the inverse of the width of spectral transitions (e.g. about 1 s for a 1 Hz highpass or 1 Hz-wide notch filter). Temporal distortion is inconsistent with the common claim of “millisecond temporal resolution” for MEG, although its impact is hard to assess because impulse responses are rarely published. Data quality would be enhanced if spectral filtering could be avoided.

A fourth approach is spatial filtering. Linear combinations of sensor signals are formed to attenuate noise and/or enhance brain activity. Examples are synthetic gradiometers (already mentioned), the Laplacian (e.g. Kayser and Tenke, 2006), Principal Component Analysis (PCA) (e.g. Ahissar et al., 2001; Kayser and Tenke, 2003, 2006; Spencer et al., 2001), Independent Component Analysis (ICA) (e.g. Makeig et al., 1996; Vigário et al., 1998; Barbati et al. 2004), Signal Space Projection (SSP) (Tesche et al., 1995), Signal Space Separation (SSS) (Taulu et al., 2005), beamforming (e.g. Sekihara et al., 2001, 2006) and other linear techniques (Parra et al., 2005). Spatial filtering is useful to tease apart the activity of multiple sources within the brain. While it can also remove environmental noise, using it for that purpose constrains the options for brain source analysis (Nolte and Curio, 1999). Spatial filtering distorts the spatial signature of sources of interest, and forward models (required for source modeling) may need adjusting.

Finally, a very common procedure is to average responses over multiple repetitions of the stimulus. Stimulus-evoked brain activity adds constructively, while noise components tend to cancel each other out. Measurement of the steady-state response (SSR) in the frequency domain obeys the same principle. Drawbacks are that only repeatable “evoked” activity may be observed in this way, the signal-to-noise ratio (SNR) improvement is modest (it varies with the square root of repetitions), and the procedure is costly in experimental time. Effective denoising would allow cheaper experiments, and possibly useful recordings of single-trial activity.

To summarize, a wide range of noise-reduction tools is available. Together, they allow high quality measurements of brain activity, as evident from the MEG literature. Nevertheless, some have drawbacks that interfere with the observation of brain response morphology. For others, prior removal of environmental noise would allow them to be optimized for the purpose of brain source analysis.

Some MEG systems are equipped with reference sensors that measure environmental fields. Regression of brain sensor signals on the subspace spanned by reference sensor signals allows the contribution of environmental noise to be attenuated without the need for spectral filtering, or spatial filtering of the brain sensor array. Several methods have been proposed for that purpose (e.g. Vrba and Robinson, 2001; Adachi, 2001; Volegov et al., 2004; Ahmar and Simon, 2005). Assuming that noise sources are distant and their fields homogenous, three sensors should suffice to capture the three spatial components of the noise field, regardless of the number of sources. However a larger number of reference sensors may be useful if field gradients differ between noise sources. Assuming instantaneous propagation at the relatively low frequencies of interest (Hämäläinen et al., 1993), the responses of two sensors to the same noise component differ only by a scalar factor. One should thus expect projection techniques to be highly effective. However, electromagnetic shielding is known to be frequency-dependent ((Hämäläinen et al., 1993), and the electronics (flux lock loop, hardware filters) may introduce convolutive mismatch between channels, in which case scalar regression does not work well.

The method to be described extends these techniques by augmenting the array of reference signals by delayed versions of the same. The linear combination of delayed signals constitutes, in effect, a finite impulse response (FIR) filter that is applied to each reference signal before subtraction from each brain sensor signal. As we shall see, this greatly improves the effectiveness of denoising.

II Methods

Signal model

We observe K brain sensor signals and J reference sensor signals. For example the MEG system described below has K=157 gradiometers placed over the brain and J=3 reference magnetometers placed far from the brain and oriented orthogonally to each other. Denoting vectors with bold-faced letters, S(t) = [s₁(t), … , s_K(t)]^Τ, the K brain sensor signals reflect a combination of brain activity, environmental noise and sensor noise:

$$\mathbf{S}\left(t\right)={\mathbf{S}}_b\left(t\right)+{\mathbf{S}}_e\left(t\right)+{\mathbf{S}}_s\left(t\right)$$ (1)

whereas the J reference sensors R(t) = [r₁(t), … , s_J(t)]^Τ reflect only noise. Sensor noise S_s(t) is supposed negligible (see de Cheveigné and Simon, 2007). Signals are sampled and we use t to represent the time series index. Environmental noise in both sensor arrays originates from L noise sources within the environment, E(t) = [e₁(t), … , e_L(t)]^Τ. If the relation between each noise source and each sensor were scalar (no filtering or delay), the dependency could be described in matrix notation as:

$$\begin{array}{cc}\hfill {\mathbf{S}}_e\left(t\right)=& \mathbf{A}\mathbf{E}\left(t\right)\hfill \\ \hfill \mathbf{R}\left(t\right)=& \mathbf{B}\mathbf{E}\left(t\right)+{\mathbf{R}}_s\left(t\right)\hfill \end{array}$$ (2)

where A = [a_kl] and B = [b_jl] are mixing matrices with a_kl and b_jl scalar and R_s(t) is reference sensor noise. Reference sensor noise is supposed negligible (the question is discussed further on). If the relation between noise and sensor signals is convolutive (filtering and/or delay) the same notation can be used supposing that each element a_kl or b_jl of the mixing matrices A or B represents an impulse response, and replacing multiplication by convolution in Eq. 2. For example:

$$r_{\mathit{jl}}\left(t\right)=(b_{\mathit{jl}}\ast e_l)\left(t\right).$$ (3)

where r_jl(t) is the contribution of noise source l to sensor j. The brain activity term S_b(t) in Eq. 1 presumably also reflects multiple sources within the brain, however we do not need to detail this dependency. To summarize the signal model, brain sensors and reference sensors pick up the same noise sources, but the relation between noise and sensor may have convolutive properties that differ between brain and reference sensors.

Algorithm

The TSPCA algorithm is straightforward. First, the reference channels R(t) are time-shifted by a series of multiples of the sampling period, both positive and negative: R(t+n), n = −N/2+1, …, N/2. Second, the set of time-shifted reference signals is orthogonalized by applying PCA, to obtain a basis of JN orthogonal time-domain signals. Third, each brain sensor signal is projected onto this basis, and the projection removed. The result is the “clean” signal.

For brain sensor k the overall process can be described as:

$${\widehat{s}}_k\left(t\right)=s_k\left(t\right)-\underset{j=1}{\overset{J}{\Sigma }}\underset{n=1}{\overset{N}{\Sigma }}{\alpha }_{\mathit{kj}}\left(n\right)r_j(t-n-N∕2)$$ (4)

where Ŝ_k(t) is the cleaned signal and the [α_kj(n)] emerge from the combination of orthogonalization and projection. Coefficient α_kj(n) can be understood as the n-th coefficient of an N-tap finite impulse response (FIR) filter applied to reference signal j before subtraction from brain signal k. This filter is optimal, in a least-squares sense, to minimize the contribution of noise components to the brain sensor signal. Note that the brain sensor signals S_k(t) are not filtered, and thus there is no spectral distortion of brain activity S_b(t) (we return to this question later). Processing can be summarized in matrix notation as:

$$\widehat{\mathbf{S}}=I\mathbf{S}-𝒜\tilde{\mathbf{R}}$$ (5)

where I is the identity matrix, A = [α_kj] the matrix of coefficients found by orthogonalization and projection, and R̃ represents the set of time-shifted reference channel signals.

Implementation

The algorithm was implemented in Matlab. The number of taps is an arbitrary tradeoff: effectiveness, computational cost, and risk of overfitting, all increase with N. The value N=200 (shift range of ±200 ms for a 500 Hz sampling rate) was chosen for our simulations yielding 600 time-shifted reference channels. After PCA, components with variance (relative to the first) below an arbitrary threshold (10⁻⁶ in our simulations) were discarded to avoid numerical problems in the next steps. The algorithm can be applied to data blocks or files of arbitrary size: smaller blocks allow the algorithm to accommodate eventual fluctuations in reference/brain sensor relations, while larger blocks reduce the risk of overfitting. We typically used a block size of 10⁵ samples (200 s), but we did not observe ill effects with larger or smaller sizes.

III Results

We first evaluate the method with MEG data from one particular system to illustrate its effectiveness as a practical tool. Next we use synthetic data to quantify eventual side-effects. Later on we give more examples with data from other systems.

A MEG data

Setup

Magnetic signals were recorded using a 160-channel, whole-head system with 157 axial gradiometer sensors that measure fields from the brain and 3 magnetometer reference sensors oriented along orthogonal directions (KIT, Kanazawa, Japan; Kado et al., 1999). The system is situated within a magnetically shielded room to reduce magnetic fields from the environment. Except where noted, DC and very low frequency fields are removed by a high-pass filter in hardware at 1 Hz, line noise is suppressed by a notch filter at 60 Hz, and aliasing is prevented by a low-pass filter at 200 Hz (for 500 Hz sampling) or 400 Hz (for 1 kHz sampling).

Empty machine

Figure 1 (a) (red) illustrates the power spectrum averaged over channels in normal conditions but with no subject within the system. It consists essentially of environmental power that has eluded magnetic shielding, cancellation by the gradiometers, and attenuation by hardware filters. The power spectrum is dominated by several sharp components at 120 Hz and beyond, several narrow modes at intermediate frequencies (10 to 120 Hz), and a diffuse distribution of low-frequency power below 10 Hz [expanded in Fig. 1 (d), red].

Fig. 1.

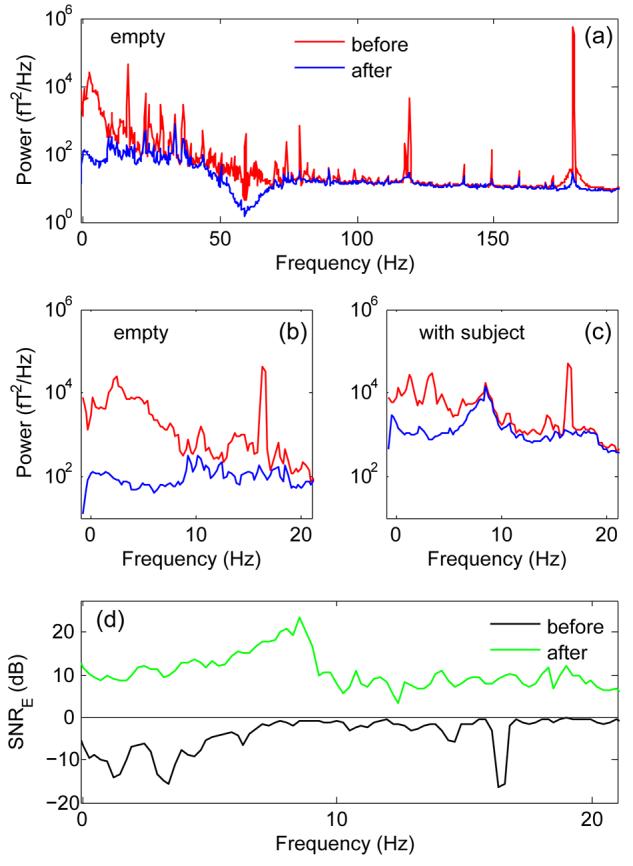
MEG responses before and after denoising. (a): Power spectrum recorded from an empty machine averaged over all channels, before (red) and after (blue) denoising. (b) Same, with an enlarged abscissa. (c) Same, in the presence of a subject. (d) Estimated signal-to-environmental noise ratio (SNR_E) of brain fields before (black) and after (green) denoising. The estimate of SNR_E before denoising was made by comparing power recorded with and without a subject in the MEG machine. The estimate of SNR_E after denoising was made by comparing power after denoising to power before denoising. Both estimates are rough approximations.

Figure 1 (a) (blue) shows the power spectrum after applying our algorithm to the same data as in Fig. 1 (a) (red). 98% of the variance has been discarded, leaving only 2% of residual noise power. Sharp high-frequency components are virtually eliminated, and mid-frequency peaks are greatly reduced. The dip near 60 Hz reflects the hardware notch filter, not noticeable in raw data because it coincides with the 60 Hz line power component (see below). The low-frequency region is expanded in Fig. 1 (b). Noise power in this region is reduced by a factor of about 100 (20 dB).

Brain activity

Fig. 1 (c) illustrates data recorded with a subject performing an auditory task (Chait et al., 2005), before (red) and after (blue) denoising. Before denoising, the brain activity of the subject is hard to distinguish from environmental noise. After denoising the brain activity emerges more clearly. Assuming that brain activity and environmental noise are orthogonal, we can estimate the approximate power of the brain response by subtraction, and thus derive a rough estimate of the power ratio of the signal (defined in this context as activity other than environmental noise) to the estimated environmental noise (SNR_E). Note that this definition of signal includes all activity other than environmental noise. After denoising, SNR_E approaches 10 dB over the 0-20 Hz frequency range that includes many important components of brain activity, with a peak of about 20 dB just below 10 Hz (Fig. 1 (d)). It should be stressed that these are “single-trial” data, without spatial filtering, spectral filtering other than in hardware, or averaging over epochs.

Recording without hardware filters

The previous responses were recorded with hardware high-pass and 60 Hz notch filters, as is standard in most MEG studies. As mentioned in the Introduction, filtering distorts the observations and it would be useful to avoid it, if possible. Figure 2 shows data recorded with high-pass and notch filters deactivated (in red). The waveform [Fig. 2 (a)] is dominated by a 60 Hz component visible as a peak in the power spectrum [Fig. 2 (b)], as well as slower fluctuations visible in Fig. 2 (b) as a prominent peak at very low frequencies. After denoising, both are greatly reduced, by about 40 dB for the former and 35 dB for the latter. On average over the spectrum, the power has been reduced by about 99%. This suggests that, with adequate denoising, hardware filters could be omitted (however filters may still be required to avoid overloading of analog-to-digital converters by noise components if the resolution of the converters is insufficient).

Fig. 2.

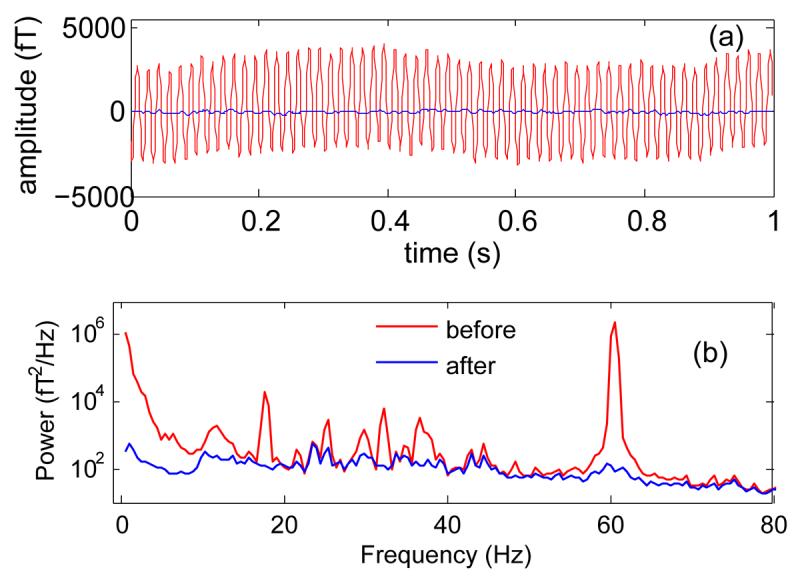
Effect of denoising on data recorded in the absence of hardware high-pass and 60 Hz band-reject (notch) filters. (a) Waveform of one channel before (red) and after (blue) denoising. (b) Power spectrum averaged over channels before (red) and after (blue) denoising.

Is the target distorted?

An obvious concern is whether denoising distorts brain activity. It was already mentioned that brain activity does not undergo spatial or spectral filtering (Eq. 4) as long as reference channels do not pick up brain activity. Spurious correlations might conceivably appear by chance between brain and delayed-reference subspaces, in which case genuine brain components might be stripped together with the noise. However, given that brain and environmental activity are unrelated, the power of any such component should be small.

We tested this conclusion with synthetic data for which the target and noise were both known. In a first simulation we used a target consisting of wide-band gaussian noise independent between channels. For “noise”, we used data recorded in the absence of a subject in the MEG machine, modified by subtracting the residual power (about 2 %) leftover after denoising. This is very similar to real environmental noise, but with the nice property that denoising removes it completely so that target distortion may be observed in isolation. Target and noise were added in sensor space to produce synthetic “noise-contaminated data” that were then processed by the TSPCA algorithm to obtain “denoised data”. After denoising, target power was reduced (uniformly over the spectrum) by less than 1 dB as N was varied from 1 to 200 (not shown).

A second simulation used as a target data recorded from the MEG with a subject performing an auditory task, denoised by application of TSPCA. This is our best approximation, in terms of amplitude and spectral content, of brain activity as measured in sensor space (real brain activity being obviously inaccessible). Figure 3 (a) shows the power spectrum of the brain activity (green, thick), the noise-contaminated activity (red), and the denoised activity (blue) plotted over a 0-50 Hz range. Denoising supresses noise components, but the target itself is not seriously distorted: comparing the green and blue plots, the differences are small. Our target is the result of a denoising process and thus conceivably less susceptible to distortion than “real” brain activity, but it is our best approximation in the absence of direct access to brain source activity.

Fig. 3.

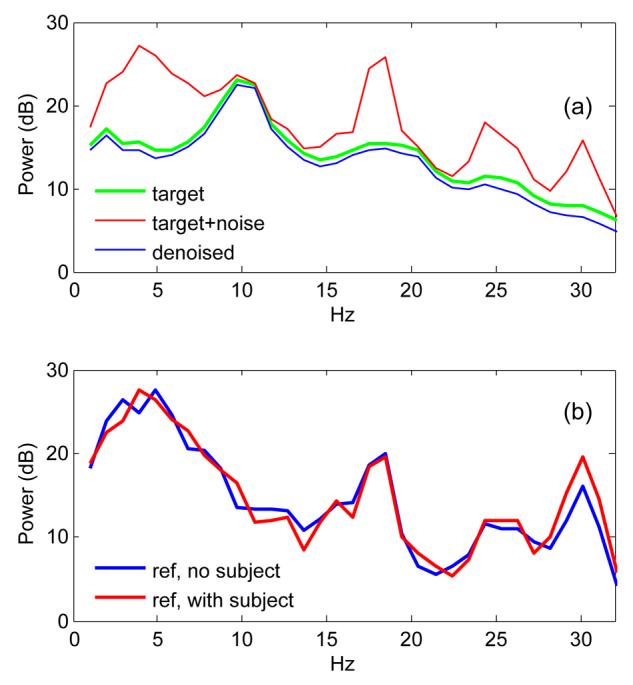
The top plot shows the effect of denoising on synthetic data. Green: synthetic “brain activity”. Red: same after addition of synthetic “noise”. Blue: same after denoising. The bottom plot illustrates estimating leakage of brain activity into reference channels. Blue: power spectrum of reference channels recorded in the absence of a subject. Red: same in the presence of a subject. The lack of a systematic difference between reference power spectra (red, blue) at frequencies where brain activity is intense suggest that leakage is weak.

Taken together, these arguments suggest that it is safe to assume that brain activity is not significantly distorted by TSPCA. Note that the assumption of uncorrelated brain and environmental noise might not hold if, say, the stimulus apparatus produced a magnetic field synchronized to the stimulus, or if reference sensors picked up appreciable brain activity. Overfitting could occur if the number of data samples were small relative to the number of free parameters in the model (600 for N=200). In those cases, target distortion could be significant.

Is it reasonable to assume that reference sensors pick up no brain activity?

If the reference sensors pick up fields from the brain, it is possible that some brain components are removed together with the noise. For data from a real system this possibility cannot be ruled out completely, but two arguments suggest that leakage of brain activity into reference channels is too small to be of practical concern for our setup. First, if there were significant leakage, we would expect the power spectrum of the reference channel signals to differ according to whether a subject is present or not. Figure 3(b) compares reference channel power spectra measured without (blue) and with a subject (red). The spectra differ in detail, as expected from different samples of ongoing environmental noise, but the difference does not follow the shape of the brain power [Fig. 3(a), green]. Second, significant leakage should show up as brain-like characteristics within the residual (noise) signal removed by denoising, for example after averaging over many repetitions of a stimulus. No such characteristics were found (not shown).

Leakage of brain activity into reference channels appears to be negligible for our setup. However, if the reference sensors picked up more brain activity, or less environmental noise as might occur with better shielding, leakage could lead to significant subtraction of brain activity. This should be checked for before introducing the method to a particular machine.

Are delays useful?

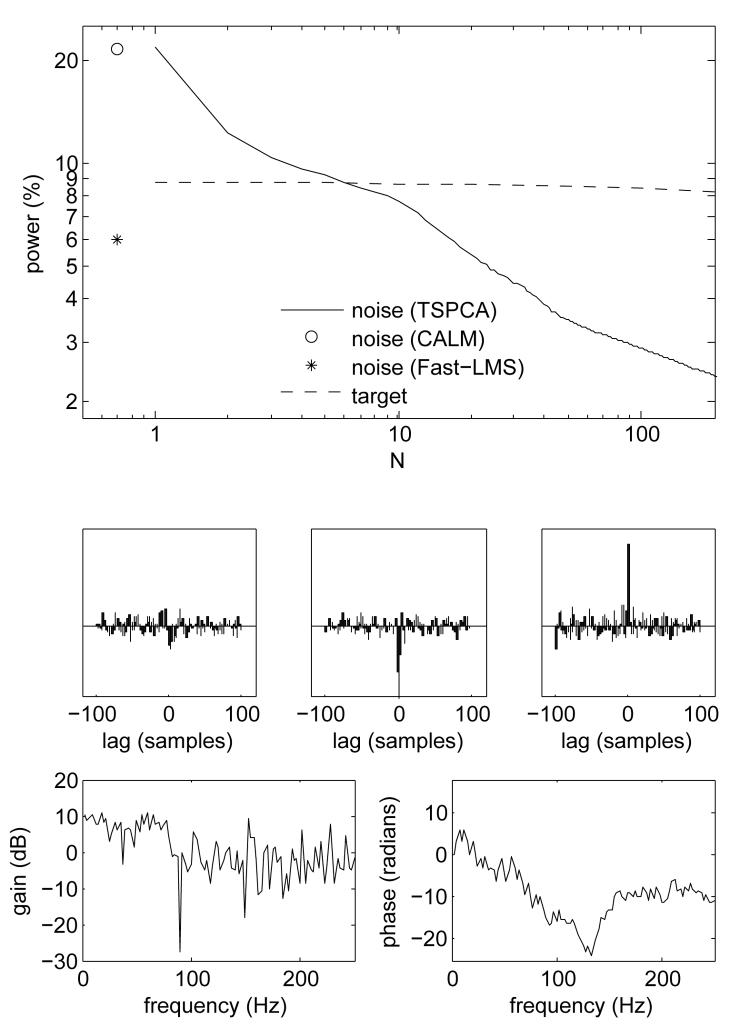
With N=1 the method defaults to scalar regression (see Introduction). The amount of residual environmental noise as a function of N is plotted in Fig. 4 (top, full line). As N is increased from 1 to 200, the residual noise power drops from about 20% to about 2% while the power of the target (dashed line) is almost constant, with the result that the signal-to-environmental noise ratio (dB) becomes positive for about N > 8. Multiple delays are obviously useful. Crucially, this shows that TSPCA is not indiscriminate as to how it removes power from a noisy signal. The power decrease affects only the noise (full line) but not significantly the target (dashed line).

Fig. 4.

Top, full line: percentage of noise power remaining after denoising as a function of number of taps, N. Dotted line: target power. Symbols are data for algorithms CALM (Adachi et al., 2001) and Fast-LMS (Ahmar and Simon, 2005). Intermediate: impulse responses of filters applied to each of the three reference sensor signals, for one particular brain sensor. Bottom: magnitude and phase plot of the rightmost filter.

The middle panels of Fig. 4 show the three reference-brain impulse responses for one particular brain channel for N=200, and the bottom panels of Fig. 4 show the amplitude and phase transfer functions of the third of these filters. The shapes, resulting from the automatic regression procedure, are not easily interpretable. Non-zero values of the impulse response at lags other than the origin reflect the fact that the corresponding lags contribute to reduce noise.

As described above, the power of the delays to better isolate and remove noise can arise simply from non-instantaneous mixing of noise across channels. Additionally, multiple delays can further aid noise reduction if some independent noise components are differentially spectrally filtered with respect to another (since the effect of summing and delaying noise channels can also create spectral filtering).

Are MEG data typically that noisy?

Our illustrations were based on data from one rather noisy MEG system, and one might wonder whether other systems would also benefit. Figure 5 shows data from a variety of systems from different makers and installed in different locations (details in caption). For each system, the power spectrum of a single channel is shown before (red) and after (blue) denoising. In each case the spectrum of the raw MEG data comprises low frequency and line frequency harmonics that denoising removes. The benefit of TSPCA is not restricted to one particular system.

Fig. 5.

Data from a selection of systems. For each, the power spectrum of one arbitrary channel is plotted with a logarithmic frequency axis and a dB ordinate (with arbitrary origin). MEG system 1 is a 157-channel axial gradiometer system with 3 reference channels, built by Yokogawa and installed in a high-quality MSR (60 dB at 0.01 Hz) in a quiet suburban environment. MEG system 2 is a 440-channel system also built by Yokogawa. Reference channel data were not available for this recording; instead, “synthetic reference” signals were obtained by applying ICA and selecting the three components most strongly dominated by DC and power line harmonics. MEG system 3 is a 306 channel system built by Elekta Neuromag, for which six synthetic references were derived by ICA. The green line represents the result of applying instead the SSS algorithm provided with the system. MEG system 4 is a 151-channel system built by CTF with 29 reference channels. The EEG system was a 16-channel system installed within an electromagnetically shielded booth. Four channels were devoted to ‘reference’ channels: two were attached to the subject's wrists and the other two were attached to the metallic floor and wall of the booth.

Reference channels were unavailable for two systems (MEG systems 2 and 3). To apply TSPCA nevertheless, we derived “synthetic reference channels” by applying ICA and selecting the three components with the largest proportion of DC and line noise. This appears to be effective, but it amounts to a form of spatial filtering and shares its potential drawbacks. Real reference sensors would be preferable. The green line in the plot for system 3 is the result of applying the SSS algorithm available with that system. TSPCA appears to be competitive with this implementation of that denoising method. The purpose of these examples is to show that TSPCA may be of use for a range of MEG systems. They should not be interpreted as reflecting the relative quality of systems or sites.

How does TSPCA compare with other methods?

Methods differ in their requirements and side-effects, and a level ground for comparison is hard to find. Easiest to compare are methods that use reference channels. Setting N=1, TSPCA is equivalent to scalar regression, a standard technique used in different forms (e.g. Volegov et al., 2004). From Fig. 4 (top) it is clear that TSPCA is superior to scalar regression for N>1. We compared TSPCA with two other methods, CALM (Adachi et al., 2001) that is widely used with KIT/Yokogawa systems, and Fast-LMS (Ahmar and Simon, 2006), a state-of-the-art LMS algorithm developed by our group. TSPCA surpasses both methods (Fig. 4, top). Many other signal processing techniques can make use of reference channels (Haykin, 1991) but a comprehensive review is beyond the scope of this paper. Suffice to say that we are not aware of a method in widespread use with performance comparable to TSPCA.

Comparison with techniques that do not engage reference channels is of limited use because TSPCA can be used together with them. TSPCA alters neither spectral nor spatial characteristics, and it is fully compatible with noise reduction measures that precede it (passive or active shielding) or follow it (spectral or spatial filtering). Of interest is whether combining those methods with TSPCA offers an advantage over applying them alone. Data in Fig. 1 were recorded from gradiometers with hardware filters (1 Hz highpass and 60 Hz notch): obviously applying TSPCA is an improvement over mere filtering, and Fig. 2 suggests that TSPCA might even replace such filters. Similar arguments can be made for spatial filtering, which is involved in a wide range of techniques (PCA, ICA, SSS, etc.).

Another standard approach to reduce noise (environmental and physiological) is to average responses over multiple repetitions of the same stimulus. Figure 6 shows responses from an auditory study (Chait et al., 2005) averaged over 100 repetitions. Plotted in (a) is the root-mean-square field RMS averaged over channels before (red) and after (blue) denoising. The stimulus onset is at 0 ms and at about 100 ms appears the typical ‘M100’ onset response (Roberts et al., 2000). The field distribution over the sensor array shows a typical ‘auditory’ configuration (hemispherically antisymmetric pair of magnetic dipoles) that is visible in the raw data (b, left), but is much more clear in the denoised data (c, left). At about 200 ms post onset, an additional peak is visible in the denoised data, with a similar ‘auditory’ configuration of opposite polarity. In the raw data, however, that peak is no more prominent than spurious peaks at other times (e.g. 400 ms), and the distribution in Fig. 6 (b right) is dominated by noise. TSPCA followed by averaging offers improvement over averageing alone.

Fig. 6.

MEG responses of one subject to an auditory stimulus, averaged over 100 repetitions (Chait et al. 2005). (a) Time course of RMS over all channels before (red) and after (blue) denoising. (b) Topography of field over subject's head before denoising at ∼100 ms and ∼200 ms post stimulus onset. (c): Topographies after denoising.

Reference sensor noise

Reference sensor noise is typically small compared to the amplitude of the environmental fields, and unlikely to affect the outcome of the calculation of orthogonalization and projection matrices. However, reference sensor noise is injected into the denoised data via Eq. 5, and may contribute to the new noise floor remaining after TSPCA. Therefore it is especially important that the reference sensors exhibit minimal sensor noise. Another way to reduce the impact of reference sensor noise is to increase the number of reference sensors beyond the number (usually 3) required to describe the environmental noise field, as redundant sensors allow sensor noise to be reduced (see de Cheveigné and Simon, 2007).

IV Discussion

The TSPCA algorithm has the following useful features:

• It is effective in removing environmental noise: in our simulations the single trial SNR_E improved from −10 dB to about +10 dB overall.

• It does not involve spectral or spatial filtering, and thus does not distort brain activity.

• It is relatively efficient and easy to implement, and should be suitable for a real-time implementation in BMI applications.

• Once it has been validated for a system, it is suitable as a systematic unsupervised data preprocessing tool. It does not require tuning, calibration, component selection, or other expert intervention.

• It is applicable to recordings other than MEG. So far only EEG has been tested, but it is expected that the technique might benefit electrophysiology in general.

• It is complementary (and compatible) with other methods of noise reduction and source analysis.

The method does not address other sources of noise such as sensor noise or unwanted physiological activity such as heartbeat, eyeblinks, muscle activity, brain activity other than of interest, etc. Other noise-reduction or data analysis techniques are available for that purpose, with which TSPCA is complementary. Note that, if an independent measurement of a physiological artifact is available, TSPCA may be used to optimize the rejection of that artifact, and that it is possible to include non-linear transforms in addition to delays, for example to compensate for eventual sensor nonlinearities.

Effective denoising can replace spectral and spatial filtering, but hardware high-pass or notch filters may nevertheless be necessary to preserve dynamic range. Equation 4 suggests, and simulations confirm, that the method does not appreciably distort brain activity. This implies that forward models do not need to be modified, and the method can be used together with techniques such as source modeling, PCA, ICA, SSA, etc. (Baillet et al., 2001, Ahissar et al., 2001, Parra et al., 2005, Makeig et al., 1996). Indeed, removing a major source of noise may help make those techniques more effective.

Reference sensors must be available, although we saw that TSPCA can make use of a “synthetic reference”. Regression on a synthetic reference amounts to a form of spatial filtering, and real reference sensors should be preferred if available. References should not be sensitive to physiological fields of interest. This should be verified when the method is applied to a new system, either directly with phantom sources, or indirectly by looking for traces of brain activity in the reference signals.

Our method extends previous methods that perform regression on reference sensor signals (Adachi et al. 2001, Vrba and Robinson, 2001, Volegov et al. 2004). It is superior to those methods in that it augments the reference signals with time-shifted versions of the same, thus allowing the synthesis of filters that compensate for eventual latency or filtering mismatches. In this respect it resembles frequency-domain regression (e.g. Woestenburg et al., 1983, Vrba, 2000). It can be understood loosely as a way to enhance the effectiveness of regression by compensating for convolutional mismatch. It should be applicable to other sources of artifact for which a brain-independent measurement is available, such as heartbeat or eye movements, and to other measurement techniques such as EEG.

This new MEG denoising technique is related to dynamic PCA used in process control (Ku et al., 1995), Singular Spectrum Analysis (SSA) used in geophysics (Vautard and Ghil, 1989, Allen and Smith, 1997, Ghil et al., 2002), the delayed coordinate methods of Gruber et al. (2006), or the delayed correlation ICA methods of Ziehe et al. (2000) or Sander et al. (2002). All of these techniques involve augmenting a set of signals with delayed versions. To the best of our knowledge this is the first application of such ideas to MEG or EEG noise suppression (see however He et al., 2004).

V Conclusions

The TSPCA method is effective for denoising MEG signals on the basis of reference channels that pick up environmental noise. Sensor channels are projected on a subspace spanned by the time-shifted reference signals. This effectively synthesizes filters that are optimal (in a least-squares sense) to compensate for any mismatch between data and reference sensor channels. Tests with data recorded from an empty MEG system found that 98% of noise variance were removed, in particular within frequency bands important for the study of brain responses. While recording from a subject during an auditory task, estimated single-trial signal-to-noise ratios approaching 10 dB were obtained across the low-frequency band (0 - 20 Hz), with a peak of 20 dB at about 10 Hz. The method is of considerable practical interest, as it may allow MEG systems to be designed more cheaply, to be deployed in less controlled (especially clinical) environments, and require less time per experiment. It may be of use to improve the quality of information about the brain that is gathered by this brain imaging technique, as well as other recording techniques sensitive to noise.