Phospholipid composition of the mammalian red cell membrane can be rationalized by a superlattice model

Abstract

Although the phospholipid composition of the erythrocyte membrane has been studied extensively, it remains an enigma as to how the observed composition arises and is maintained. We show here that the phospholipid composition of the human erythrocyte membrane as a whole, as well as the composition of its individual leaflets, is closely predicted by a model proposing that phospholipid head groups tend to adopt regular, superlattice-like lateral distributions. The phospholipid composition of the erythrocyte membrane from most other mammalian species, as well as of the platelet plasma membrane, also agrees closely with the predictions of the superlattice model. Statistical analyses indicate that the agreement between the observed and predicted compositions is highly significant, thus suggesting that head group superlattices may indeed play a central role in the maintenance of the phospholipid composition of the erythrocyte membrane.

Despite recent progress in understanding the structure and function of biological membranes, certain crucial issues remain unresolved. For example, it is not well understood how the particular lipid compositions of the cellular membranes arise and are maintained. Regarding this, there is some evidence that the components of binary bilayers have a tendency to acquire regular, superlattice (SL)-like lateral distributions (1–9). A consequence of such a behavior would be that a number of predictable “critical” compositions, corresponding to optimal lateral arrangements of the components (7, 8), occur. It is an intriguing possibility that such “critical” compositions play a role in regulating lipid compositions of natural membranes. To study this, we have compared the previously determined phospholipid compositions of the erythrocyte membrane from various mammals with the critical compositions predicted by the SL model. The erythrocyte membrane was selected because its composition has been studied in considerable detail and because it may be close to compositional equilibrium because of a lack of de novo lipid synthesis (10) and membrane traffic. Furthermore, the erythrocyte membrane is commonly considered as a model of mammalian cell membranes, and therefore, the information obtained should be of more general relevance.

The results show that there is a highly significant agreement between the experimental and predicted values, thus supporting the involvement of SL formation in the regulation of the phospholipid composition of the erythrocyte membrane.

THEORY

The Head Group SL Model.

The general principles of the membrane SL model have been described previously (1, 2). The present head group SL model is similar to the earlier model but makes two specific assumptions. First, phospholipid head groups represent the basic lattice elements. Second, phospholipid species with an identical or similar (in terms of size and/or charge) polar head group are considered equivalent, i.e., they form a single equivalency class. Accordingly, the choline phospholipids (CPs), phosphatidylcholine (PC) and sphingomyelin (SM), form one class; the acidic phospholipids (APs), phosphatidylserine (PS), phosphatidylinositol (PI), and phosphatidic acid (PA), form another; and phosphatidylethanolamine (PE) alone forms the third class. Such classification greatly simplifies the analysis of membrane compositions in terms of lipid SLs. The assignment of PS, PI, and PA to a single group is justified because (i) each of these lipids has a negatively charged head group and (ii) mutual coulombic repulsion is likely to be the principal factor governing the lateral distribution of these lipids in multicomponent membranes.

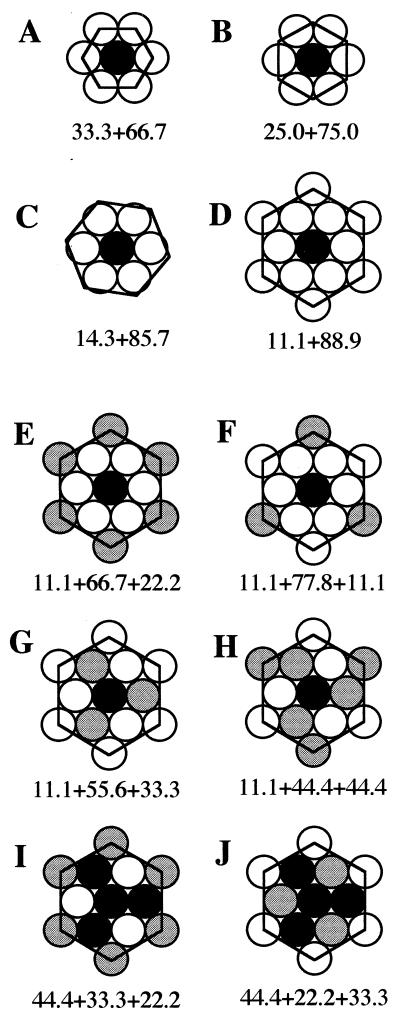
SLs are best defined in terms of unit cells. In case of binary hexagonal lattices the smallest unit cells consist of 3, 4, 7, or 9 elements as shown in Fig. 1 A–D. The unit cells are defined by the equation

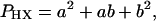1

where P_HX is the total number of elements (lattice sites) in the unit cell and a and b are integers (2). The composition of the corresponding lattice is obtained from the equation

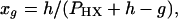2

where x_g is the guest mole fraction and h and g indicate the number of lattice sites occupied by a host and a guest molecule, respectively. Because each polar head group is assumed to occupy one lattice site, h = 1 and g = 1 and therefore x_g = 1/P_HX and x_h = 1 − 1/P_HX.

Figure 1.

Small unit cells for binary and ternary hexagonal SLs. (A–D) The smallest binary hexagonal unit cells contain 3, 4, 7, or 9 lattice sites, respectively. The molar percentages of the host (white) and guest (black) elements in the corresponding lattices are given below each unit cell. (E–J) Ternary unit cells derived from the 9-site binary cell. There are five different ternary cells with 9-lattice sites because J is a permuted form of I. The percentages of the black, white, and gray elements are shown below each unit cell, in that order. The lattice space groups are: E, p6mm; F, p3m1; G, p31m; H, p3; I and J, p31m.

The head group composition of the outer leaflet of the erythrocyte membrane can be analyzed in terms of binary unit cells because there are only two different head group classes present (see below). The inner leaflet, however, contains three head group classes, and thus ternary unit cells have to employed. These can be derived from the binary ones by substituting certain host (white) elements at symmetrically equivalent sites by the original (black) or new (gray) guest elements (Fig. 1 E–I). Unit cells with 9 elements turn out to be most relevant for the erythrocyte membrane (see below), and five different 9-element ternary unit cells can be generated. The composition of the corresponding lattices can be determined simply by counting the different elements within the unit cells.

In a lattice defined by 9-element unit cells the mole fractions of the components are multiples of 1/9, i.e., 0.111, 0.222, 0.333, etc. (x_PLC = m/9; Fig. 1 E–I). These numbers are valid for a single membrane leaflet. When the composition of the whole bilayer is considered, the critical mole fractions will be averages of any pair of these numbers—i.e., 0.0556, 0.111, 0.167, 0.222, etc.—provided that there is an equal number of phospholipid molecules in the inner and outer membrane leaflets, which indeed seems to be the case (Tables 1 and 2).

Table 1.

The phospholipid composition of the human erythrocyte membrane

Phospholipid	% of whole membrane, ±SD	Outer leaflet, %	Inner leaflet, %
PC	29.3  ±  1.5	44.8	14.0
SM	25.5  ±  1.4	42.1	9.1
LPC	1.0  ±  0.8	2.0	—
CPs	55.8  ±  2.2 (55.6)	88.9 (88.9)	23.1 (22.2)
PE	27.6  ±  1.5 (27.8)	11.1 (11.1)	43.9 (44.4)
PS	14.9  ±  1.7	—	29.6
PI	0.6  ±  0.5	—	1.2
PA	1.1  ±  0.5	—	2.2
APs	16.6  ±  1.8 (16.7)	0.0 (0.0)	32.9 (33.3)

The overall composition was taken from ref. 13. Very similar values have been obtained by many independent investigators (cf. ref. 14). The compositions of the individual leaflets were calculated based on the overall composition and transbilayer distribution data (15–17). The values were corrected assuming 100% recovery (determined recovery was 99.6%). The relative amounts of phospholipid in the outer and inner leaflets were calculated to be 49.7 and 50.3 mol %, respectively. Lysophosphatidylcholine was assumed to localize exclusively to the outer leaflet, because it can be rapidly depleted upon incubation with lipoprotein acceptors (18), and second, the cytoplasm of erythrocytes contains a lysophospholipase (19) and a reacylating enzyme (20), which are expected to degrade or acylate, respectively, any lysolipids entering the inner leaflet. The model-predicted values closest to the experimental ones are shown in parentheses. SD is for a group of 10 individuals. 

Table 2.

The total and leaflet phospholipid compositions of the erythrocyte membrane from various mammalian species

Phospholipid	Monkey			Horse			Rat			Mouse			Rabbit
	Total	OL	IL	Total	OL	IL	Total	OL	IL	Total	OL	IL	Total	OL	IL
CPs	56.5 (55.6)	89.4 (88.9)	23.1 (22.2)	56.3 (55.6)	79.7 (77.8)	33.2 (33.3)	59.0 (61.0)	87.8 (88.9)	31.3 (33.3)	60.8 (61.0)	86.3 (88.9)	37.8 (33.3)	57.3 (55.6)	87.8 (88.9)	26.1 (22.2)
APs	15.9 (16.7)	0.0 (0.0)	33.9 (33.3)	15.7 (16.7)	0.0 (0.0)	31.2 (33.3)	16.0 (16.7)	2.0 (0.0)	29.5 (33.3)	14.9 (16.7)	3.5 (0.0)	25.2 (22.2)	8.4 (11.1)	0.0 (0.0)	16.9 (22.2)
PE	27.6 (27.8)	10.6 (11.1)	43.0 (44.4)	28.0 (27.8)	20.3 (22.2)	35.6 (33.3)	25.0 (22.2)	10.2 (11.1)	39.2 (33.3)	24.3 (22.2)	10.2 (11.1)	37.0 (44.4)	34.4 (33.3)	12.2 (11.1)	56.9 (55.6)
Phospholipid in leaflet, %		50.2	49.8		49.7	50.3		49.0	51.0		47.5	52.5		50.5	49.5

The inner and outer leaflet compositions were calculated based on published overall compositions and transbilayer distribution data (20–23). The unit is mol %. Standard deviations are, when given, similar to those in Table 1. When a range was given for the fraction of total lipid in the outer leaflet, the upper limit was chosen because this brings the transbilayer distribution of total phospholipids closer to the expected and generally observed 50:50 distribution. Incomplete digestion of the outer leaflet lipids is a common problem in the determination of transbilayer distributions (24). Lysophosphatidylcholine, which represents about 5, 4, and 2.5% of rat, mouse, and monkey erythrocyte phospholipids, respectively, was assumed to be present exclusively in the outer leaflet (see legend of Table 1). IL, inner leaflet; OL, outer leaflet. 

Statistical Analysis.

The fit between the experimental and predicted compositions was analyzed by employing the symmetric multivariate distribution method (11). Because the SL model predicts several critical mole fractions (see above), each experimental value has to be compared with the closest predicted one, i.e., the values falling between n⋅d − d/2 and n⋅d + d/2 should be compared with the theoretical one at n⋅d (n = 1, 2, 3 etc. and d is 0.111 for a single leaflet and 0.0556 for the whole membrane). Thus in the case of a single leaflet, an experimental value falling between—e.g., 0.0556 and 0.166 is compared with the predicted value of 0.111, an experimental value of 0.167–0.277 with the predicted one of 0.222, and so forth.

For example, when the fit between the predicted and observed composition of the outer and inner leaflets is analyzed collectively, there will be three independent compositional variables (one for the outer and two for inner leaflet; see above), i.e., the mole fractions x₁, x₂, and x₃, which define a point in a three-dimensional space. Correspondingly, the closest predicted mole fractions, x_t,1, x_t,2, and x_t,3 define another point in this three-dimensional space. If the experimental mole fractions are not confined by SL formation (or by some other principle favoring lateral regularity), they should distribute randomly over the intervals n⋅0.111 ± d/2, i.e., the point corresponding to the experimental values (x₁, x₂, x₃) would locate with equal probability anywhere inside a cube with a volume V_c = d³. However, if the membrane phospholipid composition is confined by SL formation, the points defined by the experimental and predicted mole fractions, respectively, should lie close to each other, i.e., their separation,

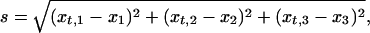would be small. All points at a distance s from the theoretical point are located inside a sphere of a volume, V = 4πs³/3. The probability (P) that a random point inside the cube is also inside this sphere, i.e., that an observed composition fortuitously coincides with the predicted one, is V_s/V_c = 4πs³/3d³. Analogously, it is possible to analyze the fit between the experimental and predicted values of a single lipid class for membranes from n species. In this case the space is n-dimensional. Yet, a collective analysis can be carried out for m lipid classes and n species by employing a (n⋅m)-dimensional space. By noting n⋅m = N, the volume of the N sphere will be

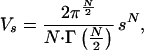3

where Γ function is as defined in ref. 12. Because the volume of the N cube is d^N, the probability for a fortuitous fit in this N-dimensional case will be

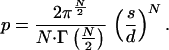4

RESULTS AND DISCUSSION

Table 1 displays the observed and model-predicted (in parentheses) phospholipid compositions for the human erythrocyte membrane as a whole as well as for the individual leaflets. Clearly, there is a striking similarity between the measured and predicted head group class distributions in each case. It is important to note that whereas the model allows for other compositions beside the ones shown in Table 1, these other values are far from the experimental ones. As an example, the measured concentration of CPs in the membrane, i.e., 55.8 mol %, is very similar to the predicted value of 55.6 mol % but quite different from the next closest predicted values, i.e., 50.0 and 61.1 mol %.

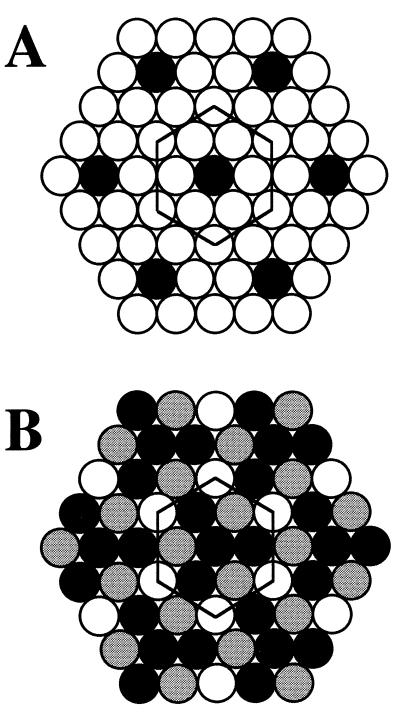
To examine the possibility that agreement between the predicted and determined compositions would have arisen simply by chance, the data were subjected to statistical analysis (see Theory). The probability for a coincidental agreement was found to be very small, i.e., less than 3⋅10⁻³, thus supporting the idea that the tendency of the phospholipids to adopt SL-like lateral arrangements may determine the phospholipid (class) composition of the red cell membrane. The mean lateral arrangement of the head groups in the outer leaflet is thus predicted to be as depicted in Fig. 2A where the open and closed circles represent the choline and ethanolamine head groups, respectively. The preferred arrangement of the head groups in the inner leaflet is suggested to correspond with that shown in Fig. 2B, where the gray symbols represent APs and the white and black symbols CPs and PEs, respectively. We stress that the regular structures depicted in Fig. 2 are not suggested to permanent but should be considered as minimum energy arrangements, which are both spatially and temporally limited (7, 8).

Figure 2.

The proposed mean lateral arrangements of phospholipid classes in the outer and inner leaflet of the human erythrocyte membrane. (A) The proposed lateral arrangement of the head groups in the outer leaflet. The SL is based on unit cell D in Fig. 1, which predicts the abundance of 11.1 and 88.9 mol % of ethanolamine (black) and choline (white) lipids, respectively. (B) The proposed lateral arrangement in the inner leaflet. The SL is based on the ternary unit cell J in Fig. 1, predicting the molar percentages of 44.4, 33.3, and 22.2 for the ethanolamine (black), acidic (gray), and choline (white) phospholipid classes, respectively.

If the proposed tendency of the phospholipid to adopt SL-like arrangements is indeed responsible for the particular compositions of the human erythrocyte membrane, as suggested by the data given above, one would expect that this would be the case with the erythrocytes from other species as well. Table 2 displays the compositions of erythrocytes from the species for which both the overall and the leaflet compositions are known. The overall compositions generally fall close to one of the predicted values, as do the outer leaflet compositions. Regarding the latter, the choline derivatives and PE represent 86–89% and 10–12% of the total phospholipids, respectively, as was observed for the human erythrocyte. The horse erythrocyte differs from the others in that it contains less CP lipids and more PE lipids in the outer leaflet, but importantly, the concentrations of CPs and PE now coincide with another set of predicted values, i.e., 77.7 and 22.2 mol %, respectively. It is also noteworthy that the CP content of the outer leaflet is nearly invariant (excluding the horse) in spite of the fact that the PC to SM ratio varies nearly 4-fold from human (1.1) to mouse (3.9). This suggests that there is a tendency to maintain a constant head group composition rather than a constant sphingolipid/glycerolipid ratio in the outer leaflet. This would be in accordance with the predictions of the SL model as well as with the proposition that PC and SM are completely miscible in fluid bilayers (25).

Except for the human, monkey, and horse erythrocytes, the inner leaflet compositions do not coincide as closely with the predicted values as they do for the outer leaflet. The lack of close agreement in the case of those other species does not, however, necessarily imply that the model is incorrect for the following reasons. First, the inner leaflet composition is based on two determinations (i.e., overall composition and the composition of outer leaflet) whereas a single one is needed to obtain the composition of the outer leaflet. Thus inner leaflet values are inherently more prone to error. Second, significant amounts of PS are reported to be present in the outer leaflet of rat and mouse erythrocytes. This is probably an experimental artifact, because PS is a highly potential initiator of the coagulation cascade and also a marker for sequestration of blood cells from circulation (26). Third, rat and mouse erythrocytes also contain relatively high levels of lysophosphatidylcholine (5 and 4%, respectively). It has not been established how this lysophosphatidylcholine is distributed over the membrane.

When the outer leaflet compositions of erythrocytes from six species (Tables 1 and 2) were analyzed collectively, the probability of a fortuitous agreement between the experimental and predicted values was found to be very low, i.e., 2.5⋅10⁻⁴. For the inner leaflet the probability is higher, i.e., 10⁻², probably because of the experimental uncertainties discussed above.

Table 3 displays the head group class distributions in the erythrocyte membrane from species for which only the overall composition is known. For the guinea pig, sheep, dog, cat, and camel erythrocytes the observed composition agrees closely with one of the predicted values. For the goat, pig, and cow erythrocytes the fit is satisfactory although it is poor for the buffalo. However, considering the experimental uncertainties and the fact that in each case data are available from a single study only, these deviations may not be significant. Notably, the phospholipid composition of the plasma membrane from human and pig platelets also agrees very well with one of the predicted compositions (Table 3). When the compositions given in Table 3 were analyzed collectively, the probability of a fortuitous agreement was found to be 5⋅10⁻³. When all independent values given in Tables 1–3 were analyzed collectively, the probability of a fortuitous fit was found to be very low indeed, i.e., 10⁻⁸. To further assess the significance of the observed fits, the distribution of deviations of the overall compositions (Tables 1–3) from the predicted values was determined for each head group class. As indicated in the legend of Table 3, the standard deviation varies from 1.2 to 1.5 mol %. This is only slightly more than the standard deviation found for a single species, i.e., human (cf. Table 1), thus suggesting that the deviations may be largely because of experimental uncertainties.

Table 3.

Overall phospholipid head group class composition of the erythrocyte and platelet plasma membrane from various mammals

Phospholipid	Erythrocytes									Platelets
	Guinea pig	Sheep	Cat	Camel	Dog	Goat	Pig	Cow	Buffalo	Man	Pig
CPs	55.3 (55.6)	54.2 (55.6)	56.4 (55.6)	54.1 (55.6)	59.5 (61.0)	46.3 (44.4)	50.7 (50.0)	52.5 (55.6)	52.5 (55.6)	56.3 (55.6)	56.6 (55.6)
APs	16.4 (16.7)	18.0 (16.7)	21.4 (22.2)	23.2 (22.2)	18.1 (16.7)	25.6 (27.8)	19.6 (22.2)	15.4 (16.7)	11.6 (11.1)	16.2 (16.7)	16.1 (16.7)
PE	28.3 (27.8)	27.8 (27.8)	22.2 (22.2)	22.7 (22.2)	22.4 (22.2)	28.1 (27.8)	29.7 (27.8)	32.4 (33.3)	35.9 (33.3)	27.5 (27.8)	27.3 (27.8)

The head group class distributions were calculated from published data (27–32). Unidentified lipids, present in sheep, camel, and goat erythrocytes (4.8, 3.4, and 0.8 mol %, respectively), were excluded from the analysis, and the percentages of the other lipids were corrected accordingly to add to 100%. The data fits collectively to the equations: x_CP = n_CP⋅5.56 + 0.45 ± 1.5; x_AP = n_AP⋅5.56 − 0.3 ± 1.5; x_PE = n_PE⋅5.56 − 0.15 ± 1.2 (n_CP + n_AP + n_PE = 9), where x and n⋅5.56 are the observed and the closest predicted mole fractions, respectively. The last figures are standard deviations. 

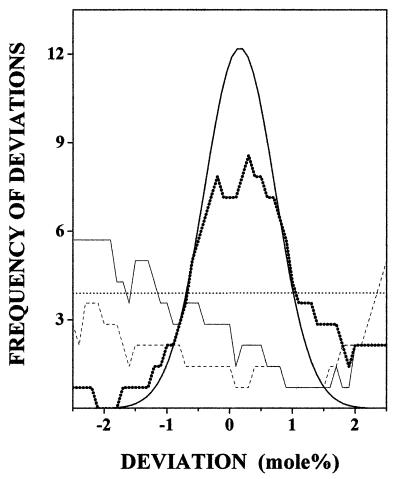
The significance of the observed fits can also be demonstrated graphically. In Fig. 3 the distribution of deviations of the PE mole fraction from the closest predicted one is plotted for a set of 17 different membranes (Tables 1–3). Intriguingly, the distribution of deviations (boldface line) resembles closely the distribution predicted by the model (the Gaussian curve) while allowing for an experimental error of 0.8 mol % (cf. legend of Fig. 3). That this similarity is not trivial is shown by the fact that if the model-predicted critical mole fraction interval (1/9) is replaced by a slightly different (arbitrary) value of 1/8 or 1/10, the similarity is completely lost (Fig. 3), as it is if one assumes that no preferred compositions exist, i.e., that the PE concentrations fall randomly between the observed extremes of 22.2 mol % (cat) and 35.9 mol % (buffalo).

Figure 3.

Graphical demonstration of the significance of the fit between observed and predicted compositions. The deviation of the overall PE molar percentages from the predicted ones was calculated for 17 different membranes (Tables 1–3), and the frequency of deviations was plotted against the magnitude of deviations (thick dotted line). The plot was smoothed by using the running point average method and 1.4 mol % window. The Gaussian curve represents the distribution of deviations predicted by the SL model with the assumption that the error in the experimental values (means) is 0.8 mol % on the average. This value, which defines the half-width of the Gaussian, was obtained by dividing SD by the square root of the number of determinations (assumed to be 4). The Gaussian has been shifted slightly (0.16 mol %) along the x axis to make comparison with the experimental curve easier. The distributions are plotted also for the hypothetical cases that: (i) the critical mole fraction interval would be 1/8 (thin continuous line) or (ii) 1/10 (dashed line) instead of the model predicted value of 1/9, or (iii) that no preferred compositions would exist, i.e., the concentration of PE could obtain any value between the experimental extremes 22.2 mol % (cat) and 35.9 mol % (buffalo) with equal probability (horizontal dotted line).

One may wonder why only 9-element unit cells would be feasible among the many different unit cells suggested by the SL model (cf. Eq. 1)? One feasible explanation becomes apparent on examination of the lateral arrangement of the elements in the different ternary lattices allowed for by the model. It turns out that only when P_HX = 9 or 12 are the APs evenly distributed (Fig. 2B and not shown, respectively). When P_HX = 7, 13, 16, or 19, APs cluster, which goes against a basic principle of the model (see Theory). Therefore these unit cells are not feasible. Notably, they also do not give a good fit to the experimental data (data not shown). When the unit cell is very large (P_HX ≥ 21), the critical mole fractions become so closely spaced that an (apparent) fit would be frequently observed. However, for such large unit cells to be stable, the organizing forces (see below) should extend beyond more than 5 head group layers. This seems highly unlikely for a liquid–crystalline membrane.

Apart from phospholipids, the erythrocyte membrane also contains cholesterol and glycosphingolipids. Cholesterol was not included in the SL model simply because it has a very small polar moiety, which is located well below phospholipid head groups (refs. 33 and 34; and see below). The feasibility of phospholipid head group SL formation in the presence of cholesterol is supported by theoretical studies (J.A.V. and P.S., unpublished data) as well as by experimental data obtained for PE/PC/cholesterol bilayers (unpublished data). Glycosphingolipids were omitted from the SL model because they are probably segregated into distinct domains (35–37). However, direct experimental evidence supporting such segregation of glycosphingolipids in erythrocyte membranes is lacking.

Also the integral membrane proteins present in the erythrocyte membrane could in principle interfere with the formation of the lipid SLs, for example by selectively attracting APs (38). However, inspection of the putative inner leaflet lattice in Fig. 2B reveals that wherever a membrane protein would be inserted, there would be many APs in the protein boundary, independent of the number of membrane-spanning helices or other structural details of the protein molecule. Therefore, the affinity of a protein for acidic species could be fully satisfied without perturbing the lipid SL. Another distinct issue is that proteins, when inserted to the SL, could substitute different lipid classes disproportionally. This would obviously distort the characteristic compositions and thus severely complicate the present type of analysis. However, theoretical analyses (unpublished data) show that such disproportional replacement would occur only in the very unlikely case that (i) the protein molecules also adopt a SL distribution and (ii) the lattice constant of this protein lattice is identical to or a multiple of that of the lipid SL. On the other hand, Rodgers and Glaser (39) have shown that fluorescent phospholipid derivatives introduced to the erythrocyte ghost membrane are not evenly distributed but concentrate in distinct macroscopic domains in a head group-dependent manner. It was suggested that selective interactions between some membrane proteins and lipids are responsible for the presence of such domains. Those findings obviously contradict the present model, which proposes macroscopically even lateral distribution of the phospholipid species in the erythrocyte membrane.

At this time, it is only possible to make some suggestions regarding the interactions responsible for the formation of the putative head group SLs in the erythrocyte membrane. It is probable that both steric and coulombic interactions are involved. We have recently obtained some evidence that in liquid–crystalline PC/PE bilayers the components tend to adopt SL-like arrangements (40). It was suggested that SL formation optimally relieves the packing problems (frustrations) present in bilayers consisting of only PC or PE. Liquid–crystalline PE bilayers are “curvature frustrated” because of the small effective cross-sectional area of the polar head group as compared with that of the acyl chains (41, 42). In contrast, the effective cross-sectional area of the head group of the choline lipids is typically larger than that of the acyl chains because of the extensive hydration (41, 43, 44) and/or repulsive dipole–dipole interactions between the head groups (45). Consequently, bilayers consisting of CPs alone should also be considered as “frustrated.” However, when PE and PC are mixed, the frustration should diminish and, at a particular composition, disappear because of the complementary shapes of the two lipids (41). Importantly, this “anti-frustration” effect is expected to be maximal when the components adopt a regular, SL-like distribution in the bilayer.

Notably, cholesterol also has been suggested to act as a head group spacer diminishing the packing “frustrations” present in neat PC bilayers (7, 41). Because cholesterol is abundant in the erythrocyte membrane, one may thus wonder whether any significant packing “frustration” remains to be relieved by PE. The answer depends on how cholesterol is distributed between the membrane leaflets, which is not fully established. However, because (i) cholesterol is known to associate preferably with CPs (46, 47) and (ii) the latter are markedly concentrated to the outer leaflet (Tables 1 and 2), it is very likely that also most of the cholesterol is located in this leaflet. In contrast, PE is concentrated to the inner leaflet (Tables 1 and 2). Such a complementary distribution of cholesterol and PE over the membrane suggests that the former serves as the main head group spacer in the outer leaflet whereas the latter does so in the inner leaflet.

The inner leaflet of the erythrocyte membrane is rich in APs; typically every third phospholipid in the inner leaflet is AP (Tables 1 and 2). Because of their net negative charge, mutual repulsion exists between APs. Although this repulsion is difficult to quantitate, it is likely to prevent APs from occupying proximal lattice sites. This would be adequate to bring about the proposed regular distribution of APs in the inner leaflet (cf. Fig. 2B). Previously, Berclaz and McConnell (48) have provided evidence for regular lateral arrangements in fluid bilayers consisting of a negatively charged phospholipid and PC.

Because the (putative) random state-to-SL transition is probably a second order one, the relative areas occupied by the two types of organization can be estimated from the Bolzmann equation. This equation predicts that the SLs would cover 50% of the membrane area even if the difference in free energy of the random and SL “phases” is equal to zero. However, this figure is probably an overestimate because the formation of a SL is likely to be a significantly less favorable process than its melting to a random phase. Therefore, the Bolzmann equation is not directly applicable even if a partition function can be applied to study phase transitions (49). Further studies are needed to resolve this issue. On the other hand, it is essential to point out here that the SLs do not even need to cover a major fraction of membrane area at any time to play a crucial role in compositional regulation; a smaller coverage would only mean that there is more fluctuation around the SL-determined composition. It is also relevant to note that recent studies indicate that SL formation in hard-sphere systems is, perhaps unexpectedly, driven by entropy (50). The favorable entropy effect probably derives from the fact that the rotation and vibration of the elements are less hindered in a SL as compared with less organized systems (51, 52). In the case of phospholipid membranes the entropy gain because of SL formation is likely to be even more important because the (horizontal) rotation of the elongated, asymmetric head groups is expected to be more sensitive to “crowding” than that of hard spheres (52).

In conclusion, the present data show that there is an intriguing correlation between the experimentally determined phospholipid compositions of the erythrocyte membrane and those predicted by the SL model. However, the SL model makes several simplifying assumptions regarding intermolecular interactions in a complex membrane and must therefore be considered as a tentative one until more evidence is available. Although it is not easy to devise experiments for critical testing of the proposed model, some of the following could be useful. First, one could manipulate the phospholipid composition of the erythrocyte membrane by using a lipid transfer protein (53) and then determine the effect on some membrane property. Because the SL model predicts that optimal lateral packing of the lipids occurs only at particular, “critical” compositions, deviations from those compositions should lead to coexistence of domains with different SLs as well as domain boundaries with imperfect lateral packing (8). The appearance of such packing defects should enhance membrane permeability (54), which could be monitored. Alternatively, packing defects could be detected by studying the susceptibility of erythrocyte membrane phospholipids to endogenous (55) or exogenous phospholipases. Phospholipases typically act only on bilayers where lateral packing defects are present (56). Also Merocyanine 540, a fluorescent probe, is sensitive to the lipid packing order (57) and could thus be employed. Second, diffraction methods or atomic force microscopy could provide information on the presence of SLs. Wide angle neutron diffraction studies on membranes containing a deuterated phospholipid species (58) could be particularly useful. Although it is not certain whether these physical techniques are suitable to study the erythrocyte membrane, they are likely to provide relevant information on model membranes. Even this would be most valuable, because the evidence for SL formation in any membrane is still limited, indirect, and often based on the use of unphysiological, potentially perturbing probes. Finally, theoretical approaches, such as Monte-Carlo simulations (8), should also be helpful when testing the predictions of the SL model.

ABBREVIATIONS

SL

superlattice

CP

choline phospholipid

PC

phosphatidylcholine

SM

sphingomyelin

AP

acidic phospholipid

PS

phosphatidylserine

PI

phosphatidylinositol

PA

phosphatidic acid

PE

phosphatidylethanolamine

PLC

phospholipid class