Dynamics of different functional parts of bacteriorhodopsin: H-²H labeling and neutron scattering

Abstract

We show that dynamics of specific amino acids within a protein can be characterized by neutron spectroscopy and hydrogen–deuterium labeling, and we present data on the motions of a selected set of groups within bacteriorhodopsin (BR), the retinal-based proton pump in the purple membrane of halophilic Archaea. Elastic incoherent neutron scattering experiments allow the definition of motions in the nano- to picosecond time scale and have revealed a dynamical transition from a harmonic to a softer, anharmonic atomic fluctuation regime in the global behavior of proteins. Biological activity in proteins is correlated with this transition, suggesting that flexibility is required for function. Elastic incoherent neutron scattering is dominated by H atom scattering, and to study the dynamics of a selected part of BR, fully deuterated purple membrane with BR containing H-retinal, H-tryptophan, and H-methionine was prepared biosynthetically in Halobacterium salinarum. These amino acids cluster in the functional center of the protein. In contrast to the protein globally, the thermal motions of the labeled atoms were found to be shielded from solvent melting effects at 260 K. Above this temperature, the labeled groups appear as more rigid than the rest of the protein, with a significantly smaller mean square amplitude of motion. These experimental results quantify the dynamical heterogeneity of BR (which meets the functional requirements of global flexibility), on the one hand, to allow large conformational changes in the molecule and of a more rigid region in the protein, on the other, to control stereo-specific selection of retinal conformations.

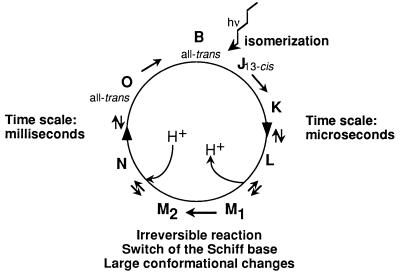
Bacteriorhodopsin (BR) functions as a light-driven proton pump (1–3). It is the only protein in the purple membrane (PM) of Halobacterium salinarum, in which it is organized with lipids in a highly ordered two-dimensional lattice. The structure of BR is known to relatively high resolution for a membrane protein in its natural lipid environment from cryoelectron microscopy (4, 5). Recently, a 2.5-Å structure was published from an x-ray crystallography study of BR detergent crystals obtained from cubic lipid phases (6), and glycolipids closely associated with BR have been localized in PM by neutron diffraction and deuterium labeling (44). Its main features are seven α-helices, arranged in a bundle around a retinal molecule that is bound, via a Schiff base, to a lysine residue. Upon illumination, BR undergoes a catalytic cycle with a frequency of the order of milliseconds causing proton translocation (1) (Fig. 1). A subset of intermediates with different colors comprises a photocycle that has been analyzed in detail by spectroscopy. The first part of the photocycle, until the photointermediate M, is achieved in a few microseconds. The amount of time for relaxation from M back to B is in the order of milliseconds. Within M there is an irreversible transition between two substates of almost identical absorption characteristics, M1 and M2, involving a large structural change (7–9). Ferrand et al. (10) have shown that the ability of the protein to relax functionally from M and complete the photocycle is correlated strongly with the onset of low frequency anharmonic atomic motions in the membrane. For a normally hydrated sample, this occurs at ≈230 K, where a dynamical transition is observed. Motions within BR as a function of hydration have been characterized further by quasielastic neutron scattering (11, 12). Other experimental and theoretical studies also have provided evidence that biological activity in proteins is correlated with a dynamical transition from a harmonic to a softer, anharmonic atomic fluctuation regime (13–18), suggesting that flexibility is required for function (17). Before the present work, experiments had only explored this transition in the global behavior of a few proteins.

Figure 1.

The bacteriorhodopsin photocycle. B, initial state of BR. Predominant features associated with the dynamics–function hypothesis in the present study are shown schematically.

To focus on the motions of selected groups in BR, which may be involved more directly in the functioning of the protein, we used neutron spectroscopy combined with selective H-²H labeling. Natural abundance hydrogen (99.985% ¹H) has an incoherent neutron cross-section of 79.91 barns, compared with <1 barn for other atoms in proteins (19). The cross-section of ²H is 2.04 barns, making H-²H labeling a powerful approach to separate the scattering of various parts of a complex structure.

The part of BR selected for study is located toward the extracellular (EC) half of the protein and includes the retinal and its close environment. Electron microscopy studies have suggested first that the main conformational changes involved in the M1 to M2 transition reside in the CP half of BR and, second, that the atoms in the CP half have larger Debye–Waller factors than those in the EC half (4, 8, 9). In molecular dynamics simulations, the fluctuations of the helix extremities in the CP half of BR appeared twice as large as those in the EC half (20) and the movements of the helices in the M state required more flexibility in the CP region of BR (21). The photoisomerization of the retinal from all-trans to 13-cis initiates the photocycle. This specific isomerization is assumed to be ensured by the close packing of surrounding amino acids. Furthermore, the retinal binding pocket is implicated in the irreversible transition within the M state of the photocycle, during which the Schiff base changes its accessibility from the EC part of the protein—which releases the proton—to the CP part—where proton uptake takes place (22, 23). This “switch” of the Schiff base allows the vectorial transport of the proton. The retinal pocket then can be seen as a proton “valve” between EC and CP parts of BR. Clearly, the isomerization of the retinal molecule as well as its “switch” function would be best exerted in a “rigid” environment.

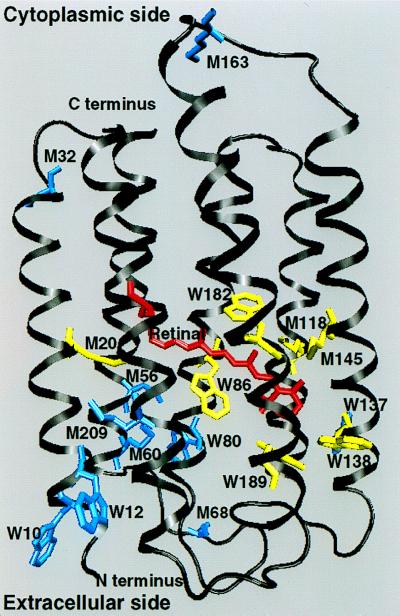
To explore whether the retinal pocket and EC parts of BR present more rigid dynamics than the protein globally, we took advantage of the fact that methionine and tryptophan residues are not distributed homogeneously in the protein. A special PM sample was prepared biosynthetically in H. salinarum (24). The membrane was fully deuterated except for the retinal, tryptophan, and methionine residues, which contained hydrogen with natural isotope abundance (see Fig. 2). Four tryptophan residues (out of a total of eight in BR) are located in this pocket (W86, W182, W138, and W189). Three of them are highly conserved in all bacterial opsins and are described as constraining the motions of the retinal during photoisomerization [W86, W182, and W189 (25, 26)]. Three out of a total of nine methionines in BR are near the retinal (M20, M118, and M145). Two of these are particularly close to the retinal and have an influence on the photocycle (M118 and M145); their mutations to alanine lead to a decrease in the efficiency of the proton pump (27). The remaining labeled residues are all in the EC half of the transmembrane helices except for three methionines found in the loops.

Figure 2.

Labeled BR viewed from within the plane of the membrane: Red, retinal molecule; yellow, Trp (W86, W182, W138, and W189) and Met (M20, M118, and M45) residues in the retinal pocket; blue, Trp (W10, W12, W80, and W137) and Met (M32, M56, M60, M68, M163, and M209) residues out of the retinal pocket [Protein Data Bank atomic coordinates from Grigorieff et al. (4)].

MATERIALS AND METHODS

PM Sample Preparations.

Three samples were prepared in different states of deuteration.

Natural abundance PM and fully deuterated PM were obtained by growing H. salinarum strain S9 on standard medium (28) and on a completely deuterated medium (24), respectively.

For the specifically hydrogenated PM, BR was labeled with natural abundance hydrogen (H-)retinal, (H-)tryptophan (Trp), and (H-)methionine (Met) residues in otherwise fully deuterated PM. The retinal-negative strain JW5 (28) was grown on a completely deuterated medium (24) to which hydrogenated Met and Trp residues were added in excess (2.5 mM and 0.5 mM, respectively). After the onset of growth (3–5 days), a total of 14 μmol hydrogenated all-trans-retinal in isopropyl alcohol (1.4 ml) per 700 ml of culture was administered in 4 aliquots, every 2nd day.

All PM samples were isolated and purified by standard methods (28). H₂O in the samples was replaced by ²H₂O in three successive centrifugation steps (100,000 × g, 10°C, 1 h) of the isolated fraction in 99.8% ²H₂O, to give a H₂O dilution of (1:35)³. Wet samples then were equilibrated with ²H₂O in 93% (for deuterated and labeled PM) and 100% (for hydrogenated PM) relative humidity, corresponding to 0.45 and 0.55 g of ²H₂O/g of PM, by vapor exchange over a saturated KNO₃ solution and water solution (5–6 days, 25°C), respectively. A lower relative humidity was chosen for the deuterated samples to decrease the solvent scattering. At 100% and 93% relative humidity, the photocycle shows the same kinetics and includes the same transients as PM fragments suspended in water (29). The dry sample was obtained by moderate drying over silica gel. It corresponds to a water content of 0.02 g of ²H₂O/g of PM. For the scattering experiments, samples were deposited inside standard aluminum containers (≈20 cm² in beam area, with a defined path length of 0.5 mm).

Elastic Incoherent Neutron Scattering.

In a coherent radiation scattering experiment, the atomic distribution in a particle is measured from the angular distribution of scattered intensities. The scattering pattern results from the interference between waves scattered coherently by the atoms at different positions. In an elastic incoherent neutron scattering (EINS) experiment, the waves that interfere with each other are scattered by a single nucleus occupying different positions as a function of time (19). Similarly to the coherent case, the angular distribution of the EINS intensity contains information on the spatial distribution of each atom as it moves during an effective exposure time (approximately nanoseconds for the experiments presented), i.e., the method describes the shapes of the “blurred” atoms. This similarity is expressed by Eq. 1 (30), which is analogous to the Guinier approximation in classical small angle scattering (31):

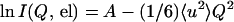1

where I(Q, el) is the EINS as a function of scattering vector Q (4πsinθ/λ, 2θ is the scattering angle), 〈u²〉 is the mean square amplitude describing the spatial extent of the atomic “blurs,” and A is a constant. Note that we have followed the definition of 〈u²〉 given by Smith (30), which refers to the full amplitude of the motion. It differs by a factor of 2 from the definition of Ferrand et al. (10) in the first EINS studies of BR, which referred to displacements from average atomic positions (in the harmonic approximation). Formally, Eq. 1 is valid in the limit of Q → 0, but similarly to the Guinier approximation, it holds for 〈u²〉Q² ≈ 2 (32). The effective exposure (coherence) time is related to the energy resolution (ΔE) of the spectrometer used in the experiment. Longer times correspond to smaller ΔE values. In practice, the measured 〈u²〉 values correspond to the H atoms, whose scattering cross section is strongly dominant. In the selectively hydrogenated PM, although the label H atoms represent only 6% of the total H or ²H. their incoherent signal contributes 72% of the total scattering from the membrane. The 〈u²〉 obtained for this sample then is dominated by the motion amplitudes of the labeled atoms. In the fully deuterated PM sample, 97% of the incoherent signal from the membrane is due to the ²H atoms.

The integrated elastic intensities I(Q, el) were collected on the IN10 backscattering spectrometer at the Institut Laue Langevin (ILL) in Grenoble (λ = 6.27 Å, energy resolution, ΔE = 1 μeV, corresponding to a coherence time for neutron scattering <2 ns) as a function of temperature. Samples were in a helium cryostat to allow measurements at different temperatures. At first, the sample temperature was decreased to 15 K (at ≈1.5 K/min), then it was increased from 15 to 300 K in steps of 1.5 K. The acquisition time at each temperature was 5 min for the hydrogenated PM. For deuterated and labeled PM, it was 20 min because of their low scattering cross-section. For each Q value, EINS data were corrected for cell scattering and detector response and normalized by the I(Q, el) obtained at the lowest temperature (see following paragraph). For each temperature, a linear fit of log[I(Q, el)_normalized] as a function of Q² was performed, according to Eq. 1, to extract 〈u²〉, the hydrogen mean square amplitudes. The 〈u²〉 values calculated corresponded to motions occurring in a time shorter than 2 ns, corresponding to the energy resolution of IN10 in the conditions used for the experiments. The Q range was 0.6–1.8 Å⁻¹, corresponding to observable amplitudes close to 1 Å.

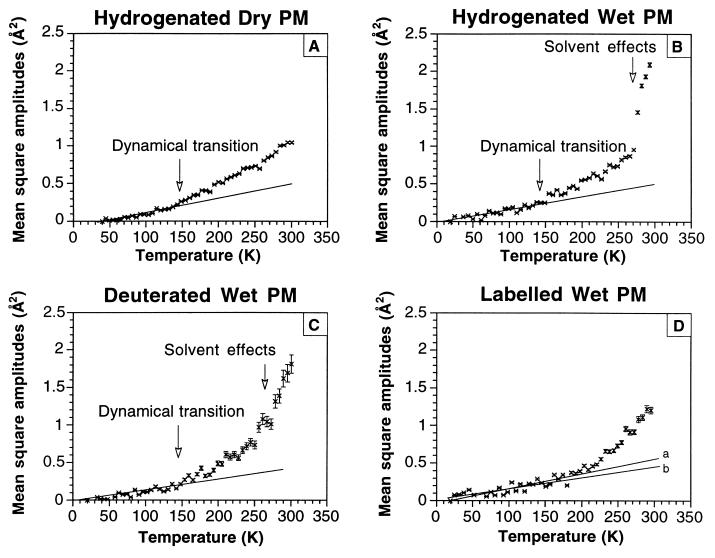
Because the EINS intensities were normalized by the values measured at the lowest temperature examined (T_min) each mean square amplitude plotted in Fig. 4 is equal to 〈u²〉(T) − 〈u²〉(T_min). Because of this, the plots do not extrapolate to either zero or to a small positive value at T = 0 as expected in classical or quantum mechanics, respectively. The values of T_min were: 40 K for hydrogenated dry PM, 18 K for hydrogenated wet PM, 19 K for deuterated wet PM, and 20 K for labeled wet PM. The values of 〈u²〉(T_min) were estimated to be <0.1 Ų. For a harmonic system, 〈u²〉 as a function of T is a straight line. Error weighted straight line fits of the data were performed for all samples between the minimum temperature and 150 K by using the Marquardt–Levenberg algorithm in the gnufit routine under gnuplot on a Unix system (program version 3.5, Dartmouth University, Dartmouth, NH). The slopes obtained, respectively, for Figs. 4 A-C were 1.82 (10⁻³ ŲK⁻¹), 1.68 (10⁻³ ŲK⁻¹), and 1.62 (10⁻³ ŲK⁻¹). In the case of the labeled wet PM sample (Fig. 4D), points between 150 and 200 K did not deviate significantly from this line [the slope for the fit to 150 K is 1.92 ± 0.18 (10⁻³ ŲK⁻¹); the slope for the fit to 200 K is 2.00 ± 0.18 (10⁻³ ŲK⁻¹)]. For this sample, the fit obtained by giving equal weights to the data points also is shown [slope 1.44 (10⁻³ ŲK⁻¹)]. The difference between the two lines is due to the fact that, in the “weighted” fit, the relative errors are very large for the points at the lowest temperatures (where 〈u²〉 are close to zero).

Figure 4.

Hydrogen mean square amplitudes 〈u²〉 – 〈u²〉(T_min) plotted as function of temperature for the different samples and conditions. Experimental errors in 〈u²〉 are shown. The solid lines correspond to linear fits of the data points for T_min < T < 150 K as described in Materials and Methods. (D) Line a corresponds to the error-weighted fit, and line b corresponds to the fit with equal weights attributed to the data points.

RESULTS

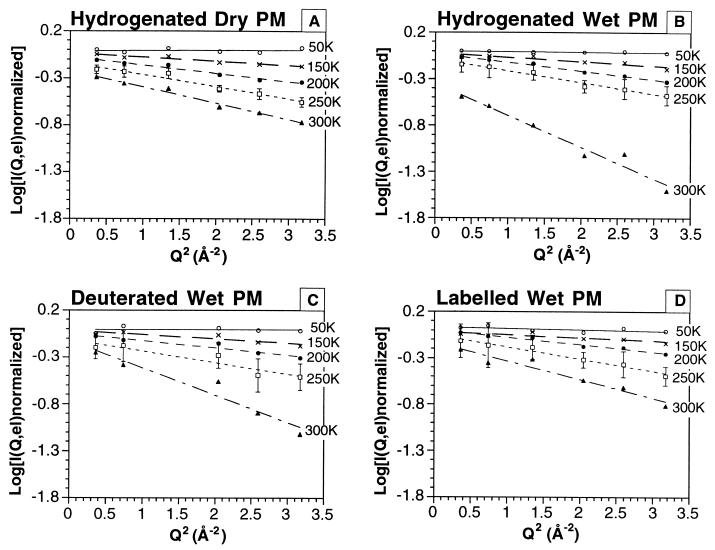
The EINS data obtained for the four samples were plotted as log[I(Q, el)_normalized] as a function of Q² (Fig. 3), after usual corrections and normalizations (see Materials and Methods). Data are displayed only for five chosen temperatures. Error bars corresponding to statistical errors were similar at all temperatures for each sample and are indicated only for one temperature. They are larger for the deuterated samples because of the lower signal-to-noise ratio. The straight lines represent the linear fits to Eq. 1 in the Q range 0.6–1.8 Å⁻¹, from which the mean square amplitudes plotted against temperature in Fig. 4 were determined. The mean square amplitudes were fitted by straight lines between the minimum temperature and 150 K, following the procedure described in Materials and Methods. A deviation from the straight line indicates a dynamical transition away from harmonic behavior. In the harmonic approximation, the slope of 〈u²〉 vs. T is inversely proportional to the force constant, so that a smaller slope indicates a more “rigid” oscillator and vice versa.

Figure 3.

Variation of ln I(Q, el) normalized as a function of Q² for the different samples and conditions, from which mean square displacements, 〈u²〉 – 〈u²〉(T_min) (see Materials and Methods), were calculated by using Eq. 1.

A dynamical transition at 150 K is observed in the fully H-dry sample (Fig. 4A). The fully H- (Fig. 4B) and fully ²H- (Fig. 4C) wet samples show quantitatively identical plots, except for the poorer statistical accuracy of the ²H- data arising from its lower scattering cross-section. The data from the fully ²H- sample provide an important control, showing that, in the time domain examined, the dynamical behavior of the sample is not modified by an isotope effect. Amplitudes in the nanosecond time range are dominated by the thermal fluctuations of amino acid side chains (5, 23) so that H or ²H nuclei reflect the motions of the larger chemical groups to which they are bound. Fig. 4 B and C, therefore, represent the mean square amplitudes of all atoms in PM. In Fig. 4 B and C, a second break in the curve is observed at ≈260 K, probably because of the onset of larger amplitude fluctuations of the atoms in the membrane allowed by the melting of solvent water.

There are significant differences between the data in Fig. 4 B and D (the specifically labeled wet PM sample). First, within experimental errors, either the harmonic regime is maintained to above 200 K (as shown by line a, the “weighted” fit) or (as shown by line b) the points above a dynamical transition at 150 K deviate less from harmonic values than in Fig. 4B. Second, the break putatively due to solvent melting at 260 K is absent and 〈u²〉 increases less steeply with temperature (indicating more “rigid” dynamics for the labeled groups). At room temperature, the mean square amplitude is significantly smaller than for PM globally (1.2 Ų compared with 2.1 Ų). These data quantify the atomic thermal motions of different parts of the BR molecule. They show that the labeled groups are more “rigid” than the rest of the protein and that they do not respond to the melting of solvent water, even though the apparent increase in slope at ≈220 K in Fig. 4D might be correlated with the melting of bound hydration water.

In the specifically H-labeled sample, the labeled amino acids are located mainly in the retinal pocket and the EC half of the BR helices, and the data in Fig. 4D essentially represent motions in these parts of BR. An approximate calculation based on incoherent neutron cross-sections and PM composition showed that, in this sample, the scattering signal by the H-labeled groups accounts for ≈72% of the total scattering from the membrane; of the remaining 28%, ≈7% is from ²H in lipids and ≈21% is from ²H in the unlabeled part of the protein. The signal from the H-labels is broken up in the following way: four of the eight labeled Trp and three of the nine labeled Met are in the retinal binding pocket (i.e., 84 out of the total of 164 H atoms, corresponding to 51% of the signal). There are three Met in the loops (corresponding to 15% of the signal), and all other labeled residues (four Trp and three Met) are in the EC half of the BR transmembrane helices (3) (corresponding to 34% of the signal) (Fig. 2). The mean square amplitudes in the labeled sample are mean values of contributions from the groups in the transmembrane parts (85%) and from the loops (15%). The loop amplitudes are expected to be larger than the amplitudes corresponding to the transmembrane parts of the protein and to be influenced by solvent melting. We can conclude that the mean square amplitudes of atoms in the retinal pocket and EC part of BR are likely to be smaller than the values in Fig. 4D.

DISCUSSION

The first EINS measurements on a protein were performed on myoglobin (13). Plotting 〈u²〉 vs. T (absolute temperature) allowed these authors to investigate the nature of protein motions. A classical harmonic regime at low temperatures was described, where 〈u²〉 is proportional to T and extrapolates to close to T = 0. The dynamical transition was shown by a break in the line, leading to an anharmonic regime with a steeper increase in 〈u²〉 vs. temperature. Protein motions in the higher temperature regime can be modeled in various ways (13, 30). For example, the dynamical transition can be related to a simple interpretation within the conformational substate (CS) model (33). Each protein molecule, at low temperatures, is trapped in one of many possible conformational substate potential wells, where it vibrates harmonically. At the dynamical transition temperature, it can acquire sufficient activation energy to move anharmonically between conformational substate potential wells. In hydrated myoglobin, a dynamical transition was observed at ≈180 K that could be accounted for by a jump model between a ground state and an excited state in a common potential energy surface for hydrogen atoms (13). Such a model is certainly an oversimplification, however, because proteins have many more than two accessible conformations, and it is likely that hydrogen atoms will move in a complex hierarchy of potential surfaces (33). In an analysis of the dynamical transition in myoglobin by molecular dynamics simulations, Smith (30) introduced temperature-dependent, quasi-harmonic potentials and highlighted the importance of configurational degeneracy and the nonequivalence of H-atoms contributing to the observed amplitudes.

The dynamics of the iron and heme in myoglobin was compared with the global dynamics of the protein by applying complementary spectroscopic methods and molecular dynamics calculations (34). The motion of the iron with respect to the heme was probed by absorption spectroscopy, Mössbauer spectroscopy probed the overall motion of the heme, and neutron scattering probed the motions of all of the atoms in the protein molecule. The three experimental methods probe different time domains (nanoseconds to picoseconds for neutrons; shorter than 10⁻¹ ms for Mössbauer spectroscopy; and picoseconds for light absorption spectroscopy). Comparison of the mean square displacements obtained showed that the fluctuations of the protein backbone are larger than the fluctuations of the heme, which, in turn, are larger than the fluctuations of the iron with respect to the heme plane. The temperature of the dynamical transition, however, remained approximately constant at ≈180 K for the three sets of motions observed.

Mössbauer spectroscopy experiments on the dynamics of iron bound nonspecifically to BR showed dynamical transitions at ≈220 K, with some differences in the behavior depending on the oxidation state of the Fe ion (16). This result suggested that the hydrophilic loops of BR on either side of the PM also undergo a transition in flexibility. Ferrand et al. (10) have shown that, for a hydrogenated wet PM sample, a dynamical transition at ≈230 K can be correlated to the ability of the protein to functionally relax and complete the photocycle initiated by the absorption of a photon. These previous EINS measurements (10) on hydrogenated PM, wet or dry, showed two significantly different results from those described in the present study. First, mean square amplitude values in this work were about two times higher than those in the study by Ferrand et al. (10), after allowing for the difference in the definition of 〈u²〉 between the Ferrand work (10) and this work (see Materials and Methods). Second, the transition at 150 K observed here (Fig. 4 A and B) was not observed by Ferrand et al. (10) in the wet sample or in the dry sample. These differences arise from the differences in the Q ranges of the spectrometers used: 1 < Q < 4.5 Å⁻¹ on IN13 (at ILL) in Ferrand et al. (10) and 0.6 < Q < 1.8 Å⁻¹ on IN10 (at ILL) in the present work. In the range of large Q values, the experiment is more sensitive to the small motion amplitudes and conversely. The 〈u²〉 values reported here therefore are weighted toward the population of atoms having motions of larger amplitudes that show a dynamical transition at ≈150 K (32).

The catalytic and photochemical properties of BR well could be reflected in the dynamical heterogeneity observed when data from the wet hydrogenated and labeled PM samples are compared. The stereospecific initial photoisomerization from all-trans to 13-cis must be selected by the retinal binding pocket and is best done in a “rigid” environment. Furthermore, Delaney et al. (35) have shown that a restricted flexibility of retinal, ensured by van der Waals contact with Leu-93, is necessary for its re-isomerization from the 13-cis to the all-trans state at the end of the photocycle. Schweiger et al. (36) have shown that BR could function without a covalent linkage between retinal and protein, which may suggest that the retinal is embedded tightly by its local environment. The Schiff base, after having released a proton to the extracellular side of the protein, must change its accessibility to the cytoplasmic side for re-uptake of a proton, thus allowing vectorial translocation of the proton (2, 3). This, also, is a switch that is best conceived in a “rigid” local environment. On the other hand, the accessibility change of the Schiff base is connected to a substantial conformational change of the protein (7, 9), essentially located in the CP half of the protein, and requires flexibility of the “soft body” around a “rigid” anchor perhaps provided by the retinal pocket and EC transmembrane half of BR. Of course, the terms “soft” and “rigid” are relative. At functional temperatures, both regions have gone through their dynamical transitions. Of interest, the protein conformational change corresponding to the transition between the intermediates M1 and M2 of the catalytic cycle is frozen out at temperatures below ≈260 K (43), which correspond to the transition observed in global behavior and are attributed to solvent effects. These structural changes also are inhibited at low hydration levels even though, under these conditions, the chromophore color shows that the Schiff base is deprotonated and an M-state is formed (37, 38). It is important to note that either below 260 K or at low relative humidity, the proton from Asp-85 reprotonates the Schiff base instead of going out toward the EC part of the membrane (39–41). This point strongly suggests that solvent effects allow the required flexibility for the structural changes.

Thermal motions can be seen as the “lubricant” for all necessary conformational changes in a protein (30). Dynamical transitions have been correlated to active site accessibility for myoglobin (13) and ribonuclease A (17). In BR, a global dynamical transition observed for large Q values (small amplitudes) was correlated with the capability to complete the thermal relaxation steps of the photocycle (10). Simulations have suggested different dynamical behavior for the cytoplasmic and extracellular parts of the protein (20). Because the labels are located predominantly in the extracellular half of BR (85% of the incoherent signal: retinal pocket + Trp and Met in the EC half transmembrane helices), the present EINS experiments provide quantitative data for a further understanding of this function-related behavior through molecular dynamics studies.

Atomic fluctuation amplitudes, on the one hand, and displacements associated with different conformational substates, on the other, depend on their location in a protein. The analysis of Debye–Waller factors in x-ray crystallography have shown that, in general, displacements from mean positions are smaller for atoms in the core of a protein than for atoms on the macromolecular surface (42). We have shown here that protein atoms move in potential wells of different shapes and temperature characteristics, depending on their location in the structure. The EINS experiments have proven to be sufficiently sensitive to quantify this dynamical heterogeneity. The labeled H atoms, in the present study, represent 6% of the total H in the protein, which demonstrates the sensitivity of the method.

It is stressed that the neutron approach yields the most direct and possibly unique quantitative data to test models from molecular dynamics simulations because the observable ranges of amplitude and time scale coincide for theory and experiment. With more such data on hand, it will be possible to address important questions: Has a dynamics-function relation put evolutionary pressure on the specific dynamics of proteins? Does specific dynamics have to compromise between the requirements of stability and those of function? in the case of extremophiles, for example, has specific dynamics adapted to different conditions of solvent environment, temperature, or pressure?