How evolution makes proteins fold quickly

Abstract

Sequences of fast-folding model proteins (48 residues long on a cubic lattice) were generated by an evolution-like selection toward fast folding. We find that fast-folding proteins exhibit a specific folding mechanism in which all transition state conformations share a smaller subset of common contacts (folding nucleus). Acceleration of folding was accompanied by dramatic strengthening of interactions in the folding nucleus whereas average energy of nonnucleus interactions remained largely unchanged. Furthermore, the residues involved in the nucleus are the most conserved ones within families of evolved sequences. Our results imply that for each protein structure there is a small number of conserved positions that are key determinants of fast folding into that structure. This conjecture was tested on two protein superfamilies: the first having the classical monophosphate binding fold (CMBF; 98 families) and the second having type-III repeat fold (47 families). For each superfamily, we discovered a few positions that exhibit very strong and statistically significant “conservatism of conservatism”—amino acids in those positions are conserved within every family whereas the actual types of amino acids varied from family to family. Those amino acids are in spatial contact with each other. The experimental data of Serrano and coworkers [Lopez-Hernandez, E. & Serrano, L. (1996) Fold. Des. (London) 1, 43–55]. for one of the proteins of the CMBF superfamily (CheY) show that residues identified this way indeed belong to the folding nucleus. Further analysis revealed deep connections between nucleation in CMBF proteins and their function.

One of the most important goals of bioinformatics is to learn how to recognize, through alignment of numerous homologous sequences, the structural and functional features of the proteins that they encode. The bioinformatics approach is based on the idea of “recognition” and identification of features of a new sequence common to those of another sequence for which structure and function are known. However, this approach encounters significant difficulties because of a lack of understanding of what features of sequences have evolved to encode stability and fast folding, which ones are functional and which ones may be “adventitious” because of insufficient divergence of sequences from their common ancestor.

Better understanding of general principles that govern kinetics and thermodynamics of protein folding can help to reveal the signatures of protein sequences that are related to folding. Understanding of these “signatures” is of a great importance for creating more unambiguous approaches to fold recognition, especially in the most difficult cases of low sequence homology.

A computationally tractable lattice model of protein folding was developed recently in which folding of protein-like chains of realistic lengths (up to 175 monomers; refs. 1 and 2) has been demonstrated. Because the conformational space of such chains is comparable with that of real proteins, and the model solves its “Levinthal paradox” efficiently, there are good reasons to believe that folding mechanism(s) used by model proteins may be similar, in their essential features, to the mechanism(s) of real protein folding. The fact that the thermodynamics of model proteins is qualitatively similar to the thermodynamics of real proteins (cooperative folding transition) provides additional confidence in the validity of simple models of folding.

One important result of theoretical studies is the conjecture that protein code is multiple degenerate, i.e., that many sequences may encode a given structure (3–5). This is fully consistent with reality, which shows that very different sequences that have no obvious common evolutionary roots or functional relation fold to structurally similar conformations (evolutionary convergence). This observation poses a major challenge to bioinformatics. In spite of a very low similarity of sequences, one needs to recognize a “signal” (of physical or evolutionary origin) that calls for similarity of their tertiary structures.

A natural first step in this direction is to study lattice model proteins that represent a replica of the universe of real proteins as far as the basics of folding are concerned (2, 6, 7). It is natural, in the realm of the lattice model, to mimic protein evolution to obtain a large “database” of sequences that fold fast into the same native conformation. In the world of model proteins, we can simulate convergent evolution-like selection that presses for the generation of fast-folding sequences and creates families of model proteins that fold rapidly into the same native structure and analyze their persistent features, which for the studied model reflect the requirement of fast folding and stability for the evolved sequences. The “signals” from lattice model studies can be tested directly on sequence/structure databases of real proteins. This is the approach taken in the present paper.

First, we use a simple lattice model whereby a protein conformation is represented by a walk on a cubic lattice. Residues are located at the nodes of the lattice. The energy of a protein conformation is the sum of energies of all pairwise interactions between residues, which are not sequence neighbors:

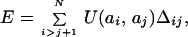where Δ_ij equals 1 if residues i and j are located in adjacent nodes of the lattice and 0; otherwise, a_i denotes the identity of residue i, and U(u, v) is the energy of interaction between residue types u and v. In this work, we use a matrix of interactions U(u, v) derived by Miyazawa and Jernigan (8). Protein folding is simulated by a dynamic Monte Carlo (MC) algorithm (9–11) at constant temperature T = 0.16. Each simulation run starts from a random chain conformation. A run is terminated when the native conformation is reached, and the number of MC steps required to reach the native conformation is counted as folding first passage time (FPT).

Evolution is simulated by a series of successive random point mutations and a selection procedure, which accepts a mutation if it makes folding to the same native state faster and rejects it otherwise (12). To eliminate dramatically decelerating mutations at minimal computational cost, we use a system of five successive filters applied as follows. Each mutant is subject to 100 MC runs. After every 20 runs, the MFPT is estimated. If the estimated MFPT exceeds the MFPT of the “wild-type” sequence by >5%, then the mutation is rejected. This system of filters effectively eliminates mutations that dramatically slow down folding and accepts the majority of neutral and accelerating mutations. As a final filter, the MFPT is evaluated over 400 runs, and if the MFPT of the mutated sequence is lower than the MFPT of the current, wild-type sequence, a mutation is accepted. Finally, after a mutation is accepted, 400 additional runs are carried out to obtain an unbiased estimate of the MFPT, which serves as a new wild-type MFPT. The MFPT can be determined only to an approximation. This factor introduces “noise” into the algorithm, which occasionally allows for the occasional acceptance of decelerating mutations. This factor allows to explore the sequence space in a systematic manner by occasionally accepting a mutation that slows down folding with subsequent compensating mutations, which is equivalent to allowing (with some probability) multiple mutation.

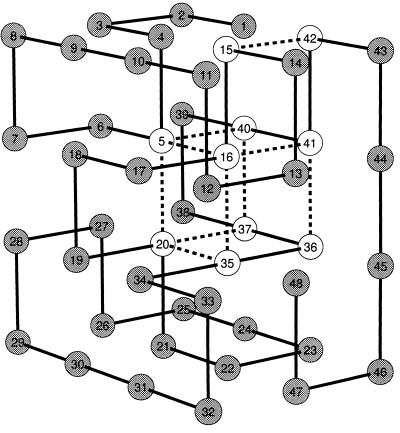
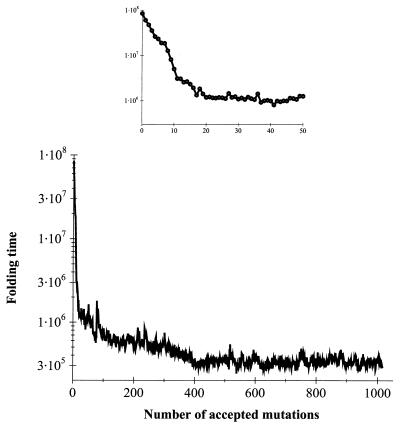
We applied the selection algorithm to generate fast-folding sequences of a 48-mer lattice model protein (Fig. 1). The initial sequence folded into its native structure (Fig. 1) in about 9 × 10⁷ MC steps (approximately as fast as the fastest random sequences; ref. 13). We performed long (10⁹ steps) equilibrium MC run to make sure that the initial sequence had the structure shown in Fig. 1 as its native state (global energy minimum). However, it was designed relatively “weakly”: its z-score (which is often used as a measure of protein stability; refs. 14 and 16) was −7.6, i.e., it was much higher than for the best designed sequences (15) (for them z ≈ −13). After ≈400 accepted mutations, the steady–state was reached with folding time fluctuating ≈3 × 10⁵ steps. (Fig. 2). For the vast majority of evolved sequences, the native structures (global energy minima) were identical to the one shown in Fig. 1. However, for a few sequences, structures that were very close (not more than one small loop rearrangement) to the native state of the original sequence (Fig. 1) were identified as global minima.

Figure 1.

The native conformation of the studied 48-mer. Broken lines show the contacts in the folding nucleus defined and determined as explained in refs. 17 and 15. “Cold” positions in which no mutations were observed over the whole steady–state part of the evolution (last 500 sequences) are shown in white.

Figure 2.

The progress of the evolutionary algorithm showing acceleration of folding (MFPT in MC steps) for the 48-mer model. (Inset) The first 50 accepted mutations.

Thus, we obtained the database of sequences whose folding rates differ more than two orders of magnitude. We aligned the evolved fast-folding sequences to seek the features that distinguish them from slow-folders. For this analysis, we took only sequences generated at the later steady–state stage of evolutionary selection. Indeed, we find that only 10 residues totally were conserved in >500-evolved fast-folding sequences (see Fig. 1). Two other residues mutated only once. Mutations at all of the other positions were frequent. What is so special about those conserved residues?

In our earlier work (15), a nucleation mechanism of folding was found for model 48-mers having the same native structure as shown in Fig. 1, but with sequences designed using the MC algorithm in sequence space, to provide high thermodynamic stability to the native conformation. Nucleation mechanism implies that certain amino acids (folding nucleus) form their contacts predominantly in the transition state. We found as shown in ref. 15 that the location of the folding nucleus was the same for sequences designed using different sets of potentials (though sequences were of course quite different), suggesting that it may be determined predominantly by the structure (15).

The striking result of the present study is that all of the residues conserved in the steady–state part of the evolution-like selection of fast folders happened to be in the positions identified in ref. 15 as the folding nucleus for that structure. The probability that the nucleus residues are conserved in evolved fast-folding sequences just by chance is negligible (≈10⁻¹⁰). Two other residues that mutated only once also belong to the nucleus.

To verify further the kinetic importance of conserved positions for evolved fast-folding sequences, we searched for their folding nucleus directly by using the method described in ref. 17. We found that the folding nucleus of evolved fast-folding sequences was identical to the folding nucleus of sequences which were designed (using the MC algorithm in sequence space) to fold into the same structure (17). Further, we applied the same method to determine the folding nucleus in the slow-folding sequence from which we started our selection. The search for the specific folding nucleus for these sequences gave negative results, i.e., no contacts were found whose appearance were necessary and sufficient for subsequent rapid descent to the native conformation. This result suggests that the original slow-folding sequences did not fold via a specific nucleus mechanism. From that, we conclude that in the present simulations, a specific nucleus mechanism evolved as a result of “Darwinian” evolutionary pressure toward fast folding.

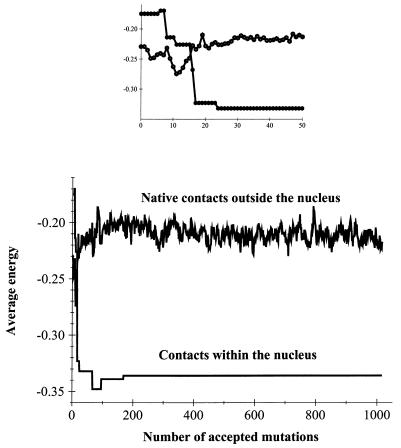
These results point out that a possible explanation for fast folding of evolved sequences, may be in the special properties of their folding nucleus. Strikingly, we observed that after the first 30 or so mutations, the average energy of a nucleus contact dropped from −0.16 to −0.34, whereas the average energy of all nonnucleus native contacts was unchanged (within the noise level of sequence fluctuations) (see Fig. 3). Thus, we found that a pronounced acceleration of folding was accompanied by dramatic stabilization of nucleus contacts (shown by broken lines in Fig. 1) whereas the overall stability did not change significantly as compared with the sequence from which we started the selection.

Figure 3.

Evolution of the average energy (per contact) of the nonnucleus native contacts and of the average energy of nucleus contacts. Nucleus contacts are shown by dashed lines in Fig. 1. (Inset) The first 50 accepted mutations.

This conclusion is in remarkable agreement with the results of the recent study by Ladurner et al. (18) who presented evidence that a small protein CI2 may have been optimized for folding rate (stability of the nucleus) rather than overall stability.

These model results bear a straightforward analogy to folding and evolution of real proteins. Each run of the evolutionary selection algorithm that starts from a new “weakly designed” sequence generates a set of fast-folding “evolutionary related” sequences, that diverged from the same root sequence, i.e., a protein family. The fact that, for a small number of sequences in the family, their native states are not identical but structurally very similar to the native state of the “root sequence” makes this analogy with protein families even closer. Different runs of selection algorithm generate different families of model proteins that have unrelated sequences but fold to the same structure, i.e., a protein superfamily. Do different families have anything in common at all? Our theory predicts a peculiar phenomenon of a “conservatism of conservatism” (CoC): amino acids belonging to the positions equivalent to the nucleus in structurally aligned superfamily are conserved within each family. We stress that amino acids of different types may be placed into nucleus positions in different families, so that amino acid alignment across the families may not reveal any special (nucleation) positions. It is the structural alignment of intrafamily conservatism profiles that may carry the signal about common nucleation in families of proteins that fold into similar three-dimensional structures.

This crucial prediction from our simulations was tested on several protein superfamilies including the classical monophosphate binding fold (CMBF) (19) and the type III repeat fold superfamilies. We will present the results for CMBF in some detail as most statistically reliable. There are 198 low homology families in the CMBF superfamily, according to the families of structurally similar proteins (FSSP) database (20) of proteins. For 98 of them, HSSP intrafamily alignments, are sufficiently large and divergent (21). Most importantly, folding of one protein from the CMBF superfamily, CheY, was studied using protein-engineering methods, and its folding transition state was characterized (22).

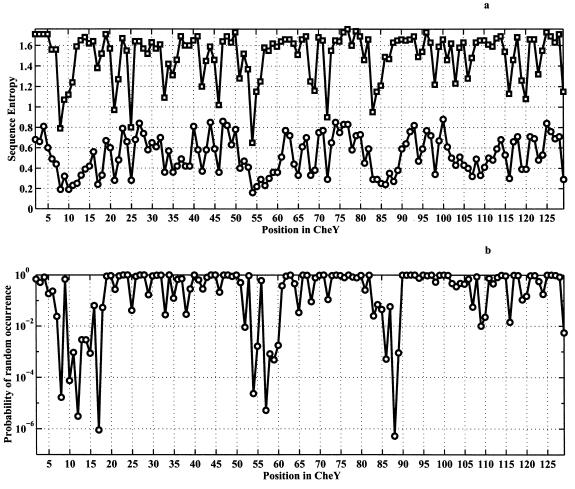
First, we used the families of structurally similar proteins database (20) to identify families of proteins that are structurally, but not by sequence, related to CheY. Next, for each family, we determined the degree of conservation (sequence entropy, see refs. 15 and 21) for each position within each family, using the homology-derived secondary structure of proteins (HSSP) database (21). Finally, the 98 intrafamily conservatism profiles were aligned according to the structural alignment between families. Fig. 4a (circles) shows the intrafamily sequence entropy at each position, averaged over all of the 98 families (in cases of gaps for some families at some positions the average is taken only over families where amino acids were present). Strikingly, we see that indeed there exist a few positions at which amino acids are conserved within each family, i.e., CoC. It is crucial to establish whether this conclusion is statistically significant. This is even more important given the fact that the structural alignments have gaps at some positions and therefore the average sequence entropy shown in Fig. 4a is calculated over a different number of occurrences for different positions. A zero hypothesis against which the obtained results must be tested is that the values of intrafamily sequence entropies are not correlated between families. If the zero hypothesis was correct, the probability distribution of average sequence entropies plotted in Fig. 4a (circles) would be Gaussian according to the Central Limit theorem. The average and dispersion of such Gaussian distribution can be evaluated in the straightforward way from the average value and dispersion of intrafamily conservatism at each position, as prescribed by the Central Limit theorem (23). It is natural to expect that the degree of intrafamily conservatism at each position in the structure should depend on its solvent accessibility, with buried positions being more likely to be conserved than exposed ones. To take this factor into account, we calculated the average value and dispersion of intrafamily conservatism, as a function of solvent accessibility, for all of the proteins in the protein data bank (using the whole HSSP database). These numbers were taken as the average value and dispersion for intrafamily conservatism at each position with a given solvent accessibility in the CMBF superfamily. Then the average and dispersion of the Gaussian probability density distribution of average conservatism was calculated for each position in CMBF superfamily according to the Central Limit theorem.

Figure 4.

Analysis for the CMBF superfamily. Ninety-eight families were used (the list is available from authors on request). All listed proteins are structurally homologous to CheY with Z > 3 and RMSD < 4A, according to the families of structurally similar proteins (FSSP) database (19). We used a coarse-grained six-letter amino-acid alphabet whereby amino acids were grouped according to their physical properties into following six classes: “aliphatic + Cys”: A, L, I, V, M, C; “aromatic”: F, Y, W, H; small nonpolar: G, P; polar: T, S, Q, N; basic: R, K; and acidic: E, D. The analysis using all 20 types of amino acids gives results that are qualitatively similar. Horizontal axes denote position in the CheY, which was taken as reference. (a, circles) CoC analysis: intrafamily sequence entropy averaged over all 98 families (excluding gaps), calculated as S_CoC(l) = ∑_F=1^M S_intra^F(l)/M. Here, the sum is taken over all of the 98 families used in the analysis, excluding gaps. Intrafamily sequence entropy for every position, for a given family, F, is calculated as follows: S_intra^F(l) = −∑_i=1⁶ p_i^F(l)log p_i^F(l), where p_i^F(l) represents the normalized frequency of observing residue of class i (i = 1–6) at position l in all homologous sequences belonging to the family F. The sum is taken over all possible residue classes. (a, squares) sequence entropy calculated across all families. To obtain this quantity, we evaluated frequencies of occurrence of amino acids of each class i at each position l for all families [p_i^across(l)] and then calculated sequence entropy for a position l as S_across(l) = −∑_i=1⁶ p_i^across(l)log p_i^across(l). (b) The probability that equal or lower S_CoC will be observed under zero hypothesis that conservatism of a residue in the structure is related primarily to its degree of buriedness.

We evaluate the statistical significance of CoC at each position in terms of the probability that the apparent value of average conservatism is just by chance, as it would have been under the zero hypothesis. The results are presented in Fig. 4b. We see that for most positions the observed average conservatism indeed can be very well explained by the zero hypothesis that intrafamily conservatism is a function of solvent accessibility only. The overall correlation coefficient between observed average conservatism and the one expected under the zero hypothesis is 0.87. However, strikingly, we find a number of positions that have pronounced, statistically significant CoC. Specifically, the following positions exhibit >99% statistically significant CoC: F8, V10, V11, D12, D13, F14, S15, M17, V54, I55, D57, W58, N59, M60, V86, A88, and E89 (here and below we provide the notation for the residues for the CMBF superfamily in terms of positions in CheY.)

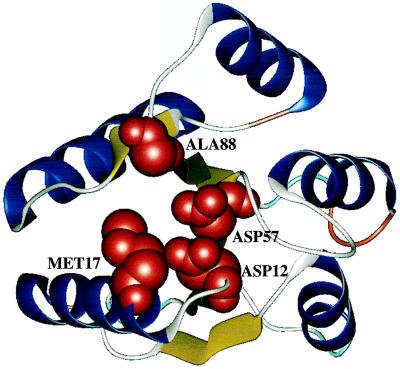
It follows from the lattice simulations that one of the reasons for CoC may be the optimization of kinetics (folding nucleus). A number of observations show that is indeed the case for the CMBF superfamily. First, the folding nucleus interpretation of CoC implies that amino acids at the positions that exhibit CoC must be in contact with each other. Indeed, F8, V10, V11, D12, D13, M17, R18, D57, M60, and V86 form a tightly packed cluster: their Cβ atoms are not farther than 7.5 Å from each other. Remarkably, D12 and D57 exhibiting very strong CoC with statistical significance close to 1 − 10⁻⁶ are in perfectly tight contact, their Cβ atoms being <4.5 Å apart. (Fig. 5) with side chains almost parallel.

Figure 5.

Ribbon diagram of the CheY structure where the four residues showing most statistically significant CoC (D12, M17, D57, A88) are shown as solid models.

Convincing evidence that CoC is related to the folding nucleus comes from the experimental study of Serrano and coworkers (22), who measured φ values for a large number of amino acids in CheY. They reported 10 positions for which the measured φ values are higher than 0.5. Of those, six (V10, V11, D12, D13, V54, and D57) belong to the group with >99% statistically significant CoC. Of the remaining amino acids from this group, the φ value for I55 is also high (0.3), and for F14 it is reported to be −0.03. However, this number is not very reliable because the change in free energy upon F14A mutation is very small (0.8 kcal/M). A88, which is located in the interface between the β strand and a long loop, does not belong to the nucleus cluster (it contacts only K109). It is possible that A88 plays an important role in defining the so-called “topology” of the structure, being one of the important bending residues (24). φ values for the remaining positions of the group with higher than 99% significant CoC (F8, S15, M17, W58, N59, M60, V86, E89, and K109) were not reported in ref. 21. Four amino acids not exhibiting high CoC have high φ value [residues V33, A36, D38 (D38G mutation, ref. 22), and A42]. However, V33 and D38 also exhibit some CoC (with 95% statistical significance). A36 and A42 do not show significant CoC; these two positions may belong to “an extended folding nucleus”, which is likely to vary from family to family and therefore may not be detected by the CoC analysis. The probability that 6 of 10 nucleus residues belong to the set of the 17 most significant CoC positions by chance is close to 10⁻³.

An alternative explanation of the observed statistically significant CoC may be along the lines of the “profile” analysis proposed in ref. 14, which suggests that there may be structure-dependent, self-consistent “one-particle” potential which would, in all families, in certain positions, bias evolution toward certain types of amino acids. If such a factor exists, then simple alignment across families would reveal the amino acid preferences. The plot of conservatism across the families is presented in Fig. 4a (squares). There are only two positions in the CMBF superfamily in which amino acids noticeably are conserved across the families (F8, V54). These positions are central to the hydrophobic core of the protein. There is a noticeable but not very high CoC at those two positions. We see that environment factors, such as accessibility, certainly play a role in determining amino acid conservatism, but these factors alone cannot explain the observed strong CoC in the CMBF superfamily. Another example is the superfamily of proteins having the structure of type III repeats of fibronectin. A protein from this superfamily, tensacin was shown to fold via a simple two-state mechanism (25, 26).

We considered 47 families having type III repeat fold (20). A few positions exhibited strong CoC with statistical significance exceeding 99%. Those are A17, V19, W21, L33, V69, L71, A83, and F87 (notation of amino acids as in tenascin, 1ten is used), which are in close contact with each other. An interesting feature of the nucleus for that superfamily is that in many families it contains 100% conserved Trp. However, the location of the 100% conserved Trp in the nucleus may vary from family to family because of peculiar “cyclic permutations”: the 100% invariant Trp appears in position 21 of tenascin, but in other type III structures, it appears in other possible nucleation positions; e.g., in both CD8 and 1BEC, it is in the position equivalent to L33 of tenascin (W35 in CD8 and W32 in 1bec); whereas in the second domain of cd4, it appears as the structural equivalent of V69 in tenascin (W157 in the second domain of cd4). Sometimes strong nucleus contacts in type III repeat structure are supplemented/replaced by a disulfide bond (e.g., the nucleus contact W21-L71 is replaced by disulfide C23-C92 in 1bec or by C23-C94 in cd8).

It is important to note that the Mg²⁺ binding site of CheY involves D12, D13, and D57 (27), and D57 is phosphorylated in the process of signal transduction by CheY (27). At the same time, those residues belong to the folding nucleus as revealed by experiments (22) and CoC analysis. Such a dual role of these residues in CheY explains why the similarly charged amino acids were placed in the folding nucleus of CheY (mutation to A of either D12 or D57 stabilizes the protein and makes it fold faster; ref. 22). This fact may call into question the conclusions about the connection between CoC and nucleation. However, not all of the members of the CMBF superfamily have their active site at the same position: e.g., in p21ras, the Mg²⁺ binding site is located at the different site. However, interestingly, the putative nucleation sites in p21ras, G10, G15, and V81, corresponding to D12, M17, and D57 in CheY are used to conformationally constrain the P-loop, which participates in the binding of the phosphate (28). It is important to note that residues that are involved directly in Mg²⁺ or phosphate binding in kinases (e.g., S17 and D57 in p21Ras and R19 and E35 in CheY) do not show any CoC (Fig. 4). Additionally, we note that, although strong CoC was found in the type III repeat superfamily, it is not related to function of those proteins that usually participate in protein–protein interactions (receptors, antibodies, etc.).

Recently, Ptitsyn (29) analyzes families of CytC proteins and came to the similar conclusions that there may be a number of residues that are conserved for folding, rather than functional, reasons. A possible explanation for the correlation between the active site and folding nucleus in CheY superfamily may come from the observation that vast majority of proteins from that superfamily bind a cofactor (in contrast to type III repeat superfamily). If strong binding of a cofactor is important, then rigid fixation of coordinating amino acids in space by the structure of the protein may be crucial. In that case, folding nucleus may indeed serve as an ideal location for the active site. Indeed, folding nucleus generally appears to be most protected from local unfolding fluctuations (see Fig. 8 of ref. 17), and that is the case for CheY (30).

The results and analysis presented here point out that, for each protein structure, there is a small number of positions that are most crucial for fast folding into that structure. Protein sequences that fold fast into that structure may have evolved by placing such amino acids into those strategic nucleus positions that provide stabilization of the nucleus.

ABBREVIATIONS

CMBF

classical monophosphate binding fold

CoC

conservatism of conservatism

MC

Monte Carlo

FPT

first passage time

MFPT

mean FPT