Summary
This article develops a probability distribution for the lead time in periodic cancer screening examinations. The general aim is to allow statistical inference for a screening program's lead time, the length of time the diagnosis is advanced by screening. The program's lead time is distributed as a mixture of a point mass and a piecewise continuous distribution. Simulation studies using the HIP (Health Insurance Plan for Greater New York) study's data provide estimates of different characteristics of a screening program under different screening frequencies. The components of this mixture represent two aspects of screening's benefit, namely, a reduction in the number of interval cases and the extent by which screening advanced the age of diagnosis. We present estimates of these two measures for participants in a breast cancer screening program. We also provide the mean, mode, variance, and density curve of the program's lead time. The model can provide policy makers with important information regarding the screening period, frequency, and the endpoints that may serve as surrogates for the benefit to women who take part in a periodic screening program. Though the study focuses on breast cancer screening, it is also applicable to other kinds of chronic disease.
Keywords: Breast cancer, Early detection, Lead time, Periodic screening exams, Sensitivity, Sojourn time, Transition probability
1. Introduction
A potentially effective way to increase the cure rate or prolong survival of cancer patients is to detect the disease early and treat it at an early state. The primary technique for implementing early detection is periodic screening examinations, by which the disease may be found before the onset of symptoms. According to a recent report (NIH, 2000), breast cancer is the most common form of cancer among women in the United States and the second leading cause of cancer deaths among women. There is great interest in studying the relative contribution of chemotherapy and screening on the reduction of breast cancer mortality seen in the United States (Berry et al., 2005).
The past four decades have seen many large randomized breast cancer screening trials, as well as some observational studies. Accompanying the increased effort at early detection, questions have arisen concerning the efficient design of a periodic cancer screening program, such as at what age to initiate screening programs and the best exam frequencies (Eddy, 1980). Optimal design of screening trials is hampered, however, because the theory of screening has not been fully developed to date. In particular, there has been a major controversy over the benefits of mammography to detect breast cancer for women in their 40s (NIH, 1997). Very often the recommended frequency in a periodic screening program is arbitrary.
The effectiveness of a screening program directly depends on the availability of effective therapy and improved outcome if one receives treatment for the disease in its earliest stages of development. When evaluating the effectiveness of a screening program, one should account for the fact that the age at diagnosis is earlier if the disease is detected by screening rather than by the onset of clinical symptoms. The difference between the age of diagnosis with screening and the future onset of clinical disease without screening is called the lead time. Even in the absence of effective therapy, screening will appear to lengthen the time from diagnosis until death. If one does not account for the lead time when analyzing the benefit of screening, then one's inference is subject to lead-time bias.
We assume the commonly followed disease progression model (Zelen and Feinleib, 1969). According to this model, the disease develops by progressing through three states, denoted by S0 → Sp → Sc. Respectively, these states refer to the disease-free state; the preclinical disease state, in which an asymptomatic individual unknowingly has disease that a screening exam can detect; and the disease state at which the disease manifests itself in clinical symptoms. We allow for the sensitivity of the screening exam to be less than 100%, so that an exam might yield a false-negative call. We do not consider false positives in this model.
If a person enters the preclinical state (Sp) at age t1 and becomes clinically incident (Sc) later at age t2, then (t2 − t1) is the sojourn time in the preclinical state. If, however, this person undergoes a screening exam at time t within the time interval (t1, t2) and cancer is diagnosed, then the length of time (t2 − t) is the person's lead time. This is illustrated in Figure 1.
Figure 1.

Illustration of disease development and lead time.
As mentioned earlier, the rationale behind screening is that early detection and treatment hopefully lead to a better prognosis. For a particular case detected by the screening exam, the lead time is, of course, unobservable. The distribution of the lead time depends on the distributions of the sojourn time, the sensitivity, and the transition probability into the preclinical state. Our model may be an aid in characterizing the effectiveness of screening programs and determining the optimal interval of periodic screenings.
Many researchers have proposed methods to infer lead time among participants in a screening program, whether within a randomized study or not. Prorok (1982) made a major contribution by deriving the conditional probability distribution of the lead time, given detection at the ith screening exam. He then applied his model in simulations to study the properties of the lead time, assuming different sojourn time distributions. He noted that when one increases the number of exams, keeping the between-exam interval fixed, the local lead time properties appeared to stop changing after four or five screening exams in his examples. The stabilization of the local lead-time properties suggested a stopping rule for comparative studies, in that further screening exams will not yield more information about the benefit of screening versus no screening. His work, however, has limited applicability. He considered only screen-detected cases, ignoring interval cases for whom the lead time is zero. His results apply to cases who are screen detected at the ith screening exam. He did not estimate the whole proportion of cases who were not detected by the periodic screening.
Straatman, Peer, and Verbeek (1997) estimated the mean lead time among participants in a screening program, applying ideas similar to Prorok (1982). They assumed an exponential distribution for the sojourn time in the preclinical state. Because of the memoryless nature of the exponential distribution, the lead time had the same exponential distribution as the sojourn time in their models. Walter and Day (1983) considered other distributions, such as a lognormal distribution and a step-function for the sojourn time, in addition to an exponential distribution. They derived a formula to estimate the mean lead time. Other publications (Kafadar and Prorok, 1994, 1996, 2003; Xu and Prorok 1995; Kafadar, Prorok, and Smith, 1998; Xu, Fagerstorm, and Prorok, 1999) have provided estimates of the mean and variance of the lead time. The main focus of these papers is on screen-detected cases and on the survival benefits, rather than on the inference of the lead time.
In this article, we derive the exact probability distribution of the lead time for the whole cohort taking part in the screening program, including screen-detected cases and interval-incident cases. Our model includes the result of Prorok (1982) as a special case. Hence, our model allows estimation of the proportion of patients whose lead time is zero and the proportion that truly benefits from the program. We apply our methodology to a periodic screening program that involves at least 10 screening exams (e.g., for women from 50 to 80 years old, who will take annual exams) to get information on the benefits of the screening program. This inference will help determine how a long-term screening program may contribute to public health.
The remainder of the article is organized as follows. In Section 2, we set up the probability model and derive the distribution for the lead time for the whole cohort. We also derive the lead-time distribution for the screen-detected cases, which will lead to the same result as in the formula (2) in Prorok (1982). In Section 3, we present some simulation results for different screening intervals and apply our method to the HIP data using Bayesian inference. We conclude with a discussion in Section 4.
2. Methods
Consider a cohort of initially asymptomatic individuals who enroll in a screening program. Let β(t) be the sensitivity of the screening modality; that is, the probability that the screening exam is positive conditional on the individual being in the preclinical state, where t is the individual's age at the screening exam. Define w(t) dt as the probability of a transition from S0 to Sp during (t, t + dt). Let q(·) be the probability density function of the sojourn time in Sp, and let be the survivor function of the sojourn time in the preclinical state Sp. Throughout this article, the time variable t represents the participating individual's age.
2.1 Lead-Time Distribution for Potential Patients
When we consider the concept of the lead time (i.e., the time gained because of early detection by screening), we assume that the person will develop symptomatic cancer. Therefore, the lead time distribution is, in fact, a conditional distribution given that someone will ultimately develop clinical disease before death. We will study the case of an initially asymptomatic woman with no history of cancer who goes through a series of periodic screening exams and develops breast cancer later in her life. Define D as a binary random variable, with D = 1 indicating development of clinical disease and D = 0 indicating the absence of the clinical disease before death.
Denote as L the lead time for individuals detected on screening. We consider the lead time to be 0 for individuals whose disease is not detected by the screening exam but who develop clinical symptoms. The distribution of the lead time for a woman will be a mixture of a point mass at zero and the density of a piecewise continuous, positive random variable. That is, the distribution of the lead time is a mixture of the conditional probability P(L = 0 | D = 1) and the conditional density function fL(z | D = 1), for ∀0 < z < (T − t0). Here, T represents the span of the human life, and t0 is the woman's age at her initial screening exam. One might consider treating T as a random variable and allow for competing causes of death when modeling T. We implicitly condition on a fixed upper bound, T, in our model and do not pursue the more complicated model in this article.
We need to calculate several probabilities to compute these conditional probabilities explicitly. In particular, we need P(D = 1), the probability of developing breast cancer during one's lifetime after age t0, the joint probability P(L = 0, D = 1), and the joint probability density function fL(z, D = 1). We assume that the individual is asymptomatic at age t0.
The probability of developing breast cancer after the initial screening exam (at age t0) is the following. Suppose a woman is incident with clinical disease at age t ∈ (t0, T). Then, one must move from S0 to Sp before age t, say at age x. The sojourn time in the preclinical state is (t − x). Hence,
| (1) |
We illustrate the key ideas underlying the formulation of P(L = 0, D = 1) and fL(z, D = 1) using as an example a periodic screening program with two screening exams. At the end of this section, we give the general results for the distribution of the lead time for any number of examinations.
Consider a cohort of initially asymptomatic women who are aged t0 (usually t0 ≥ 40) at study entry and who will develop breast cancer at some time before dying. The study offered two screening exams, one at age t0 and the other at age t1(>t0).
If a woman goes through the two screening exams without being detected, then her lead time will be zero, and she will not benefit from the screening program at all. We now calculate this probability. Define t−1 ≡ 0 and the first screening interval as (t0, t1), and the second screening interval as (t1, T). Correspondingly, the ith generation of women consists of those who enter Sp during the ith screening interval (i = 1, 2). The 0th generation includes all women who enter Sp before t0, the age at the initial screening exam. A participant's lead time is zero if and only if she is diagnosed in the clinical state Sc within the intervals (t0, t1) or (t1, T); that is, if she is an interval case. Hence,
where I2,1 is the probability of being an interval case in (t0, t1), and I2,2 is the probability of being an interval case in (t1, T). The first index reminds us that there are two screening exams in the program. For a woman to be an incident case in (t0, t1), either she belongs to the 0th generation (i.e., she entered Sp before t0) and has a false-negative screening result at t0, or she belongs to the first generation (i.e., entered Sp in (t0, t1)). Hence,
where βi = β(ti) is the sensitivity at age ti. Similarly, we obtain
The lead time will be greater than zero for the screen-detected cases. These are the people who might truly benefit from periodic screening exams, because their disease is detected and treated at an early stage.
We derive the probability density function in the following way. We partition the support of z into (0, T − t1] and (T − t1, T − t0]. When the lead time z ∈ (0, T − t1], there are two possibilities: either this person is detected at t0 and would have entered the clinical state Sc at age tc = t0 + z without the screening exam at t0; or she is detected at t1 and would have entered Sc at age t1 + z without screening. See Figure 2, where x represents onset of the Sp, and tc indicates the age at the transition into Sc.
Figure 2.
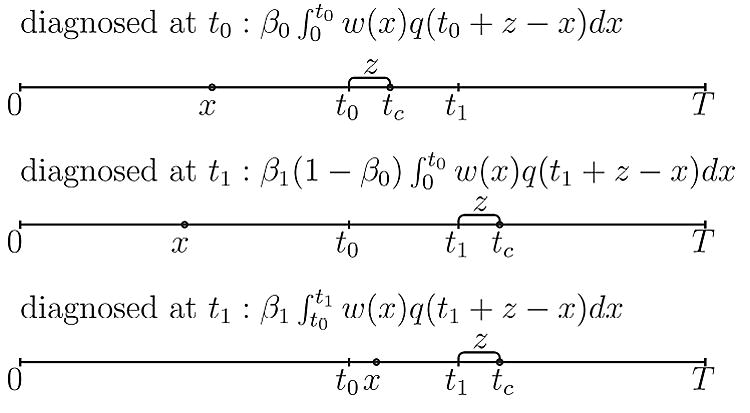
Calculation of the joint density fL(z, D = 1) with 2 screening exams.
Therefore, the joint density is
When the lead time z ∈(T − t1, T − t0], there is only one possibility: she must have been detected at t0 because her lifetime is bounded by T. Hence
Combining the above results, the distribution for the lead time is
| (2) |
| (3) |
The validity of this mixed or semicontinuous distribution can be verified by
| (4) |
Now we generalize this result to any number of screening exams. Assume the protocol calls for K-ordered screening examinations that occur at ages t0 < t1 < · · · < tK−1. The ith generation of women are those who enter Sp between the ith and the (i + 1)th screening exams (i.e., between ti−1 and ti), i = 1, 2, … , K − 1. The 0th generation includes all who enter Sp before the initial screening exam. We let t−1 ≡ 0, and tK = T. In order to calculate the distribution, we need to calculate the joint probability P(L = 0, D = 1) and the joint probability density function fL(z, D = 1).
The lead time is zero if and only if an individual is an interval case. Let IK,i denote the probability of being an interval case in the ith interval (ti−1, ti) in a sequence of K-screening exams. Then
where
| (5) |
It can be proved by mathematical induction that, if the sensitivity is less than 1, then for any fixed sequence t0 < t1 < · · · < tK−1 < T,
In other words, more screening reduces the probability that the lead time equals zero among women who would go on to develop cancer.
For the cases whose lead times are greater than zero, we calculate the joint probability density function fL(z, D = 1), where z ∈(0, T − t0]. When T − t1 < z ≤ T − t0, detection must have occurred at t0. In general, when T − tj < z ≤ T − tj−1, j = 2, 3, … , K, one was screen detected at ti, i = 0, … , j − 1. Thus, with T − tj < z ≤ T − tj−1, j = 2, 3, … , K (i.e., tc = ti + z < T, i = 0, … , j − 1),
| (6) |
When j = 1 and T − t1 < z ≤ T − t0 (i.e., one must have been detected at t0), the above formula becomes
| (7) |
Again, the validity of this probability distribution can be verified by
where P(D = 1) is given in equation (1). Hence, the lead-time distribution is a mixture of a point mass and a piecewise continuous distribution. The probability density function of the lead time is not continuous at the points (T −tj), j = 1, … , K − 1, which can be verified easily from (6) and (7).
2.2 Lead-Time Distribution for the Screening-Detected Cases
Prorok (1982) derived the probability distribution for the lead time if one were diagnosed at the ith screening exam. The derivation used properties of forward and backward recurrence times from renewal process theory. He did not take into consideration the interval cases, whose lead time is zero. We will obtain the same result as in Prorok (1982) by conditioning on detection by the ith screening exam.
Assume K exams and define events:
The (conditional) probability density function for the lead time given Aj is
| (8) |
The numerator is
| (9) |
The denominator is
| (10) |
This is exactly the same result in the formula (2) in Prorok (1982) (which he called the local lead-time p.d.f. [probability density function]) without the use of forward and backward recurrence times.
3. Application to the HIP Study
According to the results in Section 2, it is clear that the lead-time distribution depends on the sensitivity β(·), the transition probability w(·), and the sojourn time distribution in the preclinical state q(·). Hence, accurate estimation of these parameters is essential in the estimation of the lead-time distribution.
We applied our method to the Health Insurance Plan for Greater New York (HIP) data (Shapiro et al., 1988). Wu, Rosner, and Broemeling (2005) estimated the age-dependent sensitivity β (t), the transition probability w(t), and the sojourn time distribution q(·) from the HIP study group data. They characterized the sensitivity β(t) as a function of age t using a logistic model,
where t̄. is the average age at entry in the study group. The transition density function was
which is the probability density function of a lognormal(μ, σ2) multiplied by 20% (the upper limit corresponding to a lifetime risk). The log-logistic distribution was adopted as the distribution for the sojourn time in the preclinical state, so that the survivor function and the hazard function are, respectively,
where x is the sojourn time in the state of Sp. The density is q(x) = h(x) Q(x). (See section 2.2 in Wu et al. [2005] for details.)
The unknown parameters in the above model are θ = (b0, b1, μ, σ2, κ, ρ). Let H represent the HIP data. The likelihood function L(θ | H) was derived in section 2.1 in Wu et al. (2005). Let π(θ) be the prior distribution of θ. The posterior distribution is
We used Markov chain Monte Carlo (MCMC) to draw posterior samples from f(θ | H). The MCMC sample size was 2000 draws from two parallel chains with overdispersed starting values (Wu et al., 2005).
Given the HIP data, the posterior predictive distribution of the lead time can be estimated as follows:
| (11) |
| (12) |
| (13) |
| (14) |
where is a random sample drawn from the posterior distribution f(θ | H). The last step is Monte Carlo simulation (see Gilks, Richardson, and Spiegelhalter, 1996, p. 4).
We combined our earlier results with the current model to make inference in the case of a program consisting of periodic screening exams for women aged 50–80 years. We examined various screening intervals. The results are for both screen-detected and interval cases, that is, inference concerns the program's lead time that includes the point mass at zero and the piecewise continuous density function.
Table 1 summarizes the Bayesian posterior inference. The time interval Δ between screens was 6, 9, 12, 18, and 24 months within ages 50 (t0) and 80 years (T). The density curves for the lead time are shown in Figure 3 for different screening intervals.
Table 1.
Application for the HIP data using Bayesian posterior samples
| Δa | Number of screenings | P1b | 1 − P1 | Mode | Meanc | SD |
|---|---|---|---|---|---|---|
| 6 months | 60 | 8.95 | 91.05 | 0.50 | 1.418 | 2.111 |
| 9 months | 45 | 16.04 | 83.96 | 0.38 | 1.282 | 2.075 |
| 12 months | 30 | 23.37 | 76.63 | 0.30 | 1.168 | 2.040 |
| 18 months | 20 | 36.52 | 63.48 | 0.16 | 0.988 | 1.969 |
| 24 months | 15 | 46.68 | 53.32 | 0.08 | 0.856 | 1.901 |
Δ = ti − ti−1 is the time interval between screens.
P1 = P(L = 0 | D = 1) is the probability of “no benefit.” Both columns 3 and 4 are in percentages. Columns 5–7 are in years.
The mean is E(L | D = 1), which equals to P(L > 0 | D = 1)E(L | L > 0, D = 1), the fraction detected on screening multiplied by the benefit of detection.
The mode, the mean, and the standard deviation (SD) in the table are for the mixture distribution.
Figure 3.
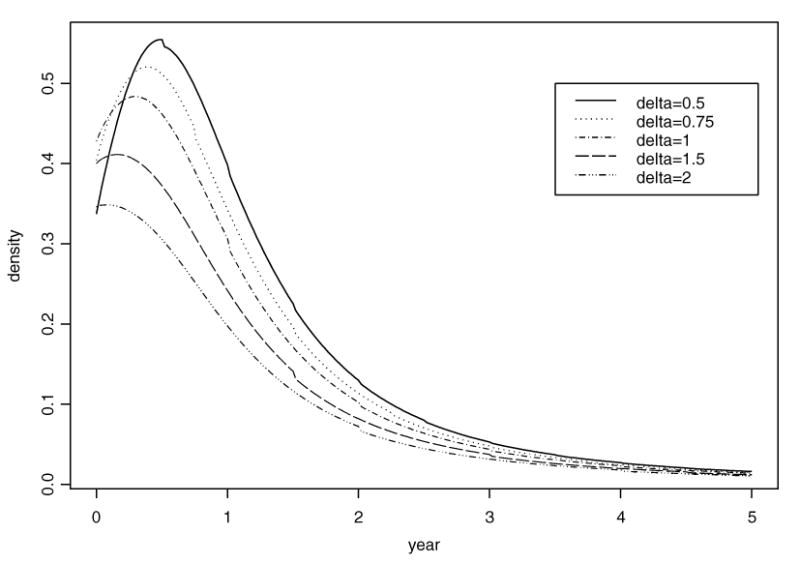
Density curve for the lead time in the HIP study using Bayesian inference.
From these results, we see that if a woman begins annual screening (i.e., Δ = 12 months) when she is 50 years old and continues until she reaches 80, then there is a 23.37% chance that she will not benefit from early detection by the screening program if she develops breast cancer during those 30 years. Her chance of no benefit from the screening program decreases to 8.95% if the exams are 6 months apart.
Table 1 shows that the mean lead-time increases as the screening time interval decreases. In other words, more screening exams will contribute to a longer lead time, which would translate to treatment of the disease at an earlier stage and, potentially improved prognosis. The increase in the mean lead time is partly due to the smaller point mass for zero lead time when screening exams are closer together.
The standard error of the lead time decreases as the time between screening exams increases. Table 1 also reveals that the standard deviation for the program's lead time is larger than the mean lead time. In the table, the largest mode is 0.5 years (6 months), corresponding to screening exams every 6 months. With annual exams, the mode value for the lead time is 0.3 years (3.6 months).
4. Discussion
We provided the exact probability distribution for the lead time in a periodic screening scenario. We consider the distribution of the lead time as a mixture of a point mass at zero and a piecewise continuous density function. The mixture formulation considers all cases among participants in a screening program, namely, those diagnosed by screening and interval cases. Our model includes the local lead-time distribution given in Prorok (1982) as a special case.
Our model characterizes two aspects of a screening program's benefit. One aspect is the proportion of interval cases among the program's participants (that is, the probability assigned to the point mass at zero). The second aspect is the length of time by which screening advances the age of diagnosis of cancer. This length of time will hopefully lead to treatment of disease in earlier stages of development and a better prognosis. The P(L = 0 | D = 1), the fraction of participants who will develop clinical cancer and diagnosed as interval case, was used in the Appendix A of Baker et al. (2006). The other measure is the mean lead time E(L | D = 1), which is equivalent to P(L > 0 | D = 1)E(L | L > 0, D = 1), that is, the fraction of persons detected on screening times the benefit of detection. This endpoint was used in Dwyer et al. (1983) in their study of scheduling follow-up exams for cancer patients after the initial detection of cancer. The ultimate goal of a screening program in cancer is to reduce cancer mortality. Reduction in cancer mortality is discussed in Baker et al. (2003), Flanders and Longini (1990) and Chen et al. (1997) in the context of evaluating periodic screening.
Our model contributes to the study of a screening program in other ways. First, the model allows inference about the lead-time distribution for the whole cohort who will develop breast cancer in their lifetime. Previous work on the lead time focused on screen-detected cases only. Second, predictive inference can extend easily to any number of screening exams with our model. Thus, one can use the model to infer outcome measures that relate to different scenarios of periodic screening, such as the proportion of people who stand to benefit from various screening programs. One can thus use our model to evaluate and compare the characteristics of different possible screening programs. For example, the model can provide answers to questions, such as what may be the outcomes of periodic screening exams for a woman in her 50s or 60s? How do these outcomes change as the frequency of screening exams changes (e.g., screening every 6, 12, or 24 months)? What is the probability that a woman's cancer will be detected early if she has cancer? How does changing the screening program affect the lead-time distribution? Our model showed that the mean lead time increases as the interval between screening exams becomes shorter.
When evaluating a screening program, one has to consider benefits and costs. In the case of a cancer screening program, for example, the benefit is reduction in cancer mortality. The costs may include invasive biopsies that are not necessary, possible side effects of the screening modality or follow-up action, needless anxiety, time, and financial cost. In addition, more screening exams may lead to more false-positive results, which we have not yet incorporated into the model. Any decision-theoretic approach should account for false-positive and false-negative screening errors and consequences of these assessments.
We have not incorporated information on mortality after detection into the model. The effect of a screening program on disease-specific mortality is a very important consideration. Although one might incorporate a screening-and-subsequent-treatment effect in the model, it would be complex and would require additional assumptions. Including mortality would also require long-term follow-up, which is not necessary to apply in our approach.
Zelen (1993) proposed a utility function to find the optimal scheduling for (n + 1) exams by assigning different weights to probabilities of screen-detected cases and interval-incident cases. His simulation was based on the assumptions that the sensitivity is independent of age, and the sojourn time is exponentially distributed.
In Prorok (1982), the local lead-time distribution stabilized after four or five exams when β = 0.9, w = 0.002, or 0.004, and the screening interval was 1 year. In his simulations, he assumed that the local lead-time distribution has domain (0, ∞). In our simulations, if we fix β, w, and the screening interval as Prorok did, the probability P(L > 0 | D = 1) (equivalently, P(L = 0 | D = 1)) will also stabilize after four or five exams. Our lead time has finite support (0, T − t0); however, the mean and the standard error increase as T increases. When the sensitivity and the transition probability are both age dependent as in our model, an asymptotic distribution for the lead time does not exist within the realm of realistic scenarios.
Further work to individualizing risk assessment would include considering other covariates besides age. Each woman probably has a different risk of developing breast cancer during her lifetime. If she has a close relative who had breast cancer, then her risk of developing breast cancer increases. This risk is reflected in the w(t) in our model, which could be modeled with covariates to individualize risk assessment.
Our model has conditioned on the event that the person will ultimately develop clinical disease (e.g., symptomatic breast cancer). This conditioning effectively removes from consideration cancers that never reach the clinical state. A further improvement to the model would incorporate the competing risk of death from other causes. Parmigiani (2002) discusses a decision model based on transitions between health states. His approach allows one to model the transition intensities, thus allowing for the competing risk of death before the transition to clinical disease. By incorporating the possibility of death from a cause other than breast cancer, for example, the inference can extend to provide information about how a screening program may affect a woman's risk of dying from breast cancer or even her risk of a diagnosis of breast cancer during her lifetime. We are working on this model.
5. Supplementary Materials
The 2000 posterior samples referenced in Section 3 are available under the Paper Information link at the Biometrics web site http://www.tibs.org/biometrics.
Acknowledgments
We thank an anonymous reviewer for helpful comments that improved the article. This research was partially supported by the National Institutes of Health grant CA-115012. The third author was partially supported by the National Cancer Institute grant CA-093459.
References
- Baker SG, Erwin D, Kramer BS, Prorok PC. Using observational data to estimate an upper bound on the reduction in cancer mortality due to periodic screening. BMC Medical Research Methodology. 2003;3:4. doi: 10.1186/1471-2288-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker SG, Kramer BS, McIntosh M, Patterson BH, Shyr Y, Skates S. Evaluating markers for the early detection of cancer: Overview of study designs and methods. Clinical Trials. 2006;3:43–56. doi: 10.1191/1740774506cn130oa. [DOI] [PubMed] [Google Scholar]
- Berry DA, Cronin KA, Plevritis SK, Fryback DG, Clarke L, Zelen M, Mandelblatt JS, Yakovlev AY, Habbema JDF, Feuer E. Effect of screening and adjuvant therapy on mortality from breast cancer. New England Journal of Medicine. 2005;353:1784–1792. doi: 10.1056/NEJMoa050518. [DOI] [PubMed] [Google Scholar]
- Chen HH, Duffy SW, Tabar L, Day NE. Markov chain models for progression of breast cancer part II: Prediction of outcomes for different screening regimes. Journal of Epidemiology and Biostatistics. 1997;2:25–35. [Google Scholar]
- Dwyer AJ, Prewitt JMS, Ecker JG, Plunkett J. Use of the hazard rate to schedule follow-up exams efficiently: An optimization approach to patient management. Medical Decision Making. 1983;3:229–244. doi: 10.1177/0272989X8300300211. [DOI] [PubMed] [Google Scholar]
- Eddy DM. Screening for Cancer: Theory, Analysis and Design. Englewood Cliffs, New Jersey: Prentice Hall; 1980. [Google Scholar]
- Flanders WD, Longini IM. Estimating benefits of screening from observational cohort studies. Statistics in Medicine. 1990;9:969–980. doi: 10.1002/sim.4780090812. [DOI] [PubMed] [Google Scholar]
- Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. Boca Raton, Florida: Chapman & Hall/CRC; 1996. [Google Scholar]
- Kafadar K, Prorok PC. A data-analytic approach for estimating lead time and screening benefit based on survival curves in randomized cancer screening trials. Statistics in Medicine. 1994;13:569–586. doi: 10.1002/sim.4780130519. [DOI] [PubMed] [Google Scholar]
- Kafadar K, Prorok PC. Computer simulation of randomized cancer screening trials to compare methods of estimating lead time and benefit time. Computational Statistics and Data Analysis. 1996;23:263–291. [Google Scholar]
- Kafadar K, Prorok PC. Alternative definitions of comparable case groups and estimates of lead time and benefit time in randomized cancer screening trials. Statistics in Medicine. 2003;22:83–111. doi: 10.1002/sim.1331. [DOI] [PubMed] [Google Scholar]
- Kafadar K, Prorok PC, Smith PJ. An estimate of the variance of estimators for lead time and screening benefit time in randomized cancer screening trials. Biometrical Journal. 1998;40:801–821. [Google Scholar]
- National Institutes of Health. NIH Publication No 103. Bethesda, Maryland: 1997. Jan 21–23, 1997. Breast cancer screening for women ages 40–49. [Google Scholar]
- National Institutes of Health. NIH Publication No 00-1556. Bethesda, Maryland: 2000. Dec 12, 2000. What you need to know about breast cancer. [Google Scholar]
- Parmigiani G. Modeling in Medical Decision Making: A Bayesian Approach. Chichester, UK: Wiley; 2002. [Google Scholar]
- Prorok PC. Bounded recurrence times and lead time in the design of a repetitive screening program. Journal of Applied Probability. 1982;19:10–19. [Google Scholar]
- Shapiro S, Venet W, Strax P, Venet L. Periodic Screening for Breast Cancer. The Health Insurance Plan Project and its Sequelae, 1963–1986. Baltimore, Maryland: The Johns Hopkins University Press; 1988. [Google Scholar]
- Straatman H, Peer PGM, Verbeek ALM. Estimating lead time and sensitivity in a screening program without estimating the incidence in the screened group. Biometrics. 1997;53:217–229. [PubMed] [Google Scholar]
- Walter SD, Day NE. Estimation of the duration of a preclinical disease state using screening data. American Journal of Epidemiology. 1983;118:856–886. doi: 10.1093/oxfordjournals.aje.a113705. [DOI] [PubMed] [Google Scholar]
- Wu D, Rosner G, Broemeling L. MLE and Bayesian inference of age-dependent sensitivity and transition probability in periodic screening. Biometrics. 2005;61:1056–1063. doi: 10.1111/j.1541-0420.2005.00361.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Prorok PC. Non-parametric estimation of the post-lead-time survival distribution of screen-detected cancer cases. Statistics in Medicine. 1995;14:2715–2725. doi: 10.1002/sim.4780142410. [DOI] [PubMed] [Google Scholar]
- Xu J, Fagerstrom RM, Prorok PC. Estimation of post-lead-time survival under dependence between lead-time and post-lead-time survival. Statistics in Medicine. 1999;18:155–162. doi: 10.1002/(sici)1097-0258(19990130)18:2<155::aid-sim12>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Zelen M. Using observational data to estimate an upper bound on the reduction in cancer mortality due to periodic screening. Biometrika. 1993;80:279–293. doi: 10.1186/1471-2288-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelen M, Feinleib M. On the theory of screening for chronic diseases. Biometrika. 1969;56:601–614. [Google Scholar]


