Human and Automated Detection of High-Frequency Oscillations in Clinical Intracranial EEG Recordings

Abstract

Objective

Recent studies indicate that pathologic high-frequency oscillations (HFOs) are signatures of epileptogenic brain. Automated tools are required to characterize these events. We present a new algorithm tuned to detect HFOs from 30 – 85 Hz, and validate it against human expert electroencephalographers.

Methods

We randomly selected 28 3-minute single-channel epochs of intracranial EEG (IEEG) from two patients. Three human reviewers and three automated detectors marked all records to identify candidate HFOs. Subsequently, human reviewers verified all markings.

Results

A total of 1,330 events were collectively identified. The new method presented here achieved 89.7% accuracy against a consensus set of human expert markings. A one-way ANOVA determined no difference between the mean F-measures of the human reviewers and automated algorithm. Human Kappa statistics (mean κ = 0.38) demonstrated marginal identification consistency, primarily due to false negative errors.

Conclusions

We present an HFO detector that improves upon existing algorithms, and performs as well as human experts on our test data set. Validation of detector performance must be compared to more than one expert because of interrater variability.

Significance

This algorithm will be useful for analyzing large EEG databases to determine the pathophysiological significance of HFO events in human epileptic networks.

Introduction

The human electroencephalogram (EEG) is composed of a wide range of neuronal oscillations with spectral activity extending well beyond what was first reported by Berger (Berger, 1929), and what is commonly used in clinical practice and pre-surgical evaluation (0.1 – 40 Hz) (Sperling, 1986; Niedermeyer, 1987; Schiller et al., 1998; Quesney, 2000; Spencer and Lee, 2000). Recent studies using pre-surgical intracranial EEG (IEEG) recordings report gamma oscillations (∼ 40 – 80 Hz) (Buzsaki, 1996; Buzsaki, 1998; Bragin et al., 1999a; Grenier et al., 2003a) and ripple oscillations (∼80 – 200 Hz) that may be important for learning and memory consolidation (Llinas, 1988; Lisman and Idiart, 1995; Buzsaki, 1996; Buzsaki, 1998; Bragin et al., 1999a; Grenier et al., 2003a). In addition to their role in normal brain function, high-frequency activity has been described at seizure onset (Grenier et al., 2003a; Alarcon et al., 1995; Allen et al., 1992; Bragin et al., 1999b; Fisher et al., 1992; Worrell et al., 2004; Jirsch et al., 2006) and interictally in human epileptogenic foci at times temporally remote from seizure onset (Fisher et al., 1992; Bragin et al., 1999a; Worrell et al., 2004). There is accumulating evidence that high-frequency oscillations (HFOs), which we collectively term as all activity > 40 Hz (including gamma, high-gamma, ripple, and fast ripple oscillations), may have a fundamental role in the generation and spread of focal seizures (Bragin et al., 2002; Grenier et al., 2003b; Worrell et al., 2004), and that certain classes of these events are electrophysiological signatures of epileptogenic brain. Understanding the relationship between HFOs, ictogenesis, and seizure propagation requires robust automated detection algorithms for detailed spatiotemporal mapping of these events in large EEG databases.

To date, a few studies have utilized digital IEEG recordings to demonstrate high-frequency activity at the onset of human neocortical (Allen et al., 1992; Fisher et al., 1992; Alarcon et al., 1995; Worrell et al., 2004; Jirsch et al., 2006) and mesial temporal lobe seizures (Bragin et al., 1999b; Bragin et al., 2002; Jirsch et al., 2006). These studies relied on manual visual review of IEEG to identify oscillations of interest and subsequently applied digital signal processing techniques to characterize them, e.g., oscillation amplitude distribution, duration, and spectral characteristics. None of these studies addressed the selection bias, potential lack of reproducibility, and interrater reliability issues that have plagued the spike- and seizure detection literature (Webber et al., 1994; Gotman, 1999). Similarly, in animals where ripple and fast ripple osciallations were first described (eg. Buzsaki et al. 1992, Khalilov et al., 2003) there has been little discussion of the difficulties associated with the broad class of supervised energy and amplitude threshold detectors generally used to detect HFOs. However, understanding these issues is an important prerequisite for researchers studying HFOs using large-scale modern clinical IEEG databases. Indeed, despite the widespread availability of automated algorithms for the detection of seizures and interictal spikes and sharp waves, we are aware of only one study investigating automated detection of brief paroxysmal pathologic HFOs in multichannel human intracranial EEG (Staba et al., 2002). This study reported on a detection algorithm for fast ripple oscillations (80 – 500 Hz) from human hippocampal microwire recordings. No rigorous validation of the automated algorithm with human reviewers was performed, and gamma frequency oscillations (observable in standard clinical recordings) were not considered. While the potential clinical importance of HFOs to localize epileptic networks and their possible mechanistic role in generating focal seizures remain active areas of research, it is clear that reliable, robust automated event detection is a prerequisite for progress.

In this paper, we present the results of a study of more than 1300 HFO events to validate a new algorithm for detecting brief focal paroxysmal HFOs in clinical IEEG (∼0.1 – 100 Hz). We compare the performance of our algorithm to that obtained from two implementations of a benchmark detector (Staba et al., 2002), and to markings from three board-certified epileptologists performing blinded visual identification and verification of HFO events. Finally, we discuss the merits of this algorithm for large-scale data mining of EEG databases.

Methods

Clinical Data Collection

We examined IEEG recordings from two patients who underwent continuous long-term monitoring for presurgical evaluation of intractable epilepsy. The patients were chosen for the clear presence of HFOs upon initial review of their EEG, and for their disparate diagnoses—one pediatric patient with lesional (cortical dysplasia) neocortical epilepsy, one adult patient with non-lesional extratemporal lobe epilepsy—and EEG background characteristics. Informed consent for participation in these studies was obtained with the approval of the Emory University, University of Pennsylvania, and The Children's Hospital of Philadelphia (CHOP) Internal Review Boards.

Each patient underwent implantation of intracranial electrodes according to standard presurgical evaluation protocols (Engel, 1987; Quesney et al., 1992; Quesney, 2000). Ad-Tech subdural grids, strips, and depth electrodes (AD-Tech Medical Instrument Corporation, Racine, WI) were used. Referential EEGs were recorded using Nicolet BMS-5000 (Nicolet Biomedical, WI) and Astro-Med Grass-Telefactor (Astro-Med Corporation, Warwick, RI) (CHOP) epilepsy monitoring systems. Data were sampled at 200 Hz and bandpass-filtered (0.1 – 100 Hz) during acquisition. Data were further digitally bandpass-filtered (4^th-order Butterworth, forward-backward filtering, 0.1 – 85 Hz) to minimize potential artifacts due to aliasing. Recordings were reviewed by three clinical epileptologists (G.W., E.M., and D.D.) to identify representative channels exhibiting frequent HFO activity for each patient. Fourteen three-minute epochs were randomly selected from a single channel from each patient's EEG for further analysis using custom MATLAB (Mathworks, Natick, MA) scripts. Representative EEGs for each patient are shown in Figure 1.

Figure 1.

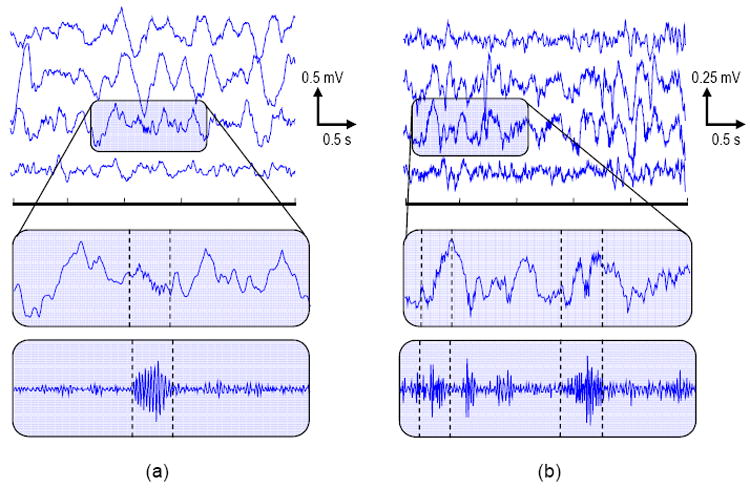
Representative EEGs with HFO events showing: (top) multichannel recordings, (middle) single channel with event zoom, (bottom) single channel high-pass (fc = 35 Hz) zoom. (a) Pediatric patient, recorded from four neighboring frontal grid electrodes (marked event frequency ∼ 48 Hz). (b) Adult patient, recorded from four neighboring frontal grid electrodes (marked event frequencies ∼ 72 Hz, 73Hz). (Dashed lines) HFO event onset/offset times. Note the heterogeneous EEG amplitude and background characteristics between the patients.

Automated HFO Identification

Existing methods for identifying HFOs (Staba et al., 2002; Khalilov et al., 2005) implicitly model the events as short-duration, high-frequency oscillatory transients additively combined with background EEG. A general block diagram describing these approaches is shown in Figure 2. Events are identified by analyzing EEG in two stages: preprocessing and detection. During preprocessing, EEG data are bandpass-filtered to restrict the range of frequencies under consideration. Additional filtering may also be performed, e.g., spectral equalization (also known as preemphasis, whitening, and prewhitening) via first-order backward differencing (Shiro and Utzhak, 1982). Detection consists of measuring the short-time energy (or similar signal) and thresholding, first by amplitude (e.g., are event amplitude values “significantly” higher than those corresponding to normal background EEG?) and then by duration (e.g., is this event of physiologically significant duration?). Sometimes post-detection filtering, such as ripple counting (not shown in Figure 2), is performed as a further confirmation of detections.

Figure 2.

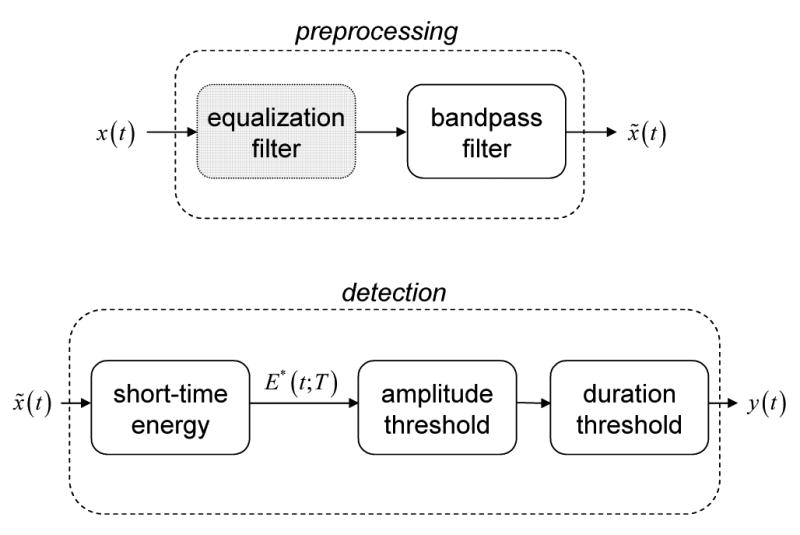
Block diagram of basic EEG processing for bandpass energy-based HFO detection. The EEG signal, x(t), is analyzed first by preprocessing, then by detection, to produce an indicator, y(t), of HFO events. The short-time energy, E* (t;T), may be replaced by similar measures, e.g., line length. (Gray) Equalization may be applied during preprocessing to compensate for EEG spectral rolloff.

We implemented two automated detection algorithms for comparison in this study: one new method (X), and one benchmark method (Y₁, Y₂) (Staba et al., 2002). Our motivation for developing method X was to introduce three algorithmic improvements to the benchmark method. First, we performed simple spectral equalization, as described previously, to compensate for the significant spectral rolloff present in clinical EEG over the frequency range 30 – 100 Hz. Second, we replaced the short-time energy estimate,

$$E^{\ast }(t)=\sqrt{\frac{1}{N}\underset{k=t-N+1}{\overset{t}{\Sigma }}{\stackrel{\sim }{x}}^2(k)}$$ (1)

with another measure, short-time line length,

$$E^{\ast }\left(t\right)=\underset{k=t-N+2}{\overset{t}{\Sigma }}\left|\stackrel{\sim }{x}\left(k\right)-\stackrel{\sim }{x}\left(k-1\right)\right|$$ (2)

which weights outlying amplitude values less heavily. Our qualitative observation is that the line length statistic is more robust against false positive detections produced by spikes and large-amplitude artifacts than the energy statistic. The precise relationship between line length, energy, and signal frequency is complex, but this statistic has proven robust and broadly applicable in clinical EEG, for example, in seizure detection (Esteller et al., 2001). Third, we selected a nonparametric threshold by examining the empirical cumulative distribution function (cdf) of line length values from a small training set (not included in further analysis), and noting that thresholds corresponding to the 95 – 98 percentile of the cdf appeared to be natural “breakpoints.” We heuristically selected the 97.5 percentile, and applied this to each epoch during processing, yielding epoch-specific (e.g., data dependent) threshold values. Proper threshold selection is crucial to algorithm performance, and we have observed that the distributions of short-time energy and short-time line length are both skewed and kurtotic (Figure 3). A Kolmogorov-Smirnov test for one sample on line length values, for instance, indicates that they are not normally distributed (p ≪ 0.01). This suggests that the use of standard deviation derived thresholds (e.g., parametric thresholding) may be inappropriate, at least for low-bandwidth recordings.

Figure 3.

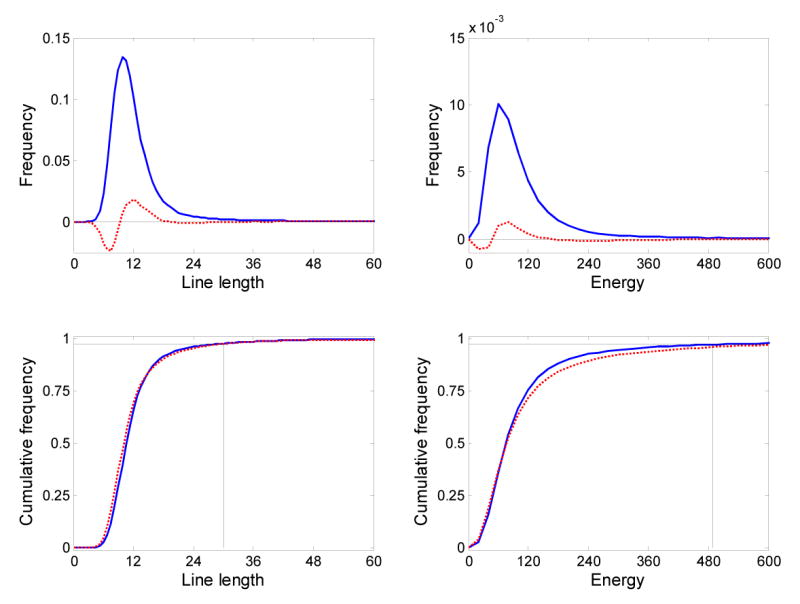
(Top row) Distribution of line length and energy values for patient 1 (solid blue lines), and difference between distributions for patients 1 and 2 (dashed red lines). (Bottom row) The cumulative distributions of line length and energy values for patient 1 (solid blue lines) and patient 2 (dashed red lines) used to select a threshold for the automated detection algorithm. Thresholds are shown for patient 1 for the 0.975 quantile.

A direct implementation of the benchmark algorithm was not possible for the low-bandwidth clinical IEEG we analyzed, so we introduced two “translational” modifications: (1) a bandpass filter with lower frequency cutoffs (30 – 85 Hz) was used during EEG preprocessing, and (2) longer event duration thresholds were used for detection. We made three additional modifications to the benchmark method to improve its performance. First, we replaced the global threshold specified for short-time energy with a threshold computed in a per-epoch fashion. Our justification for this change is that the total duration of HFO events is a small fraction of the total epoch duration, so each 3-minute epoch should provide a reasonable estimate of the local background bandpass energy. Second, we did not perform any event merging for HFO events. Finally, we implemented two versions of the benchmark method (Y₁, Y₂) with different thresholding rules: Y₁ had a lower threshold designed to improve detection sensitivity, while Y₂ used the benchmark threshold (Staba et al., 2002). Table 1 summarizes the key parameter values used in each detector, as well as the reference values from the benchmark algorithm (Staba et al., 2002).

Table 1.

Summary of automated detector characteristics.

	X	Y1	Y2	Benchmark (Staba et al., 2002)
Data Bandwidth	0.1 – 100 Hz	0.1 – 100 Hz	0.1 – 100 Hz	0.1 – 5,000 Hz
Spectral Equalization	1st-order difference	-	-	-
Bandpass Filtering	30 – 85 Hz 4th-order Butterworth	30 – 85 Hz 4th-order Butterworth	30 – 85 Hz 4th-order Butterworth	100 – 500 Hz Finite Impulse Response (FIR) -33 dB/octave
Energy Measure	Line length	RMS amplitude	RMS amplitude	RMS amplitude
Energy Measure Window Size	85 ms (17 samples)	85 ms (17 samples)	85 ms (17 samples)	3 ms (30 samples)
Threshold	97.5 percentilea (per epoch)	μ + 2.5σa (global)	μ + 5σa (global)	μ + 5σb (global)
Minimum Event Duration	80 ms	80 ms	80 ms	6 ms
Ripple Count Criteria	None	None	None	6-peak minimum

^aEstimated from the empirical distribution of energy-measure values for each epoch

^bEstimated from the empirical distribution of energy-measure values using all available data

Human Identification

We developed a custom MATLAB graphical user interface (GUI) to present two-second screens of single-channel EEG (0.1 – 100 Hz) and its highpass-filtered counterpart (30 – 100 Hz) for visual identification of HFOs. The display gain was calibrated to 7 μV/mm for both signals.

In our first human identification experiment, each reader was asked to use the GUI to independently mark the start- and stop times of every HFO event (frequency > 40 Hz, duration > 85 ms) they observed in each of the 28 3-minute epochs available. The identification task was untimed, and the reviewer was able to modify his selections for an epoch until declaring it “processed,” at which time the marked events were automatically saved to a database for future analysis and comparison to computerized detections. Three months later, a second identification experiment was performed in the same manner using a subset of 14 of the 28 total epochs available. Reviews were conducted in a blinded fashion to test the reproducibility of human expert markings.

Human Verification

An additional experiment required the human reviewers to verify the existence of each of the candidate HFOs identified by either human or computer. The candidate events were presented via a separate custom MATLAB GUI with one second of unfiltered EEG displayed per page at a gain of 7 μV/mm. Each candidate event was highlighted and centered in the window, and reviewers were asked to either accept or reject the highlighted EEG interval as an HFO. The verification task was untimed, and binary scores were saved at the end of presentation for further analysis.

Statistical Methods

A Kolmogorov-Smirnov test for one sample was used to test the normality assumption of line length values. We used accuracy, A, defined as the percentage of correct (true positive) detections compared to a ground truth data set, to compare the performance of the automated detectors. A paired t-test identified significant accuracy differences between detectors.

Precision (3), P, and recall (4), R, were used to compute F-measures (5), F, to compare the performance of human and automated detectors when a ground truth set of detections was defined.

$$P=\frac{TP}{TP+FP}$$ (3)

$$R=\frac{TP}{TP+FN}$$ (4)

$$F=\frac{2TP}{2TP+FP+FN}$$ (5)

TP, FP, and FN are the total number of true positives, false positives, and false negatives, respectively. Note that these performance measures do not require the specification of true negative (TN) events (which is both problematic and a source of specificity bias in rare event detection problems). For this task it is difficult to define true negatives, and their occurrence highly skews the sensitivity and specificity. F-measures were computed by partitioning the total set of EEG available into 20 consecutive segments, each containing the same number of ground truth events. We performed a one-way ANOVA to test the null hypothesis that human and automated detectors performed consistently with the same mean F-measure value. We note that the F-measure is especially appropriate for evaluating interrater agreement as it does not require the specification of true negative events (often a problematic task) (Hripcsak and Rothschild, 2005).

The Kappa statistic, κ, was used to evaluate human reviewer reproducibility at identifying HFOs. We compared the relative detection rate between detectors using Pearson's correlation coefficient, ρ.

Results

A total of 1,330 events from both patients (612 for patient 1, 718 for patient 2) were identified by human and automated detectors. The total duration of all events corresponds to approximately 2.8% of the total duration of the data analyzed and confirms that HFO events occur sparsely in time. Figure 4 shows the events identified in four representative epochs from both patients. The results highlighted by gray background in each plot correspond to events identified by the automated detectors. In analyses where we compare detections from multiple detectors (human or automated), we consider two events to be identical if they overlap in time by at least one sample.

Figure 4.

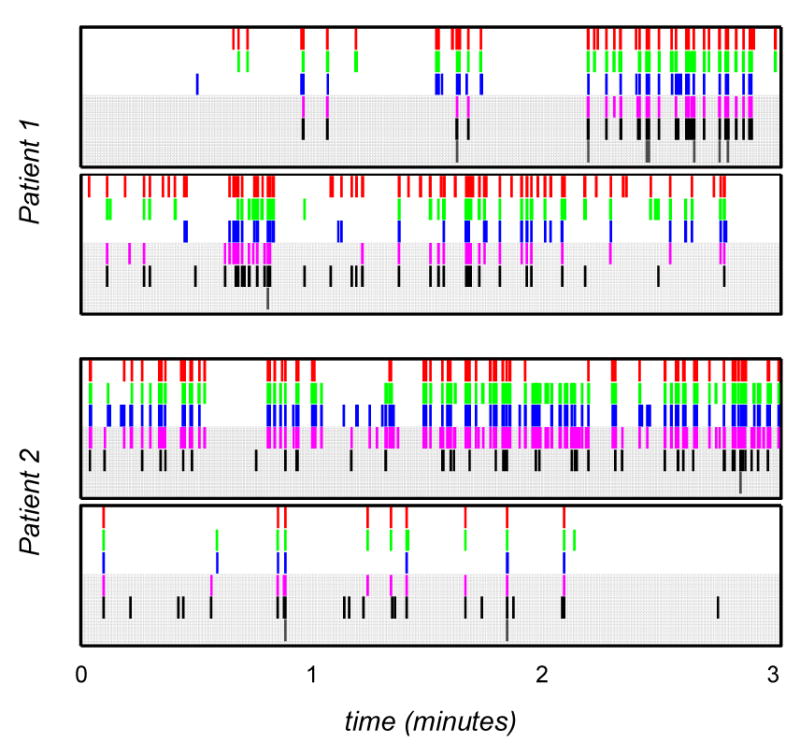
Representative HFO identifications for both patients for each detector. (Top-to-bottom in each plot) Detection sequences correspond to A (red), B (green), C (blue), X (magenta), Y₁ (black), Y₂ (charcoal). Gray background highlights detections by automated detectors.

Comparison of Automated Detectors

We compared the detections produced by the three automated detector implementations (X, Y₁, and Y₂) to a ground truth set of detections. The ground truth set included all events which were independently identified by all of the reviewers in the identification experiment. While it is likely that such an event set may not include all HFOs (e.g., some events may be marked by only one or two reviewers), the study was designed based upon the hypothesis that any events included in this ground truth set were likely to be true HFO events and should be detected by an automated algorithm.

Figure 5 shows the patient-specific and combined detection results of the automated methods. Misses (red bars) correspond to ground truth events that went undetected (false negatives). Detections (green and gray bars) may represent either true positives (if they correspond to ground truth), true HFO events that went undetected by all three human experts, or false positives. Due to this ambiguity in determining the appropriate labels for some detections, we chose to compare the automated algorithms strictly by their accuracy.

Figure 5.

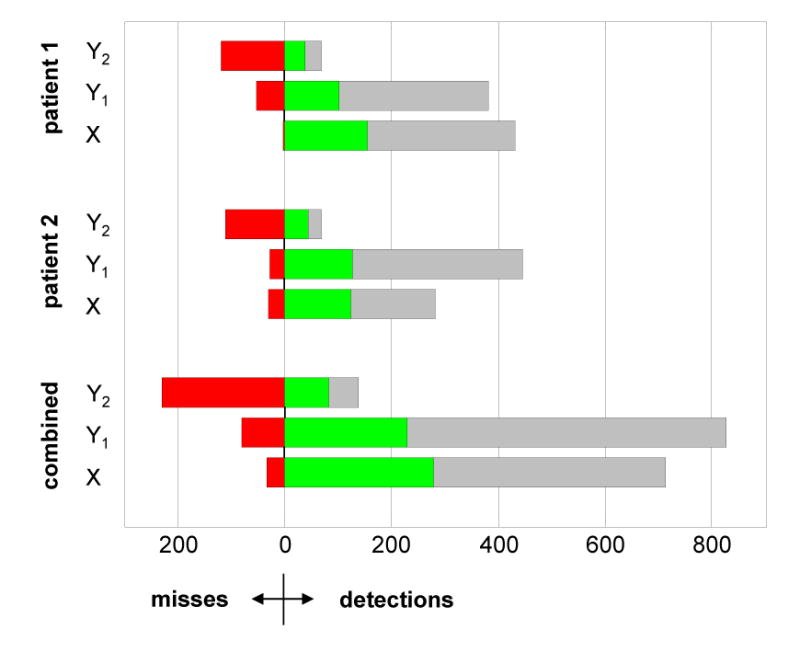
Comparison of automated detections (X, Y₁, Y₂) with the ground truth set of events identified by all three human reviewers. (Red) Number of ground truth events undetected (false negatives). (Green) Number of ground truth events successfully detected (true positives). (Gray) Number of unlabeled detections—these events include an unknown mixture of false positive detections made by the automated detectors, and false negative detections made by the human reviewers.

Detector Y₂ performed uniformly poorly for both patients, and only achieved 26.4% accuracy on the combined data set. Both detectors X (89.7%) and Y₁ (74.0%) performed better than Y₂, showing greater accuracy and more uniform results across each patient. A paired t-test comparing detector outputs (X, Y₁) allowed us to reject the null hypothesis that the detector accuracies were equivalent (p ≪ 0.01, n = 280). Based on these results, we deemed X to be the most accurate automated algorithm available and did not consider Y₁ or Y₂ further. Of significant interest is the clarification of unlabeled detections (gray bars in Figure 5), exploring whether these detections are false positive automated detections, false negative human detections, or both. We address this task in section 3.2.

Comparison of Automated vs. Human Detectors

To compare the performance of the best automated method (X) against humans we examined data from the first human identification experiment and the verification experiment. We again defined a ground truth set so that all identifications could be labeled appropriately (e.g., a true positive, false positive, or false negative). However, for this analysis the ground truth selection rule was modified as follows: an event was deemed a ground truth event if it was independently identified or verified by two or more detectors (including the automated detector, X). Aside from the heuristic justification for this rule change (e.g., majority voting), we note the following: (1) if we insist upon unanimous human consensus as the definition of a ground truth event, we do not allow for human false negative errors, (2) human verification is required for disambiguation of unlabeled detections from the automated detector. It is precisely the extent of human false negatives that we wish to explore (c.f. 3.1) to fully understand the performance of the automated algorithm, and the modified ground truth rule facilitates this exploration.

Detector results are presented by patient in Table 2. We note that humans generally exhibit low false positive detection rates: the errors that human reviewers make are false negatives. We hypothesize that these errors arise from fatigue and distraction during marking tasks. The automated detector seems to consistently, slightly over-detect with respect to ground truth. Reviewing these false positives, we observed qualitatively that these HFOs consisted of a small number of artifacts, and a large mixture of both spike-like transients and transients with very low amplitude and/or short-duration high-frequency components. The telling error for the automated detection is the large number of false negative detections for patient 2. Upon visual review of patient 2's ground truth set, we observed that HFOs were lower-amplitude than those for patient 1. We also note from Table 2 that reviewer C more closely agrees with X. A one-way ANOVA analysis of the mean F-measures for each detector does not allow us to reject the null hypothesis that the human detector performance differed from the automated algorithm (p = 0.68, n = 888).

Table 2.

Summary of detection statistics^† and performance^* for human reviewers (A, B, C) and the automated detector (X): true positives (TP), false positives (FP), false negatives, mean precision (P̄), mean recall (R̄), and mean F-measure (F̄). Ground truth set included all events declared as HFOs by two or more detectors during identification or review. Mean values were calculated from 20 partitions of the ground truth set.

	Patient 1				Patient 2				Combined
	A	B	C	X	A	B	C	X	A	B	C	X
TP	187	242	269	347	406	338	240	243	593	580	509	590
FP	0	5	9	69	40	19	35	25	40	24	44	94
FN	203	148	121	43	92	160	258	255	295	308	379	298
P̄	1.00	0.98	0.96	0.83	0.91	0.95	0.89	0.92	0.96	0.97	0.93	0.88
R̄	0.48	0.64	0.71	0.99	0.89	0.71	0.52	0.52	0.68	0.67	0.61	0.75
F̄	0.64	0.75	0.80	0.90	0.89	0.81	0.64	0.64	0.77	0.78	0.72	0.77

^†(TP + FN) is constant for a patient, and is equal to the number of ground truth events

^*Best values for each row and patient are emphasized in bold

Detector Reproducibility

We evaluated the consistency of detectors in two ways. First, we examined human identification consistency by computing Kappa statistics for the two identification trials (Table 3). The Kappa statistic measures the degree of reproducibility between repeated trials, where: 0 ≤ κ < 0.4 indicates marginal reproducibility, 0.4 ≤ κ ≤ 0.75 indicates good reproducibility, and κ > 0.75 indicates excellent reproducibility (Rossner, 1995). We note that the interval nature of our detections requires us to make special assumptions regarding true negative events when calculating Kappa statistics. We included in our analysis a 3-way consensus detector, which represents the intersection of identifications by A, B, and C. Thus 3-way consensus detections correspond to events unanimously identified in a trial by all three human reviewers. We had hypothesized that this 3-way set of detections would be highly reproducible, but in fact the Kappa statistics indicate that this reproducibility is less than excellent. We also note from Table 3 that human reproducibility is only marginal to slightly-good for all reviewers.

Table 3.

Consistency of human experts (A, B, C) and their unanimous consensus (3-way) at HFO identification as measured by the Kappa statistic. The total number of events considered is in parentheses.

	A	B	C	3-way
Patient 1	0.29 (175)	0.49 (215)	0.39 (212)	0.61 (125)
Patient 2	0.34 (169)	0.46 (159)	0.31 (141)	0.65 (61)
Combined	0.30 (344)	0.47 (374)	0.34 (353)	0.64 (186)

Subsequently, we examined the reproducibility between identifications and verifications. Three inferences are apparent from the data (Table 2). First, humans are reasonably consistent amongst each other at both identification and verification. Second, a 3-way consensus verification finds nearly all 3-way consensus identification events, but also finds an almost equal number of new events. This provides very strong evidence for the hypothesis that human reviewers tend to make many false negative errors, but few false positive errors. Third, the automated detector, X, tends to over-detect and produce more false positive identifications than humans, but also identifies the most 3-way verifications.

Relative Detection Rate Consistency Is Observed

We observed that the sequence of detection counts, that is the sequence formed by taking the total number of HFO identifications for each epoch for a fixed detector, was consistent. We measured this consistency by calculating correlation values between these sequences for each detector pair (Table 4). We note that there is no difference between the mean human-human values (0.85) and the mean human-automated values (0.85). The phenomenon of relative detection rate consistency has been reported previously in experiments assessing human spike rating consistency (Webber et al., 1993). One interpretation is that detectors tend to generate a number of markings per record that is a multiple of the true number of events present. Thus, while the difference between identifications in a record between two detectors may vary significantly, the ratio tends to agree across a sequence of records. The implication of detection rate consistency is that even if one concluded that an automated algorithm was a poor absolute event detector, it may be very good at comparing the rate of events over long intervals of EEG, and therefore an acceptable tool to mine large EEG databases..

Table 4.

Relative detection rate consistency between detectors. The value in each cell corresponds to the Pearson correlation coefficient between the total number of events identified per record by two detectors (A, B, C: human, X: automated).

	Patient 1			Patient 2
	A	B	C	A	B	C
B	0.98	-	-	0.83	-	-
C	0.93	0.97	-	0.59	0.78	0.83
X	0.89	0.95	0.99	0.64	0.78	0.83

Discussion

The results of this study suggest that, given a properly chosen threshold, our new automated method performs better than the benchmark method (Staba et al., 2002), and as well as human experts at identifying gamma-band HFO oscillations in clinical IEEG. Additionally, it is clear from our experiments that human experts are only marginally consistent at visually identifying HFO events, primarily due to the large number of false negative errors they make, but are very good at labeling candidate HFOs when presented with short EEG segments for review. While these results arise from an analysis of just two patients, over 1300 events were studied: we feel that the performance of both human and automated methods is unlikely to improve simply by “adding more patients.” These important points support two central motivations for this study: (1) to validate our new method, in preparation for deploying it to track the spatial and temporal evolution of multi-scale oscillations during seizure generation; and (2) to present important concepts and techniques for benchmarking automated algorithms for tracking physiological oscillations in human recordings. As more algorithms focused on tracking similar, multi-scale, signature events in normal and pathological brain activity are developed, similar validation against human experts will be required.

Automated Detection

The discrepancy between the high-bandwidth recordings previously analyzed (Staba et al., 2002), and the clinical bandwidth data available for this study implies that direct comparisons between the methods is not exact. In addition, the reference implementation is only approximate, as discussed in section 2.2. In particular, the number of samples per event for clinical data sampled at 200 Hz is smaller (∼ 17 – 75 samples) than previously used (Staba et al., 2002). This makes confirmation of candidate HFO events more difficult, either by spectral estimation or by duration thresholding. For the bandwidth considered (0.1 – 85 Hz) in this study, however, comparison of the results of the automated detector implementations (X, Y₁, Y₂) (cf. 3.1) show that X performs best with regard to specificity and sensitivity when compared to a ground truth of human consensus markings. We attribute this to the three algorithm improvements we introduced—nonparametric thresholding, spectral equalization, and an alternative energy measure. A more complete comparison of X and Y methods over a broad parameter range is necessary, however, to unequivocally compare the relative performance of each.

Clearly the proper choice of a threshold is the most important factor for automated detector performance, while spectral equalization is necessary to compensate for the spectral rolloff present in clinical EEG. For both patient data sets in this study, the 97.5 percentile was an acceptable threshold that was easily, visually determined from the cdf of line length values on a small training set. As noted previously, both energy and line length values were not normally distributed, hence our non-parametric thresholding strategy appeared more suitable than other proposed methods (e.g., mean-plus-standard-deviation based rules (Staba et al., 2002)). However, it is unlikely that a single quantile threshold will perform optimally across multi-patient data sets. Ultimately, a better method for threshold calibration will be required for fully automated HFO detection. We also note that this problem, threshold selection, still exists for more computationally expensive detection methods, e.g., time-frequency methods like matching pursuit, and is non-trivial not because of the nature of HFO events themselves (simple oscillations), but rather the nature of the diversity of background EEG they coincide with.

Automated vs. Human Performance

The automated detector, X, clearly detected the majority (89.7%) of unanimous human consensus set events, but it also produced nearly twice as many “extra” detections. This raised an important question about the performance of the automated algorithm: were the majority of unlabeled, extra events due to errors made by the human experts during identification (e.g., false negatives), or errors made by the automated detector (e.g., false positives)? Only if the former were confirmed would we consider the automated algorithm acceptable. The results in Table 2 suggest that this was indeed the case, and that the automated algorithm performs at least as well human experts.

Additional insights into human versus automated performance are also apparent: it is clear from Table 2 that the majority of human errors are false negatives. In retrospect, this seems plausible: fatigue, vigilance, and distractions make it easy to miss HFOs during marking tasks. Surprisingly, it also appears that false negatives are the most serious error made by the automated detector: the sensitivity of the detector for patient 2 was simply too low, resulting in many false negative errors. This reinforces our previous conclusion that threshold selection (especially in a patient-specific manner) is the key determinant of automated detector performance.

Human Performance

The results of our experiments suggest that human performance on a marking task is not consistent across the full range of HFOs, and is only marginally reproducible. Based on the experts' previous EEG reading experiences prior to this study (e.g., spike detection, seizure onset localization, and other event identification), we anticipated some degree of poor performance; however, the results were worse than expected. Humans miss many events (false negative) when asked to visually identify HFOs in EEG. However, when an expert does identify an HFO, other experts are also likely to agree with that marking upon review. This highlights the finding that human experts are very consistent (and accurate) when presented with short clips (1-2 s) of candidate EEG to confirm HFOs. We attribute this asymmetry of performance between identification and review to the different vigilance requirements of each task.

One major implication of the poor human performance is that the determination of a ground truth data set (e.g., “the gold standard”) is difficult. In the limit, it is likely that unanimous agreement among EEG readers would result in an empty ground truth data set. In our case, a unanimous consensus data set accounted for only 21% of all events identified, while review consensus was 67%. Human ground truth data is still not precise, which makes the validation of any detection algorithm difficult. We believe one possible improvement to ground truth determination is to implement subjective event scoring during the identification task (e.g., HFOs are rated on a scale of 1 – 10). By scoring each event, the expert is qualitatively stating the degree of HFO-ness observed, and providing an indication of their internal threshold for marking events. We hypothesize that changes in this internal threshold which occur throughout a marking session—in addition to vigilance changes—are a major contributor to false negative errors and confounder of reproducibility. We note, however, that such a scoring system requires much more effort and time on the part of the marker, and may not provide a clear indication of how to form a ground truth set.

Future Work

In addition to improving algorithm precision and speed, experiments are underway within our group to use this and similar automated approaches to track important physiological oscillations in normal and pathological recordings of neuronal activity. While the automated detector, X, performed well in our study, a method for calibrating the threshold on a per-patient basis is required prior to analyzing large patient databases. An acceptable calibration technique may be semi-supervised, where human experts review sampled candidate events identified by the automated detector to determine the “best” threshold. The method presented in the paper should also be benchmarked more exhaustively against a larger patient database to study its performance against a greater range of background EEG. In particular it would be interesting to characterize the sensitivity of this detector to spikes and other non-HFO, epileptiform activity since basic bandpass energy-based detection strategies operate as weak spike detectors. Finally, mapping events detected from multichannel, multi-patient databases will allow characterization of the spatiotemporal distribution of gamma-band HFOs, and their spectral characteristics in patients with epilepsy. Improved automated HFO detection tools will facilitate the exploration of associations between HFO location, ictal onset zone, and pathological tissue.