Abstract
Evidence suggests that inertial cavitation plays an important role in the renal injury incurred during shock-wave lithotripsy. However, it is unclear how tissue damage is initiated, and significant injury typically occurs only after a sufficient dose of shock waves. While it has been suggested that shock-induced shearing might initiate injury, estimates indicate that individual shocks do not produce sufficient shear to do so. In this paper, we hypothesize that the cumulative shear of the many shocks is damaging. This mechanism depends upon whether there is sufficient time between shocks for tissue to relax to its unstrained state. We investigate the mechanism with a physics-based simulation model wherein the the basement membranes that define the tubules and vessels in the inner medulla are represented as elastic shells surrounded by viscous fluid. Material properties are estimated from in vitro tests of renal basement membranes and documented mechanical properties of cells and extracellular gels. Estimates for the net shear deformation from a typical lithotripter shock (~ 0.1%) are found from a separate dynamic shock simulation. The results suggest that the larger interstitial volume (~ 40%) near the papilla tip gives the tissue there a relaxation time comparable to clinical shock delivery rates (~ 1Hz), thus allowing shear to accumulate. Away from the papilla tip, where the interstitial volume is smaller (≲ 20%), the model tissue relaxes completely before the next shock would be delivered. Implications of the model are that slower delivery rates and broader focal zones should both decrease injury, consistent with some recent observations.
Keywords: Shock-wave lithotripsy, renal injury, tissue damage, numerical simulation
Introduction
Shock wave lithotripsy (SWL) is a widely used treatment for urinary tract calculi, but it has been found that more renal trauma accompanies treatment than initially thought (Evan and McAteer, 1996; Evan et al., 1998). Acute renal injury occurs to some degree in virtually all patients, and some cases have been reported in which damage is severe. This trauma is thought to lead to chronic complications such as an increased risk of hypertension (Lingeman et al., 2003; Krambeck et al., 2006) and there appears to be a link between SWL and the occurrence of new-onset diabetes (Krambeck et al., 2006). Studies of pig kidneys (e.g. Evan et al., 1996) just after treatment with SWL show that the damage is extensive and that it occurs during treatment rather than from longer-term hypoxia resulting from vascular damage (Shao et al., 2003). It appears that as they are delivered the shock-waves themselves rupture the basement membranes of vessels and tubules and destroy cells (Shao et al., 2003).
Inertial cavitation is thought to be the mechanism responsible for the greatest part of the observed damage (Bailey et al., 2003). The precise mechanism(s) of bubble action in vascular injury, however, are not known, but bubble expansion or bubble collapse and rebound may all be involved. The rapid collapse and rebound of bubbles is known to be potentially destructive to surrounding material (Sturtevant, 1996; Zhong et al., 2001). The importance of cavitation in renal injury is supported by results for inverted shock waves, which are generated via a pressure release reflector. These are significantly less destructive (Evan et al., 2002), presumably because the trailing wave is compressive and therefore suppresses cavitation. Inverted shock waves have also been shown to reduce hemolysis relative to the standard lithotripter shocks when directed at in vitro samples of red blood cells (Evan et al., 2002). The acoustic signature of inertial cavitation has been observed in pig kidney tissue after around 1000 shocks (Bailey et al., 2005), which is comparable to the number necessary for significant tissue injury (Evan et al., 1998), though specific thresholds have not yet been determined.
Questions remain, however, as to how cavitation and cavitation damage are initiated. For example, why are so many (~ 1000) shock waves necessary before cavitation signatures and significant injury are observed in kidney tissue (Bailey et al., 2005)? It has been suggested that bleeding is a necessary prelude to extensive cavitation (Shao et al., 2003). In this view, the accumulation of non-circulating blood in the lesion would provide favorable conditions for extensive and spreading cavitation damage. At normal physiological conditions, blood flow speeds, which are estimated to be ~ 0.5mm/s in the vasa recta (Jamison and Kriz, 1982) and would probably have a similar speed in the capillaries, seems fast enough to remove nucleation sites before more than a few shocks could grow them into damaging cavitation bubbles. It has been proposed in conjunction with in vitro models that the initial rupture might be caused by expanding cavitation bubbles (Zhong et al., 2001), though this has not yet been observed in vivo.
It is also possible that the initial hemorrhage does not involve bubbles at all. Though damage was modest and localized, inverted wave studies still showed hemorrhaging near the papilla tip (Evan et al., 2002). Shock-wave induced shearing is another proposed injury mechanism, but as we discuss in more detail in following sections, the shear due to a single shock is estimated to be insufficient to tear basement membranes. It has been proposed that the renal papilla structure makes it particularly prone to the focusing of shock waves scattered by its acoustic inhomogeneities (Howard and Sturtevant, 1997). However, based on the speed of sound in its constituent components, the papilla is not expected to be significantly more acoustically inhomogeneous than other parts of the kidney that seem to be less susceptible to damage in the absence of cavitation (Evan et al., 2002).
In this paper we investigate the possibility that the greater interstitial volume near the papilla tip makes it particularly susceptible to shear accumulation during repeated shock applications, leading eventually to damage and hemorrhage. Once hemorrhage has occurred, pooled blood could then give rise to more extensive cavitation damage as previously discussed. The net shear displacement that remains after the passing of the focused wave is computed from the simulation results of Tanguay and Colonius (2003). A simulation model of the inner medulla, which is constructed based on its known structure and estimates of the material properties of its components, suggests that shear strain can indeed accumulate near the papilla tip.
Materials and Methods
Tissue: Structure and Approximate Properties
The structural properties of the tissue of the inner medulla (figure 1) appear to be set by the relatively stiff and strong basement membranes of the thin limbs of the loops of Henle, larger collecting ducts, and small blood vessels (vasa recta and capillaries). Collectively, we refer to these simply as tubes. Though there are a few branch points, these tubes are generally aligned in parallel (Jamison and Kriz, 1982). The interstitial space between the tubes in the inner medulla is filled with interstitial cells surrounded by extracellular matrix material referred to here as an interstitial gel. The cells typically span between two or more tubes or vessels suggesting a structural role (Madsen and Tisher, 2004). Higher in the medulla and the cortex they are less ordered and resemble typical fibroblasts (Jamison and Kriz, 1982). The interstitial gel is made of a flocculent polysaccharide material (Madsen and Tisher, 2004). The fraction of the inner medulla that is interstitial space increases into the papilla and toward its tip as discussed in the following, where we discuss our model’s geometric parametrization.
Fig 1.
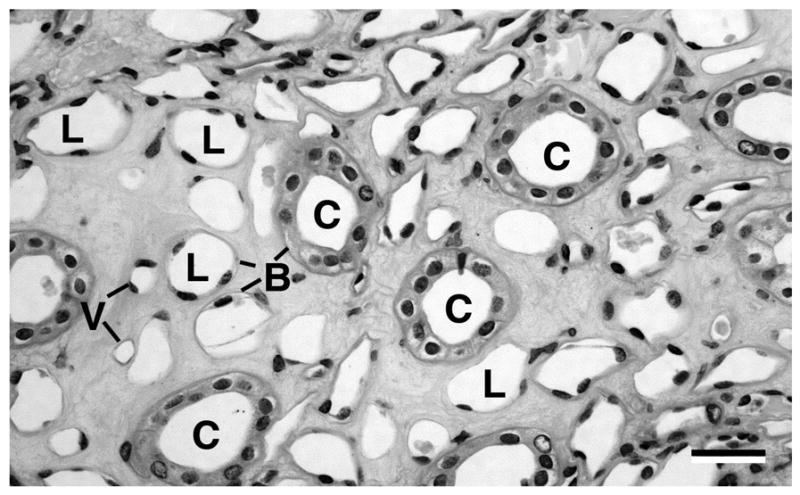
A light micrograph of a transverse cross section of an inner medulla near the papilla tip (human): collecting ducts (C), loop limbs (L), and blood vessels (V). Each tubule is defined by a basement membrane (B) as discussed in the text. The scale bar is ~40μm.
The pressure-diameter relation of rabbit renal tubule basement membranes has been measured by Welling et al. (1995), with additional references therein. These were found similar to properties of the basement membranes of frog capillaries and rat venules (Swane et al., 1989), which suggests at least a degree of universality to basement membrane properties. They are surprisingly stiff, with elasticity comparable to that of tendon (Welling et al., 1995). A luminal pressure increase of up to 980 Pa (10cmH20) increases the diameter approximately linearly up to about 5μm, which gives a tension modulus per unit length of the tubule of T = 0.16N/m. For larger deformations, the membranes become considerably stiffer. It is straightforward to fit these diameter-pressure curves with appropriate nonlinear functions of the deformation gradient tensor, but this is unnecessary for the present investigation as we only seek to assess whether small shears can accumulate. The local membrane tension is thus related to the local stretch as
| (1) |
where s is the deformed arc length and so is its reference zero-strain length. If we assume that the properties of a h = 0.2μm-thick membrane are uniform across its thickness, the bending modulus of the tubule wall will be M = Th2/12 = 5.2 × 10−16 Nm per unit length. The bending moment that results from curvature of C relative to the reference curvature Co is b = M(C − Co).
Welling et al. (1995) compared the elastic properties of tubules before and after the epithelial cells were removed by a sodium deoxycholate bath. They found that the membrane material properties were essentially unchanged, demonstrating that the net elastic effect of the cells is small compared to the basement membrane. These results provide justification for neglecting these cells in our model.
To test our hypothesis with a simulation model, we also require properties of the interstitial cells and gel. It does not appear that these have been measured for interstitial kidney cells, but various methods [micropipette aspiration (Evans and Yeung, 1989), magnetocytometry (Wang et al., 1993), microplate manipulation (Thoumine and Ott, 1997), atomic-force microscopy (Mathura et al., 2001) and several others reviewed by Brown (2000)] have been used to study a variety of cells [fibroblasts (Thoumine and Ott, 1997; Karcher et al., 2003), myogenic cells (Desprat et al., 2005), respiratory epithelial cells (Alcaraz et al., 2003), ovary cells (Canetta et al., 2005), muscles cells of multiple types (Mathura et al., 2001), and others]. Despite differences in measurement methods, the types of cells measured, varying capacities for active transduction and motion, and different viscoelastic constitutive frameworks used to describe data, nearly all cells measured have relatively small elasticity, with linear elastic moduli typically around 1kPa, and relaxation times typically greater than 1s due to their high relative viscosity. Cyclically applied forces with periods of 1s have been observed to cause accumulating displacement each cycle (Karcher et al., 2003). More rapid strains (100Hz oscillations) have shown that the principal resistance to rapid distortion is viscous (Alcaraz et al., 2003). Even models that do not include simple moduli and relaxation times, such as the power law creep function proposed by Desprat et al. (2005), suggest that recovery from deformation should occur on the time scale of seconds. Since kidney interstitial cells have a fibroblast character, and the shock application rate is on the order 1Hz, the fibroblast cyclic force loading study of Karcher et al. (2003) is perhaps the most directly relevant, both for the cell type and for the rate. They observe a clear drift in displacement for this rate. It has also been observed that mechanical properties of cells can evolve over periods of tens of minutes, which is thought to be the results of active cytoskeletal rearrangement (Thoumine and Ott, 1997; Desprat et al., 2005). If the repeated application of shocks is viewed as a continuous loading—the repeated shocks would indeed exert a mean load—then it might induce cytoskeletal changes that would facilitate additional tissue displacement.
The viscoelastic properties of the extracellular interstitial gel in the kidney are not well characterized, and in general extracellular matrix material is less well characterized than those of cells. However, data indicate that it too has a long relaxation time. The notable lack of collagen fibers (Osvaldo and Latta, 1966) in kidney interstitial gel would suggest that its elasticity would be particularly small, even for interstitial gels. Zeng et al. (2006) studied a collagen gel in a rheometer and fit results with a generalized Maxwell viscoelastic model with two relaxation times: λ1 ≈ 0.6s and λ2 ≈ 5s. The coefficients that weight these two terms suggested equal importance to the overall response. Similar viscoelastic properties were found by Hsu et al. (1994), again suggesting a long relaxation period.
More quantitative analysis of the medulla tissue will require specific measurement of the mechanical properties of the various components for the types of deformation they are expected to experience when shocked. For our current purposes, however, precise measures are unnecessary. It is sufficient for us that the interstitial material does not recover completely in the about 1.0s time scale of shock application in standard treatments. If the structure is such that the basement membrane elasticity does not bring the tissue back to its pre-shocked state, the entire tissue will not recover before the following shock deforms it still further.
Shear due to focused shocks
We make estimates of shock induced shear based on the lithotripter shock-wave characterization of Cleveland et al. (2000) for the Dornier HM3 (Dornier GmbH, Germany). The shock focuses at F2 with a pressure around 40MPa and pressure drops to 0 across a distance perpendicular to its propagation of ~ 1cm, defining the width of the focus. As estimated for lithotriptor shocks by Lokhandwalla and Sturtevant (2001), this gives a peak particle velocity of approximately v = p/ρc = 26m/s. Assuming that the peak pressure drops linearly over 2μs, this gives a maximum displacement of 26μm. Since the affected region is long in the direction of the shock’s propagation, a maximum shear strain of approximately 26μm/1cm = 0.26 percent is achieved. Though these estimates are relatively crude given that the wave is finite amplitude and not planar, it is nevertheless unlikely that a single shock can produce the strains of over 10 percent (for renal tubules) that would be needed to rupture basement membranes (Welling et al., 1995). Similarly, the critical tension for basement membranes is approximately a factor of 20 larger (Tc = 200 to 500mN/m) than the value used by Lokhandwalla and Sturtevant (2001) in their analysis for shock-shear driven hemolysis. Even considerable local shock focusing by the mechanisms proposed by Howard and Sturtevant (1997) would be insufficient to immediately tear the basement membranes by a single-shock mechanism (Lokhandwalla and Sturtevant, 2001).
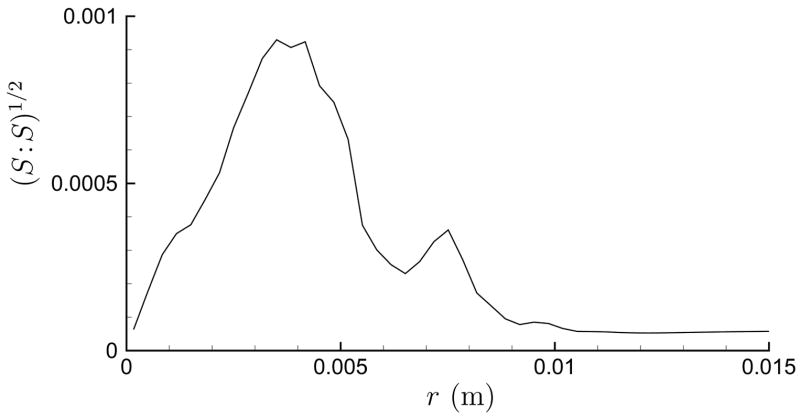
In making these shear estimates, it was assumed that the damage was caused by maximum shear, which would be associated with the compressive portion of the wave, and it was therefore appropriate to neglect the weaker negative pressure that follows (Cleveland et al., 2000). This expansive portion of the wave causes displacements counter to the compressive portion and undoes some, though not all, of the displacement caused by the leading portion of the wave. That the compressive and trailing expansive portions of the pressure signal do not need to cancel pointwise has been previously recognized (Bailey et al., 1999), though without discussion of implications for the net displacement. We estimate this net displacement field by time integrating the velocity fields computed in the shock-dynamic simulations of Tanguay and Colonius (2003). These simulations suggest that a 0.1 percent strain remains in the neighborhood of F2 after the wave has completely passed. Figure 2, for example, shows a radial profile of at F2, where S is the strain tensor in cylindrical coordinates
Fig 2.
Strain norm near F2 for an axisymmetric focus shock obtained by time integrating computed velocity fields (Tanguay and Colonius, 2003).
| (2) |
with ux and ur being the displacements in the x (shock propagation) and radial r directions, respectively. This strain is much less than the peak during the passing of the compressive shock front and thus even less likely to cause any significant damage on its own. However, since it remains after the passing of the entire wave it can only be removed by the elasticity of the kidney tissue. If the relaxation time is too slow, this strain will be increased with each additional shock.
We study this relaxation process in our simulation model discussed below. We show that in all cases the relaxation time is significantly longer than the ~ 6μs of the physical deformation. Thus, we will neglect the viscous phase of deformation, as defined by Lokhandwalla and Sturtevant (2001), and assume the shock’s influence is strictly inertial.
Model design
In rabbit kidneys Knepper et al. (1977) found that the interstitial volume fraction Γi changes from about 0.4 near the papilla tip to 0.2 midway up the medulla. These extrema set the range we study. These changes are clear in images of the rabbit inner medulla Jamison and Kriz (1982). Pigs, which have been the subject of the most detailed injury tests, follow the same trend. We show this in figure 3, which contrasts an image of the inner stripe of an outer medulla with one of the inner medulla near the papilla tip. In figure 3 (a), we see the closely packed vascular bundles, limbs and ducts whose structure we attempt to model, hypothesizing that the close spacing of all the tubules will make the tissue here fast to recover from deformation. In contrast, in figure 3 (b) there are extensive regions of interstitial material between the vessels and larger collecting ducts. Humans show essentially the same structural change; the micrograph in figure 1 shows the relatively high interstitial volume fraction near the papilla tip.
Fig 3.
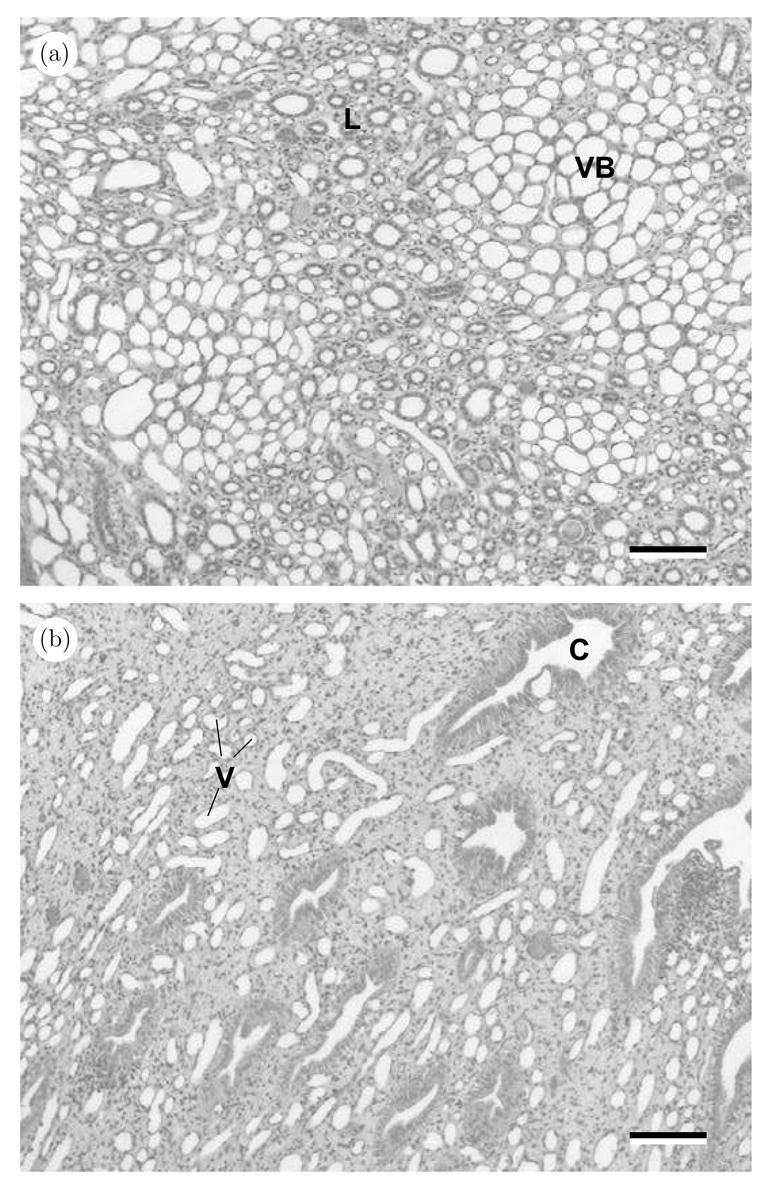
Photomicgrographs of an (a) outer medulla (inner stripe) and an (b) inner medulla near the papilla tip (pig). In (a), closely packed vascular bundles (VB) alternate in space with regions (L) in which ascending and descending thin limbs and thick ascending limbs intermingle with vessels and collecting ducts. In (b), large collecting ducts (C) and small vessels (V) are separated by extensive regions of interstitial material. The nuclei of the interstitial cells appear as black dots in the interstitium. The scale bars are ~ 60μm.
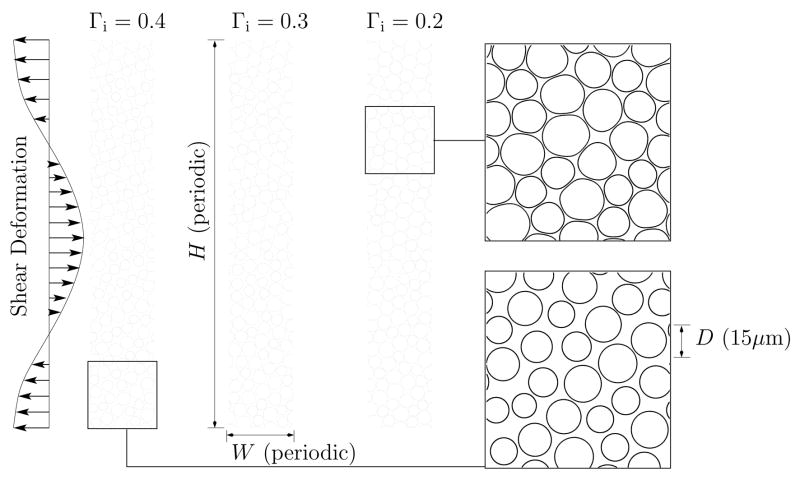
As shown schematically in figure 4, we model the medulla tissue as parallel tubes with different interstitial volume fractions Γi. Similar to Howard and Sturtevant (1997) we assume that the tubes are long and thus only consider their two-dimensional geometry. We represent only a small sub-region of the medulla, using periodic boundary conditions in order to avoid artifacts that would be associated with other potential choices of boundary conditions (e.g. fixed or stress free). Periodic boundary conditions are also the most compatible with the numerical methods we employ. Simulations for two domain sizes will be presented. The larger, which is shown in figure 4 has 150 tube cross sections in a H × W = 75 × 450μm2 domain and the smaller has 30 tubes in a H × W = 50×150μm2 domain. These domains are, of course, significantly smaller than the region over which the shear would occur in a kidney, but they satisfy two key conditions necessary for their results to be applicable. The first condition is that the length over which shear is applied (by the shock wave) is significantly greater than the tube diameters. Similar results for the large and small domain cases confirm insensitivity to this. The second condition is that the relaxation rate of the small simulated regions can be related to the larger-scale shear relaxation in the kidney. If the net effective elasticity and viscosity of the material are linear, than relaxation is independent of transverse length scale. This was also confirmed with tests of the model.
Fig 4.
The simulation model configuration.
The model tissue was constructed by “growing” the tube diameters of a uniform distribution of small tubes until the target volume fraction was reached. While they were grown, they flowed into the random configurations we see in the figure. The resulting average tube diameters in the model were 13μm for Γi = 0.4, 14μm for Γi = 0.3 and 15μm for Γi = 0.2. The randomness of tube sizes in the medulla was modeled with uniform diameter distribution of ±20%. These diameters are appropriate for modeling the vasa recta and capillaries in the inner medulla (e.g. Jamison and Kriz, 1982).
The relaxation time of the interstitial cells and extracellular matrix is expected to be comparable to standard shock delivery rates. In this study, we neglect its elastic character and model it simply as a Newtonian fluid. The small scales and high viscosity allow us to neglect inertia in the relaxation process. For some of the results presented, the interstitial region was set to be λ = 5 times more viscous than the tube’s Newtonian fluid contents (blood) with viscosity μ = 0.035kg/(m·s). However, for finite viscosity ratio the simulation are much more computationally intense. Therefore, to focus our resources on longer time series and larger domains we mostly used λ = 1. We shall see that the key conclusion of this paper is in fact independent of λ.
Numerical algorithm
The boundary integral algorithm used to solve the governing equations for Stokes flow is similar to that used in a previous study of microcirculatory mechanics (Freund, 2007). The velocity at a point x depends upon the stresses applied to the fluid by the deformed tube walls,
| (3) |
via an implicit integral expression,
| (4) |
where s is the arc-length coordinate around any particular shell membrane tube wall, Sij and Tijk are the appropriate periodic versions of the fundamental solutions of the Stokes operator for velocity (Sij, the Stokeslet ) and stress (Tijk, the Stokes stresslet ), and Ωm designates the m-th membrane. Freund (2007) used λ = 1 for all cases, so (4) was an explicit expression for the velocity, but the complete details of the formulation for λ ≠ 1 case are well known (Pozrikidis, 1992), and the fast numerical solution approach we use is outlined also for the this case by Metsi (Metsi, 2000). For the present solutions, each membrane was discretized with 128 Fourier-spectral collocation points, which were used to evaluate (3) for use in (4). The quadratures were computed for these same points as simple sums as appropriate for Fourier basis functions, and the time advancement was by a second-order Runge–Kutta algorithm. The linear system for the unknown velocities that results from (4) in λ ≠ 1 cases was solved with a GMRES(10) algorithm (Saad and Schultz, 1986).
Simulation procedure
After the tissue was constructed, the system was simulated for a long enough time (over 1 second) to insure that it was in equilibrium. During this period all velocities became effectively zero. Then the deformation was applied instantaneously. It was a horizontal displacement of Δx = Ao cos(2πy/H), which is compatible with the periodic boundary conditions. After this deformation, the evolution of the tissue was tracked by computing the x displacement of the basement membranes from their initial conditions: Δx = x(t) − x(0), where t is the time measured from that of the applied shear. Figure 5 shows an example shear deformation relaxation for the Γi = 0.2 cases. It is clear that the response is approximately linear, maintaining its cosine shape. The amplitude of this deformation in time, A(t), is determined by the cosine transform for wavenumber 2π/H. We took Ao = 7.5μm or 15μm for different results presented in this paper. Comparisons with a Ao = 0.75μm case showed essentially the same behavior for A(t)/Ao.
Fig 5.
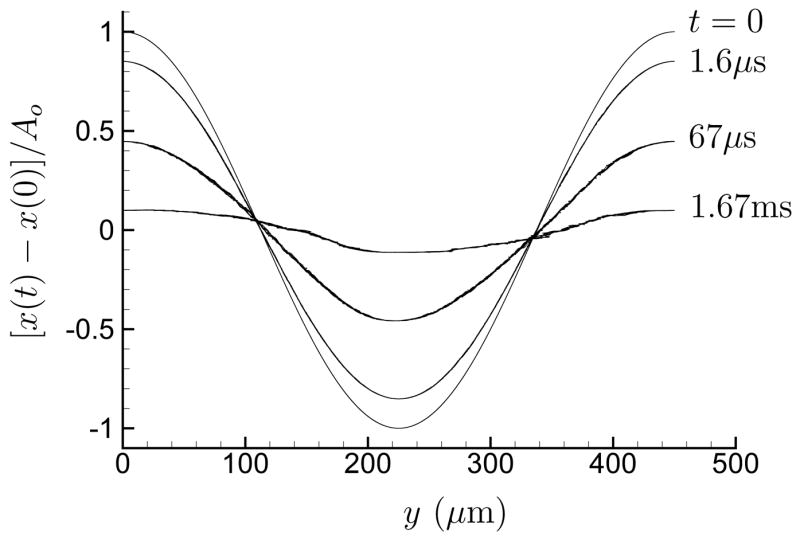
Relaxation of strain for large large domain with λ = 1.0 and Γi = 0.2 (see text). Shown are the discrete collocation points representing the membranes.
Results
Figure 6 (a) shows the relaxation, A(t), for the small domain case with λ = 5 and figure 6 (b) shows the same for the large domain case with λ = 1. We see similar behavior for both cases: for Γi = 0.2, as seen higher in the medulla, the tissue rapidly relaxes to its initial position while for the larger Γi nearer the papilla tip it does not. In the Γi = 0.4 cases, the relaxation is initially rapid, corresponding to the rapid response of the membranes, but effectively stops well short of returning to zero. The actual small elasticity of the interstitial cells and gel would probably cause a continued slow decrease in deformation in this case, but it would only be complete for times significantly longer than 1 second. This qualitative behavior is insensitive to λ. The Γi = 0.3 cases show a behavior that is, as expected, intermediate.
Fig 6.
Effect of a single shocks for (a) small system with λ = 5 and (b) large system with λ = 1:———Γi = 0.4; – – – – Γi = 0.3; and -------- Γi = 0.2.
The effect of repeated shocks is shown in figure 7. Since nearly all the relaxation occurred in the first 0.15s after a model shock deformation, the delivery rate was increased to 6Hz in order to reduce the computation time required. It is clear that the Γi = 0.4 case shows significantly more accumulated deformation than the Γi = 0.3 case, and that the Γi = 0.2 case shows none.
Fig 7.
Effect of shocks applied at 6Hz on the small model system with λ = 1.0: ———Γi = 0.4; – – – – Γi = 0.3; and -------- Γi = 0.2.
Discussion
These results suggest that the ~ 0.1 percent net shear deformation per shock would be completely relaxed when the basement membranes of the renal structures are effectively in contact, as when Γi = 0.2. However, for the larger interstitial volume cases the relaxation is both slower and, in absence of interstitial elasticity, incomplete. Figure 6 (a) shows that after 1 second the Γi = 0.4 case still retains over 15 percent of the strain caused by the shock after 1 second. For zero interstitial elasticity, 1000 shocks would yield a strain of approximately 15 percent, assuming a homogeneous material. However, since the basement membranes themselves relax in all cases, the local strains of the tissue between the vessels would be considerably higher. Such strains may be sufficient to cause damage even in absence of cavitation. Any tissue fatigue due to the cyclic character of the straining would tend to further promote damage. In the Γi = 0.3 case, the net strain of the material after 1 second of relaxation is lower, but it would be even more concentrated in the interstitial space than in the Γi = 0.4 case and therefore also potentially damaging.
We studied this system with a two-dimensional model and therefore neglected restoration of the material due to any induced longitudinal tension in the vessels. An elastic response in this coordinate direction would accelerate relaxation toward the undeformed condition, but it is unclear what appropriate boundary conditions for displacements in that direction would be. The vessels would not be expected to be held taut outside of neighborhood of F2. Indeed, they are not even particularly straight (e.g. Jamison and Kriz, 1982, figure 15-1, p. 224), and may therefore potentially be straightened with little elastic resistance.
Our viscous fluid model suggests that any deformation recovery that will occur is nearly complete by the first 0.15s after the shock, so in this case the proposed mechanism would be independent of shock delivery rate so long as it is slower than ~ 6Hz. However, the actual viscoelasticity of the interstitial material, with a relaxation time ~ 1s, would be expected to introduce a sensitivity to the shock delivery rate. The greater the time between shocks, the more deformation recovery could result via the interstitial material’s relatively small elasticity. Assuming an interstitial-material relaxation time of 1s, we would expect significantly decreased damage for delivery rates slower than ~ 1Hz. Conversely, damage should increase for faster delivery rates. Unfortunately from the perspective of investigation with, say, animal models, this is not the only damage initiation mechanism that would be expected to show this trend. Damage initiation via the growth of bubbles up to the point of violent cavitational collapse (e.g. Zhong et al., 2001) should show a similar trend if cavitation nuclei can advect away or dissolve in the time between shocks. However, it could be tested with inverted shock waves. For the proposed cumulative shear mechanism, these should cause less bleeding of the type observed (Evan et al., 2002) at slower delivery rates. On the other hand, if it is direct shear damage (Lokhandwalla and Sturtevant, 2001) that causes the observed bleeding in this cavitation-free case, that should be insensitive to delivery rate.
The cumulative shear mechanism clearly predicts that hemorrhage should first appear in the inner medulla. Initiation location is difficult to assess and does not appear to have been the subject of extensive investigations. However, automatic digital sectioning identifying regions of hemorrhage do suggest this location (Blomgren et al., 1997). For the 2000 shocks at 24 kV delivered by a Dornier HM3 in that study, hemorrhage is identified in several papilla only toward the tip and not elsewhere in the kidney. Connors et al. (2000) also show a greater propensity for lesions near the papilla tip, but also to a lesser degree in the cortex near the renal capsule.
Another implication of the model is that broader focal zones, even at the same peak pressure, should be less damaging because there should be less shear. Focal zone width, shock strength and delivery rate have not been studied independently, but preliminary results with broader focal zones at lower peak shock pressures and relatively slow rate (27/min) do indeed show a marked decrease in injury (Evan et al., 2006). A reduction of shock strength of a standard narrower focus machine reduces shear and is observed also to reduce injury (Connors et al., 2000), but more tests are needed to confirm the exact mechanism(s). If the cumulative shear mechanism is confirmed to be important, rate adjustment and wave tailoring to reduce net shear should offer means of reducing injury without compromising stone commutation.
Acknowledgments
We are grateful to J. McAteer for comments on a draft of this paper. Portions of this work were supported by NIH grant PO1-DK043881.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farré R, Navajas D. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophysical J. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey MR, Blackstock DT, Cleveland RO, Crum LA. Comparison of electrohydraulic lithotripters with rigid and pressure-release ellipsoidal reflectors. II. Cavitation fields. J of Acoust Soc Am. 1999;106:1149–1160. doi: 10.1121/1.427123. [DOI] [PubMed] [Google Scholar]
- Bailey MR, Crum LA, Evan AP, McAteer JA, Williams JC, Jr, Sapozhnikov OA, Cleve-land RO, Colonius T. Cavitation in shock wave lithotripsy. The Fifth International Symposium on Cavitation, Cav03-OS-2-1-006; Osaka, Japan. 2003. [Google Scholar]
- Bailey MR, Pishchalnikov YA, Sapozhnikov OA, Cleveland RO, McAteer JA, Miller NA, Pishchalnikova IV, Connors BA, Crum LA, Evan AP. Cavitation detection during shock-wave lithotripsy. Ultrasound in Med & Biol. 2005;31:1245–1256. doi: 10.1016/j.ultrasmedbio.2005.02.017. [DOI] [PubMed] [Google Scholar]
- Blomgren PM, Connors BA, Lingeman JE, Willis LR, Evan AP. Quantitation of shock wave lithotripsy-induced lesion in small and large pig kidneys. Anatomical Record. 1997;249:341–348. doi: 10.1002/(SICI)1097-0185(199711)249:3<341::AID-AR4>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- Brown TD. Techniques for mechanical stimulation of cells in vitro: a review. J Biomech. 2000;33:3–14. doi: 10.1016/s0021-9290(99)00177-3. [DOI] [PubMed] [Google Scholar]
- Canetta E, Duperray A, Leyrat A, Verdier C. Measuring cell visoelastic peroperties using a force-spectrometer: Influence of protien-cytoplasm interactions. Biorheology. 2005;42:321–333. [PMC free article] [PubMed] [Google Scholar]
- Cleveland RO, Bailey MR, Fineberg N, Hartenbaum B, Kokhandwalla M, McAteer GA, Sturtevant B. Design and characterization of a research electrohydraulic lithotripter patterned after the Dornier HM3. Rev Sci Instr. 2000;71:2514–2525. [Google Scholar]
- Connors BA, Evan AP, Willis LR, Blomgren PM, Lingeman JE, Fineberg NS. The effect of discharge voltage on renal injury and impairment caused by lithotripsy in the pig. J Am Soc Nephrol. 2000;11:310–318. doi: 10.1681/ASN.V112310. [DOI] [PubMed] [Google Scholar]
- Desprat N, Richert A, Simeon J, Asnaciosx A. Creep function of a single living cell. Biophysical J. 2005;88:2224–2233. doi: 10.1529/biophysj.104.050278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evan AP, Connors BA, Lingeman JE, Blomgren P, Willis JR. Branching patterns of the renal artery of the pig. The Anatomical Record. 1996;246:217–223. doi: 10.1002/(SICI)1097-0185(199610)246:2<217::AID-AR8>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Evan AP, McAteer JA. Q-effects of shock-wave lithotripsy. In: Coe FL, Favus MJ, Pak CYC, Parks JH, Preminger GM, editors. Kidney stones: medical and surgical management. Philadelphia: Lippincott-Raven; 1996. pp. 549–570. [Google Scholar]
- Evan AP, Willis LR, Lingeman JE, McAteer JA. Renal trauma and the risk of long-term complications in shock wave lithotripsy. Nephron. 1998;78:1–8. doi: 10.1159/000044874. [DOI] [PubMed] [Google Scholar]
- Evan AP, Willis LR, McAteer JA, Bailey MR, Connors BA, Shao Y, Lingeman JE, Williams JC, Jr, Fineberg NS, Crum LA. Kidney damage and renal functional changes are minimized by waveform control that suppresses caviation in shockwave lithotripsy. The Journal of Urology. 2002;168:1556–1562. doi: 10.1016/S0022-5347(05)64520-X. [DOI] [PubMed] [Google Scholar]
- Evan AP, Pishchalnikov YA, Williams JC, Jr, McAteer JA, Connors BA, Handa R, Willis LR, Kim S, Lingeman JE. Minimal tissue injury and effective stone breakage in the pig model using the eisenmenger broad focal zone, low-pressure lithotripter. Journal of Urology. 2006;175(1668 Suppl):538–538. [Google Scholar]
- Evans E, Yeung A. Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration. Biophysical J. 1989;56:151–160. doi: 10.1016/S0006-3495(89)82660-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund JB. Leukocyte margination in a model microvessel. Physics of Fluids. 2007 in press. [Google Scholar]
- Howard D, Sturtevant B. In vitro study of the mechanical effects of shock-wave lithotripsy. Ultrasound in Med & Biol. 1997;23:1107–1122. doi: 10.1016/s0301-5629(97)00081-1. [DOI] [PubMed] [Google Scholar]
- Hsu S, Jamison AM, Blackwell J. Viscoelastic studies of extracellular matrix interactions in a model native collagen gel system. Biorheology. 1994;31:21–36. doi: 10.3233/bir-1994-31103. [DOI] [PubMed] [Google Scholar]
- Jamison RL, Kriz W. Urinary concentrating mechanism: structure and function. New York: Oxford University Press; 1982. [Google Scholar]
- Karcher H, Lammerding J, Huang H, Lee RT, Kamm RD, Kaazempur-Mofrad M. A three-dimensional viscoelastic model for cell deformation with experimental verification. Biophysical J. 2003;85:3336–3349. doi: 10.1016/S0006-3495(03)74753-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knepper MA, Danielson RA, Saidel GM, Post RS. Quantitative analysis of renal medulary anatomy in rats and rabbits. Kidney International. 1977;12:313–323. doi: 10.1038/ki.1977.118. [DOI] [PubMed] [Google Scholar]
- Krambeck AE, Gettman MT, Rohlinger A, Lohse CM, E PD, Segura JW. Diabetes mellitus and hypertension associated with shock wave lithotripsy of renal and proximal ureteral stones at 19 years of followup. J Urology. 2006;175:1742–1747. doi: 10.1016/S0022-5347(05)00989-4. [DOI] [PubMed] [Google Scholar]
- Lingeman JE, Delius M, Evan AP, Gupta M, Sarica K, Strohmaier W, McAteer JA, Williams J., Jr . Bioeffects and physical mechanisms of SW effects in SWL. In: Segura J, Conort P, Khoury S, Pak C, Preminger GM, Tolley D, editors. Stone Disease, 1st International Consultation on Stone Disease. Paris: Health Publishers; 2003. pp. 287–356. [Google Scholar]
- Lokhandwalla M, Sturtevant B. Mechanical haemolysis in shock wave lithotripsy (SWL): I. Analysis of cell deformation due to SWL flow-fields. Physics in Med and Bio. 2001;46:413–437. doi: 10.1088/0031-9155/46/2/310. [DOI] [PubMed] [Google Scholar]
- Madsen KM, Tisher CC. Anatomy of the kidney. In: Brenner BM, Levine SA, editors. Brenner & Rector’s the kidney. 7 Philadelphia: 2004. pp. 2–72. [Google Scholar]
- Mathura AB, Collinswortha AM, Reicherta WM, Krausb WE, Truskey GA. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J Biomech. 2001;34:1545–1553. doi: 10.1016/s0021-9290(01)00149-x. [DOI] [PubMed] [Google Scholar]
- Metsi E. PhD thesis. University of Illinois: Urbana-Champaign; 2000. Large scale simulations of bidisperse emulsions and foams. [Google Scholar]
- Osvaldo L, Latta H. Interstitial cells and the renal medulla. J Ultrastructure Res. 1966;15:589–613. doi: 10.1016/s0022-5320(66)80129-6. [DOI] [PubMed] [Google Scholar]
- Pozrikidis C. Boundary integral and singularity methods for linearized viscous flow. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- Saad Y, Schultz MH. GMRES: A generalized minimal residual algorithm for solveing non-symmetric linear systems. SIAM J Sci Stat Comp. 1986;7:856–869. [Google Scholar]
- Shao Y, Connors BA, Evan AP, Willis LR, Lifshitz DA, Lingeman JE. Morphological changes induced in the pig kidney by extracorporeal shock wave lithotripsy. The Anatomical Record Part A. 2003;275A:979–989. doi: 10.1002/ar.a.10115. [DOI] [PubMed] [Google Scholar]
- Sturtevant B. Shock wave physics of lithotriptors. In: Smith AD, editor. Smith’s Textbook of Endourology. Vol. 1. St. Louis, Missouri: Quality Medical Publishing, Inc; 1996. pp. 529–552. [Google Scholar]
- Swane GTG, Smaje LH, Bergel DH. Distensibility of single capillaries and venules in the rat and frog mesentry. Int J Microcirc Clin Exp. 1989;8:25–42. [PubMed] [Google Scholar]
- Tanguay M, Colonius T. Progress in modeling and simulation of shock wave lithotripsy (SWL). In Fifth International Symposium on Cavitation (CAV2003); Osaka, Japan. 2003. pp. 1–11. [Google Scholar]
- Thoumine O, Ott A. Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- Wang N, Butler JP, Ingber DE. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 1993;260:1124–1127. doi: 10.1126/science.7684161. [DOI] [PubMed] [Google Scholar]
- Welling LW, Zupka MT, Welling DJ. Mechanical properties of basement-membrane. News In Physiological Sciences. 1995;10:30–35. [Google Scholar]
- Zeng D, Ferrari A, Ulmer J, Veligodskiy A, Fischer P, Spatz J, Ventikos Y, Poulikakos D, Kroschewski R. Three-dimensional modeling of mechanical forces in the extracellular matrix during epithelial lumen formation. Biophysical J. 2006;90:4380–4391. doi: 10.1529/biophysj.105.073494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong P, Zhou Y, Zhu S. Dynamics of bubble oscillations in constrained media and mechanisms of vesel rupture in SWL. Ultrasound in Med & Biol. 2001;27:119–134. doi: 10.1016/s0301-5629(00)00322-7. [DOI] [PubMed] [Google Scholar]