Abstract
The purpose of this study was to develop a method for identifying subject-specific passive elastic joint moment-angle relationships in the lower extremity, which could subsequently be used to estimate passive contributions to joint kinetics during gait. Twenty healthy young adults participated in the study. Subjects were positioned sidelying with their dominant limb supported on a table via low-friction carts. A physical therapist slowly manipulated the limb through full sagittal hip, knee, and ankle ranges of motion using two hand-held 3D load cells. Lower extremity kinematics, measured with a passive marker motion capture system, and load cell readings were used to compute joint angles and associated passive joint moments. We formulated a passive joint moment-angle model that included eight exponential functions to account for forces generated via the passive stretch of uni-articular structures and bi-articular muscles. Model parameters were estimated for individual subjects by minimizing the sum of squared errors between model predicted and experimentally measured moments. The model predictions closely replicated measured joint moments with average root-mean-squared errors of 2.5 Nm, 1.4 Nm, and 0.7 Nm about the hip, knee, and ankle respectively. We show that the models can be coupled with gait kinematics to estimate passive joint moments during walking. Passive hip moments were substantial from terminal stance through initial swing, with energy being stored as the hip extended and subsequently returned during pre- and initial swing. We conclude that the proposed methodology could provide quantitative insights into the potentially important role that passive mechanisms play in both normal and abnormal gait.
Keywords: passive tension, gait, bi-articular muscles
INTRODUCTION
The stretch of soft tissue about a joint generates a passive joint moment that can influence functional movement. Furthermore, the passive elastic moment at one joint is influenced by motion at a neighboring joint due to the stretch of bi-articular muscles such as the rectus femoris, hamstrings, and gastrocnemius. Bi-articulate coupling enables the transfer of energy between joints (Kaya, et al., 2005), and is thus important to consider when evaluating the contributions of passive stiffness to gait kinematics and kinetics (Ishikawa, et al., 2005; Mansour and Audu, 1986; Yoon and Mansour, 1982).
A double exponential model of passive moment-angle relationships (Davy and Audu, 1987) has previously been used to capture the sharp increase in force that occurs near end-range joint motion. However, the use of exponential models requires accurate kinematic measures since a small deviation in joint angle can cause a large change in the estimated joint moment, and therefore substantially impact the mechanics attributed to passive properties. This factor may contribute to the widely varying estimates of passive contributions to the work and power done during walking (Riener and Edrich, 1999; Vrahas, et al., 1990; Yoon and Mansour, 1982). Furthermore, the identification of subject-specific passive moment-angle relationships is often not done, yet is thought to be relevant for understanding the role of passive forces during both normal (Edrich, et al., 2000; Ishikawa, et al., 2005; McGibbon, 2003; Muraoka, et al., 2005) and abnormal (Cooney, et al., 2006) gait. Finally, prior approaches of measuring passive joint moments have only considered a limited number of joint angle combinations (Edrich, et al., 2000; Mansour and Audu, 1986; Vrahas, et al., 1990) when estimating bi-articular properties, which limits the robustness of the approach.
The purpose of this study was to develop a method for identifying subject-specific passive elastic joint moment-angle relationships about the hip, knee, and ankle, which could then be used to estimate passive contributions to joint kinetics during gait. A key aspect to our approach is the use of the same methodology for measuring joint kinematics in passive and gait analysis, allowing for more consistent estimates of passive joint mechanics than has been achieved previously. We demonstrate this approach by using the identified models to estimate the hip moments arising from the passive stretch of soft tissues during normal walking.
METHODS
Experiment
Twenty healthy young adults participated in the study (Table 1). Subjects had no history of major orthopedic diagnosis, musculoskeletal trauma, or persistent joint pain. Each subject gave informed consent according to a protocol approved by the University of Wisconsin’s Health Sciences Institutional Review Board.
Table 1.
Mean (s.d.) age, mass, and height of the 20 subjects tested.
| Males | Females | |
|---|---|---|
| Number of subjects | 9 | 11 |
| Age (yrs) | 26.1 (4.1) | 25.5 (3.1) |
| Mass (kg) | 79.2 (7.6) | 59.3 (13.2) |
| Height (m) | 1.82 (0.10) | 1.66 (0.10) |
The experimental setup (Fig. 1a), was designed to simultaneously measure the joint angles and sagittal plane passive joint moments about the hip, knee, and ankle. Subjects were positioned side-lying with their dominant limb supported on a table via low-friction carts placed under the medial side of the thigh and leg. A padded brace prevented rotation and translation of the pelvis during testing. With the subject relaxed, a physical therapist slowly manipulated the hip, knee, and ankle through full ranges of motion in 15 unique trials using two hand-held three dimensional (3D) load cells (model 45E15A, range 250 lbs; JR3 Inc., Woodland, CA). Load cell forces and moments were recorded at 2000 Hz. The trials were designed to decouple the passive sagittal contributions from the major uni- and bi-articular soft tissues acting about the hip, knee, and ankle joints (Table 2).
Fig. 1.
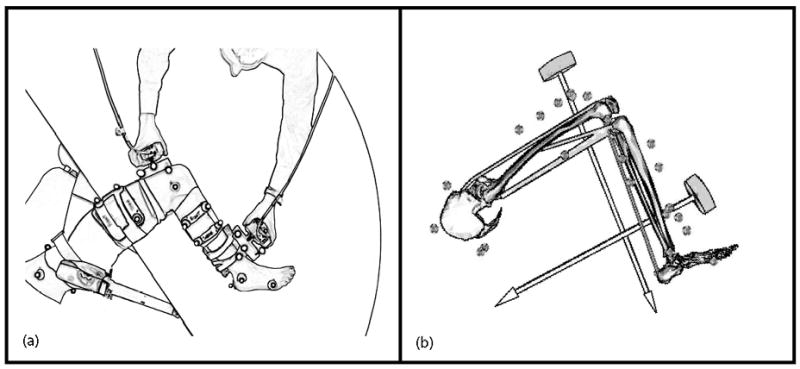
(a) A top view of the apparatus used to simultaneously measure the passive elastic properties of the hip, knee, and ankle. The pelvis was secured to prevent rotation and translation during testing. The positions of reflective markers were monitored to characterize the three-dimensional kinematics of the lower extremity and two hand-held load cells. (b) Measured forces and kinemaitcs were input to a 12 degree of freedom linked segment model to compute the passive moments about the joints of the lower extremity.
Table 2.
Fifteen separate trials were used to identify the passive moment-angle relationships. Shown are the approximate joint angles, joint excursions, and the muscles that were stretched. Positive angles represent hip flexion, knee flexion, and ankle dorsiflexion. Negative angles represent hip extension and ankle plantarflexion.
| Trial | Hip Flexion (deg) | Knee Flexion (deg) | Ankle Dorsiflexion (deg) | Muscles Stretched |
|---|---|---|---|---|
| 1 | −15–0 | 0–60 | ~ −20 | RF, HF |
| 2 | −15–0 | 0–10 | ~ −20 | RF, HF |
| 3 | −15–0 | 0–135 | ~ −20 | RF, HF |
| 4 | 0 | 0–135 | ~ −20 | RF, HF |
| 5 | 0–30 | 0–35 | ~ −20 | HAM, HE |
| 6 | 0–30 | 0–135 | ~ −20 | RF, HF, HE |
| 7 | 0–60 | 0–35 | ~ −20 | HAM, HE |
| 8 | 0–60 | 0–135 | ~ −20 | RF, HF, HE |
| 9 | 0–85 | 0–35 | ~ −20 | HAM, HE |
| 10 | 0–85 | 0–135 | ~ −20 | HAM, RF, HE |
| 11 | ~ 15 | 0 | −20–20 | GAS, PF |
| 12 | ~ 15 | 0–60 | −20–20 | GAS, PF |
| 13 | ~ 15 | 0–135 | −20–20 | GAS, PF |
| 14 | −15–0 | 0–25 | ~ −20 | HF |
| 15 | 0–100 | 0–25 | ~ −20 | HE |
Abbreviations: rectus femoris (RF), hamstrings (HAM), gastrocnemius (GAS), uni-articular ankle plantarflexors (PF), hip extensors (HE), hip flexors (HF), knee extensors (KE), and knee flexors (KF)
Three-dimensional kinematics of the load cells and lower extremity were recorded (100 Hz) using an optical, passive marker motion capture system (Motion Analysis Corporation, Santa Rosa, CA). The position and orientation of each load cell was monitored by four markers rigidly fixed to the load cell frame. Lower extremity motion was tracked via eight markers placed on palpable anatomical landmarks on the pelvis and lower extremity, and an additional seven tracking markers on rigid plates attached to the thigh and shank (Fig. 1). An initial recording using 35 markers was performed with the subject in an upright standing posture to establish bilateral joint centers, body segment coordinate systems, and segment lengths. In addition, two trials were performed in which the subject circumducted his/her right and left limbs to establish hip joint center locations in the pelvis reference frame (Piazza, et al., 2004).
Electromyographic (EMG) signals from seven lower extremity muscles (rectus femoris, vastus lateralis, medial hamstrings, lateral hamstrings, tibialis anterior, soleus, gastrocnemius) were recorded using pre-amplified single differential surface electrodes with a fixed inter-electrode distance of 10mm (DE-2.1, DelSys, Inc, Boston, MA). In preparation for electrode placement, the skin was shaved, cleaned with alcohol, and conductive gel was applied to the electrodes. Muscles of interest were identified, with the same investigator placing the electrodes for all subjects. Electrode and load cell cabling was interfaced to an amplifier/processor unit (CMRR >84 dB at 60 Hz; input impedance > 100 MΩ). Amplification of each channel was adjusted to maximize signal resolution, with EMG data sampled at 2000 Hz using a 12-bit A/D converter interfaced to the collection computer. EMG signals were visually monitored during testing and any trial with detectable muscle activity was repeated.
The pelvis and lower extremity were represented by a 12 degree of freedom (DOF) model (Fig. 1b). The pelvis was the base segment with six DOF. The hip was represented as a spherical joint with three DOF. The knee was represented as a one DOF joint in which non-sagittal rotations and tibiofemoral translations were computed as a function of the knee flexion-extension angle (Walker, et al., 1988). The ankle and subtalar joints were represented as pin joints aligned with the anatomical axes (Delp, et al., 1990). The dimensions of each segment in the generic model were scaled to individual subjects such that joint centers and measured marker locations corresponded to virtual locations in the model. At each time step in motion trials, the pelvis position, pelvis orientation, and lower extremity joint angles were computed using an inverse kinematics routine that minimized the sum of squared differences between measured marker positions and corresponding positions of those markers on the model (Lu and O’Connor, 1999). Inverse dynamics analysis was then used to compute the sagittal plane hip, knee, and ankle joint moments from the measured load cell forces and joint angles.
Each subject also performed a series of walking trials at his/her preferred walking speed. Kinematics were recorded using a full body marker set that included, as a subset, the markers used in the passive trials. Ground reaction forces for two successive foot strikes were recorded at 2000 Hz (AMTI, Watertown, MA). Three-dimensional joint angles and joint moments during walking were computed in a manner consistent with the passive testing.
Mathematical Model of Passive Joint Moments
A set of eight exponential functions were developed to account for the stretch of uni-articular structures about the hip, knee, and ankle along with the bi-articular rectus femoris, hamstrings, and gastrocnemius muscles. Uni-articular exponential functions were described by two parameters, gain (β) and offset (α) angle. Bi-articular functions included a third parameter, which ensured the conservation of energy storage and release across joints (see Appendix). As a result, the predicted passive hip moment (M̂h) was a function of hip (θh) and knee (θk) angles. The predicted passive knee moment (M̂k) was a function of hip, knee, and ankle (θa) angles, and the predicted passive ankle moment (M̂a) was a function of knee and ankle angles.
| (eq.1) |
Model parameters were estimated for each subject by minimizing the sum of squared differences between the measured and predicted passive moments (lsqcurvefit, MATLAB, The Mathworks Inc.). Root mean square (RMS) errors between the measured and predicted passive moments were compared for all subjects and trials. For a subset (n=7) of subjects, the estimated model parameters were used to predict joint moments in eight representative trials not used in the parameter estimation phase. These representative trials traversed a full range of hip, knee, and ankle motion, allowing for an assessment of the validity of the model to represent novel loading scenarios. The passive hip moment during walking was estimated using the joint angles measured during gait as inputs to the passive hip moment-angle function (A.5).
RESULTS
Subject-specific models were able to closely replicate the measured joint moments at the hip, knee, and ankle with average root mean square errors of 2.5 Nm in hip flexion-extension, 1.4 Nm in knee flexion-extension, and 0.7 Nm in ankle plantar-dorsiflexion. These RMS errors did not significantly increase when using subject-specific models to estimate joint moments for the validation trials not used in the parameter estimation phase (Table 3). Within subjects, the repeated trials produced qualitatively similar results (Fig. 2). Between subjects, the gains in the exponential models exhibited greater similarity across subjects than the offset angles (Table 4). This contributed to more variability in the passive moments at end-range than at mid-range motion (Fig. 3).
Table 3.
Mean (s.d.) root mean square (RMS) errors between measured and predicted moments (Nm). Subject-specific model parameters were used to predict joint moments in eight additional validations not including in the parameter estimation. Errors between the measured and model predicted moments did not significantly (tested via paired t-tests) vary between the identification and validation trials.
| Hip | Knee | Ankle | |
|---|---|---|---|
| Identification Trials | 2.5 (0.5) | 1.4 (0.3) | 0.7 (0.2) |
| Validation Trials | 2.1 (0.6) | 1.2 (0.3) | 0.4 (0.1) |
Fig. 2.
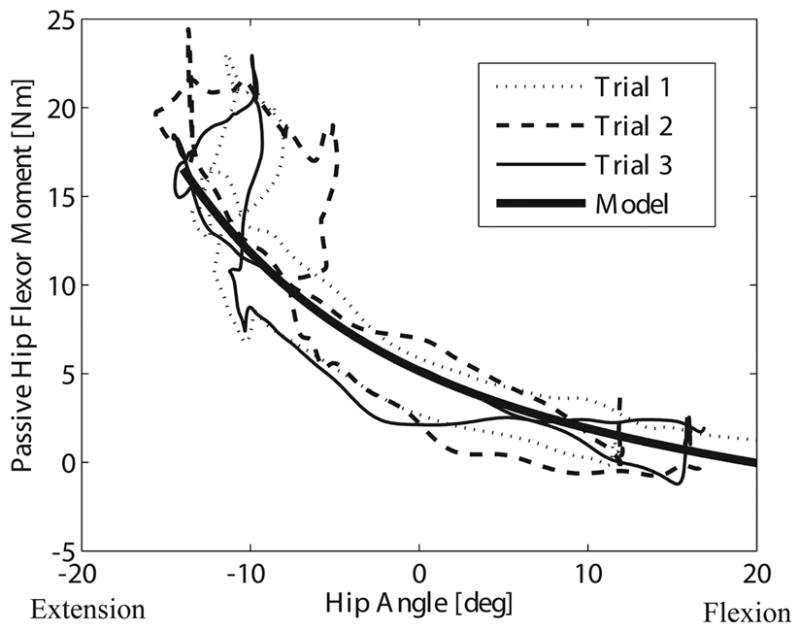
Three representative, repeated trials, in which the hip was first extended and the knee was then flexed. Overlaid is the model-predicted moments using subject-specific parameter estimates. Joint angles from one of the three repeated trials were used as inputs for hip, knee, and ankle angles in the model functions. Both the experimental data and the model contain a loop near full hip extension due to bi-articular rectus femoris stretch as a result of the knee flexion. A slight hysteresis is present in the experimental data, with the moments slightly lower when the hip is flexing than when it is extending.
Table 4.
Mean (s.d.) model parameter estimates across the 20 subjects tested.
| Muscle Function | Gain, β | Offset, α [deg] | |
|---|---|---|---|
| Proximal | Distal | ||
| Rectus Femoris (RF) | 3.1 (1.4) | 1.9 (0.7) | 24.4 (9.0) |
| Hamstrings (HAM) | 5.1 (2.0) | 3.9 (2.5) | 30.8 (14.9) |
| Gastrocnemius (GAS) | 4.5 (1.6) | 4.7 (3.4) | 26.0 (28.9) |
| Hip Flexors (HF) | 5.1 (0.9) | 19.5 (10.0) | |
| Hip Extensors (HE) | 2.0 (0.9) | 27.3 (18.0) | |
| Knee Flexors (KF) | 5.8 (4.2) | 12.8 (13.1) | |
| Knee Extensors (KE) | 3.5 (1.7) | 101.9 (11.9) | |
| Ankle Plantarflexors (PF) | 4.9 (1.5) | −3.4 (5.0) | |
Fig. 3.
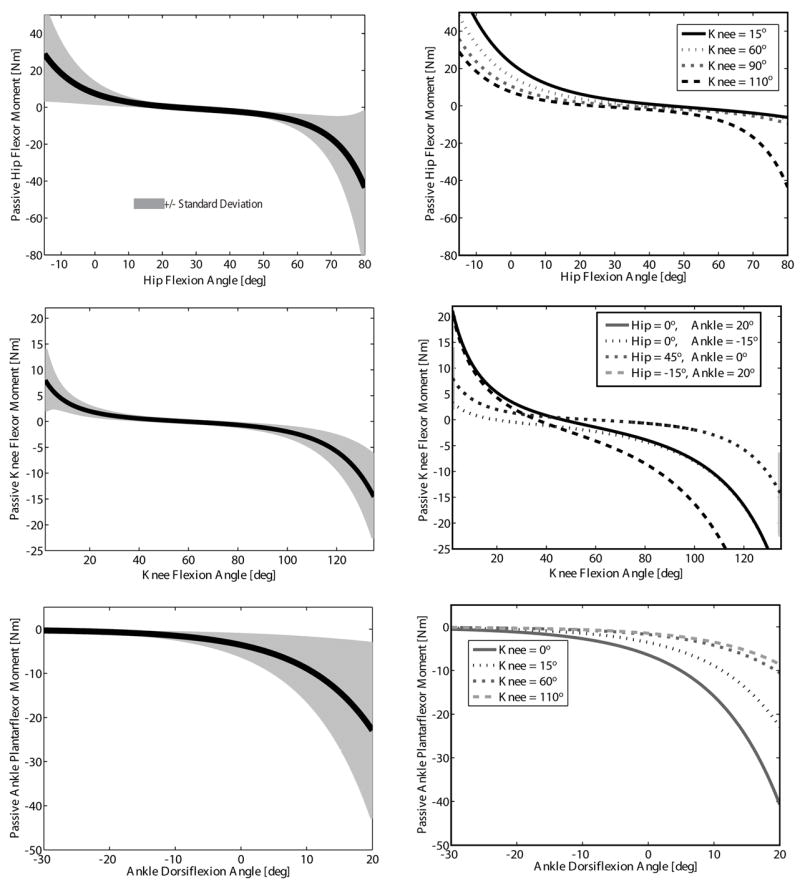
Averaged model predicted joint moment-angle relationships for all 20 subjects. The mean (thick line) and standard deviation (shaded area) were emphasized at representative joint angles (dotted lines) for the hip (knee = 15°), knee (hip = 45°, ankle = 0°), and ankle (knee = 15°). The passive moment changed as the adjacent joint angle(s) varied (dotted lines) demonstrating the contributions of the bi-articular rectus femoris, hamstrings and gastrocnemius.
Substantial hip flexor moments were estimated when joint angle kinematics during gait were used as inputs to the passive hip moment-angle relationship (A.5). Energy was passively absorbed while the hip was extending from terminal-stance to pre-swing (50–60% of the gait cycle). A peak passive hip flexor moment of ~20 Nm occurred just prior to toe-off. Slightly more energy was subsequently returned during pre- and initial-swing (50–73% GC) due to the bi-articular rectus femoris passively transferring energy from the knee to the hip (Fig. 4).
Fig. 4.
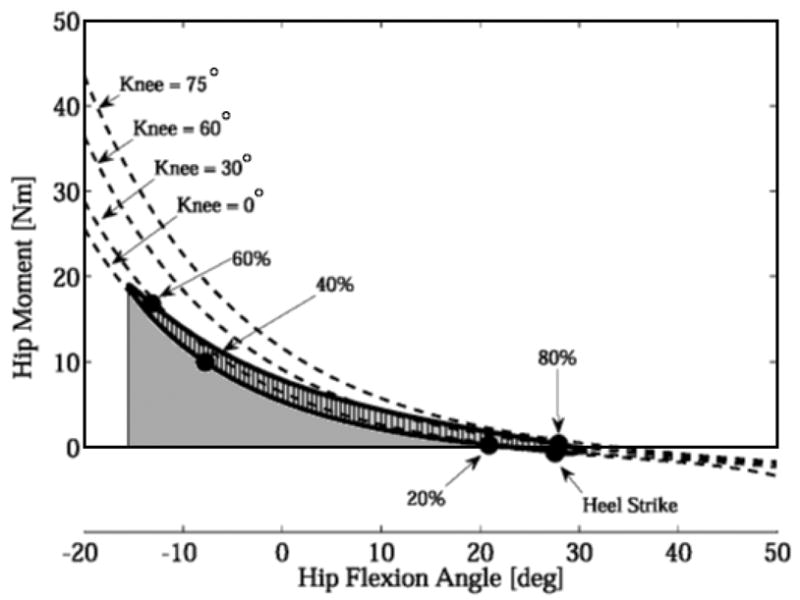
The passive joint moments during walking were estimated by applying the derived moment-angle functions to joint angles measured during walking. The passive hip flexor moment is shown for a single subject at a preferred walking speed. Also shown are the passive hip-flexor moments at 4 fixed knee angles (0°, 30°, 60°, and 75°). Passive energy was absorbed while the hip was extending and returned from approximately pre- to initial-swing (50–73% gait cycle). Slightly greater energy return (cross-hatched area) is achieved via the stretched rectus femoris transferring energy from the knee to the hip.
DISCUSSION
We have introduced a simple experimental setup and mathematical model that can be used to describe the passive joint moment-angle relationships about the hip, knee, and ankle for individual subjects. A unique aspect of our approach was the use of a kinematic marker set that can be directly applied during functional movement, enabling a more consistent description of joint angles and passive moments during movement. This is critical due to the exponential nature of passive forces and the large variability, particularly at end range motion, that can be introduced due to slight measurement errors in joint angles.
Our model includes the effects of both uni-articular structures (single joint muscles, ligaments, joint capsule, skin) and bi-articular muscles. Other researchers have also shown the need to account for the contribution of bi-articular muscle stretch to passive moments (Edrich, et al., 2000; Mansour and Audu, 1986; Riener and Edrich, 1999). However, previous models have not been formulated in a consistent manner that ensures the conservation of energy, i.e. that the energy stored via stretch of a bi-articular muscle is equal to the energy returned by that muscle when it shortens. Enforcing this requirement results in a three parameter model for bi-articular components, rather than a four parameter model that would result from coupling two uni-articular components together (see Appendix). Our formulation allows for bi-articular muscles to absorb energy via stretch at one joint and then release that energy via shortening at the neighboring joint, as has been observed experimentally (Ishikawa, et al., 2005; Kaya, et al., 2005).
The simultaneous identification of passive properties about three joints requires that passive measurements be collected over a full range of motion that decouples the contribution of individual components. Our setup was therefore designed to allow each joint to be passively manipulated in the sagittal plane using hand held load cells. The use of motion capture enabled us to monitor three-dimensional joint angles continuously throughout the trials (Table 2). Previous investigators have relied upon the use of a discrete number of joint angles (Edrich, et al., 2000; Mansour and Audu, 1986; Vrahas, et al., 1990) to elicit bi-articular responses, as well as ensemble averaged passive joint moments across subjects to estimate parameters (Edrich, et al., 2000; Mansour and Audu, 1986; Riener and Edrich, 1999; Yoon and Mansour, 1982). Such simplifications could limit the resolution with which passive properties can be identified. It should be noted that in our approach, the use of data from a subset of trials could be used if one is only interested in select muscles. For example, we have been able to obtain reasonable estimates of the parameters of the hamstrings in healthy subjects by including only those trials that involve substantial hip and knee extension.
A limitation of the proposed mathematical model is that it does not account for a slight hysteresis present in the passive moment-angle data (Fig. 2). Our parameter estimation includes both the increasing and decreasing parts of the moment-angle curve, thereby splitting the difference in the fit. This compromise likely results in a slight underestimation of the peak passive moment and an over-estimation of the passive energy returned. Identifying the parameters of a model that includes viscoelastic effects is much more challenging since this would also require manipulation of the joint velocity (Vrahas, et al., 1990; Yoon and Mansour, 1982).
Others (Edrich, et al., 2000; Vrahas, et al., 1990) have demonstrated relatively small between-trial variability in passive joint moments as we observed (Fig. 2). Due to the length of our entire testing procedure, we did not repeat the entire set of calibration trials necessary to re-estimate the model parameters. However, we did use the identified models to estimate moments during unique trials not using in the model fitting, and found good agreement between the measured and predicted moments.
A potential source of error in our procedure arises from the calculation of joint angles and joint centers from skin-mounted markers. We minimized these errors by taking extra care that the markers remained fixed between the upright calibration trials and the side-lying testing procedures. We also employed a functional hip joint center identification method, which has been shown to reduce errors in locating the hip joint center (Piazza, et al., 2004). However, it remains possible that errors in the estimate of the hip joint center location led to the larger errors in passive moments at the hip compared to the knee and ankle (Table 3).
Electrical activity in select muscles was monitored to ensure a truly passive test. We occasionally observed some reflex activity, for example in the tibialis anterior during dorsiflexion trials. In these cases, the trials were repeated and all of our subjects were capable of eliminating the activity levels upon repeat testing. However the suppression of reflex activities may be challenging for individuals with neuromuscular impairments, in which case it may be necessary to account for active responses superimposed on the passive measures. In addition, muscle activities were recorded on only seven selected superficial muscles so the relaxed state of other muscles, e.g. deeper muscles like the iliopsoas, could not be directly confirmed.
In using the passive moment-angle relationships to estimate passive contributions during movement such as gait, one inherently assumes that the passive properties are additive with the active components present. This is likely a reasonable assumption for fully passive structures such as the joint capsule, ligaments, and skin. However, the interaction of passive and active components in muscle remains an area of active research (Epstein and Herzog, 2003), making it more challenging to quantify precisely how passive components are utilized in movement. Furthermore, our methodology only considered the influence of sagittal plane passive joint moments, which may be reasonable in normal gait. However, further investigation is needed to apply these techniques to pathological gait, e.g. cerebral palsy or stroke, where non-sagittal motion may be considerable.
Applying the passive moment-angle curves to gait demonstrates the potential for substantial contribution of both passive uni- and bi-articular muscle stretch to the joint moments observed (Fig. 4). Our results suggest that passive mechanisms may contribute substantially to the hip flexor moment seen during normal gait. Hip flexor moments are estimated to reach ~50 Nm during normal adult walking (Kerrigan, et al., 1998). We estimated a passive moment of ~20 Nm, meaning that nearly one-half of the hip flexor moment may arise from passive structures. Others have estimated the passive hip flexor moments at toe-off as between 10–50% (Vrahas, et al., 1990; Yoon and Mansour, 1982) of the net component, putting our estimate near the upper end of this range. This moment occurs due to the passive stretch of the uni-articular hip flexors and bi-articular rectus femoris, enabling the absorption of energy during terminal stance and passive return during pre- and initial-swing. The ability of passive structures to store and release energy during normal gait may substantially reduce the active generation of energy required to initiate swing and generate propulsion.
Our methodology could be used to investigate the role that impairments play in abnormal gait. For example, it has been suggested that hip flexion contractures may be used by impaired elderly to passively assist the initiation of limb swing motion (McGibbon, 2003). In addition, it is thought that passive forces arising from tight hamstrings may contribute to diminished terminal swing knee extension commonly seen in children with cerebral palsy (Cooney, et al., 2006). Quantifying the contributions of passive properties to the joint moments and powers observed during abnormal gait may provide new insights into the biomechanical function of impairments during walking.
Acknowledgments
This work was supported by NIH AG 24276, NFL Charities, and NSF pre-doctoral fellowship (AS).
APPENDIX
A mathematical model was used to describe the relationship between the sagittal plane joint angles and passive joint moments about the hip (h), knee (k), and ankle (a). The model included five uni-articular and three bi-articular components. The uni-articular components account for the net moments generated via the single-joint dependent stretch of soft tissue such as ligaments, skin, relaxed uni-articular musculotendons, and the joint capsule. The uni-articular components in the model were divided into the hip flexors (HF), hip extensors (HE), knee flexors (KF), knee extensors (KE), and ankle plantarflexors (PF). The passive ankle dorsiflexor moments were not included since they are not thought to contribute substantially during human gait. The bi-articular muscles in the model were the rectus femoris (RF), hamstrings (HAM), and gastrocnemius (GAS). Model inputs included experimentally measured hip, knee, and ankle angles (θjoint) and joint moments.
Each uni-articular component was represented by an exponential function parameterized by a gain (β) and offset angle (α)
| (A.1) |
where θ is the measured angle of the joint of interest. Note that the predicted uni-articular moment, M̂, reduces to a value of 1 Nm when the joint angle θ is equal to the offset angle α.
Bi-articular muscles generate moments about both the proximal and distal joints they span, and thus have the potential to do simultaneous positive or negative work at either joint while also storing or releasing energy. We formulated the passive bi-articular functions to allow such energy transfer between joints, while ensuring that net energy was neither lost nor created. In general, energy conservation is ensured when the joint moments are the differential of a potential energy function with respect to the proximal (prox) or distal (dist) joint angle. Defining the potential energy function as
| (A.2) |
and differentiating with respect to the proximal and distal angles results in the following expressions used to represent the bi-articular joint moment-angle relationships.
| (A.3) |
| (A.4) |
Bi-articular offset angles were described with respect to the muscle’s more proximal joint (i.e. the value of αRF could be directly compared to θh). The ratio, βdist/βprox, can be interpreted as the instantaneous ratio of the distal and proximal moment arms of a bi-articular muscle. For the bi-articular case, the passive moment reduces to a value of 1 Nm when the distal joint angle is zero and proximal joint angle is at the offset angle.
Considering the joints that each of the uni- and bi-articular components crosses, one obtains the following model for predicting the hip (M̂h), knee (M̂k), and ankle (M̂a) moments from the experimentally measured hip, knee, and ankle angles. A total of 19 parameters were used in the model including 11 gain constants and 8 offset angles (αmuscle).
| (A.5) |
| (A.6) |
| (A.7) |
Model parameters were estimated by determining the set of parameters that minimized the sum of squared errors between model-predicted and measured moments over all passive motion trials.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Cooney KM, Sanders JO, Concha MC, Buczek FL. Novel biomechanics demonstrate gait dysfunction due to hamstring tightness. Clinical Biomechanics. 2006;21:59–66. doi: 10.1016/j.clinbiomech.2005.08.014. [DOI] [PubMed] [Google Scholar]
- Davy DT, Audu ML. A dynamic optimization technique for predicting muscle forces in the swing phase of gait. Journal of Biomechanics. 1987;20:187–201. doi: 10.1016/0021-9290(87)90310-1. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions on Biomedical-Engineering. 1990;37:757–67. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- Edrich T, Riener R, Quintern J. Analysis of passive elastic joint moments in paraplegics. IEEE Transactions on Biomedical Engineering. 2000;47:1058–65. doi: 10.1109/10.855933. [DOI] [PubMed] [Google Scholar]
- Epstein M, Herzog W. Aspects of skeletal muscle modelling. Philosophical Transactions of the Royal Society B: Biological Sciences. 2003;358:1445–52. doi: 10.1098/rstb.2003.1344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishikawa M, Komi PV, Grey MJ, Lepola V, Bruggemann GP. Muscle-tendon interaction and elastic energy usage in human walking. Journal of Applied Physiology. 2005;99:603–8. doi: 10.1152/japplphysiol.00189.2005. [DOI] [PubMed] [Google Scholar]
- Kaya M, Jinha A, Leonard TR, Herzog W. Multi-functionality of the cat medical gastrocnemius during locomotion. Journal of Biomechanics. 2005;38:1291–301. doi: 10.1016/j.jbiomech.2004.06.009. [DOI] [PubMed] [Google Scholar]
- Kerrigan DC, Todd MK, Della Croce U, Lipsitz LA, Collins JJ. Biomechanical gait alterations independent of speed in the healthy elderly: evidence for specific limiting impairments. Archives of Physical Medicine and Rehabilitation. 1998;79:317–22. doi: 10.1016/s0003-9993(98)90013-2. [DOI] [PubMed] [Google Scholar]
- Lu TW, O’Connor JJ. Bone position estimation from skin marker coordinates using global optimisation with joint constraints. Journal of Biomechanics. 1999;32:129–34. doi: 10.1016/s0021-9290(98)00158-4. [DOI] [PubMed] [Google Scholar]
- Mansour JM, Audu ML. The passive elastic moment at the knee and its influence on human gait. Journal of Biomechanics. 1986;19:369–73. doi: 10.1016/0021-9290(86)90013-8. [DOI] [PubMed] [Google Scholar]
- McGibbon CA. Toward a better understanding of gait changes with age and disablement: neuromuscular adaptation. Exercise & Sport Sciences Reviews. 2003;31:102–8. doi: 10.1097/00003677-200304000-00009. [DOI] [PubMed] [Google Scholar]
- Muraoka T, Chino K, Muramatsu T, Fukunaga T, Kanehisa H. In vivo passive mechanical properties of the human gastrocnemius muscle belly. Journal of Biomechanics. 2005;38:1213–9. doi: 10.1016/j.jbiomech.2004.06.012. [DOI] [PubMed] [Google Scholar]
- Piazza SJ, Erdemir A, Okita N, Cavanagh PR. Assessment of the functional method of hip joint center location subject to reduced range of hip motion. Journal of Biomechanics. 2004;37:349–56. doi: 10.1016/s0021-9290(03)00288-4. [DOI] [PubMed] [Google Scholar]
- Riener R, Edrich T. Identification of passive elastic joint moments in the lower extremities. Journal of Biomechanics. 1999;32:539–44. doi: 10.1016/s0021-9290(99)00009-3. [DOI] [PubMed] [Google Scholar]
- Vrahas MS, Brand RA, Brown TD, Andrews JG. Contribution of passive tissues to the intersegmental moments at the hip. Journal of Biomechanics. 1990;23:357–62. doi: 10.1016/0021-9290(90)90065-b. [DOI] [PubMed] [Google Scholar]
- Walker PS, Rovick JS, Robertson DD. The effects of knee brace hinge design and placement on joint mechanics. Journal of Biomechanics. 1988;21:965–74. doi: 10.1016/0021-9290(88)90135-2. [DOI] [PubMed] [Google Scholar]
- Yoon YS, Mansour JM. The passive elastic moment at the hip. Journal of Biomechanics. 1982;15:905–10. doi: 10.1016/0021-9290(82)90008-2. [DOI] [PubMed] [Google Scholar]


