Insulin Transport within Skeletal Muscle Transverse Tubule Networks

Abstract

It has recently been observed in situ in mice that insulin takes ∼10 min to be transported 20 μm into the t-tubule networks of skeletal muscle fibers. The mechanisms for this slow transport are unknown. It has been suggested that the biochemical composition of the t-tubular space that may include large molecules acting as gels and increased viscosity in the narrow tubules may explain this slow diffusion. In this article, we construct a mathematical model of insulin transport within the t-tubule network to determine potential mechanisms responsible for this slow insulin transport process. Our model includes insulin diffusion, insulin binding to insulin receptors, t-tubule network tortuosity, interstitial fluid viscosity, hydrodynamic wall effects, and insulin receptor internalization and recycling. The model predicted that depending on fiber type there is a 2–15 min delay in the arrival time of insulin between the sarcolemma and inner t-tubules (located 20 μm from the sarcolemma) after insulin injection. This is consistent with the experimental data. Increased viscosity in the narrow t-tubules and large molecules acting as gels are not the primary mechanisms responsible for the slow insulin diffusion. The primary mechanisms responsible for the slow insulin transport are insulin binding to insulin receptors and network tortuosity.

INTRODUCTION

Insulin is an important hormone that controls glucose transport within skeletal muscle cells. Insulin binds to insulin receptors located within the t-tubules of skeletal muscle fibers and allows the entry of glucose into muscle cells (1). The t-tubule networks of skeletal muscle fibers allow for propagation of electrical and chemical signals into the muscle fiber. These t-tubule networks are highly branched spacefilling networks that are located near sarcomere Z-lines and have primarily transverse branches. It has been observed in situ in mice that there is a 10 min delay in insulin transport between the sarcolemma and inner t-tubules located 20 μm from the sarcolemma (2). Diffusive insulin transport in the t-tubules is therefore ∼1000 times slower than in free solution. It was suggested by Lauritzen et al. (2) that the biochemical composition of the t-tubular space that may include large molecules acting as gels and increased viscosity in the narrow tubules may explain this slow diffusion of insulin through the t-tubule network. In this article, we construct a theoretical model of insulin diffusion within the skeletal muscle t-tubule network to help determine potential mechanisms responsible for this slow insulin transport process. The model includes insulin diffusion, insulin binding to insulin receptors within the t-tubules, t-tubule network tortuosity, interstitial fluid viscosity, hydrodynamic wall effects, and insulin receptor internalization and recycling. Our investigation shows that large molecules acting as gels and increased viscosity in the narrow tubules are not the major factors responsible for the slow insulin diffusion in the t-tubules. Based on our modeling analysis we conclude that the primary mechanisms responsible for the slow insulin transport within the t-tubules are insulin binding to insulin receptors and t-tubule network tortuosity.

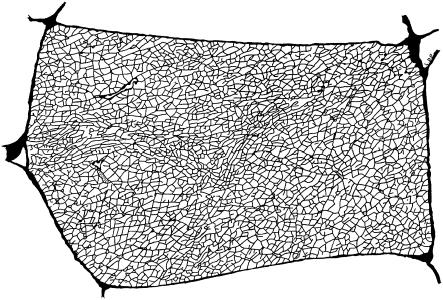
A reconstruction of the t-tubule network by Peachey and Eisenberg (3) using electron microscope slices of frog sartorius muscle fibers is shown in Fig. 1. The extensive network is largely an isotropic irregular network and the diameter of the t-tubules is ∼18 nm (4). The tortuous structure of the t-tubule network impedes the diffusion and transport of material through the t-tubule network and it has been observed experimentally that the effective diffusion coefficient for ions in the t-tubule network is five times smaller than in free solution (5). In this article, we investigate the effect of t-tubule network geometry on the transport of insulin through the t-tubule networks of skeletal muscle fibers.

FIGURE 1.

A reconstruction of the t-tubule network made by Peachey and Eisenberg (3) using electron microscope slices of frog sartorius muscle fibers (×1400; fiber is ∼40 × 80 μm). The boundary of the t-tubule network represents the sarcolemma. Reprinted with permission from the Biophysical Society and L. D. Peachey.

RESULTS

Mathematical model

The simplest conceptual model of insulin (I) binding to the insulin receptor (R), receptor internalization (IR*), and recycling is

where k₊ and k₋ are the rates of insulin binding and unbinding to the receptor, A₁ and A₂ are the rates of internalization of insulin bound and unbound receptors, and G is the rate of receptor recycling. Internalized insulin is not returned to the t-tubules. The transport of insulin in the t-tubules of a skeletal muscle fiber with a circular cross section is then described by the homogenized system of equations

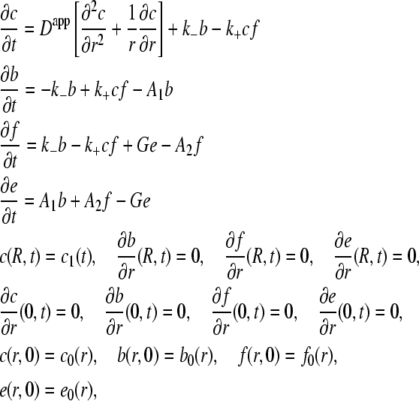(1)

where c(r,t) is the insulin concentration in the t-tubules at radial location r from the center of the fiber at time t, f is the concentration of insulin receptors, b is the concentration of insulin-bound receptors, e is the concentration of internalized receptors, R is the fiber radius, D^app = τD is the apparent insulin diffusion coefficient, where τ is the total t-tubule network tortuosity factor and D is the insulin diffusion coefficient in free solution, c₁(t) is the interstitial insulin concentration at time t, c₀ is the equilibrium insulin concentration, and b₀, f₀, and e₀ are the equilibrium concentrations of insulin-bound, unbound, and internalized receptors. Because receptors are uniformly distributed within the t-tubule network (2) and receptors are not transported/removed from the t-tubule network, the total concentration of insulin receptors, b(r,t) + f(r,t) + e(r,t), is independent of r,t and is therefore constant.

Model parameterization

Insulin exists as a monomer in blood, and the diffusion coefficient of insulin in monomer-form in water at 20°C is 150 μm² s⁻¹ (6). The diffusion coefficient (D) is given by the Einstein-Stokes relationship

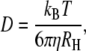(2)

where T is absolute temperature, k_B is the Boltzmann constant, η is the viscosity of the solvent, and R_H is the molecular radius of the solute. Because the viscosity of water at 20°C is 1 × 10⁻³ Pa·s, the viscosity of water at 37°C is 0.69 × 10⁻³ Pa·s, and the viscosity of the interstitial fluid at 37°C is 1.2 × 10⁻³ Pa·s (7), it follows that the diffusion coefficient of insulin in monomer-form at 37°C in the interstitial fluid is D = 116 μm² s⁻¹.

The resistive properties of tissue are described by tortuosity factors (τ) (8), which have been calculated for a number of different tissue types and different fixed regular geometries (9). Although there are no direct measurements of the tortuosity factor for insulin in skeletal muscle t-tubules, it can be estimated from measurements of the K⁺ tortuosity factor in the t-tubules. For example, Almers (5) investigated K⁺ diffusion in frog sartorius t-tubules in Ringer solution using a voltage-clamp technique at 22°C. Using a computer model of the radial spread of K⁺ within a fiber, they found that their data were consistent with an apparent t-tubule K⁺ diffusion coefficient of 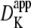= 3.8 × 10⁻⁶ cm²/s. The K⁺ diffusion coefficient in free solution at 25°C is 18.3 × 10⁻⁶ cm²/s (10). These data are, therefore, consistent with a t-tubule network total tortuosity factor of τ = 0.21, which includes geometric and hydrodynamic factors. Friedrich et al. (11) identified that hydrodynamic wall effects reduce the diffusion of molecules in the tubules (D^Tube) relative to that in free solution (D^sol) because of the small diameter of the t-tubules. This hydrodynamic effect is dependent on the size of the diffusing molecule. Potassium has an atomic radius of 0.22 nm and therefore the solute/t-tubule size ratio is

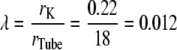(3)

and the reduction in diffusion is (12)

(4)

so that the K⁺ diffusion coefficient is 8% smaller within an 18 nm t-tubule. Insulin in monomer form has a molecular radius of 1.34 nm and therefore the solute/t-tubule size ratio is λ = 0.074 and the reduction in diffusion is so that the insulin diffusion coefficient is 33% smaller within an 18 nm t-tubule. The small diameter of the t-tubules therefore has a significant effect on insulin diffusion within the t-tubules. It follows that the total tortuosity factor for insulin in the t-tubules is τ = 0.21 × 0.67/0.92 = 0.153.

Insulin binds to the insulin receptor and promotes the entry of glucose into muscle cells. Burdett et al. (13) have measured the concentration of insulin receptors in rat skeletal muscle to be 0.43 pmol/mg t-tubule membrane protein. Skeletal muscle has a density of ∼1.06 g/cm³ (14) and therefore the concentration of insulin receptors in rodent t-tubules is ∼456 nM. Koerker et al. (15) observed that the concentration of insulin binding sites in rat skeletal muscle was fiber-dependent and ranged from 0.25 to 1.6 pmol/g fresh muscle. Because the t-tubules constitute 0.3% of the fiber volume (16) the average concentration of insulin binding sites within the t-tubules of rat skeletal muscle is therefore ∼b_t = b + f = 327 nM. In the absence of insulin, 90% of the receptors are located at the cell surface (17) so that the total concentration of insulin receptors is

The insulin receptor dissociation constant (K = k₋/k₊) is 0.13–0.28 nM in ovine and bovine skeletal muscle (18,19) and 0.29–0.42 nM in rodent skeletal muscle (20). For the modeling purposes in this article we have used K = 0.355 nM as the insulin receptor dissociation constant in rodents. Reported values for k₋ for the insulin receptor range from 1 × 10⁻⁴ to 4 × 10⁻³ s⁻¹ (21) and we assume an average value of k₋ = 2 × 10⁻³ s⁻¹. From the definition of the dissociation constant it follows that k₊ = k₋/K = 0.0056 nM⁻¹ s⁻¹.

The fasting blood insulin concentration is 7 μU/mL in mice (22). Because 1 μU/mL = 0.006 nM (23), it follows that the basal insulin level in mice is therefore c₀(R) = 0.042 nM. Lauritzen et al. (2) injected mice with a 16.8 μL insulin bolus at 656 mU and then measured insulin transport in muscle fibers. Mice have a blood volume of 6–8 mL per 100 g of body weight (24) and a 30 g mouse therefore has a blood volume of 2.1 mL. The initial interstitial insulin blood concentration in these mice due to bolus injection is therefore ∼c₁(t) = c₁ = 1.87 nM and for model simplicity we ignore the degradation of blood insulin with time.

Myocyte insulin receptors are downregulated by an insulin-induced increase in insulin receptor internalization. Standaert and Pollet (17) observed that 20 nM of insulin reduced the number of insulin binding sites by 50% after 20 h according to a first-order process with rate constant 0.22 h⁻¹. They found that the receptor internalization rate constants were A₁ = 30.6 × 10⁻⁶ s⁻¹ and A₂ = 3.33 × 10⁻⁶ s⁻¹, and the receptor recycling rate constant was G = 30.6 × 10⁻⁶ s⁻¹.

The complete set of model parameter values and definitions are listed in Table 1. The system of nonlinear partial differential equations (Eq. 1) was solved using the MatLab software package (The MathWorks; www.mathworks.com) with the PDE toolbox.

TABLE 1.

Model parameter values and definitions

Parameter	Definition	Value
k−	Rate of insulin unbinding from the receptor.	2 × 10−3 s−1
K	Insulin receptor dissociation constant.	0.355 nM
k+ = k−/K	Rate of insulin binding to the receptor.	0.0056 nM−1 s−1
Dapp	Insulin apparent diffusion coefficient.	17.8 μm2 s−1
D	Insulin diffusion coefficient in free solution.	116 μm2 s−1
τ	Insulin tortuosity factor.	0.153
A1	Rate of internalization of insulin bound receptors.	30.6 × 10−6 s−1
A2	Rate of internalization of insulin unbound receptors.	3.33 × 10−6 s−1
G	Receptor recycling rate constant.	30.6 × 10−6 s−1
bt	Total concentration of insulin binding sites.	327 nM
R	Radius of muscle fiber.	20 μm
c0(R)	Basal insulin level.	0.042 nM
c1	Initial interstitial insulin blood concentration.	1.87 nM

Model prediction of insulin transport in the t-tubules

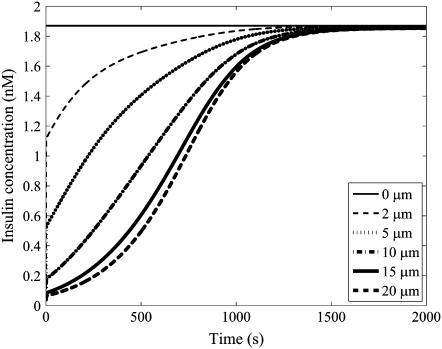
The mathematical model of the insulin concentration dynamics within the t-tubules of a 40-μm-diameter skeletal muscle fiber with circular cross section (Eq. 1) was simulated with the parameter set in Table 1. The simulated insulin concentration dynamics after insulin bolus injection (1.87 nM) at locations 0, 2, 5, 10, 15, and 20 μm from the sarcolemma is shown in Fig. 2 (compare with Fig. 5 b in (2)). Insulin transport in the t-tubules is very slow and is ∼1000 times slower than diffusive transport in free solution. The model simulation is consistent with the observation by Lauritzen et al. (2) that after insulin injection there was a 10 min delay in the arrival of sulforhodamine B-labeled insulin and PIP₃ production (a product of insulin activation) between inner t-tubules (20 μm from the sarcolemma) and the sarcolemma. Insulin binding to the insulin receptors in skeletal muscle t-tubules and t-tubule network tortuosity therefore significantly impedes the transport of insulin through the t-tubule network.

FIGURE 2.

The simulated insulin transport within the t-tubules of a 40-μm-diameter skeletal muscle fiber with circular cross section after insulin bolus injection (1.87 nM) at 0, 2, 5, 10, 15, and 20 μm from the sarcolemma. The horizontal line denotes the equilibrium insulin concentration.

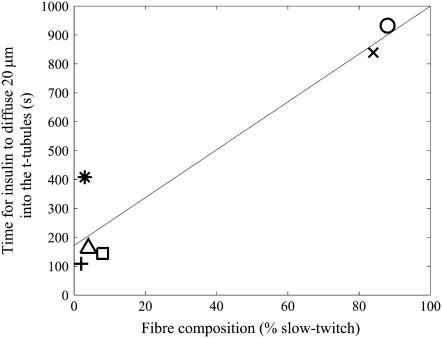
FIGURE 5.

The predicted times for insulin to reach 0.75 nM at a location 20 μm from the sarcolemma after the insulin injection as a function of muscle fiber composition. The skeletal muscles are rat adductor longus (○), soleus (X), quadriceps (□), EDL (∗), anterior tibialis (+), and medial gastrocnemius (▵). Also shown is a linear regression fit to these insulin travel times that explains 90% of the variance (—).

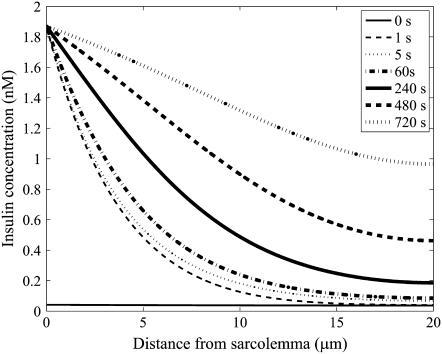
The simulated insulin concentration gradient within the t-tubules of a 40-μm-diameter skeletal muscle fiber with circular cross-section after insulin bolus injection (1.87 nM) at 0, 1, 5, 60, 240, 480, and 720 s is shown in Fig. 3. The horizontal line denotes the equilibrium insulin concentration. Also shown in Fig. 4 are the corresponding concentrations of bound insulin receptors within the t-tubules of the muscle fiber after insulin bolus injection (1.87 nM) at 0, 1, 5, 60, 240, 480, and 720 s. After 5 s, a significant insulin concentration gradient is established across the fiber with little change in the concentration of insulin-bound (b) and unbound receptors (f). The insulin concentration profile that is rapidly established after 5 s is therefore well approximated by the solution to

(5)

which for c₀, b₀, and f₀ constant has steady-state solution

(6)

where I₀ is the modified Bessel function of the first kind. This steady-state solution closely correlates with the insulin concentration profile generated 5 s after insulin bolus injection in Fig. 3. The insulin concentration profile that establishes after 5 s is due to the binding of insulin to the receptors.

FIGURE 3.

The simulated insulin concentration gradient within the t-tubules of a 40-μm-diameter skeletal muscle fiber with circular cross section after insulin bolus injection (1.87 nM) at 0, 5, 60, 240, 480, and 720 s.

FIGURE 4.

The simulated concentrations of bound insulin receptors within the t-tubules of a 40-μm-diameter skeletal muscle fiber after insulin bolus injection (1.87 nM) at 0, 1, 5, 60, 240, 480, and 720 s.

The t-tubule network geometry is different in different muscle fiber types. For example, the t-tubule network from slow-twitch guinea pig skeletal muscle is more nonplanar than that from fast-twitch skeletal muscle (25). Franzini-Armstrong et al. (25) found that t-tubule branches are 3/30% greater in length than they appear in two-dimensional transverse images of t-tubule networks of fast/slow-twitch fibers. This has a significant effect on network tortuosity. From the relationship between the diffusion coefficient, space, and time, it follows that that the effective diffusion coefficient on this nonplanar t-tubule network is reduced by the factor 1/1.03² = 0.94 in fast-twitch fibers and 1/1.3² = 0.59 in slow-twitch fibers. This suggests that the effective diffusion coefficient on the t-tubule network in slow-twitch fibers is 37% smaller than in fast-twitch fibers. Frog sartorius muscle contains 90% fast-twitch fibers (26), and because the structure of the t-tubule network is similar in frog (27) and mammalian fibers (25), we assume that τ = 0.153 in fast-twitch fibers and τ = 0.096 in slow-twitch fibers. Insulin transport is, therefore, significantly faster in fast-twitch fibers because their t-tubules are less tortuous.

There is also significant variability in both the concentration of insulin receptors and the receptor affinity for insulin in rat skeletal muscle fibers (15). The measured receptor concentration, affinity values, and fiber type composition are listed in Table 2. These data along with the tortuosity estimates in different fiber types can then be used with the mathematical model to investigate insulin transport in different skeletal muscles. We found that the times for insulin to reach 0.75 nM at a location 20 μm from the sarcolemma for rat adductor longus, soleus, quadriceps, EDL, anterior tibialis, and medial gastrocnemius muscle fibers after the insulin injection described by Lauritzen et al. (2) are 932, 839, 144, 408, 109, and 162 s, respectively. These insulin transport times are shown in Fig. 5 as a function of fiber type composition. The model therefore indicates that the transport of insulin into the t-tubule network of rat skeletal muscles is highly variable between muscles. Furthermore, fiber composition explains 90% of this variability. Because the time required to transport insulin into the t-tubules partially determines the speed of tissue responsiveness to insulin, differences in fiber type composition between species or age-groups can therefore potentially impact on the speed of tissue responsiveness to insulin.

TABLE 2.

Insulin receptor affinities, concentrations, and fiber composition measured in different rat muscle fibers

Muscle	Total concentration of insulin binding sites (bt)*	Receptor affinity (K)	Fiber composition (% slow twitch)	Rate of insulin binding (k+ = k−/K)†
Adductor longus	503 nM	0.92 nM	88	0.0022 nM−1 s−1
Soleus	596 nM	2.06 nM	84	0.0010 nM−1 s−1
Quadriceps	88 nM	0.258 nM	8	0.0078 nM−1 s−1
EDL	479 nM	1.82 nM	3	0.0011 nM−1 s−1
Anterior tibialis	165 nM	1.03 nM	2	0.0019 nM−1 s−1
Medial gastrocnemius	188 nM	1.01 nM	4	0.0020 nM−1 s−1

Data is from Koerker et al. (15).

^*Assuming t-tubules constitute 0.3% of the fiber volume (16).

^†k₋ = 2 × 10⁻³ s⁻¹ (21).

The mathematical model can also be used to investigate the effect of different factors such as receptor internalization and recycling on insulin transport in the t-tubules. In our simulations a 1000 s exposure of insulin at 1.87 nM decreases the concentration of insulin binding sites in the t-tubules from 304 to 294 nM due to receptor internalization. For this scenario, the time for insulin to reach 0.75 nM at a location 20 μm from the sarcolemma is 628 s. If receptor internalization and recycling processes are not included in the model, then the time for insulin to reach 0.75 nM at a location 20 μm from the sarcolemma is 624 s. Receptor internalization and recycling is therefore too slow a process to have a significant effect on insulin transport into the t-tubules.

The insulin transport model described by Eq. 1 can therefore be significantly simplified by ignoring the slow receptor internalization and recycling processes (A₁ = A₂ = G = 0). In addition, if the receptor kinetics are assumed to be fast (i.e., 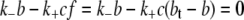), then

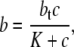(7)

and from Eq. 1 and Eq. 7 it follows that (28)

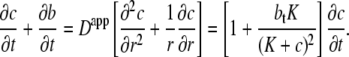(8)

The transport of insulin in the t-tubules of a skeletal muscle fiber with a circular cross section is then described by the equation (28)

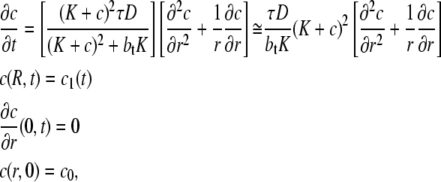(9)

where c(r,t) is the insulin concentration in the t-tubules at radial location r from the center of the fiber at time t, K = k₋/k₊ is the insulin receptor dissociation constant for insulin, and b_t = b + f is the constant total concentration of insulin receptor binding sites in the t-tubules. The diffusive transport of insulin into the t-tubules therefore approximately satisfies a diffusion equation with a diffusion coefficient that is a nonlinear function of insulin concentration. This diffusion coefficient increases with increasing insulin concentration and decreases with increasing receptor concentration. The functional form of this diffusion coefficient provides insight into the slow transport phenomenon: the term τ/b_tK = 1/759 ensures transport is much slower than in free solution and the nonlinear quadratic term also provides a further restriction on transport (because (K + c)² ≤ 1 for c ≤ 0.65 nM, which is the case for the leading edge of the traveling front). Equation 9 also has the advantage of being easier to parameterize than Eq. 1 and the insulin transport dynamics are also clearer. However, Eq. 1 is necessary to accurately describe the diffusive transport of insulin into the t-tubules and the significant effect of long-term insulin infusion on receptor internalization and recycling.

DISCUSSION

It has been observed in situ in mice that there is a 10 min delay in the time for insulin to diffuse from the sarcolemma to a distance 20 μm inside the t-tubule network after insulin injection (2). It was suggested by Lauritzen et al. (2) that the biochemical composition of the t-tubular space that may include large molecules acting as gels and increased viscosity in the narrow tubules may explain this slow diffusion of insulin through the t-tubule network. Although these factors contribute to the slow diffusion of insulin through the t-tubules, our investigation shows that these are not the major factors responsible for the slow diffusion. Here we explain why. Because the viscosity of water at 37°C is 0.69 × 10⁻³ Pa·s and the viscosity of the interstitial fluid at 37°C is 1.2 × 10⁻³ Pa·s (7), the increased interstitial fluid viscosity does not explain the very slow insulin diffusion time in the t-tubules. Furthermore, since insulin has a molecular diameter of ∼2.7 nm, a t-tubular gel made from large molecules would need to have a mesh size of <3 nm to generate the very slow insulin diffusion time in the t-tubules. However, it is known that peroxidase (4 nm diameter; Mr = 44,000), used as an extracellular marker, enters the t-tubule system of rat muscle fibers (29). Ferritin (11 nm diameter, Mr = 445,000) similarly enters the t-tubules of frog muscle (29,30). Krolenko et al. (31) were also able to transport plasmid DNA (Mr = 2.7 × 10⁶) into the t-tubules. This plasmid DNA has a diameter of ∼20 nm, which is very close to the diameter of the t-tubules (18–30 nm). Given that these large molecules can be transported into the t-tubule system, it is unlikely that the t-tubules contain large molecules acting as gels. Increased viscosity in the narrow t-tubules and large molecules acting as gels therefore do not appear to be the primary mechanisms responsible for the slow insulin diffusion time in the t-tubules.

To help ascertain potential mechanisms responsible for the slow transport of insulin through the t-tubule network, we have constructed a theoretical model of insulin transport within the skeletal muscle t-tubule network. Our model includes insulin diffusion, insulin binding to insulin receptors within the t-tubules, t-tubule network tortuosity, interstitial fluid viscosity, hydrodynamic wall effects, and insulin receptor internalization and recycling. The model predicted that, depending on fiber type, there is a 2–15 min delay in the arrival time of insulin between the sarcolemma and inner t-tubules (located 20 μm from the sarcolemma) after insulin injection. Our model simulations of insulin transport in the t-tubules are therefore consistent with the observed 10 min delay in the arrival time of insulin between the sarcolemma and inner t-tubules after insulin injection.

The contribution of the different factors toward this delay in insulin diffusive transport can be estimated by selectively removing each factor from the model and calculating the insulin transport delay. The delay in insulin transport between the sarcolemma and inner t-tubules (located 20 μm from the sarcolemma) after insulin injection with the selective removal of different individual factors from the generic model (with a transport delay of 628 s) in order of importance are: insulin binding to insulin receptors within the t-tubules (3 s), t-tubule network tortuosity (67 s), interstitial fluid viscosity (334 s), hydrodynamic wall effects (441 s), and insulin receptor internalization and recycling (624 s). Insulin receptor internalization and recycling had very little effect on insulin transport into the t-tubules. The main factor responsible for the delay in insulin transport within the t-tubules, based on our modeling analysis, is therefore insulin binding onto the receptor. This is because during the initial period of up to ∼60 s after the insulin bolus injection, the concentration of bound receptors is low (Fig. 4), implying a high concentration of unbound receptors that strongly take up insulin and prevent it from diffusing far into the fiber (Fig. 3). At later times, as the concentration of bound receptors increases (Fig. 4), the rate of insulin uptake by unbound receptors decreases, and insulin can penetrate in significant amounts to the interior of the fiber (Fig. 3).

The t-tubule network therefore significantly impedes insulin transport into the t-tubules and consequently delays the translocation of GLUT4 glucose transporters to the t-tubule membrane and the uptake of glucose by skeletal muscle. It is possible that pathological conditions such as diabetes are associated with altered insulin transport in the t-tubule network and are due, for example, to changes in the t-tubule network structure or the insulin receptor distribution within the network. If the t-tubule network geometry is known for a pathological condition, then the consequent impact on insulin transport in the t-tubules can be calculated by the methods described in Saxton (32).

The functional importance of glucose transport via the t-tubules is not clear. It is known that the surface area of the t-tubule network is 1–3 times greater than that of the sarcolemma and that the t-tubules contain a significant proportion of the insulin receptors and GLUT4 transporters. The spacefilling nature of the t-tubule network ensures the targeted delivery of electrical and chemical signals throughout a muscle cell. The t-tubule network therefore appears to allow glucose to be delivered in a targeted manner to the intracellular metabolic machinery within a skeletal muscle cell.