Protein Aggregation/Crystallization and Minor Structural Changes: Universal versus Specific Aspects

Abstract

Protein association covers wide interests in biophysics, protein science, and biotechnologies, and it is often viewed as governed by conformation details. More recently, the existence of a universal physical principle governing aggregation/crystallization processes has been suggested by a series of experiments and shown to be linked to the universal scaling properties of concentration fluctuations occurring in the proximity of a phase transition (spinodal demixing in the specific case). Such properties have provided a quantitative basis for capturing kinetic association data on a universal master curve, ruled by the normalized distance of the state of the system from its instability region. Here we report new data on lysozyme crystal nucleation. They strengthen the evidence in favor of universality and show that the system enters the region of universal behavior in a stepwise manner as a result of minor conformation changes. Results also show that the link between conformation details and universal behavior is actuated by interactions mediated by the solvent. Outside the region of universal behavior, nucleation rates become unpredictable and undetectably long.

INTRODUCTION

A wide variety of interests in protein science and physiology, biotechnologies, nanophysics, pathologies related to deposits of protein aggregates, and protein-solvent interactions are covered by processes of aggregation of proteins (1–9). They include the growth of protein crystals, currently the bottleneck to protein structure determination (10–15).

Protein association leading to aggregation/crystallization has often been viewed as governed by details of structure and of chemical physical conditions. Efforts to gain a somewhat more general view have produced, e.g., George and Wilson's notion of crystallization slot (16). Other efforts have also been reported (17,18). More recently, the existence of a universal physical principle governing aggregation/crystallization processes has been suggested by a series of experiments and shown to be linked to the universal behavior of concentration fluctuations (19–21) occurring in proximity of the “spinodal line.” The latter is the line in the (T,c) plane, encompassing a region of instability of the solution against spontaneous, nonnucleated demixing (22). On approaching the spinodal line from the stability region, amplitudes and lifetimes of spontaneous concentration fluctuations are known to undergo critical divergences (22) following a universal scaling law. This is an inverse power dependence on the parameter ɛ = (T − T_s)/T_s, where T is the actual temperature and T_s is the spinodal temperature. By definition, the ɛ parameter measures the normalized distance of the representative point of the solution from the spinodal line. It expresses the overall effect of all system parameters (temperature, buffer, salts, pH, concentrations, additives …) on the stability of the solution. Consequently, the same ɛ value can be obtained by widely different choices of system parameters. The presence of anomalous fluctuations and the temperature range where their divergences follow the known universal law are measured by light-scattering experiments in slow temperature scans (23,24). These also provide spinodal temperature values. Experiments on a variety of systems had already shown that the phase transition of demixing, as well as anomalous fluctuations occurring in its vicinity (that can be viewed as transient demixing), play a central role in promoting aggregation of proteins and other polymers (25–30).

Previously (20,21), we have experimentally shown that nucleation rates of lysozyme crystals as well as of deoxy-Sickle Cell hemoglobin (deoxy-HbS) fibers exhibit a universal behavior governed solely by the value of the ɛ parameter. This is proven by the fact that all nucleation rates for both systems fall on one and the same universal curve (or “master curve”) as shown in Fig. 1 (20,21). Remarkably, such a master curve covers a span of several orders of magnitude of nucleation rates. Both systems had previously been the subject of ample studies. As to HbS, very valuable studies on kinetics of fiber formations had been done (31). A phase diagram including a spinodal line had been independently determined (26), and a role of demixing in aggregation had been suggested on qualitative (26) and, more recently, quantitative (19,32) bases. As to lysozyme, crystal nucleation rates had been the object of pioneering, semiquantitative studies (33) as well as of more recent quantitative ones (17,34). In this case as well, independent studies of the phase diagrams in a variety of conditions (pH and salts) have taken into consideration binodal (18) and spinodal (18,35) lines, that is, the two lines jointly delimiting the metastability region of the solution. Relations of nucleation rates to the location of the representative points corresponding to actual experimental conditions were qualitatively sought with interesting preliminary results (17).

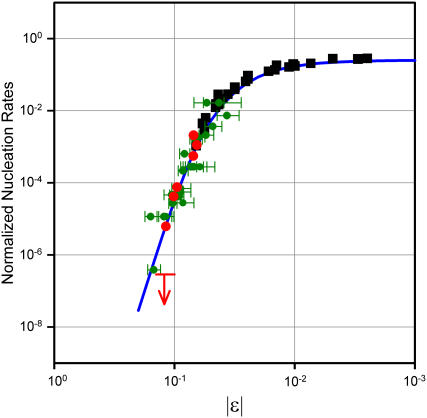
FIGURE 1.

Master curve governing many orders of magnitude of nucleation rates versus the normalized distance ɛ = (T – T_S)/T_S of the actual state of the system (at temperature T) from the instability region. The curve (continuous line) is derived from the universal scaling properties of critical fluctuations (20,21). The ɛ parameter expresses the overall effects of all system parameters (temperature, buffers, salts, pH, concentrations, additives. etc.). Consequently, the same ɛ value can be obtained by widely different choices of system parameters. (Green symbols) lysozyme crystallization induction times from literature and from Pullara and Pullara et al. (20,21). (Red symbols) data on lysozyme crystallization. Data (by different authors) are relative to different pH, temperature, and protein and salt concentrations. (Black squares) sickle hemoglobin (HbS) fiber induction times (19,30). The arrow refers to an experiment that was done in conditions of nonvalidity of the master curve and in which nucleation was not observed (see text).

The existence of a master curve allows a novel synthetic understanding and predictability of nucleation rates. Its shape has been rationalized in terms of a simple two-stage model. In the first stage, fluctuations generate sufficiently ample and long-lived liquid regions where proteins cluster. In the second stage, clustered proteins rearrange themselves within a characteristic time into a crystalline nucleus (20,21). The existence of a master curve for nucleation rates is thus a direct consequence of the existence of a region of thermodynamic instability of the solution against spontaneous demixing. Its dependence on the sole parameter ɛ and its universal shape are direct consequences of the existence and universal divergence properties of the related critical fluctuations. As already mentioned, these views are reinforced by other results concerning a number of different systems, which legitimate similar conclusions (if only in qualitative terms because of the current nonavailability of similarly complete sets of quantitative data).

These results do not conflict with the possible mechanistic role of the details of protein structure and conformation. Rather, they clearly show that such details also cover thermodynamic aspects. In fact, minor protein structural/conformational changes have proven to affect aggregation properties via both the location and shape of the instability region. A paradigmatic example is provided by a comparison of the already mentioned case of deoxy-HbS and that of CO-liganded HbS (CO-HbS) (30). A subtle conformational change is implied in the passage from the liganded to the unliganded form of HbS (36). This has been shown to alter the region of thermodynamic stability of the solution (as encompassed by the spinodal line). As a consequence, demixing/aggregation of CO-HbS can still be observed, but at physiologically irrelevant temperatures. In addition to these crucial thermodynamic effects of the slight conformational change, equally important “local” effects are observed. Indeed, the slight conformational difference of CO-HbS is incompatible with the topology of the classic helicoidal fiber structure of deoxy-HbS (30), and amorphous aggregates are now formed. Another significant case is that of a polyoligomer of elastin. In that case it was found that the spinodal and the binodal lines cannot be described, as they should, in terms of the same thermodynamic parameters. The reason was clearly traced to conformational changes occurring in response to the temperature scan operated on approaching the binodal line. Such conformational changes give rise to a binodal line governed by thermodynamic parameters different from those governing the spinodal line (37).

These examples prove that the effects of even slight protein conformational changes are not limited to the topology and energetics of contacts within aggregates. Actually, they also significantly affect the thermodynamic drive toward aggregation and the ranges of related parameters for which aggregation/crystallization occurs and shows universality features. In fact, such changes add to and interact with those more often taken into consideration, e.g., other parameters (such as pH, salts, etc.), on the location and shape of the spinodal line and hence on the ɛ value relative to the given experimental conditions. Values of all these other parameters and hence their effects on T_S remain, of course, constant in temperature scan experiments aimed at checking the occurrence and the universal divergence properties of anomalous fluctuations and at measuring T_S values. Conformational changes, however, remain free to occur in response to temperature changes in the course of T-scan experiments. As just seen, this may cause T_S changes during T-scans, thus limiting the temperature range where the expected universal behavior of critical fluctuations is observed.

Interest in exploring in greater depth the issue of the ther-modynamic effects of the temperature dependence of protein conformation (in addition to local effects) prompted this study. The system chosen (lysozyme) offers the advantage of allowing use of the qualitative and quantitative information contained in the already established master curve for crystallization times. In our experiments we made joint use of static and dynamic light scattering and circular dichroism techniques. Our results show that, indeed, the occurrence of (minor) protein structural changes in the course of temperature scans set the limits of the region where critical fluctuations and crystal nucleation show universal features. Further, our results highlight a novel mechanism whereby an abrupt change of the solution T_S values can be linked to a similar abrupt change of the generalized forces stabilizing protein conformation rather than to a similar change of conformation itself. This novel effect is reasonably ascribed to a stepwise change of protein hydration and related solution thermodynamics.

MATERIALS AND METHODS

Experiments were performed on Chicken Egg White lysozyme L-6876, Lot 57H7045 (Sigma, St. Louis, MO). Samples were prepared by dissolving lysozyme in acetate buffer solution at the selected pH and at temperature ∼37°C. The lysozyme and buffer concentrations values were twice the final values. These solutions were successively mixed with equal amounts of NaCl solutions, also at twice the final concentration, and also at temperature ∼40°C. Addition of NaCl after protein dissolution avoided formation of crystal nuclei during preparation. Buffers were sodium acetate, 100 mM for pH 4.2 and 40 mM for pH 4.6 (final concentrations). This choice facilitated contact among this data and those available from literature. Solutions were filtered through 20-nm pore size filters directly into a preheated cuvette.

For static and dynamic light-scattering measurements we used a precision, fast-switching multiangle instrument (MK3) built under a joint European Community and INFM contract with our department (INFM Patent #01309135). As light source we used a frequency-doubled and stabilized Nd-doped solid-state laser (λ = 532 nm). In the detection and correlation channel, we used a Perkin-Elmer Optoelectronics avalanche diode (SPCM-AQR-14) and a Flex-01 1088 channel multitau correlator. Temperature scan experiments (from 40°C to 5°C at 1.3°C/h scanning rate) allowed determination of the spinodal temperature T_S. As already noted, when T_S is approached from the solution stability region, the intensity of light scattering diverges because of the divergence properties of amplitude and lifetime of anomalous fluctuations (23,24). The scattered intensity is proportional to the square amplitude of concentration fluctuations in the sample. Within mean-field approximation, the latter increases according to a well-known universal law: 〈|Δc²|〉 ∝ ɛ⁻¹ so that we get I_scatt ∝ ɛ⁻¹ or, equivalently, I⁻¹ ∝ (T − T_S)/T_S (23,24). The photon correlation time τ = 1/Dq² (where q is the scattering vector and D the diffusion constant) measures the fluctuation lifetime. In the so-called hydrodynamic approximation, the fluctuation correlation length ξ is related to D by ξ = k_BT/6πηD. Again, within the mean-field approximation, ξ also obeys a universal law: ξ ∝ ɛ^−½, which, for our purposes, is more conveniently written as ξ⁻² ∝ (T − T_S)/T_S. Within the validity of these approximations, plots of I⁻¹ and ξ⁻² versus T are expected and indeed found to be linear, and their extrapolations are expected to individuate the same value T = T_S on the temperature axis.

Precise determinations of statistical delay times of crystallization were performed using a homemade low-angle light-scattering instrument. This instrument (to be presented in detail elsewhere) uses a single longitudinal mode green (λ = 532 nm) laser. Light collection is done by a CCD camera. The zero-order light beam is stopped by a micromirror. Light intensity reflected by the micromirror is continuously monitored to account for laser power fluctuations and scattered light not collected by the CCD camera. Total scattered light intensity was measured by averaging over 10 frames/s and was monitored every 4 s.

Circular dichroism (CD) measurements were performed using a Peltier temperature-controlled Jasco J-715 spectropolarimeter, kindly made available by Prof. L. Cordone. Spectra in the far UV (190 nm < λ < 250 nm) and in the near UV (250 nm < λ < 350 nm) ranges were taken at selected temperatures during 1°C/h temperature scans and averaged over four acquisitions made at 40 nm/min scan rates. Quartz cuvette path lengths used were 1 mm (far UV) and 10 mm (near UV) for 0.01% lysozyme concentration; 0.1 mm (far UV) and 1 mm (near UV) for 2.0% lysozyme concentration; 0.01 mm (far UV) and 0.1 mm (near UV) for 6.5% lysozyme concentration. Spectra of the solvent were taken using the same temperature scan rate and the same cuvettes reported above to subtract background CD signal. Simultaneous recording of the photomultiplier voltage (HT signal) allowed selecting fully reliable CD data only.

RESULTS

As is clearly evident from Fig. 1, data points concerning deoxy-HbS fiber nucleation (black squares) are far better aligned on the master curve than most of those related to lysozyme crystal nucleation. This is not surprising, given the higher average experimental accuracy of available HbS data. The ample available data on lysozyme crystal nucleation (even if sometimes only semiquantitative) has nevertheless allowed Pullara and colleagues (20,21) to substantiate on statistically meaningful grounds the existence of the master curve of Fig. 1 and confirm its validity over several orders of magnitude of nucleation time. In this work we have taken advantage of the possibility of precise measurements of nucleation times offered by our low-angle light-scattering instrument (see Materials and Methods). The combined use of this instrument and of our fast switching multiangle light-scattering spectrometer (20,21) has allowed accurate determination of T_S and ɛ values and nucleation times on aliquots of one and the same preparation of lysozyme solutions. This was instrumental to avoid allowing subtle, yet important, effects to be obscured or flawed by minor differences in preparations of samples used in different measurements. The occurrence of protein structural changes was also monitored by CD spectroscopy in the same conditions. The excellent alignment of these data points (red dots in Fig. 1) evidences the higher accuracy now attained over a span of some three orders of magnitude of nucleation times.

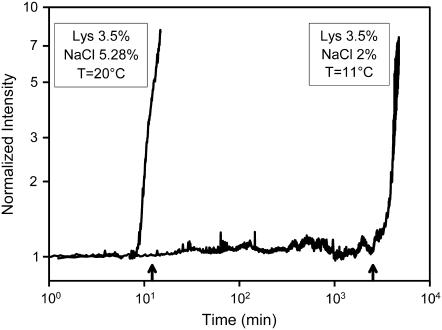
Spinodal temperatures T_S were measured by downward temperature scans, as specified in Materials and Methods, for solutions listed in Table 1. Knowledge of T_S values made it possible to choose (by referring to the master curve) temperatures and related ɛ values such that the expected crystal nucleation times would cover a range of several orders of magnitude. For each solution, chosen temperatures and related ɛ values are also shown in Table 1. Examples of actual tracings obtained in constant-temperature low-angle light-scattering experiments allowing precise nucleation time determinations are shown in Fig. 2. Measurements under conditions corresponding to larger ɛ values (say, 0.2–0.25), although desirable, would require prohibitively long observation times (months or years).

TABLE 1.

Crystallization temperatures and related values

	Lysozyme (w/w)*	NaCl (w/w)	pH	T (°C)	ɛ
i	3%	3%	4.6	5	0.065
ii	6.5%	3%	4.6	18	0.07
iii	3.5%	5.28%	4.2	20	0.073
iv	2%	3%	4.6	1	0.087
v	2.23%	5.28%	4.2	14	0.095
vi	6.5%	3%	4.6	32	0.12
vii	3.5%	2%	4.2	11	0.12

^*The order of listing corresponds to right-to-left order of red points in Fig. 1.

FIGURE 2.

Examples of nucleation time measurements. Normalized low-angle scattered light intensity is recorded versus time for monitoring the occurrence of nucleation. Arrows on the time axis indicate nucleation times predicted from the master curve.

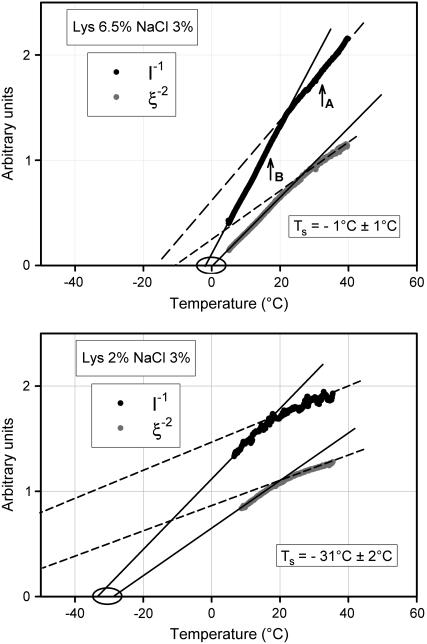
In Fig. 3 we show for two different conditions (ii and iv in Table 1) examples of typical plots of I⁻¹ and ξ⁻² (with I being the scattered light intensity and ξ the fluctuation correlation length) and of extrapolations used to obtain T_S values. In each panel of the figure, two distinct and consecutive temperature intervals are identified, where plots are essentially linear but have different slopes, so as to give origin to elbows. Reasonably defined sets of T_S values that can be nicely fitted to a theoretical spinodal line are obtained only from extrapolations of the higher-slope (lower temperature) segments of the plots. With such T_S values and related ɛ values, measured nucleation rates actually fall on the master curve (red data points in Fig. 1). This does not occur for T_S values obtained from extrapolation of the upper temperature segments of the plots in Fig. 3. That is, only in the lower temperature segments (below the elbows) does the linearity of I⁻¹ and ξ⁻² plots reflect the universal divergences of critical fluctuations (related to the spinodal demixing line), which drive crystal nucleation. Actually, in some sporadic cases such as that of Fig. 3 (top), extrapolations from the upper temperature parts may seem to converge to the same T_S temperature. Yet, this does not identify true T_S values, because such behavior is only exceptionally observed, so that a spinodal line cannot be obtained. Indeed, for most other cases (such as in Fig. 3, bottom) extrapolations from the upper temperature part do not converge to the same (or nearly the same) temperature. This conclusion should not obscure the fact that in this range, too, the observed changes of scattered light reveal some kind of reversible local concentration fluctuations.

FIGURE 3.

(Top) Static and dynamic light-scattering experiments. Downward: T-scans from 40°C to 5°C; lysozyme 6.5% + NaCl 3% in NaAc 40 mM pH 4.6 buffer. The ξ⁻² as well as the I⁻¹ plot evidence of “elbows”, that is, narrow regions where slopes change stepwise although tracings themselves remain continuous. Extrapolations providing meaningful spinodal temperature T_S that can be fitted to theoretical expressions of a spinodal line are obtained only from the linear parts of the tracings below the elbows. Crystallization experiments reported in the text were performed at temperatures indicated as T_A and T_B. (Bottom) Same as top panel; lysozyme 2% + NaCl 3% in NaAc 40 mM pH 4.6 buffer.

These observations have prompted further questions and related experiments concerning 1), predictability of nucleation rates outside the range of critical fluctuations and 2), origin and significance of the elbow in the I⁻¹ and ξ⁻² plots. In a first set of experiments, we have studied nucleation kinetics (as in Fig. 2) in temperature conditions falling on the upper linear branch of plots such as in Fig. 3. A typical case is that of crystal nucleation at 32°C, in the conditions of Fig. 3, (top, point A). Indeed, in these conditions, the temperature of 32°C is unmistakably above the elbow. The spinodal temperature is T_S = −1°C, which would correspond to a predicted nucleation time of 1.15 d. Contrary to such prediction, no crystallization was observed (neither by low-angle light scattering nor by visual inspection of the sample at the end of the experiment) over weeks. This result is represented by the arrow in Fig. 1. Predictions proved instead veridical for incubation temperatures below the elbow, such as point B in Fig. 3 (top) as well as for all similar cases. Indeed, all dots referring to lysozyme data reported in Fig. 1 are relative to extrapolations and incubation temperatures below the elbow. Further attempts to predict and to observe nucleation in a number of different solutions at temperatures above the respective elbows gave consistently negative results. Consequently, in those conditions crystallization is either slowed down toward extremely long times (becoming undetectable in actual practice) or is prevented by some other phenomenon occurring at, or close to, the elbow.

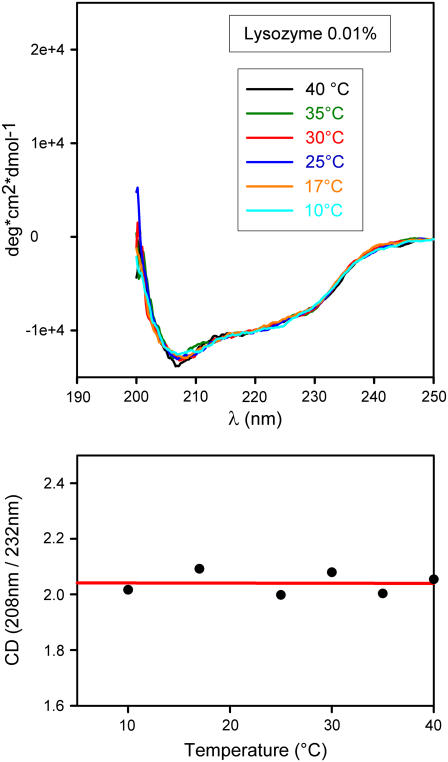
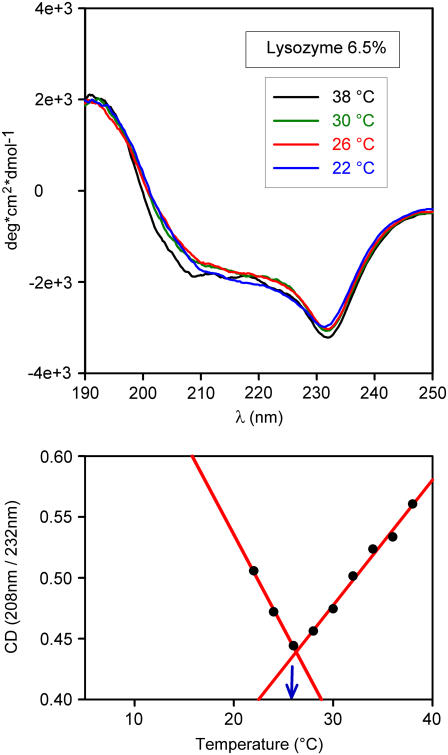
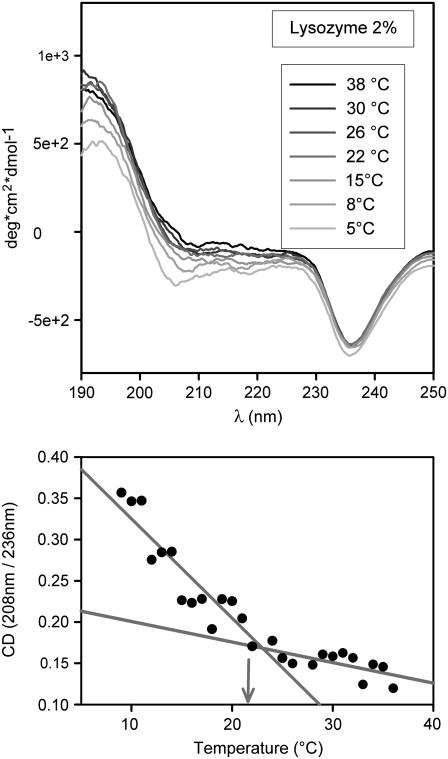
This takes us to a second set of experiments. As recalled in Introduction, in several other systems we have observed a dependence of the spinodal temperature on protein conformation (27,30,37). This was done to ascertain whether some structural change occurred at (or near) the elbow. For this purpose, we performed CD measurements in the near and far UV in diverse conditions. Here we report far-UV spectra only because near UV provided similar but not equally clear-cut information. CD spectra at different temperatures are shown in Figs. 4–6 for different lysozyme concentrations (NaCl 3% and pH 4.6 in all cases). Fig. 4 refers to a highly diluted solution (0.01%), whereas Figs. 5 and 6 refer to the same solutions used in light-scattering experiments of Fig. 3. For the high-dilution case (Fig. 4), scattered light is undetectable, thus barring a comparison between the two types of data. It is of interest, however, to note that a comparison of spectra in Fig. 4 with analogous ones available from literature (38) shows that at such a low concentration (that is, in a condition of negligible protein-protein interaction) the lysozyme structure is scarcely affected by even large changes of pH and salt concentration. We also see that at this low concentration the CD spectrum is temperature independent, at variance with what we observe at higher concentrations. Spectra in Figs. 5 and 6 are indeed considerably different from those of highly diluted solutions. It is here useful to note that the remarkable differences seen in CD signals at different concentrations may at least in part be caused by a well-known lack of linearity in their dependence on concentration (36). This is conceivably the reason for the nonavailability of literature data on CD spectra at high concentration. However, this lack of linearity can hardly affect the temperature dependence of the CD signal at fixed concentration, which is the main interest of this work. To evidence spectral shape changes with temperature, we have taken the ratio of CD signals at two wavelengths corresponding to well-defined features of the spectra. These are 208 nm and a second value in the range 230–240 nm, in correspondence to the spectral minimum (see bottom panels of Figs. 4–6). We see that the ratio is temperature independent at high dilution only. An unmistakable slope change of the CD ratio versus temperature plots occurs in both cases of Figs. 5 and 6 at the same temperatures of elbows shown in Fig. 3. As Figs. 5 and 6 show, this change becomes more notable at high protein concentration. We may therefore conclude that temperature affects the structure of lysozyme molecules, but only if the concentration is sufficiently high to allow their interaction, not at concentrations sufficiently low for protein-protein interactions to be ignored.

FIGURE 4.

(Top) CD spectra of dilute lysozyme solution (lysozyme 0.01% + NaCl 3% in NaAc 40 mM pH 4.6 buffer) taken at selected temperatures in the course of a slow temperature scan from 40°C to 5°C. Scanning rate 1.3°C/h. (Bottom) Plot of the 208 nm/232 nm CD signal ratio versus temperature. Note the absence of changes.

FIGURE 5.

(Top) As in Fig. 4 top; lysozyme 6.5% + NaCl 3% in NaAc 40 mM pH 4.6 buffer. (Bottom) As in Fig. 4 bottom. Note the slope change occurring at the same temperature (blue arrow) where an elbow is observed in light-scattering data (Fig. 3 top).

FIGURE 6.

(Top) As in Fig. 4 top; lysozyme 2% + NaCl 3% in NaAc 40 mM pH 4.6 buffer. (Bottom) As in Fig. 4 bottom. Note the slope change occurring at the same temperature (arrow) where an elbow is observed in light-scattering data (Fig. 3 bottom). Note that the slope change analogous to that in Fig. 5 is even less pronounced here, indicating a marked dependence on lysozyme concentration.

As already noted, the temperature at which an elbow is observed in Fig. 3 coincides with the temperature at which a slope change is observed in the plots of CD ratios (Figs. 5 and 6, lower panels). This, together with the mentioned independence of CD spectra of isolated, noninteracting lysozyme molecules on temperature, pH, and salt concentration, leads to the conclusion that the elbow temperature marks a sharp change in the dependence of lysozyme-lysozyme interaction on temperature. Such interaction change is seen to correlate very closely with the proteins' structural changes responsible for the CD signal and are discussed in the forthcoming section.

DISCUSSION AND CONCLUSIONS

Data we have presented follow in the path of previous findings (discussed in Introduction), which have brought into light the central role played in the nucleation of aggregates and crystals by critical fluctuations associated with the phase transition of demixing. In turn, and based on the universal scaling properties of critical fluctuations, those findings have allowed a novel understanding and predictability of nucleation rates by bringing them all on the same master curve. In this work we have addressed by CD and light-scattering experiments the relevance of small, temperature-induced changes of protein conformation and interactions and, specifically, the thermodynamic grounds of their relation to the validity limits of the universal behavior of nucleation rates. As discussed below, the onset of the universal behavior captured by the master curve is marked by the sharp changes evidenced by “elbows” in Fig. 3 and lower panels of Figs. 5 and 6.

The observed existence of a temperature-dependent (thermoreversible) scattered light intensity can only be a result of the presence of similarly temperature-dependent inhomogeneities of the solution, corresponding to local fluctuations of protein concentration. The observed closely parallel behavior of scattering and CD data makes it clear that significant (if small) protein structural changes correlate very closely with the existence and behavior of such fluctuations of concentration.

These data are better understood with reference to some basic concepts discussed in greater detail elsewehere (39–45). As is well known, the stable configuration of a single protein in solution can be viewed in terms of a minimum in a free energy landscape (41–43,45) whose entropy term makes it temperature dependent and is essentially dominated by the multiplicity of rapidly interchanging, thermally available configurations of the solvent. Changes of this free energy landscape depend nonadditively on the presence and distance of other solutes (44,46–48). Also, by its very nature, “thermodynamic averaging” (39–43) causes a marked temperature dependence and a strong nonadditivity (that is, context dependence) of solvent-induced interactions (43,44). As an example, we recall that the subtle T-R conformational change of hemoglobin has been shown to cause abrupt and conspicuous changes of hydration and of related solvent-induced interactions (27). Similar sharp changes have also been observed in simulation work related to other systems (49) and can be expected to occur as well in interprotein solvent-induced interactions because the latter do not distinguish between residues belonging to the same or to different proteins when at comparable distances. Recalling that the thermodynamics of demixing and related binodal and spinodal lines are to a large extent governed by solvent-induced interactions, one sees how apparently minor conformational changes can also cause (as seen, e.g., in the case of T-R conformational change of hemoglobin) a shift of the spinodal line toward (or away from) useful and significant regions.

Within this view, it is easily understood that a global minimum of free energy (that is, a stable state of the whole protein solution at a given temperature) can be attained via intraprotein configuration changes (protein structural readjustments) as well as via interprotein configuration changes (onset of concentration inhomogeneities, including permanent or transient demixing) (25,37) as well as in both ways, all involving changes of thermodynamically available solvent configurations and, therefore, a contribution of solvent-induced interactions. In turn, this makes configurational minima of single proteins markedly context dependent. That is, they may depend not only on temperature but also on local concentrations of solutes (43).

Results reported in the foregoing section are readily understood by referring them to the above concepts. In downward scannings from higher temperatures, we see the correlated progress of minor conformational readjustments (by CD) and local concentration fluctuations (by light scattering). Because conformational readjustments are not seen in the very dilute solution, we conclude that they are the synergistic effect of temperature and local fluctuations of concentration. Synergism is the expected effect of the above discussed temperature and concentration dependence of solvent-induced inter- and intraprotein interactions. We note, however, that above the elbows shown in Fig. 3 and lower panels of Figs. 5 and 6, such fluctuations (as already seen in Results) are not related to an approaching phase transition (such as demixing) and therefore are not expected to show universal features. Below the elbows, the situation is drastically different. Indeed, we have seen that scannings in these lower temperature ranges allow determination of a set of spinodal temperatures that can be accurately fitted to a theoretical expression of a spinodal line. On approaching such temperatures, fluctuations follow the universal scaling behavior proper of phase transitions, thus causing the universal behavior of nucleation times to be accurately expressed over several orders of magnitude by the master curve governed by the sole parameter ɛ = (T − T_S)/T_S.

The question is of the nature of the elbows, where CD data show an abrupt change in their temperature dependence, not in their actual values. This evidences a similarly abrupt change of the temperature dependence of the generalized forces responsible for protein conformation rather than a change of conformation itself. Such a change cannot be caused by intraprotein direct interactions among residues because it does not occur in dilute solutions (compare Figs. 4–6). On the other hand, it is difficult to envisage how direct interprotein interactions (that is, interactions not involving a sizable entropy term, such as in the case of solvent-induced ones) alone could cause such a sharp change of the temperature dependence of conformation not accompanied by analogous changes of conformation itself. A straightforward explanation, however, is at hand if the elbows are thought to correspond to stepwise changes of hydration (and of related forces concurring in determining conformation) occurring in the course of the observed progressive conformation changes. An attempt to use dielectric relaxation techniques to gain a better view of such expected stepwise hydration changes is now being made in collaboration with Professor Bruni at Università degli Studi Roma Tre. Note that, as mentioned previously in this section, such stepwise changes of hydration, entailing similarly stepwise changes of solvent-induced free energy and forces, have been evidenced by experiments (27) as well as by simulations (50) to occur in other systems.

All in all, a marked dependence of protein conformation on temperature implies an equally sizable entropy term (such as one caused by solvent-induced interactions) concurring in conformation stability. On the other hand, solvent-induced interactions do not distinguish between residues belonging to the same or to different proteins if at comparable distances. Accordingly, at not too low concentrations, abrupt changes of interprotein interactions (affecting the solution stability) can be expected to occur concurrently with intraprotein ones (such as evidenced in Figs. 5 and 6) affecting the conformational stability and stiffness of individual proteins. This expectation is confirmed by these data evidencing that a spinodal instability of the solution becomes detectable as soon as the state of the latter is brought below the “elbow.” Anomalous fluctuations associated with this instability, and their universal scaling properties, are the origin of the universal scaling behavior of aggregate/crystal nucleation rates reflected in the master curve of Fig. 1.