Kinetics of Proton Binding to the Sarcoplasmic Reticulum Ca-ATPase in the E₁ State

Abstract

A new caged proton, 2-methoxy-5-nitrophenyl sulfate, was synthesized and used in time-resolved pH jump experiments to study proton binding in the sarcoplasmic reticulum Ca-ATPase. The major advantage of this compound is that it does not produce significant artifacts in experiments in which the fluorescent styryl dye 2BITC is used to monitor ion movements in the Ca pump. Two rate-limiting processes were resolved and their dependence on pH, Ca²⁺ concentration, and temperature investigated. The faster process showed a relaxation time between 4 and 8 ms independent on pH and Ca²⁺ concentration, and the time constant of the slower process varied between 31 ms (0 Ca²⁺) and 100 ms (100 μM Ca²⁺). A consistent mechanism to explain the results was derived in agreement with previous studies and the generally accepted Post-Albers scheme of the pump cycle. This mechanism requires that under physiological conditions the ion-binding sites are always occupied and two protons and a Ca²⁺ ion replace each other. In the absence of ATP at low pH a nonphysiological state can be induced in which up to four protons bind to the Ca pump in the E₁ conformation. So far it could not be verified whether these additional protons bind to amino acid side chains or are coordinated as hydronium ions.

INTRODUCTION

The Ca-ATPase of the sarcoplasmic reticulum (SR) is the first P-type ATPase that allows an advanced analysis of its structure-function relation since its structure became available in a resolution of a few Angstrom in various conformational states (1–6). Functional details have been known for several years and were discussed on the basis of the so-called Post-Albers pump cycle (7–9). It describes the transport of two Ca²⁺ from the cytosol to the SR lumen and countertransport of two protons in a ping-pong mode while the enzyme becomes phosphorylated in the first and dephosphorylated in the second half-cycle. The enzymatic partial reactions catalyze the transition between both basic conformations, E₁, in which the ion-binding sites are accessible from the cytoplasm, and P-E₂, in which the binding sites are open to the luminal aqueous phase. It was shown that the ion-binding and -release steps in both conformations are electrogenic, i.e., net electric charges are moved into and out of the membrane dielectric (10–12). These findings can be explained—in agreement with the structural insights—by the concept that the ion-binding sites are located (almost) in the middle of the membrane domain of the SR Ca-ATPase (13).

The fact that the ion-binding and -release steps are electrogenic means that the access pathways (or “ion wells” (9)) are narrow channels through which the ions have to diffuse to reach their binding moieties. Entering the ion-binding site is accompanied by interaction with the amino acid side chains known to form the binding site (1). This coordination process requires conformational rearrangements of the participating amino acids and, consequently, of the respective transmembrane α helices of the protein to provide a state of low potential energy according to the concept of a binding site. In preceding studies we could show that in the case of Ca²⁺ binding in both principal conformations of the Ca-pump, E₁ and P-E₂, the rate-limiting reaction steps were such conformational relaxations which are intercalated between ion subsequent fast ion movements from the aqueous phase into the binding sites, such as (12)

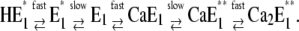This sequence indicates that only one site is accessible at a time, and experimental studies with ⁴⁵Ca²⁺ have provided strong evidence for this mechanism (7). An interesting question is now whether the same functional principle also holds for proton binding or release. The two protons transported as counterions of Ca²⁺ are not necessary for the energetics of the transport process since the SR membrane is quite permeable for cations other than Ca²⁺; however, protons are discussed as stabilizers of the binding sites in the absence of Ca²⁺ ions (14). If such stabilization is maintained by protonation of carboxyl residues, it is rather probable that proton binding or release does not require or induce significant conformational rearrangements in the binding sites. If the species bound to the binding sites is a hydronium ion, H₃O⁺, coordination in the site should be expected, and kinetics may be expected different from that of a more or less diffusion-controlled protonation.

To contribute to an answer to this open question, we present this study in which we used a newly synthesized caged proton to investigate the time-resolved kinetics of proton binding to the SR Ca-ATPase in its E₁ conformation.

Recently we applied caged calcium to determine successfully the Ca²⁺-binding kinetics in E₁ (12) and used a fluorescence assay to detect the ion movements into and out of the membrane domain of the Ca-ATPase. Due to high leak conductance of the SR membrane, direct electrophysiological measurements are not easy to perform. Electrochromic styryl dyes, however, monitor local electric fields in membranes and are extremely sensitive to charge movements in membranes with such a high protein density as the SR membranes. With this method it is possible to monitor specifically the electrogenic Ca²⁺ and H⁺ binding in (and release from) the ion-binding sites inside the membrane domain (15,16).

MATERIALS AND METHODS

Materials

Phosphoenolpyruvate, pyruvate kinase, lactate dehydrogenase, NADH, and the Ca²⁺ carrier A23187 were obtained from Boehringer (Mannheim, Germany). DMNP-EDTA, caged calcium (1-(4,5-dimethoxy-2-nitrophenyl)-1,2-diaminoethane-N,N,N′,N′-tetraacetic acid), and the chelator BAPTA (1,2bis(2-aminophenoxy)-ethane-N,N,N9,-tetrasodium salt, B1214) were obtained from MoBiTec (Göttingen, Germany). Thapsigargin was purchased from Alomone Labs (Jerusalem, Israel). The styryl dye 2BITC (16) was a gift from Dr. H.-D. Martin, University of Düsseldorf, Düsseldorf, Germany. All other reagents were of the highest grade commercially available.

Synthesis of the caged proton, 2-methoxy-5-nitrophenyl sulfate

The photosensitivity of nitrophenyl phosphates and sulfates was noted in 1956 when the metaisomer was shown to undergo photohydrolysis 34 times faster than the ortho- or paraisomers (17). De Jongh and Havinga rationalized these results by proposing that the carbon atom next to the nitro group becomes electron deficient in the excited state, and therefore it is susceptible to a nucleophilic attack by hydroxide. Later, Kirby and Varvoglis demonstrated the generality of the “metanitro effect” by showing that 3,5-dinitrophenyl phosphate was stable for months in darkness but is hydrolyzed when irradiated (18).

After several, less well-reproducible trials with published preparation prescriptions of nitrophenyl sulfates, the following synthesis provided reproducible results with 70% of the theoretical yield. The procedure is based on the reaction of 2-methoxy-5-nitrophenol (MNP; EMS-Dottikon, Dottikon, Switzerland) with chlorosulfuric acid in pyridine according to Ragan (19): Pyridine (∼5 ml) was cooled to −20°C, and 0.115 mol chlorosulfuric acid was added dropwise under stirring and efficient cooling. This procedure has to be performed in an extremely cautious manner to avoid a violent reaction! Then a solution of 17 g MNP in pyridine (∼30 ml) was added in one portion, and the solution was stirred overnight at room temperature. Thereafter, the solvent was evaporated in vacuo (< 40°C). The reaction product was dissolved in distilled water (200 ml) and the pH adjusted to 8.0–8.5 with diluted aqueous NaOH. The solvent was removed in vacuo (<35°C). The precipitate was dissolved in ethanol and the solute immediately filtered and cooled to −4°C. The crystalline precipitate was filtered under suction. The crystallization procedure was repeated. The final product was dried in vacuo and stored at −30°C in the dark. A total of 19 g of the sodium salt of 2-methoxy-5-nitrophenyl sulfate was obtained in the form of slightly yellow, needle-like crystals; 2-methoxy-5-nitrophenyl sulfate sodium will be abbreviated as MNPS·Na in the following.

The purity of MNPS·Na was checked by ¹H-NMR. The compound was dissolved in d₆-DMSO (dimethylsulfoxide) and measured in a JEOL (Tokyo, Japan) JNM-LA-400 FT NMR system at 30°C. The purity of the recrystalized product was >98%.

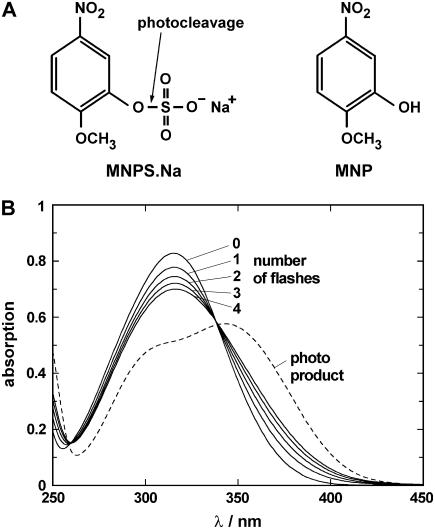
The ultraviolet (UV)-flash-induced effect on MNPS·Na was determined by absorption spectroscopy. The caged proton was dissolved in quartz-distilled water to a concentration of 100 μM and filled into a cuvette with a profile of 2 mm × 10 mm. Light from a flash lamp (model 5M-3; EG&G Electro Optics, Salem, MA) was transmitted through a band-pass filter (270–380 nm; Schott UG 11) and applied to the cuvette positioned so that the flash passed through the 2-mm pathway. The absorption of the solution was measured in a spectrophotometer (Lambda 40; Perkin Elmer, Rodgau, Germany) along the 10-mm pathway before the first and after each UV flash. Typical spectra are shown in Fig. 1 B to demonstrate the effect of the first four flashes. The pH of the (unbuffered) solution was determined in corresponding experiments in which 10 μM phenol red were added as a pH indicator (not shown). Typical pH values in these experiments were 9.2 before flashing and pH 8.1, 7.7, 7.3, and 7.0 for the first four flashes. After 12 flashes pH was ∼5.5. For comparison the absorption spectrum of the photoproduct, MNP, is plotted in Fig. 1 B as the dashed line.

FIGURE 1.

Caged proton, MNPS·Na and its photoproduct, MNP. (A) Chemical structure. The UV-flash-induced hydrolyzation of the compound is indicated by the arrow and occurs according to the reaction, (B) Absorption spectra of 100 μM unexposed MNPS·Na (0) after 1–4 UV flashes and 100 μM (pure) photoproduct, all dissolved in distilled water.

Enzyme preparations

Ca-ATPase was prepared from psoas muscles of rabbits by a slightly modified method of Heilmann and collaborators (20). The whole procedure was performed at temperatures below 4°C. The determination of the protein content of the membrane preparation was performed according to Markwell et al. (21). The most active fractions of the final density gradient separation had a protein content of 2–3 mg per ml. The enzyme activity was determined by the linked pyruvate kinase/lactate dehydrogenase assay (22). Background enzyme activity of the isolated preparation was measured by addition of 1 μM thapsigargin that blocked the SR Ca-ATPase completely. The Ca-ATPase-specific activity was 175 μmol P_i per mg protein and h at 37°C and could be increased up to 310 μmol P_i per mg protein and h in the presence of A23187 to short circuit the vesicles forming membranes for Ca²⁺. With a molecular mass of 110.000 Da and a specific activity of 5.2 units × mg⁻¹ was determined. The turnover rate of the pump is 9.5 s⁻¹ in this preparation. In control experiments the effect of the styryl dye 2BITC on the enzymatic activity was checked. Up to a dye concentration of 1.2 mM no changes of the enzymatic activity could be observed.

Protein-free lipid vesicles, which were used in control experiments, were made from dioleoylphosphatidylcholine (DOPC) in electrolyte of 10 mM NaCl without pH-buffering substances by dialysis, as described elsewhere (23). Before the experiments, electrolyte pH was adjusted by addition of diluted NaOH or HCl.

Detection of partial reactions with 2BITC

For data recording of fluorescence signals with high time resolution, a setup was modified, whose design was published earlier (24). A cylindrical quartz cuvette (internal diameter, 7.8 mm) containing 300 μl electrolyte solution (layer height, ∼5 mm) was placed in the upper focus of an ellipsoidal mirror (Melles Griot, Zevenaar, The Netherlands) whose opening was directed downward. The electrolyte for pH jump experiments contained 10 mM NaCl, 10 μM EDTA, or BAPTA, 200–600 nM 2BITC, 9 μg/ml Ca-ATPase preparation, and 300 μM MNPS·Na . The initial pH was set by addition of HCl or NaOH. The absence of pH-buffering agents made it necessary for the pH to always be measured again immediately before each pH jump. The dye was excited by a 543 nm HeNe laser from the top of the setup. A quartz lens was adjusted to widen the laser beam and to illuminate the whole solution almost homogeneously. The emitted light was collected by the ellipsoidal mirror and reflected into the second focus of the mirror. An interference light filter (589 ± 10 nm) selected the emitted light of the styryl dye before passing the entrance window of a photomultiplier (PM, R928, Hamamatsu Photonics, Hamamatsu, Japan).

An additional UV cutoff filter reduced the effect of the UV-laser flash used to photocleave the caged compound. The output current was amplified by a current/voltage converter and fed into a 12-bit data-acquisition board of a PC with sampling frequencies between 1 and 500 kHz. The bottom of the cuvette was in contact with a thermostated copper socket (that also stopped the incident light). To release a proton from MNPS·Na, a UV-light flash (mean duration 14 ns, wavelength 351 nm, maximum power 6 MW) was generated by an EMG 100 excimer laser (Lambda Physics, Göttingen, Germany) and directed through a quartz lens into the cuvette, illuminating the whole buffer volume. The amount of released protons was dependent on the intensity of the UV flash and the concentration of the caged compound. At a concentration of 300 μM and an initial pH between 7 and 7.2 the first UV flash produced pH jumps on the order of −0.4 to −0.7. With successive light flashes the pH of the electrolyte could be decreased stepwise. Typically, four flashes were applied to the same cuvette filling to collect kinetic data of proton binding to the Ca-ATPase.

The time course of the fluorescence signal was analyzed by a numerical fit of the data with a sum of two exponential functions,

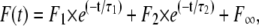(1)

which provided the time constants, τ₁ and τ₂, as well as the respective fluorescence amplitudes, F₁ and F₂, and the new stationary fluorescence level, F_∞, after the relaxation process, which was used to determine the pH of the electrolyte.

pH determination by fluorescence measurements

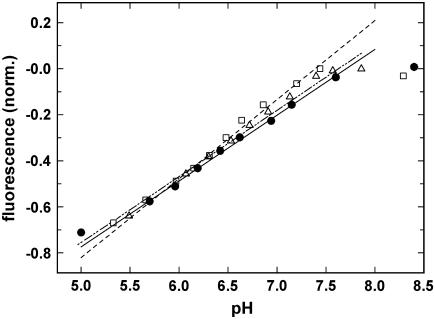
To determine pH of the electrolyte solutions in situ and immediately after a pH jump, we made use of the fact that in the E₁ (and P-E₂) conformation of the Ca-ATPase a monotonous relation holds between buffer pH and the specific fluorescence level of the styryl dye. This dependence has been measured by equilibrium titration experiments. Three representative experiments are shown in Fig. 2. The solutions contained 20 mM Bis-Tris, 0.2 mM EDTA, 9 μg/ml SR Ca-ATPase, 200 nM 2BITC, and the indicated concentrations of NaCl or KCl. The initial pH was adjusted by NaOH or KOH. The titration was performed by addition of small aliquots of HCl. The fluorescence signal was normalized to the initial level at high pH (pH 8.2–8.5). As indicated by the lines in Fig. 2, a linear relation existed between normalized fluorescence intensity and pH in the pH range between pH 5.5 and 7.5. In each series of the time-resolved experiments presented below, the pH at the beginning of the experiment was set to a value <7.5 and again measured at the end directly in the cuvette by a pH microelectrode (AMANI 1000-Flex; Harvard Apparatus, Tampa, FL). With the two data pairs of pH and fluorescence levels, the intermediate stationary pH after each pH jump could be calculated numerically by interpolation.

FIGURE 2.

Dependence of the 2BITC fluorescence on pH in Ca-ATPase-containing SR vesicles. Equilibrium titration experiments were started at high pH and performed by addition of appropriate aliquots of HCl. The electrolyte contained besides 20 mM Bis-Tris, 0.2 mM EDTA, 9 μg/ml SR Ca-ATPase, 200 nM 2BITC 10 mM NaCl (•), 10 mM KCl (□), or 100 mM KCl (Δ). The respective lines are regression lines calculated through the data point in the pH range 5.5–7.5. (T = 21°C).

RESULTS

According to previous investigations with SR Ca-ATPase it was shown that H⁺ binding/release occurs in an electrogenic manner in the pH range between 7.5 and 5 (10). The previous studies were performed as equilibrium titration experiments, which allowed the determination of equilibrium dissociation constants of protons in the cytoplasmic-binding sites of the ion pump as well as competition of protons with Ca²⁺ and Mg²⁺ for the ion sites. The availability of MNPS·Na now provides the opportunity to perform time-resolved kinetic experiments and obtain access to rate constants of the proton binding and dissociation in the E₁ conformation of the Ca-ATPase. Since the presence of Mg²⁺ ions produces only an apparent shift of binding affinities with respect to Ca²⁺ and H⁺ binding, all experiments were performed in the absence of Mg²⁺.

MNPS·Na-induced fluorescence changes

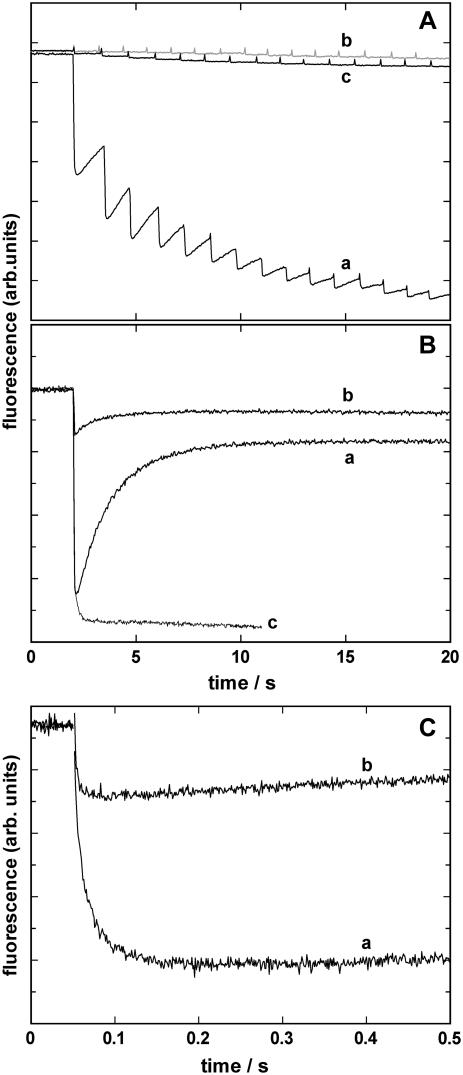
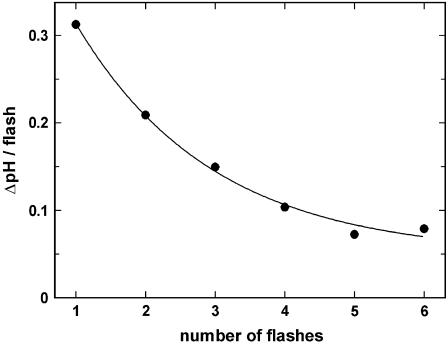
To test and identify effects produced by the so far unstudied caged proton, a series of control experiments was performed. Essential experiments are summarized in Fig. 3. In Fig. 3 A 15 UV flashes were applied to a cuvette with different fillings in the fluorescence setup. The light flashes were administered with a frequency of ∼1/s. Trace a shows the result when the buffer contained 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, 9 μg/ml Ca-ATPase, and 300 μM MNPS·Na; the initial pH was 6.8. Upon a fast fluorescence decrease within the first 200 ms after the UV-flash-induced pH jump, a partial recovery of the fluorescence intensity can be observed, which can be seen more clearly in Fig. 3 B, trace a, where only a single flash was triggered. When the pH of the electrolyte was measured after 1–6 flashes it was found that ΔpH decreased with each subsequent flash (Fig. 4), and after six flashes the total pH drop was ∼1 unit. When the experiment was repeated with 300 μM of MNP, the inert photoproduct of the caged proton, in the cuvette no significant fluorescence decrease could be observed (trace b in Fig. 3 A). When in a similar experiment the Ca-ATPase-containing SR vesicles were left out and 300 μM MNPS·Na were present, again no significant fluorescence decrease could be observed (trace c).

FIGURE 3.

Time course of pH jump induced 2BITC fluorescence signals. (A) A sequence of 15 UV flashes was applied to cuvettes filled with electrolyte containing 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, and (a) 9 μg/ml Ca-ATPase and 300 μM MNPS·Na, (b) 9 μg/ml Ca-ATPase and 300 μM of MNP, (c) no Ca-ATPase but 300 μM MNPS·Na . (B) A single UV flash was applied to visualize the partial recovery of the fluorescence amplitude in the case of a pH jump in the presence of 9 μg/ml Ca-ATPase and 300 μM MNPS·Na (trace a). For comparison the same experiment was repeated in the presence of 300 μM MNPS·Na and DOPC vesicles (trace b) or open membrane fragments containing SR Ca-ATPase and 300 μM MNPS·Na (trace c). (C) Experiments as shown in panel B were repeated with higher time resolution to show the initial fluorescence decrease. Trace a represents the experiment in the presence of 300 μM MNPS·Na and 9μg/ml Ca-ATPase (2.5 μg/ml lipid) in the form of SR vesicles. In trace b 9 μg/ml pure DOPC vesicles were added instead of the SR vesicles.

FIGURE 4.

Effect of proton release from MNPS·Na on electrolyte pH. In these experiments between one and six UV flashes were applied to a cuvette filled with electrolyte containing 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, 9 μg/ml Ca-ATPase, and 300 μM MNPS·Na, pH 7.0. After the illuminations pH was measured by a microelectrode. ΔpH between two consecutive flashes was determined and plotted against the number of applied flashes. The line fitted through the data points is an exponential decay and corresponds to an average release of 0.125 μM H⁺ per flash (corresponding to 0.33% of the initial amount of caged proton).

In Fig. 3 B, trace a, the same electrolyte composition was chosen as in panel A, trace a, but only a single UV flash was administered. The fast fluorescence drop was followed by a slower increase with a new equilibrium state below that before the light flash. The time constant of the raising phase was on the order of 2–5 s. A possible explanation of such a slow process is that there exists a slowly accessible H⁺ buffering compartment that scavenges H⁺ from the electrolyte and thus removes protons from the binding sites in the Ca-ATPase. To test this hypothesis we performed experiments with pure DOPC vesicles. An experiment corresponding to that of trace a, in which the Ca-ATPase-containing SR vesicles were replaced by 9 mg/ml unilamellar lipid vesicles, is shown as trace b. The amplitude of the fluorescence response may not be compared since the amount of lipid in both experiments was not the same (the lipid concentration was higher by about a factor of 2 in the case of the protein-free vesicles), and the specific fluorescence in lecithin vesicles is different from that in membranes containing different lipids and proteins.

It is nevertheless obvious that pH jump also caused an effect on the styryl dye in pure lipid vesicles. The time constants and the fluorescence change were, however, significantly smaller than in the SR vesicles. Another control experiment was performed with open membrane fragments prepared from SR vesicles by a procedure derived from the method used to obtain the purified microsomal membrane preparation of Na,K-ATPase (25). When those membranes, both sides of which are simultaneously accessible in the electrolyte solutions, were used in experiments corresponding to that of trace a, a biphasic time course of the fluorescence response on a pH jump was no longer visible (Fig. 3 B, trace c). The absence of the rising phase strongly supports the idea that the delayed buffering of protons is caused by the slowly accessible luminal compartment in the case of a vesicular membrane shape.

Since the rising phase of the fluorescence signal has a time constant on the order of seconds whereas the initial fluorescence decrease is much faster, with time constants from a few milliseconds to less than 100 ms, both phases are well separable, as can be seen in Fig. 3 C. Both traces show identical experiments to that of Fig. 3 B with a higher time resolution, 500 ms instead of 20 s, for Ca-ATPase-containing SR vesicles (trace a) and DOPC vesicles (trace b). The experiments were performed at 21°C and show that the unspecific 2BITC-fluorescence decrease is significantly faster than that of the Ca-ATPase-mediated effect. In Fig. 3 C the time course of the fluorescence signals were fitted by the sum of two exponentials according to Eq. 1, and the time constants were 3.2 ms and 22.2 ms for trace a. The falling phase of trace b could be fitted by a single exponential with a time constant of 4 ± 1 ms. To normalize the fluorescence amplitude to the same lipid concentration in the cuvette (5.4 μg/ml in trace a, 9 μg/ml in trace b), the amplitude of trace b has to be reduced by a factor of 0.6 to allow a comparison of both fluorescence responses under the assumption that the specific fluorescence is not significantly different in both lipid compositions. The unspecific fluorescence response (trace b) would then be ∼10% of the response generated by proton binding to the Ca-ATPase.

Analysis of pH-dependent proton binding to the E₁ state of the Ca-ATPase

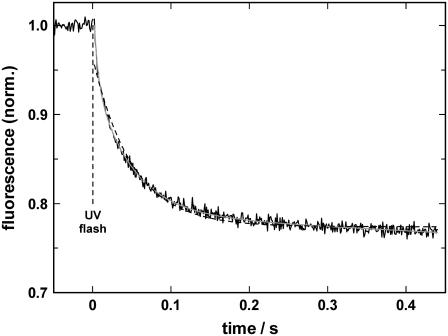
To study the time-resolved kinetics of proton binding to the ion-binding sites in the E₁ conformation of the SR Ca-ATPase, pH jump experiments were performed with high time resolution. A typical experiment is shown in Fig. 5. The cuvette was filled with 300 μl of electrolyte containing 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, 9 μg/ml Ca-ATPase, and 300 μM MNPS·Na . The initial pH was 7.2, the temperature was 6.5°C. The level of the 2BITC fluorescence reflects the occupation state of the ion-binding sites and was continuously monitored. Under the given conditions the binding sites were virtually empty before the first flash (10). At time t = 0 a UV laser flash was triggered and caused the hydrolysis of ∼0.125 μM MNPS·Na and a (transient) pH jump of ∼0.5 units from pH 7.2, according to Figs. 2 and 3. The time course of the fluorescence was fitted by a least square method with one or the sum of two exponentials as shown in Fig. 5 (dashed or solid line, respectively). The single exponential with a time constant of 50.4 ms did not reproduce the experimental data in a satisfactory manner. When fitted with the sum of two exponentials, the time constants of τ₁ = 14.5 ms and τ₂ = 65 ms produced a perfect fit of the experimental time course. The amplitude of both processes were comparable, F₁ = 0.1 and F₂ = 0.12, which indicates that about the same amount of positive charge was moved into the membrane domain of the ion pump. In the experiments described in the following, the falling phase was always fitted with a sum of two exponentials to obtain an accurate representation of the data.

FIGURE 5.

pH jump induced proton binding to the SR Ca-ATPase in its E₁ conformation. After a UV-flash-induced release of protons, binding of H⁺ induces a decrease in 2BITC fluorescence. The experiment was performed in electrolyte containing 10 mM NaCl and 10 μM BAPTA, pH 7.2. The temperature was 6.5°C. The time course of the fluorescence signal could be perfectly fitted by the sum of two exponentials (solid gray line) with time constants, τ₁ = 14.5 ms and τ₂ = 65 ms. Fitting the data with a single exponential led to no satisfactory result (dashed line).

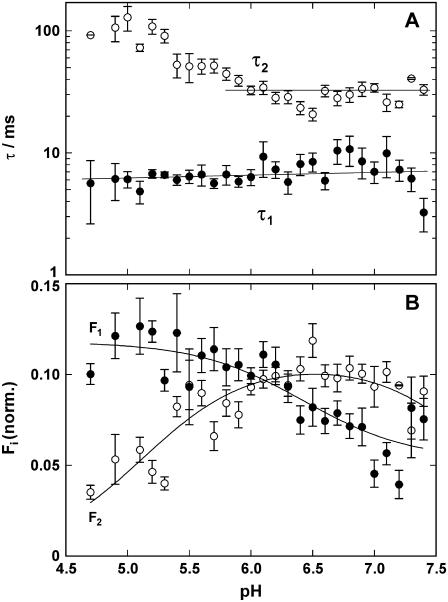
Experiments as shown in Fig. 5 could be performed four times in sequence with one filling in the cuvette. Electrolyte pH was measured by a microelectrode before the first and after the last experiment. The respective fluorescence levels were also recorded at the beginning and at the end. With the pH dependence of 2BITC fluorescence of the respective electrolyte composition (cf. Fig. 2), the appropriate pH was determined immediately before and after each UV flash. For each pH jump relaxation the data were fitted with the sum of two exponentials (Eq. 1), and the time constants, τ₁ and τ ₂, as well as the amplitudes, F₁ and F₂, were determined. The time constants and amplitudes of experiments within the same pH interval of 0.1 were averaged and plotted against pH (after the pH jump). For each interval of 0.1 between pH 5.0 and 7.2, 6–20 experiments were performed and the results averaged. The overview over the experiments in 10 mM NaCl, 0.1 μM BAPTA, 600 nM 2BITC, 300 μM MNPS·Na (T = 20°C) is shown in Fig. 6.

FIGURE 6.

Analysis of pH jump experiments in the absence of CaCl₂. The time course of the fluorescence decrease was fitted with the sum of two exponentials (Eq. 1), and (A) the time constants, τ_i, and (B) amplitudes, ΔF_i, were plotted against the electrolyte pH after the pH jump. The UV-flash-induced release of protons was ∼0.125 μM, independent of pH in the buffer. (A) The faster of the two rate-limiting processes, controlled by τ₁ is not significantly dependent on pH in the pH range covered by the experiments. The slower process is decelerated below pH 6 with increasing proton concentrations. (B) The fluorescence amplitude revealed a pH dependence for both processes. Since it reflects binding of protons to the Ca-ATPase, it is obvious that below pH 6 the faster process carried more protons into the membrane domain than the slower one. Above pH 6 it was vice versa.

According to the principles of chemical kinetics, the time course of a signal that is controlled by two exponential functions represents a reaction sequence with (at least) two rate-limiting steps. The faster of both processes was not significantly pH dependent. The mean value of τ₁ averaged for all 338 experiments was 6.6 ± 0.3 ms. The slower process has a constant time constant in the more “physiological” pH range of 5.9–7.4 with a τ₂ = 31.4 ± 1.5 ms. At pH below 6 the relevant process was decelerated. This finding indicates that it could not be proton binding since then it would have to be expected that the reaction rate is accelerated with increasing H⁺ concentration (i.e., the time constant is smaller). The most probable explanation of the observed effect at low pH is that certain amino acid side chains of the protein become protonated below pH 6, and this modification has an allosteric effect, influencing conformational rearrangements of the Ca-ATPase related to proton binding.

The pH dependence of the (modulus of the) fluorescence amplitudes, F₁ and F₂, as shown in Fig. 6 B cannot be interpreted simply. With each pH jump experiment the proton concentration was stepwise increased by ∼0.125 μM, and the respective induced fluorescence amplitude changes are plotted against the pH after the jump. When the total fluorescence decrease per pH jump, ΔF = F₁ + F₂, was calculated in the pH range between 5.0 and 7.0, it was constant with ΔF = 0.176 ± 0.004 (not shown). For the few data points at pH < 5.0 a smaller ΔF could be observed. This result indicates that in the pH range covered by the experiments the amount of protons bound to the pump was the same for each pH jump. The second piece of information that can be taken from the pH dependence of the amplitudes in Fig. 6 B is the normalized fluorescence amplitudes, F₁/ΔF and F₂/ΔF. These amplitudes reveal that at pH 6.2 both amplitudes are equal, whereas at lower pH the faster process carried more charge into the binding sites than the slower one; and for pH > 6.2 the contributions are reversed. The increase/decrease of the normalized fluorescence amplitude is linearly related to the pH (not shown).

Interaction of Ca²⁺ and H⁺ ions in pH jump experiments

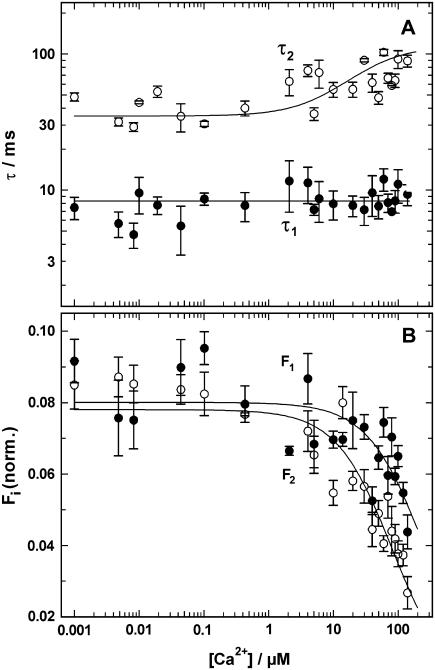
Since it is known that protons and Ca²⁺ ions compete for the same binding sites in the Ca-ATPase, the effect of Ca²⁺ on proton-binding kinetics was studied. Experiments as shown in Fig. 5 were performed in the presence of various concentrations of CaCl₂. In an electrolyte with 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, 9 μg/ml Ca-ATPase, and 300 μM MNPS·Na concentrations of free Ca²⁺ were chosen between 1 nM and 140 μM. Above 140 μM Ca²⁺ the fluorescence amplitudes induced by a pH jump were so small that no reliable analysis was possible. Electrolyte pH after a single flash-induced proton release was between 7.0 and 6.7 in these experiments. At each Ca²⁺ concentration 4–10 experiments were performed and analyzed by fitting the time course with two exponentials (Eq. 1). In Fig. 7 the time constants, τ₁ and τ₂, and the amplitudes, F₁ and F₂, of the fluorescence decrease are plotted against the free Ca²⁺ concentration. For the faster process the time constant, τ₁, was completely independent of the Ca²⁺ concentration. The average value was 8.3 ± 0.4 ms and varied over five orders of magnitude in Ca²⁺ concentration by less than a factor of 2. The slower process could be fitted with time constants between 30 ms and 100 ms. To visualize possible concentration dependence, a binding isotherm was plotted through the data with a half-saturating concentration of 30 μM.

FIGURE 7.

Ca²⁺-concentration dependence of the pH jump induced fluorescence relaxation. Experiments as shown in Fig. 5 were performed in the presence of various Ca²⁺ concentrations. The time course of the fluorescence signal was fitted with the sum of two exponentials (Eq. 1). The time constants, τ_i, and the fluorescence amplitudes, F_i, were plotted against the concentration of free Ca²⁺ in the electrolyte. (A) The time constant of the fast process, τ₁ = 8.3 ms, was Ca²⁺-concentration independent whereas the slower process was decelerated at Ca²⁺ concentrations above 1 μM. (B) The amplitude of both components of the fluorescence signal decreased at concentrations >5 μM. Above 400 μM Ca²⁺ no significant fluorescence changes could be detected.

This dependence indicates that at higher Ca²⁺ concentrations a different and slower rate-limiting reaction step became prominent, i.e., when Ca²⁺ ions have to be assumed to occupy the binding sites. This interpretation is supported by the Ca²⁺ concentration dependence of the fluorescence amplitude (Fig. 7 B). Both amplitudes can be fitted by a binding isotherm with estimated half-binding Ca²⁺ concentrations of 80 μM (F₁) and 25 μM (F₂). The reduction of the fluorescence amplitude for both amplitudes reflects less positive net charge movement into the membrane domain of the ion pump at high Ca²⁺ concentrations. A reasonable assumption to explain this observation is that at low Ca²⁺ concentrations the binding sites were free of Ca²⁺ and uncompensated proton binding occurred, and at intermediate Ca²⁺ concentrations two or more protons were exchanged against a Ca²⁺ ion. At sufficiently high Ca²⁺ concentrations both binding sites were occupied by Ca²⁺ and no exchange occurred at all. This assumption is in agreement with the results from previous equilibrium titration experiments with the same enzyme (10). From the fluorescence amplitudes of both components, F₁ and F₂, it can also be seen that at low Ca²⁺ concentrations in the fast and slow process about the same amount of positive charge is moved into the membrane domain. At concentrations above 1 μM the faster reaction step is related to a larger charge movement than the slower one.

To study the interaction of protons and Ca²⁺ ions in the cytoplasmic ion-binding sites, the pH dependence of the fluorescence signal was investigated in the pH range between 7.5 and 5.0 in the presence of 50 μM free Ca²⁺. Since the half-saturating Ca²⁺ concentration at pH 7.2 (and in the absence of Mg²⁺) is 185 nM (10) and ∼380 nM at pH 6.3 (data not shown), the occupation of the binding sites with Ca²⁺ should be almost complete at 50 μM Ca²⁺.

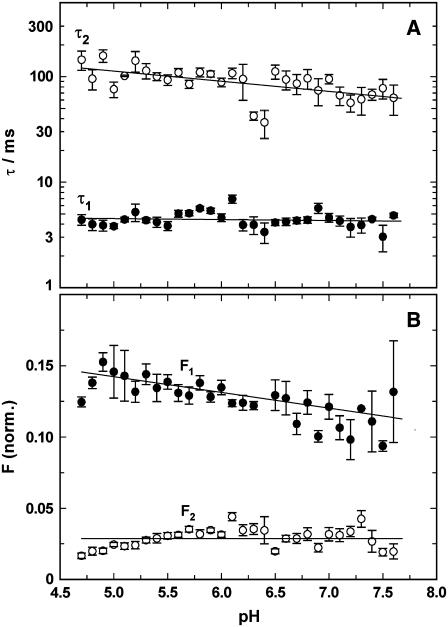
pH jump experiments were performed as in the absence of Ca²⁺ (described above). Electrolyte composition was 10 mM NaCl, 10 μM BAPTA, 600 nM 2BITC, 9 μg/ml Ca-ATPase, 300 μM MNPS·Na, and 60 μM CaCl₂ (corresponding to 50 μM free Ca²⁺). The results are presented in Fig. 8. The enzyme batch used in these experiments differed slightly in its kinetic properties. The faster process, represented by τ₁, was found (again) to be pH independent (Fig. 8 A); however, its value was 4.41 ± 0.14 ms, which is about a factor of 2 smaller than the corresponding point in Fig. 7 A. The time constant of the slower process, τ₂, is in agreement with the corresponding data in Fig. 7 A. It showed a slight pH dependence with a minor increase with decreasing pH. In the physiologically interesting pH range between 6 and 7.5, τ₂ was determined to be 78.5 ± 5.5 ms.

FIGURE 8.

Analysis of pH jump experiments in the presence of 50 μM CaCl₂. The time course of the fluorescence decrease was fitted with the sum of two exponentials (Eq. 1), and (A) the time constants, τ_i, and (B) amplitudes, ΔF_i, were plotted against the electrolyte pH after the pH jump. The UV-flash-induced release of protons was ∼0.125 μM, independent of pH in the buffer. (A) Both rate-limiting processes, controlled by τ₁ and τ₂ are not significantly dependent on pH in the pH range covered by the experiments. (B) The fluorescence amplitude of the faster process, F₁, showed a slight decrease with a decreasing proton concentration, whereas the fluorescence amplitude of the slower process, F₂, was virtually independent of the electrolyte pH. It was by a factor of 3–4 smaller than the faster component.

The pH dependence of the fluorescence amplitudes in the presence of 50 μM Ca²⁺ (Fig. 8 B) differed significantly from that in the absence of Ca²⁺ (Fig. 6 B). F₁ increased only slightly from pH 7.5 (0.11) to pH 5 (0.14), whereas in the absence of Ca²⁺ the increase was about a factor of 2. A comparison of the charge moved by the faster process into the binding sites reveals that in the presence of 50 μM Ca²⁺ a slightly higher amount was found at all pH values. In the presence of 50 μM Ca²⁺ the fluorescence amplitude of the slow process, F₂, was almost pH independent, with an average amplitude of 0.03 (Fig. 8 B), in contrast to the findings in the absence of Ca²⁺ (Fig. 6 B); and the amount of (net) charge entering the membrane domain of the Ca-ATPase related to the slower process was only a fraction of that in the absence of Ca²⁺ (∼30%–40%) at a pH > 6.

Activation energies of the rate-limiting reaction steps

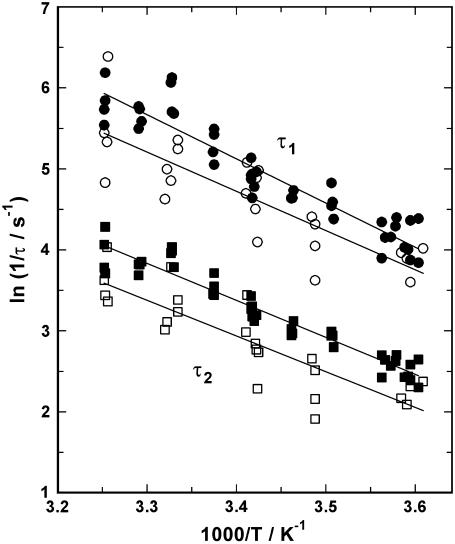
pH jump experiments were also performed in the temperature range between 4°C and 34°C, in the absence and presence of 40 μM free Ca²⁺ and in the pH range between 7.0 and 6.5. The fluorescence signals were fitted with Eq. 1, and both resulting time constants, τ₁ and τ₂, were plotted as an Arrhenius plot (i.e., ln(1/τ) versus 1/T), as shown in Fig. 9. The activation energies, E_A, of the respective rate-limiting reaction steps can be determined from the slope, m, of the regression line through the plotted data, according to E_A = −m × R (R = 8.13 J mol⁻¹ K⁻¹). In the absence of Ca²⁺ the activation energies were E_A (τ₁) = 45.3 ± 2.5 kJ/mol and E_A (τ₂) = 38.0 ± 1.6 kJ/mol. In the presence of 40 μM Ca²⁺ the activation energies were E_A (τ₁) = 40.3 ± 5.7 kJ/mol and E_A (τ₂) = 36.7 ± 4.8 kJ/mol. Thus, the presence of Ca²⁺ did not significantly alter the activation energy, and the difference between E_A (τ₁) and E_A (τ₂) was only minor. In summary, these activation energies correspond to a Q₁₀ value of 1.68 ± 0.04.

FIGURE 9.

Temperature dependence of the relaxation time constants. The experimentally determined time constants, τ₁ (circles) and τ₂ (squares), are shown as an Arrhenius plot. The flash-induced pH jump experiments were performed in the absence of Ca²⁺ (solid symbols) or in the presence of 50 μM free Ca²⁺ (open symbols). The lines drawn through the data are linear regression fits, and the absolute value of their slopes is proportional to the activation energy of the rate-limiting process.

DISCUSSION

The advantage of relaxation studies of ion-transport systems was recognized in the early years of this field and exploited by detailed mathematical formalisms to determine the kinetic parameters, such as rate constants and partition coefficients (for a review, see Läuger et al. (26)). Concentration-jump experiments became especially useful after the introduction of so-called caged compounds, which are utilized to release a substrate for a transport protein by a light-induced release from an inactive precursor (27–32). In the case of ion pumps, concentration jumps of transported ions are of prominent interest since their application affords important insights into kinetics and mechanisms of transport. For the SR Ca-ATPase it is a lucky chance that both transported cations, Ca²⁺ and H⁺, are available as caged compounds. Caged Ca²⁺, which is a photolabile chelator that selectively binds Ca²⁺ (33–35), has been successfully applied to study binding to the ion sites in the E₁ conformation on the cytoplasmic side (12). To produce fast pH jumps in aqueous solutions, a number of caged compounds were synthesized which differed in aqueous solubility and quantum yield (36–38).

In our experiments a styryl dye is used to monitor charge movements in the membrane domain of the ion pumps by their effect on the local electric fields in the hydrophobic domain of the membrane (16). Local electric fields in membranes are controlled also by the dielectric coefficient of the lipid phase, and therefore it is crucial that the photoproduct after cleavage of the caged proton is highly water soluble and/or does not affect the dielectric coefficient of the membrane. At least, it should not interfere with the styryl dyes by production of unspecific fluorescence changes. The newly synthesized caged proton, MNPS·Na, which actually is a caged sulfate similar to the recently introduced 1-(2-nitrophenyl)ethyl sulfate (38), meets all the requirements necessary to study proton binding to the Ca-ATPase: It is highly soluble in the aqueous phase, the photoproduct does not significantly affect the styryl dyes in the lipid phase of the membrane, and in the setup used for our experiments it produced proton-concentration jumps of ∼0.125 μM free H⁺ under optimized conditions in low buffered systems. Since each flash hydrolyzed less than 1% of the caged proton present, numerous successive flashes can be applied, and typically four experiments were performed with one cuvette filling. They generated a total pH jump on the order of 1–2 pH units, depending on the initial pH before the first flash (Fig. 4). Due to the lack of appropriate equipment we were not able to resolve the kinetics of the hydrolysis of MNPS·Na. Preliminary experiments with indicator solutions and textbook knowledge on the principles of similar hydrolysis reactions indicate, however, that the release reaction may be expected to be considerably faster than the observed reaction processes of the Ca-ATPase on the order of 1 ms and above. A detailed analysis is planned in a collaboration.

Analysis of the fluorescence amplitudes

The experiments were performed with SR membrane vesicles in which the cytoplasmic side of the membrane faces the outside and allows unrestricted access to the binding sites in the E₁ conformation of the ion pump. At times t > 0.5 s a fluorescence increase could be observed which reflects a pH increase in the electrolyte (Fig. 3). Since this effect disappeared in experiments with nonvesicular membrane preparations, this increase may be explained by the diffusion of protons into the lumen of the vesicles where they are buffered by the internal lipid surface and the aqueous compartment. The analyzed reaction steps of proton binding to the E₁ conformation were fast enough (<0.4 s, Fig. 5) so that this unspecific effect could be neglected.

The average concentration of protons released by a UV flash from caged proton was 0.125 μM (Fig. 4). (The concentration of Ca-ATPase was ∼0.072 μM.) The experimentally determined relation between H⁺ concentrations in the electrolyte and the amount of charge bound after a pH jump was found to be linear and indicates that the experiments were performed under conditions far from saturation of the ion-binding sites.

Independent of the initial pH in all pH jump experiments, the total fluorescence change, ΔF_total = F₁ + F₂, was approximately constant (0.184 ± 0.004 in the absence of Ca²⁺ and 0.155 ± 0.003 in the presence of 50 μM Ca²⁺). From Ca²⁺-titration experiments in the tested pH range between pH 5 and 7.6 we know that the maximum fluorescence change upon addition of saturating concentrations of Ca²⁺ produced a fluorescence drop of |ΔF_max| = 0.70 ± 0.02 at pH 7.6 and room temperature. This value allows an estimate of the effect of four elementary charges entering the binding sites on the fluorescence amplitude. Typical fluorescence changes produced by pH jump experiments on the order of 0.17 correspond to the addition of a single elementary charge (or one proton).

In the experiments with several successive flash-induced pH jump experiments a total fluorescence decrease of 0.75–0.9 could be observed which matches an uptake of about four positive elementary charges in the binding sites. This finding is in agreement with equilibrium pH-titration experiments as shown in Fig. 2 or in a previously published study (10) performed with the same detection method. These results indicate that under nonphysiological conditions the binding sites may be forced to accept more than the two transported protons, when the Ca pump is confined to the states in the E₁ conformation due to the absence of ATP.

According to the (physiological) Post-Albers cycle of the SR Ca-ATPase, the reaction steps accessible in the absence of ATP and inorganic phosphate are confined to the sequence

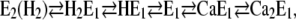(Scheme 1)

or are further reduced in the absence of Ca²⁺ to

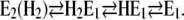(Scheme 2)

As mentioned above, previously published experiments (10,39) indicated that more than two H⁺ may be bound to the pump under nonphysiological conditions,

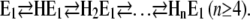(Scheme 3)

In recent work it was found that the transport stoichiometry possibly varies in a pH-dependent manner (40,41).

When pH jump experiments were performed in the absence of Ca²⁺, the equilibrium distribution between the states in the reaction sequence (Scheme 3) is shifted slightly to the right after each pH jump, indicating a higher occupation of the states in which one or more protons are bound to the ion-binding sites in the Ca-ATPase.

From time-resolved experiments with the styryl dye, 2BITC, the fluorescence signal upon a pH jump had to be described by the sum of two exponential functions (Eq. 1), and two types of information are obtained: 1), the amplitude of the fluorescence changes, F₁ and F₂; and 2), the time constant of the exponentials, τ₁ and τ₂.

To analyze the amplitudes, one has to keep in mind that for each pH jump the H⁺ concentrations increased only by such a small amount that on the average only a fraction of an elementary charge per pump is shifted into the binding sites and that this process also depends on the electrolyte pH before the experiment. The maximum fluorescence decrease after a series of 15 proton-releasing UV flashes also produced a total drop of ≥0.9, equivalent to binding about four protons. Since it was convincingly shown that the SR Ca-ATPase transports only two H⁺ per cycle (39,42), two further H⁺ have to bind to additional “sites” in the membrane domain, probably in or at least close to the Ca²⁺-binding sites. When starting experiments with Ca²⁺ ions in the binding sites no transient fluorescence increase was observed which would correspond to the state E₁ with empty binding sites. This fact leads to the suggestion that a fast exchange of Ca²⁺ against H⁺ takes place, as it was observed in the case of the Na,K-ATPase for Na⁺ against H⁺ (43). In the pH jump experiments performed, the pH after the jump as well as ΔpH itself varied, and the total charge movements was shared between (at least) two electrogenic reaction steps. Due to this complex situation the fluorescence amplitudes, F₁ and F₂, as a function of pH were less meaningful than the ratio of both amplitudes, F₁/F₂, that provides information on which of both steps more charge was moved into the membrane domain. In the absence of Ca²⁺ ions, when displacements of the steady state are possible only in the restricted reaction Scheme 3, this ratio reveals which of the observed partial reactions transfers more charge. From the pH dependence of this ratio, arguments are gained on how to assign both detected processes to the ion-binding scheme of the pump (see below).

In the absence of Ca²⁺ ions, it was found (Fig. 6) that at pH < 6 more protons were entering the protein in the faster process (1 < F₁/F₂ < 3), in contrast to the experiments at pH > 6 when the contribution of the slower process was greater (0.5 < F₁/F₂ < 1). Analysis of the measurements in the presence of 50 μM Ca²⁺ (Fig. 8) showed that the amplitude of the faster process, F₁, was larger in the whole pH range covered by the experiments (3.5 < F₁/F₂ < 8). Between pH 5.5 and 7.5 the ratio was constant with an average value of 3.9 ± 0.12, and below pH 5.5 it increased to ∼8 at the lowest pH.

Analysis of the time constants

The time constants, τ₁ and τ₂, or their reciprocal values, which are relaxation rates, k₁ = 1/τ₁ and k₂ = 1/τ₂, are complex compound values of the forward and backward rate constants of the underlying reaction scheme, as can easily be verified in textbooks of chemical kinetics (e.g., Bamford and Tipper (44)). Nevertheless, it can be concluded from the order of magnitude of the detected time constants (1–100 ms) that the rate-limiting processes are no diffusion-controlled ion movements through the access channels (which would occur in the time domain of τ < 1 μs).

The faster process, represented by the time constant τ₁, is not significantly dependent on the concentrations of H⁺. The averaged values were 6.9 ± 0.3 ms in the absence and 4.4 ± 0.1 ms in the presence of 50 μM Ca²⁺. When we studied Ca²⁺ binding to the SR Ca-ATPase in a recent article (12), two time constants were also found of which the faster process had a τ₁ of 4.7 ± 0.5 at pH 7 and various Ca²⁺ concentrations (and in an electrolyte buffered with 50 mM Hepes). If this process describes proton binding to the pump, such as E₁ + H⁺ → HE₁ (or more probably, E₁ + 2H⁺ → H₂E₁), then it has to be expected that the rate would become faster with increasing H⁺ concentration or, correspondingly, the time constant would be reduced with decreasing pH. The pH independence of τ₁ indicates, however—similar to what was observed in the case of Ca²⁺ binding—that the electrogenic entry of H⁺ into the sites and its binding to a site has to be fast compared to the observed rate-limiting step and has to be subsequent to the observed (slower) step.

The second time constant, τ₂, represents another rate-limiting reaction step with 31.4 ± 1.5 ms in the absence of Ca²⁺ and in the pH range of 5.9–7.4. Decreasing pH below 5.9 led to increasing time constants (or smaller rate constants). Such a behavior is in contradiction to a proton-binding reaction, which would be accelerated in the presence of a higher H⁺ concentration and may be explained more consistently by an allosteric reaction, such as an amino acid side-chain protonation (outside the binding site) that reduces the speed of the detected rate-limiting process. In the more physiological pH range around 7, pH independence again suggests that the detectable process is not related to proton binding but preferentially represents an electroneutral conformation relaxation which is followed by an electrogenic proton movement and binding.

When pH jump experiments were performed in the presence of increasing Ca²⁺ concentrations, the average initial state of the Ca-ATPase before the pH jump was shifted to the right in the reaction sequence, 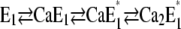(12). In a previous article we showed that the conformational relaxation, 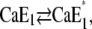is a rate-limiting step. 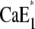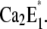Therefore, it has to be expected that this conformation transition affects the time course of the fluorescence signal in pH jump experiments that start from state or Release of a Ca²⁺ ion earlier than H⁺ binding would lead to the higher fluorescence level of state E1, followed by a fluorescence decrease when H⁺ binds. Since the time constant τ₂ rises with increasing Ca²⁺ concentrations from 34 ms ([Ca²⁺] < 1 μM) to 100 ms ([Ca²⁺] = 100 μM), the transition 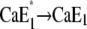obviously came into effect. The relaxation time constant of 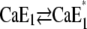was determined to be 200 ms (in a buffered electrolyte composition) (12). However, no transient fluorescence increase was observed. This is in agreement with published equilibrium titration experiments (10) in which pH titrations in the presence of 100 μM Ca²⁺ also exhibited no transient fluorescence increase in the course of the experiment when pH was decreased from pH 7.5 to pH 5. Possible explanations for these observations are that either the “empty” state E₁, which has to have the highest fluorescence level, is unfavorable in this pH range and exists only during a period too short to be detected or it virtually does not exist at all due to rapid displacement reactions for Ca²⁺ by protons in the binding sites.

To find further constraints on the nature of the rate-limiting processes, their temperature dependence was investigated, and their activation energies were found to be on the order of 40 kJ/mol (Fig. 9). The average Q₁₀ value of 1.68 ± 0.04 obtained from the activation energies indicates that the reaction steps controlling the detected kinetic behavior are a conformational rearrangement rather than ion binding or release. This result is in agreement with the findings of Ca²⁺ binding to the ion pump (12), which also showed high activation energies for the rate-limiting steps. This behavior was explained by rate-limiting conformational rearrangements in the binding moieties which precede the diffusion-controlled electrogenic ion movement and binding to the sites.

Proposal of a reaction mechanism

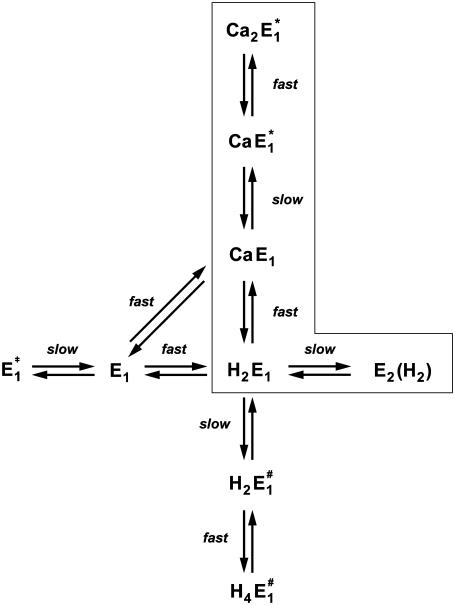
When all results of this study were taken into account it became immediately clear that the part of the Post-Albers cycle accessible in the absence of ATP and inorganic phosphate (Scheme 1) is not sufficient to explain the experimental findings. Even the scheme introduced upon a detailed study of cytoplasmic Ca²⁺ binding (12) was inadequate to explain all the new results in the presence and absence of Ca²⁺. Therefore, we were forced to expand the previously applied reaction mechanism. The simplest proposal based on a physiological Post-Albers scheme is shown in Fig. 10. To simplify matters, although there is no experimental evidence that two protons bind cooperatively, such as E₁ → H₂E₁ or 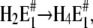successive binding of the two protons was assumed to be so fast compared to the other reaction steps that it can be treated as a single step.

FIGURE 10.

Proposal of a reaction scheme accounting for Ca²⁺ and H⁺ ion interaction with the binding sites of the SR Ca-ATPase in the E₁ conformation. The transitions between states of the ion pump enclosed by the box represent the reaction sequence under physiological conditions; they are part of the Post-Albers cycle. The labeling as “fast” and “slow” transitions indicates the two classes of reaction steps in which, respectively, diffusion-controlled ion movements and binding/coordination of ions happen or conformational rearrangements of the protein occur which modify the access to binding sites.

In the reaction scheme of Fig. 10 the main difference in the canonical sequence is that Ca²⁺ displaces 2 H⁺ (and vice versa) with the consequence that in the presence of Ca²⁺ and H⁺ the binding sites are always occupied by ions. This is possible when acidic amino acid side chains of the Ca-binding site I possess pK values which are high enough that they are protonated under moderate pH conditions (<7.5). A comparable condition has been reported recently for the Na,K-ATPase (43) and was requested for the SR Ca-ATPase in its E₂ conformation (14). In recent electrostatic calculations (40,41) protonation of those amino acid side chains in site I, Glu-771, Asp-800, and Glu-908, was shown to be most likely to occur at neutral pH. Steady-state electrogenic events of Ca²⁺/H⁺ exchange led to the conclusion that Glu-771 and Asp-800 are possible candidates that release H⁺ when a Ca²⁺ binds (42). For the assumption that empty binding sites do not exist in a considerable fraction, our experimental evidence is that upon a pH jump in the presence of Ca²⁺ (in the binding sites) no transient increase of the fluorescence level of 2BITC could be observed. This would have to occur when the number of positive charges in the membrane domain is transiently reduced as in the reaction sequence, CaE₁ → E₁ → H₂E₁.

The state H₂E₁ is in a thermodynamic equilibrium with the preceding state of the Post-Albers cycle, E₂(H₂), which is an occluded dephosphorylated E2 state. Since it is occluded we rule out further proton binding to this state when pH is decreased in the electrolyte. Therefore, we propose another (nonphysiological) side reaction branching from state H₂E₁. To allow additional H⁺ binding in the ion sites, we assume a conformational rearrangement of the binding moiety, namely 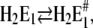which is different from the overall transition into the E₂ conformation. Such minor rearrangements by which the α helices that form the ion-binding moiety respond after the binding (or release) of an ion inside the binding sites to accomplish energetically favored positions. Such relaxations are essential to form optimized structural conditions necessary for the next reaction step. The state 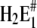either provides access to other side chains in the binding site that may be protonated, such as amino acids involved in site II, or creates polarized structures which are able to coordinate hydronium ions, H₃O⁺.

Obara et al. (41) showed that numerous water molecules fill the binding moiety, and it is not too farfetched to propose that minor side-chain rearrangements provide energetic premises that are able to coordinate hydronium ions. The experimental evidence for this additional partial reaction is the observation that with decreasing pH of the electrolyte, the 2BITC fluorescence decreases to levels that correspond to the presence of four H⁺ inside the membrane domain of the Ca-ATPase (Fig. 4 A). Corresponding results were found by equilibrium titration experiments (10) which could be reproduced (data not shown). Other evidence for this proposal is that in the reaction sequence of proton binding two rate-limiting reaction steps were found of which the faster is assigned to 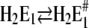(see below). Since this process is pH independent it cannot relate to proton binding, and the high activation energy suggests that it represents a conformational rearrangement.

On the other hand, with respect to state H₂E₁ it may be estimated that at high pH and in the absence of Ca²⁺ an uncompensated deprotonation in the binding sites will occur, and the modified electrostatics inside the membrane domain will provoke another conformational rearrangement of the α helices that form the ion-binding moiety. Therefore, we introduced the reaction sequenc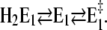e State 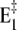is assumed to not bind any ions. To account for Ca²⁺ binding to the Ca-ATPase at high pH, a respective binding step additionally has to be included, 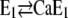(Fig. 10).

To assign the observed rate-limiting processes to appropriate steps in the reaction scheme (Fig. 10), we first consider the experiments in the absence of Ca²⁺. In the pH jump experiments the faster process with τ₁ ≈ 6.6 ms (Fig. 6 A) was not significantly dependent on pH (and Ca²⁺ concentration). It was found also in the presence of Ca²⁺, τ₁ ≈ 8 ms (Fig. 7 A) and τ₁ ≈ 4.4 (Fig. 8 A) and, therefore, should be the rate-limiting step that is present in the sequence of all pH jump experiments. According to Fig. 10 this is true for the reaction step, 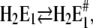that precedes the fast binding of additional protons,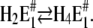

The second, slower process with a time constant of τ₂ ≈ 31 ms observed in the absence of Ca²⁺ may be assigned, according to Fig. 10, to two slow reaction steps, 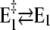or 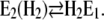In the first case, after a pH jump the total reaction sequence, 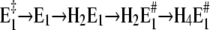includes two (electrogenic) H⁺-binding steps, whereas in the second case, starting from E₂(H₂), only one (electrogenic) H⁺-binding step is present, 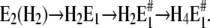The amount of bound ions is reflected in the monitored fluorescence amplitude. Above pH 6 the fluorescence amplitude of the slow process is larger than the faster one, which indicates predominant binding of the first two protons, E₁ → H₂E₁ . When the pH is below 6, the amplitude of the faster rate-limiting process prevails, 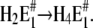There are two reasons to explain this finding: 1), before the pH jump, the equilibrium between the states 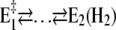is shifted to the left with increasing pH, and therefore, more protons will be bound after a pH jump in the slower step; and 2), at low pH, due to the higher H⁺ concentration, state E₂(H₂) is more strongly populated, and the probability is increased that (finally) up to 4 H⁺ are bound.

The analysis of the time course of the fluorescence signals in the presence of various concentrations of Ca²⁺ is also represented by two exponentials. As discussed above, the faster process can be assigned to a conformational rearrangement, 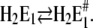The slower process is Ca²⁺-concentration dependent, and the characteristic time constant τ₂ increased from ∼30 ms in the absence of Ca²⁺ to ∼100 ms at 100 μM Ca²⁺ (Fig. 7 A). This shift indicates an increasing control of the slower process by the conformational step 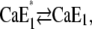which is a consequence of a higher population of the state Ca₂E₁* at higher Ca²⁺ concentrations. When the Ca²⁺ concentration is high enough (>100 μM) most of the pumps are occupied by 2 Ca²⁺ and upon a (small) pH jump the exchange of Ca²⁺ against H⁺ is suppressed for the most part. This is reflected by vanishing fluorescence amplitudes at high Ca²⁺ concentrations (Fig. 7 B). Accordingly, at 50 μM Ca²⁺ the slow process displayed a significantly smaller fluorescence change (and charge exchange) than the faster process (Fig. 8 B).

CONCLUSION

The time-resolved pH jump experiments with the SR Ca-ATPase in its E₁ conformation revealed that the amount of charge entering the binding sites as well as the independence of the reaction rates on pH made it necessary to modify the classical Post-Albers pump cycle by additional reaction steps and states. The observed fluorescence changes require the binding of up to four protons at nonphysiological low pH. Ion-binding and -release steps are all electrogenic since the ions pass through narrow access channels and thus produce changes of the local electrical fields in the membrane domain of the Ca-ATPase. These changes are detected by the styryl dye; however, they are fast compared to the preceding rate-limiting steps. Therefore, the time course of the fluorescence signals is controlled by preceding slow conformational relaxations in the binding moieties. Those relaxations are proposed to be minor rearrangements of amino acid side chains necessary to optimize the potential energy of the protein structure according to the number of ions present. Taking together all the observations and arguments discussed above, the reaction scheme proposed in Fig. 10 allows a consistent description of the ion-binding and -release steps for both transported species of cation to the SR Ca-ATPase in the E₁ conformation. It is an extension of the well-established Post-Albers pump cycle that accounts for the pump function under physiological conditions.

The mechanistic constraints in terms of acidic amino acid side chains that may be protonated in the absence of Ca²⁺ fit well with model calculations. Therefore, we present our proposal as a working hypothesis for further experimental studies.