Abstract
Uropathogenic Escherichia coli express pili that mediate binding to host tissue cells. We demonstrate with in situ force measuring optical tweezers that the ability of P and type 1 pili to elongate by unfolding under exposure to stress is a shared property with some differences. The unfolding force of the quaternary structures under equilibrium conditions is similar, 28 ± 2 and 30 ± 2 pN for P pili and type 1 pili, respectively. However, type 1 pili are found to be more rigid than P pili through their stronger layer-to-layer bonds. It was found that type 1 pili enter a dynamic regime at elongation speeds of 6 nm/s, compared to 400 nm/s for P pili; i.e., it responds faster to an external force. This possibly helps type 1 to withstand the irregular urine flow in the urethra as compared to the more constant urine flow in the upper urinary tract. Also, it was found that type 1 pili refold during retraction at two different levels that possibly could be related to several possible configurations. Our findings highlight functions that are believed to be of importance for the bacterial ability to sustain a basic antimicrobial mechanism of the host and for bacterial colonization.
INTRODUCTION
P pili and type 1 pili are surface organelles anchored to the outer membrane and commonly found on uropathogenic isolates of Escherichia coli bacteria. They facilitate adherence to host cells and are important in the first step of colonization and necessary for biofilm formation (1,2). Depending on the environment, different types of pili are involved in the infection process. Bacteria expressing P pili are most frequently associated with infections in the upper urinary tract and kidney region causing pyelonephritis, whereas bacteria expressing type 1 pili are commonly found in the lower urinary tract and bladder causing cystitis (3). Both P and type 1 pili are ∼1-μm long and 6–7 nm in diameter composed of >1000 subunits of similar size and a comparable higher order structure, in a right-handed helical arrangement with 3.28 and 3.36 subunits per turn, respectively (4,5). At the end of the helix-like rods, a short thin thread (tip fibrillum) is expressed, which anchors the adhesin that binds to the receptors expressed by host cells (6).
Since bacteria in the urinary tract are exposed to mechanical host defenses, primarily urine flow, that expose the bacteria to shear forces, it is suggested that their pili possess elongation properties that are of importance for the ability of bacteria to adhere to host cells and for colonization of tissue at different locations. Bacterial adhesion mediated by a large number of pili acting in parallel would, if the attachment organelles are nonflexible, presumably be considerably weaker than the sum of the individual bonds when a bacterium is exposed to shear forces, since the adhesion bonds then will rupture in a serial mode (like a zipper). If the pili instead have a significant degree of flexibility (mainly an ability to elongate under the presence of a force), shear forces can be distributed among a larger number of pili, thereby exposing each adhesion bond to a smaller force, even if the bacterium-host distance is widely dissimilar at different parts of the binding area (4,7–10).
We have previously shown by the use of force measuring optical tweezers that P pili have the ability to unfold and refold in different modes of elongation and thereby distribute the load over numerous pili (7–10). The elongation can be divided into three distinct regions: region I shows a linear increase in force that corresponds to an elastic stretching of all bonds, region II shows a constant force that represents a sequential unfolding of the quaternary structure, and finally region III, which is represented by a reconfiguration of the head-to-tail bond. Miller et al. recently reported on similar force measurements using atomic force microscopy (AFM) on P and type 1 pili, measurements that confirmed the conclusions reached on the basis of our results on P pili and pointed out biomechanical similarities of the two pili organelles (11). Furthermore, Forero et al. investigated the dynamic properties of the layer-to-layer bond of type 1 pili with AFM (12). However, the limited force resolution of the AFM technique restricted their measurement to assessment of the general biomechanical function of type 1 but did not allow for analysis of its detailed force characteristics, details that can be assessed by the use of force measuring optical tweezers due to its higher force resolution. We have therefore, in this work, used force measuring optical tweezers (7,13) to compare the biomechanical properties of individual P pili expressed from E. coli strain HB101/pPAP5 with the properties of type 1 pili from strain HB101/pPKL4. Our findings show that the differences in their biomechanical properties can be correlated to the host environment in which the pili structures and their role presumably have evolved.
MATERIALS AND METHODS
Bacterial strains and growth conditions
To avoid possible interference of other similar (i.e., fimbrial) surface structures, P pili and type 1 pili were expressed by the otherwise afimbriated E. coli strain HB101 from the plasmid pPAP5 and pPKL4, respectively. The E. coli strain HB101/pPAP5 carries the entire pap gene cluster on the vector pBR322 and expresses normal P pili (14) and the E. coli strain HB101/pPKL4 expresses functional type 1 pili (15). The bacteria were cultured on trypticase soy agar at 37°C and the expression of functional pili was assessed by hemagglutination assays (10).
Optical tweezers force measuring system and measurement procedures
Individual bacteria were mounted on 9.0 μm in diameter polystyrene beads that were immobilized (by heating) to the coverslip and functionalized with poly-L-lysine (7). A typical sample volume (30 μl) for a measurement consists of 1× PBS (pH 7.4), 3.2-μm diameter hydrophobic polystyrene beads and diluted bacteria.
Force measurements were performed by the use of an optical tweezers system, with a force resolution of ∼0.4 pN, which is described in detail elsewhere (7,13). Before each measurement the force constant of the trap was calibrated with the power spectrum method described in Fällman et al. (9). Therefore, the trap stiffness, κ, was individually calibrated in each experiment (∼150 pN/μm). The force responses of the two pili systems were assessed at elongation speeds of 0.05–120 μm/s as well as under a stationary relaxation process described below. The force measurements were combined with a number of control measurements involving measurements on purified P pili as well as on nonpili-producing strain HB101/pBR322 so as to assess irrefutably the measured response to individual pili, and, for example, not the deformation of the bacterial membrane.
Rate theory for unfolding and refolding of a helix-like polymer
The constant force-versus-elongation response in region II is a direct result of the configuration of the quaternary structure of the pilus. As mentioned above, units are appended in a long backbone filament forming a helix-like rod that is connected by ∼3 layer-to-layer bonds per turn. Each bond within the rod will experience one-third of the applied force, the outermost unit will, however, experience the total force. Moreover, opening a bond in the interior of the rod requires that three bonds open simultaneously, which is very unlikely. These two effects lead to a sequential bond breaking of the rod that is mathematically described below.
The rate at which the outermost bond opens can be described by the rate equation,
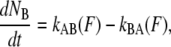 |
(1) |
where  is the number of open layer-to-layer bonds,
is the number of open layer-to-layer bonds, 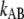 and
and 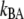 are the bond opening and closure rates under an applied force F. The rates are described by Bell (16),
are the bond opening and closure rates under an applied force F. The rates are described by Bell (16),
 |
(2) |
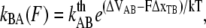 |
(3) |
where 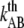 is the thermal bond opening rate in the absence of force,
is the thermal bond opening rate in the absence of force, 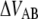 the energy difference between the open and close state,
the energy difference between the open and close state, 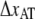 and
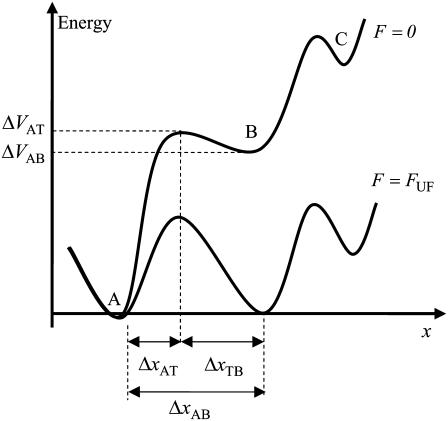
and 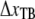 the distance between the closed state A and the transition state T and the distance between the transition state T and the open state B, respectively. Finally, k is the Boltzmann factor and T the temperature. A schematic description of the energy landscape is given in Fig. 1.
the distance between the closed state A and the transition state T and the distance between the transition state T and the open state B, respectively. Finally, k is the Boltzmann factor and T the temperature. A schematic description of the energy landscape is given in Fig. 1.
FIGURE 1.
Schematic energy landscape diagram of the interactions between neighboring units elongated along the long axis of the pilus rod (the reaction coordinate, denoted by x). State A represents the closed layer-to-layer bond, state B the head-to-tail interaction that makes up the backbone of the rod. The position of the maximum of the energy landscape curve between the states A and B are referred to as the transition state, and is denoted by t. The uppermost curve represents the energy landscape for a pilus not exposed to any force, whereas the lower curve refers to the case when the pilus is exposed to a force equal to the unfolding force of the quaternary structure of the rod, 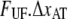 represents the distance from the minimum of state A (in the presence of a force) to the transition state, whereas
represents the distance from the minimum of state A (in the presence of a force) to the transition state, whereas 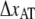 is the distance from the transition state to the minimum of state B.
is the distance from the transition state to the minimum of state B. 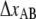 represents the bond opening length along the reaction coordinate. The energies
represents the bond opening length along the reaction coordinate. The energies 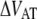 and
and 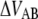 are those of the energy barrier and the difference between state A and B, respectively. State C represents an alternative configuration of the head-to-tail bond.
are those of the energy barrier and the difference between state A and B, respectively. State C represents an alternative configuration of the head-to-tail bond.
Equation 1 gives at equilibrium, i.e., when the two rates are at balance (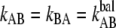 ) an expression for the stationary unfolding force,
) an expression for the stationary unfolding force, 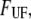 as;
as;
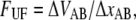 |
(4) |
where 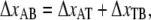 i.e., the bond opening length (8). The effective bond opening rate can also be related to the elongation speed,
i.e., the bond opening length (8). The effective bond opening rate can also be related to the elongation speed, 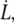 as
as 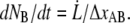 Using this relation and neglecting the refolding rate, which is appropriate for speeds above the corner velocity
Using this relation and neglecting the refolding rate, which is appropriate for speeds above the corner velocity 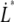 (7), results in an expression that relates the force and elongation speed,
(7), results in an expression that relates the force and elongation speed,
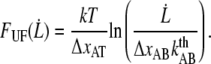 |
(5) |
It is thereby possible to use the unfolding force-versus-elongation speed data to assess 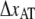 and
and  a method referred to as dynamic force spectroscopy (DFS) (7,12,17,18). This method was used for assessment of
a method referred to as dynamic force spectroscopy (DFS) (7,12,17,18). This method was used for assessment of 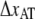 and
and 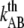 in P pili. However, due to the low corner velocity of type 1 pili, DFS is not suitable for assessment of its parameters (see Discussion below). These parameters can instead preferably be assessed by an alternative technique, which is built upon the monitoring of the decay in force that follows when the elongation to which the pilus is exposed is suddenly halted.
in P pili. However, due to the low corner velocity of type 1 pili, DFS is not suitable for assessment of its parameters (see Discussion below). These parameters can instead preferably be assessed by an alternative technique, which is built upon the monitoring of the decay in force that follows when the elongation to which the pilus is exposed is suddenly halted.
The decaying force, measured with a force transducer, is related to the elongation speed and the stiffness of the trap, 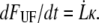 Using this relation and
Using this relation and 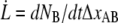 in combination with Eqs. 1–3 gives an expression for the time-dependent unfolding force,
in combination with Eqs. 1–3 gives an expression for the time-dependent unfolding force,
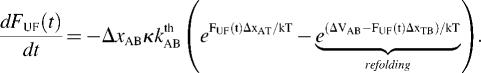 |
(6) |
At high forces the refolding rate can be neglected (7) and Eq. 6 becomes a separable differential equation from which an analytical expression of the unfolding force can be derived,
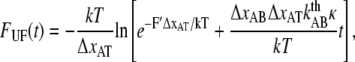 |
(7) |
where F′ is the initial force.
Region III is governed by random transitions from state B to C that give a soft wave-like shape in the force-versus-elongation curve, i.e., an entropic softening. Since all bonds are involved in the length regulation of region III and not just the last bond of the rod, which is the case of region II, region III reacts much faster. Therefore, region III is in its steady-state region for all elongation speeds used. This implies that energy landscape parameters, such as 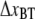 and
and 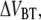 cannot be readily assessed.
cannot be readily assessed.
The force measured during elongation of a biopolymer is a direct result of the energy landscape of the bonds and the applied elongation speed as shown in Eqs. 1–7. Therefore, a trustworthy comparison of similar biopolymers requires measurements either at steady state or an assessment of their dynamic behavior. We have therefore in this work investigated both P and type 1 pili under as equal conditions as possible, both regarding sample preparation and force measurements.
RESULT
Typical single pilus responses to elongation forces
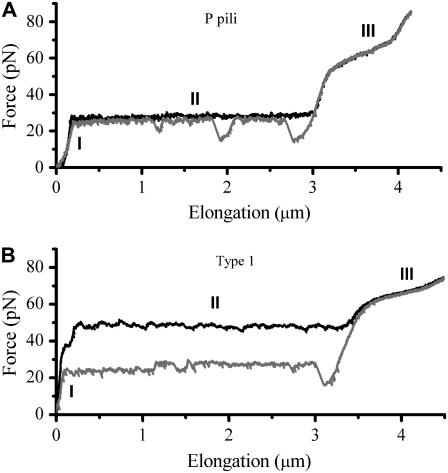
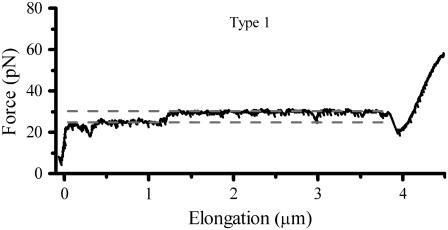
Several in situ measurements on both P and type 1 pili have been performed using force measuring optical tweezers. Fig. 2 shows, by the two panels, a typical unfolding and refolding response of (A) P pili and (B) type 1 pili, respectively. Both measurements were performed at an elongation speed of 0.1 μm/s with the same optical tweezers setup. For P pili, it has been shown that elongation speeds below ∼0.4 μm/s is in the steady-state force regime (7). Moreover, the steady-state unfolding (black curve) and refolding force (gray curve) is 28 ± 2 pN and the bond opening length of the quaternary structure is 3.5 nm (8). As mentioned above, region III was only measured at steady-state conditions with an average force level, ∼65 pN, at the middle of the inclined plateau (8), further elongation gives rise to a force that increases linearly up to a few hundred piconewton (11,12).
FIGURE 2.
Panels A and B show a typical force-versus-elongation response of a single P pili and type 1 pili during unfolding (black curve) and refolding (gray curve) at an elongation speed of 0.1 μm/s.
As can be seen in Fig. 2 B, type 1 pili have a characteristic response largely similar to that of P pili, i.e., same unfolding sequence (black curve); elastic elongation, unfolding at a constant force (opening of the quaternary structure in a sequential manner), and an overstretching of the linearized form, which has partly been shown in recent studies by the use of atomic force microscopy (11). The elastic elongation (almost a constant increasing force, i.e., no entropic behavior) of region I, is very similar to P pili, which indicates that the pili are very straight (long persistence length) (19). Region II shows, for this particular speed, an unfolding force of 50 pN, which is significantly higher than for P pili. Finally, the transition of individual units in region III has a “center of the plateau” value of ∼68 pN that is close to that of P pili.
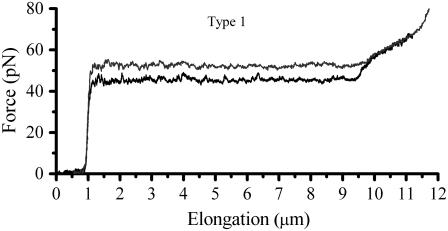
Fig. 3 show a single type 1 pilus elongated at two different speeds, 0.05 and 0.5 μm/s, respectively. The difference in the unfolding force at region II for such an increment in speed indicates that the response was caused by a dynamic effect.
FIGURE 3.
Comparison of the force-versus-elongation response of a type 1 pilus extended at a speed of 0.1 and 0.5 μm/s, respectively. It is clearly seen that the unfolding of region II is in dynamic regime whereas region III is unaffected by the difference in elongation speed.
Since the lowest possible speed of our piezo stage is 0.05 μm/s, which is above the steady-state elongation speed of type 1 pili, it was not possible to measure the elongation of type 1 pili under equilibrium condition. Instead, to assess the equilibrium force that appears when there is a balance between the unfolding and refolding rate, several measurements (>40) were performed in which the elongation was stopped at a fixed elongation in the middle of region II.
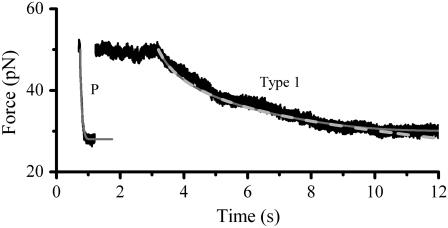
Fig. 4 shows typical relaxation data of P and type 1 pili. Starting at 50 pN type 1 pili typically reach the steady-state force after ∼7 s whereas P pili reach it within ∼0.2 s. The mean steady-state force of type 1 pili was assessed to 30 ± 2 pN, which is about half of what Miller et al. measured (11) and very close to 28 pN assessed for P pili (7).
FIGURE 4.
Typical force-versus-time responses for relaxation of P and type 1 pili from an initial force of ∼50 pN to steady state. An initial force of 50 pN was set through elongation at a fixed speed, 40 μm/s for P pili and 0.3 μm/s for type 1 pili. When the elongation was stopped the pili relaxed to steady state. Type 1 pili reached steady state in ∼7 s and P pili in ∼0.2 s. The dashed line is a fit of Eq. 7 over the force interval 35–50 pN. The solid line corresponds to a numerical simulation of Eq. 6 using the assessed parameters. The overlap of the two curves justifies that 35 pN is high enough to neglect refolding.
For type 1 pili the two fitted lines are the logarithmic decline according to Eqs. 6 and 7 (where the dashed line corresponds to the cases without refolding). The good agreements of the fit (without refolding) to the data show that the force decline is well described by the theory and that the refolding rate can be neglected at forces ∼2 pN above equilibrium. Through a fit of Eq. 7 to 24 relaxation sequences from 15 different pili and by the use of 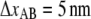 (12), the distance to the transition barrier,
(12), the distance to the transition barrier, 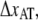 and the thermal bond opening rate,
and the thermal bond opening rate, 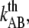 were assessed to 0.59 ± 0.06 nm and 0.016 ± 0.009 Hz, respectively. For the P pilus in this particular plot, the corresponding parameter values were found to be 0.65 nm and 0.8 Hz, respectively. These values show good agreement with the values previously assessed with DFS measurements, 0.76 ± 0.11 nm and 0.8 ± 0.5 Hz, respectively (7).
were assessed to 0.59 ± 0.06 nm and 0.016 ± 0.009 Hz, respectively. For the P pilus in this particular plot, the corresponding parameter values were found to be 0.65 nm and 0.8 Hz, respectively. These values show good agreement with the values previously assessed with DFS measurements, 0.76 ± 0.11 nm and 0.8 ± 0.5 Hz, respectively (7).
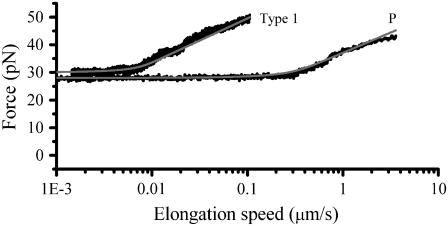
To further elucidate the implication of 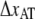 and
and 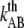 on the force response, the unfolding force-versus-elongation speed was derived and plotted in Fig. 5. At relaxation experiments the elongation speed is set by the properties of the pilus wherefore the elongation speed is based on the parameter assessed by the fit in Fig. 4,
on the force response, the unfolding force-versus-elongation speed was derived and plotted in Fig. 5. At relaxation experiments the elongation speed is set by the properties of the pilus wherefore the elongation speed is based on the parameter assessed by the fit in Fig. 4,
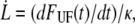 |
(8) |
where 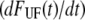 is given by Eq. 6. Fig. 5 shows a typical dynamic response, i.e., a constant unfolding force up to the corner velocity, where after the unfolding force increases logarithmically, in agreement with Eq. 5.
is given by Eq. 6. Fig. 5 shows a typical dynamic response, i.e., a constant unfolding force up to the corner velocity, where after the unfolding force increases logarithmically, in agreement with Eq. 5.
FIGURE 5.
Force-versus-elongation speed where the elongation speed was derived through 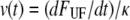 using the parameters assessed via the fit in Fig. 4. The solid curve is a simulation of the force data, based on Eq. 6.
using the parameters assessed via the fit in Fig. 4. The solid curve is a simulation of the force data, based on Eq. 6.
Two levels of refolding
Type 1 pili can, in contrast to P pili, refold at two different force levels, separated by ∼5 pN as can be seen in the refolding curve in Fig. 6. The upper level had an average stationary force level of 30 pN, whereas the lower level is located at 25.5 pN, for this particular set of data.
FIGURE 6.
A refolding sequence of a type 1 pilus that shows a force drop, which almost always is permanent whenever it occurs.
DISCUSSION
The pili structures expressed by uropathogenic E. coli have evolved to delicate organelles with many important and interesting properties that seems to be optimized for bacterial adhesion. It has recently been proposed that a pilus is a flexible structure that plays an important role when it comes to extending the adhesion time by acting as a damper of external forces (11,12). Also, its unfolding and refolding capabilities help the bacterium to keep a close contact to host cells during and after the rinsing action of urine flow (9). This study shows that the biomechanical properties of the type 1 pili are in many perspectives similar to those of P pili but also that there are distinct differences, which possibly can be related to the differences in the local environment. To further elucidate the similarities/differences of the two pili structures a summary of the measured/calculated structure parameters are summarized in Table 1.
TABLE 1.
Parameter values of P and type 1 pili
| Type 1
|
Type 1
|
Type 1
|
P pili
|
|
|---|---|---|---|---|
| Parameters | Our results | Miller et al. (11) | Forero et al. (12) | Andersson et al. (7,8) |
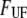 (pN) (pN) |
30 ± 2 | 60* | 22 | 28 ± 2 |
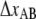 (nm) (nm) |
– | – | 5 ± 0.3 | 3.5 ± 0.1 |
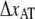 (nm) (nm) |
0.59 ± 0.06 | 0.2 | 0.26 ± 0.01 | 0.76 ± 0.11 |
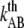 (Hz) (Hz) |
0.016 ± 0.009 | 0.05 | 0.5 | 0.8 ± 0.5 |
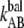 (Hz) (Hz) |
1.2 ± 0.9 | 0.8 | 2.2 | 120 ± 75 |
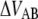 (kT) (kT) |
37 ± 2 | 16† | 25 | 24 ± 1 |
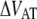 (kT) (kT) |
27 ± 2 | 26† | 29 | 23 ± 1 |
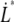 (nm/s) (nm/s) |
6 | – | – | 400 |
Measured at 1–3 μm/s, which is according to our measurements not at steady state.
At an attempt rate of 1010 Hz.
In general, the model agrees well with the experimental data and the fitted values showed little spread from the mean value. The parameter values that best fitted all data for type 1 pili, as presented in Fig. 4, gave an estimate of the bond length of the quaternary structure, of 0.59 ± 0.06 nm, slightly larger than what has been reported using AFM (11,12), but shorter than for P pili, previously assessed to 0.76 ± 0.11 nm (7). The small difference of the bond lengths of type 1 and P pili confirms their structural similarities found through scanning transmission electron microscopy (5).
The thermal bond opening rate for type 1 pili, 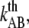 was assessed to 0.016 ± 0.009 Hz, which is significantly lower than what was found for P pili, 0.8 Hz (7). Since the thermal rate,
was assessed to 0.016 ± 0.009 Hz, which is significantly lower than what was found for P pili, 0.8 Hz (7). Since the thermal rate, 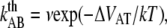 (where ν is the attempt rate), directly depends on the energy of the transition barrier, it can be concluded that a layer-to-layer bond in type 1 pili is bound harder. A ratio of 50 of the thermal bond opening rates of P pili and type 1 pili corresponds to a difference in barrier height of 4 kT. Assuming an attempt rate of 1010 Hz leads to a
(where ν is the attempt rate), directly depends on the energy of the transition barrier, it can be concluded that a layer-to-layer bond in type 1 pili is bound harder. A ratio of 50 of the thermal bond opening rates of P pili and type 1 pili corresponds to a difference in barrier height of 4 kT. Assuming an attempt rate of 1010 Hz leads to a 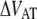 of 23 kT for P and 27 kT for type 1 pili, respectively. The value for type 1 pili is in good agreement with those found by others, 26 kT (17 kT with an attempt rate of 106) by Miller et al. (11) and 29 kT reported by Forero et al. (12).
of 23 kT for P and 27 kT for type 1 pili, respectively. The value for type 1 pili is in good agreement with those found by others, 26 kT (17 kT with an attempt rate of 106) by Miller et al. (11) and 29 kT reported by Forero et al. (12).
The higher transition barrier in combination with a shorter bond length in the energy landscape for type 1 pili in comparison to P pili has a large influence on the pilus' response to stress. Also, the form of the type 1 pili energy landscape is in agreement with a hypothesis that the shape of the energy landscape reflects the bond functioning, i.e., that a bond with a sharp potential can hold a high force for a short time whereas a bond with a soft potential can hold a small force for a long time. Therefore, the steeper and higher transition barrier implies that unfolding is more unlikely and that the rate of unfolding is slower at a particular force, i.e., that it requires a higher force to unfold the type 1 pili with the same speed as the P pili. Furthermore, the steeper potential can be seen as a consequence that the type 1 pili structure has evolved to support higher forces at shorter time events, originating from the irregular urine flow in the bladder and the urethra as compared to the constant urine flow in the upper urinary tracts. It is therefore possible that the much stiffer bond potential for type 1 pili is optimized for a fast shock damping effect.
Moreover, a higher transition barrier implies that the bond opening/closing rate in region II under balanced conditions, 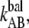 is lower for type 1 pili. We assessed the rate to 1.2 Hz, whereas Forero et al. assessed it to 2.2 Hz using AFM in a force feedback mode (12). Both these values are much lower than the rate balance of P pili (120 Hz), which is in line with the fact that P pili reaches its stationary force balance much faster than type 1 pili; see Fig. 4. The good agreement between the values obtained for P pili from the relaxation fit, and the previously assessed thermal bond opening rate and bond opening length through DFS, shows that the model correctly describes the unfolding of the quaternary structure and that it is justified to use Eq. 7 as a model of force relaxation.
is lower for type 1 pili. We assessed the rate to 1.2 Hz, whereas Forero et al. assessed it to 2.2 Hz using AFM in a force feedback mode (12). Both these values are much lower than the rate balance of P pili (120 Hz), which is in line with the fact that P pili reaches its stationary force balance much faster than type 1 pili; see Fig. 4. The good agreement between the values obtained for P pili from the relaxation fit, and the previously assessed thermal bond opening rate and bond opening length through DFS, shows that the model correctly describes the unfolding of the quaternary structure and that it is justified to use Eq. 7 as a model of force relaxation.
Measurements at stationary elongation showed that the steady-state unfolding force of P and type 1 pili are comparable, 28 ± 2 pN and 30 ± 2 pN, respectively. That implies that the ratio of the bond opening energy and bond opening length, 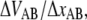 are similar for the two structures. A direct comparison of unfolding forces requires that both measurements are performed at equilibrium speed or at stationary conditions (below the corner velocity
are similar for the two structures. A direct comparison of unfolding forces requires that both measurements are performed at equilibrium speed or at stationary conditions (below the corner velocity  which is 400 nm/s for P pili and 6 nm/s for type 1 pili). This implies that our value for the unfolding force of the type 1 pilus cannot directly be compared to the unfolding force of 60 pN reported by Miller et al. (11) since their assessment was done at an elongation speed of 1–3 μm/s. However, according to our model parameters and Eq. 5, a measurement at an elongation speed of 1 μm/s should result in a force of 65 pN, which is in line with their data.
which is 400 nm/s for P pili and 6 nm/s for type 1 pili). This implies that our value for the unfolding force of the type 1 pilus cannot directly be compared to the unfolding force of 60 pN reported by Miller et al. (11) since their assessment was done at an elongation speed of 1–3 μm/s. However, according to our model parameters and Eq. 5, a measurement at an elongation speed of 1 μm/s should result in a force of 65 pN, which is in line with their data.
The energy difference 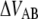 of P and type 1 pili is 24 kT and 37 kT, respectively, i.e., the energy level of the unfolded state is higher than the transition barrier,
of P and type 1 pili is 24 kT and 37 kT, respectively, i.e., the energy level of the unfolded state is higher than the transition barrier, 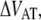 wherefore neither type 1 pili nor P pili possesses a bound unfolded state. Therefore, whenever a bond is open it will close with the attempt rate, i.e., none of the structures will be found in an unfolded state unless an external force is applied. Consequently, images of unfolded pili shown in the literature are most likely a result of the treatment during sample preparation before imaging.
wherefore neither type 1 pili nor P pili possesses a bound unfolded state. Therefore, whenever a bond is open it will close with the attempt rate, i.e., none of the structures will be found in an unfolded state unless an external force is applied. Consequently, images of unfolded pili shown in the literature are most likely a result of the treatment during sample preparation before imaging.
Small force fluctuations revealed by optical tweezers
Optical tweezers have soft spring constants that provide a better force resolution than the stiffer cantilever used in AFM systems. Therefore, small force variations, <10 pN, that are hidden in the noise of the AFM data are revealed by optical tweezers. The last part of the force-versus-elongation response measured with optical tweezers, clearly shows the linearized phase transition as a soft wave-like force-versus-elongation region with an inclining plateau at ∼65 pN, i.e., at the same level as for P pili. This part is not visible in the response data collected in AFM measurements due to their higher loading rates (11,12). Moreover, region III involves random transitions of all bonds, which requires elongation speeds that are ∼1000 times higher to enter the dynamic region (7). Such elongation speeds are, however, not achievable with our instrumental setup due to technical limitations (7). The two force traces shown in Fig. 3, taken at 0.1 and 0.5 μm/s, respectively, illustrate this dynamic phenomenon. It shows the dynamic effect at region II where the unfolding speed affects the unfolding force, whereas the unfolding of region III is independent of the elongation speed. The similar response of region III for both studied types of pili is what one would expect since the sequence of PapA in P pili and FimA in type 1 pili are very similar and that both types of subunits are connected via a donor strand complementation (19,20).
The fact that region III does not show any dynamic effect at moderate elongation speeds implies that whenever the unfolding force of region II reaches the level of transition of region III, i.e., ∼65 pN, units will immediately jump from state A to state C. This implies that, if the bond length 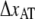 is to be assessed, the elongation speed has to be low enough to prevent direct transitions. To measure the bond length of type 1 pili without this effect, the elongation speed has to be <1 μm/s. The low useable elongation speed interval 0.05–1 μm/s results in large inaccuracies in DFS assessment of
is to be assessed, the elongation speed has to be low enough to prevent direct transitions. To measure the bond length of type 1 pili without this effect, the elongation speed has to be <1 μm/s. The low useable elongation speed interval 0.05–1 μm/s results in large inaccuracies in DFS assessment of 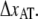 Our assessment of
Our assessment of 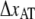 using relaxation measurements from ∼50 pN down to the steady-state force is therefore believed to give a more accurate value of the bond length. The larger speed interval of P pili, 0.05–100 μm/s, however, makes DFS appropriate (7).
using relaxation measurements from ∼50 pN down to the steady-state force is therefore believed to give a more accurate value of the bond length. The larger speed interval of P pili, 0.05–100 μm/s, however, makes DFS appropriate (7).
The presence of the refolding dip in the force curves, ∼15 pN, at the transition from region III to II in all measurements on both P and type 1 pili, is a clear indication that the refolding process requires the formation of a nucleation kernel that can only be formed at lower force levels, i.e., the pilus must have a large amount of slack before the formation of the first layer-to-layer bond can take place. In our P pili measurements similar dips were sometimes found in the middle of the refolding sequences and the number increased with refolding speed, which could be a consequence of misfoldings. The number of misfoldings is typically 1–3 per refolding sequence, i.e., 1 out of ∼700 subunits misfold. Misfoldings are not repeated in consecutive measurements on a single pilus, which indicates that misfoldings are not caused by a fatigue of the structure but rather a sporadic blockage of layer-to-layer bonds (21).
These misfoldings are, however, seldom found in refolding sequences of type 1 pili. A hypothetical explanation could be that its quaternary structure is mediated by more than one binding site whereas that of the P pili is mediated by a single site, i.e., if one bond/site is blocked the folding would be interrupted in P pili and would require a reformation of a nucleation kernel. Type 1 pili, on the other hand, would only misfold if all sites are blocked at the same time, which presumably is less likely. Small spikes, where the force goes down and up (<5 pN) are, however, frequently seen and this is interpreted as an indication of blockage of one of the sites, a blockage that does not necessarily require reformation of the nucleation kernel.
Another indication of multiple or complex binding sites in the type 1 pilus layer-to-layer bond is that the refolding force occasionally changed ∼5 pN with a distinct step response, i.e., type 1 pili have the ability to refold its quaternary structure at two different force levels, ∼30 and ∼25 pN. This behavior is believed to reflect the possibility of reassembling the structure in two different ways, one where all interactions are aligned and another where the units do not go back to the original orientation. Such a force change was almost always permanent and prolonged until the whole pili structure was refolded, which is a clear indication of an alternative configuration and that the position of each subunit is set by its neighbor (Fig. 6). This alternative configuration was never observed in the case of P pili, which retract with a constant force during the complete refolding of the quaternary structure except for some short misfoldings that do not contribute to any changes in their mechanical properties over time (13).
The ability to study the unfolding-refolding mechanism of pili structures in real time allows further dissection of pilus biogenesis (21). Our detailed assessment of the biomechanical properties of the pili structures and its significance in the context of specific adhesion and its catch-bond effect (22–24) elucidate the importance of the biomechanical function of the rod on the efficiency of the bacteria to withstand host defense mechanism. The flexibility of the pilus has not only evolved for shock absorption but presumably it has coevolved with the adhesin function to optimize its bond lifetime in its particular host environment (12). This gives a clear indication that the flexibility of the pilus is of much greater importance to the bacteria's ability to infect than earlier has been recognized and also thereby suggests a novel candidate target for the development of new antiinfectious agents.
Acknowledgments
The authors thank Prof. Ove Axner for valuable discussions and Monica Persson for assistance with the preparations of bacteria.
This work was made within the Umeå Center for Microbial Research (UCMR) and was supported by grants from the Swedish Research Council. We acknowledge economical support for the construction of a force-measuring optical tweezers system from the Kempe foundation and from Magnus Bergvall's foundation.
Editor: Marileen Dogterom.
References
- 1.Sauer, F. G., M. A. Mulvey, J. D. Schilling, J. J. Martinez, and S. J. Hultgren. 2000. Bacterial pili: molecular mechanisms of pathogenesis. Curr. Opin. Microbiol. 3:65–72. [DOI] [PubMed] [Google Scholar]
- 2.Anderson, G. G., J. J. Palermo, J. D. Schilling, R. Roth, J. Heuser, and S. J. Hultgren. 2003. Intracellular bacterial biofilm-like pods in urinary tract infections. Science. 301:105–107. [DOI] [PubMed] [Google Scholar]
- 3.Ruiz, J., K. Simon, J. P. Horcajada, M. Velasco, M. Barranco, G. Roig, A. Moreno-Martinez, J. A. Martinez, T. J. de Anta, J. Mensa, and J. Vila. 2002. Differences in virulence factors among clinical isolates of Escherichia coli causing cystitis and pyelonephritis in women and prostatitis in men. J. Clin. Microbiol. 40:4445–4449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bullitt, E., and L. Makowski. 1995. Structural polymorphism of bacterial adhesion pili. Nature. 373:164–167. [DOI] [PubMed] [Google Scholar]
- 5.Hahn, E., P. Wild, U. Hermanns, P. Sebbel, R. Glockshuber, M. Haner, N. Taschner, P. Burkhard, U. Aebi, and S. A. Muller. 2002. Exploring the 3D molecular architecture of Escherichia coli type 1 pili. J. Mol. Biol. 323:845–857. [DOI] [PubMed] [Google Scholar]
- 6.Jacobdubuisson, F., J. Heuser, K. Dodson, S. Normark, and S. Hultgren. 1993. Initiation of assembly and association of the structural elements of a bacterial pilus depend on two specialized tip proteins. EMBO J. 12:837–847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Andersson, M., E. Fällman, B. E. Uhlin, and O. Axner. 2006. Dynamic force spectroscopy of the unfolding of P pili. Biophys. J. 91:2717–2725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Andersson, M., E. Fällman, B. E. Uhlin, and O. Axner. 2006. A sticky chain model of the elongation of Escherichia coli P pili under strain. Biophys. J. 90:1521–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fällman, E., S. Schedin, J. Jass, B. E. Uhlin, and O. Axner. 2005. The unfolding of the P pili quaternary structure by stretching is reversible, not plastic. EMBO Rep. 6:52–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jass, J., S. Schedin, E. Fällman, J. Ohlsson, U. Nilsson, B. E. Uhlin, and O. Axner. 2004. Physical properties of Escherichia coli P pili measured by optical tweezers. Biophys. J. 87:4271–4283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Miller, E., T. I. Garcia, S. Hultgren, and A. Oberhauser. 2006. The mechanical properties of E. coli type 1 pili measured by atomic force microscopy techniques. Biophys. J. 91:3848–3856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Forero, M., O. Yakovenko, E. V. Sokurenko, W. E. Thomas, and V. Vogel. 2006. Uncoiling mechanics of Escherichia coli type I fimbriae are optimized for catch bonds. PLoS Biol. 4:1509–1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Andersson, M., E. Fällman, B. E. Uhlin, and O. Axner. 2006. Force measuring optical tweezers system for long time measurements of pili stability. SPIE. 6088:286–295. [Google Scholar]
- 14.Lindberg, F. P., B. Lund, and S. Normark. 1984. Genes of pyelonephritogenic E. coli required for digalactosidase-specific agglutination of human cells. EMBO J. 3:1167–1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sokurenko, E. V., H. S. Courtney, S. N. Abraham, P. Klemm, and D. L. Hasty. 1992. Functional-heterogeneity of type-1 fimbriae of Escherichia coli. Infect. Immun. 60:4709–4719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bell, M. G. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 17.Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- 18.Strunz, T., K. Oroszlan, I. Schumakovitch, H. J. Guntherodt, and M. Hegner. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bullitt, E., and L. Makowski. 1998. Bacterial adhesion pili are heterologous assemblies of similar subunits. Biophys. J. 74:623–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Choudhury, D., A. Thompson, V. Stojanoff, S. Langermann, J. Pinkner, S. J. Hultgren, and S. D. Knight. 1999. X-ray structure of the FimC-FimH chaperone-adhesin complex from uropathogenic Escherichia coli. Science. 285:1061–1066. [DOI] [PubMed] [Google Scholar]
- 21.Åberg, V., E. Fällman, O. Axner, B. E. Uhlin, S. J. Hultgren, and F. Almqvist. 2007. Pilicides block pilus formation without affecting their structure or dynamics. Mol. Biosyst. 3:214–218. [DOI] [PubMed] [Google Scholar]
- 22.Duncan, M. J., E. L. Mann, M. S. Cohen, I. Ofek, N. Sharon, and S. N. Abraham. 2005. The distinct binding specificities exhibited by enterobacterial type 1 fimbriae are determined by their fimbrial shafts. J. Biol. Chem. 280:37707–37716. [DOI] [PubMed] [Google Scholar]
- 23.Nilsson, L. M., W. E. Thornas, E. V. Sokurenko, and V. Vogel. 2006. Elevated shear stress protects Escherichia coli cells adhering to surfaces via catch bonds from detachment by soluble inhibitors. Appl. Environ. Microbiol. 72:3005–3010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thomas, W. E., E. Trintchina, M. Forero, V. Vogel, and E. V. Sokurenko. 2002. Bacterial adhesion to target cells enhanced by shear force. Cell. 109:913–923. [DOI] [PubMed] [Google Scholar]