Abstract
α-Helical secondary structure occurs widely in globular proteins and its formation is a key step in their folding. As a consequence, understanding the energetics of helix formation is crucial to understanding protein folding and stability. We have measured the helix propensities of the nonpolar amino acids for an α-helix in an intact protein, ribonuclease T1, and for a 17-residue peptide with a sequence identical to that of the α-helix in the protein. The helix propensities are in excellent agreement. This shows that when compared in the same sequence context, the helix propensities of the nonpolar amino acids are identical in helical peptides and intact proteins, and that conclusions based on studies of the helix-to-coil transitions of peptides may, in favorable cases, be directly applicable to proteins. Our helix propensities based on ribonuclease T1 are in good agreement with those from similar studies of barnase and T4 lysozyme. In contrast, our helix propensities differ substantially from those derived from studies of alanine-stabilized or salt bridge-stabilized model α-helical peptides.
Predicting the three-dimensional structure of a protein from its amino acid sequence and gaining a detailed understanding of the mechanism of protein folding remain two of the most difficult, unsolved problems in biochemistry. In both cases, understanding the many forces that contribute to the conformational stability of a protein and their interplay is a major difficulty. One approach to this problem is to uncouple the formation of secondary structure from overall protein folding by studying the factors that influence secondary structure formation in model peptides. α-Helices are of primary interest because they occur widely in proteins and the isolated peptides often form helical structures in solution so that they can be used as convenient models for protein folding and stability (1–5). Although model α-helical peptides have been studied in detail, the relevance of these models to the folding of intact proteins has not been carefully explored. Here we present a direct comparison of the helix propensity of the nonpolar amino acids measured in an α-helix in an intact protein, and in an α-helical peptide with the identical sequence.
Ribonuclease T1 (RNase T1) is a small (104 residue), monomeric protein, which has proven to be a useful model for the study of protein folding and stability (6). RNase T1 is an α+β class protein with several strands of β-sheet packed against a relatively long (17 residues and 4.5 turns) α-helix, forming a hydrophobic core (7). The sequence of the single α-helix in wild-type RNase T1 is: SSDVSTAQAAGYKLHED, which corresponds to Ser-13 through Asp-29 in the intact protein (Fig. 1). The helical portion of the RNase T1 protein has a near ideal site at which to measure helix propensities: alanine 21 is in the exact center of the helix, on the solvent exposed face, and the side chains of residues (i, i+3) and (i, i+4), which could interact with residues at position 21 are all involved in other interactions. No residues outside of the helical region of the protein appear to be close enough to interact with side chains at position 21. Here we compare the differences in helix propensity for the nonpolar amino acids in the context of the intact RNase T1 protein and in a helical peptide derived from RNase T1.
Figure 1.
A ribbon drawing of RNase T1 generated from the crystal structure (Protein Data Base entry 9RNT) determined by Martinez-Oyanedel et al. (7). The ribbon drawing was made with molscript (8). The single α-helix in RNase T1 spans residues 13–29. The site of substitution, Ala-21, is shown.
MATERIALS AND METHODS
Mutants were constructed by the polymerase chain reaction single-mutagenic primer technique (9) and the proteins were purified as described (10). Purity was confirmed by SDS/PAGE. The peptides were synthesized using an Applied Biosystems automated peptide synthesizer (model 431A) and standard fluorenylmethoxycarbonyl chemistry. The N and C termini of the peptides are blocked with acetyl and carboxamide, respectively. The peptides were purified using reversed-phase liquid chromatography and the identity was confirmed using matrix-assisted laser desorption spectroscopy–time-of-flight mass spectrometry.
The stability of the mutant proteins was determined using urea denaturation. Usually, 22 tubes were prepared for each denaturation curve; each sample tube contained 0.01 mg/ml−1 protein in 30 mM glycine (pH 2.5), along with various concentrations of urea (Sigma ultrapure). A urea stock solution was prepared fresh for each curve; the urea concentration was measured by refractive index using a relation given previously (11). These tubes were incubated at 25.0°C for at least 16 hr before measurements were taken to ensure that the tubes had come to equilibrium. The intrinsic fluorescence of each sample (kept at 25.0 ± 0.1°C by a circulating water bath and stirred using a magnetic stirring apparatus) was measured by exciting at 278 nm and monitoring emission at 320 nm in a SLM AB2 fluorescence spectrometer (Aminco). Analysis of the denaturation curves was performed using the two-state unfolding model and the linear extrapolation method (11). These two methods were combined into a single equation to describe the shape of the denaturation curve (12, 13):
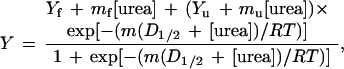 |
where Y is the observed fluorescence (after subtracting out the intrinsic fluorescence of buffer and urea), mf and Yf are the slope and intercept, respectively, of the pretransition baseline, mu and Yu are the slope and intercept, respectively, of the posttransition baseline, m is the dependence of free energy of unfolding on urea concentration, and D1/2 is the midpoint of the denaturation curve. The experimental curves were fit by the above equation using standard data analysis software. The free energy of unfolding in the absence of denaturant (defined as the conformational stability of the protein) is the product of m and D1/2. By calculating ΔΔG from the difference in midpoints times an average m value, a long extrapolation back to 0 M urea is avoided. Denaturation curves were performed at least twice for each mutant, and two mutants were measured four times. The standard deviations in these sets of four give an estimated error in D1/2 of 0.04 M and an error in m of 50 kcal mol−1 M−1. This gives a maximum error in ΔΔG of 0.07 kcal mol−1.
Helicity of the peptides was measured using circular dichroism (CD) on an Aviv model 62DS CD spectropolarimeter. Samples contained 30 μM peptide in CD buffer (1 mM each potassium phosphate, borate, and citrate) (pH 2.5) in a 0.5-cm pathlength cuvette, maintained at 0°C by a built-in temperature controlling unit. Peptide stock solutions were made in water and the peptide concentration was determined by the absorbance of the single tyrosine residue at 276 nm using an extinction coefficient of 1390 M−1 cm−1 (14). To convert the measured CD signal at 222 nm of the peptides into a free energy scale it is necessary to use Lifson–Roig helix–coil theory (15). Raw CD signal (in millidegrees) was converted to mean residue ellipticity ([θ]obs) and then to fraction helix using
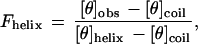 |
where [θ]helix and [θ]coil represent the mean residue ellipticity of a complete helix (−42,500·(1 − (3/n)), where n is the number of residues in the peptide and complete random coil (+640), respectively (16). The units of mean residue ellipticity are deg/cm2 dmol−1.
For analysis of the peptide data we define the wt* peptide (see below) as the “host” peptide and all the other peptides contained guest residues at position 21. The helix propensities of the host and guest residues were calculated using a version of the Lifson–Roig model for the helix–coil transition described previously (17). The model employs the single-sequence approximation, meaning that only one stretch of helical residues was allowed to exist in any one peptide molecule in the partition function (one nucleation site per molecule). For peptides of this length, this model is equivalent to the full treatment of Lifson–Roig theory (17). The nucleation constant, v2, was taken to be 0.0023 (16). The model treats the host peptide as a homopolymer, assigning only one propagation parameter (whost) to the whole peptide based on the measured helicity. The helix propagation parameters for the guest residues (wguest) are determined from the changes in measured helicity. Relative free energy changes were calculated using ΔG = −RT ln (w/(1 + v)). We define ΔΔG = ΔGmut − ΔGwt*, such that a positive ΔΔG indicates destabilization of the helix.
RESULTS AND DISCUSSION
The sequence of the single α-helix in wild-type RNase T1 is: SSDVSTAQAAGYKLHED (Ser-13 through Asp-29). A peptide of this sequence shows a CD spectrum characteristic of a random coil conformation, with at most only a few percent helix. The G23A mutation (Gly-23 underlined in the sequence above) increases the helicity of the peptide to 30% so that it becomes a useful model. This variant, denoted wt*, serves as the host for our helix propensity studies. The nonpolar amino acids are substituted at position 21 (double underlined alanine above) in the wt* peptide and wt* protein (also containing the G23A mutation). We have substituted six nonpolar amino acids at position 21 in the wt* RNase T1 protein and measured the resulting changes in conformational stability using urea denaturation. The data and analysis are presented in Table 1. All mutations resulted in stable, active ribonucleases. These types of surface substitutions are not expected to cause large changes in the structure of the protein (18, 19). The RNase T1 with alanine at position 21 is the most stable and that with glycine is the least stable. Alanine is typically found to be the best helix former and glycine the worst (excluding proline) in studies of other peptides and proteins.
Table 1.
Protein urea denaturation and peptide helicity data
| Residue 21 | D1/2, M | m, kcal mol−1 M−1 | Δ(ΔG)† kcal mol−1 | −[Θ]222, deg cm2 dmol−1 | Fhelix | Δ(ΔG)‡ kcal mol−1 |
|---|---|---|---|---|---|---|
| Ala | 2.78 | 1.58 | 0 | 9,900 | 0.30 | 0 |
| Leu | 2.70 | 1.64 | 0.13 | 7,800 | 0.24 | 0.25 |
| Met | 2.69 | 1.60 | 0.14 | 8,300 | 0.25 | 0.18 |
| Ile | 2.51 | 1.57 | 0.44 | 6,600 | 0.20 | 0.38 |
| Phe | 2.43 | 1.69 | 0.56 | 5,100 | 0.16 | 0.61 |
| Val | 2.38 | 1.77 | 0.65 | 4,800 | 0.15 | 0.66 |
| Gly | 2.23 | 1.71 | 0.90 | 3,200 | 0.11 | 0.98 |
Change in conformational stability of the protein relative to wt* with alanine at position 21. Calculated using Δ(ΔG) = mavg·(D1/2[wt*] − D1/2[mutant]), where mavg is the average m value for the seven proteins (1.65 kcal mol−1 M−1). Positive values of Δ(ΔG) indicate that the mutation is destabilizing. Errors in D1/2 and m are approximately 0.04 M and 0.05 kcal mol−1 M−1, respectively.
Change in free energy for helix formation of the peptides calculated from Lifson–Roig helix–coil theory (see Materials and Methods).
We synthesized seven 17-residue peptides with sequences identical to the α-helix in wt* RNase T1 and the six nonpolar mutants. Our peptide model, wt*, shows a CD spectrum characteristic of an α-helix, with minima at 222 nm and 208 nm, and a maximum around 190 nm (data not shown). This helical structure shows no dependence on peptide concentration, suggesting that the peptide exists as a monomer. The helical contents of the seven peptides, as measured by CD at 222 nm, are given in Table 1. The fractional helix contents ranged from 11 to 30%. We used Lifson–Roig helix–coil theory to translate these fractional helicities into a relative scale of free energies as described above. The range of free energies is about 1 kcal mol−1, just as in the mutant proteins.
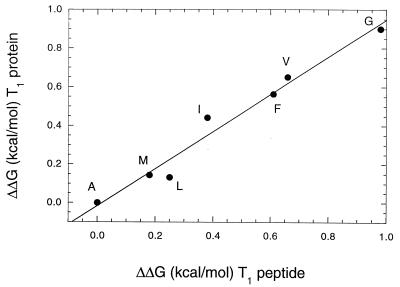
Fig. 2 compares helix propensities measured in intact RNase T1 with those measured in peptides with sequences identical to those of the α-helices of RNase T1. There is excellent agreement between the two systems, with a slope of unity, a y-intercept near zero, and a correlation coefficient of 0.98. This is an important result. It shows that results from studies of the helix-to-coil transition of a peptide may, in favorable cases, be directly applicable to proteins. In earlier work, we also found excellent agreement between studies of interactions at the carboxyl terminus of the wt* peptide and similar studies of intact RNase T1 (20, 21).
Figure 2.
Comparison of measured helix propensity in the RNase T1 peptide and protein systems. The differences in ΔG are expressed relative to alanine for the other nonpolar amino acids. Data are from Table 1.
Helix propensities were measured earlier in two other proteins, barnase (22) and T4 lysozyme (18, 19). These results are compared with our RNase T1 results in Table 2 and Fig. 3A. The agreement between results from three proteins and the RNase T1 peptide suggests that the helix propensities given in Table 1 provide a good measure of helix propensity at an exposed site near the center of an α-helix in a protein.
Table 2.
Helix propensity measured in various systems
| Model system† (sequence) | ΔG(Gly) − ΔG(Ala), kcal mol−1 | Intercept | Slope | Correlation coefficient |
|---|---|---|---|---|
| Peptides | ||||
| RNase T1 peptide | 0.98 | (0.00)‡ | (1.00)‡ | (1.00)‡ |
| (-STAQXAAYK-) | ||||
| AK | 1.97 | 0.00 | 1.84 | 0.97 |
| (-AAKAXAAKA-) | ||||
| E4K4 | 0.74 | 0.06 | 0.70 | 0.97 |
| (-KKKXXXEEE-) | ||||
| EAK | 1.95 | −0.04 | 1.79 | 0.90 |
| (-AKEAXAKEA-) | ||||
| Host–guest | 0.35 | −0.11 | 0.35 | 0.80 |
| (HBLP or HPLG) | ||||
| AGADIR | 1.10 | −0.04 | 1.02 | 0.96 |
| (various) | ||||
| Proteins | ||||
| RNase T1 protein-21 | 0.90 | −0.02 | 0.96 | 0.98 |
| (-STAQXAAYK-) | ||||
| Barnase-32 | 0.91 | 0.19 | 0.88 | 0.88 |
| (-KSAQXLG-) | ||||
| T4 lysozyme-44 | 0.96 | −0.13 | 0.92 | 0.93 |
| (-QAAKXELDK-) | ||||
| Coiled–coil | 0.77 | 0.07 | 0.74 | 0.90 |
| (-AALEXKLQA-) |
The peptide or protein systems being compared to the RNase T1 peptide are shown along with the sequence near the substitution site (X), given as one-letter amino acid codes. For the peptide model systems, the AK data are from Baldwin’s group (16), the E4K4 data are from Kallenbach’s group (5), the EAK data are from Stellwagen’s group (23) as analyzed by Chakrabartty and Baldwin (3), the host–guest studies of Scheraga (24) and the algorithm AGADIR is from Muñoz and Serrano (25). HPLG and HBLG refer to the host, hydroxypropyl- or hydroxybutyl-l-glutamine, respectively (24). The protein models are from site 32 in barnase (22), site 44 in T4 lysozyme (18, 19) and a solvent-exposed site in a model coiled–coil peptide (26).
The intercept, slope, and correlation coefficient are derived by plotting the data from the indicated model system against the results for the RNase T1 peptide.
Figure 3.
(A) Comparison of measured helix propensity in the wt* peptide and T4 lysozyme (18, 19) (•) and barnase (22) (□).Values given are the change in ΔG of folding relative to alanine. (B) Comparison of measured helix propensity values for the nonpolar amino acids in the RNase T1 wt* peptide and alanine-based peptides (16) (•) and salt bridge-stabilized peptides (5) (□). Values are the change in ΔG of helix formation relative to alanine. Slopes, intercepts, and correlation coefficients for best-fit linear regressions of the data in A and B are given in Table 2.
Intrinsic helical propensities of the amino acids were first measured systematically by Scheraga and coworkers using a host–guest random polymer system (24). These studies suggested that the helical propensities of the amino acids, with the exception of proline, did not vary greatly, and that short peptides (<20 residues) would not exhibit significant helix formation in aqueous solution. However, in 1968, Klee showed that the S-peptide of ribonuclease A does form significant amounts of α-helix in aqueous solution (27, 28). This triggered studies, first by the Baldwin laboratory and then by several other laboratories, to find simpler model α-helices that could be used to probe the determinants of α-helix stability. It was found that short, monomeric helices composed mostly of alanine exhibit significant helix formation in water (29, 30). This helix formation occurred even without favorable side-chain interactions, showing that the helical propensity of alanine is higher than indicated by host–guest studies. These alanine-stabilized peptides have been widely used to model protein folding (1–5, 16). An important question is whether these and other model α-helices give results directly applicable to the α-helices found in proteins. With regard to the helix propensities of nonpolar amino acids, our results suggest that in some cases they do not.
A comparison of our peptide results with those from the alanine-stabilized peptides studied by Baldwin and coworkers (16) and with the salt bridge-stabilized peptides studied by Kallenbach and coworkers (5) is shown in Fig. 3B. In both cases, the correlation is excellent (Table 2), but there is a sizable discrepancy in the range of propensities. The propensities measured in alanine-stabilized helices are almost twice those found with the ribonuclease T1 helices, whereas those for the salt bridge-stabilized helices are about 30% less (Table 2). The propensities measured by Stellwagen’s group (23) (see also ref. 3) with peptides stabilized by both alanine residues and salt bridges are very similar to those measured in the alanine-stabilized peptides (Table 2). In contrast, our peptide data are in excellent agreement with results from the program AGADIR developed by Muñoz and Serrano (23) (Table 2). The parameters used in AGADIR were obtained from an analysis of the measured fractional helicities of over 400 peptides. It is also obvious from Table 2 that propensities from host–guest studies are not applicable to either proteins or other peptides.
The major discrepancy is that the Δ(ΔG) values from the alanine-stabilized peptides are twice as large as the those measured in RNase T1 and in other proteins. When the amino acid sequences of the various systems are compared, important differences are found (Table 2). In the alanine-stabilized peptides, the variable residue has adjacent alanines and has alanines at three of the four (i, i+3) and (i, i+4) positions. The RNase T1 helix has bulkier residues at some of these positions, as do the T4 lysozyme and barnase helices. The residues in the salt bridge-stabilized peptides of Kallenbach are even bulkier, with glutamic acid or lysine present at most positions. The host–guest polymers consist mainly of very large host residues (hydroxypropyl- or hydroxybutyl-l-glutamine). It appears that the range of propensities scales with the size of the residues surrounding the variable position. This suggests that the hydration of backbone amides and carbonyls might be an important factor (for an example, see ref. 31). The local sequence might also change the flexibility of the backbone or side chain and thereby influence conformational entropy. It is surprising that these differences in sequence exert such a large effect on the measured helix propensities. It will be interesting to see if the theoreticians who study the helix-to-coil transition can explain this difference in behavior.
It has been suggested that the disagreement between alanine-based peptides and other systems is due to oversimplification in applying complex helix–coil theories (32). Our peptide results confirm that the problem does not lie in helix–coil theory. One recent attempt to explain the discrepancy between propensities measured in peptides and proteins was made by Qian and Chan (33). In their model, protein-based systems and isolated peptides should only give identical measures of helix propensity when helix formation and global protein folding are tightly coupled. The excellent agreement between our peptide and protein data suggests that secondary and tertiary structure formation are indeed tightly coupled in RNase T1.
Several explanations for the different propensities exhibited by the amino acids with nonpolar side chains have been proposed. These include differences in conformational entropy (34), in the hydrophobic effect (19), and in hydration of the backbone (35). The helix propensities calculated by Hermans et al. (32) using molecular dynamics simulations are in remarkably good agreement with the results in Table 1. They predict a Δ(ΔG) of ≈0.2 kcal mol−1 for leucine and methionine (based on their calculations with α-amino-n-butyric acid), of ≈0.7 kcal mol−1 for valine, and ≈1.2 kcal mol−1 for glycine. They attribute the difference between alanine and glycine entirely to differences in backbone conformational entropy, and those between alanine and the other side chains mainly to differences in side-chain conformational entropy. These and other calculations (19, 34, 36, 37) suggest that the differences in helix propensity for the nonpolar amino acids are due mainly to differences in conformational entropy.
Recently, a structure-based thermodynamic scale for α-helix propensity has been developed (38). In this approach, the differences in helical propensity between the amino acids cannot solely be explained by differences in side-chain conformational entropy, but can be faithfully calculated when backbone conformational entropy, solvation entropy, and enthalpic contributions are included. Using this approach, good agreement is found between predicted and observed helix propensities in T4 lysozyme, barnase, and coiled-coils (see Table 2).
The conformational stability of proteins is remarkably low, only 5–10 kcal mol−1. The large conformational entropy [≈1.7 kcal mol−1 per residue at 300 K (36, 37, 39)] that favors the unfolded state is barely surmounted by a large number of weak, stabilizing interactions: ≈1 kcal mol−1 per -CH2-group buried (40) and ≈1 kcal mol−1 per intramolecular hydrogen bond formed (41). Even though the helix propensities discussed here are similarly weak, they are important because proteins typically contain 30% of their residues in α-helical conformations. Intrinsic propensities are also very important for determining the conformational preferences of peptides. However, the contributions from helix propensity are generally destabilizing. As pointed out (1–5, 34), only alanine residues contribute favorably to the stability of α-helices, all other amino acids are either neutral or destabilizing and make their contributions mainly through unfavorable conformational entropy.
In summary, one important unresolved question has been (1–5): Do helix propensities make an equivalent energetic contribution in peptides and proteins? Our results suggest that the answer is YES.
Acknowledgments
We thank R. L. Baldwin and the Pace and Scholtz lab groups for helpful discussion, Geoff Horn for DNA sequencing, and Kevin Shaw for generating Fig. 1. We acknowledge the National Institutes of Health for financial support (Grants GM52483 to J.M.S. and GM37039 to C.N.P. and Predoctoral Training Grant T32 GM08523 to J.K.M.) and the Robert A. Welch Foundation (Grants A-1281 to J.M.S. and A-1060 to C.N.P.). C.N.P. is also supported by the Tom and Jean McMullin Professorship and J.M.S. is an American Cancer Society Junior Faculty Research Awardee (Grant JFRA-577).
ABBREVIATIONS
- RNase T1
ribonuclease T1
- CD
circular dichroism
References
- 1.Scholtz J M, Baldwin R L. Annu Rev Biophys Biomol Struct. 1992;21:95–118. doi: 10.1146/annurev.bb.21.060192.000523. [DOI] [PubMed] [Google Scholar]
- 2.Scholtz J M, Baldwin R L. In: Peptides: Synthesis, Structures, and Applications. Gutte B, editor. San Diego: Academic; 1995. pp. 171–192. [Google Scholar]
- 3.Chakrabartty A, Baldwin R L. Adv Protein Chem. 1995;46:141–176. [PubMed] [Google Scholar]
- 4.Bryson J W, Betz S F, Lu H S, Suich D J, Zhou H X, O’Neil K T, DeGrado W F. Science. 1995;270:935–941. doi: 10.1126/science.270.5238.935. [DOI] [PubMed] [Google Scholar]
- 5.Kallenbach N R, Lyu P, Zhou H. In: Circular Dichroism and the Conformational Analysis of Biopolymers. Fasman G D, editor. New York: Plenum; 1996. pp. 201–259. [Google Scholar]
- 6.Pace C N, Heinemann U, Hahn U, Saenger W. Angew Chem Int Ed Engl. 1991;30:343–360. [Google Scholar]
- 7.Martinez-Oyanedel J, Choe H W, Heinemann U, Saenger W. J Mol Biol. 1991;222:335–352. doi: 10.1016/0022-2836(91)90215-r. [DOI] [PubMed] [Google Scholar]
- 8.Kraulis P J. J Appl Crystallogr. 1991;24:946–950. [Google Scholar]
- 9.Landt O, Grunert H P, Hahn U. Gene. 1990;96:125–128. doi: 10.1016/0378-1119(90)90351-q. [DOI] [PubMed] [Google Scholar]
- 10.Shirley B A, Laurents D V. J Biochem Biophys Methods. 1990;20:181–188. doi: 10.1016/0165-022x(90)90076-o. [DOI] [PubMed] [Google Scholar]
- 11.Pace C N. Methods Enzymol. 1986;131:266–280. doi: 10.1016/0076-6879(86)31045-0. [DOI] [PubMed] [Google Scholar]
- 12.Santoro M M, Bolen D W. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 13.Scholtz J M. Protein Sci. 1995;4:35–43. doi: 10.1002/pro.5560040106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pace C N, Vajdos F, Fee L, Grimsley G, Gray T. Protein Sci. 1995;4:2411–2423. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lifson S, Roig A. J Chem Phys. 1961;34:1963–1974. [Google Scholar]
- 16.Rohl C R, Chakrabartty A, Baldwin R L. Protein Sci. 1996;5:2623–2637. doi: 10.1002/pro.5560051225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qian H. Biopolymers. 1993;33:1605–1616. doi: 10.1002/bip.360331010. [DOI] [PubMed] [Google Scholar]
- 18.Blaber M, Zhang X-J, Matthews B W. Science. 1993;260:1637–1640. doi: 10.1126/science.8503008. [DOI] [PubMed] [Google Scholar]
- 19.Blaber M, Zhang X-J, Lindstrom J D, Peipot S D, Baase W A, Matthews B W. J Mol Biol. 1994;236:600–624. doi: 10.1006/jmbi.1994.1016. [DOI] [PubMed] [Google Scholar]
- 20.Myers J K, Smith J S, Pace C N, Scholtz J M. J Mol Biol. 1996;263:390–395. doi: 10.1006/jmbi.1996.0583. [DOI] [PubMed] [Google Scholar]
- 21.Walter S, Hubner B, Hahn U, Schmid F X. J Mol Biol. 1995;252:133–143. doi: 10.1006/jmbi.1995.0480. [DOI] [PubMed] [Google Scholar]
- 22.Horovitz A, Matthews J M, Fersht A R. J Mol Biol. 1992;227:560–568. doi: 10.1016/0022-2836(92)90907-2. [DOI] [PubMed] [Google Scholar]
- 23.Park S-H, Shalongo W, Stellwagen E. Biochemistry. 1993;32:7048–7053. doi: 10.1021/bi00078a033. [DOI] [PubMed] [Google Scholar]
- 24.Wójcik J, Altman K H, Scheraga H A. Biopolymers. 1990;30:121–134. doi: 10.1002/bip.360300112. [DOI] [PubMed] [Google Scholar]
- 25.Muñoz V, Serrano L. J Mol Biol. 1995;245:275–296. doi: 10.1006/jmbi.1994.0023. [DOI] [PubMed] [Google Scholar]
- 26.O’Neil K T, DeGrado W F. Science. 1990;250:646–651. doi: 10.1126/science.2237415. [DOI] [PubMed] [Google Scholar]
- 27.Klee W A. Biochemistry. 1968;7:2731–2736. doi: 10.1021/bi00848a006. [DOI] [PubMed] [Google Scholar]
- 28.Brown J E, Klee W A. Biochemistry. 1971;10:470–476. doi: 10.1021/bi00779a019. [DOI] [PubMed] [Google Scholar]
- 29.Marqusee S, Baldwin R L. Proc Natl Acad Sci USA. 1987;84:8898–8902. doi: 10.1073/pnas.84.24.8898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marqusee S, Robbins V H, Baldwin R L. Proc Natl Acad Sci USA. 1989;86:5286–5290. doi: 10.1073/pnas.86.14.5286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Blaber M, Baase W A, Gassner N, Matthews B W. J Mol Biol. 1995;246:317–330. doi: 10.1006/jmbi.1994.0087. [DOI] [PubMed] [Google Scholar]
- 32.Hermans J, Anderson A G, Yun R H. Biochemistry. 1992;31:5646–5653. doi: 10.1021/bi00139a031. [DOI] [PubMed] [Google Scholar]
- 33.Qian H, Chan S I. J Mol Biol. 1996;261:279–288. doi: 10.1006/jmbi.1996.0459. [DOI] [PubMed] [Google Scholar]
- 34.Creamer T P, Rose G D. Proc Natl Acad Sci USA. 1992;89:5937–5941. doi: 10.1073/pnas.89.13.5937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Avbelj F, Moult J. Biochemistry. 1995;34:755–764. doi: 10.1021/bi00003a008. [DOI] [PubMed] [Google Scholar]
- 36.D’Aquino J A, Gómez J, Hilser V J, Lee K H, Amzel L M, Freire E. Proteins Struct Funct Genet. 1996;25:143–156. doi: 10.1002/(SICI)1097-0134(199606)25:2<143::AID-PROT1>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 37.Lee K H, Xie D, Freire E, Amzel L M. Proteins. 1994;20:68–84. doi: 10.1002/prot.340200108. [DOI] [PubMed] [Google Scholar]
- 38.Luque I, Mayorga O L, Freire E. Biochemistry. 1996;35:13681–13688. doi: 10.1021/bi961319s. [DOI] [PubMed] [Google Scholar]
- 39.Spolar R S, Record M T., Jr Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 40.Pace C N. J Mol Biol. 1992;226:29–35. doi: 10.1016/0022-2836(92)90121-y. [DOI] [PubMed] [Google Scholar]
- 41.Myers J K, Pace C N. Biophys J. 1996;71:2033–2039. doi: 10.1016/S0006-3495(96)79401-8. [DOI] [PMC free article] [PubMed] [Google Scholar]