Three-dimensional Inhomogeneous Triphasic Finite Element Analysis of Physical Signals and Solute Transport in Human Intervertebral Disc under Axial Compression

Abstract

A 3D inhomogeneous finite element model for charged hydrated soft tissues containing charged/uncharged solutes was developed and applied to analyze the mechanical, chemical and electrical signals within the human intervertebral disc during an axial unconfined compression. The effects of tissue properties and boundary conditions on the physical signals and the transport of fluid and solute were investigated. The numerical simulation showed that, during disc compression, the fluid pressurization and the effective (von Misses) solid stress were more pronounced in the annulus fibrosus (AF) region near the interface between AF and nucleus pulposus (NP). In NP, the distributions of the fluid pressure, effective stress, and electrical potential were more uniform than those in AF. The electrical signals were very sensitive to fixed charge density. Changes in material properties of NP (water content, fixed charge density, and modulus) affected fluid pressure, electrical potential, effective stress, and solute transport in the disc. This study is important for understanding disc biomechanics, disc nutrition and disc mechanobiology.

INTRODUCTION

The intervertebral disc (IVD) is the largest cartilaginous structure in human body that contributes to flexibility and load support in the spine. To accomplish these functions, the disc has a unique architecture consisting of a centrally-located nucleus pulposus (NP) surrounded superiorly and inferiorly by cartilage endplates and peripherally by the annulus fibrosus (AF) (Lundon and Bolton, 2001). Because the disc is avascular and experiences mechanical loads, the cells in IVD tissues live in a complex physical environment. Many studies have shown that changes in nutrient levels and physical signals will affect the activity of disc cells (Horner and Urban, 2001; Urban, 2002). The cellular response, in turn, can alter matrix and thereby initiate structural remodeling. These processes are important for disc homeostasis, yet they can also lead to tissue disorganization and dysfunction (e.g., disc degeneration). During the past decade, increasing attention has been focused on the biological responses of IVD to mechanical forces and other physical stimuli to understand cellular mechanotransduction mechanisms. The identification of such mechanisms will give rise to tremendous potential for clarifying disease mechanisms, establishing prevention strategies, and defining regeneration techniques. However, the physical stimuli are very complex, comprised of mechano-electrochemical events within the extracellular matrix (ECM), such as stress, strain, ion concentrations, fluid pressure, electrical potential, transport of water, ions, and other solutes, etc. As a first step in understanding the relationships between physical stimuli and cell response, it is essential to quantify the physicochemical environment within the disc tissues with an appropriate theoretical model. To this end, many attempts have been done by different investigators using various computational models [see recent papers by (Soukane D.M. et al., 2005; Yao and Gu, 2006b) for summary].

From an engineering point of view, IVD is an inhomogeneous, anisotropic, charged, porous fibrous material. Due to its unique structure, it is a challenge to simulate its mechanical, chemical, and electrical signals as well as solute transport under different loading conditions. The objective of this study was to develop a three-dimensional (3D), inhomogeneous finite element model (FEM) for human IVD for analyzing the physical environment and solute transport within the tissue under different mechanical loading conditions. A case of IVD under axial compression was simulated and reported. Because of the complex nature of the problem, the analysis of this simple loading condition is useful for elucidating the effects of changes in material properties (due to degeneration or growth) on solute (nutrients or growth factors) transport in IVD. It could also serve as a baseline for comparison of different theoretical models as well as for experimentally extracting material properties that may be difficult to measure directly.

METHODS

In this study, the IVD is modeled as an inhomogeneous material with two distinguishing regions, i.e., NP and AF regions (Figure 1a). Responses of physical signals and solute transport in the human lumbar disc (Figure 1a) to unconfined compression (stress-relaxation test, Figure 1) were analyzed in this study. The size and geometry of a representative disc was shown in Figure 1a (Iatridis et al., 2003). The thickness of the disc was h =10mm. The disc sample was initially equilibrated with a bathing solution of 0.15M NaCl. An uncharged solute was introduced into the bathing solution at t=0, and the disc was subjected to a ramp compression (10% strain in 10,000s) between two endplates (Figure 1d). For the control case, two endplates were assumed to be perfectly permeable to water and solutes. The effect of endplate calcification on water and solute transport was investigated by assigning impermeable boundary condition to the portion of endplate adjacent to AF or to the portion adjacent to NP (Figure 1c). In this study, the human disc was modeled as an isotropic inhomogeneous mixture consisting of an intrinsically incompressible elastic solid (with fixed charge), water, ion (Na⁺ and Cl⁻) and uncharged solute (uncharged growth factor) phases.

Figure 1.

(a) Disc geometry, (b) mesh, (c) test configuration, and (d) testing protocol.

A theoretical model (Yao and Gu, 2006b), developed based on the works by (Lai et al., 1991) and (Gu et al., 1998), was used in this study. In the model, strain-dependent hydraulic permeability and strain-dependent diffusivity were considered (Table 1) using the constitutive relations for AF and gels (Gu et al., 2003; Gu and Yao, 2003; Gu et al., 2004). The FEM formulation (weak form) was based on the work by (Sun et al., 1999). The formulation of this 3D initial- and boundary- value problem was solved using FEMLAB software (FEMLAB3.1, COSMOL Inc., Burlington, MA).

Table 1.

Inhomogeneous material properties.

	Annulus fibrosus (AF)	Nucleus pulposus (NP)
Initial water content ${\phi }_0^w$	0.75	0.86 (0.82, low WC NP)
Initial fixed charge density $c_0^F$ (mEq/ml)	0.15	0.25 (0.15, low FCD NP)
Elastic constant λ (MPa)	0.2	0.02 (0.002, soft NP)
Elastic constant μ (MPa)	0.15	0.015 (0.0015, soft NP)
Darcy permeability (nm2) κ = a1 (φw/φs)b1	a1 =0.00044, b1=7.193	a1 =0.00339, b1=3.24
Relative diffusivity $\begin{array}{l}\frac{D^{\alpha }}{D_0^a}=exp\left[-a_2{\left(\frac{r_s^a}{\sqrt{\kappa }}\right)}^{b_2}\right]\\ \alpha =+,-,\text{o}\end{array}$	a2=1.29, b2=0.372	a2 =1.25, b2=0.681

The upper quadrant of the disc was modeled with a mesh of 4306 second-order, tetrahedral Lagrange elements (Figure 1b). The maximum time-step of 100s was used during the ramp phase, and variable maximum time-steps from 5s to 1000s were used during the relaxation phase. The convergence of the numerical model was examined by refining the mesh and tightening the tolerance. The accuracy of the numerical method was also checked with the results of a 3D homogeneous case published in the literature (Yao and Gu, 2006b).

The following baseline parameters were used in the simulation: temperature T = 298 K, bathing solution c* = 0.15M NaCl, neutral solute concentration (in bathing solution) c^o* = 4 10⁻⁵ mol/m³, and coupling coefficient B_w = 0. The Stokes radii of cation (Na⁺) r⁺_s = 0.197 nm, anion (Cl⁻) r⁻_s = 0.142nm, and uncharged solute radius r^o_s = 1.146 nm were calculated based on the corresponding diffusivity values in the aqueous solution at 25 °C using Stokes-Einstein equation. The diffusivity values in solution for cation, anion and neutral solute were 1.28×10⁻⁹m²/s, 1.77×10⁻⁹m²/s and 2.2×10⁻¹⁰m²/s, respectively. For uncharged solute, the diffusivity value was similar to that of IGF-1 and the partition coefficient was Φ= 0.1. For small ions, activity coefficient γ_±/γ_±* = 1 and osmotic coefficient φ=1 were used. The convection coefficients (hindrance factors) H^α (α =+,−,o ) have not been determined for IVD tissues. In this study, the values of these parameters were assumed to be unity. The inhomogeneous material properties for AF and NP were listed in Table 1(Iatridis et al., 1995; Iatridis et al., 1996; Iatridis et al., 1997b; Iatridis et al., 1997a; Iatridis et al., 1998; Iatridis et al., 2003; Urban and McMullin, 1988).

RESULTS

This inhomogeneous model predicted more uniform distributions of fixed charge density (Figure 2a), fluid pressure (Figure 2b), electrical potential (Figure 2c), and effective (Von Misses) stress (Figure 2d) in NP, compared to those calculated from the homogeneous model in the literature (Yao and Gu, 2006b).

Figure 2.

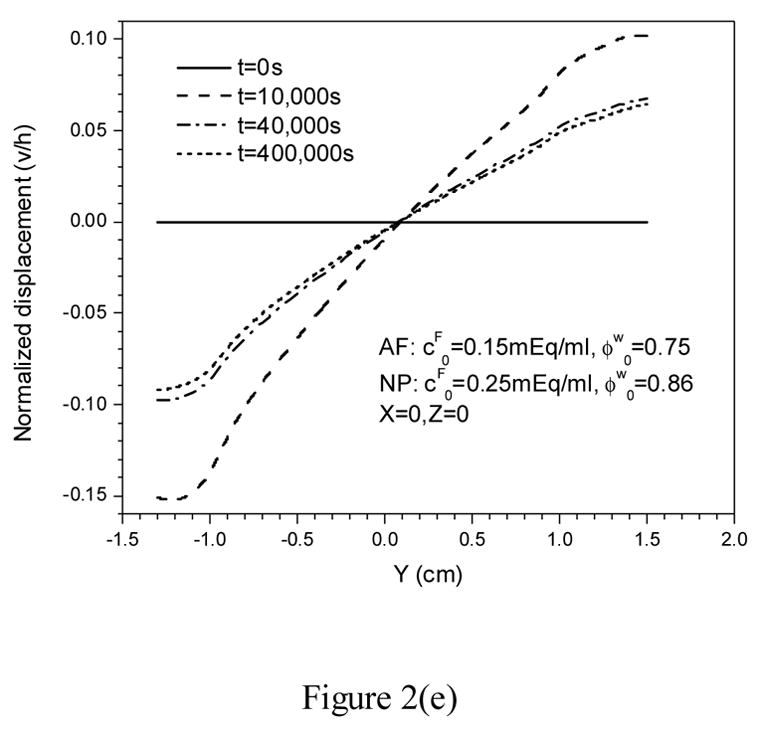
Transient response of fixed charge density (a), fluid pressure (b), electrical potential (c), effective (von Misses) stress (d), and tissue displacement in y-direction (e) during stress-relaxation.

The inhomogeneous model also predicted greater solid displacement in the posterior (negative y) direction than that in the anterior (positive y) direction when IVD is subjected to axial compression (Figure 2e).

Mechanical stiffness affected distributions of effective stress and fluid pressure. For example, a decrease in NP modulus by one order of magnitude (Table 1) increased the effective stress in AF, but reduced the effective stress and pressure in the NP region (Figure 3a,b). The solid displacement in the y-direction also increased (Figure 3c).

Figure 3.

Effect of NP stiffness on effective stress (a), fluid pressure (b), and tissue displacement in y-direction (c).

A reduction of water content for NP from 86% to 82% increased slightly the fluid pressure in the NP (Figure 4a), but reduced slightly the magnitude of electrical potential (Figure 4b). It also slightly increased the solid displacement (Figure 4c) and effective stress (not shown).

Figure 4.

Effect of NP water content on fluid pressure (a), electrical potential (b), and tissue displacement in y-direction (c).

The distribution of electrical potential varied significantly when the FCD of NP was reduced from 0.25 to 0.15 mEq/ml, see Figure 5a. However, the fluid pressure in the NP decreased slightly (Figure 5b).

Figure 5.

Effect of FCD on the distribution of electrical potential (a) and fluid pressure (b) in IVD.

Changes in NP properties (water content, FCD, modulus) affected the distributions of uncharged solute concentration within the tissue (Figures 6a, b). A reduction of endplate permeability in the NP region decreased the solute concentration dramatically (Figures 6a, b).

Figure 6.

Effects of NP stiffness, water content, and FCD on solute concentration. A decrease in endplate permeability reduces solute concentration. (a) Concentration distribution in x-direction. (b) Concentration distribution in z-direction.

DISCUSSION

The distribution of physical signals within the disc under axial compression was determined using the triphasic, inhomogeneous finite element model. The solute transport was also investigated. Results of this study clearly show that inhomogeneous material properties have a significant effect on the distributions of physical signals within the IVD. One of the most interesting phenomena is that, in NP, the distribution of effective solid stress, fluid pressure, electrical potential, and FCD (or dilatation, not shown) are very uniform compared to those in AF (Figure 2). There are sharp peaks in effective solid stress distribution in AF near the interface between AF and NP (Figure 2d). This is due mainly to the discontinuity in material properties at the interface used in the model. However, even though the material properties were homogeneous, the maximum effective stresses would occur at the same region (Yao and Gu, 2006b). These results are important for understanding load-sharing mechanisms in IVD as well as disc failure under axial compression.

The most significant biochemical change seen in a degenerated disc is the loss of proteoglycan, resulting in the decrease in FCD (Lyons et al., 1981). In this study, the electrical signals, such as the electrical potential, were found to be very sensitive to FCD (Figure 5a). Thus, the measurement of this electrical signal might be used as an indicator for disc degeneration. A decrease in FCD also reduces the contribution of osmotic pressure to the fluid pressure.

The mechanism of dynamic mechanical loading on the solute transport has been investigated numerically (Huang and Gu, 2006; Yao and Gu, 2006a). In the present study, the effect of endplate boundary conditions on the transport of uncharged solute in IVD under static compression was analyzed. The results indicate that the permeability of endplate affects solute transport rate into the tissue as does its concentration distributions (Figure 6).

A decrease in tissue water content will reduce its hydraulic permeability, leading to higher fluid pressurization effect (Figure 4a). It will also reduce solute diffusivity (Gu et al, 2004). Consequently, lower value of water content reduces both convection and diffusion effects, resulting in a lower solute concentration (Figure 6).

It is known that the mechanical interaction between solute and matrix may restrict solute transport in cartilaginous tissue for both diffusion and convection (Garcia et al., 1996). For diffusion, the intra-tissue diffusivities (D^α) were always smaller than their corresponding values in free solution ( $D_0^{\alpha }$), and its value is compression-dependent (Leddy and Guilak, 2003; Quinn et al., 2001). For convection, the restriction effect is considered by the convection coefficient (H^α) of the solutes. The value of H^α should be in the range of $\left(D^{\alpha }/D_0^{\alpha }\right)\le H^{\alpha }\le 1$ (Yao and Gu, 2006a). Note that H^α might be significantly less than 1 for large solutes (Evans and Quinn, 2006), while its value is close to unity for small solutes. In this study, the values of H^α =1 were used for both small and large solutes, since there is no data available for IVD tissue. Consequently, the concentration of large solute might be overestimated in our results. This is one of the limitations of this study.

The IVD was assumed to be isotropic mixture in this study. This assumption does not reflect the real material behavior of AF (Elliott and Setton, 2001). In the future, this finite element model needs to be improved to address this issue.

In summary, this is the first report of 3D inhomogeneous triphasic finite element analysis of mechanical, chemical and electrical signals within the human disc under axial compression. The effects of tissue porosity, FCD, and modulus on physical signals and fluid transport have been investigated parametrically. The effect of endplate permeability on solute transport and its concentration has also been studied. The results of this study provide additional insights into physical signals and solute transport within the human disc under mechanical loading.