Kinetic Analysis of [¹¹C]McN5652: A Serotonin Transporter Radioligand

Summary

The impulse response function of a radioligand is the most fundamental way to describe its pharmacokinetics and to assess its tissue uptake and retention pattern. This study investigates the impulse response function of [¹¹C](+)McN5652, a radioligand used for positron emission tomography (PET) imaging of the serotonin transporter (SERT) in the brain. Dynamic PET studies were performed in eight healthy volunteers injected with [¹¹C](+)McN5652 and subsequently with its pharmacologically inactive enantiomer [¹¹C](−)McN5652. The impulse response function was calculated by deconvolution analysis of regional time-activity curves, and its peak value (f_max), its retention value at 75 minutes (f_T), and its normalized retention (f_rel = f_r/f_max) were obtained. Alternatively, compartmental models were applied to calculate the apparent total distribution volume (DV_T) and its specific binding component (DV_S). Both the noncompartmental (f_T, f_rel) and the compartmental parameters (DV) were investigated with and without correction for nonspecific binding by simple subtraction of the corresponding value obtained with [¹¹C](−)McN5652. The impulse response function obtained by deconvolution analysis demonstrated high tracer extraction followed by a slow decline in the form of a monoexponential function. Statistical analysis revealed that the best compartmental model in terms of analysis of variance F and condition number of the parameter variance-covariance matrix was the one that was based on a single tissue compartment with parameters k₁and k₂ and that also included the parameter of regional cerebral blood volume (BV). The parameter f_rel demonstrated low between-subject variance (coefficient of variation [CV] = 19%), a midbrain to cerebellum ratio of 1.85, and high correlation with the known density of SERT (r = 0.787 where r is the coefficient of linear correlation between the parameter and the known density of SERT). After correction for nonspecific binding, f_rel demonstrated further improvement in correlation (r = 0.814) and midbrain to cerebellum ratio (3.09). The variance of the distribution volumes was acceptable when the logarithmic transform lnDV was used instead of DV (17% for the three-parameter model), but correlation of this compartmental parameter was slightly less (r = 0.652 for the three-parameter model) than the correlation of the noncompartmental f_rel with the known density of SERT, and the midbrain to cerebellum ratio was only 1.5 (uncorrected) and 1.8 (corrected). At the expense of increasing variance, the correlation was increased after correction for nonspecific binding using the inactive enantiomer (r = 0.694; CV = 22%). These results indicate that the kinetics of [¹¹C](+)McN5652 can best be described by a one-tissue compartment model with three parameters (k₁, k₂, and BV), and that both the noncompartmental parameter f_rel and the compartmental distribution volumes have the potential for quantitative estimation of the density of SERT. Further validation of the radioligand in experimental and clinical situations is warranted.

Positron emission tomography (PET) imaging of the serotonin transporter (SERT) is based on the rationale that SERT is expressed by serotonergic (5-HT) neurons (Blakely et al. 1991) and the premise that the regional density of SERT correlates with regional density of 5-HT axon terminals under circumstances of hyposerotonergic, normoserotonergic, and hyperserotonergic innervation, as well as under pathologic situations causing 5-HT denervation.

The radioligand [¹¹C]McN5652 (1,2,3,5,6,10βhexahydro6[4(methylthio) phenyl] pyrrolo[2,1-a]isoquinoline) selectively labels the SERT in vivo. Its geometrical trans, optical (+) isomer has a subnanomolar inhibitory constant for synaptosomal 5-HT uptake and a potency similar to paroxetine and sertraline, two high affinity ligands of SERT. (Maryanoff et al., 1984; Shank et al., 1988). Pharmacologic and behavioral experiments show that (+)McN5652 has at least two orders of magnitude higher potency to block the SERT than its inactive enantiomer (−)McN5652 (Smith et al., 1991). In vitro inhibition studies reveal that the potency of (+)McN5652 to prevent 5-HT uptake is much higher than its potency to prevent norepinephrine uptake, whereas its potency for dopamine uptake is negligible (Shank et al., 1988). In vivo ligand selectivity is even greater; pretreatment of mice with 5 mg/kg intravenous injections of either a norepinephrine transporter inhibitor (desipramine), a dopamine transporter inhibitor (GBR-12,909), or a SERT inhibitor (paroxetine) reveals that only paroxetine reduces tissue-to-cerebellum ratios in the hypothalamus, striatum, thalamus, and cerebral cortex; desipramine or GBR-12,909 have no effect (Suehiro et al., 1993b).

In humans and nonhuman primates, initial uptake into the brain is similar for the pharmacologically active enantiomer [¹¹C](+)McN5652 and the pharmacologically inactive enantiomer [¹¹C](−)McN5652, but 60 to 120 minutes after intravenous administration of the radioligand, only [¹¹C](+)McN5652 shows a distribution pattern that corresponds to the distribution of SERT in the brain. The PET studies in baboons after treatment with the 5-HT neurotoxins methylene-dioxy-metamphetamine or fenfluramine demonstrate reduced radioligand binding and a correlation with loss of tissue 5-HT (Scheffel et al., 1995, 1996a).

Significant problems confounding quantitative evaluation of [¹¹C](+)McN5652 PET studies are a relatively high nonspecific binding of the radioligand and a rapid equilibration between specific and nonspecific binding pools. Furthermore, there is no reference brain region without a significant quantity of SERT, and nonspecific binding cannot be assessed from PET scans with [¹¹C](+)McN5652 alone.

Despite these shortcomings, [¹¹C](+)McN5652 offers compelling advantages. It is a PET radioligand with brain uptake and retention corresponding to the distribution of SERT in rodents (Suehiro et al., 1993a), nonhuman primates (Szabo et al., 1995b), and humans (Szabo et al., 1995a;). Preliminary observations in subjects with neurodegenerative diseases and in animals and human subjects previously exposed to serotonergic neurotoxins show that binding of [¹¹C](+)McN5652 is reduced when 5-HT terminals are damaged (Suehiro et al., 1993b; Scheffel et al., 1995, 1996a; Szabo et al., 1996; Ricaurte et al., 1996). Animal studies demonstrate that accumulation of radioactive extrinsically or intrinsically formed metabolites of [¹¹C](+)McN5652 or [¹¹C](−)McN5652 in brain tissue is negligible (Scheffel and Szabo, unpublished data, 1993).

With compartmental modeling, radioligand kinetics can be described by state-space equations. The core of these differential equations is the impulse response function, the parameters of which are related to exchange rates between and distribution within virtual body spaces called compartments. Recently, alternative models based on model-free calculation of the impulse response function have emerged. These models characterize the impulse response function by probability distributions, the independent variable of which is either the vector of time (Szabo et al., 1993) or a set of continuous exponential coefficients (Cunningham and Jones, 1993). A link between the noncompartmental and compartmental models can be established, and the most applicable compartmental model is directly implicated by the configuration of the impulse response function (Szabo et al., 1985).

The current work investigates the kinetics of [¹¹C](+)McN5652 and [¹¹C](−)McN5652 using the impulse response function calculated by deconvolution analysis and applies the impulse response function to derive an applicable compartmental model. This hypothetical compartmental model was compared with alternative compartmental models by statistical tests including analysis of variance (ANOVA) and eigenvalue analysis of the parameter variance-covariance matrix. Parameter reliability was explored in healthy individuals by three criteria: between-subject reproducibility/variance, correlation with the known density of SERT, and the midbrain-to-cerebellum ratio. The use of the pharmacologically inactive enantiomer [¹¹C](−)McN5652 to correct for nonspecific binding also was explored: two PET studies were performed in each subject, one with [¹¹C](+)McN5652 and another with [¹¹C](−)McN5652, and correction for nonspecific binding was achieved by subtraction of the parameters derived from these two studies.

METHODS

Radioligand preparation

Both [¹¹C](+)McN5652 and [¹¹C](−)McN5652 were synthesized as previously described (Suehiro et al., 1993b). Purification was achieved by HPLC using a semipreparative reversed-phase C-18 column.

Volunteers

Eight healthy volunteers (five women and three men) with an average age of 28 ± 7 years were included. In each of the volunteers, organic diseases and neurologic and psychiatric disorders were ruled out using clinical history, physical examination, and blood and urine chemical studies. Urine toxicology tests were performed to rule out recent drug abuse.

Magnetic resonance imaging

A magnetic resonance imaging (MRI) study was performed in each subject for reproducible positioning and for placement of regions of interest (ROI) on coregistered PET/MRI scans. Before MRI, the volunteers obtained a custom-made face mask (TRU-SCAN, Annapolis, MD, U.S.A.). This thermoplastic-mask was molded to the subject’s face and prepared so that it could be attached firmly to a head-holder fitting both the PET scanner and the MRI scanner. An MRI slice from the sagittal midplane of the brain was used to identify the anterior commissural-posterior commissural (AC-PC) line. The intersection of the AC-PC plane was labeled on the mask as a reference for both MRI and PET. The lowest PET slice was plated parallel and caudal to this plane at a distance of five PET slices (32.5 mm). Thus, in each PET scan, the AC-PC line was located in the sixth slice. This technique yields reproducible positioning of the basal ganglia and thalami with a positioning error of ± 1 mm (Muller-Gärtner et al., 1992).

Magnetic resonance imaging was performed using a GE Signa 1.5-T scanner (GE Medical Systems. Milwaukee. WI. U.S.A.). Two sequences were obtained: one for identification of the AC-PC plane and another for coregistration with PET. The first sequence was a set of T1-weighted scout images used to identify the AC-PC line. Imaging parameters were as follows: repetition time 500, echo time 20, slice thickness 5 mm with 0 gap, 128 × 256 matrix, and 1 nex. The second sequence was an axial spin density/T1-weighted three-dimensional volumetric scan using radiofrequency “spoiled” gradient echoes. This data set was used to identify gray and white matter. Imaging parameters were as follows: repetition time 35, echo time 5, flip angle 45 degrees, 1.5-mm effective slice thickness, 0 gap, 124 slices with inplane 192 × 256 matrix, 24 cm field of view, and 1 nex.

Positron emission tomography

The PET studies were performed with a GE 4096 Plus whole-body PET scanner, which acquires 15 simultaneous slices spaced 6.5 mm apiirt. The spatial resolution of this scanner equals 6 mm. The subjects were positioned in the scanner using the previously drawn coregistration line. A transmission scan was acquired for 10 minutes using a 10-mCi ⁶⁸Ge/⁶⁸Ga pin source. Two PET studies were performed in each subject, one with [¹¹C](+)McN5652 (pharmacologically active enantiomer of McN5652] and another with [¹¹C](−)McN5652 (pharmacologically inactive enantiomer of McN5652), with a time difference of 150 minutes between injections.

The injected dose at time of injection was 17.8 ± 1.5 mCi (mean ± 1SD) at a specific activity of 1555 ± 357 mCi/(μmol for [¹¹C](+)McN5652, and 18.5 ± 1.3 mCi at a specific activity of 1223 ± 233 mCi/μmol for [¹¹C](−)McN5652. Eighteen serial PET scans were obtained in dynamic mode during 95 minutes. The following image sequence was used: 4 × 15 seconds, 3 × 1 minutes, 3 × 2 minutes, 3 × 5 minutes, 3 × 10 minutes, and 2 × 20 minutes. Positioning was closely monitored during acquisition, and any deviation from the original line labeled on the mask was corrected by repositioning. The PET scans were corrected for radioactive decay and were reconstructed using ramp-filtered back-projection in a 128 × 128 matrix, with a transaxial pixel size of 2 × 2 mm. The PET scans also were attenuation-corrected using the transmission scan. The sequential PET scans were transferred to a personal computer equipped with a 300-MHz Pentium CPU and a Windows NT 4.0 (Microsoft, Redmond, WA. U.S.A.) operating system running custom image analysis software developed in house (JHU Imager-3D).

Input function

Arterial blood samples were obtained every 3 to 7 seconds during the first 2 to 3 minutes after injection, and at increasing time intervals thereafter, until 95 minutes after injection. The arterial plasma samples were analyzed by HPLC, and the input function was corrected for metabolized radioligand activity. The HPLC was performed after loading the plasma on SEP-PAK columns and extracting the radioactivity by methanol. An Econosil C18 column (Alltech, Deerfield. IL, U.S.A.) was used as the solid phase, and 50%50% acetonitrile/water buffered with 0.1 mol/L ammonium formate as the mobile phase for HPLC. Measured radioactivity was digitally stored and analyzed by the Dynamax software package (Rainin).

Time-activity curves

Regions of interest placement was based on coregistered MRI/PET images using linear trans formations of the MRI images. The ROI included the frontal cortex, parietal cortex, temporal cortex, occipital and circulate cortices, caudate, putamen, thalamus, midbrain, pons, hypothalamus, and cerebellum. The average size of the ROI was 44 pixels. Typically, the number of ROI for cortical regions was six (three on each side of the brain). This was equivalent to a total tissue volume of 6.86 cm³, whereas the number of ROI for subcortical structures was one (equivalent to 1.14 cm³; pons, midbrain, hypothalamus), two (equivalent to 2.29 cm³; caudate heads combined, thalami combined), or four (equivalent to 4.58 cm³; right and left anterior and posterior putamen combined). The ROI from three planes of the brain are shown in Fig. 1.

FIG. 1.

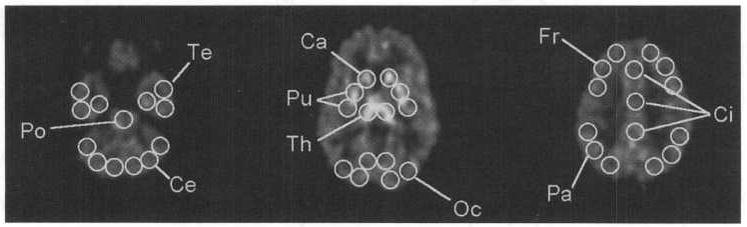
Regions of interest (ROI) used to derive time-activity curves from the cerebellum (Ce), temporal cortex (Te), pons (Po). caudate head (Ca), putamen (Pu), thalamus (Th), occipital cortex (Oc), frontal cortex (Fr), cingulate gyrus (Ci), and parietal cortex (Pa). Additional regions were placed over the hypothalamus and midbrain (not shown).

Noncompartmental model

Tissue time-activity curves derived from the ROI are the result of uptake, retention, and recirculation of the radioactive ligand. Mathematically, they represent a convolution integral of two functions: the impulse response function, which would be measured after instantaneous introduction of the radioligand into the tissue, and the input function, which is represented by the time course of radioligand concentration in arterial blood. The tissue curve and the input function are complex because they both result from the distribution of the radioligand in multiple compartments, a phenomenon referred to as a high model order. A high postulated model order results in over-parametrization and instability during parameter estimation.

To reduce model order, the impulse response function can be calculated from tissue time-activity curves by deconvolution analysis using the metabolite-corrected arterial plasma time-concentration curve as input function (Szabo et al., 1987). The resulting impulse response function is, at least theoretically, unique and can be used to reconstruct the tissue response to any shape of input function as long as two conditions are fulfilled: linearity and stationarity.

A tracer kinetic process is considered linear when a radioligand with high specific activity is injected and the ligand mass is low compared with the density of specific binding sites (i.e., the density of SERT). This likely is the case with [¹¹C](+)McN5652. In healthy subjects, the maximal brain concentration of (¹¹C](+)McN5652 is 0.6 pmol/L, less than 1% of 350, 450 pmol/L, the k_i of unlabeled (+)McN5652 needed to displace 5-HT from the SERT (Shank et al., 1988).

The stationary condition of the tracer kinetic process is represented by the fact that the rate constants remain unchanged for the time of the investigation. The stationary condition in time also is likely to be fulfilled for the following reasons:

1. Physiologic determinants of radioligand uptake: Since subjects have 30 to 40 minutes to acclimate to the PET scanner, and sensory input is minimized and standardized during imaging, it is unlikely that significant changes in regional cerebral blood volume, blood flow, or in the blood–brain permeability occur during the PET study.

2. Determinants of radioligand binding/retention: Nonspecific binding of the radioligand depends on the presence of nonspecific binding membranes and proteins, whereas specific binding depends on the presence of SERT. In the well-established environment of the PET laboratory, there is no reason to believe that any of these parameters will change significantly during the PET study.

To perform deconvolution analysis, the time-activity curves representing the input function and tissue activity need to be sampled at equidistant time intervals. In our experiments, this interval was set at Δt = 0.5 minutes. Since both the PET images and the arterial blood samples were sampled at variable time intervals, missing values were calculated by linear interpolation. The equidistantly spaced values of the input function, x(t), tissue time-activity curve, y(t), and impulse response function, f(t), were described by a series of discrete values x₁…x_n, y₁…y_n, and f₁…f_n; where, x_i = x(t_i), c_i = c(t_i), and f_i = f(t_i), respectively, and n is the number of data points (180 for a 90-minute measurement). These discrete values were used to construct the vectors of the impulse response function, f, and the tissue time-activity curve, y, as well as the lower triangular matrix of input function X:

$$\mathbf{f}=\mid \begin{array}{l}{f}_1\hfill \\ f_2\hfill \\ f_3\hfill \\ \dots \hfill \\ f_{\text{n}}\hfill \end{array}\mid ,\mathbf{y}=\mid \begin{array}{l}{y}_1\hfill \\ y_2\hfill \\ y_3\hfill \\ \dots \hfill \\ y_{\text{n}}\hfill \end{array}\mid ,\hspace{0.17em}\text{and\hspace{0.17em}}\mathbf{X}=\mid \begin{array}{lllll}{x}_1\hfill & 0\hfill & \dots \hfill & \dots \hfill & \dots \hfill \\ x_2\hfill & x_1\hfill & \dots \hfill & \dots \hfill & \dots \hfill \\ x_3\hfill & x_2\hfill & x_1\hfill & \dots \hfill & \dots \hfill \\ \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill & \dots \hfill \\ x_{\text{n}}\hfill & x_{\text{n}-1}\hfill & x_{\text{n}-2}\hfill & \dots \hfill & x_1\hfill \end{array}\mid$$ (1)

The time-activity vector y is the result of convolution, which in matrix notation is equivalent to

$$\mathbf{y}=\mathbf{Xf}+\mathbf{e}$$ (2)

Because of the presence of noise, e, it is not sufficient to multiply both sides of Equation 2 by the matrix inverse X⁻¹ to obtain f. Such a maneuver would amplify noise and deform the shape of the impulse response function. Equation 2 is said to be ill-conditioned with regard to inversion of X, a phenomenon also referred to as the singularity problem. The procedure of regularization was introduced by Tihonov (1963) to resolve or at least minimize the problem of singularity encountered during deconvolution. This technique was further elaborated by Twomey (1965) and Phillips (1962) and was adapted to processing biomedical signals by Hunt (1970, 1972). Hunt’s regularization entails combining the minimum squared difference estimator with a filter function G:

$$\mathbf{f}={[{\mathbf{X}}^{\text{T}}\mathbf{X}+\gamma {\mathbf{G}}^{\text{T}}\mathbf{G}]}^{-1}{\mathbf{X}}^{\text{T}}\mathbf{y}$$ (3)

Matrix G can be designed to minimize first, second, or higher differences of the impulse response function f. The influence of G on f is weighted by the power of regularization γ. For the data presented here, a second difference minimization matrix G with γ = 0.1 were found adequate to reduce noise-dependent oscillations without significantly degrading f(t).

From the impulse response function of [¹¹C]McN5652, three parameters were derived: (1) maximum or peak value f_max to express radioligand uptake; (2) value at time T = 75 minutes, f_T, to express radioligand retention; and (3) the ratio f_rel = f_T/f_max to express radioligand retention independent of its delivery to the ROI. The principle of impulse response function (the “black-box” model) (Zierler, 1965; Lassen and Perl, 1979) is depicted at the top of Fig. 2; four compartmental models are shown below. The impulse response function is helpful to assess model order because, as it can be shown by Laplace transformation that first-order kinetics yields a single exponential function, second-order kinetics yields a double exponential function and so on (DiStefano and Landaw, 1984; Szabo, 1995).

FIG. 2.

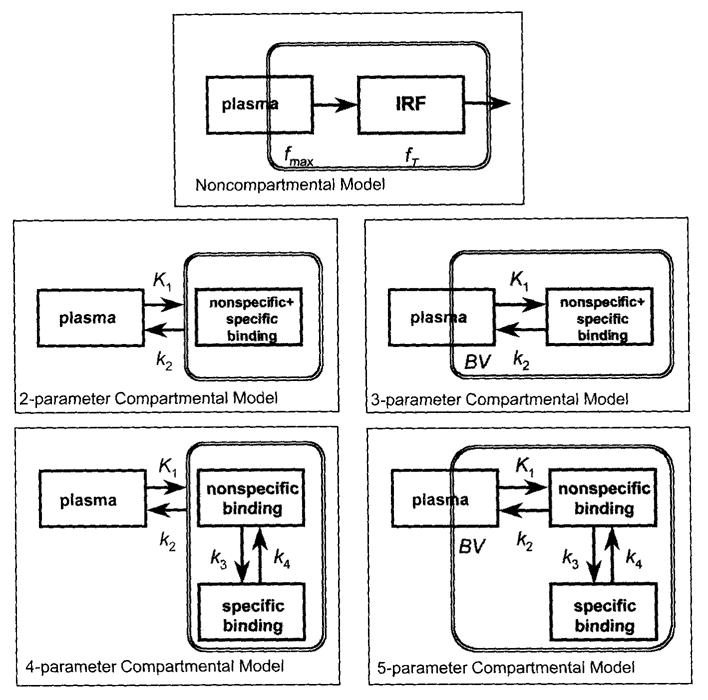
Kinetic models applied: non-compartmental model, two-parameter compartmental model (one tissue compartment), three-parameter compartmental model (one tissue compartment plus vascular pool), four-parameter compartmental model (two tissue compartments), and five-parameter compartmental model (two tissue compartments plus vascular pool). BV, Regional cerebral blood volume, k₁…k₄, compartmental rate constants, f_max … f_T = parameters of the impulse response function. The shaded area represents the model components that are in the field of view of the positron emission tomography (PET) scanner. The presence of vascular blood pool is indicated by partial inclusion in the field of view of the PET scanner.

Compartmental models

Several compartmental models were evaluated (Fig. 2).

With the one-tissue compartment model, the assumption was made that a single compartment can describe all identifiable aspects of radioligand behavior in the brain. With the two-tissue compartment model, the assumption was made that at least two compartments are needed for this purpose: one to describe nonspecific and another to describe specific binding. Although free, unbound ligand is presented as a separate compartment in some models, in most models it is incorporated into the nonspecific binding compartment. For each model, parameter k₁ was used to describe radioligand uptake in brain and k₂ was used to describe radioligand washout from the brain. For the two-tissue compartment model, k₃ and k₄ were included to describe binding and release of the radioligand at the site of the SERT. For both models, two situations were investigated: one with significant blood activity present in the PET scanner field of view (described by parameter BV) and one without. This resulted in four models with two, three, four, and five parameters (Fig. 2), respectively, which are indicated in the subscripts of each parameter. Thus k_2,4par and k_2,5par represented k₂ of the four- and five-parameter models and corresponded to k₂′ in the works of Koeppe et al. (1996) and Frey et al. (1996). Similarly, in comparison with Koeppe et al. (1996) and Frey et al. (1996), in this presentation, k_3,4par and k_3,5par corresponded to k₃′.

The model parameters were estimated by minimizing the summed squared difference between actual tissue activity measured with PET and estimated tissue activity C_T(t) using the Marquardt technique (Marquardt, 1963). Time-activity curves were synthesized by the fourth-order Runge-Kutta technique (Press et al., 1986) using the following set of differential equations:

$$\begin{array}{l}\mathit{PET}(I)={\int }_{t_1}^{t_2}[(BV)(C_A(t)+(1-BV))(C_T(t))]dt\\ C_T(t)=C_S(t)+C_{NS}(t)\\ \frac{d{C}_{NS}(t)}{dt}=K_1{C}_A(t)-k_2{C}_{NS}(t)+k_4{C}_S(t)-k_3{C}_{NS}(t)\\ \frac{d{C}_S(t)}{dt}=K_3{C}_{NS}(t)-k_4{C}_S(t)\end{array}$$ (4)

where C_T(t), C_NS(t), and C_S(t) represent total tissue activity, nonspecific binding, and specific binding, respectively; C_T(t) is identical to vector y of the noncompartmental model of Equations 1 through 3 with different sampling rates; and C_A(t) = arterial activity (input function) is identical to the main diagonal of X of the noncompartmental model of Equations 1 through 3 with different sampling rates.

Model subsets

Of this set of equations the following four model subsets were derived and tested:

One tissue compartment, two-parameter model

There is no significant (identifiable) vascular activity present in the brain tissue curves, and the specific and nonspecific compartmental radioactivities are inseparable. Parameters k_1,2par and k₂,_2par are estimated, and parameters k₃ and k₄ vanish.

One tissue compartment, three-parameter model

There is significant vascular activity present in the brain tissue curves, and the specific and nonspecific compartmental radioactivities are inseparable. Parameters BV, k_1,3par, and k_2,3par are estimated.

Two tissue compartment, four-parameter model

There is no significant (identifiable) vascular activity present in the brain tissue curves, but specific and nonspecific compartmental radioactivities are separable, that is, the two tissue compartments are separately identifiable. The following parameters were estimated: k_1,4par and k_2,4par, k_3,4par, and k_4,4par.

Two tissue compartment, five-parameter model

There is significant vascular activity present in the brain tissue curves, but specific and nonspecific compartmental radioactivities are separable, that is, the two tissue compartments are separately identifiable. The following parameters were estimated:BV, k_1,4par and k_2,4par, k_3,4par, and k_4,4par.

Data sampling

The tissue time-activity vector was sampled as follows:

1. The PET measurement was acquired at unequal time points with increasing time intervals to account for noise caused by radionuclide decay.

2. Deconvolution was performed on brain tissue curves at steps of 0.5 minutes.

3. Tissue curve synthesis by Runge-Kutta simulation was achieved at equidistant steps of 1 second. The synthesized curve then was resampled at the nonequidistant sampling rate of the PET scans to obtain the squared differences needed for parameter estimation by the Marquardt algorithm.

Radioligand concentration of arterial plasma (the input function) was sampled at three different sampling patterns identical to those of the tissue curve.

Since separation of a third tissue component (e.g., of free radioligand) is unlikely to be achieved for lipophilic tracers, the five-parameter model is the most desirable one, although accurate estimation of the individual rate constants may not be possible because of the overparametrization and numerical instability of the parameter estimator. Another significant problem is collinearity of parameters (Slinker and Glantz, 1985), a phenomenon that can be minimized by using parameter ratios for estimation of radioligand binding. One widely used parameter ratio is the binding potential k₃/k₄ (Mintun et al., 1984), which is used when two tissue compartments are separable and the parameters of specific binding k₃ and k₄ can be determined with high confidence. As an alternative, apparent radioligand tissue distribution volumes can be derived that are relatively insensitive to the instabilities of parameter estimates (Koeppe et al., 1996; Frey et al., 1996). Such distribution volumes were calculated from the parameters of [¹¹C]McN5652:

The total apparent tissue distribution volume for the one-tissue compartment (two- or three-parameter) model is as follows:

$$D{V}_{\text{t},2\text{par}}=K_{1,2\text{par}}/k_{2,2\text{par}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}D{V}_{\text{t},3\text{par}}=K_{1,3\text{par}}/k_{2,3\text{par}}$$ (5)

Total apparent tissue distribution volume for the two-tissue compartment (four- or five parameter) model is as follows:

$$\begin{array}{l}D{V}_{\text{t},4\text{par}}=(K_{1,4\text{par}}/k_{2,4\text{par}})\hspace{0.17em}(1+k_{3,4\text{par}}/k_{4,4\text{par}});\\ D{V}_{\text{t},5\text{par}}=(K_{1,5\text{par}}/k_{2,5\text{par}})\hspace{0.17em}(1+k_{3,5\text{par}}/k_{4,5\text{par}})\end{array}$$ (6)

Specific binding component of the apparent tissue distribution volume of the two-tissue compartment (four- or five parameter) model is as follows:

$$\begin{array}{l}D{V}_{\text{s},4\text{par}}=(K_{1,4\text{par}}/k_{2,4\text{par}})\hspace{0.17em}(k_{3,4\text{par}}/k_{4,4\text{par}});\\ D{V}_{\text{s},5\text{par}}=(K_{1,5\text{par}}/k_{2,5\text{par}})\hspace{0.17em}(k_{3,5\text{par}}/k_{4,5\text{par}})\end{array}$$ (7)

Statistical analysis

Conditioning of the parameter variance—covariance matrix

The Marquardt algorithm uses the parameter variance-covariance matrix S to estimate parameters by adjusting the parameter vector p iteratively using the recursive formula (Dell et al., 1973):

$${\mathbf{p}}_{\text{k}}={\mathbf{p}}_{\text{k}-1}+\mathrm{\Delta }\mathbf{p};\hspace{0.17em}\mathrm{\Delta }\mathbf{p}={({\mathbf{S}}^{\mathbf{T}}\mathbf{WS})}^{-1}{\mathbf{S}}^{\mathbf{T}}\mathbf{WS}\mathrm{\Delta }Y$$ (8)

The parameter variance-covariance matrix S has a size of n_p × n_p, with n_p being the number of parameters, and is derived from the partial derivatives of the synthesized tissue-activity curve over every estimated parameter. Diagonal elements of weighting matrix W usually are chosen to apportion the effect of individual measurements on parameter estimates based on their statistical significance. For the current study, these diagonal elements were assigned the value of the measured radioactivity (Koeppe et al., 1994); off-diagonal elements of W were assigned zeros. Accurate solutions of p require the information matrix S^TWS to be easily invertible (e.g., nonsingular) (Delforge et al., 1989). Unfortunately, the information matrix often is nearly singular because of the effects of noise, limited data sampling, and model overparametrization (Landaw and DiStefano, 1984; Slinker and Glantz, 1985). Singularity was graded by the condition number, which was calculated from the ratio of the largest and smallest eigenvalues of the parameter variance-covariance matrix (Delforge et al., 1989; Muzik et al., 1997).

If the model parameters are completely independent and their variances comparable, the eigenvectors of the parameter variance-covariance matrix will be orthogonal to each other, and the eigenvalues of this matrix will be of comparable magnitude. If parameter variances are different, the distribution of the parameters will become elliptical in the multiparametric space. The principal axes of this ellipse or ellipsoid correspond to the eigenvectors (direction) and eigenvalues (magnitude) of the parameter variance-covariance matrix. The larger the difference of the eigenvalues (e.g., the higher the condition number), the more likely it is that the parameter variances are nonhomogeneous and parameter collinearity exists.

Goodness of fit

For statistical estimation of model order, the ANOVA F value was calculated from the sums of squared residuals SS₁, and SS₂ over n measurements of two models of order p₁, and p₂, which were compared (Landaw and DiStefano, 1984; Muzik et al., 1997):

$$F_{p_2-p_1,n-p_2}=\frac{(S{S}_1-S{S}_2)(n-p_2)}{S{S}_2(p_2-p_1)}$$ (9)

Parameter variance and parameter bias

When the condition number increases, parameter identifiability decreases and the variance of the estimated parameters is higher because of numerical instability or singularity. The variance in the variance–covariance matrix, however, does not encompass the variances caused by error occurring during performance of the experiments or by biological differences between the individuals. Thus, to assess between-subject variance, the standard deviation (SD) and coefficient of variation (CV) were calculated.

The applicability of each parameter to represent the regional density of SERT was tested by correlating the average parameter values obtained in 12 brain regions with [³H]paroxetine binding to human brain tissue of the same regions measured in vitro (Laruelle et al., 1988; Laruelle and Maloteaux, 1989). The zero intercept of the regression line between the PET-derived parameters and the in vitro densities is a nonzero positive value, which has been referred to as the parameter bias (Frey et al., 1996). Since the density of the SERT measured in vitro in the cerebellum is only 6% to 7% of the density in the region of the raphe nuclei (midbrain and pons), the midbrain to cerebellum ratio was used to assess bias, and a parameter with a higher midbrain to cerebellum ratio was interpreted as one with lower bias.

Dependence of f_rel k₁

Since CBF may affect both the uptake and release of a radioligand, it also may affect the parameter f_rel. To estimate this effect, computer simulations based on the impulse response function defined by k₁, and k₂ were performed. Assuming that the extraction fraction of the radioligand is high and that k₁ therefore represents blood flow, the effect of k₁ on f_rel, was investigated. The average parameters obtained for the hypothalamus were used for these computer simulations. For the active enantiomer [¹¹C](+)McN5652, k₁, = 0.33685 and DV = 114.56; for the inactive enantiomer [¹¹C](−)McN5652, k₁, = 0.2231 and DV = 14.34. By systematically increasing k₁, from 0.2 to 0.5 at steps of 0.002, f_rel was calculated at T = 75 minutes as exp(−75k₁,/DV). Correction for nonspecific binding was achieved by subtracting the f_rel values of the two enantiomers.

Deconvolution analysis, compartmental parameter estimation, and numerical simulations were performed using the numerical software package MATLAB/Windows version 5 (The Mathworks, Nattick, MA, U.S.A.). Statistical computations were performed with the SPSS/Windows statistical package version 7 (SPSS, Inc., Chicago, IL, U.S.A.).

RESULTS

Input function

The time-integral of the total arterial plasma activity for [¹¹C](−)McN5652 was 865 ± 184 (nCi)(min)/cm³/mCi injected dose (ID) (mean ± SD), a value substantially higher than the 612 ± 112 (nCi)(min)/cm³/mCi ID of [¹¹C](+)McN5652. The SEP-PAK-extracted fraction or average recovery was 75%. As revealed by HPLC, unmetabolized [¹¹C](+)McN5652 accounted for 89 ± 5% of recovered activity at 5 minutes, but only for 14 ± 6% at 60 minutes. In comparison, the unmetabolized fraction of the [¹¹C](−)McN5652 enantiomer decreased from 93 ± 5% at 5 minutes to 26 ± 12% at 60 minutes.

Noncompartmental model

The impulse response function obtained by deconvolution analysis demonstrated noise-dependent fluctuations. Despite these noise effects, two parameters (f_max, representing uptake, and f_T, representing retention or binding at T = 75 minutes) could be identified (Fig. 3). The shape of the model-free impulse response function was monoexponential, consistent with a first-order tracer kinetic model (e.g., with a single identifiable tissue compartment). Although there was a small early peak (f_max) corresponding to radioligand appearance within the brain vessels (Fig. 4), this peak often was indistinguishable from noise oscillations. In addition to noise, high extraction of the radioligand and slow release from brain were probable reasons for insufficient separation of this vascular component from the rest of the impulse response function. The slope of the slow tissue component of the impulse response function of [¹¹C](−)McN5652 was steeper and more uniform in various regions of the brain than the slope of the impulse response function of [¹¹C](+)McN5652.

FIG. 3.

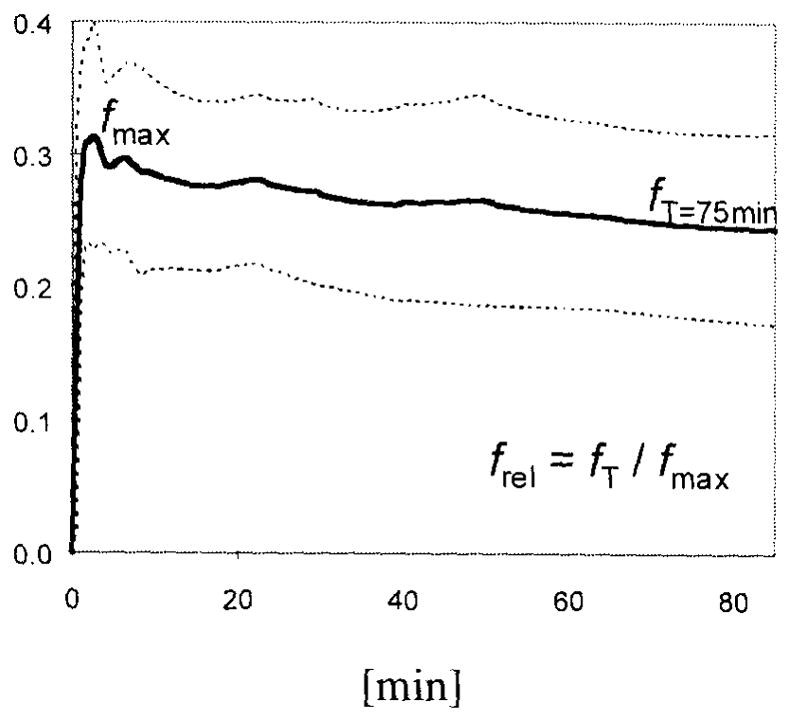
Noncompartmental impulse response function calculated from the thalamus: shown are mean ± SD of the impulse response function from eight healthy controls. f_max, maximum value; f_T, value at T = 75 minutes.

FIG. 4.

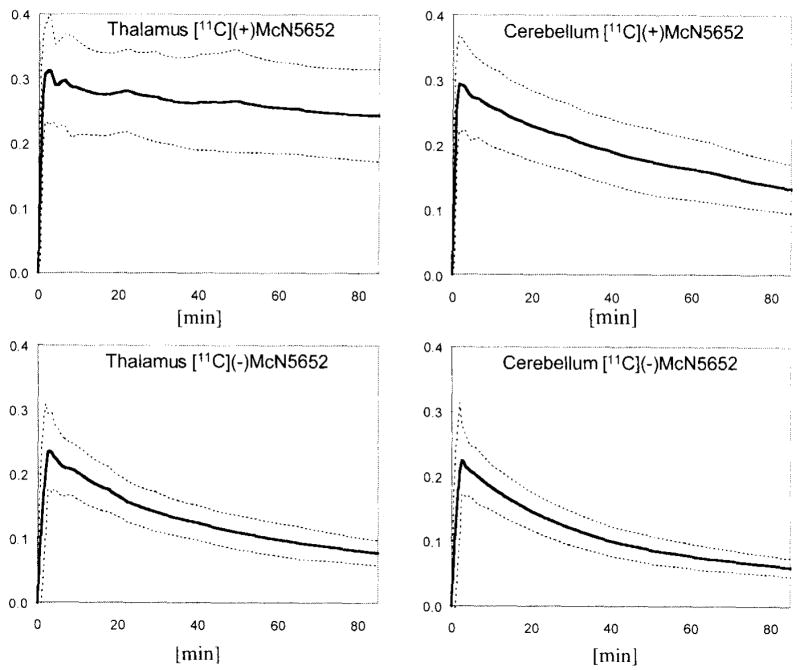
Impulse response functions of [¹¹C](+)McN5652 and [¹¹C](−)McN5652 measured in the thalamus and in the cerebellum. Shown are mean ± SD from eight healthy controls.

Compartmental models

The condition number of the two-parameter model was 2.48 to 3.58 (2.93 ± 0.22), which is consistent with a well-conditioned model. With the three-parameter model, the condition number was 2.87 to 6.09 (3.74 ± 0.55), which is consistent with minimal instability because of overparametrization compared with the two-parameter model. There was a significant improvement in curve fit with the three-parameter versus the two-parameter model (F = 57.27, P < 0.0001), which indicates that in addition to k₁ and k₂, it was necessary to include BV during parameter estimation. Both the four-and five-parameter model represent curve fits that were significantly worse than the three-parameter fit (F_4par/3par = −10.20 and F_5par/3par = − 3.95, respectively). Also, using the three-parameter model as a reference, the four-and five-parameter models resulted in 9.6- and 12.4-fold increases in the condition number of the parameter variance-covariance matrix.

Model parameters

For simplicity, in this presentation variance is used to describe parameter variance and its measure, the coefficient of variation, in units of percent. Correlation is used to describe parameter correlation with the known density of SERT. From the noncompartmental model, the most dependable parameter was f_rel, both in terms of low variance (19%) and high correlation (0.787). Correlation was further improved (0.814) at a cost of increased variance (36%) when f_rel was corrected for nonspecific binding. The parameter f_T demonstrated a variance of 26% and a correlation of 0.511 (Table 1).

TABLE 1.

Between-subject variance (CV = coefficient of variation) of individual noncompartmental and compartmental parameters and their correlation (r = correlation coefficient) with the known density of the SERT

	Uncorrected		Corrected
Parameter	CV	r	CV	r
Tissue radioactivity at T = 85 minutes
A85	33.83	0.541	44.45	0.661
Impulse response function (noncompartmental)
fmax	20.27	− 0.179
fT	25.93	0.511	34.69	0.623
frel	18.69	0.787	36.45	0.814
Two-parameter model (compartmental)
K1,2par	16.74	− 0.343
k2,2par	55.75	− 0.789
Three-parameter model (compartmental)
BV3par	30.50	− 0.391
K1,3par	17.92	− 0.336
k2,3par	57.31	− 0.769
Four-parameter model (compartmental)
K1,4par	23.93	− 0.130
k2,4par	52.37	0.212
k3,4par	62.80	0.111
k4,4par	137.18	− 0.436
Five-parameter model (compartmental)
BV5par	42.75	−0.106
K1,5par	23.75	−0.196
k2,5par	54.78	0.116
k3,5par	66.56	0.254
k4,5par	135.67	0.061
Distribution volumes
DVt,2par	79.04	0.622	90.71	0.622
DVt,3par	79.08	0.322	91.03	0.322
DVt,4par	125.32	0.308	141.87	0.308
DVt,5par	101.91	0.368	112.14	0.395
DVs,4par	133.77	0.308
DVs,5par	111.43	0.395
lnDVt,2par	16.70	0.715	22.29	0.742
lnDVt,3par	16.85	0.652	22.61	0.694
lnDVt,4par	22.42	0.796	32.24	0.816
lnDVt,5par	21.02	0.696	26.58	0.730
lnDVs,4par	28.60	0.800
lnDVs,5par	25.58	0.673

Uncorrected parameters represent those derived from [¹¹C](+)McN5652 while corrected parameters represent those corrected for nonspecific binding by subtraction of the identical parameter obtained with [¹¹C](−)McN5652. A₈₅, Activity (nCi/cc/mCi injected dose) measured with PET 75–95 minutes post injection; f_max, maximum value of the impulse response function; f_T, value of the impulse response function at T = 75 minutes post injection; f_rel, f_T/f_max; k₁, compartmental uptake; k₂, compartmental washout; BV, blood volume; 2par, 2 parameter model; DV, total apparent tissue distribution volume; DV_S, apparent distribution volume of specific binding.

The total apparent tissue distribution volume of the three-parameter model, DV_t,3par, demonstrated a variance of 79% and a correlation of 0.322. Using the logarithmic transform of this parameter, lnDV_t,3par, the variance could be reduced to 17% and the correlation increased to 0.652. The variance of lnDV_t,2par was slightly lower and its correlation slightly higher than those of lnDV_t,3par (Table 1). The correlation of the distribution volumes derived from more complex models, lnDV_t,4par and lnDV_t,5par, was higher, but their variances also were higher. The variances of lnDV values corrected for nonspecific binding remained within an acceptable range (22% to 32%), whereas their correlation was improved (0.694 to 0.816, Table 1).

Although the F test indicates that the most robust model was the three-parameter model, the variances and the correlations of the lnDV values of both the more and less complex models (i.e., the three- and five-parameter models, respectively) were comparable.

The variance of tissue radioactivity, measured 75 to 95 minutes after injection expressed in nanocuries per cubic centimeter per millicuries of the injected dose, was 34%, and the con-elation was 0.541. Variance of this parameter was slightly higher (44%) and the correlation slightly better (0.661) after it was corrected for nonspecific binding (Table 1).

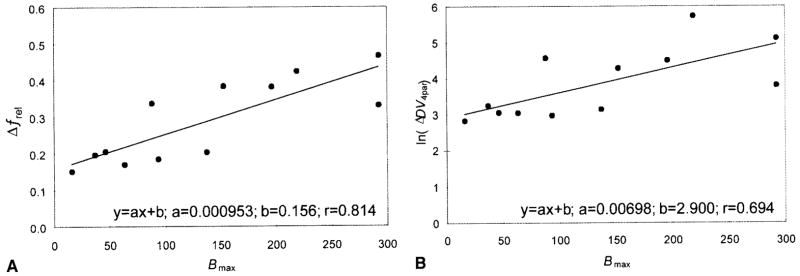
Table 2 shows means and SD values for four parameters of potential clinical use in the 12 brain regions investigated: lnDV_t,3par, lnΔDV_t,3par, f_rel, and Δf_rel. The Δ symbol represents the parameter difference between [¹¹C](+)McN5652 and [¹¹C](−)McN5652. All four parameters demonstrate lowest values in the cerebellum, corresponding to the known low density of SERT in this part of the brain. Highest values were observed in the midbrain and hypothalamus. Correction for nonspecific binding resulted in an increased midbrain to cerebellum ratio, a parameter often used to assess specific binding.

TABLE 2.

Regional values of the noncompartmental parameter f_rel and compartmental parameter lnDV_t1,3par (mean ± SD; n = 8)

	Uncorrected		Corrected
	frel	lnDVt,3par	Δfrel	lnΔDVt,3par
Hypothalamus	0.80 ± 0.24	5.95 ± 2.54	0.42 + 0.24	5.73 ±2.77
Midbrain	0.84 ±0.06	5.22± 1.14	0.47 ± 0.05	5.11 ± 1.20
Thalamus	0.69 ±0.14	4.85 ± 1.64	0.34 + 0.18	4.56 ± 1.85
Putamen	0.73 + 0.16	4.71 +0.84	0.38 ±0.13	4.49 ± 0.99
Caudate	0.71 ±0.09	4.49 ± 0.53	0.38 ± 0.07	4.28 ± 0.62
Pons	0.70 ± 0.08	4.09 ±0.51	0.33 ± 0.06	3.80 ±0.64
Temporal	0.62 ±0.08	3.73 ± 0.43	0.20 ±0.11	3.24 ± 0.62
Cingulate	0.52 + 0.10	3.61 ±0.38	0.20 ± 0.07	3.13 + 0.52
Frontal	0.55 ±0.12	3.58 ± 0.33	0.20 ± 0.05	3.05 ± 0.49
Parietal	0.57 + 0.18	3.60 ± 0.37	0.17 + 0.08	3.04 ± 0.57
Occipital	0.54 ±0.11	3.52 ± 0.42	0.18 ±0.08	2.96 ± 0.59
Cerebellum	0.46 + 0.07	3.42 + 0.30	0.15 + 0.06	2.82 ± 0.43
Midbrain/cerebellum	1.85	1.52	3.09	1.81

Uncorrected represents the parameter calculated from [¹¹C](+)McN5652 without correction for nonspecific binding. Corrected represents the parameter corrected for nonspecific binding, e.g. the difference of the identical parameters obtained with [¹¹C](+)McN5652 and [¹¹C](−)McN5652. Shown is also the midbrain/cerebellum ratio for each parameter.

Correlations between parameters of [¹¹C](+)McN5652 and [¹¹C](−)McN5652

There was a linear correlation between the parameters describing the uptake of the two enantiomers k₁ and f_max (r = 0.595 to 0.766), indicating comparable uptake of the two enantiomers. No such correlation could be found between the other noncompartmental and compartmental parameters of the two enantiomers, which is consistent with the differences in the kinetics of the two radioligands. Unexpectedly, the correlation between the radioactivities, measured 75 to 95 minutes after injection also was high (r = 0.796), indicating that the absolute radioactivity measured with PET was strongly determined by the uptake of the radioligands.

Correlations between the compartmental and noncompartmental models

The parameter k₁ of the compartmental models and f_max of the noncompartmental model describe the same process (i.e., uptake of radioligand into brain tissue). In fact, there was a strong correlation between the k₁ values obtained with the four compartmental models (0.953 to 0.997) as well as between the compartmental k₁ values and the noncompartmental f_max (0.905 to 0.940).

Parameter f_T describes radioligand retention at T = 75 minutes independent of any specific kinetic model. To compare parameters derived from the compartmental and noncompartmental models, f_max and f_T were used to calculate an apparent distribution volume of a first-order model. The correlation of the lnDV_noncomp with lnDV_t,3par was high (r = 0.927 for [¹¹C](+)McN5652; r = 0.917 for [¹¹C](−)McN5652).

Effect of k₁, and BV on f_T, (simulations)

There was a small effect of k₁ on f_rel, with a decrease of uncorrected f_rel with increasing k₁,. On the other hand, the corrected f_rel, showed a slight increase with increasing k₁. The difference between uncorrected and corrected f_rel values decreased with increasing k₁ (Fig. 5).

FIG. 5.

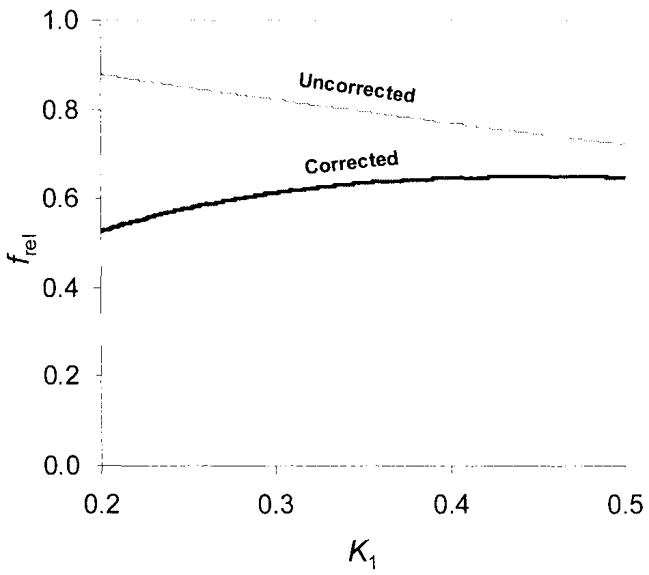
Computer simulation demonstrating the dependence of a computationally derived f_rel on k₁, in the hypothalamus. “Uncorrected” means f_rel not corrected for nonspecific binding. “Corrected” means f_rel, corrected for nonspecific binding.

DISCUSSION

Preliminary studies indicate the usefulness of the radioligand [¹¹C](+)McN5652 to study the integrity of the serotonergic system (Szabo et al., 1996; Ricaurte et al., 1996; Scheffel et al., 1996a,b). Understanding its kinetic properties is important to extend its application. The data presented here demonstrate that quantitative kinetic parameters can be derived for this radioligand that correlate with the density of SERT, an established marker of serotonin axon terminals. The binding of the radioligand is stereospecific, since the distribution of its pharmacologically inactive enantiomer [¹¹C](−)McN5652 does not correlate with the density of SERT. Two types of quantitative parameters emerge: parameters that describe the retention of the radioligand derived from a noncompartmental model (f_T and f_rel), and apparent tissue distribution volumes derived from compartmental models (DV).

Input function

Tissue radioactivity measured with [¹¹C](+)McN5652 without any mathematical analysis of the data does not appear to provide a reproducible estimate of the SERT. This probably results from the fact that the amount of activity in the brain at any time to a large degree depends on the delivery of the radioligand by way of circulation and its uptake into brain tissue by way of blood-brain barrier permeation. The importance of the input function is demonstrated by the substantial difference between the time-integrals of the arterial plasma activity curves of the two enantiomers of McN5652. The integral of the active enantiomer is smaller than the integral of the inactive one. This difference can be explained by faster metabolism of the active enantiomer or higher removal of the active radioligand because of a rapid binding to both peripheral and central SERT sites. Whichever the reason, the available amount of radioligand is significantly less for the active than the inactive enantiomer, underscoring the significant effect of extracerebral processes on the total radioactivity entering the brain and the importance of determining the input function as accurately as possible.

Compartmental parameters

Based on the ANOVA F values and the condition numbers, the most suitable compartmental model is the one that describes the kinetics of [¹¹C](+)McN5652 with the aid of one tissue compartment and three parameters (e.g., regional blood volume BV, radioligand uptake in tissue k_1,3par, and radioligand release from tissue k_2,3par). Although none of these parameters show a direct, positive correlation with the known density of the SERT in the human brain, the apparent distribution volume calculated from the ratio DV_t,3par = k₁/k₂ shows correlation. This correlation is improved after logarithmic transformation (lnDV_t,3par), particularly if the distribution volume of the [¹¹C](−)McN5652 enantiomer has been subtracted. When the logarithmic transform of the tissue distribution volumes obtained using any of the alternative compartmental models is compared with the density of SERT, the correlation remains significant and the intersubject parameter variance is acceptable for routine applications.

Accurate estimation of the distribution volume of nonspecific binding is difficult, but the high degree of reproducibility of this parameter measured with [¹¹C](−)McN5652 across brain regions and between subjects is remarkable (Table 3). This reproducibility makes [¹¹C](−)McN5652 more appropriate to correct for nonspecific binding if such a correction appears necessary. The overall effect of this correction on the distribution volumes, however, is minor, which is demonstrated by the fact that the midbrain to cerebellum ratio of the parameter lnDV_t,3par is increased only from 1.52 to 1.81.

TABLE 3.

Regional values (original and natural logarithm) of the apparent total tissue distribution volume DV_t,3par of [¹¹C](−)McN5652 (mean ± SD; n = 8)

	DVt,3par	InDVt,3par
Hypothalamus	15.29 ± 2.34	2.73 ± 0.85
Midbrain	14.47 ± 3.07	2.67 ± 1.12
Thalamus	17.34 ± 2.59	2.85 ± 0.95
Putamen	16.79 ± 2.09	2.82 ± 0.74
Caudate	15.87 ± 2.81	2.76 ± 1.03
Pons	13.86 ± 1.46	2.63 ± 0.38
Temporal	14.90 ± 1.78	2.70 ± 0.57
Cingulate	13.63 ± 1.72	2.61 ± 0.54
Frontal	14.20 ± 1.69	2.65 ± 0.53
Parietal	14.24 ± 1.81	2.66 ± 0.60
Occipital	13.73 ± 2.00	2.62 ± 0.69
Cerebellum	13.65 ± 1.80	2.61 ± 0.59

Noncompartmental model

The most established way of analyzing radioligand kinetics involves application of compartmental models. Unfortunately, compartmental modeling has many inherent problems that make derivation of reliable and reproducible physiologic parameters difficult. For example, according to the principles of compartmental modeling, a radioligand is distributed within virtual spaces called compartments, and its movement between the compartments is described by a set of compartmental rate constants. Relative to data sampling, mixing of the radioligand within each separable compartment of the system is assumed to be instantaneous (Anderson, 1983). However, instantaneous mixing is unlikely to occur in the brain, an organ composed of an infinite abundance of membranes and other molecular barriers. Surprisingly, both compartmental and noncompartmental analyses of time–activity curves result in impulse response functions, which are compatible with radioligand distribution within a finite, rather than infinite, number of compartments. Moreover, when quantitative parameters are derived from time–activity curves, some of them correlate with statistically coherent molecular interactions between the radioligand and its specific binding sites.

The second inherent problem of compartmental modeling is poor separability of compartmental responses. Compartments, even if they are well separated physiologically or anatomically, may be inseparable in the time–activity curves. Poor separation is caused by slow ligand distribution within and rapid ligand exchange between the compartments. This appears to be the case with [¹¹C](+)McN5652 and many other radioligands with potential clinical use.

In addition to the nonideal biokinetics of a radioligand, the inferior statistical properties of the PET measurements and uncertainties intrinsic to numerical computational techniques are additional factors resulting in derived kinetic parameters that are inaccurate and imprecise.

These problems of compartmental modeling call for exploration of alternative, noncompartmental kinetic models. The impulse response function method represents an approach to radioligand kinetic analysis that is based on a nondeterministic, stochastic kinetic model (Szabo et al., 1993). Classic parameters derived from the impulse response function have been tracer residence times and distribution volumes (Carson, 1996). Unfortunately, the slow release of [¹¹C](+)McN5652 from the brain precludes the calculation of these parameters. Alternative parameters such as f_max and f_T, as used here, describe radioligand uptake and retention in a simplified yet quantitative way, particularly when release of the radioligand is as uncomplicated as that of [¹¹C](+)McN5652.

The impulse response function provides a generalized, statistical representation of tracer kinetics. The here-proposed peak value of the impulse response function, f_max, represents the probability that a tracer molecule will enter the tissue ROI when presented in unit amount to the organ-feeding artery. Subsequent values of the impulse response function f(t) represent the probability that a tracer molecule entering the brain at the input (arterial) side will remain in the region of interest until the time point t. Since the f_max parameter of a highly lipophilic radioligand such as [¹¹C](+)McN5652 will be strongly influenced by regional CBF, it is conceivable that the normalized value f_rel = f_T/f_max will correlate better than f_T with the density of SERT determined in vitro. Figure 5 shows only a weak effect of radioligand uptake (k₁) on f_rel in brain areas rich in SERT.

In compartmental models, it is usual to assume that exchange of radioligand across the blood-brain barrier is relatively rapid in both directions and that the tissue distribution volume is of reasonable magnitude, which depends on regional CBF. The large distribution volume of the pharmacologically inactive enantiomer, [¹¹C](−)McN5652, however, demonstrates that it is not always the case and that binding to nonspecific binding sites may be a much stronger determinant of the apparent tissue distribution volume than blood flow. This concept is supported by the finding that the apparent tissue distribution volume of [¹¹C](−)McN5652 is relatively constant across brain regions, although these brain regions have significantly different regional blood flow values.

Regional impulse response functions are probability functions that depend only on the destiny of the radioligand within the particular brain region of interest. In contrast, actually measured time–activity curves represent convolution integrals of this probability distribution function with the arterial input function. The model order of the measured tissue time–activity curves is high because they comprise both the kinetics intrinsic to the brain and the kinetics because of extracerebral radioligand distribution, metabolism, recirculation, and binding. Deconvolution analysis eliminates all of these extracerebral effects, reduces model order, and permits focusing on the kinetic process of interest.

Data sampling, noise, and curve filtering may distort the first-pass peak of the impulse response function (f_max), a parameter that theoretically corresponds to regional blood flow. In the experiments presented here, f_max of both the active and inactive radioligand correlated with compartmental k₁. High lipophilicity and high extraction fraction of both enantiomers explain this correlation, since k₁ represents the product of regional blood flow and radioligand extraction fraction. There also was high correlation between the f_max values of the two enantiomers. This was expected, since both enantiomers were injected in a small mass, which made differences caused by pharmacodynamic effects on CBF and blood–brain barrier permeability unlikely.

The vascular peak of the impulse response function is followed by a slowly descending tissue component (Figs. 3 and 4). If radioligand retention follows the rules of a compartmental model, such a tissue component will be composed of one, two, or more exponential functions. The number of exponentials will represent the number of compartments or the model order, and the exponential rate constants will be identical to the macroparameters of the most applicable compartmental model. In compartmental modeling terminology the macroparameters or model-of-data parameters are arithmetically related to the compartmental rate constants, called microparameters or model-of-system parameters (DiStefano and Landaw, 1984). Knowing the number of components of the impulse response function aids in determining the model order; including more compartments than implied by the impulse response function ultimately leads to poor conditioning and an increase in parameter variance (Table 1).

With the matrix regularization technique used in this study, the effect of noise on the impulse response function was acceptable, and noise did not interfere with the recognition of the shape of the impulse response function. The noncompartmental impulse response function (Figs. 3 and 4), in accordance with statistical comparisons of the investigated compartmental models, indicates that for [¹¹C](+)McN5652 (and more so, for its pharmacologically inactive enantiomer [¹¹C](−)McN5652), only one tissue compartment can be identified. Of course, this single compartment is not clearly outlined physiologically and is composed of many inseparable virtual spaces, including those of specific and nonspecific binding. Hence DV_t is composed of apparent distribution volumes of both specific and nonspecific binding (Koeppe et al., 1994).

In addition to the parameter f_max, which describes radioligand uptake, two parameters were derived from the noncompartmental impulse response function to describe radioligand retention: f_T (T = 75 minutes) and f_rel. Using 75 minutes for determination of radioligand retention is arbitrary. For the current setup of experiments, the time interval of 70 to 80 minutes was used to calculate an average value of f_T because the impulse response function in this domain was unaffected by distorting oscillations caused by domain truncation of the tissue time-activity curve.

The retention parameter f_T corresponds to tissue activity free of recirculating radioligand. Determination of f_T and f_rel represents a practical way to quantify radioligand kinetics in the brain. The only, and probably most important computational step, deconvolution analysis, is performed in a straightforward fashion using fast Fourier transformation (Hunt, 1970; Hunt, 1972; Mitler et al, 1990). Application of f_T and f_rel in research studies is justified by their statistical robustness (Tables 1 and 2), by their correlation with the apparent compartmental distribution volumes, and, most importantly, by their correlation with the known density of SERT (Fig. 6). There is a tradeoff here as well. Computer simulation of the impulse response function indicates that the parameter f_rel depends on tissue uptake k₁, although this effect is not strong (Fig. 5). Also, the difference between f_rel parameters of the two enantiomers, used to account for nonspecific binding, depends on k₁ with a decreasing difference between unconnected f_rel and corrected f_rel with increasing k₁ (Fig. 5).

FIG. 6.

Correlation between the noncompartmental parameter Δf_rel and regional density of serotonin transporter (SERT) (A) and compartmental parameter lnΔDV (B) and regional density of SERT. Each point for each of the 12 brain regions represents an average obtained from eight subjects. The Δ symbol signifies the difference between [¹¹C](+)McN5652 and [¹¹C](−)McN5652 (correction for nonspecific binding).

Physiologic interpretation of the impulse response function

The noncompartmental and the compartmental models can be interrelated through the apparent tissue distribution volume of the radioligand (DV), since the area under the impulse response function is equivalent to DV. The following integral equation can be used to calculate DV (Lassen and Perl, 1979) of a radioligand from the measured time-activity curve y(t) and input function x(t):

$$DV=\frac{{\int }_0^{\infty }y(t)dt}{{\int }_0^{\infty }x(t)dt}$$ (10)

If the radioligand is delivered as a unit impulse δ(t), the time-activity curve y(t) becomes f(t); assuming identity of distribution volumes for any form of input function, the numerator of Equation 10 becomes the area under the impulse response function, and the denominator becomes unity. Thus, the time integral of the impulse response function is identical to DV. Yet, to calculate Equation 10, sampling would have to last much longer than the mean retention time of the radioligand, and proper integration still would require extrapolation of the impulse response function. When the impulse response function is monoexponential f(t) = k₁e^−k₂t, its area can be derived by Laplace transformation and is identical to k₁/k₂, that is, the DV calculated from the compartmental model. The apparent distribution volume depends both on k₁ and k₂; however, the parameter that is related to the regional binding of the radioligand is k₂. For [¹¹C](+)McN5652, the values of k₂ are small in areas rich in SERT, such as the caudate or midbrain. The variance of a small, near-zero k₂ in the denominator will result in a numerically unstable k₁/k₂ ratio. Indeed, DV demonstrated a variance unacceptable for routine use. The variance was improved by logarithmic transformation, lnDV, without loss of correlation with the density of SERT.

For many radioligands used for imaging receptors and transporters in the brain, a reference region void of specific binding is used to account for nonspecific binding. For such radioligands, specific binding can be assessed from the difference between the distribution volumes of the ROI and the reference region. Unfortunately, such a reference region does not exist for [¹¹C](+)McN5652. Even the cerebellum, which has the lowest concentration of SERT, contains too many of these binding sites to be used as a reference region. Thus, in this study, the compartmental distribution volume of the inactive enantiomer and the retention parameters of the noncompartmental impulse response function of the inactive enantiomer were used to assess nonspecific binding.

It is well known that both compartmental analysis and deconvolution analysis are numerically unstable operations. Because of the excellent curve fits perceived with compartment analysis, there has been a misconception that quantitative parameters derived from compartmental models are less sensitive to noise than those derived by deconvolution analysis. The small variance of both f₇₅ and f_rel demonstrates that this does not need to be the case. When the noncompartmental and compartmental parameters were compared with the density of SERT, the highest correlation at the lowest parameter variance was obtained with f_rel.

Which of the kinetic parameters is best suited for routine applications? Without knowing the alterations of these parameters in subjects with a diminished density of SERT, this is difficult to predict. Based on the data presented here, there are two candidate parameters: a noncompartmental parameter f_rel and a compartmental parameter lnDV_t,3par. They both demonstrate good correlation with the density of SERT at acceptable variance. Yet, their bias is high because of nonspecific binding. This bias can be reduced by using the inactive enantiomer [¹¹C](−)McN5652 and by calculating the corrected parameters Δf_T, Δf_rel, and lnΔDV. By doing so, variance is not augmented significantly; however, study expense and patient inconvenience are increased.

If the goal is to estimate the “absolute” loss of the SERT, the use of both enantiomers of [¹¹C]McN5652 and correction for nonspecific binding should be considered. On the other hand, to answer the questions whether SERT is reduced in a disease at all, granted that reductions are large enough to be observed, or whether certain clinical manifestations of 5-HT deficiency (i.e., aggression, impulsiveness, depression, anxiety) correlate with SERT losses, using the pharmacologically active enantiomer [¹¹C](+)McN5652 alone could be considered.

The impulse response function represents a curve measured after rapid intraarterial injection at no recirculation. Such experiments have been performed in primates (Buck et al.,1996) and have resulted in brain time-activity curves similar to the impulse response functions in humans, presented in this work. The main advantage of direct intraarterial injection is elimination of the effects of extracerebral radioligand kinetics on the tissue response function. Another advantage is improved counting statistics because of a higher amount of radioactivity reaching the brain. Deconvolution analysis, on the other hand, is better suited for human studies, since it avoids the need for intracarotid injection. Since there is no method for calibration, radioligand uptake cannot be assessed after intraarterial injection, yet it can be estimated after intravenous injection both with the compartmental parameter k₁ or the noncompartmental parameter f_max.

Further validation of [¹¹C]McN5652 and the noncompartmental and compartmental parameters used to analyze the data require experiments that incorporate interventions affecting both the availability of SERT and the delivery of the radioligand to specific binding sites. Reduced SERT availability occurs in animals and humans previously exposed to serotonin-specific neurotoxins. An effective model for SERT reduction is exposure to amphetamine derivatives, such as methylene-dioxy-metamphetamine (MDMA) and fenfluramine which have specific affinity for the SERT. Animal models with altered CBF could be designed to measure the effects of CBF on radioligand kinetics. In human subjects with neurodegenerative or cerebrovascular diseases, measuring CBF and assessing its effect on the kinetic parameters of [¹¹C](+)McN5652 would be helpful to differentiate the effects of reduced radioligand binding from reduced delivery.

CONCLUSION

The impulse response function of [¹¹C](+)McN5652 can be calculated both by deconvolution analysis and compartmental modeling. Deconvolution analysis resembles intraarterial tracer injection and provides simple kinetic parameters, which describe radioligand uptake and retention.

In the healthy subjects investigated in this study, noncompartmental radioligand retention parameters correlated with the known density of SERT and offered a variance acceptable for clinical applications. Compartmental analysis provided an apparent distribution volume of the radioligand, which also correlated with the known density of SERT and had acceptable variance after logarithmic transformation. Based on multiple statistical criteria, the most applicable compartmental model for [¹¹C](+)McN5652 consisted of a single tissue compartment with three parameters, BV, k_1,3par, and k_2,3par, and an apparent tissue distribution volume computed as DV_t,3par = k_1,3par/k_2,3par.

Both the noncompartmental retention parameters and the compartmental distribution volumes can be corrected for nonspecific binding by subtracting the corresponding parameter measured with the pharmacologically inactive enantiomer [¹¹C](−)McN5652, but such a correction may not be needed to test every scientific hypothesis. Further validation of the kinetic parameters of [¹¹C](+)McN5652 is warranted and should include assessment of the effects of altered CBF and altered SERT availability.

Abbreviations used

PET

positron emission tomography

SERT

serotonin transporter

kinetic model

McN5652