Pharmacogenetics and anti-arrhythmic drug therapy: a theoretical investigation

Abstract

Pharmacological management of cardiac arrhythmias has been a long and widely sought goal. One of the difficulties in treating arrhythmia stems, in part, from incomplete understanding of the mechanisms of drug block and how intrinsic properties of channel gating affect drug access, binding affinity, and unblock. In the last decade, a plethora of genetic information has revealed that genetics may play a critical role in determining arrhythmia susceptibility and in efficacy of pharmacological therapy. In this context, we present a theoretical approach for investigating effects of drug-channel interaction. We use as an example open-channel or inactivated-channel block by the local anesthetics mexiletine and lidocaine, respectively, of normal and ΔKPQ mutant Na⁺ channels associated with the long-QT syndrome type 3. Results show how kinetic properties of channel gating, which are affected by mutations, are important determinants of drug efficacy. Investigations of Na⁺ channel blockade are conducted at multiple scales (single channel and macroscopic current) and, importantly, during the cardiac action potential (AP). Our findings suggest that channel mean open time is a primary determinant of open state blocker efficacy. Channels that remain in the open state longer, such as the ΔKPQ mutant channels in the abnormal burst mode, are blocked preferentially by low mexiletine concentrations. AP simulations confirm that a low dose of mexiletine can remove early afterdepolarizations and restore normal repolarization without affecting the AP upstroke. The simulations also suggest that inactivation state block by lidocaine is less effective in restoring normal repolarization and adversely suppresses peak Na⁺ current.

Existing ion channel blocking drugs have failed to prove effective in managing cardiac arrhythmias, and drugs that have undergone testing in large randomized and placebo controlled studies have not been proven to reduce mortality (21, 49, 54a, 58, 62). These poor outcomes exist in part because the majority of antiarrhythmic drugs were developed when little was known about the molecular and physiochemical basis of drug-receptor interactions. However, since the advent of gene cloning, a wealth of information has been gathered regarding the processes of drug binding and how factors such as drug structure and charge affect interaction with the target ion channel. These new concepts have also been tested within the framework of the modulated receptor hypothesis, which derives from the concept of conformational dependence of the binding affinity of allosteric enzymes and was first proposed by Hille to describe interaction of local anesthetic molecules with Na⁺ channels (23, 27, 28, 30, 36, 37, 61). The idea is that the drug binding affinity is determined, and modulated by, the conformational state of the channel (closed, open, or inactactivated). Moreover, once bound, a drug alters the gating kinetics of the channel.

As a result, understanding the basis for drug-receptor interactions is much more comprehensive (7, 23, 36, 37, 43, 44, 55, 61, 63, 65–68). These findings have occurred concomitantly with the realization and identification of the genetic origins of, or increased predisposition to, some forms of arrhythmia, including drug-induced arrhythmia (1, 10, 11, 15, 35, 52, 53, 72). Improvement in the understanding of drug-channel interactions in the context of genotype-phenotype relationships may set the stage for a new era of “genetic medicine,” where pharmacological agents can be developed to treat patients based on individual genotypic profiles (51).

Cardiac Na⁺ channels as therapeutic targets

Block of cardiac Na⁺ channels for the intended management of cardiac arrhythmia has been widely used (46, 48, 71). Despite the prospective therapeutic value of the inherent voltage- and use-dependent properties of channel block by these drugs in the treatment of tachyarrhythmias, it is precisely these complex effects that have led to unpredictable and unforeseen toxic side effects, most notably arrhythmia induction (47, 70).

The presence of polymorphisms and mutations in the drug target can also influence outcomes (36, 37). Nonetheless, defective channels suggest themselves as prime targets for disease-specific and perhaps even mutation-specific pharmacological interventions (37). Here, we aim to test the feasibility of such an approach within a computational framework that allows not only the testing of effects of pharmacological intervention on ion channels under various conditions but also the emergent effects of block on the cellular action potential (AP). An absolute requirement for testing the effects of pharmacological intervention on voltage-gated cardiac ion channels via computational methods is the development of sufficiently detailed models that recapitulate all of the basic features of channel gating (31–33, 57). At this stage, the models that we propose here will likely be mostly useful for predicting drug effects on normal tissue or in the presence of a single mutation or polymorphism. In the future, these models might be expanded for use in simulated tissue with variable genetic background or in tissue with simulated ischemia or infarction.

Accurate models for drug testing

To date, the majority of cellular AP models have used Hodgkin-Huxley (29)-type models as a paradigm to represent currents. However, this framework is insufficient to reproduce even basic features of voltage-gated channels, in part, because the Hodgkin-Huxley formalism presumes independence between kinetic transitions (33, 56). Representation of coupling between discrete structural states (i.e., via activation and inactivation transitions) is required to reproduce complex gating behaviors that will affect whole cell activity.

We have previously formulated Markovian-based models of normal and mutant cardiac Na⁺ channels encoded by Na_V1.5, which represent discrete structural states and their interactions (16–20). The models have been repeatedly validated and improved as new experimentally obtained data have become available (17–20). The models are now able to accurately simulate single channel properties such as latency to first opening, distribution of mean open times, voltage dependence of mean open times, distribution of channel closed times, and gating behavior of single channels. Macroscopic current properties are also accurately reproduced, including current-voltage relations, voltage dependence of activation and availability, and time and voltage dependence of channel recovery from inactivation. These accurate channel models can be used to investigate state-specific binding of drugs to the channels within the complex integrative cell.

The development of theoretical structurally based models of ion channels reflects advancements in our understanding of channel gating. Since most data are collected outside of the physiological cellular environment, the model provides a tool for integrating single-channel properties into the cell and for simulating physiological conditions that cannot be maintained during experiments (e.g., dynamic ion concentration changes and current interactions during the AP). Using models, we can relate the integrated electrophysiological behavior of the cell to state-specific, single-channel events (17). This is important, because it is difficult to predict the effect of a mutation or drug intervention that alters a single voltage-dependent transition of an ion channel, or even more complex, multiple discrete transitions, on the whole cell behavior due to multiple complex interactions within the cellular environment. Even more challenging is to foresee how a drug interacting with a mutant channel might affect cellular dynamics. The present study presents a theoretical framework for testing the interactions of pharmacological agents with normal and mutant cardiac Na⁺ channels and for predicting the cellular response to bridge this gap. We use, as an example, a cardiac Na⁺ channel mutation ΔKPQ that is associated with the long-QT syndrome (LQT3), ventricular arrhythmias and sudden cardiac death (7), and block of the channel by the local anesthetics mexiletine and lidocaine.

MATERIALS AND METHODS

Simulation of single channel gating

Stochastic properties of individual channels can be simulated as follows: Consider a simplified two-state model C↔O, (C, closed; O, open) where the rate constant for the forward transition (C to O) is aa and the rate for the reverse transition (O to C) is bb. At time t = 0, the channel resides in the C state; the probability that the channel will move to the O state is determined by

$$e^{-(aa)\text{T}}=r,$$ (1)

where r is a random number between 0 and 1. When time = T, then the channel will make a transition. Similarly, the transition from O→C is determined by

$$e^{-(bb)\text{T}}=r.$$ (2)

The random number is generated by the computer function that is seeded by the internal clock, thereby ensuring that the sequence of random number generation is distinct each time.

Simulation of Na⁺ channel block by drugs

For open-state block, assume a two-state model with the two states O (open) and B (blocked), O→B, where the rate constant for the forward transition (O to B) is on and the rate for the reverse transition is off. The on rate of the drug is assumed to be limited by diffusion (1 × 10⁸ M⁻¹s⁻¹) and is given by [D] · 1 × 10⁵ ms⁻¹ (65), where [D] is the drug concentration. The off rate is K_d · 1 × 10⁵ ms⁻¹ and is assumed the same for each state that can bind the drug. The K_d for mexiletine, which binds to the open state is 2.5 μM (65). The same approach is applied to inactivated state block by lidocaine. The K_d for lidocaine is 4.0 μM (34).

Simulation of Markov macroscopic current

Whole cell current densities are described by

$$I_{\text{s}}=G_{\text{s}}\cdot {\text{PO}}_{\text{s}}\cdot (V_{\text{m}}-E_{\text{rev}}),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where\hspace{0.17em}}{G}_{\text{s}}=\hspace{0.17em}\{\cdot \hspace{0.17em}{g}_{\text{s}}$$ (3)

PO_s is the sum of all open probabilities of the channel, V_m is the membrane potential, and E_rev is the reversal potential of the channel. G_s is the maximum membrane conductance for the stimulus current (I_s), and is equal to the product of the channel density { times the unitary channel conductance g_s. A Markovian scheme is used to describe the gating kinetics of the Na⁺ channels and to compute the open probabilities (17, 18). In this scheme, discrete channel states (i.e., open, closed, inactivated) are represented explicitly. Each state is coupled to other states by transition rates that depend on the membrane potential.

The change in channel state probability is described by a first-order differential equation. When N discrete channel states is assumed, then the probability of the channel residing in a particular state P_i at any time satisfies the following:

$$\text{d}{P}_i/\text{d}t=\sum _{j=1}^N[k_{ji}\cdot P_j(t,V_{\text{m}})]-\sum _{j=1}^N[k_{ij}\cdot P_i(t,V_{\text{m}})]$$ (4)

for i = 1,2, . . . . , N−1; i ≠ j, and ${\sum }_{i=1}^N{P}_i=1$, the voltage (V_m)-dependent rate constants (k_ij) describe the transition from state i to state j. Initial conditions are obtained by finding values for state probabilities from the steady-state equation

$$\text{d}{P}_i/\text{d}t=0$$ (5)

When it is assumed that the probability in each state i at time t_n is

$$P1(t_n),P2(t_n),\dots PN(t_n)$$

then at t_n + 1 = t_n + Δt

$$P_i(t_n+1)=P_i(t_n)+\mathrm{\Delta }{P}_i$$ (6)

P_i is calculated in Eq. 6 at each time step. Picard iterates are computed by a second-order Runge-Kutta procedure to obtain the dynamic values of P_i. The steady-state probability obtained from Eq. 5 is used for P_i(t₀).

Simulation of the cardiac ventricular AP

We use the Luo-Rudy (LRd) model of the cardiac AP for simulations of cellular level behavior (39). The formulation is based on a numerical reconstruction of the AP using the following differential equation that describes the rate of change of the V_m:

$$\text{d}{V}_{\text{m}}/\text{d}t=-(1/C_{\text{m}})(I_{\text{ion}}+I_{\text{st}})$$ (7)

where C_m is the membrane capacitance, I_st is a stimulus current, and I_ion is the sum of all the ionic currents through the membrane. In the model, I_ion includes currents carried through voltage-gated channels, pumps, and exchangers:

$$\begin{array}{l}{I}_{\text{ion}}=I_{\text{Na}}+I_{\text{Ca}(\text{L})}+I_{\text{Ca}(\text{T})}+I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{K}1}+I_{\text{Kp}}\\ +I_{\text{NaK}}+I_{\text{NaCa}}+I_{\text{p}(\text{Ca})}+I_{\text{Nab}}+I_{\text{Cab}}\end{array}$$ (8)

The currents are the following: I_Na, fast sodium current; I_Ca(L), calcium current through L-type channels; I_ca(T), calcium current through T-type channels; I_Kr, fast component of the delayed rectifier potassium current; I_Ks, slow component of the delayed rectifier potassium current; I_K1, inward rectifier potassium current; I_Kp, plateau potassium current; I_NaK, sodium-potassium pump current; I_NaCa, sodium-calcium exchange current; I_P(Ca), calcium pump in the sarcolemma; I_Na,b, sodium background current; and I_Ca,b, calcium back-ground current (22, 38). All the ionic currents are computed as current densities for 1 μF of cell membrane capacitance. Specific membrane capacity is set to 1 μF/cm². The formulation is based on data adjusted to 37°C. The LRd model accounts for dynamic changes of ionic concentrations of Na⁺, K⁺, and Ca²⁺ during the AP. The rate of change of ionic concentration is given by:

$$\text{d}{[\text{B}]}_i/\text{d}t=-(I_{\text{B}}\cdot A_{\text{cap}})/(V_{\text{c}}\cdot Z_{\text{B}}\cdot F)$$ (9)

where [B] is the concentration of ion B, I_B is the sum of the currents carried by B, A_cap is the capacitive membrane area, V_C is the volume of the compartment where B is updated, Z_B is the valence of the ion, and F is Faraday’s constant. The model accounts for handling of intracellular Ca²⁺ by the sarcoplasmic reticulum and by Ca²⁺ buffers, including troponin, calmodulin, and calsequestrin. Details of the LRd model can be found in Refs. 22 and 38 and in the Research Section of http://rudylab.wustl.edu.

RESULTS

In this study, we have expanded on a previously developed Markovian model of the cardiac Na⁺ channel Na_V1.5 (18) to include additional model states that represent state-specific binding sites for the local anesthetic molecules mexiletine and lidocaine. We assume that mexiletine binds only to open states and lidocaine only to fast-inactivated states of the Na⁺ channel. We investigate the gating of wild-type (WT) and Long-QT associated ΔKPQ mutant channels during open and inactivated channel block and their effects on channel and whole cell current during the AP. In doing so, we gain unexpected insights into important characteristics of channel block. These theoretical findings suggest potential experimental directions in exploring channel-gating kinetics and efficacy of local anesthetic interactions with cardiac Na⁺ channels.

The Markov model of Na_V1.5 I_Na with incorporated drug binding states is shown in Fig. 1. The model framework is shown in Fig. 1A, left, for open state block (e.g., by mexiletine) of the normal or “wild-type (WT)” cardiac Na⁺ channels. In WT channels, drug block is represented with a single drug-binding site to represent open state block (Fig. 1A, left, green block state adjacent to O). The ΔKPQ mutant channel and its block via open channel binding is shown in Fig. 1B, left, and consists of a background gating mode (top nine states in black) similar to WT and an additional gating mode [burst mode shown as the lower 4 states in red (17, 18)], with two discrete possible drug-binding sites to the open states (green block and red block).

Fig. 1.

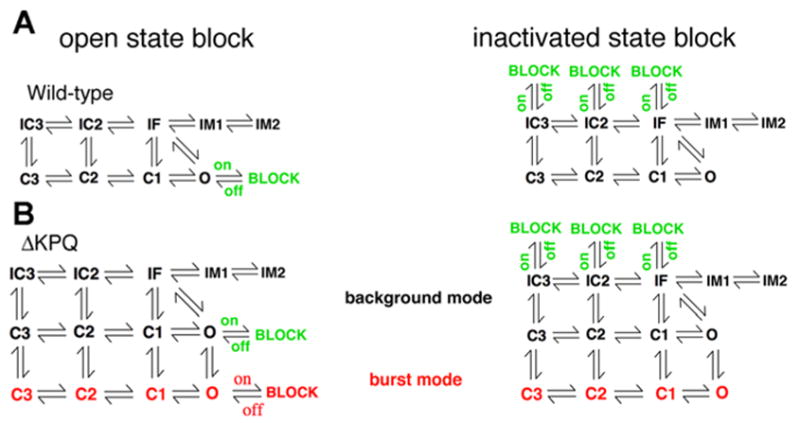
Naturally occurring mutations (or polymorphisms) in cardiac ion channels can lead to complex drug effects and reduced predictability of drug action. A schematic example depicting open-state drug binding in the Markov model framework for open channel block (A, left) of a wild-type (WT) Na⁺ channel with a single drug-binding site (BLOCK state in green adjacent to O). Inactivated state block of WT channels is also shown (A, right). The ΔKPQ mutant channel (B) contains a background gating mode (top 9 states in black) similar to WT and an additional gating mode (burst mode shown as the lower 4 states in red), with 2 discrete possible open channel blocker drug-binding sites (green BLOCK and red BLOCK shown in B, left). Inactivated state block of the ΔKPQ mutant channel is in B, right.

In Fig. 1 [right, A (WT) and B (ΔKPQ mutant)], inactivated state block (e.g., by lidocaine) is represented as block of fast closed inactivated states (from IC3 → BLOCK and IC2 → BLOCK) and as block of the fast inactivation state that the channel enters subsequent to channel opening (IF → BLOCK). Experimental data are consistent with this scheme, because lidocaine block induces a leftward shift in the steady-state availability curve (36).

We have shown in several previous studies that the Markov channel model scheme of Fig. 1 is sufficient to accurately simulate experimentally measured kinetic properties of WT and ΔKPQ mutant cardiac Na⁺ channels (17–19) in the absence of drugs. Briefly, the background or normal gating mode has nine discrete states consisting of three closed states (C3, C2, C1), a conducting open state (O), a fast inactivation state (IF), and two intermediate inactivation states (IM1 and IM2), the latter three of which are required to reproduce the complex fast and slow features of recovery from inactivation. Channel closed state inactivation is achieved via the inclusion of two closed-inactivation states (IC2 and IC3). The burst mode in the ΔKPQ model represents a small population of channels that fail to inactivate because of the mutation. The transitions between the background and burst modes are not explicitly voltage dependent, rather they represent the probability of a channel that can inactivate (i.e., in the upper background mode) switching to a mode where it fails to inactivate (i.e., in the lower burst mode). This type of modal gating has been observed and quantified experimentally (8, 12, 19).

We first used the Markov model to investigate the dose-dependent reduction of wild-type and mutant (ΔKPQ) cardiac Na⁺ channel peak macroscopic current resulting from open channel block by mexiletine or inactivated state block by lidocaine, shown in Fig. 2, A and B, respectively. Simulated cells were held at −100 mV until steady state was reached (no change in computed parameters) and subjected to depolarization to the indicated test potential for 100 ms. The peak current values for WT (Fig. 2, left) and ΔKPQ (Fig. 2, right) mutant channels at each test potential were calculated and used to construct the peak current voltage relations, shown in the absence (no drug) and presence of a range of mexiletine or lidocaine concentrations (no drug, 10.0 μM, 100.0 μM, and 1.0 mM) as indicated. Interestingly, the simulation results reveal little differences in the relative reduction of macroscopic current by open state block in simulated cells containing WT and ΔKPQ mutant channels. However, subsequent simulations suggest that these results may not tell the whole story and that study of open channel block of cardiac Na⁺ channels requires more detailed investigation to reveal true efficacy.

Fig. 2.

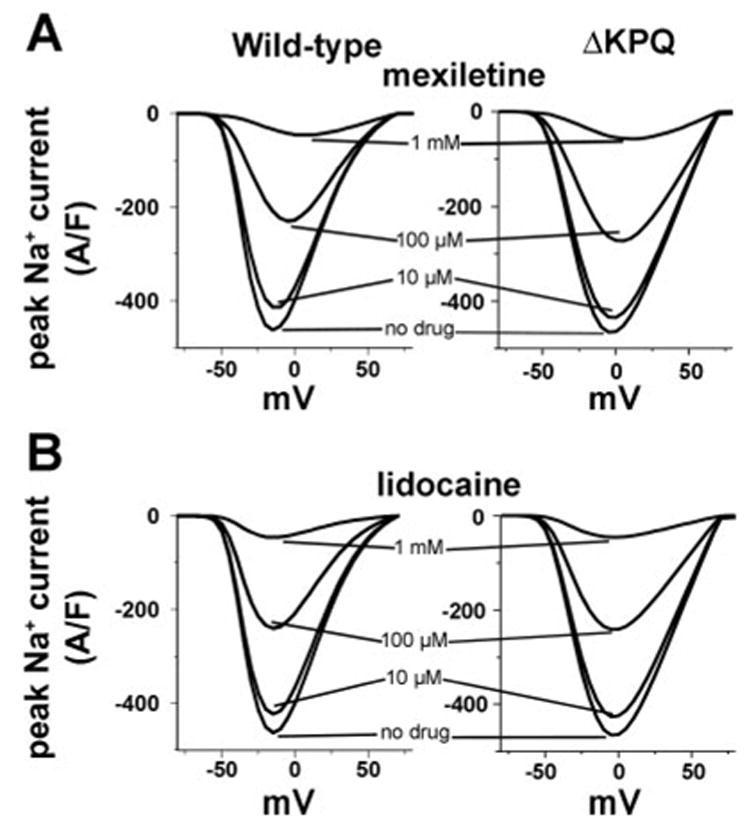
Effect of open channel and inactivated state block on peak currents. The dose-dependent reduction of WT and mutant (ΔKPQ) cardiac Na⁺ channel peak macroscopic current by open and inactivated channel block by mexiletine and lidocaine, respectively. A: current voltage relations are shown in the absence (no drug) and presence of a range of mexiletine concentrations (10.0 μM, 100.0 μM, and 1 mM) as indicated. The relative reduction of macroscopic current appears comparable, erroneously suggesting similar affinity of WT and mutant channels to block by mexiletine. B: steady-state effect of lidocaine-inactivated state block on peak currents is shown for WT and ΔKPQ mutant channels (left and right, respectively).

The lidocaine simulations (Fig. 2B) suggest that inactivated state binding blocks WT and ΔKPQ mutant channels equally well and that the extent of block is similar to that observed with open state block by mexiletine as shown in Fig. 2A. Interestingly, this effect is observed because the simulations are performed under steady-state conditions.

Even though the steady-state effects of block by mexiletine and lidocaine appear comparable, the mechanisms of channel block are different. Under conditions of open state block by mexiletine, channels must open before the drug has access to the binding site. Hence, the reduction in current observed with increasing drug concentration occurs because the probability of drug binding increases dramatically with increased drug concentration as open channels rapidly enter a drug-bound state. The peak current is reduced due to the rapid block of channels in the open state. Inactivation state block by lidocaine occurs by a completely different mechanism. The dependence of block by lidocaine on drug concentration looks similar to that observed with mexiletine because channels are “incubated” with lidocaine at the holding potential until steady-state equilibrium is reached before depolarization. Hence, channels that undergo closed-state inactivation are increasingly likely to enter a drug-bound state as the drug concentration increases. Because the probability of closed-state inactivation, even at the −100-mV holding potential, is not zero, the long duration required for the system to reach steady state permits more closed-state inactivation and therefore opportunity for drug binding to occur.

In Fig. 3, we show the results of simulating the effects of mexiletine block of single cardiac Na⁺ channels and the apparent relationship between channel mean open time and efficacy of block. For WT channels, the mean open time is relatively short (0.18 ms) as shown in Fig. 3A, left. A low-dose drug application has a minimal effect on the observed single channel behavior (compare Fig. 3A, middle with right). However, the drug affects ΔKPQ mutant channels differently from WT channels. The mutation results in two types of abnormal gating. In Fig. 3B, mutant channels in the background mode (top black states in the gating model shown in Fig. 1B) in the absence of open more frequently than WT (Fig. 3B, middle), but like WT have short mean open times (0.12 ms) (Fig. 3B, left). Application of a low dose of mexiletine has little effect (Fig. 3B, right). In contrast, ΔKPQ mutant channels in the burst mode, characterized by long channel open times (1.2 ms) (Fig. 3C, left) are effectively blocked by a low dose of drug (compare Fig. 3C, middle with right). Block by mexiletine can only occur from the channel open state, therefore, we reasoned that block may be increased by an increase in the number of channel openings (i.e., frequency of reopening) and/or by the amount of time that the channel stays open (reflected in the channel mean open time). In fact, these simulations suggest that the channel open time is more important. An increased number of openings [compare mutant channels in the background mode (Fig. 3B, center) that open more frequently than WT channels (Fig. 3A, center)] does not increase the propensity of the channels to block (compare Fig. 3B with Fig. 3A). However, channel mean open time is an important determinant of block (Fig. 3C). For a channel in the open state, there are several transition options. The open channel can inactivate (O → IF transition), deactivate (O → C1 transition), or become blocked by entering the block state (O → BLOCK transition). The probability of each of these transitions is determined by their relative transition rates. The open time of the channel is determined by 1/(sum of the transition rates out of the open state), so a single (relatively) fast transition will dominate the other possible transitions. In this case, fast voltage-dependent inactivation that is present in WT channels and in ΔKPQ channels in the background gating mode is much faster than the blocking rate because the drug concentration is low. However, for ΔKPQ channels in the burst mode, the fast inactivation transition is absent and the block rate is faster than the deactivation transition. Hence, the block transition becomes dominant. Mean open time will clearly not affect efficacy of block by lidocaine, because the drug does not bind to open channels.

Fig. 3.

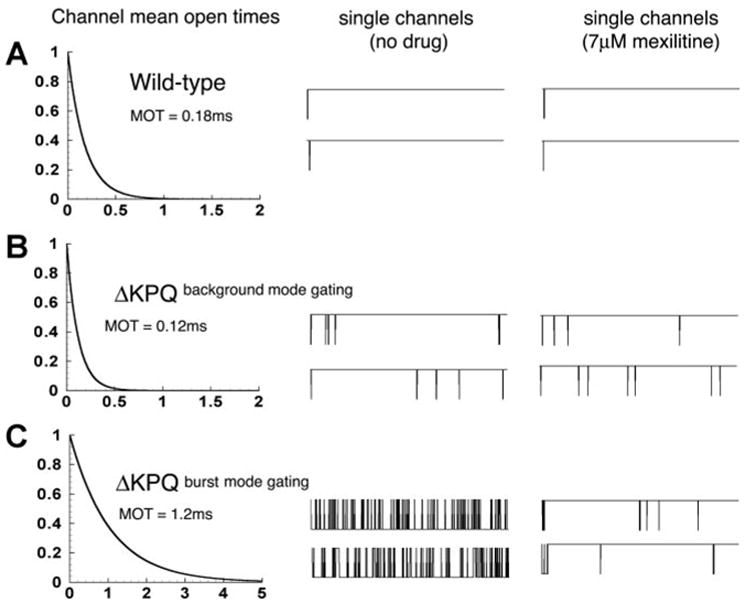
Mexiletine block of single cardiac Na⁺ channels and the relationship between channel mean open time and efficacy of block. A, left: for WT channels, the mean open time is relatively short (0.18 ms). There is little observed effect of a low-dose drug application on single channel behavior (compare A, middle with right). The ΔKPQ mutation results in two types of abnormal gating. B: mutant channels in the background mode (center) open more frequently than WT, but like WT, have short mean open times (0.12 ms) (left). Application of a low dose of mexiletine has little effect (right). In contrast, ΔKPQ mutant channels in the burst mode, characterized by long channel open times (1.2 ms) (C, left) are effectively blocked by a low dose of drug (compare C, center with right).

Figure 4A shows the steady-state channel availability curves for WT and ΔKPQ in the absence and presence of lidocaine as indicated. Availability curves show normalized peak current plotted after a long (sufficient to allow for steady state where the derivatives of the simulated channel state probabilities are zero) prepulse to the indicated test potential. The ΔKPQ mutation alone does not cause a significant shift in channel availability compared with WT, which is consistent with experimental findings (4, 12). However, in the presence of lidocaine, which binds to inactivated channels, the availability curve exhibits a characteristic leftward shift, a phenomenon also observed experimentally (36). In the presence of 10 μM lidocaine, the WT and mutant curves are shifted by −9 mV and in the presence of 100 μM, the shift is −24 mV.

Fig. 4.

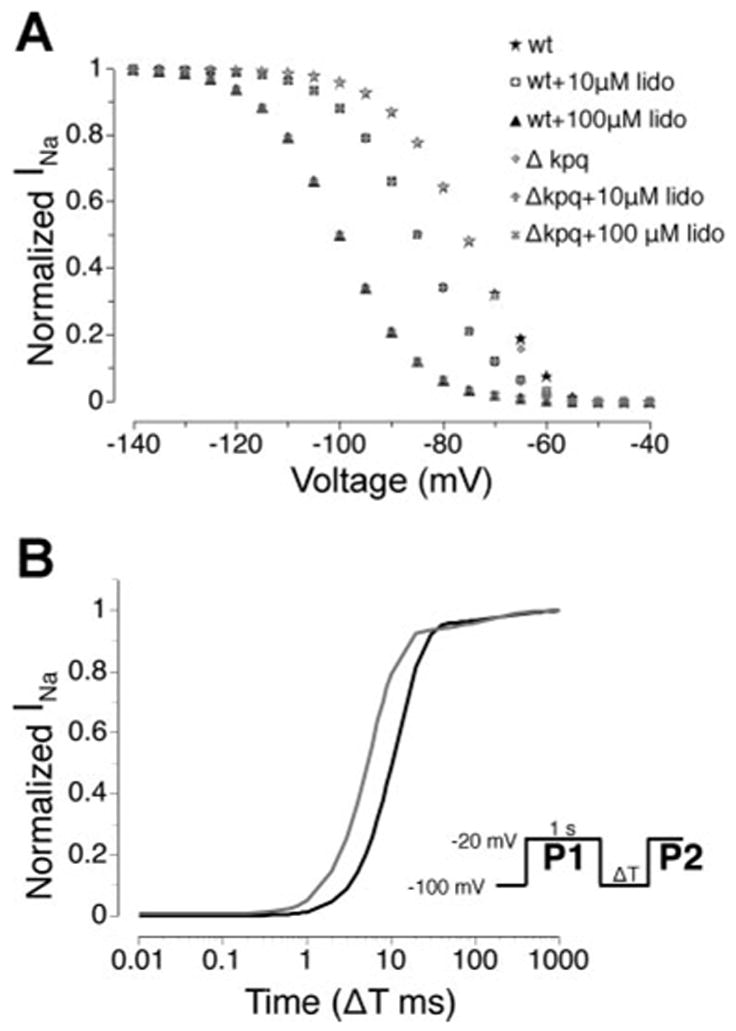
Lidocaine reduces channel availability. A: steady-state channel availability curves for WT and ΔKPQ in the absence and presence of lidocaine. Availability curves reflect the relative reduction of peak current at −20 mV following a long (sufficient to allow for steady state where the derivatives of the simulated channel state probabilities are zero) prepulse to the test potential. The ΔKPQ mutation alone does not cause a significant shift in channel availability compared with WT. Lidocaine shifts the availability curve leftward. For 10 μM lidocaine, the WT and mutant curves are shifted by −9 mV and in the presence of 100 μM lidocaine the shift is −24 mV. B: simulated time course of recovery from inactivation for WT (black) and ΔKPQ (gray) channels (protocol shown as inset). The ratio of peak macroscopic Na⁺ current (I_Na) during a test pulse (P2) to peak current during the conditioning pulse (P1) is shown for WT and ΔKPQ channels. The leftward shift of the ΔKPQ recovery curve relative to WT indicates faster recovery from inactivation, as observed experimentally.

Figure 4B compares the simulated time course of recovery from inactivation for WT (black) and ΔKPQ (gray) channels (protocol shown as inset). The ratio of peak macroscopic I_Na during a test pulse (P2) to peak current during the conditioning pulse (P1) is shown for WT and ΔKPQ channels. The leftward shift of the ΔKPQ recovery curve relative to WT indicates faster recovery from inactivation. These simulated results are consistent with the experimentally observed values published previously (4, 12). In an earlier study, we examined various aspects of model behavior but did not specifically examine the kinetics of recovery from inactivation for ΔKPQ channels (17). We include these simulation results as additional validation of the model to reproduce channel properties that likely influence drug interactions.

Previously published studies have shown that the primary hallmark of the ΔKPQ mutation, a persistent noninactivating current, is rate dependent (17, 19). When subjected to a series of depolarizing pulses, the interpulse interval (or recovery interval) affects the amplitude of late current observed during subsequent depolarization. The shorter the recovery period, the more rate-dependent reduction in the late current is observed. This is an important observation, because it provides an explanation for the slow heart rate (bradycardia) dependence of LQT3 phenotypes (arrhythmias occur during sleep or relaxation at slow heart rates) (50). Moreover, a number of studies investigating ion channel block have shown that drug block may also be rate- or so-called use dependent (36, 37). However, these studies suggest that drugs block channels more effectively at fast rates. In the case of ΔKPQ an ideal blocker would also be effective at slow rates to preempt the onset of the tachyarrhythmia, which presumably occurs as the result of propagating triggered activity in a substrate with increased dispersion of repolarization. As a result, we investigated the effects of rate on open state block of ΔKPQ mutant Na⁺ channels. The results, shown in Fig. 5, suggest that open state block (Fig. 5A) by mexiletine completely normalizes arrhythmogenic ΔKPQ late current and that the effect on late current is independent of interpulse interval (i.e., pacing rate). Shown in Fig. 5A is the current elicited in response to a train of 20 depolarizing pulses at short (Fig. 5A, top, depolarizing pulse to −10 mV from −100 mV for 500 ms with 20-ms recovery intervals) and long (Fig. 5A, bottom, pulse to −10 mV from −100 mV for 500 ms with 1,000-ms recovery intervals) recovery intervals.

Fig. 5.

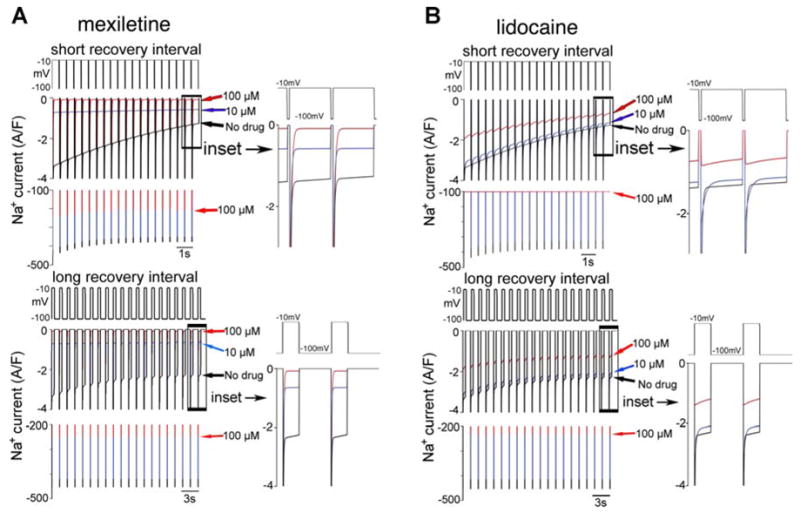
Unlike lidocaine (B), mexiletine (A) preferentially blocks ΔKPQ late current and does so independently of pacing frequency. Whereas the amplitude of late current resulting from the ΔKPQ mutation exhibits rate-dependent changes, application of relatively low doses of mexiletine completely removes rate dependence and preferentially reduces the late current, whereas lidocaine appears to preferentially block the peak current. Shown is the I_Na elicited in response to a train of 20 depolarizing pulses with short recovery intervals (top, depolarizing pulse to −10 mV from −100 mV for 500 ms with 20-ms recovery intervals) and long recovery intervals (bottom, pulse to −10 mV from −100 mV for 500 ms with 1,000-ms recovery intervals). Arrows indicate the late current amplitude at the 20th pulse for control [no drug, (black), 10 μM (blue), and 100 μM (red) drug concentrations]. Additional red arrow (bottom in each panel) indicates peak current amplitude for 100 μM drug concentration. Insets show a magnified time course of current elicited during the last two pulses. In each panel, top trace shows the pacing protocol, middle trace shows I_Na on a scale that emphasizes the late current, and the bottom trace emphasizes the peak current on a larger scale. Note that 100 μM mexiletine completely blocks the late current but not the peak current. Like with mexiletine, at all concentrations of lidocaine (B: no drug, 10 μM, and 100μM), the peak currents recorded at slow rates with long recovery intervals (top) are larger than at fast rates with short recovery intervals (bottom). However, at a high concentration (100 μM) of lidocaine during rapid pacing the peak current was ablated (top, red lines). At both fast and slow pacing frequencies in the presence of low or high lidocaine concentrations, lidocaine fails to reduce the late component of current by more than 50%. Rather, the simulations suggest that lidocaine preferentially reduces peak current.

In contrast to the effects of open state block, inactivated state block by lidocaine does not preferentially reduce late current, as shown in Fig. 5B. Rather, during rapid pacing (Fig. 5B, top), a high concentration of lidocaine (100 μM, red line) abolishes the peak current after the first depolarization. This occurs because the drug binds to channel inactivation states and prevents the channels from recovering from inactivation during the repolarizing inter-pulse interval. When the drug concentration is sufficiently high, very few channels can recover from drug block and do not recover from inactivation. The current that remains is due to channels that are trapped in the burst mode and fail to inactivate. These channels do not have opportunity to enter a drug bound state. During slower pacing with longer recovery intervals (Fig. 5B, bottom) there is sufficient time for channels to recover from drug block and inactivation between depolarizing pulses. Hence, the effect of lidocaine during slow pacing appears minimal. The drug also does not cause a substantial reduction in the late current resulting from the mutation, suggesting limited capacity for correcting the LQT disease phenotype.

In Fig. 6A, summary data are shown at indicated levels of mexiletine for peak currents recorded after 20 applied pulses with short or long recovery intervals (corresponding to “fast” and “slow” pacing, respectively) using the protocols described for Fig. 5. At all concentrations of mexiletine (no drug, 10 μM, and 100 μM), the peak currents recorded at slow rates with long recovery intervals (solid bars) are larger than at fast rates with short recovery intervals (shaded bars). This is an expected result, because long recovery intervals during slow pacing permit complete recovery of Na⁺ channels from inactivation, allowing for full repriming of I_Na between depolarizing pulses. However, the ratio of slow to fast paced peak currents (indicated above the bar graphs for each concentration) is unchanged, regardless of the mexiletine concentration. This suggests that the drug reduced the peak current amplitudes equally, regardless of pacing frequency. Moreover, a relatively low concentration (10 μM) had very little effect on the peak current amplitude (Fig. 6A, middle), and a high concentration (100 μM) was required to substantially reduce the peak current (Fig. 6A, right). Interestingly, the effect of mexiletine on ΔKPQ late current was different from its effect on peak current. As shown in Fig. 6B, in the absence of drug application (left bars), the amplitude of persistent (late) current resulting from the ΔKPQ mutation at the end of the twentieth depolarization at the slow rate (solid bar) is more than double that observed at the fast rate (shaded bar), indicated by the slow-to-fast ratio = 1.81. This is not surprising and has been explored in detail in other publications (19). However, in the presence of low drug concentration (10 μM mexiletine in the middle panel), the rate-dependent differences are completely abolished. These findings are important for two reasons: 1) The open channel blocker works effectively, independently of rate and will effectively reduce the larger late current observed at slow rates where arrhythmias occur, and 2) the late current is reduced substantially at concentrations that have little effect on peak Na⁺ current (Fig. 6A, middle), which is essential for normal AP depolarization and conduction.

Fig. 6.

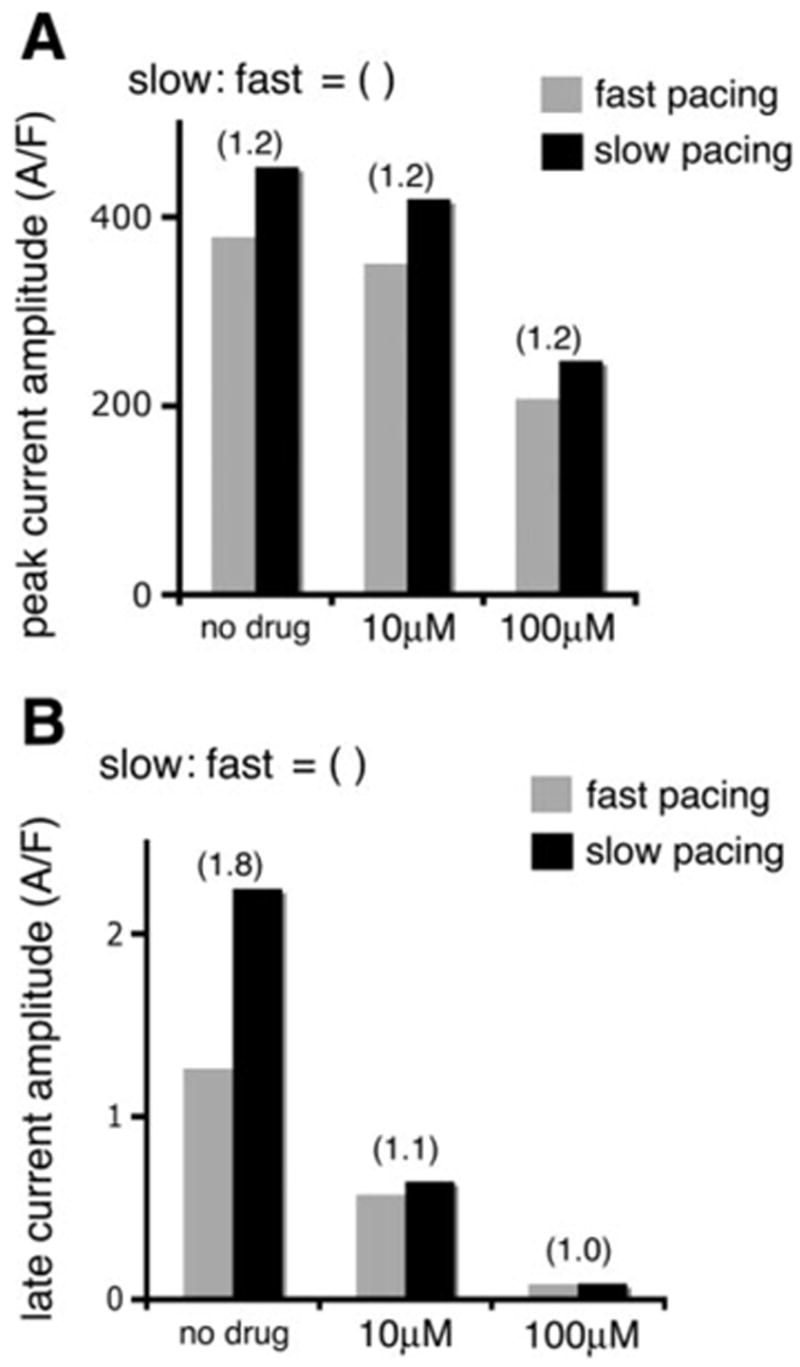
Mexiletine differentially affects the two components (peak vs. late) of ΔKPQ current. Summary data are shown at indicated levels of mexiletine for peak currents from ΔKPQ mutant channels (A) recorded after 20 applied pulses with short or long recovery intervals (“fast” and “slow” pacing, respectively) using the protocols described for Fig. 5. At all concentrations of mexiletine (no drug, 10 μM, and 100 μM), the peak currents recorded at slow rates with long recovery intervals (solid bars) are larger by a factor of 1.2 than at fast rates with short recovery intervals (shaded bars). A low concentration of mexiletine (10 μM) had very little effect on the peak current amplitude (center) and a high concentration (100 μM) was required to substantially reduce the peak current (right). B: in the absence of drug application (left), the amplitude of ΔKPQ late current at the end of the 20th depolarization pulse at the slow rate (solid bar) is almost double that observed at the fast rate (shaded bar), indicated by the slow-to-fast amplitude ratio = 1.8. In the presence of low drug concentration (10 μM mexiletine, middle), the rate-dependent differences are completely abolished and the ΔKPQ late current at a slow rate is greatly and preferentially reduced. At a higher concentration (100 μM mexiletine, right), the late current is fully suppressed at fast and slow pacing rates.

Finally, we investigate the effects of simulated application of mexiletine and lidocaine on the cardiac ventricular AP in the presence of the ΔKPQ Long-QT mutation. These results are shown in Fig. 7. The simulated cells were paced for 10 beats at a cycle length of 1,000 ms from rest (at steady state) and the tenth AP is shown. In the absence of any drug intervention, the cell with mutant Na⁺ channels displays characteristic arrhythmogenic early afterdepolarizations (Fig. 7A). With increasing titration of the Na⁺ channel blocker mexiletine, albeit at low doses, preferential block of late Na⁺ current results in AP shortening (Fig. 7B) and ultimately, at a relatively low dose, a normal AP morphology and duration (Fig. 7C). In contrast, at the higher concentration of lidocaine, the abnormal cellular phenotype persists, while peak current is greatly reduced, suggesting that lidocaine may be less useful as a therapeutic agent for treating LQT-3.

Fig. 7.

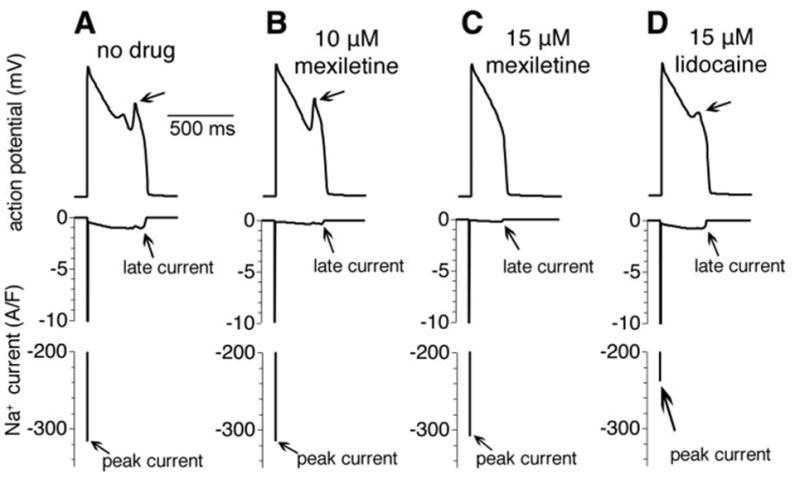
Simulated effects of mexiletine and lidocaine on the cardiac ventricular action potential (AP) in the presence of the ΔKPQ Long-QT mutation. In the absence of any drug intervention, the cell with mutant Na⁺ channels displays characteristic arrhythmogenic early afterdepolarizations (EADs) (A). With increasing titration of the Na⁺ channel blocker mexiletine, preferential block of late I_Na results in AP shortening (10 μM) (B), and ultimately, at a relatively low dose (15 μM), EADs are abolished and the AP morphology and duration are normalized without any significant effect on peak I_Na (C). In the presence of 15 μM lidocaine, the EAD persists and peak current is significantly reduced, which may affect conduction velocity (D).

DISCUSSION

In this study we demonstrate the first necessary step toward developing a theoretical framework for testing the interactions of pharmacological agents with both normal and mutant cardiac Na⁺ channels. We apply this approach to the cardiac Na⁺ channel using recent experimental observations (7, 19, 36, 37, 63, 65). The importance of such a tool is clear, given that a specific pharmacological intervention can result in profoundly diverse outcomes among individuals (15, 35, 53). Whereas there are a number of possible explanations for variability of drug response, recent work has suggested a major role for distinct genetic backgrounds in determining pathways and outcomes of drug action (36, 37). The nascent field of pharmacogenetics aims in part to determine how gene defects may alter the efficacy of pharmacological therapeutic interventions.

In the past decade a wealth of genetic information has revealed that a number of cardiac arrhythmia syndromes are causally linked to mutations in genes encoding cardiac ion channels (3, 6, 15, 60). The discovery of the link between genes and disease has led to a large number of genetic, basic science, and clinical science studies that have focused on improved understanding of the mechanistic basis of these diseases (2, 15, 52). Dozens of mutations have been identified in the gene SCN5A, which encodes the α-subunit of the cardiac Na⁺ channel, and have been causally linked to a wide spectrum of cardiac arrhythmic disorders, including Long-QT syndrome type 3 (LQT3), Brugada Syndrome (BrS), cardiac conduction disease (CCD), sick sinus syndrome (SSS), or a combination of these syndromes (8, 9, 14, 15, 25, 54, 59).

LQT3, manifests as prolongation of the QT interval on the ECG and predisposes the patients to polymorphic ventricular tachycardia (torsade de pointes). It is shown to result from “gain-of-function” mutations in SCN5A, such as the deletion of three residues in the III-IV linker of the channel protein (ΔKPQ) (8) and mutations in the COOH-terminus (20, 45, 69). These mutations evoke a small, persistent current during the AP plateau that delays AP repolarization.

There are multiple recent examples of the importance of pharmacogenetic considerations in drug therapy. For example, the recent discovery of a common polymorphism present in 13% of African Americans that predisposes carriers to drug-induced arrhythmia (53). In addition, other studies have shown that Na⁺ channel blockade by flecainide can reduce QT prolongation in carriers of some Na⁺ channel-linked LQT3 mutations (24, 41, 42). However, the same drug treatment can evoke ST-segment elevation, a hallmark of the BrS, in patients with a predisposition to the disease (41). Thus in the case of LQT3, flecainide has potential therapeutic application, whereas for BrS it has proven useful as a diagnostic tool (24, 41). Interestingly, in some cases, flecainide has been reported to provoke BrS symptoms (ST-segment elevation) in patients harboring LQT3 mutations (24, 40, 41). Furthermore, flecainide preferentially blocks certain LQT3- or BrS-linked mutant Na⁺ channels (1, 26, 36, 61).

Here we use a virtual transgenic cell to examine the effects of the Na⁺ channel open-state blocker mexiletine and the inactivation-state blocker lidocaine on LQT3-associated ΔKPQ mutant channels as a “proof of concept” and to suggest experimental testing in vitro and in transgenic animals harboring mutations. We show that our simulation study suggests that mexiletine, or other open-state blockers, preferentially reduce the arrhythmogenic-persistent current that is the hallmark of LQT3 mutations in cardiac Na⁺ channels. Moreover, this preferential block is achieved at low doses of the drug that have little effect on the large transient peak currents that underlie the AP upstroke and permit conduction of excitable impulses throughout the myocardium. These simulations suggest that the increase in channel mean open time is the determinant parameter for dose-dependent efficacy. This is evidenced by the fact that the repeated reopenings observed for mutant channels in the background-gating mode that have short open times are not preferentially blocked, whereas channels in the burst mode, characterized by long open times, are preferentially blocked. This preferential block in the burst mode occurs because block is so much faster than the channel deactivation transition but is absent in the background mode because fast voltage-dependent inactivation that is present in this mode occurs before the drug accessing the binding site. Because the channel open time is determined by the expression, 1/(sum of the transition rates out of the open state), a single fast transition will dominate the other possible transitions. As the drug concentration is substantially increased, the likelihood of block increases due to increased probability of drug interaction with the receptor. Our simulations also suggest that drugs that preferentially bind to inactivated channels (e.g., lidocaine) may not be useful in treating LQT-3-linked arrhythmia syndromes.

This study demonstrates the importance of consideration of the modulated receptor hypothesis in prediction of drug action. The modulated receptor hypothesis (23, 27, 28, 30, 36, 37, 61) suggests that the drug-binding affinity is determined, and modulated by, the conformational state of the channel (closed, open, or inactivated). Moreover, once bound, a drug alters the gating kinetics of the channel. Our results show an interesting differential effect of state-specific drug binding and modulation of the channel (Figs. 5 and 6) on late Na⁺ current versus peak current. At a low concentration, mexiletine has no appreciable effect on peak Na⁺ current but a significant effect on the late current, which is generated by the burst mode. Lidocaine has much less effect on late current at any concentration tested but reduces peak current substantially at higher concentrations. As indicated in Fig. 6, in the absence of drug, the amplitude of persistent current during slow pacing is larger than at fast rates (17, 19). However, in the presence of even low mexiletine concentration, the late current at slow rates is preferentially reduced by open-state block, and the rate dependence is completely abolished, which is not the case for inactivated-state block by lidocaine. This is because at slow rates more channels recover from inactivation to closed states in the background mode, from which they can transit to the burst mode. In the burst mode, the channels reside longer in the open state due to the failure of the channels to inactivate. This promotes drug binding to the open channel, which can only occur in the open state, and reduces the likelihood of binding to inactivated channels. This property suggests that an open channel blocker with the simulated characteristics will preferentially reduce the larger late currents observed at slow rates where arrhythmias occur. Hence, the channel behavior in the presence of the drug (rate-independent late current magnitude) is fundamentally different from that in the absence of drug, demonstrating that binding of the drug alters the gating kinetics of the channel.

Whereas our study does not explicitly consider the charge on the drug, the voltage dependence of mexiletine is nonetheless accounted for. Because the drug requires channel opening to reach the binding site in the pore, it will have reduced access particularly at low voltages where the probability of channel opening is low. The drug will have reduced affinity at very positive voltages, too, since the channels, despite high probability for opening, will remain in the open state for a very short time before they rapidly undergo fast voltage-dependent inactivation, thereby reducing the probability of drug interaction.

Our results suggest that low doses of mexiletine will effectively normalize AP duration at slow heart rates in the presence of the Long-QT-associated ΔKPQ mutation, whereas application of lidocaine will not. Moreover, the model suggests that the effective dose of mexiletine required to reverse the Long-QT phenotype has minimal effects on peak current, and therefore on the AP upstroke velocity, a primary determinant of conduction velocity. Lidocaine, on the other hand, causes large reduction of peak current. The results presented here point to Na⁺ channel open state block as a genotype-driven potential therapeutic target. We suggest that testing of these findings in ΔKPQ transgenic animals might constitute a next reasonable step towards the development of genotype-specific interventions for genetic arrhythmia syndromes.