An Exact Sampling Formula for the Wright–Fisher Model and a Solution to a Conjecture About the Finite-Island Model

Abstract

An exact sampling formula for a Wright–Fisher population of fixed size N under the infinitely many neutral alleles model is deduced. This extends the Ewens formula for the configuration of a random sample to the case where the sample is drawn from a population of small size, that is, without the usual large-N and small-mutation-rate assumption. The formula is used to prove a conjecture ascertaining the validity of a diffusion approximation for the frequency of a mutant-type allele under weak selection in segregation with a wild-type allele in the limit finite-island model, namely, a population that is subdivided into a finite number of demes of size N and that receives an expected fraction m of migrants from a common migrant pool each generation, as the number of demes goes to infinity. This is done by applying the formula to the migrant ancestors of a single deme and sampling their types at random. The proof of the conjecture confirms an analogy between the island model and a random-mating population, but with a different timescale that has implications for estimation procedures.

WAKELEY (2003) has provided a theoretical framework for statistical inference about mutation, selection, and divergence time made from molecular data at unlinked nucleotide sites as in Sawyer and Hartl (1992) but in the case of a population subdivided into many subpopulations or demes. Assuming an island model of migration (Wright 1931; Moran 1959) but with a finite number of finite demes, it has been argued that the frequency of a mutant allele segregating with a wild-type allele at the same locus in the whole population should be governed in the limit of a large number of demes by a diffusion process that is identical to the standard diffusion approximation used for a panmictic population (see, e.g., Ewens 2004, Chap. 4), with the exception that it occurs on a longer timescale.

More precisely, consider a haploid population subdivided into D demes with N individuals in each deme and suppose discrete, nonoverlapping generations. At the beginning of each generation, every individual in every deme produces the same large number of offspring, which then disperse independently and randomly among all the demes with probability m (0 < m ≤ 1) or stay in their original deme with probability 1 − m. In other words, m is the fraction of offspring in each deme that come from a deme chosen at random. Two alleles at a single locus are segregating in the population, a mutant allele A and a wild-type allele B, and viability selection takes place among the offspring within each deme (what is known as soft selection) such that the mutant type has fitness 1 + γ/(ND) compared to 1 for the wild type. The population structure is restored before the beginning of the next generation by sampling N survivors within each deme according to a classical Wright–Fisher model (Fisher 1930; Wright 1931). The frequency of A in all the demes is then described by a multidimensional discrete-time Markov chain. The same chain is obtained in the case of a diploid population with gametic migration followed by random union of gametes and additive selection.

Measuring time in units of ND/(1 − F) generations, where F is the fixation index given by

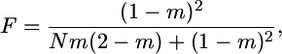(1)

it has been shown that the frequency of A in the whole population in the limit as D goes to infinity should be described by a diffusion continuous-time process on the interval [0, 1] having drift and diffusion coefficients given by

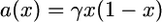(2)

and

(3)

respectively. This is exactly what is obtained for a panmictic population of size ND with ND generations taken as unit of time (see, e.g., Ewens 2004, Chap. 5). Therefore, in the limit of a large D, the only difference between the two models is the timescale, the unit of time in the island model being longer by a factor 1/(1 − F). Note that the parameter F represents the probability under neutrality and assuming a large number of demes that the lineages of two individuals chosen at random in the same deme coalesce backward in time before one of them migrates to another deme.

The limit diffusion for the island model results from a separation of timescales as in Ethier and Nagylaki (1980), drift within demes occurring on a faster timescale than drift between demes and selection pressure. Moreover, a rigorous proof relies on the following assumption:

Conjecture (Wakeley 2003): If ν = (ν₀, ν₁, …, ν_N) is the probability distribution satisfying

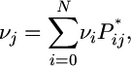(4)

where

(5)

and x represents the frequency of A in the current generation, then there exist some coefficients r₁, …, r_N such that from one generation to the next

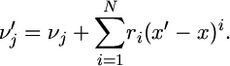(6)

Moreover, these coefficients may depend on N, j, m, and x.

It has been noted that the conjecture is true when ν is approximated with a hypergeometric distribution exhibiting the same mean and variance; namely,

(7)

where

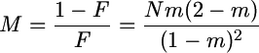(8)

and

(9)

with Γ(a + 1) = aΓ(a) for a > 0 (see, e.g., Feller 1968, p. 66, for properties of the gamma function). Such an approximation can be justified by exchangeability properties (Rothman et al. 1974). The accuracy of the approximation has been illustrated by numerical calculations for a deme of size as small as 10 (see Wakeley 2003 for more details). Moreover, numerical simulations in the case of a large deme size have shown little discrepancy with the stochastic dynamics predicted from the diffusion approximation (Cherry and Wakeley 2003). This is consistent with analytical results for a large deme size with Nm kept constant, in which case both Nν and approach the density of a beta distribution evaluated at y = j/N; namely,

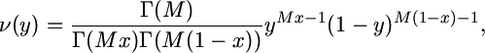(10)

where M takes its limit value 2Nm (see, e.g., Moran 1962, Chap. 6). This distribution corresponds to the stationary distribution in a deme of large size that receives an expected fraction m of migrants each generation from an infinite population, possibly subdivided into an infinite number of demes, in which the frequencies of A and B are kept constant and equal to x and 1 − x, respectively (Wright 1931).

On the other hand, the hypergeometric distribution where

(11)

is the solution of the system of equations

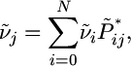(12)

where

(13)

(14)

(15)

and otherwise. This distribution comes into play when a Moran-type model (Moran 1958) is used for reproduction, one individual at a time being replaced with an offspring of an individual either in the same deme with probability 1 − m or in the entire population with probability m (Wakeley and Takahashi 2004). This is also the distribution of allele types in an island population of size N generated by a birth-and-death process with immigration (BDI) from a large mainland population in which the frequencies of alleles A and B are x and 1 − x, respectively, if M is defined as the ratio of the immigration rate over the individual birth rate (Rannala 1996).

In the case of infinitely many alleles in the mainland population of a BDI process (Joyce and Tavaré 1987; Tavaré 1989), the distribution of allele types in an island or a subpopulation is related to the Ewens sampling formula. This formula gives the likelihood of the configuration of alleles at a single locus in a small sample drawn at random from a large population assuming that every mutation leads to a novel type. It was conjectured by Ewens (1972) from the stationary frequency spectrum based on a diffusion approximation and proved formally by induction by Karlin and McGregor (1972). The formula holds in the limit of a wide range of exchangeable models, including the Wright–Fisher model and the Moran model, and is a basic tool for estimating the mutation rate and testing neutrality (see, e.g., Ewens 1990). An analogy with a Polya urn model has been pointed out (Hoppe 1984, 1987). The formula has been proved by a simple combinatorial argument (Griffiths and Lessard 2005) based on the coalescent approach as the population size goes to infinity (Kingman 1982).

The Ewens sampling formula or any related asymptotic formula cannot be used, however, to get the distribution ν since the deme size is fixed and finite. What is needed is an exact formula for the neutral Wright–Fisher model. More precisely, the distribution ν that is to be determined corresponds to the stationary distribution in a Wright–Fisher population of fixed size N that receives an expected fraction m of migrants each generation from an infinite population in which the frequencies of A and B are kept constant and equal to x and 1 − x, respectively. Equivalently, this is the stationary distribution in a Wright–Fisher population in which mutation occurs with probability m per gene per generation and leads either to an allele A with probability x or to an allele B with probability 1 − x.

In this note, the stationary distribution ν is obtained from an exact sampling formula for the Wright–Fisher model under infinitely many alleles mutation that is deduced in the next section (see Fu 2006 for a study of the exact coalescent in this model without mutation). The proof of the conjecture and some concluding remarks follow.

EXACT SAMPLING FORMULA FOR THE NEUTRAL WRIGHT–FISHER INFINITELY MANY ALLELES MODEL

We consider the neutral Wright–Fisher model for a population of N genes at a single locus with discrete, nonoverlapping generations and a probability of mutation to a novel allelic type u per gene per generation. We are interested in the probability of having k different types, labeled arbitrarily from 1 to k and represented n₁,…, n_k times, respectively, in a sample of 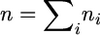genes drawn at random without replacement in a given generation (say, generation g₀). The sample size satisfies 1 ≤ n ≤ N.

Let us assign the labeled types to the sampled genes. There are

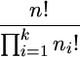(16)

possibilities. The probability of the sample configuration is obtained by reconstructing the history of the sample genes.

Backward in time, the sampled genes are lost by mutation or coalescence. We consider first only the generations with such mutation or coalescence events that define ordered steps of gene loss backward in time. Let step t correspond to generation g_t for t = 1,…, T, where T represents the total number of steps. We introduce the notation r_i,t for the number of genes of type i remaining at the beginning of step t. This number decreases from n_i to 1 as t increases from 1 to t_i, this step corresponding to the loss of type i by mutation, so that 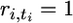and r_i,t = 0 for all t > t_i. Moreover, define the total number of genes remaining at the beginning of step t, and m_t, the number of mutation events occurring at step t, that is, the number of i such that t_i = t. (See Table 1.)

TABLE 1.

Notation and inequalities for the numbers of genes of the different types (i = 1,…, k) at the beginning of the successive steps of gene loss (t = 1,…, T)

1

…

t

t + 1

…

ti

ti + 1

…

T

n1

…

r1,t

≥

r1,t+1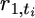

…

≥

…

r1,T

≥

0

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

ni

…

ri,t

≥

ri,t+1

…

1

>

0

…

0

=

0

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

·

nk

…

rk,t

≥

rk,t+1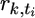

…

≥

…

rk,T

≥

0

n

…

rt

>

rt+1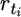

…

>

…

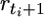rT

>

0

The number of mutations at step t, represented by m_t, is the number of types i such that r_i,t = 1 and r_i,t+1 = 0 and satisfies .

Then, assuming that the parent of each gene in any given generation is a gene chosen at random in the previous generation independently of all others, step t as defined from the numbers of genes of each type remaining at the beginning of steps t and t + 1, that is, r_i,t+1 for all i given r_i,t for all i with 0 ≤ r_i,t+1 ≤ r_i,t for all i following at least one, and possibly multiple, mutation or coalescence events (see Figure 1 for an example), has probability

(17)

where N^[r] = N(N − 1) … (N − r + 1), while S_rs represents the number of ways that r distinct elements can be partitioned into s nonvoid subsets. This is a Stirling number of the second kind given by the formula

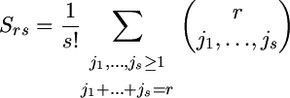(18)

(see, e.g., Abramowitz and Stegun 1965). Note that, in Equation 17, we use the equalities N^[0] = 1 and S₀₀ = S₁₀ = 1.

Figure 1.—

Example of types 1, 2, 3, 4, 5 represented 3, 1, 2, 1, 4 times at step t and 1, 0, 2, 0, 3 times at step t + 1 as a result of mutation events, represented by dots, and coalescence events. Note that the coalescence event between the gene of type 4, prior to the mutation event, and one of the genes of type 5 has no effect on the sample configuration.

Considering all steps of gene loss from 1 to T = max{t₁, … , t_k} and using the identity 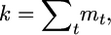we get the probability

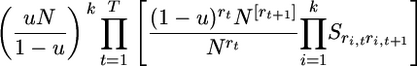(19)

On the other hand, the probability of neither mutation nor coalescence in all intermediate generations separating the generations of gene loss is

(20)

which reduces to

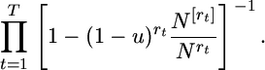(21)

Multiplying (16) with (19) and (21) and dividing by k!, which is the number of ways that the mutant types can be labeled, the probability of the sample configuration for the labeled types, denoted by p(n; n₁, … , n_k), is found to be

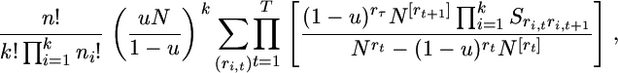(22)

where 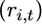is an array of nonnegative integers satisfying r_i,t ≥ r_i,t+1 for i = 1,…, k and t ≥ 1 with r_i,1 = n_i and 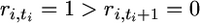for some t_i for all i and 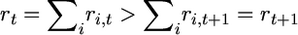as long as r_t ≥ 1, which occurs for t = 1, … , T.

PROOF OF THE CONJECTURE

Suppose a neutral Wright–Fisher model for a population of N genes at a single locus without mutation but in which each gene in each generation, with probability m and independently of all others, comes from a large surrounding population where two alleles A and B are segregating and maintained at equilibrium frequencies x and 1 − x, respectively. In the population of size N, it is as if a mutation event to a novel type would occur with probability u = m per gene per generation and that the novel type would be either in class A with probability x or in class B with the complementary probability 1 − x.

In the Wright–Fisher population at stationarity, the number of genes in class A can be expressed as

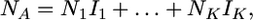(23)

where K is the number of types in the population, N₁, … , N_K are the numbers of times that these types once labeled from 1 to K are represented in the population, and I₁,…, I_K are independent random variables that take the value 1 with probability x and 0 otherwise. Given that K = k, the numbers N₁,…, N_k are exchangeable random variables and the sum I₁ + … + I_k follows a binomial distribution with parameters k and x. Therefore, the probability of having j genes in class A in the Wright–Fisher population at stationarity is

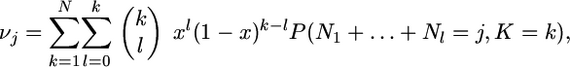(24)

where, using the sampling formula of the previous section for the whole population (n = N), we have

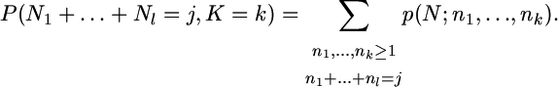(25)

We conclude that

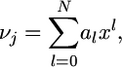(26)

where the coefficients a₀, a₁,…, a_N depend on m, j, and N.

Let us write

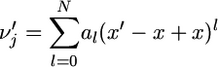(27)

for the probability of having j genes in class A in the Wright–Fisher population at stationarity when the frequency of A in the surrounding population is x′ different from x. Then, the binomial formula

(28)

and a rearrangement of terms yield the expression

(29)

where

(30)

This coefficient for i = 1, … , N depends on N, j, m, and x and the stated conjecture is established.

CONCLUDING REMARKS

The proof of the conjecture relies on the fact that the probability of having a given number of genes in class A in a haploid Wright–Fisher population of size N with a backward migration probability of m per individual per generation is a polynomial of degree N with respect to the frequency of A among migrants that is kept constant. Note that the proof does not require an exact expression for p(N; n₁,…, n_k), which represents the probability for the population at stationarity to have k migrant ancestors labeled from 1 to k and having n₁, … , n_k descendants, respectively. However, the analogy with an infinitely many alleles mutation model with a mutation rate u = m per gene per generation and the importance of sampling formulas for drawing inferences about genetic and demographic parameters make of interest such an expression for any sample size n, in which case the probability is represented by p(n; n₁, … , n_k). The number of terms to sum up to compute this probability corresponds to the number of ways that the sampled genes can be lost backward in time by mutation or coalescence and this number increases rapidly with the sample size. Unless the population size N is large, all these terms have to be considered.

If we let N go to infinity and u to zero and keep θ = 2Nu constant, then only the arrays for the gene losses with r_τ+1 = r_τ − 1 for τ = 1,…, n will contribute to the probability of the sample configuration since

(31)

There are 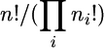such arrays with r_i,τ+1 = r_i,τ − 1 for one and only one type i, denoted by i_τ, for each τ = 1, … , n. Then, using the identity S_r,r−1 = r(r − 1)/2 for r ≥ 2 and S_1,0 = 1, we find that the probability is the same for each array and that the probability for all arrays is

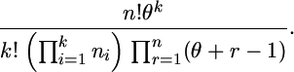(32)

This is the Ewens sampling formula for labeled types (Ewens 1972; Karlin and Mcgregor 1972; see Ewens 2004, Section 3.6, for more details on its deduction from a diffusion approximation, and Griffiths and Lessard 2005, for a combinatorial proof based on a coalescent approximation).

The difference between the exact sampling formula for a fixed population size and a fixed mutation rate and the large-N, small-u approximation comes mainly from the occurrence of simultaneous mutation or coalescence events that cannot be neglected in the general case. This is particularly relevant when N corresponds to a deme size in a subdivided population, which can be quite small (<10), and u to a migration rate from one deme to any other, which can be very high (>10⁻¹).

The exact formula has been deduced by considering all generations backward in time and unconditional transition probabilities for the sample configuration from one generation to the previous one. An alternative approach would be to consider only the generations with a change by mutation or coalescence and conditional transition probabilities given such a change, but this approach would be equivalent and not simpler.