Abstract
The shrinkage estimate of a quantitative trait locus (QTL) effect is the posterior mean of the QTL effect when a normal prior distribution is assigned to the QTL. This note gives the derivation of the shrinkage estimate under the multivariate linear model. An important lemma regarding the posterior mean of a normal likelihood combined with a normal prior is introduced. The lemma is then used to derive the Bayesian shrinkage estimates of the QTL effects.
THE Bayesian shrinkage estimation of quantitative trait locus (QTL) effects was first introduced by Xu (2003) and later formalized by Wang et al. (2005). The multivariate version of the shrinkage estimation of QTL effects was recently developed by Yang and Xu (2007). The main purpose of the shrinkage estimation is to avoid variable selection for mapping multiple QTL. Once a normal prior distribution for each regression coefficient is incorporated into the QTL mapping program, the method can handle substantially more QTL effects than the classical maximum-likelihood (ML) method. In addition, the shrinkage method produces much clearer signals of QTL on the genome than the ML method. As a result, shrinkage mapping appears to have pointed to a new direction for future research in QTL mapping.
The key issue of shrinkage estimation is the normal prior distribution assigned to the regression coefficient (QTL effect). More importantly, different regression coefficients are assigned different normal priors. Because the variances in the prior distributions determine the degrees of shrinkage, assigning different prior variances to different regression coefficients allows the method to differentially shrink regression coefficients. A smaller prior variance will cause the regression coefficient to shrink more while a larger prior variance will lead to less shrinkage. This phenomenon is called selective shrinkage.
After incorporating the normal prior distribution into the likelihood function, we can derive the posterior distribution of the regression coefficient, which remains normal due to the conjugate nature of the normal prior. The posterior mean and posterior variance are used to generate a posterior sample of the regression coefficient. Formulas for the posterior mean and posterior variance are mathematically attractive (see Xu 2003; Wang et al. 2005; Yang and Xu 2007). However, due to page limitations of these publications, derivation of the formulas was not provided in these articles.
Derivation of the univariate shrinkage estimation closely followed Box and Tiao's (1973, Appendix A1.1) combination of a univariate normal likelihood and a univariate normal prior. Derivation of the multivariate shrinkage estimation followed the general Bayesian linear model of Lindley and Smith (1972) and the best linear unbiased prediction (BLUP) of Robinson (1991). The derivations presented by these authors were particularly targeted to statisticians and often difficult to understand by the audience of the genetics community. I have been regularly receiving e-mails and calls from readers asking for the derivation. These readers (almost all genetics professionals and students) are often interested in extending the shrinkage method to handle QTL mapping in different mapping populations. Understanding the derivation of these formulas is crucial to the development of new shrinkage methods. Simply pointing them to the above references often does not help too much because intermediate steps are needed to lead to the shrinkage estimate presented by Xu (2003). By doing this, I often give them an impression of irresponsibility. Therefore, I prepared a short note for the derivation and distributed the note to these interested readers. The note briefly summarizes the derivation using a language that is easy to understand by geneticists with basic statistical training. Given the increasing interest of the derivation from the QTL mapping community, it is more efficient to publish the note in Genetics where the very first shrinkage method (Xu 2003) was published.
THEORY AND MODEL
Shrinkage estimates:
Let 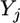 be an
be an 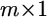 vector for the phenotypic values of m traits collected from the jth individual for
vector for the phenotypic values of m traits collected from the jth individual for 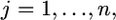 where n is the sample size. This vector is described by the following linear model,
where n is the sample size. This vector is described by the following linear model,
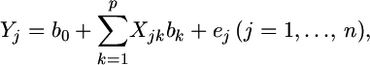 |
(1) |
where 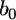 is an
is an 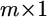 vector for the population means (or intercept),
vector for the population means (or intercept), 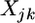 is an
is an 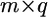 design matrix (determined by the genotypes of the jth individual at the kth locus),
design matrix (determined by the genotypes of the jth individual at the kth locus), 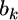 is a
is a 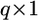 vector for the regression coefficients (QTL effects) for locus k (
vector for the regression coefficients (QTL effects) for locus k (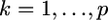 ),
), 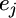 is an
is an 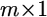 vector of residual errors with an assumed
vector of residual errors with an assumed 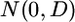 distribution, and D is an
distribution, and D is an 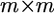 positive definite covariance matrix. When the kth regression coefficient is considered, all other regression coefficients are treated as constants and thus model (1) can be rewritten as
positive definite covariance matrix. When the kth regression coefficient is considered, all other regression coefficients are treated as constants and thus model (1) can be rewritten as
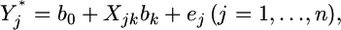 |
(2) |
where
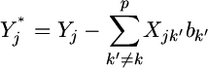 |
(3) |
is the phenotypic value adjusted by all other regression coefficients that are not currently under consideration. Let us describe 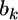 by the following normal prior
by the following normal prior 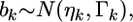 where
where 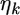 is a
is a 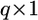 vector for the means and
vector for the means and 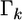 is a
is a 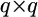 prior variance–covariance matrix. The posterior distribution of
prior variance–covariance matrix. The posterior distribution of 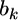 is multivariate normal with mean
is multivariate normal with mean
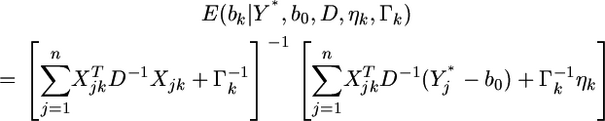 |
(4) |
and variance–covariance matrix
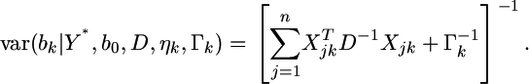 |
(5) |
In shrinkage analysis, we often set 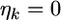 for
for 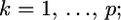 as such the posterior mean becomes
as such the posterior mean becomes
 |
(6) |
This posterior mean is called the shrinkage estimate of the regression coefficient  When
When  the prior is flat, leading to the usual least-squares estimate,
the prior is flat, leading to the usual least-squares estimate,
 |
(7) |
When 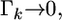 we have
we have 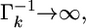 which leads to
which leads to 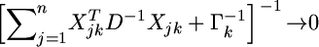 and thus
and thus 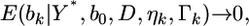 an estimate shrunken to zero. Therefore, matrix
an estimate shrunken to zero. Therefore, matrix 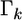 serves as a factor to determine the degree of shrinkage for the estimate of
serves as a factor to determine the degree of shrinkage for the estimate of 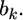 Because
Because 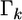 varies, the degree of shrinkage also varies across k. To prove the shrinkage estimate, I first introduce the following lemma:
varies, the degree of shrinkage also varies across k. To prove the shrinkage estimate, I first introduce the following lemma:
Lemma. Assume that parameter b can be inferred from two independent sources of information. Let 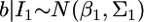 and
and 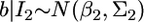 be the distributions of the two sources of information. When we combine
be the distributions of the two sources of information. When we combine 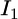 and
and 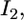 the distribution of b remains multivariate normal
the distribution of b remains multivariate normal 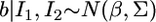 with mean
with mean 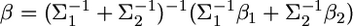 and variance–covariance matrix
and variance–covariance matrix 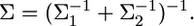
Proof of the lemma. The distribution of b given the two sources of information is described by
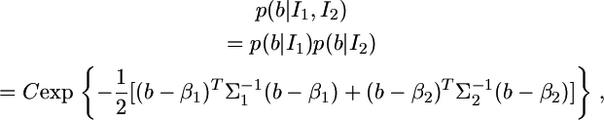 |
(8) |
where C is a constant with respect to b. When deriving a distribution, we are interested only in the kernel of the distribution. A kernel of a distribution is the central part of the distribution function, the part that remains when constants are disregarded. In the above distribution, the logarithm of the kernel is
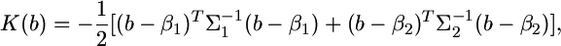 |
(9) |
which is further expressed by
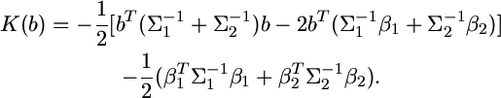 |
(10) |
We can see that this kernel involves another constant, 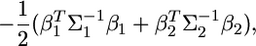 which can be ignored also. Therefore, the actual kernel that contains only the linear and quadratic functions of b is
which can be ignored also. Therefore, the actual kernel that contains only the linear and quadratic functions of b is
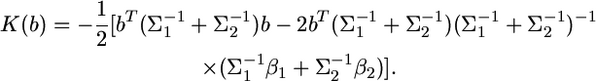 |
(11) |
Let 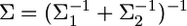 and
and 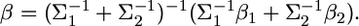 The kernel is simplified into
The kernel is simplified into
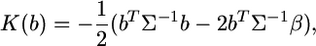 |
(12) |
which turns out to be the kernel of 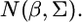 Therefore, we conclude that
Therefore, we conclude that 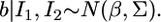
Derivation of the shrinkage estimates:
We now use the above lemma to derive the shrinkage estimate of 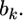 The two sources of information for
The two sources of information for 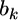 come from the data (
come from the data (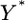 ) and the prior. Information from the data is used to infer
) and the prior. Information from the data is used to infer 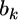 through the maximum-likelihood method. The log-likelihood function is
through the maximum-likelihood method. The log-likelihood function is
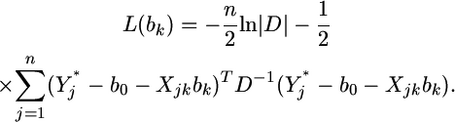 |
(13) |
The maximum-likelihood estimate of 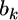 is
is
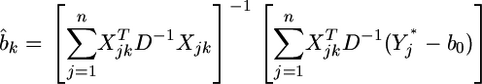 |
(14) |
and the variance of this estimate is
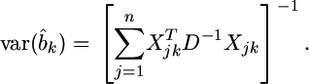 |
(15) |
Let 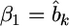 and
and 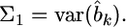 After some algebraic manipulation on the likelihood function, we find that Equation 13 has the following normal kernel with respect to
After some algebraic manipulation on the likelihood function, we find that Equation 13 has the following normal kernel with respect to 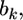
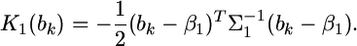 |
(16) |
Therefore, the distribution of 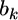 inferred from the data is
inferred from the data is 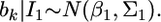 The second source of information for
The second source of information for 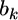 is the prior distribution
is the prior distribution 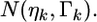 If we let
If we let 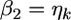 and
and 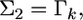 the distribution of
the distribution of 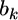 from the second source of information is
from the second source of information is 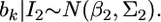 According to the lemma, the posterior mean of
According to the lemma, the posterior mean of 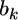 is
is
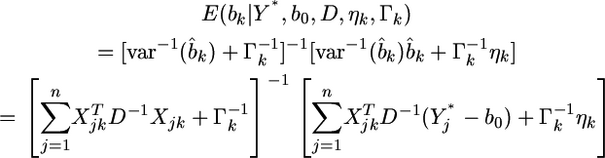 |
(17) |
and the posterior variance is
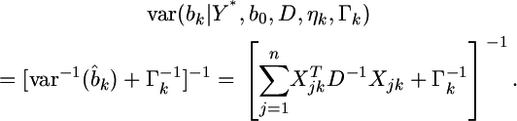 |
(18) |
This concludes the derivation of the shrinkage estimate of 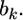
Univariate version of the shrinkage estimate:
The shrinkage estimate of the regression coefficient given by Xu (2003) is a special case of the general shrinkage estimate. The regression model of Xu (2003) is
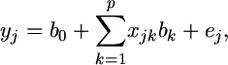 |
(19) |
where every variable in the equation is a scalar rather than a matrix. When focused on the kth regression coefficient, the model is rewritten as
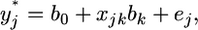 |
(20) |
where 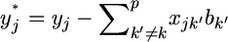 is the adjusted data. Let us assume
is the adjusted data. Let us assume 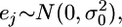 where
where 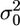 is the univariate version of matrix D. Assume that the prior distribution for
is the univariate version of matrix D. Assume that the prior distribution for 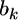 is
is 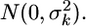 Therefore, the univariate versions of
Therefore, the univariate versions of 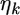 and
and 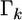 are
are 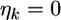 and
and 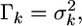 respectively. Substituting all the parameters of Equations 4 and 5 by their univariate counterparts, we have
respectively. Substituting all the parameters of Equations 4 and 5 by their univariate counterparts, we have
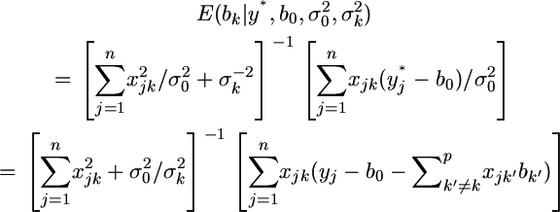 |
(21) |
and
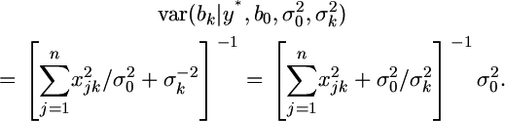 |
(22) |
These equations are exactly the same as Equations 5 and 6 given by Xu (2003).
DISCUSSION
There are several alternative ways to prove the shrinkage estimation, such as the conditional distribution of multivariate normal variables (Giri 1996). The method presented in this note is a generalization of Box and Tiao's (1973, Appendix A1.1) combination of a univariate normal likelihood and a univariate normal prior. Using the method of Box and Tiao (1973), we can extend the lemma to the situation of inferring b from more than two independent sources of information. Let m be the number of sources of information (independent of each other) used to infer b and the distribution from the ith source is 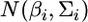 for
for 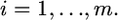 The posterior distribution of b combining all the sources of information is
The posterior distribution of b combining all the sources of information is 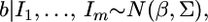 where
where
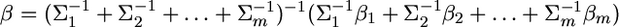 |
(23) |
and
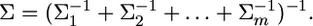 |
(24) |
One can use mathematical induction to prove Equations 23 and 24, starting from 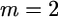 (given in the lemma) and moving to
(given in the lemma) and moving to 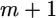 and so on.
and so on.
Bayesian shrinkage estimation refers to the biased estimation of a regression coefficient toward zero using a prior variance as a factor to control the degree of shrinkage. A normal prior is often selected because it is a conjugate prior so that the posterior distribution remains normal. A normal posterior simplifies the MCMC sampling process because the Gibbs sampler can be used to draw the regression coefficient. Other prior distributions have been proposed, e.g., the mixture prior of two normal distributions (George and Mcmulloch 1993; Yi et al. 2003) and the spike and slab model (Ishwaran and Rao 2005). A t-distribution may also be used as a prior for the regression coefficient. However, the posterior distribution using a nonnormal prior rarely has an explicit form of a distribution, making Gibbs sampling impossible and thus complicating the MCMC sampling process.
The shrinkage method for regression analysis may also be called the random model approach to regression analysis, or simply random regression, because each regression coefficient is treated as a random effect with a (prior) normal distribution. It is well known that there is no limit in the number of random effects that can be handled by a random model. The success of a random linear model analysis, however, depends on the variance components chosen for the random model. If a random model contains an excessively large number of regression coefficients, most of them will be zero or close to zero. The sparse nature of the regression coefficients cannot be characterized by the random linear model alone and it must be accompanied by an efficient method to choose the variance components. In QTL mapping, the number of variance components can be extremely large, making subjective selection of the variance components impossible. Therefore, the variance components must be estimated from the data.
The most convenient way to estimate the variance components is to use the maximum-likelihood method. The estimated variance components are used in place of the prior variances to estimate the regression coefficients. The method is called the empirical Bayes method as far as the estimation of regression coefficients is concerned (Xu 2007). To reflect the sparse nature of the regression coefficients, a prior distribution is often assigned to each variance component. This is called hierarchical modeling (Gelman 2005). Furthermore, the prior distribution should be highly concentrated around zero. Many different prior distributions can be chosen for the variance components, but the scaled inverse chi-square distribution is the most convenient and flexible prior with such a property (Lindley and Smith 1972). Exponential distribution (Tibshirani 1996) and half t-distribution (Gelman 2006) have also been used. The prior choice for variance components of the random regression analysis is a very active research area to explore. More efficient priors may be developed in the future.
In the random regression analysis, the variance of a regression coefficient is not the primary interest of the investigator; rather, it is used only for the purpose of controlling the magnitude of the shrinkage. If the regression coefficients are batched (clustered) so that regression coefficients in the same batches share the same prior distribution, the variance may be estimated accurately and the estimate of it may be meaningful (Gelman 2005). In this case, the primary interest has been shifted from the regression coefficients to the variances of the regression coefficients; the method is better called the analysis of variances (ANOVA) (Gelman 2005). In the usual shrinkage analysis, the regression coefficients are not batched; i.e., every regression coefficient has its own prior variance, and the estimated variance for a regression coefficient may vary drastically across the posterior sample. This problem may look very bad, but will not seriously harm the Bayesian shrinkage estimates of the regression coefficients. One can minimize the variation of the sampled variance across the posterior sample by using some proper prior distribution for the variance (Gelman 2005).
References
- Box, G. E. P., and G. C. Tiao, 1973. Bayesian Inference in Statistical Analysis. Wiley & Sons, New York.
- Gelman, A., 2005. Analysis of variance–why it is more important than ever. Ann. Stat. 33: 1–53. [Google Scholar]
- Gelman, A., 2006. Prior distribution for variance parameters in hierarchical models. Bayesian Anal. 1: 515–533. [Google Scholar]
- George, E. I., and R. E. McMulloch, 1993. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 91: 883–904. [Google Scholar]
- Giri, N. C., 1996. Multivariate Statistical Analysis. Marcel Dekker, New York.
- Ishwaran, H., and J. S. Rao, 2005. Spike and slab variable selection: frequentist and Bayesian strategies. Ann. Stat. 33: 730–773. [Google Scholar]
- Lindley, D. V., and A. F. M. Smith, 1972. Bayes estimates for the linear model. J. R. Stat. Soc. Ser. B 34: 1–41. [Google Scholar]
- Robinson, G. K., 1991. That BLUP is a good thing: the estimation of random effects. Stat. Sci. 6: 15–32. [Google Scholar]
- Tibshirani, R., 1996. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 58: 267–288. [Google Scholar]
- Wang, H., Y. M. Zhang, X. Li, G. L. Masinde, S. Mohan et al., 2005. Bayesian shrinkage estimation of quantitative trait loci parameters. Genetics 170: 465–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, S., 2003. Estimating polygenic effects using markers of the entire genome. Genetics 163: 789–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, S., 2007. An empirical Bayes method for estimating epistatic effects of quantitative trait loci. Biometrics 63: 513–521. [DOI] [PubMed] [Google Scholar]
- Yang, R., and S. Xu, 2007. Bayesian shrinkage analysis of quantitative trait loci for dynamic traits. Genetics 176: 1169–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi, N., V. George and D. B. Allison, 2003. Stochastic search variable selection for identifying quantitative trait loci. Genetics 164: 1129–1138. [DOI] [PMC free article] [PubMed] [Google Scholar]


