Abstract
Populations often have very complex hierarchical structure. Therefore, it is crucial in genetic monitoring and conservation biology to have a reliable estimate of the pattern of population subdivision. FST's for pairs of sampled localities or subpopulations are crucial statistics for the exploratory analysis of population structures, such as cluster analysis and multidimensional scaling. However, the estimation of FST is not precise enough to reliably estimate the population structure and the extent of heterogeneity. This article proposes an empirical Bayes procedure to estimate locus-specific pairwise FST's. The posterior mean of the pairwise FST can be interpreted as a shrinkage estimator, which reduces the variance of conventional estimators largely at the expense of a small bias. The global FST of a population generally varies among loci in the genome. Our maximum-likelihood estimates of global FST's can be used as sufficient statistics to estimate the distribution of FST in the genome. We demonstrate the efficacy and robustness of our model by simulation and by an analysis of the microsatellite allele frequencies of the Pacific herring. The heterogeneity of the global FST in the genome is discussed on the basis of the estimated distribution of the global FST for the herring and examples of human single nucleotide polymorphisms (SNPs).
INFERRING genetic population structure has been a major theme in population biology, ecology, and human genetics. The fixation index FST, introduced by Wright (1951), is a key parameter for such studies and is most commonly used to measure genetic divergence among subpopulations (Palsbøll et al. 2007). It is defined as the correlation between random gametes drawn from the same subpopulation relative to the total population. Another measure used frequently is Cockerham's (1969, 1973) coancestry coefficient, which is the probability that two random genes from different individuals are identical by descent, and the average overall pairs of individuals within the same subpopulation equal Wright's FST (Excoffier 2003). We use the notation θWC for the average coancestry coefficient and θWC = FST as shown by Weir and Cockerham (1984). Nei's (1973) GST is analogous to FST and identical to FST for diploid random-mating populations (Excoffier 2003).
Nei and Chesser (1983) proposed an estimator for FST and GST. The estimation of these parameters accounts only for the sampling error within subpopulations and therefore assumes that all subpopulations have been sampled (Cockerham and Weir 1986; Excoffier 2003). Weir and Cockerham (1984) developed the moment estimator 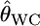 for the coancestry coefficient θWC, which takes the sampling error for the subpopulations into account. Several moment estimators with different weighting schemes have also been derived (Robertson and Hill 1984; Weir and Cockerham 1984). An alternative estimation has been discussed using the method of ordinary least squares (Reynolds et al. 1983). Weir and Hill (2002) extended θWC to a population-specific parameter to allow different levels of coancestry for different populations. They also derived an estimator for θWC with confidence intervals using a normal theory approach.
for the coancestry coefficient θWC, which takes the sampling error for the subpopulations into account. Several moment estimators with different weighting schemes have also been derived (Robertson and Hill 1984; Weir and Cockerham 1984). An alternative estimation has been discussed using the method of ordinary least squares (Reynolds et al. 1983). Weir and Hill (2002) extended θWC to a population-specific parameter to allow different levels of coancestry for different populations. They also derived an estimator for θWC with confidence intervals using a normal theory approach.
Despite the development of methods for assigning individuals to populations (Paetkau et al. 1995; Pritchard et al. 2000; Huelsenbeck and Andolfatto 2007), the differentiation estimators remain the most commonly used tools for describing population structure (Balloux and Lugon-Moulin 2002). Weir and Cockerham (1984) showed that their estimator 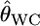 provides the smallest bias among the moment estimators. Goudet et al. (1996) confirmed this using simulations and showed that
provides the smallest bias among the moment estimators. Goudet et al. (1996) confirmed this using simulations and showed that 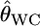 generates the least-biased estimate of FST but has the largest variance when FST is small. Raufaste and Bonhomme (2000) showed that
generates the least-biased estimate of FST but has the largest variance when FST is small. Raufaste and Bonhomme (2000) showed that 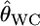 is nearly unbiased, with minimal variance for large FST, and that the estimator of Robertson and Hill (1984)
is nearly unbiased, with minimal variance for large FST, and that the estimator of Robertson and Hill (1984) 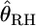 is negatively biased, with minimal variance for small FST. They proposed a correction for the bias of
is negatively biased, with minimal variance for small FST. They proposed a correction for the bias of 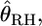 but this cannot be corrected properly in the range of [0.05, 0.1]. Therefore, a precise estimate of FST is crucial, especially for small and moderate levels of genetic differentiation.
but this cannot be corrected properly in the range of [0.05, 0.1]. Therefore, a precise estimate of FST is crucial, especially for small and moderate levels of genetic differentiation.
In addition to the estimation of FST over all subpopulations in a metapopulation (hereafter, we call this global FST), FST's for pairs of sampled localities or subpopulations (pairwise FST) are usually estimated in conservation biology and ecology. In fact, the computer programs Arlequin (Excoffier et al. 2005), FSTAT (Goudet 1995), and Genepop (Raymond and Rousset 1995) estimate these parameters and are used widely in ecological studies. These three software packages produce the same or similar values for pairwise FST estimates and provide the basic statistics for exploratory analyses of population structure, such as cluster analysis and multidimensional scaling. They are also used as a criterion for population differentiation (Waples and Gaggiotti 2006; Palsbøll et al. 2007). However, the estimation of FST's is not precise enough to reliably estimate the population structure and the extent of heterogeneity, especially for large gene flow species.
Small numbers of individuals taken from each locality should also affect the precision of  Populations often have very complex hierarchical structures, and geographical samples are usually taken from many localities to include a wide area. Therefore, the numbers of individuals from each locality are frequently limited by the large number of sampling points. Small sample sizes can result in biased estimates of the allele frequencies of each subpopulation. This bias may be larger for cases with larger numbers of alleles, such as microsatellite DNA. Uncertainty in the estimates of allele frequencies should affect the estimation of FST's. The Bayesian approach provides better estimates of allele frequencies by taking uncertainty into account (Lange 1995; Lockwood et al. 2001). Posterior distributions of global FST were simulated from posterior distributions of allele frequencies, assuming common hyperparameters across all loci (Holsinger 1999; Holsinger et al. 2002; Corander et al. 2003). However, accurate estimation of pairwise FST, the essential parameter in ecological studies, has not been fully investigated.
Populations often have very complex hierarchical structures, and geographical samples are usually taken from many localities to include a wide area. Therefore, the numbers of individuals from each locality are frequently limited by the large number of sampling points. Small sample sizes can result in biased estimates of the allele frequencies of each subpopulation. This bias may be larger for cases with larger numbers of alleles, such as microsatellite DNA. Uncertainty in the estimates of allele frequencies should affect the estimation of FST's. The Bayesian approach provides better estimates of allele frequencies by taking uncertainty into account (Lange 1995; Lockwood et al. 2001). Posterior distributions of global FST were simulated from posterior distributions of allele frequencies, assuming common hyperparameters across all loci (Holsinger 1999; Holsinger et al. 2002; Corander et al. 2003). However, accurate estimation of pairwise FST, the essential parameter in ecological studies, has not been fully investigated.
In this article, we propose an empirical Bayes procedure to estimate locus-specific pairwise FST's, taking into account the uncertainty of the allele frequencies of subpopulations. The estimation procedure has two stages. First, the hyperparameters of Dirichlet prior distributions for allele frequencies at each locus are estimated from observed allele counts by a maximum-likelihood method. The global FST is then estimated at each locus. Second, on the basis of the estimates of the hyperparameters, and given the allele counts, posterior distributions of the allele frequencies are generated for each locus, from which the posterior distributions of locus-specific pairwise FST's are simulated. The posterior mean of our empirical Bayes pairwise FST estimates can be interpreted as a shrinkage estimator (Stein 1956; Maritz and Lewin 1989) anchored to the average of the true values among pairs. It performs better than conventional differentiation estimators and robustly estimates the population structure, even for non-Dirichlet cases, as stepping-stone models. The posterior distribution of pairwise FST's can be used to calculate a criterion of population differentiation. Our maximum-likelihood estimates of the global FST's can also be used as sufficient statistics to estimate the distribution of FST among loci in the genome. Our model assumes random mating or random sampling of alleles at each locality and that linkage equilibrium holds between loci. It also assumes that allele counts at each locus, given the true allele frequencies, are independent among populations. Our method can be applied to frequency data for common genetic markers, including isozymes, mitochondrial DNA, microsatellites, and single nucleotide polymorphisms (SNPs). We show the efficacy of our model by simulation and by an analysis of microsatellite allele frequencies of the Pacific herring. The heterogeneity of FST in the genome is discussed on the basis of the estimated distribution of global FST for the herring and examples of human SNPs.
MODELS AND METHODS
The model:
Consider a simple random sampling from multiple localities in a metapopulation. Suppose that K random-mating demes or subpopulations are drawn from the metapopulation. Let 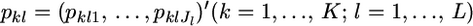 be a vector of the true allele frequencies at locus l in subpopulation k, where Jl is the number of different alleles at the locus, and
be a vector of the true allele frequencies at locus l in subpopulation k, where Jl is the number of different alleles at the locus, and 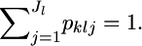 We assume a Dirichlet distribution as the prior distribution of pkl. The probability density function is
We assume a Dirichlet distribution as the prior distribution of pkl. The probability density function is
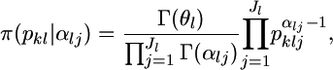 |
where 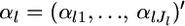 are the hyperparameters and
are the hyperparameters and 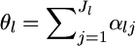 is a scale parameter that is specific for the locus. This model describes well a metapopulation that has a continuous structure and consists of an infinite number of subpopulations or demes (Pannell and Charlesworth 2000; Rousset 2003; Hanski and Gaggiotti 2004). Let
is a scale parameter that is specific for the locus. This model describes well a metapopulation that has a continuous structure and consists of an infinite number of subpopulations or demes (Pannell and Charlesworth 2000; Rousset 2003; Hanski and Gaggiotti 2004). Let 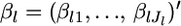 be the mean allele frequency for the metapopulation at the locus satisfying
be the mean allele frequency for the metapopulation at the locus satisfying 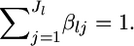 Hence, we have the relation βlj = αlj/θl.
Hence, we have the relation βlj = αlj/θl.
Under this model, the global FST (hereafter denoted as 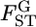 ) at each locus is expressed simply by the scale parameter, as
) at each locus is expressed simply by the scale parameter, as
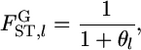 |
(1) |
as given by Wright (1969), Rannala and Hartigan (1996), Balding and Nichols (1997), Lockwood et al. (2001), Balding (2003), and Kitada and Kishino (2004). In this model, the variance of the jth allele frequency for the locus, pklj, is expressed by
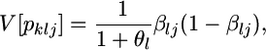 |
as given by Weir (1996), Holsinger et al. (2002), Balding (2003), and Kitakado et al. (2006). The Dirichlet distribution assumes an evolutionary equilibrium and an equal mutation rate for all alleles (Weir and Hill 2002; Ewens 2004). Under this assumption, the scale parameter θl refers to the rate of gene flow, as given by Rannala and Hartigan (1996). We use the symbol θ for the scale parameter, following Rannala and Hartigan (1996) and Balding and Nichols (1997). Weir and Cockerham (1984) also used the same symbol θ for the coancestry coefficient (= FST), so we use θWC for their θ. Our 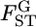 is equivalent to θWC (Weir 1996, pp. 47–48) and Holsinger's θB (Holsinger 1999; Holsinger et al. 2002).
is equivalent to θWC (Weir 1996, pp. 47–48) and Holsinger's θB (Holsinger 1999; Holsinger et al. 2002).
Maximum-likelihood estimation of hyperparameters and global FST:
The maximum-likelihood estimation of the hyperparameters has been discussed by Lange (1995), Kitada et al. (2000), and Balding (2003). A pseudo-likelihood approach was also taken by Rannala and Hartigan (1996). In the maximum-likelihood framework, a method for the simultaneous estimation of 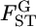 and the linkage disequilibrium coefficient between two SNPs has been proposed (Kitada and Kishino 2004). Kitakado et al. (2006) proposed an integrated-likelihood approach to reduce the negative bias of
and the linkage disequilibrium coefficient between two SNPs has been proposed (Kitada and Kishino 2004). Kitakado et al. (2006) proposed an integrated-likelihood approach to reduce the negative bias of 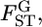 particularly for cases with few sampling points.
particularly for cases with few sampling points.
Suppose that 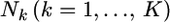 alleles of diploid organisms (Nk/2 individuals) are counted at locus l and
alleles of diploid organisms (Nk/2 individuals) are counted at locus l and 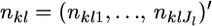 denotes a vector of observed allele counts at the locus in subpopulation k. We assume that all individuals are successfully genotyped at all loci, so
denotes a vector of observed allele counts at the locus in subpopulation k. We assume that all individuals are successfully genotyped at all loci, so 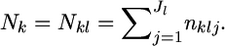 The marginal likelihood of the observed allele counts at a locus nkl has a Dirichlet-multinomial distribution (Lange 1995; Rannala and Hartigan 1996; Weir 1996; Balding and Nichols 1997; Kitada et al. 2000; Balding 2003; Rousset 2003). The parameters to be estimated are
The marginal likelihood of the observed allele counts at a locus nkl has a Dirichlet-multinomial distribution (Lange 1995; Rannala and Hartigan 1996; Weir 1996; Balding and Nichols 1997; Kitada et al. 2000; Balding 2003; Rousset 2003). The parameters to be estimated are 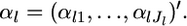 Because we assume the independence of subpopulations, the overall likelihood for these parameters is given by the product of the likelihood functions for K samples, as
Because we assume the independence of subpopulations, the overall likelihood for these parameters is given by the product of the likelihood functions for K samples, as
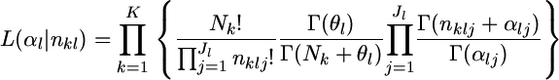 |
(2) |
The hyperparameters αl are estimated by maximizing this marginal likelihood (Lange 1995; Kitada et al. 2000). Our method can be used for both allele and haplotype counts without modification, but some notations differ slightly. For haploid organisms, Nk refers to the individuals genotyped; and nkl should be nk and αlj should be αj. Henceforth, for simplicity, we focus on diploid organisms.
The locus-specific 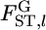 can be estimated by substituting
can be estimated by substituting 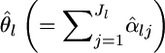 for θl in Equation 1. The variance estimator for
for θl in Equation 1. The variance estimator for 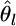 is calculated from the Fisher information matrix for αl, as
is calculated from the Fisher information matrix for αl, as 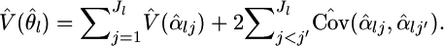 The asymptotic variance for
The asymptotic variance for 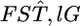 is estimated using the Delta method (Seber 1982) as
is estimated using the Delta method (Seber 1982) as
 |
(3) |
In our metapopulation model or infinite-island model, the sampled localities are regarded as a sample from all possible demes or subpopulations, including those not sampled. Hence, Equation 2 estimates the locus-specific genetic differentiation under the random-effect model of population sampling (Weir 1996). The average estimate of  for all loci is calculated as an arithmetic mean across the loci.
for all loci is calculated as an arithmetic mean across the loci.
Empirical Bayes estimation of pairwise FST:
The posterior distribution of allele frequencies pkl at locus l in subpopulation k is again a Dirichlet distribution, with parameters modified by the sample allele counts
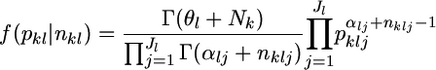 |
(4) |
(Lange 1995; Weir 1996). Given the estimates of the hyperparameters and the sampled allele counts, random numbers of pkl can be generated through this posterior distribution. The posterior distributions for any parametric functions of pkl can then be simulated by the empirical Bayes procedure (Kitada et al. 2000).
When population differentiation between or among specific subpopulations is of interest, the selected populations can be regarded as the entire set of populations. Hence, applying the fixed-effect model of population sampling (Weir 1996) is appropriate. Therefore, we use Nei's GST formula (Nei and Chesser 1983), which defines quantities with respect to fixed extant populations (Cockerham and Weir 1986), to estimate the posterior distributions of pairwise FST's (hereafter denoted as 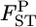 ), as did Holsinger (1999) and Corander et al. (2003) in estimating global FST. Nei's gene diversity analysis compares expected heterozygosities under Hardy–Weinberg equilibrium (HWE), and the GST estimator is expressed as a function of allele frequencies. Therefore the posterior distribution of
), as did Holsinger (1999) and Corander et al. (2003) in estimating global FST. Nei's gene diversity analysis compares expected heterozygosities under Hardy–Weinberg equilibrium (HWE), and the GST estimator is expressed as a function of allele frequencies. Therefore the posterior distribution of 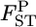 at each locus can easily be generated on the basis of the GST estimator, without using genotype frequencies. We set the number of each simulation to 10,000, so 10,000
at each locus can easily be generated on the basis of the GST estimator, without using genotype frequencies. We set the number of each simulation to 10,000, so 10,000 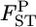 's are calculated at each locus from the 10,000 sets of allele frequencies pkl between a set of two populations. From the posterior distribution of
's are calculated at each locus from the 10,000 sets of allele frequencies pkl between a set of two populations. From the posterior distribution of 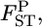 the posterior mean and 95% credible interval are calculated. We use the posterior mean as the empirical Bayes estimator of locus-specific
the posterior mean and 95% credible interval are calculated. We use the posterior mean as the empirical Bayes estimator of locus-specific 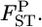 We can also calculate the probability that
We can also calculate the probability that 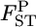 is smaller than an arbitrary value [e.g., P(
is smaller than an arbitrary value [e.g., P(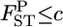 )], which can be used as the criterion for population differentiation (Waples and Gaggiotti 2006; Palsbøll et al. 2007). The average estimate of
)], which can be used as the criterion for population differentiation (Waples and Gaggiotti 2006; Palsbøll et al. 2007). The average estimate of 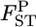 for overall loci is calculated as an arithmetic mean across the loci.
for overall loci is calculated as an arithmetic mean across the loci.
Rosenberg et al. (2003) proposed a general measure for determining the amount of information on individual ancestry on the basis of the Kullback–Leibler information. The informativeness for assignment In is defined as
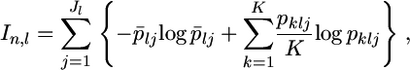 |
(5) |
where 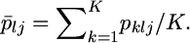 The authors showed that In and FST are very closely correlated but that In is more informative than the standard SNP-specific pairwise FST. In an additional analysis, we examine how our empirical Bayes method works to measure this under the same simulation protocol.
The authors showed that In and FST are very closely correlated but that In is more informative than the standard SNP-specific pairwise FST. In an additional analysis, we examine how our empirical Bayes method works to measure this under the same simulation protocol.
Inferring heterogeneity of global FST among loci:
We estimate locus-specific 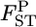 's on the basis of
's on the basis of 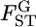 estimated at each locus. Evolutionary forces may differ among sites in the genome. Therefore, it is important to investigate the heterogeneity of FST among loci. One practical analysis is to test the null hypothesis H0, the homogeneity of
estimated at each locus. Evolutionary forces may differ among sites in the genome. Therefore, it is important to investigate the heterogeneity of FST among loci. One practical analysis is to test the null hypothesis H0, the homogeneity of 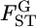 among L loci,
among L loci, 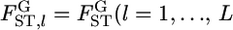 ) against the alternative hypothesis H1, the heterogeneity of
) against the alternative hypothesis H1, the heterogeneity of 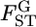 among loci, on the basis of estimates of
among loci, on the basis of estimates of 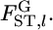 When a large number of subpopulations are sampled, the maximum-likelihood estimate
When a large number of subpopulations are sampled, the maximum-likelihood estimate 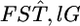 follows a normal distribution of
follows a normal distribution of 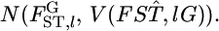 The maximum likelihood under H0 is then given as
The maximum likelihood under H0 is then given as  where
where 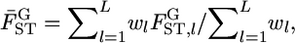
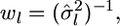 and
and 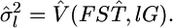 The maximum likelihood under H1 is
The maximum likelihood under H1 is 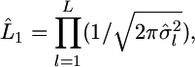 maximizing
maximizing 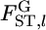 by
by 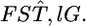 The negative twice-log-likelihood ratio is then
The negative twice-log-likelihood ratio is then 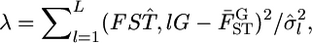 which follows the χ2-distribution with (L − 1) d.f. under the null hypothesis. We can test the heterogeneity of
which follows the χ2-distribution with (L − 1) d.f. under the null hypothesis. We can test the heterogeneity of 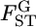 on the basis of the test statistics.
on the basis of the test statistics.
The other approach to investigate the heterogeneity of 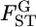 is to estimate the distribution of
is to estimate the distribution of 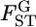 in the genome. In recent years, the number of loci analyzed has been increasing in ecological studies, but is still smaller than those used for human SNPs. For such cases, it would be difficult to directly estimate the specific distribution of
in the genome. In recent years, the number of loci analyzed has been increasing in ecological studies, but is still smaller than those used for human SNPs. For such cases, it would be difficult to directly estimate the specific distribution of 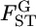 from the data. Here, we estimate the distribution of
from the data. Here, we estimate the distribution of 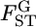 in the genome from estimates of randomly selected loci,
in the genome from estimates of randomly selected loci, 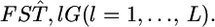 When the distribution is expressed by the parametric model
When the distribution is expressed by the parametric model 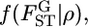 the unknown parameter
the unknown parameter 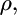 which defines the distribution of
which defines the distribution of 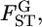 is estimated by maximizing the log marginal likelihood
is estimated by maximizing the log marginal likelihood
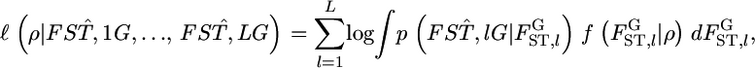 |
where 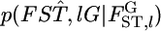 is the distribution of
is the distribution of 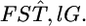 Here, we assume the independence of loci
Here, we assume the independence of loci 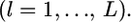 Because the maximum-likelihood estimator
Because the maximum-likelihood estimator 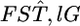 is a sufficient statistic, it is possible to estimate the distribution of
is a sufficient statistic, it is possible to estimate the distribution of 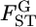 in the genome on the basis of the estimates
in the genome on the basis of the estimates 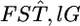 for randomly sampled loci, instead of using a direct estimation from the data.
for randomly sampled loci, instead of using a direct estimation from the data.
For the preliminary discussion here, we assume that 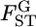 is normally distributed in the genome. When the distribution of
is normally distributed in the genome. When the distribution of 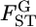 is expected to be different from 0, a simple approximation may be a normal distribution. We then assume
is expected to be different from 0, a simple approximation may be a normal distribution. We then assume 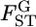 follows N(μ, σ2) as a first step in estimating the distribution of
follows N(μ, σ2) as a first step in estimating the distribution of 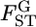 in the genome under the limited number of loci analyzed. In this case, the parameter vector ρ refers to μ and σ2. The general form of the log marginal likelihood given above becomes
in the genome under the limited number of loci analyzed. In this case, the parameter vector ρ refers to μ and σ2. The general form of the log marginal likelihood given above becomes
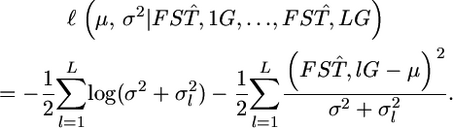 |
(6) |
Here, 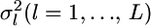 is the variance of the estimates,
is the variance of the estimates, 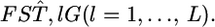 We estimate μ and σ2 numerically, regarding
We estimate μ and σ2 numerically, regarding 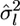 as
as 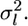 The distribution of
The distribution of 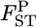 's can also be calculated with slight modifications to the above procedure.
's can also be calculated with slight modifications to the above procedure.
RESULTS
Improved precision of our empirical Bayes estimator for pairwise FST:
We investigated the performance of our method of estimating pairwise 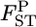 using numerical simulations. Random vectors of allele frequencies at locus l in subpopulation k, pkl's, were generated independently from the Dirichlet distribution with the parameter αl(= θl βl). Here, the number of sampling localities (K) was set at 5, 10, and 50, and the mean allele frequencies at a locus were assumed
using numerical simulations. Random vectors of allele frequencies at locus l in subpopulation k, pkl's, were generated independently from the Dirichlet distribution with the parameter αl(= θl βl). Here, the number of sampling localities (K) was set at 5, 10, and 50, and the mean allele frequencies at a locus were assumed 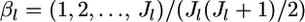 with Jl = 50. As the true values of the global FST,l's (= 1/(1 + θl)), we chose four different levels:
with Jl = 50. As the true values of the global FST,l's (= 1/(1 + θl)), we chose four different levels: 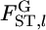 = 0.01, 0.05, 0.1, and 0.2. The sample size (Nk/2) was deemed to be common to all the localities and was set at 20, 30, and 50 individuals. Then, allele counts nkl's were drawn independently from the multinomial distribution Multi(Nk, pkl) for K localities. The pairwise
= 0.01, 0.05, 0.1, and 0.2. The sample size (Nk/2) was deemed to be common to all the localities and was set at 20, 30, and 50 individuals. Then, allele counts nkl's were drawn independently from the multinomial distribution Multi(Nk, pkl) for K localities. The pairwise 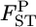 values between the first and second localities were evaluated by the conventional Nei's GST estimator and the empirical Bayes method. In the latter procedure, 500
values between the first and second localities were evaluated by the conventional Nei's GST estimator and the empirical Bayes method. In the latter procedure, 500 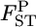 's were simulated on the basis of Nei's GST formula to save computation time, and the posterior mean was calculated as the estimator of the pairwise FST. The point estimate for the conventional GST estimator and the posterior mean of the empirical Bayes estimates were compared with the true
's were simulated on the basis of Nei's GST formula to save computation time, and the posterior mean was calculated as the estimator of the pairwise FST. The point estimate for the conventional GST estimator and the posterior mean of the empirical Bayes estimates were compared with the true 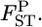 These procedures were iterated R = 1000 times.
These procedures were iterated R = 1000 times.
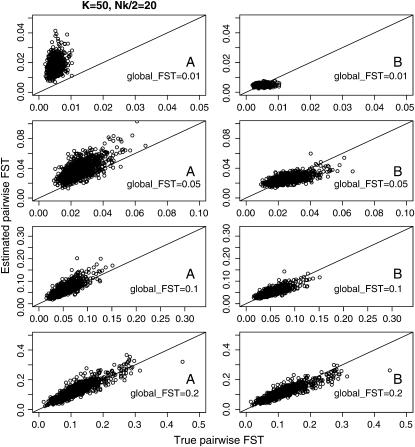
Figure 1 and supplemental Figure S1 at http://www.genetics.org/supplemental/ show the general features of the empirical Bayes estimator compared with those of the conventional GST estimator. The former examines the case of a relatively large number of sampling points and a limited sample size from each sampling point (K = 50, Nk/2 = 20). The latter investigates the case of moderately large samples from a small number of sampling points (K = 10, Nk/2 = 50), which is common in ecological studies. It is clearly apparent that the conventional GST estimator greatly overestimates the true values and has a large variance, especially for small 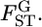 In contrast, the empirical Bayes estimates of
In contrast, the empirical Bayes estimates of 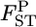 's shrink toward the average of the true
's shrink toward the average of the true 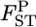 and reduce the positive bias of the conventional estimator. This is reasonable because our empirical Bayes estimator can be interpreted as a shrinkage estimator (Stein 1956; Maritz and Lewin 1989).
and reduce the positive bias of the conventional estimator. This is reasonable because our empirical Bayes estimator can be interpreted as a shrinkage estimator (Stein 1956; Maritz and Lewin 1989).
Figure 1.—
The conventional GST (A) and empirical Bayes (B) estimates of pairwise 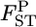 from 1000 simulations under the infinite-island model at various levels of
from 1000 simulations under the infinite-island model at various levels of 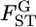 (0.01, 0.05, 0.1, 0.2) over subpopulations. The mean allele frequencies assumed were
(0.01, 0.05, 0.1, 0.2) over subpopulations. The mean allele frequencies assumed were 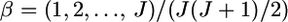 with J = 50. The number of sampling localities (K) was set at 50. The sample size Nk/2 (individuals) was common to all localities and was set at 20 individuals.
with J = 50. The number of sampling localities (K) was set at 50. The sample size Nk/2 (individuals) was common to all localities and was set at 20 individuals.
The effects of the number of sampling points K and sampled individuals Nk/2 are also shown in the supplemental material at http://www.genetics.org/supplemental/. The numbers of sampling points did not affect the positive bias of the conventional GST estimator because K was fixed at 2. The empirical Bayes procedure provided larger variation for smaller numbers of subpopulations, especially for small 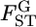 values, and vice versa (supplemental Figure S2 at http://www.genetics.org/supplemental/). Conversely, larger numbers of sampled individuals reduced the positive bias of the conventional GST estimator and the variation of the empirical Bayes estimator (supplemental Figure S3 at http://www.genetics.org/supplemental/).
values, and vice versa (supplemental Figure S2 at http://www.genetics.org/supplemental/). Conversely, larger numbers of sampled individuals reduced the positive bias of the conventional GST estimator and the variation of the empirical Bayes estimator (supplemental Figure S3 at http://www.genetics.org/supplemental/).
For a quantitative comparison of the two estimators, we used the following two measures: 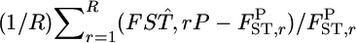 (relative mean bias) and
(relative mean bias) and 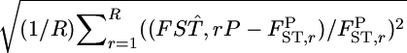 (root relative mean squared error), where
(root relative mean squared error), where 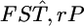 and
and 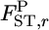 are an estimate and the true value, respectively, for pairwise
are an estimate and the true value, respectively, for pairwise 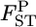 in the r th iteration. As shown in Table 1, smaller K and sample sizes (Nk/2) resulted in larger positive biases for the conventional estimator for various levels of true
in the r th iteration. As shown in Table 1, smaller K and sample sizes (Nk/2) resulted in larger positive biases for the conventional estimator for various levels of true 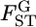 values. The bias and variation became smaller as
values. The bias and variation became smaller as 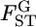 became larger. In contrast, the empirical Bayes estimator provided smaller biases and variations for all cases of
became larger. In contrast, the empirical Bayes estimator provided smaller biases and variations for all cases of 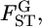 although smaller K and sample sizes resulted in a slight negative bias.
although smaller K and sample sizes resulted in a slight negative bias.
TABLE 1.
Relative mean bias and root relative mean squared error (in parentheses) of the conventional GST and empirical Bayes estimators of pairwise FST from 1000 simulations at various levels of global FST (see text)
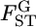 |
K | Nk/2 | Conventional | Empirical Bayes |
|---|---|---|---|---|
| 0.01 | 5 | 20 | 2.770 (3.019) | −0.726 (0.815) |
| 30 | 1.769 (1.942) | −0.541 (0.630) | ||
| 50 | 1.069 (1.192) | −0.330 (0.412) | ||
| 10 | 20 | 2.666 (2.880) | −0.325 (0.464) | |
| 30 | 1.791 (1.955) | −0.205 (0.345) | ||
| 50 | 1.081 (1.214) | −0.122 (0.270) | ||
| 50 | 20 | 2.728 (2.972) | 0.003 (0.294) | |
| 30 | 1.784 (1.967) | 0.010 (0.272) | ||
| 50 | 1.085 (1.217) | 0.033 (0.251) | ||
| 0.05 | 5 | 20 | 0.561 (0.685) | −0.136 (0.283) |
| 30 | 0.363 (0.478) | −0.097 (0.233) | ||
| 50 | 0.218 (0.304) | −0.056 (0.175) | ||
| 10 | 20 | 0.538 (0.662) | −0.039 (0.242) | |
| 30 | 0.367 (0.475) | −0.015 (0.216) | ||
| 50 | 0.233 (0.317) | 0.004 (0.169) | ||
| 50 | 20 | 0.557 (0.680) | 0.047 (0.253) | |
| 30 | 0.366 (0.480) | 0.031 (0.226) | ||
| 50 | 0.206 (0.304) | 0.015 (0.181) | ||
| 0.1 | 5 | 20 | 0.273 (0.418) | −0.053 (0.242) |
| 30 | 0.176 (0.284) | −0.036 (0.189) | ||
| 50 | 0.106 (0.194) | −0.019 (0.149) | ||
| 10 | 20 | 0.255 (0.375) | −0.006 (0.215) | |
| 30 | 0.183 (0.289) | 0.009 (0.186) | ||
| 50 | 0.098 (0.195) | −0.001 (0.151) | ||
| 50 | 20 | 0.247 (0.373) | 0.019 (0.215) | |
| 30 | 0.182 (0.287) | 0.027 (0.183) | ||
| 50 | 0.109 (0.192) | 0.020 (0.147) | ||
| 0.2 | 5 | 20 | 0.125 (0.250) | −0.017 (0.192) |
| 30 | 0.083 (0.195) | −0.007 (0.161) | ||
| 50 | 0.051 (0.134) | −0.003 (0.118) | ||
| 10 | 20 | 0.123 (0.246) | 0.009 (0.192) | |
| 30 | 0.092 (0.197) | 0.018 (0.165) | ||
| 50 | 0.049 (0.138) | 0.004 (0.122) | ||
| 50 | 20 | 0.127 (0.267) | 0.027 (0.220) | |
| 30 | 0.087 (0.188) | 0.020 (0.155) | ||
| 50 | 0.058 (0.144) | 0.018 (0.128) |
The negative bias of the empirical Bayes estimator of pairwise FST is large, especially when gene flow is large and the estimation is based on a sample from a few sampling points. Underestimation of population differences should lead to optimistic management strategies. Therefore, it is recommended in the conservation genetics of birds and fish that samples be collected from as many sampling points as possible. It is noted that the bias of the empirical Bayes estimator is reduced by increasing the number of sampling points, whereas the bias of the conventional GST estimator is not.
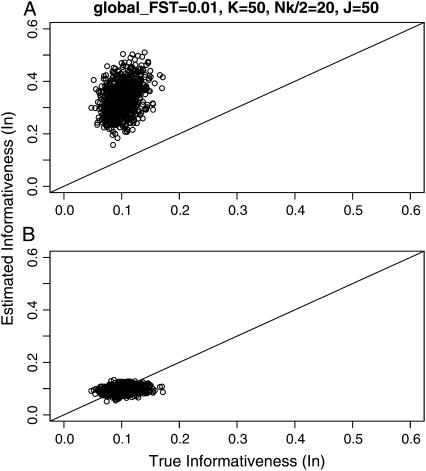
We estimated Rosenberg et al.'s informativeness of assignment In between the first and second localities using Equation 5 (K = 2) and the empirical Bayes method based on the In estimator for the case of 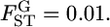 The mean allele frequencies were assumed to be
The mean allele frequencies were assumed to be 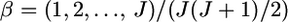 with J = 50. The number of sampling localities (K) was set at 50 and the sample size (Nk/2 individuals) was set at 20 individuals for each sampling point. Figure 2 shows that the conventional estimator for In was positively biased, whereas the empirical Bayes estimator of In performed much better, consistent with the fact that In produces upwardly biased estimates in small samples (Rosenberg et al. 2003).
with J = 50. The number of sampling localities (K) was set at 50 and the sample size (Nk/2 individuals) was set at 20 individuals for each sampling point. Figure 2 shows that the conventional estimator for In was positively biased, whereas the empirical Bayes estimator of In performed much better, consistent with the fact that In produces upwardly biased estimates in small samples (Rosenberg et al. 2003).
Figure 2.—
The conventional informativeness of assignment In (Rosenberg et al. 2003) (A) and empirical Bayes (B) estimates of In from 1000 simulations for the case of 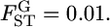 The mean allele frequencies assumed were
The mean allele frequencies assumed were 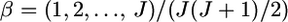 with J = 50. The number of sampling localities (K) was set at 50 and the sample size Nk/2 (individuals) was common to all localities and was set at 20 individuals.
with J = 50. The number of sampling localities (K) was set at 50 and the sample size Nk/2 (individuals) was common to all localities and was set at 20 individuals.
Robustness of our shrinkage estimator for pairwise FST:
The robustness of our 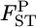 estimator was explored using numerical simulations for non-Dirichlet distributions of the allele frequencies. We considered cases in which genetic differentiation becomes larger with geographic distance. Such a stepping-stone model is biologically realistic and may be common (Palsbøll et al. 2007). We set the number of sampled subpopulations (K) to 15 and the
estimator was explored using numerical simulations for non-Dirichlet distributions of the allele frequencies. We considered cases in which genetic differentiation becomes larger with geographic distance. Such a stepping-stone model is biologically realistic and may be common (Palsbøll et al. 2007). We set the number of sampled subpopulations (K) to 15 and the 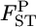 between two adjacent populations to 0.001 (case 1) or 0.0005 (case 2). We considered biallelic cases and set the allele frequencies to (0.5, 0.5) at a locus for the middle population. We then calculated the allele frequencies pkl's at the locus for another 14 subpopulations by numerical optimization. The sample size (Nk/2) was deemed to be common to all localities and was set at 20 individuals. Then, allele counts nk's were drawn independently from the multinomial distribution Multi(Nk, pkl) for 15 localities. A total of 105 pairwise FST values between all sets of the two localities were evaluated by the conventional GST and the empirical Bayes estimator following the simulation protocol described above.
between two adjacent populations to 0.001 (case 1) or 0.0005 (case 2). We considered biallelic cases and set the allele frequencies to (0.5, 0.5) at a locus for the middle population. We then calculated the allele frequencies pkl's at the locus for another 14 subpopulations by numerical optimization. The sample size (Nk/2) was deemed to be common to all localities and was set at 20 individuals. Then, allele counts nk's were drawn independently from the multinomial distribution Multi(Nk, pkl) for 15 localities. A total of 105 pairwise FST values between all sets of the two localities were evaluated by the conventional GST and the empirical Bayes estimator following the simulation protocol described above.
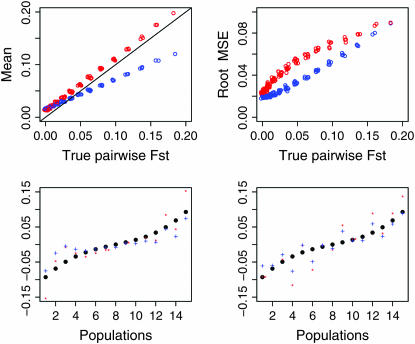
As shown in Figure 3 (case 1) and supplemental Figure S4 at http://www.genetics.org/supplemental/ (case 2, top left), our empirical Bayes procedure provided better estimates than those of the conventional GST estimator for smaller 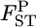 's (∼ <0.06 for case 1 and 0.04 for case 2). In conservation, management units should be defined among subpopulations with little genetic differentiation. Palsbøll et al. (2007) concluded that
's (∼ <0.06 for case 1 and 0.04 for case 2). In conservation, management units should be defined among subpopulations with little genetic differentiation. Palsbøll et al. (2007) concluded that 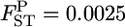 could be used as the criterion for deciding the separate management units of sockeye salmon spawning sites. For such cases with very small genetic differentiation, our method performs more efficiently, even for stepping-stone models. On the contrary, the conventional GST estimator displayed a positive bias for the whole range of
could be used as the criterion for deciding the separate management units of sockeye salmon spawning sites. For such cases with very small genetic differentiation, our method performs more efficiently, even for stepping-stone models. On the contrary, the conventional GST estimator displayed a positive bias for the whole range of 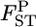 's in both cases. Our method reduced the positive bias for small
's in both cases. Our method reduced the positive bias for small 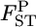 's and the bias became negative for larger
's and the bias became negative for larger 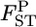 's. Reflecting the characteristics of the shrinkage estimator, the relative mean bias of the empirical Bayes estimator, which was the average of the 105 pairwise FST estimates, was slightly (1.06 times) larger than that of the conventional estimator for case 1 (Table 2). The precision of our estimates was much better for the whole range of
's. Reflecting the characteristics of the shrinkage estimator, the relative mean bias of the empirical Bayes estimator, which was the average of the 105 pairwise FST estimates, was slightly (1.06 times) larger than that of the conventional estimator for case 1 (Table 2). The precision of our estimates was much better for the whole range of 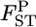 [Figure 3, top right (case 1) and supplemental Figure S4 (case 2)].
[Figure 3, top right (case 1) and supplemental Figure S4 (case 2)].
Figure 3.—
Mean (top left) and root relative mean squared error (top right) of the conventional GST (red circle) and empirical Bayes estimators (blue circle) of pairwise 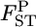 from 1000 simulations under the stepping-stone models. Means and root MSEs were plotted on the true
from 1000 simulations under the stepping-stone models. Means and root MSEs were plotted on the true 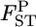 's which fluctuated very slightly when small uniform random variables were added to prevent the points overlapping heavily. The number of subpopulations (K) was set at 15 and the pairwise
's which fluctuated very slightly when small uniform random variables were added to prevent the points overlapping heavily. The number of subpopulations (K) was set at 15 and the pairwise 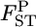 between two adjacent populations was set at 0.001 (case 1) and 0.0005 (case 2). The sample size Nk/2 (individuals) was common to all localities and set at 20 individuals. Only the results for case 1 are shown. The results of the MDS analysis of two data sets are given in the bottom section; black circles show the true population structure, and the estimated population structure based on the conventional (red “*”) and empirical Bayes estimates (blue “+”) of
between two adjacent populations was set at 0.001 (case 1) and 0.0005 (case 2). The sample size Nk/2 (individuals) was common to all localities and set at 20 individuals. Only the results for case 1 are shown. The results of the MDS analysis of two data sets are given in the bottom section; black circles show the true population structure, and the estimated population structure based on the conventional (red “*”) and empirical Bayes estimates (blue “+”) of 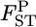 is shown.
is shown.
TABLE 2.
Relative mean bias and root relative mean squared error of the conventional GST and empirical Bayes estimators of pairwise FST from 1000 simulations under the stepping-stone models (see text)
| Relative mean bias
|
Root relative MSE
|
|||
|---|---|---|---|---|
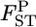 |
Conventional | Empirical Bayes | Conventional | Empirical Bayes |
| 0.001 (case 1) | 1.165 | 1.239 | 2.352 | 1.817 |
| 0.0005 (case 2) | 2.296 | 1.718 | 4.362 | 2.527 |
The number of subpopulations (K) was set at 15 and the pairwise FST between two adjacent populations was set at 0.001 (case 1) and 0.0005 (case 2). The sample size Nk/2 (individuals) was common to the localities and set at 20 individuals.
We also investigated the robustness of estimating population structure on the basis of estimated 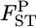 's. The results of the multidimensional scaling (MDS) (Torgerson 1952; Young and Hamer 1987) analysis of two data sets in the simulation showed that our method describes the true population structure well. The conventional GST estimator also worked, despite the larger positive bias and variance (Figure 3, bottom).
's. The results of the multidimensional scaling (MDS) (Torgerson 1952; Young and Hamer 1987) analysis of two data sets in the simulation showed that our method describes the true population structure well. The conventional GST estimator also worked, despite the larger positive bias and variance (Figure 3, bottom).
The case of Pacific herring:
We analyzed six geographical samples of the Pacific herring Clupea pallasii from spawning areas in Lake Akkeshi (AK), Yudonuma Lake (YD), and Funka Bay (FK), which are located off the east coast of Hokkaido in Japan, and Obuchinuma Lake (OB), Miyako Bay (MY), and Matsushima Bay (MT), located off the northern Pacific coast of Honshu. Hatchery fish, released and recaptured in Lake Akkeshi (AKH) and Miyako Bay (MYH), were also distinguished from wild fish on the basis of otoliths stained with alizarin complexon. A total of 2055 mature individuals were genotyped at five microsatellite loci. Allele frequencies are given in supplemental Tables S1–S5 at http://www.genetics.org/supplemental/. HWE was satisfied in each sample except at four localities for three loci, and the assumption of our metapopulation model was considered to be satisfied (supplemental Figure S5). On the basis of the estimates of the hyperparameters (supplemental Figure S6), the scale parameter θl and 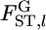 were estimated over all subpopulations (Table 3).
were estimated over all subpopulations (Table 3).
TABLE 3.
Estimated locus-specific scale parameters θ and 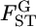 over subpopulations of the Pacific herring, with standard errors in parentheses
over subpopulations of the Pacific herring, with standard errors in parentheses
| Locus | No. alleles | θ | 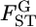 |
|---|---|---|---|
| Cha17 | 48 | 63.98 (7.88) | 0.0154 (0.0019) |
| Cha20 | 30 | 77.26 (13.13) | 0.0128 (0.0021) |
| Cha63 | 35 | 58.21 (8.60) | 0.0169 (0.0025) |
| Cha113 | 29 | 41.68 (6.59) | 0.0234 (0.0036) |
| Cha123 | 50 | 58.78 (6.68) | 0.0167 (0.0018) |
| Meana | 38.4 | 59.98 (3.98) | 0.0170 (0.0011) |
| Meanb | 0.0160 (0.0010) |
Simple mean over all loci.
Weighted mean over all loci, which was equal to the MLE obtained by Equation 3.
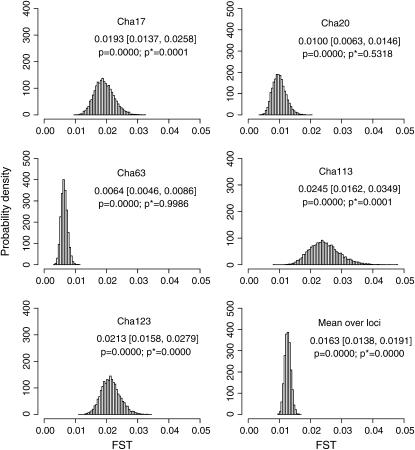
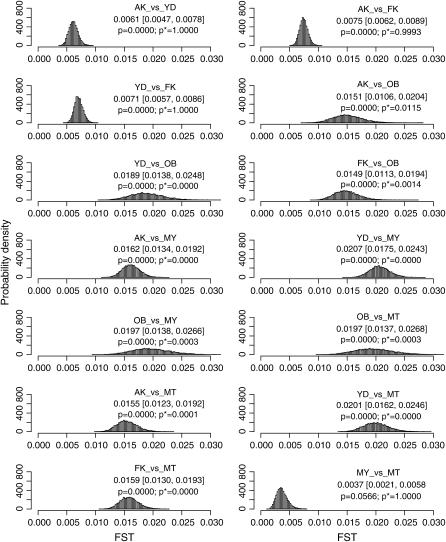
We estimated the posterior distributions of 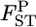 for all sets of subpopulations at all loci. As an example, the posterior distributions between FK and MY at the five loci are shown in Figure 4. The posterior means of
for all sets of subpopulations at all loci. As an example, the posterior distributions between FK and MY at the five loci are shown in Figure 4. The posterior means of 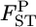 varied from 0.0064 to 0.0245, with the 95% credible intervals in parentheses (Table 4). The P-values in Figures 4 and 5 are for the homogeneity contingency test performed with Genepop (Raymond and Rousset 1995). At all loci, the allelic differences between FK and MY were highly significant (P < 0.0000). We used
varied from 0.0064 to 0.0245, with the 95% credible intervals in parentheses (Table 4). The P-values in Figures 4 and 5 are for the homogeneity contingency test performed with Genepop (Raymond and Rousset 1995). At all loci, the allelic differences between FK and MY were highly significant (P < 0.0000). We used 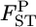 of 0.01 as a population criterion and defined the probability of
of 0.01 as a population criterion and defined the probability of 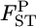 ≤ 0.01 as P*. Here,
≤ 0.01 as P*. Here, 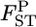 = 0.01 refers to
= 0.01 refers to 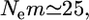 which means that the effective number of migrants is 25 individuals per generation (Waples and Gaggiotti 2006), where Ne is the effective population size and m is the migration rate. The P*-value was near 1.0 for Cha 63, indicating that the genetic differentiation at the locus was small. In contrast, P*-values were 0 or near 0 for Cha 17, Cha 113, and Cha 123 and 0.5318 for Cha 20 (Figure 4). The posterior distribution of the average
which means that the effective number of migrants is 25 individuals per generation (Waples and Gaggiotti 2006), where Ne is the effective population size and m is the migration rate. The P*-value was near 1.0 for Cha 63, indicating that the genetic differentiation at the locus was small. In contrast, P*-values were 0 or near 0 for Cha 17, Cha 113, and Cha 123 and 0.5318 for Cha 20 (Figure 4). The posterior distribution of the average 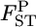 over all the loci was calculated as the mean of the posterior distributions at five loci (Figure 4, bottom right). Both the P- and P*-values coincided at 0, showing significant genetic differentiation between Funka Bay and Miyako Bay.
over all the loci was calculated as the mean of the posterior distributions at five loci (Figure 4, bottom right). Both the P- and P*-values coincided at 0, showing significant genetic differentiation between Funka Bay and Miyako Bay.
Figure 4.—
Posterior distributions of 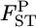 for the Pacific herring between Funka Bay and Miyako Bay at each locus, and over all loci, which were averaged over
for the Pacific herring between Funka Bay and Miyako Bay at each locus, and over all loci, which were averaged over 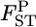 at five loci.
at five loci.
TABLE 4.
Posterior means and 95% credible and confidence intervals for pairwise FST of the Pacific herring between Funka Bay and Miyako Bay at each locus
| Locus | d.f. | Posterior mean | Empirical Bayes | Weir and Hilla |
|---|---|---|---|---|
| Cha17 | 47 | 0.0193 | [0.0137, 0.0258] | [0.0133, 0.0302] |
| Cha20 | 29 | 0.0100 | [0.0063, 0.0146] | [0.0063, 0.0180] |
| Cha63 | 34 | 0.0064 | [0.0046, 0.0086] | [0.0042, 0.0111] |
| Cha113 | 28 | 0.0245 | [0.0162, 0.0349] | [0.0154, 0.0448] |
| Cha123 | 49 | 0.0213 | [0.0158, 0.0279] | [0.0149, 0.0331] |
| Mean | 1309 | 0.0163 | [0.0138, 0.0191] | [0.0151, 0.0176] |
Estimated by Weir and Hill's (2002) normal theory approach.
Figure 5.—
Posterior distributions of 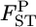 for the Pacific herring over all loci, which were averaged over
for the Pacific herring over all loci, which were averaged over 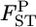 for five loci: AK, Lake Akkeshi; YD, Yudonuma Lake; FK, Funka Bay; OB, Obuchinuma Lake; MY, Miyako Bay; and MT, Matsushima Bay.
for five loci: AK, Lake Akkeshi; YD, Yudonuma Lake; FK, Funka Bay; OB, Obuchinuma Lake; MY, Miyako Bay; and MT, Matsushima Bay.
The posterior distributions of average 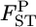 over all loci for all pairs of wild subpopulations were also simulated as simple means of the posterior distributions at five loci (Figure 5). The allelic differences were highly significant with P = 0.0000, except between MY and MT. The criterion P* resulted in a very different evaluation of population differentiation, even for the same P-value of 0.0000. This result clearly shows the difficulty in the hypothesis-testing framework in evaluating the genetic differentiation between subpopulations (e.g., Dizon et al. 1995; Ryman and Jorde 2001; Ryman et al. 2006). The P*-based criterion works well in this case and is recommended for use in hypothesis testing.
over all loci for all pairs of wild subpopulations were also simulated as simple means of the posterior distributions at five loci (Figure 5). The allelic differences were highly significant with P = 0.0000, except between MY and MT. The criterion P* resulted in a very different evaluation of population differentiation, even for the same P-value of 0.0000. This result clearly shows the difficulty in the hypothesis-testing framework in evaluating the genetic differentiation between subpopulations (e.g., Dizon et al. 1995; Ryman and Jorde 2001; Ryman et al. 2006). The P*-based criterion works well in this case and is recommended for use in hypothesis testing.
The variation in 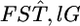 over five loci was not trivial, with a coefficient of variation (CV) of 23% (Table 3). However, the negative twice log-likelihood ratio λ was calculated to be 6.9264 and the hypothesis of constant
over five loci was not trivial, with a coefficient of variation (CV) of 23% (Table 3). However, the negative twice log-likelihood ratio λ was calculated to be 6.9264 and the hypothesis of constant 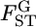 for all loci was not rejected (P = 0.8602, d.f. = 4). We estimated the distribution of
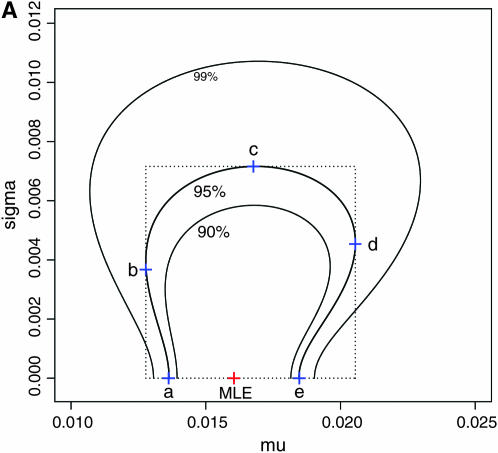
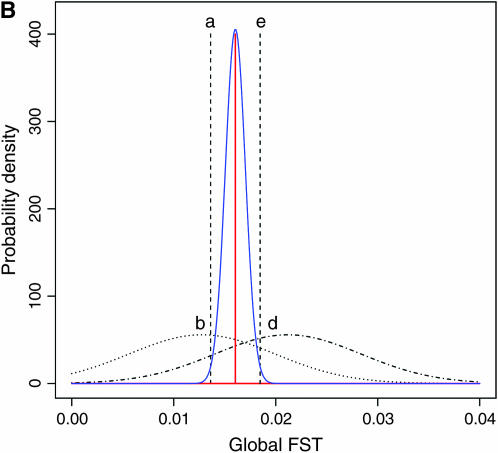
for all loci was not rejected (P = 0.8602, d.f. = 4). We estimated the distribution of 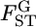 in the genome, assuming normality based on Equation 6. The maximum-likelihood estimates (MLEs) for μ and σ were obtained with 90, 95, and 99% confidence intervals, which define the distribution of
in the genome, assuming normality based on Equation 6. The maximum-likelihood estimates (MLEs) for μ and σ were obtained with 90, 95, and 99% confidence intervals, which define the distribution of 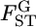 in the genome via the likelihood profile (Figure 6A). The MLE for μ, with the 95% confidence interval, was 0.0160 (0.0128, 0.0206) [Figure 6A (a, e)] and for σ was 0 (0, 0.00716) [Figure 6A (0, c)]. The weighted mean
in the genome via the likelihood profile (Figure 6A). The MLE for μ, with the 95% confidence interval, was 0.0160 (0.0128, 0.0206) [Figure 6A (a, e)] and for σ was 0 (0, 0.00716) [Figure 6A (0, c)]. The weighted mean 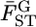 coincided with the MLE of μ (Table 3) and the distribution of the weighted mean
coincided with the MLE of μ (Table 3) and the distribution of the weighted mean 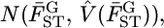 shown as the blue line in Figure 6B, described well the 95% confidence interval of μ [Figure 6A (a, e)]. Here,
shown as the blue line in Figure 6B, described well the 95% confidence interval of μ [Figure 6A (a, e)]. Here, 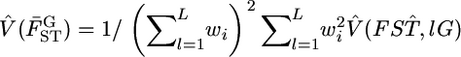 and
and 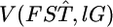 were estimated with Equation 3. The log-likelihood profile for σ was monotonic and decreasing, indicating that the point estimate of σ was 0 (supplemental Figure S7 at http://www.genetics.org/supplemental/). Hence, the point estimate of the distribution of
were estimated with Equation 3. The log-likelihood profile for σ was monotonic and decreasing, indicating that the point estimate of σ was 0 (supplemental Figure S7 at http://www.genetics.org/supplemental/). Hence, the point estimate of the distribution of 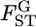 for the Pacific herring is constant, supporting the hypothesis of constant
for the Pacific herring is constant, supporting the hypothesis of constant 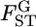 throughout the genome. However, the distribution of
throughout the genome. However, the distribution of 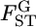 has uncertainty, which accounts for the confidence regions of μ and σ (Figure 6B).
has uncertainty, which accounts for the confidence regions of μ and σ (Figure 6B).
Figure 6.—
Confidence regions of the distribution of 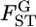 in the genome of the Pacific herring, assuming a normal distribution (see the text). (A) The confidence regions of μ and σ2, which specify the distribution. (B) The MLE distribution (red line, the delta distribution) and the representative distributions on the boundary of the confidence regions (a–e), which correspond to the points in A. The distribution of the weighted mean of
in the genome of the Pacific herring, assuming a normal distribution (see the text). (A) The confidence regions of μ and σ2, which specify the distribution. (B) The MLE distribution (red line, the delta distribution) and the representative distributions on the boundary of the confidence regions (a–e), which correspond to the points in A. The distribution of the weighted mean of 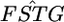 is superimposed (blue line).
is superimposed (blue line).
DISCUSSION
Our empirical Bayes estimator of 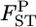 performed better than the conventional GST estimator for various levels of
performed better than the conventional GST estimator for various levels of 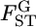 and various sampling conditions under the infinite-island model. Even for non-Dirichlet distributions of allele frequencies, such as stepping-stone models, our method provided better estimates of
and various sampling conditions under the infinite-island model. Even for non-Dirichlet distributions of allele frequencies, such as stepping-stone models, our method provided better estimates of 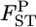 than did the conventional GST, especially for cases with large gene flow.
than did the conventional GST, especially for cases with large gene flow.
Integrated likelihood method:
The empirical Bayes estimator of 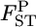 's is negatively biased, especially when the population has large gene flow and the estimation is based on a sample from only a few sampling points (Table 1, supplemental Figure S2 at http://www.genetics.org/supplemental/). With a small number of sampling points, the MLE of θ is not precise. Therefore, it is recommended in the conservation genetic analysis of such a population that the samples be collected from as many sampling points as possible. When sampling from many localities is not feasible, the integrated-likelihood method (Kitakado et al. 2006) can reduce the negative bias of
's is negatively biased, especially when the population has large gene flow and the estimation is based on a sample from only a few sampling points (Table 1, supplemental Figure S2 at http://www.genetics.org/supplemental/). With a small number of sampling points, the MLE of θ is not precise. Therefore, it is recommended in the conservation genetic analysis of such a population that the samples be collected from as many sampling points as possible. When sampling from many localities is not feasible, the integrated-likelihood method (Kitakado et al. 2006) can reduce the negative bias of 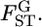 We estimated pairwise
We estimated pairwise 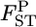 's by the empirical Bayes method based on integrated-likelihood estimates (ILEs) of θ for cases with
's by the empirical Bayes method based on integrated-likelihood estimates (ILEs) of θ for cases with 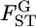 = 0.01, K = 5, and Nk/2 = 20, 30, or 50 with the same simulation protocol used for Table 1 (supplemental Figure S8 at http://www.genetics.org/supplemental/). The relative mean biases of the
= 0.01, K = 5, and Nk/2 = 20, 30, or 50 with the same simulation protocol used for Table 1 (supplemental Figure S8 at http://www.genetics.org/supplemental/). The relative mean biases of the 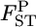 estimates, with root relative mean squared errors in parentheses, were −0.238 (0.506), −0.132 (0.365), and −0.060 (0.272), respectively. These values were much smaller than those estimated on the basis of the MLE of θ, given in Table 1 (top three rows). The negative bias of
estimates, with root relative mean squared errors in parentheses, were −0.238 (0.506), −0.132 (0.365), and −0.060 (0.272), respectively. These values were much smaller than those estimated on the basis of the MLE of θ, given in Table 1 (top three rows). The negative bias of 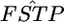 's based on the MLE was reduced to 32.8, 24.4, and 18.2% for Nk/2 = 20, 30, and 50, respectively. The integrated-likelihood method uses a uniform prior for the mean allele frequency βl and eliminates βl by integration regarding it as a nuisance parameter. By using the ILE of θ instead of the MLE, the empirical Bayes method proposed here provides nearly unbiased estimates of
's based on the MLE was reduced to 32.8, 24.4, and 18.2% for Nk/2 = 20, 30, and 50, respectively. The integrated-likelihood method uses a uniform prior for the mean allele frequency βl and eliminates βl by integration regarding it as a nuisance parameter. By using the ILE of θ instead of the MLE, the empirical Bayes method proposed here provides nearly unbiased estimates of 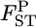 's when the sample sizes (Nk/2 individuals) are large and works more efficiently, even for cases with a small number of sampling points (supplemental Figure S8).
's when the sample sizes (Nk/2 individuals) are large and works more efficiently, even for cases with a small number of sampling points (supplemental Figure S8).
Weir and Cockerham's θ̂WC:
When we estimate genetic differentiation between two specific subpopulations, selected subpopulations can be regarded as the entire set of populations. Nei's GST formula defines quantities with respect to fixed extant populations (Cockerham and Weir 1986). In addition, GST is a function of allele frequencies under HWE, and the posterior distribution can easily be simulated from only allele frequencies. Therefore, we used the GST estimator to estimate the posterior distribution of pairwise FST.
The citation record suggests that the most widely used estimator for Wright's FST is Weir and Cockerham's 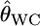 (Weir and Hill 2002). This moment estimator takes the sampling error for subpopulations into account and essentially estimates the global FST,
(Weir and Hill 2002). This moment estimator takes the sampling error for subpopulations into account and essentially estimates the global FST, 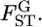 The estimator is also widely used to estimate pairwise FST's among fixed pairs of populations. With the assumption of no local inbreeding, θWC is estimated only from sample allele frequencies, but these need to be inferred from sample genotype frequencies (Weir and Hill 2002). With J alleles at a locus, the number of possible genotypes is J(J + 1)/2. In microsatellite DNA analyses, J is generally large. If J = 50, the number of genotypes is 1225. Such a situation makes our simulation more complicated and the uncertainty of the genotype counts becomes large under small or moderate sample sizes.
The estimator is also widely used to estimate pairwise FST's among fixed pairs of populations. With the assumption of no local inbreeding, θWC is estimated only from sample allele frequencies, but these need to be inferred from sample genotype frequencies (Weir and Hill 2002). With J alleles at a locus, the number of possible genotypes is J(J + 1)/2. In microsatellite DNA analyses, J is generally large. If J = 50, the number of genotypes is 1225. Such a situation makes our simulation more complicated and the uncertainty of the genotype counts becomes large under small or moderate sample sizes.
Here, we investigated the properties of 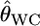 on estimating pairwise FST on the basis of the relationship between GST and θWC. Weir and Cockerham's estimates
on estimating pairwise FST on the basis of the relationship between GST and θWC. Weir and Cockerham's estimates 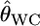 can be approximated as a function of GST by Equation 2 in Weicker et al. (2001):
can be approximated as a function of GST by Equation 2 in Weicker et al. (2001): 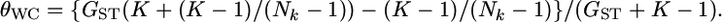 Using this equation, we calculated the conventional estimates of pairwise Weir and Cockerham's θWC from GST estimates with the simulation protocol described in results. We examined cases with a global FST of
Using this equation, we calculated the conventional estimates of pairwise Weir and Cockerham's θWC from GST estimates with the simulation protocol described in results. We examined cases with a global FST of 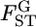 = 0.01, 0.05, 0.1, and 0.2. The mean allele frequencies were assumed
= 0.01, 0.05, 0.1, and 0.2. The mean allele frequencies were assumed 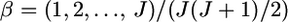 with J = 50. The number of sampling localities K was set at 10 and the sample size Nk/2 (individuals) was deemed to be common to all the localities and was set at 50 individuals. As shown in supplemental Figure S9 at http://www.genetics.org/supplemental/, the two estimators have linear relationships. Hence, our simulation results on the conventional GST estimator can be extended straightforwardly to pairwise θWC. In fact, the pairwise
with J = 50. The number of sampling localities K was set at 10 and the sample size Nk/2 (individuals) was deemed to be common to all the localities and was set at 50 individuals. As shown in supplemental Figure S9 at http://www.genetics.org/supplemental/, the two estimators have linear relationships. Hence, our simulation results on the conventional GST estimator can be extended straightforwardly to pairwise θWC. In fact, the pairwise 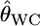 -values calculated for the Pacific herring with Genepop (Raymond and Rousset 1995) were 1.93 ± 0.47 times larger than the posterior means of
-values calculated for the Pacific herring with Genepop (Raymond and Rousset 1995) were 1.93 ± 0.47 times larger than the posterior means of 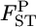 (supplemental Figure S10 at http://www.genetics.org/supplemental/), which coincides with our simulations for small
(supplemental Figure S10 at http://www.genetics.org/supplemental/), which coincides with our simulations for small 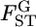 's (Figure 1, supplemental Figures S1 and S11).
's (Figure 1, supplemental Figures S1 and S11).
Weir and Cockerham's estimator 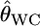 is nearly unbiased (Raufaste and Bonhomme 2000), although it has a negative bias for the two-allele case (Weir and Hill 2002). Nevertheless, when estimating the pairwise FST,
is nearly unbiased (Raufaste and Bonhomme 2000), although it has a negative bias for the two-allele case (Weir and Hill 2002). Nevertheless, when estimating the pairwise FST, 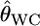 is considered to have a large positive bias, especially for species with large gene flows. Nei's GST and Rosenberg et al.'s informativeness of assignment In also showed the same phenomenon, suggesting the positive bias is irrelevant to the estimators. This positive bias of the conventional estimators was larger for smaller genetic differentiation. This might be caused by the large variation in the sample allele frequencies, which is larger for smaller sample sizes (individuals) and largely exceeded the real variation between subpopulations. The shrinkage estimator stabilizes such variation and provides better estimates.
is considered to have a large positive bias, especially for species with large gene flows. Nei's GST and Rosenberg et al.'s informativeness of assignment In also showed the same phenomenon, suggesting the positive bias is irrelevant to the estimators. This positive bias of the conventional estimators was larger for smaller genetic differentiation. This might be caused by the large variation in the sample allele frequencies, which is larger for smaller sample sizes (individuals) and largely exceeded the real variation between subpopulations. The shrinkage estimator stabilizes such variation and provides better estimates.
Weir and Hill's normal theory:
Weir and Hill's (2002) normal theory approach has the same variance as a Dirichlet distribution when i ≠ i′ in their notation. Hence, their estimator 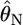 is equivalent to our
is equivalent to our 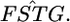
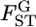 is the variance of the allele frequencies among subpopulations relative to the total population. Hence,
is the variance of the allele frequencies among subpopulations relative to the total population. Hence, 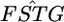 refers to a sample variance of allele frequencies, and therefore
refers to a sample variance of allele frequencies, and therefore 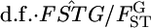 follows a χ2-distribution when the number of sampling points K is sufficiently large, as shown by Weir and Hill (2002). The shape of the posterior distribution of
follows a χ2-distribution when the number of sampling points K is sufficiently large, as shown by Weir and Hill (2002). The shape of the posterior distribution of 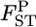 at each locus was unimodal and slightly right tailed, which reminded us of χ2-distributions (Figure 4). We estimated Weir and Hill's confidence intervals by substituting the posterior mean of
at each locus was unimodal and slightly right tailed, which reminded us of χ2-distributions (Figure 4). We estimated Weir and Hill's confidence intervals by substituting the posterior mean of 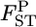 with
with 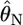 as
as 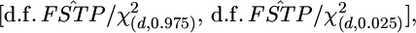 where d.f. = (K − 1)(J − 1) is the degrees of freedom. The confidence intervals of
where d.f. = (K − 1)(J − 1) is the degrees of freedom. The confidence intervals of 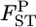 obtained with the χ2-approximation coincided well with the credible intervals calculated from the posterior distributions, although our credible intervals were narrower than the confidence intervals of the χ2-approximation, which were slightly right tailed (Table 4). The slight difference in the intervals might have been the effect of the small K(= 8) on the χ2-approximation, although it was not substantial. On the contrary, the confidence interval for the sample mean over all loci was narrower than our credible interval (Table 4). The distribution of a sample mean is normal when the sample size is large with the variance reduced by the central limit theorem. A χ2-distribution approaches a normal distribution as the degrees of freedom become larger. For our case of 1309 d.f. [
obtained with the χ2-approximation coincided well with the credible intervals calculated from the posterior distributions, although our credible intervals were narrower than the confidence intervals of the χ2-approximation, which were slightly right tailed (Table 4). The slight difference in the intervals might have been the effect of the small K(= 8) on the χ2-approximation, although it was not substantial. On the contrary, the confidence interval for the sample mean over all loci was narrower than our credible interval (Table 4). The distribution of a sample mean is normal when the sample size is large with the variance reduced by the central limit theorem. A χ2-distribution approaches a normal distribution as the degrees of freedom become larger. For our case of 1309 d.f. [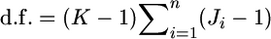 as given in Weir and Hill 2002], the two distributions are equal. The property of the sample mean should cause the narrower confidence interval of the normal theory approach. The result shows that the posterior distribution of
as given in Weir and Hill 2002], the two distributions are equal. The property of the sample mean should cause the narrower confidence interval of the normal theory approach. The result shows that the posterior distribution of 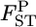 describes the distribution of
describes the distribution of 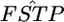 well, both for each locus and for the average over all loci.
well, both for each locus and for the average over all loci.
LD among loci:
The case study of the Pacific herring, based on a few microsatellite markers, did not detect significant variation in 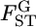 among loci in the genome (Figure 6). The assumption of normality for the MLE of
among loci in the genome (Figure 6). The assumption of normality for the MLE of 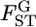 is valid when more than a few sampling points are surveyed. This assumption might be violated when the data are collected from only a few sampling points or
is valid when more than a few sampling points are surveyed. This assumption might be violated when the data are collected from only a few sampling points or 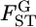 is close to 0 or 1.0. We also assumed the independence of loci
is close to 0 or 1.0. We also assumed the independence of loci 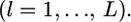 However, it is necessary to take into account the linkage disequilibrium (LD) among loci, when the molecular markers are tightly linked.
However, it is necessary to take into account the linkage disequilibrium (LD) among loci, when the molecular markers are tightly linked.
Recent progress in whole-genome analysis of human populations provides a new perspective on the inference of FST and its distribution in genomes (Garte 2003; Hinds et al. 2005; Weir et al. 2005; Walsh et al. 2006). In their Figure 1, Weir et al. (2005) showed that values for the single-locus marker 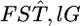 over the whole human genome for three (Perlegen) or four (HapMap) populations had a distribution very much like the χ2-distributions with 2 or 3 d.f. and suggested that values of
over the whole human genome for three (Perlegen) or four (HapMap) populations had a distribution very much like the χ2-distributions with 2 or 3 d.f. and suggested that values of 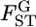 are genome-region specific. However,
are genome-region specific. However, 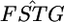 follows a χ2-distribution under constant
follows a χ2-distribution under constant 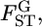 as reported by Weir and Hill (2002) and as demonstrated in our analysis of the Pacific herring. Therefore, the distributions of the values for the single-locus marker
as reported by Weir and Hill (2002) and as demonstrated in our analysis of the Pacific herring. Therefore, the distributions of the values for the single-locus marker 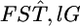 in Weir et al. (2005) do not necessarily support the genome-region-specific FST hypothesis in the human genome.
in Weir et al. (2005) do not necessarily support the genome-region-specific FST hypothesis in the human genome.
Weir et al.'s 5-Mb window average values for 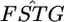 were close to normal because of the property of the sample mean. The standard deviations (SDs) of the 5-Mb window average values of
were close to normal because of the property of the sample mean. The standard deviations (SDs) of the 5-Mb window average values of 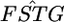 decreased substantially from single-locus estimates of 0.12 to 0.02 for HapMap and from 0.11 to 0.02 for Perlegen (Tables 2 and 3 in Weir et al. 2005). The average number of markers in a 5-Mb window was 1114 for HapMap and 1834 for Perlegen (calculated from Table 1 in Weir et al. 2005). Hence, these SDs are expected to be
decreased substantially from single-locus estimates of 0.12 to 0.02 for HapMap and from 0.11 to 0.02 for Perlegen (Tables 2 and 3 in Weir et al. 2005). The average number of markers in a 5-Mb window was 1114 for HapMap and 1834 for Perlegen (calculated from Table 1 in Weir et al. 2005). Hence, these SDs are expected to be 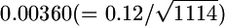 and
and 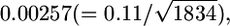 if all SNPs are independent and distributed identically in the genome. The effective sample size (Kish 1965, p. 259) could be much smaller than the real number of SNPs in the 5-Mb windows if the
if all SNPs are independent and distributed identically in the genome. The effective sample size (Kish 1965, p. 259) could be much smaller than the real number of SNPs in the 5-Mb windows if the  's are correlated, because of LD between the SNPs. A coalescent simulation of human population history implies that linkage equilibrium holds for SNPs separated by >10–100 kb (Figure 1 in Kruglyak 1999). Therefore, we can estimate the effective number of human SNPs per 100-kb window to be ∼1–20. If we assumed it to be ∼10, the effective number of SNPs per 5-Mb window becomes 500. Therefore, the SDs of the 5-Mb window
's are correlated, because of LD between the SNPs. A coalescent simulation of human population history implies that linkage equilibrium holds for SNPs separated by >10–100 kb (Figure 1 in Kruglyak 1999). Therefore, we can estimate the effective number of human SNPs per 100-kb window to be ∼1–20. If we assumed it to be ∼10, the effective number of SNPs per 5-Mb window becomes 500. Therefore, the SDs of the 5-Mb window 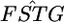 are expected to be
are expected to be 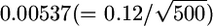 for HapMap and
for HapMap and 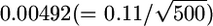 for Perlegen. The actual value (0.02) is much larger than these, even when the LD among the SNPs is taken into account. This discrepancy can be explained by the large-scale heterogeneity of FST between the 5-Mb windows. New data show that LD is highly structured into discrete blocks of sequences separated by hot spots of recombination (Goldstein 2001; McVean et al. 2004) and differs among species (Hernandez et al. 2007). The simultaneous estimation of FST's of SNPs and the LD between the SNPs should give us an accurate picture of the distribution of FST in genomes.
for Perlegen. The actual value (0.02) is much larger than these, even when the LD among the SNPs is taken into account. This discrepancy can be explained by the large-scale heterogeneity of FST between the 5-Mb windows. New data show that LD is highly structured into discrete blocks of sequences separated by hot spots of recombination (Goldstein 2001; McVean et al. 2004) and differs among species (Hernandez et al. 2007). The simultaneous estimation of FST's of SNPs and the LD between the SNPs should give us an accurate picture of the distribution of FST in genomes.
Acknowledgments
We are grateful to Bruce Weir for valuable comments on the manuscript and encouragement with this work. We also thank the anonymous reviewers for their constructive comments, which improved the earlier version of the manuscript. This work was supported by grants from the Japan Society for the Promotion of Science.
References
- Balding, D. J., 2003. Likelihood-based inference for genetic correlation coefficients. Theor. Popul. Biol. 63: 221–230. [DOI] [PubMed] [Google Scholar]
- Balding, D. J., and R. A. Nichols, 1997. Significant genetic correlations among Caucasians at forensic DNA loci. Heredity 78: 583–589. [DOI] [PubMed] [Google Scholar]
- Balloux, F., and N. Lugon-Moulin, 2002. The estimation of population differentiation with microsatellite markers. Mol. Ecol. 11: 155–165. [DOI] [PubMed] [Google Scholar]
- Cockerham, C. C., 1969. Variance of gene frequencies. Evolution 23: 72–83. [DOI] [PubMed] [Google Scholar]
- Cockerham, C. C., 1973. Analysis of gene frequencies. Genetics 74: 679–700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockerham, C. C., and B. S. Weir, 1986. Estimation of inbreeding parameters in stratified populations. Ann. Hum. Genet. 50: 271–281. [DOI] [PubMed] [Google Scholar]
- Corander, J., P. Waldmann and M. J. Sillanpää, 2003. Bayesian analysis of genetic differentiation between populations. Genetics 163: 367–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dizon, A. E., B. L. Taylor and G. M. O'Corry-Crowe, 1995. Why statistical power is necessary to link analyses of molecular variation to decisions about population structure, pp. 288–294 in Evolution and the Aquatic Ecosystem, edited by J. L. Nielsen and D. A. Powers. American Fisheries Society Symposium 17, Bethesda, MD.
- Ewens, W. J., 2004. Mathematical Population Genetics, I. Theoretical Introduction, Ed. 2. Springer, Berlin/Heidelberg, Germany/New York.
- Excoffier, L., 2003. Analysis of population subdivision, pp. 713–750 in Handbook of Statistical Genetics, Ed. 2, edited by D. J. Balding, M. Bishop and C. Cannings. Wiley, Chichester, UK.
- Excoffier, L., G. Laval and S. Schneider, 2005. Arlequin ver. 3.0: an integrated software package for population genetics data analysis. Evol. Bioinform. Online 1: 47–50. [PMC free article] [PubMed] [Google Scholar]
- Garte, S., 2003. Locus-specific genetic diversity between human populations: an analysis of the literature. Am. J. Hum. Biol. 15: 814–823. [DOI] [PubMed] [Google Scholar]
- Goldstein, D. B., 2001. Islands of linkage disequilibrium. Nat. Genet. 29: 109–111. [DOI] [PubMed] [Google Scholar]
- Goudet, J., 1995. FSTAT (version 1.2): a computer program to calculate F-statistics. J. Hered. 86: 485–486. [Google Scholar]
- Goudet, J., M. Raymond, T. de Meeüs and F. Rousset, 1996. Testing differentiation in diploid populations. Genetics 144: 1933–1940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanski, I., and O. E. Gaggiotti, 2004. Ecology, Genetics, and Evolution of Metapopulations. Academic Press, San Diego.
- Hernandez, R. D., M. J. Hubisz, D. A. Wheeler, D. G. Smith, B. Ferguson et al., 2007. Demographic histories and patterns of linkage disequilibrium in Chinese and Indian rhesus macaques. Science 316: 240–243. [DOI] [PubMed] [Google Scholar]
- Hinds, D. A., L. L. Stuve, G. B. Nelsen, E. Halperin, E. Eskin et al., 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307: 1072–1079. [DOI] [PubMed] [Google Scholar]
- Holsinger, K. E., 1999. Analysis of genetic diversity in geographically structured populations: a Bayesian perspective. Hereditas 130: 245–255. [Google Scholar]
- Holsinger, K. E., P. O. Lewis and D. K. Dey, 2002. A Bayesian approach to inferring population structure from dominant markers. Mol. Ecol. 11: 1157–1164. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck, J. P., and P. Andolfatto, 2007. Inference of population structure under a Dirichlet process model. Genetics 175: 1787–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kish, L., 1965. Survey Sampling. Wiley, New York.
- Kitada, S., and H. Kishino, 2004. Simultaneous detection of linkage disequilibrium and genetic differentiation of subdivided populations. Genetics 167: 2003–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitada, S., T. Hayashi and H. Kishino, 2000. Empirical Bayes procedure for estimating genetic distance between populations and effective population size. Genetics 156: 2063–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitakado, T., S. Kitada, H. Kishino and H. J. Skaug, 2006. An integrated-likelihood method for estimating genetic differentiation between populations. Genetics 173: 2073–2082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak, L., 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22: 139–144. [DOI] [PubMed] [Google Scholar]
- Lange, K., 1995. Application of the Dirichlet distribution to forensic match probabilities. Genetica 96: 107–117. [DOI] [PubMed] [Google Scholar]
- Lockwood, J. R., K. Roeder and B. Devlin, 2001. A Bayesian hierarchical model for allele frequencies. Genet. Epidemiol. 20: 17–33. [DOI] [PubMed] [Google Scholar]
- Maritz, J. S., and T. L. Lewin, 1989. Empirical Bayes Methods, Ed. 2. Chapman & Hall, London.
- McVean, G. A. T., S. R. Myers, S. Hunt, P. Deloukas, D. R. Bentley et al., 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]
- Nei, M., 1973. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 70: 3321–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., and R. K. Chesser, 1983. Estimation of fixation indices and gene diversities. Ann. Hum. Genet. 47: 253–259. [DOI] [PubMed] [Google Scholar]
- Paetkau, D., W. Calvert, I. Stirling and C. Strobeck, 1995. Microsatellite analysis of population structure in Canadian polar bears. Mol. Ecol. 4: 347–354. [DOI] [PubMed] [Google Scholar]
- Palsbøll, P. J., M. Bérubé and F. W. Allendorf, 2007. Identification of management units using population genetic data. Trends Ecol. Evol. 22: 11–16. [DOI] [PubMed] [Google Scholar]
- Pannell, J. R., and B. Charlesworth, 2000. Effects of metapopulation processes on measures of genetic diversity. Philos. Trans. R. Soc. Lond. B 355: 1851–1864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. Inference of population structure using multilocus genotype data. Genetics 156: 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala, B., and J. A. Hartigan, 1996. Estimating gene flow in island populations. Genet. Res. 67: 147–158. [DOI] [PubMed] [Google Scholar]
- Raufaste, N., and F. Bonhomme, 2000. Properties of bias and variance of two multiallelic estimators of FST. Theor. Popul. Biol. 57: 285–296. [DOI] [PubMed] [Google Scholar]
- Raymond, M., and F. Rousset, 1995. GENEPOP (version 3.4): population genetics software for exact tests and ecumenicism. J. Hered. 86: 248–249. [Google Scholar]
- Reynolds, J., B. S. Weirs and C. C. Cockerham, 1983. Estimation of the coancestry coefficient: basis for a short-term genetic distance. Genetics 105: 767–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson, A., and W. G. Hill, 1984. Deviation from Hardy–Weinberg proportions: sample variances and use in estimation of inbreeding coefficients. Genetics 107: 703–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg, N. A., L. M. Li, R. Ward and J. K. Pritchard, 2003. Informativeness of genetic markers for inference of ancestry. Am. J. Hum. Genet. 73: 1402–1422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset, F., 2003. Inferences from spatial population genetics, pp. 681–712 in Handbook of Statistical Genetics, Ed. 2, edited by D. J. Balding, M. Bishop and C. Cannings. John Wiley & Sons, Chichester, UK.
- Ryman, N., and P. E. Jorde, 2001. Statistical power when testing for genetic differentiation. Mol. Ecol. 10: 2361–2373. [DOI] [PubMed] [Google Scholar]
- Ryman, N., S. Palm, C. André, G. R. Carvalho, T. G. Dahlgren et al., 2006. Power for detecting genetic divergence: differences between statistical methods and marker loci. Mol. Ecol. 15: 2031–2045. [DOI] [PubMed] [Google Scholar]
- Seber, G. A. F., 1982. The Estimation of Animal Abundance and Related Parameters, Ed. 2. Griffin, London.
- Stein, C., 1956. Inadmissibility of the usual estimator for the mean of a multivariate distribution. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, California, Vol. 1, pp. 197–206. University of California Press, Berkeley, CA.
- Torgerson, W. S., 1952. Multidimensional scaling: 1. theory and methods. Psychometrika 17: 401–419. [Google Scholar]
- Walsh, R. D., P. Sabeti, H. B. Hutcheson, B. Fry, S. F. Schaffner et al., 2006. Searching for signals of evolutionary selection in 168 genes related to immune function. Hum. Genet. 119: 92–102. [DOI] [PubMed] [Google Scholar]
- Waples, R. S., and O. Gaggiotti, 2006. What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol. Ecol. 15: 1419–1439. [DOI] [PubMed] [Google Scholar]
- Weicker, J. J., R. T. Brumfield and K. Winker, 2001. Estimating the unbiased estimator θ for population genetic survey data. Evolution 55: 2601–2605. [DOI] [PubMed] [Google Scholar]
- Weir, B. S., 1996. Genetic Data Analysis II. Sinauer Associates, Sunderland, MA.
- Weir, B. S., and C. C. Cockerham, 1984. Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370. [DOI] [PubMed] [Google Scholar]
- Weir, B. S., and W. G. Hill, 2002. Estimating F-statistics. Annu. Rev. Genet. 36: 721–750. [DOI] [PubMed] [Google Scholar]
- Weir, B. S., L. R. Cardon, A. D. Anderson, D. M. Nielsen and W. G. Hill, 2005. Measures of human population structure show heterogeneity among genomic regions. Genome Res. 15: 1468–1476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S., 1951. The general structure of populations. Ann. Eugen. 15: 323–354. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1969. Evolution and the Genetics of Populations: The Theory of Gene Frequencies, Vol. 2. University of Chicago Press, Chicago.
- Young, F. W., and R. M. Hamer, 1987. Multidimensional Scaling: History, Theory and Applications. Erlbaum, New York.