Reconciling Strong Stabilizing Selection with the Maintenance of Genetic Variation in a Natural Population of Black Field Crickets (Teleogryllus commodus)

Abstract

Genetic variation in single traits, including those closely related to fitness, is pervasive and generally high. By contrast, theory predicts that several forms of selection, including stabilizing selection, will eliminate genetic variation. Stabilizing selection in natural populations tends to be stronger than that assumed in theoretical models of the maintenance of genetic variation. The widespread presence of genetic variation in the presence of strong stabilizing selection is a persistent problem in evolutionary genetics that currently has no compelling explanation. The recent insight that stabilizing selection often acts most strongly on trait combinations via correlational selection may reconcile this problem. Here we show that for a set of male call properties in the cricket Teleogryllus commodus, the pattern of multivariate stabilizing sexual selection is closely associated with the degree of additive genetic variance. The multivariate trait combinations experiencing the strongest stabilizing selection harbored very little genetic variation while combinations under weak selection contained most of the genetic variation. Our experiment provides empirical support for the prediction that a small number of trait combinations experiencing strong stabilizing selection will have reduced genetic variance and that genetically independent trait combinations experiencing weak selection can simultaneously harbor much higher levels of genetic variance.

THE presence of genetic variation in almost all traits has been exhaustively documented in natural populations (Lynch and Walsh 1998; Partridge and Barton 2000), and yet explaining the maintenance of this variation in the presence of selection represents one of the most persistent challenges in evolutionary biology (Barton and Turelli 1989; Barton and Keightley 2002; Blows and Hoffmann 2005). Traits strongly associated with fitness tend to show lower heritabilities than those less strongly associated with fitness (Gustafsson 1986; Mousseau and Roff 1987), but this is a consequence of these traits tending to have higher environmental variances (Houle 1992). When scaled appropriately, traits closely related to fitness tend to harbor more genetic variation than those more distant from fitness (Houle 1992).

Several forms of selection, particularly stabilizing selection, should deplete genetic variation (Barton and Turelli 1989; Roff 1997; Bürger 2000; Barton and Keightley 2002). Although stabilizing selection is not more common than other types of nonlinear selection in natural populations (Kingsolver et al. 2001; Brooks et al. 2005), when it occurs it is much stronger than assumed in theoretical models (Johnson and Barton 2005). Moreover, stabilizing selection is likely to be a widespread cause of stasis over longer evolutionary timescales (Estes and Arnold 2007). The ubiquity of genetic variation despite the presence of stabilizing selection currently has no compelling explanation (Johnson and Barton 2005). The conflict between these two fundamental observations has provided the impetus for the large body of theory devoted to exploring whether a balance between mutation and stabilizing selection can maintain genetic variation (Slatkin and Frank 1990; Kondrashov and Turelli 1992; Zhang et al. 2002; Zhang and Hill 2003; Johnson and Barton 2005) or whether other mechanisms are required to maintain genetic variance, such as balancing selection generated by environment- or sex-specific effects (Turelli and Barton 2004), or frequency- or density-dependent selection (Bürger 2005). Our purpose here is not to investigate any one of these potential mechanisms for maintaining genetic variance but to critically evaluate the fundamental observation of the ubiquity of genetic variance in the presence of stabilizing selection.

Direct empirical tests of the effect of stabilizing selection on the genetic variance in natural populations are difficult because genetic variances, estimates of the strength of stabilizing selection, and mutation rates must be quantified simultaneously (Zhang et al. 2002). A first step, however, is to determine the association between the strength of stabilizing selection and the magnitude of genetic variance in natural populations (Barton and Turelli 1989). There are two key difficulties in implementing this approach. First, quantifying true stabilizing selection on a set of traits, as distinct from apparent stabilizing selection generated by unmeasured traits, requires the focal traits to be manipulated in isolation from all other traits (Robertson 1967; Johnson and Barton 2005). Second, almost all single traits tend to display substantial heritabilities (Roff 1997; Lynch and Walsh 1998; Partridge and Barton 2000; Blows and Hoffmann 2005) and theory shows that many traits cannot be under true stabilizing selection simultaneously (Barton 1990). Simply associating single-trait heritabilities or estimates of genetic variance with measures of stabilizing selection on each trait is an inadequate approach to test this hypothesis (Johnson and Barton 2005), because stabilizing selection often acts most strongly on trait combinations via correlational selection (Lande and Arnold 1983; Phillips and Arnold 1989; Blows and Brooks 2003). Here we use an example of true multivariate stabilizing selection on a set of traits, which was quantified in a manipulative experiment (Brooks et al. 2005), to test the prediction that trait combinations under stronger stabilizing selection will display lower genetic variance.

MATERIALS AND METHODS

Study system:

Acoustic sexual signals in species like frogs (Ryan and Wilczynski 1988; Gerhardt 1991; Polakow et al. 1995) and crickets (Loftus-Hills et al. 1972; Loher 1979; Brooks et al. 2005) are often under stabilizing sexual selection due to sensory tuning or neuronal processing by females. Such traits provide exceptional opportunities to study stabilizing sexual selection because call properties can be manipulated independently from all other aspects of the phenotype using computer software to artificially construct calls and then measure the attractiveness of these calls in acoustic playback trials. Previously (Brooks et al. 2005), we independently manipulated five acoustic call properties: chirp pulse number (CPN); trill number (TN); inter-call duration (ICD); chirp inter-pulse duration (CIPD), and dominant frequency (DF), of the advertisement call of male Australian black field crickets (Teleogryllus commodus). We showed that these five call properties are under strong multivariate stabilizing sexual selection in controlled laboratory phonotaxis trials (Brooks et al. 2005) and in the field (Bentsen et al. 2006). Moreover, the population mean call properties of four independent samples of males, representing two different field collections and four different diet regimes, resided near the multivariate adaptive peak (Brooks et al. 2005). This experiment therefore provided support for the important prediction that populations should converge on the peak of an adaptive landscape that is characterized by stabilizing selection (Simpson 1953; Lande 1976; Arnold 2003).

Breeding design:

The laboratory stock we used originated from Smith's Lake (32° 22'S, 152° 30'E), New South Wales, Australia. After capture, the stock was bred for four generations in captivity before the start of this experiment. We mated 52 stock males to 7 dams each. This produced 301 full-sib families, as 63 dams failed to produce offspring. For each family we collected 12 offspring, at random, and reared them to adulthood in individual plastic containers (5 × 5 × 5 cm) in a constant-temperature room set to 28° ± 1° with a 10-hr-dark:14-hr-light light regime. All offspring were provided with food (Friskies Go-Cat Senior) and water ad libitum and a small piece of egg carton for shelter. Containers were cleaned and fresh food and water provided weekly.

Measuring call properties:

At 10 days posteclosion, males were set up in a constant-temperature room (28° ± 1°) in an individual plastic container (5 × 5 × 5 cm) with a condenser microphone (C1163, Dick Smith) mounted in the lid. Each microphone was connected to a junction unit to power to the microphone. Calls were recorded opportunistically (i.e., if a male was calling during the nightly 8-hr-sampling period) on high quality chrome tapes (ProCopy, Australia) using a Sony Professional Walkman (WMD6C, Sony) connected to the junction unit, which was kept outside the constant-temperature room to minimize disturbance to males when attempting to record their call. A 2-min audio sequence of the call was recorded for each male. We subsequently digitized this call sequence from tape and used Canary software (version 1.2.4; Bioacoustic Research Program, Cornell University, Ithaca, NY) to measure CPN, TN, ICD, CIPD, and DF for five random calls per sequence. The average value for each call property (across the five randomly sampled calls) was used in subsequent genetic analyses. In total, the calls of 731 males were recorded and analyzed.

Genetic analysis:

The additive genetic variance-covariance matrix was estimated using restricted maximum likelihood under a multivariate model for the standard half-sib breeding design implemented in the MIXED procedure of SAS. Two analyses were conducted. First, all traits were standardized to mean of zero and SD of 1. Second, unstandardized traits were analyzed (scores for ICD and CIPD were log transformed) and trait mean was used as a fixed effect in the genetic analysis. Genetic variance-covariance matrices were estimated by using an unconstrained covariance structure among traits at the sire level in the mixed model. Unconstrained covariance structures among traits were also modeled at the dam and residual levels.

Factor-analytic modeling of G (Hine and Blows 2006) was conducted by the sequential dropping of a dimension from a factor-analytic model at the sire level implemented in the MIXED procedure. A series of nested log likelihood ratio tests determined when the dropping of a dimension resulted in a significantly worse fit and therefore statistical support for the presence of the dimension that had been dropped. Best linear unbiased predictor (BLUP) breeding values of the 52 sires for each of the 5 composite traits (m₁ − m₅) representing the major axes of the fitness surface were extracted from a separate restricted maximum likelihood multivariate model implemented in the MIXED procedure.

RESULTS AND DISCUSSION

We compared the features of the fitness surface with the genetic basis of the same 5 call properties using the calls of 731 sons reared in a half-sib breeding design. The standardized additive genetic variance-covariance (G) matrix (Table 1) displays heritabilities for individual traits ranging between 16.7% for ICD and 71.9% for CPN. There was considerable genetic covariance among the 5 traits, with genetic correlations ranging from −0.649 between TN and CIPD to 0.401 between DF and CPN. In particular, CIPD was negatively genetically correlated with all other traits. The first eigenvector of G, g_max, reflected the negative genetic correlation of CIPD with all other traits and accounted for 51.0% of the estimated genetic variance (Table 2). We used factor-analytic modeling (Hine and Blows 2006) to determine how many genetic dimensions were present and how much of the estimated genetic variance had statistical support. We had statistical support for the presence of 3 genetic dimensions accounting for 90% of the estimated genetic variance (likelihood ratio test on dropping 3rd factor, 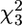= 9.21, P = 0.027). There was a suggestion of the presence of a 4th genetic dimension (g₄), explaining a further 7% of the genetic variance, but it did not reach statistical significance with the current sample size ( 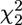= 3.79, P = 0.150). There was no support for the presence of a 5th genetic dimension; dropping g₅, which explained the remaining 3.6% of the genetic variance, left the model fit virtually unchanged ( 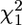= 0.59, P = 0.442).

TABLE 1.

Additive genetic variance-covariance (G) matrix of five call components of T. commodus

	CPN	CIPD	TN	ICD	DF
CPN	0.719	−0.115	0.395	0.349	0.401
CIPD	−0.061	0.388	−0.649	−0.373	−0.068
TN	0.170	−0.205	0.257	0.333	0.386
ICD	0.121	−0.095	0.069	0.167	0.379
DF	0.184	−0.023	0.106	0.084	0.293

Genetic correlations in italic are above the diagonal, and genetic covariances of traits (standardized to phenotypic SD) are below the diagonal. Genetic variances of standardized traits (equivalent to heritabilities) are along the diagonal.

TABLE 2.

Eigenvectors and eigenvalues (λ_n) of G for standardized traits

	gmax	g2	g3	g4	g5
CPN	0.793	0.460	−0.383	0.001	−0.114
CIPD	−0.281	0.782	0.209	−0.105	0.504
TN	0.362	−0.391	0.080	−0.515	0.667
ICD	0.230	−0.131	0.195	0.843	0.426
DF	0.329	0.080	0.875	−0.115	−0.326
λn	0.930	0.468	0.235	0.125	0.065
% var	51.0	25.6	12.9	6.9	3.6
gnTγgn	0.005	−0.012	−0.051	−0.097	−0.011
gnTΔG gn	0.00400 (6.6%)	−0.00283 (−7.8%)	−0.00285 (−11.0%)	−0.00212 (−13.0%)	−0.00009 (−3.8%)

The strength of nonlinear selection along each eigenvector is given by g_n^Tγg_n, and the predicted response of the genetic variance to selection along each eigenvector is given by g_n^TΔG g_n and expressed as percent change in genetic SD in parentheses.

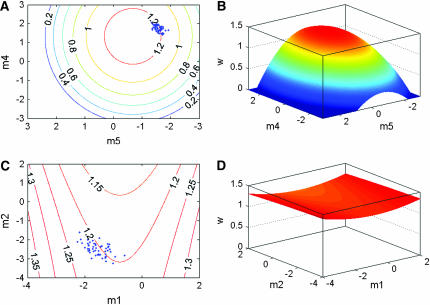
The individual fitness surface for these five call traits in this population resembles a multivariate peak, with significant stabilizing selection on the first two major axes (m₄ and m₅) of the individual fitness surface (γ) (Brooks et al. 2005) (Figure 1, A and B). Some association between the level of genetic variance and stabilizing selection is apparent for individual traits as trait genetic variances (Table 1) tend to decrease with an increase in the strength of stabilizing selection on those traits (see Table 2 in Brooks et al. 2005 for strength of selection on each trait). However, considering only the nonlinear selection on single traits ignores stabilizing and disruptive selection on trait combinations that is often stronger than that on single traits (Blows and Brooks 2003). We calculated the strength of nonlinear selection on the fitness surface along each of the genetic eigenvectors using g_n^Tγg_n. The strength of stabilizing selection was inversely proportional to the amount of genetic variance in that direction for the first four genetic eigenvectors (Table 2). The major axis of genetic variance (g_max) had weak disruptive selection acting on it, accounting for the weak (but statistically insignificant) disruptive selection that is present on the individual fitness surface (Brooks et al. 2005). Stabilizing selection increased in strength along the next 3 eigenvectors, with the strongest stabilizing selection detected on g₄, which explained only 7% of the genetic variance. However, selection on g₅ was weaker than along either g₃ or g₄, and therefore this last eigenvector was not consistent with the pattern of decreasing genetic variance with increasing stabilizing selection.

Figure 1.—

Illustration of the level of genetic variance in relation to the strength of stabilizing selection. Strong stabilizing selection along the m₄ − m₅ canonical axes of the fitness surface [contour plot (A) and 3-D surface view (B)] is associated with relatively little genetic variance represented by the distribution of BLUPs of the breeding values of the sires (diamonds on A). Stabilizing selection is weak along the ridge generated by m₁ − m₂ canonical axes [contour plot (C) and 3-D surface view (D)] and is associated with considerably more genetic variation. The elevations of Figure 1, B and D relative to one another are a consequence of the fact that call attractiveness was measured relative to a control call located at the intercept (coordinates 0, 0, 1.167) on both figures (Brooks et al. 2005).

The association between the level of genetic variance and the strength of nonlinear selection on the individual fitness surface is illustrated in Figure 1. We extracted BLUP breeding values of the 52 sires for each of the 5 composite traits (m₁ − m₅) that represent the major axes of the fitness surface. These breeding values are tightly clumped on the two axes of strongest stabilizing selection (Figure 1A). The breeding values on the two axes of weakest selection (Figure 1C) display greater variation along both axes than those under stronger stabilizing selection.

Although testing for an association between the strength of stabilizing selection and the level of genetic variance provides an intuitive approach to examine how selection shapes genetic variance, it provides an incomplete picture of how the genetic variance will change under selection. The within-generation change in G that should result from a single generation of selection is given by ΔG = G(γ − ββ^T)G (Lande and Arnold 1983; Phillips and Arnold 1989) (Table 3). To clearly discern the effect of selection on the genetic variance, we calculated the change in genetic variance along each eigenvector of G using g_n^TΔG g_n (Table 2). The genetic variance in g_max was predicted to increase by 6.6% of a genetic SD, while each subsequent eigenvector of G was predicted to experience a progressively greater decrease in genetic variance (up to 13.0% for g₄). Again, this pattern did not hold for g₅, which was predicted to experience a decrease in genetic variance of only 3.8% of a genetic SD. The absolute magnitude of the between-generation change in G along each genetic eigenvector will be less than one-half these values and will depend on the level of linkage disequilibrium generated by selection (Tallis 1987). Finally, we repeated all analyses using unstandardized trait values. A qualitatively similar result was found (Table 4), with increasing stabilizing selection along the first four eigenvalues of G, thereby illustrating that this important relationship is not an artifact of trait standardization.

TABLE 3.

The matrix of within-generational change in genetic variance (ΔG)

	CPN	CIPD	TN	ICD	DF
CPN	0.00492	0.00088	0.00174	−0.00079	0.00208
CIPD	0.00088	−0.00342	0.00255	−0.00019	−0.00180
TN	0.00174	0.00255	−0.00154	0.00075	0.00155
ICD	−0.00079	−0.00019	0.00075	−0.00217	−0.00048
DF	0.00208	−0.00180	0.00155	−0.00048	−0.00170

Elements are changes in genetic (co)variances of traits standardized to phenotypic SD.

TABLE 4.

Eigenvectors and eigenvalues (λ_n) of G for unstandardized traits

	gmax	g2	g3	g4	g5
CPN	0.582	0.812	−0.043	0.026	−0.014
CIPD	−0.054	0.068	−0.115	−0.748	0.648
TN	0.809	−0.580	−0.049	−0.056	0.056
ICD	0.036	0.009	0.701	0.401	0.589
DF	0.047	0.012	0.701	−0.526	−0.479
λn	0.683	0.293	0.006	0.006	0.002
% var	69.0	30.0	0.6	0.6	0.2
gnTγgn	−0.003	−0.007	−0.472	−0.575	−0.124
gnTΔG gn	−0.001 (−0.20%)	−0.0006 (−0.21%)	−0.00002 (−0.29%)	−0.00002 (−0.33%)	−0.0000008 (−0.03%)

The strength of nonlinear selection along each eigenvector is given by g_n^Tγg_n, and the predicted response of the genetic variance to selection along each eigenvector is given by g_n^TΔG g_n.

We have demonstrated that the strength of stabilizing selection is closely associated with the presence of over 96% of the estimated genetic variance in these 5 call properties of the advertisement call of T. commodus. Our results suggest that stabilizing selection depletes genetic variance in those trait combinations that are under the strongest selection and a lack of stabilizing selection on other trait combinations allows genetic variance to be maintained at much higher levels. However, it is important to note that the pattern of mutational covariance may also result in ill-conditioned G matrices (Griswold et al. 2007), and we cannot exclude the possibility that such biases in mutational covariance contribute to the pattern of genetic covariance we have observed.

Assuming the pattern of stabilizing selection is responsible for the pattern of genetic covariance as suggested by our analysis, we are currently unable to determine with our current experiment why the last eigenvector of G with the lowest level of genetic variance did not experience the strongest selection for a decrease in genetic variance. One explanation may be that there is in fact no genetic variance in g₅, and all the variance in this direction represents measurement error. In other words, an absolute genetic constraint (Mezey and Houle 2005) may exist in this direction, and therefore the strength of selection would not be responsible for the low variance estimated in this direction. Alternatively, if the low genetic variance indicated in this direction is not simply measurement error, this could be a consequence of selection transmitted through an unmeasured, genetically correlated trait. Such a possibility is a key limitation of all selection analyses (Lande and Arnold 1983; Mitchell-Olds and Shaw 1987). Although our manipulative experimental design allows true stabilizing selection to be estimated on the traits of interest, it does not control for selection operating on genetically correlated traits that might influence our estimates of genetic variance.

Finally, when stabilizing selection acts on multiple traits, some (Lande 1980; Cheverud 1984; Arnold et al. 2001), although not all (Hansen 2006), theory predicts that G will become aligned with the fitness surface. As our analysis shows, there is substantial similarity between the geometric orientation of G and the fitness surface, demonstrating how genetic constraints may evolve. As stabilizing selection erodes genetic variance within certain trait combinations, it constrains the potential for future evolution in that direction. Further, the evolution of G to match the fitness surface will facilitate morphological integration, enabling favored trait combinations to be co-inherited to conserve their functional integrity (Olson and Miller 1958; Cheverud 1984a, 1996).