Mating Systems and the Efficacy of Selection at the Molecular Level

Abstract

Mating systems are thought to play a key role in molecular evolution through their effects on effective population size (N_e) and effective recombination rate. Because of reduced N_e, selection in self-fertilizing species is supposed to be less efficient, allowing fixation of weakly deleterious alleles or lowering adaptation, which may jeopardize their long-term evolution. Relaxed selection pressures in selfers should be detectable at the molecular level through the analyses of the ratio of nonsynonymous and synonymous divergence, D_n/D_s, or the ratio of nonsynonymous and synonymous polymorphism, π_n/π_s. On the other hand, selfing reveals recessive alleles to selection (homozygosity effect), which may counterbalance the reduction in N_e. Through population genetics models, this study investigates which process may prevail in natural populations and which conditions are necessary to detect evidence for relaxed selection signature at the molecular level in selfers. Under a wide range of plausible population and mutation parameters, relaxed selection against deleterious mutations should be detectable, but the differences between the two mating systems can be weak. At equilibrium, differences between outcrossers and selfers should be more pronounced using divergence measures (D_n/D_s ratio) than using polymorphism data (π_n/π_s ratio). The difference in adaptive substitution rates between outcrossers and selfers is much less predictable because it critically depends on the dominance levels of new advantageous mutations, which are poorly known. Different ways of testing these predictions are suggested, and implications of these results for the evolution of self-fertilizing species are also discussed.

MATING systems are thought to have a deep impact on molecular evolution. They affect the effective population size, N_e, which plays a crucial role in molecular evolution because it controls the amount of polymorphism and the efficacy of selection (Charlesworth and Wright 2001). Inbreeding is expected to directly lower N_e by reducing the number of independent gametes sampled for reproduction. Because inbreeding also reduces the efficacy of recombination, N_e can be reduced further through hitchhiking effects: the elimination of deleterious alleles or the spread of advantageous mutations at linked loci increases the local level of genetic drift (Maynard-Smith and Haig 1974; Charlesworth et al. 1993). Finally, bottlenecks should be more severe in selfers than in outcrossers (Schoen and Brown 1991) because in selfers a single seed can found a new population (Baker 1955). The efficacy of selection depends on the product N_es, where s is the selection coefficient, such that selection should be less effective in selfers than in outcrossers. At the molecular level, selection intensity can be estimated due to the comparison of (presumably neutral) synonymous and (presumably selected) nonsynonymous polymorphisms or substitutions.

While the effect of selfing on polymorphism levels is well documented (Hamrick and Godt 1996; Nybom 2004; Glémin et al. 2006), its impact on selection efficacy has been assessed only in a few studies, without strong evidence. Bustamante et al. (2002) suggested that the self-fertilizing species Arabidopsis thaliana has mainly fixed slightly detrimental mutations, whereas Drosophila melanogaster has preferentially fixed beneficial mutations. However, Wright et al. (2002) did not find any difference in the rate of protein evolution in codon bias between A. thaliana and its outcrossing close relative A. lyrata. More recently, a survey of sequence polymorphism data in flowering plants revealed a weak increase in the π_n/π_s ratio in selfers compared to outcrossers, suggesting relaxation of selective constraints in selfers (Glémin et al. 2006).

Despite that only few studies are available, several hypotheses have been suggested to explain the weak signal of reduced selection efficacy in selfers. First, the strength of selection obviously depends on the (poorly known) genomic distribution of selection coefficients and recombination rates. For instance, under the pure neutral model with just neutral and strongly deleterious mutations, virtually no effect is expected. Second, if selfers are of recent origin, such as suggested for A. thaliana (Charlesworth and Vekemans 2005; Bechsgaard et al. 2006), the change in the selective regime could be too recent to have significantly affected the D_n/D_s ratio. According to this hypothesis, a stronger signal should be detectable in intraspecific polymorphism analyses, which may explain the results of Glémin et al. (2006). Finally, theoretical reasons can also be invoked. Indeed, selfing also affects the efficacy of selection by increasing homozygosity and thus exposing recessive alleles to selection, as in the well-known purging process of deleterious mutations through selfing (Ohta and Cockerham 1974). This effect can counteract the effect of reducing N_e. Charlesworth (1992) studied the rate of evolution in selfers through the fixation probability of mutations with any dominance level. Considering the sole reduction in N_e due to nonindependent gamete sampling under inbreeding (that is, a 50% reduction under complete selfing), he showed that selection is less efficient under partial selfing for dominant mutations but more efficient for recessive ones. Quantitatively he found a minor effect on the fixation of deleterious mutation but a significant one on the fixation of recessive advantageous alleles. However, Charlesworth (1992) did not take into account the reduction in N_e due to bottlenecks or hitchhiking effects. It is thus not clear how much N_e must be reduced beyond the twofold level to overwhelm the homozygosity effect.

To address this issue previous population genetic models are expanded by focusing on the impact of partial selfing and dominance level on several measures commonly used in molecular evolution. Genes under purifying selection are considered first, assuming constant selection against deleterious mutations or a distribution of selection and dominance coefficients. Then, the case of advantageous mutations is presented. For each case, the additional reduction in N_e that is necessary to allow detection of relaxed selection in selfers at the molecular level is determined. The effect of population subdivision is also addressed. Different ways of testing these predictions are suggested, and the implications of these results for the evolution of self-fertilizing species are also discussed.

MODEL AND RESULTS

General formulation:

The aim of this article is to develop predictions for two commonly used measures of selection in molecular evolution, namely the D_n/D_s ratio (ω hereafter) and the π_n/π_s ratio (f₀ hereafter). D_n and D_s are the mean substitution rate, per generation per nonsynonymous and per synonymous site, respectively. π_n and π_s are nonsynonymous and synonymous nucleotide diversity (Tajima 1983). As in previous studies (Piganeau and Eyre-Walker 2003; Loewe et al. 2006), the model assumes an infinite-site mutation model, autosomal inheritance, and independently evolving sites (free recombination). Mutations occur at rate μ and synonymous sites are supposed to evolve neutrally so that

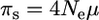(1a)

and

(1b)

Nonsynonymous mutations can be neutral, deleterious, or advantageous, in proportion c_n, c_d, and c_a, respectively (c_n + c_d + c_a = 1). Deleterious mutations may contribute both to polymorphism and to divergence, while new advantageous mutations (distinct from back mutations from a deleterious allele) can spread rapidly to fixation, contributing to substitutions but not to polymorphism (because they are likely to be rare, c_a ≪ 1, and fixation occurs rapidly). We thus have

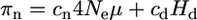(2a)

and

(2b)

where H_d is the mean equilibrium diversity at sites under purifying selection, and D_d and D_a are the mean substitution rates at sites under purifying and positive selection, respectively. It follows that

(3a)

and

(3b)

where indexes d and a stand for the contribution of deleterious and advantageous mutations to f₀ and ω. Because mating systems do not affect the neutral part of f₀ and ω, c_n is set to 0 for simplicity. Results remain unchanged since only relative values for different mating systems are considered. For simplicity, negative and positive selections are also analyzed separately.

First, consider single populations with effective population size N_e = αN/(1 + F), where N is the actual population size, and F = σ/(2 − σ) is the equilibrium Wright's fixation index with selfing rate σ. Compared with classical models, the parameter α is introduced as a simple way to summarize the reduction in effective population size due to hitchhiking and bottleneck effects. This parameter allows exploring N_e reduction in selfers without modeling explicitly bottleneck or hitchhiking effects, which would greatly increase the model complexity. To compare allogamous and autogamous populations, α = 1 in the former and α < 1 in the latter. The main aim of the model is then to seek N_e reduction that is necessary to overwhelm the homozygosity effect, that is, to derive the limit α-value for which or .

Selection against deleterious mutations:

Strong purifying selection:

Consider mutation from a wild-type allele, A, toward a deleterious allele, a. Let 1, 1 + hs, and 1 + s be the fitnesses of the three genotype AA, Aa, and aa, respectively (s < 0 for deleterious alleles, s > 0 for advantageous ones). Under strong selection (N|s| ≫ 1), deleterious alleles never reach fixation, so that D_n = 0. Mcvean and Charlesworth (1999) showed that the contribution to polymorphism of codominant () deleterious mutations is well approximated by π_n ≈ 2q, where q is their deterministic equilibrium frequency. This approximation still holds for any dominance level (see numerical results below), using q ≈ μ / (h + F − hF)|s| (Caballero and Hill 1992; Bataillon and Kirkpatrick 2000) or 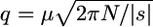for fully recessive alleles (h = 0) in a panmictic population (F = 0). This second approximation holds for 2Nμ ≪ 1 (Wright 1937; Nei 1968), which is mostly true at the nucleotide level. From these arguments we get

(4)

and

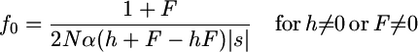(5a)

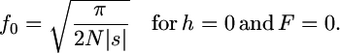(5b)

According to (5) f₀ is a decreasing function of F for and an increasing one for . Recessive alleles are more efficiently purged in self-fertilizing than in outcrossing populations and contribute less to polymorphism. Under strong selection, the f₀ ratio does depend on N, while the frequency of deleterious alleles remains constant (except for fully recessive ones). In such conditions, the interpretation of the f₀ ratio can be misleading because it does not directly estimate the strength of selection (which remains unchanged) but does estimate the fraction of deleterious mutations contributing to polymorphism. Despite this limitation, we can easily find α _limit:

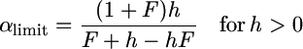(6a)

(6b)

For complete selfing, (6a) reduces to 2h and (6b) to , which is very low for recessive and nearly recessive alleles.

Arbitrary purifying selection:

If selection is weak, deleterious alleles can become fixed and then mutate back to the optimal allele. This will contribute both to polymorphism and to divergence. As far as nucleotide sequences are concerned, we have to consider four states at each site. To simplify, only two equivalence classes of selected sites are considered, namely the deleterious and optimal classes, each containing one to three variants (for instance, see Figure 2 in Loewe et al. 2006). Within each class, variants are thus neutral. This can be taken into account as in Equations 5a and 5b in Loewe et al. (2006). Provided that all mutation rates from each nucleotide are equal (which is implicitly assumed in Loewe et al. 2006), the following results do not depend on the number of variants per class because relative results between selfers and outcrossers (not absolute ones) are concerned (numerical results not shown). For clarity only the two-allele case with symmetrical mutation rates is discussed below. Mutation biases induce more complex patterns and are not treated here (for instance, see McVean and Charlesworth 1999).

Figure 2.—

f₀ (A) and ω (B) for weak deleterious mutations as a function of Ns. Deleterious alleles are recessive (h = 0, thick line), codominant (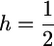, thin line), or dominant (h = 1, dashed line).

First, we need to compute the proportion of sites fixed either for the deleterious or for the optimal allele. Following Bulmer (1991) or Piganeau and Eyre-Walker (2003), the proportion of sites fixed for the deleterious allele is

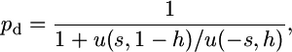(7)

where u(s, h) is the fixation probability of an allele with initial frequency 1/2N, selective advantage s > 0, and dominance level h. It is worth noting that both selection coefficients and dominance levels are reversed between the two allelic states. If the deleterious allele (−s) is recessive (h = 0), the advantageous one (s) is dominant (h = 1). According to Kimura (1962),

(8)

where 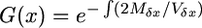. M_δx and V_δx are the infinitesimal mean and variance of the change in allele frequency of the diffusion process. In this model with partial selfing and an arbitrary level of dominance these terms are

(9a)

(9b)

(see, for instance, Charlesworth 1992). We thus have

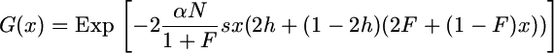(10)

π_n is then given by

(11)

and

(12)

where 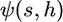is the expected contribution to heterozygosity of an allele with initial frequency 1/2N, selective advantage s > 0, and dominance level h:

(13)

(for instance, see Equation A6 in McVean and Charlesworth 1999). Similarly,

(14)

and

(15)

Expressions (12) and (15) have been computed using the NIntegrate function of the Mathematica software (Wolfram 1996).

As shown in Figure 1, f₀ and ω are decreasing functions of F for and increasing ones for . When , 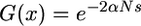; f₀ and ω are thus independent of F (see also Charlesworth 1992). Unless mating system also affects α, we do not expect any consequences of mating systems on f₀ and ω for codominant mutations. Figure 1 also shows a surprising result, which is emphasized in Figure 2. For recessive deleterious alleles (), f₀ and ω reach a maximum, >1, under (very) weak selection (Ns < 1), while they monotonically decrease with Ns when deleterious alleles are codominant or dominant. This effect is stronger for f₀ than for ω. This effect also occurs with partial selfing but the maximum is reached for very low Ns values. Under complete selfing, there is no maximum. For very weak selection, about half of the sites are fixed for the deleterious allele and the other half for the advantageous one. If the deleterious allele is recessive, its contribution to polymorphism or divergence is almost the same as the contribution of a neutral allele, while the reverse dominant advantageous mutation contributes more to polymorphism and divergence than neutral alleles. For stronger selection, most sites are fixed for the optimal allele and deleterious mutations contribute very little to both polymorphism and divergence. This explains the maximum in f₀ and ω reached for low Ns values. Similar patterns occur with mutation bias, without dominance (see Mcvean and Charlesworth 1999).

Figure 1.—

f₀ (A) and ω (B) for deleterious mutations as a function of F for different dominance levels. Ns = 1 and α = 1 is constant. Thick lines correspond to 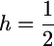. Other lines from bottom to top: h = 0, h = 0.1, h = 0.3, h = 0.7, h = 0.9, h = 1.

α_limit for weak selection:

General analytical expressions for f₀ and ω are tremendous or not available so that only numerical results are presented. Table 1 gives numerical α_limit-values obtained when allogamous populations (F = 0) and fully autogamous ones (F = 1) are compared. As expected, α_limit is lower for recessive mutations because they are easily purged by selfing so that strong reductions in N_e are necessary to overwhelm this effect. Under strong selection, numerical results are close to analytical deterministic predictions. Under weaker selection, α_limit is higher, which means that purging of recessive deleterious alleles by selfing is less efficient in small than in large populations, as already pointed out (Glémin 2003). However, for very weak selection (Ns < 1), α_limit can be low, even negative for highly recessive mutations. This result comes from the peculiar pattern of f₀ described above. If we do not assume back mutation, α_limit monotonically increases as Ns decreases. This result implies that it could be difficult to detect relaxed selection through f₀ measure in selfers because weakly deleterious mutations contribute much to polymorphism. However, such mutations are supposed to be close to the codominance level for which α_limit is high and close to one (see below).

TABLE 1.

α_limit for f₀ for various combinations of h and Ns

	Ns				Strong selection
h	0.5	1	2	5	10	50	100
0	<0	<0	0.346	0.332	0.249	0.113	0.080
					0.252	0.113	0.080
0.05	<0	<0	0.425	0.389	0.305	0.178	0.149
						0.1
0.1	<0	0.210	0.496	0.446	0.366	0.254	0.231
						0.2
0.2	<0	0.505	0.627	0.568	0.503	0.427	0.414
						0.4
0.3	0.394	0.696	0.752	0.701	0.657	0.613	0.607
						0.6
0.4	0.754	0.855	0.875	0.845	0.824	0.805	0.803
						0.8
0.45	0.884	0.929	0.937	0.921	0.911	0.902	0.901
						0.9

α_limit was computed by numerically solving for equation . Under strong selection, analytical approximations (Equations 6a and 6b) are given in italics.

Table 2 shows α_limit-values for ω. The pattern is similar to that of f₀ but absolute values are much higher and close to one, even for recessive alleles. Without additional reduction in N_e (α = 1), recessive deleterious mutations are sheltered in outcrossing populations and reach much higher frequency than in self-fertilizing ones where they are unmasked in homozygotes. Higher f₀ values are thus expected under panmixia so that α_limit needs to be rather small to compensate the homozygosity effect. However, such deleterious mutations are eventually selected against with similar intensity in outcrossing as in self-fertilizing populations, and thus rarely reach fixation in both populations. ω-values are thus similar in both populations so that α_limit-values close to one are sufficient to compensate for homozygosity. In other words, the dominance level of deleterious mutations, as well as the homozygosity effect, influences polymorphism more strongly than divergence.

TABLE 2.

α_limit for ω under purifying selection for various combinations of h and Ns

	Ns
h	0.5	1	2	5	10
0	0.055	0.684	0.833	0.930	0.965
0.05	0.314	0.719	0.848	0.935	0.968
0.1	0.441	0.753	0.864	0.941	0.971
0.2	0.625	0.818	0.897	0.954	0.977
0.3	0.768	0.881	0.930	0.968	0.984
0.4	0.890	0.941	0.965	0.983	0.991
0.45	0.947	0.971	0.982	0.991	0.995

α_limit was computed by numerically solving for equation .

Variation of α with selfing rate:

It is not easy to predict how α should vary with the selfing rate in general. For instance, no model predicts how the frequency of bottlenecks should increase with selfing. However, under the background selection (BS) hypothesis we can predict the relationship between α and F. Here, this model is used as a quantitative example of how α may decrease with F. According to Charlesworth et al. (1993), the reduction in N_e due to BS is

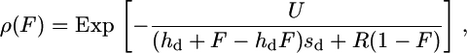(16)

where U is the genomic deleterious mutation rate, R is the genomic recombination rate, s_d is the mean selection coefficient against strongly deleterious mutations, and h_d is their dominance coefficient. We thus have

(17)

If the recombination rate is high, only highly self-fertilizing species suffer from a reduction in N_e due to BS. If the recombination rate is lower, α decreases more linearly with F. Examples are given in Figure 3. Figures 4 and 5 show how f₀ and ω vary as a function of F under the BS model.

Figure 3.—

Variation of α with F under the BS model (Equation 17) with U = 0.2, h_d = 0.1, and s_d = 0.05 and R = 5 (thin solid line), R = 1 (dotted line), or R = 0.5 (dashed line). Thick solid line: constant α.

Figure 4.—

f₀ for deleterious mutations as a function of F for constant α = 1 (thick solid line) or α decreasing with F under the BS model (same values as in Figure 3). (A) h = 0 and Ns = 2; (B) h = 0.3 and Ns = 2; (C) h = 0 and Ns = 10; (D) h = 0.3 and Ns = 10.

Figure 5.—

ω for deleterious mutations as a function of F for constant α (thick solid line) or α decreasing with F under the BS model (same values as in Figure 3). (A) h = 0 and Ns = 2; (B) h = 0.3 and Ns = 2; (C) h = 0 and Ns = 10; (D) h = 0.3 and Ns = 10.

For partially recessive alleles (h = 0.3), provided that BS is sufficiently strong (U rather high and R not too low) f₀ mainly increases with F. For fully recessive alleles, f₀ reaches a minimum at intermediate selfing rates. The decrease in ω for intermediate selfing rates is less pronounced, even for fully recessive alleles (Figure 5). In every case, only strong selfers experience significant relaxation of selection (a strong increase in both f₀ and ω).

Distribution of mutational effects:

Previous analyses considered only the fate of alleles with fixed deleterious effect and dominance level while it is much more realistic to assume variation in selective effects among mutations. Several studies showed that selection coefficients against deleterious mutations are well modeled by a gamma distribution

(18)

(Keightley 1994; Piganeau and Eyre-Walker 2003; Loewe et al. 2006), where a is the shape parameter and b the scale parameter, and Γ is the gamma function (Abramowitz and Stegun 1970). The mean and the variance of this distribution are ab and ab², respectively. Variation in dominance levels is less documented but both theoretical (Bourguet 1999) and experimental arguments (Phadnis and Fry 2005) suggest that strongly deleterious mutations (lethals, semilethals) are recessive while weakly detrimental ones are nearly codominant. One can thus assume that h and s are inversely related:

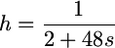(19)

(for a similar treatment see Higgins and Lynch 2001). This expression is such that for s = 0, while h = 0.02 for lethals, roughly reflecting values estimated in Drosophila (Mukai et al. 1972). Equations 12 and 15 become, respectively,

(20)

and

(21)

In this treatment, deleterious mutations and back advantageous ones follow the same gamma distribution. Integration spans from 0 (neutral alleles) to 1 (lethals), so strictly speaking, the distribution is a truncated gamma but the probability mass between 1 and ∞ is very low.

Table 3 gives some examples of the variation in ω with F assuming either that α is constant or that α decreases as F increases, as predicted under the BS hypothesis. Under the above assumptions, weakly deleterious mutations, which mostly contribute to π_n and D_n, are nearly codominant. With constant α, f₀ and ω are thus nearly invariant with F. With BS, f₀ and ω increase with F, revealing less efficient selection at the molecular level in selfers than in outcrossers. This is true even under strong recombination and therefore moderate BS effect. As in the previous case, only strong selfers show clear signals of relaxed selection. Results are very similar for f₀ but numerical integration of (20) is somewhat problematic and results may be imprecise and are not given here.

TABLE 3.

Comparison of ω for different levels of selfing (F) assuming a distribution of deleterious mutation effects (s and h)

	Exponential distribution of s (mean Ns = 2)				Skewed gamma distribution of s (mean Ns = 10)
F	Constant α	BS (high rec)	BS (medium rec)	BS (low rec)	Constant α	BS (high rec)	BS (medium rec)	BS (low rec)
0	0.427	0.427	0.427	0.427	0.665	0.665	0.665	0.665
0.2	0.427	0.429	0.439	0.449	0.664	0.665	0.667	0.669
0.5	0.426	0.437	0.474	0.504	0.664	0.667	0.675	0.682
0.7	0.426	0.451	0.527	0.578	0.664	0.670	0.687	0.698
1	0.425	0.921	0.900	0.867	0.664	0.802	0.791	0.776

α is independent of F (first column) or decreases under the BS model under high, medium, or low recombination (rec) rates (same values as in Figure 3). N = 1000; exponential distribution with mean Ns = 2 (a = 1 and b = 0.002) or strongly skewed gamma distribution with mean Ns = 10 (a = 0.1 and b = 0.1) is shown.

Positive selection:

α_limit for weak and strong positive selection:

Consider now rare advantageous mutations (s > 0). Such mutations either rapidly spread to fixation or become initially lost. They contribute to divergence, increasing D_n, but not to polymorphism. The ω-ratio is >1. The following results are mainly similar to those of Charlesworth (1992) with slight modifications. Without back mutation, we simply have

(22)

As for deleterious mutations, selection for recessive mutations 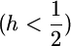is more efficient in selfers than in outcrossers while the reverse is true for dominant ones () (see Charlesworth 1992).

Under weak selection (Ns ≪ 1), according to Equation 9 in Charlesworth (1992),

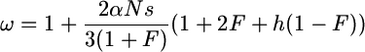(23)

from which we get

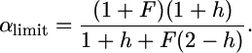(24)

This reduces to for h = 0 and F = 1.

Under strong selection (Ns ≫ 1) we can get approximations for h = 0 and either F = 0 or F = 1. From Equation 15 in Kimura (1962) when F = 0, we have

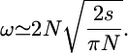(25)

When F = 1 Equation 22 becomes

(26)

We then obtain

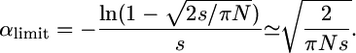(27)

α_limit is lower than for weak selection. For example, for Ns = 10 α_limit ≈ 0.25. Outcrossers hardly fix fully recessive advantageous mutations while self-fertilizing species do, even with lower N_e (see also Charlesworth 1992).

Dominance of advantageous mutations:

While both theory and experimental data support the recessivity of deleterious mutations over wild-type alleles, we know little about the distribution of dominance coefficients of newly arisen advantageous mutations. A review of pesticide resistance alleles showed that they are often dominant or codominant (Bourguet and Raymond 1997) but such alleles have been screened after selection, which is expected to skew the distribution of mutations toward dominant ones, the so-called “Haldane's sieve.” Charlesworth (1992) used data in selfers where Haldane's sieve is strongly reduced, such that the dominance spectrum of fixed mutations is very close to the one of newly arisen mutations before selection. He found a bias toward recessive mutations but he pointed out that dominant mutations should be more common among favorable mutations than deleterious ones.

To explore the effect of the dominance spectrum of mutations, one can assume that half of the mutations are recessive and the other half are dominant. Table 4 shows the evolution of ω with F for this symmetrical distribution. For constant α, ω is higher in outcrossers than in selfers if selection is weak. The reverse is true under strong selection. However, quantitatively the values are very similar. Empirically the limit is ∼2Ns² ≈ 1 but we did not find any demonstration of this result. Under weak selection, taking the average of (22), with h = 0 and h = 1 we get

(28)

which is independent of F so α_limit = 1. Under strong selection, we can show that

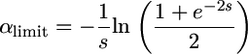(29)

(see appendix), which is always less than but rather close to 1. If N_e is reduced beyond the 50% threshold, we thus expect to detect a relaxed selection of advantageous mutations in selfers if dominance levels are distributed equally. However, if advantageous mutations are mainly recessive, adaptive evolution could go faster in self-fertilizing than in outcrossing species.

TABLE 4.

ω for advantageous mutations as a function of F and selection strength (Ns)

F	Ns = 1	Ns = 5	Ns = 10	Ns = 30
0	2.38	10.76	20.17	49.12
0.2	2.34	10.20	19.44	50.03
0.5	2.31	9.86	19.12	51.32
0.7	2.30	9.79	19.06	51.69
1	2.30	9.75	19.03	51.84

Half of the mutations are supposed to be recessive and the other half dominant.

Subdivided populations:

Most natural populations are subdivided, and geographical structure may affect population evolution. When comparing outcrossing and self-fertilizing species, population subdivision can be crucial because selfers are usually more spatially structured than outcrossers (Hamrick and Godt 1996). How does population subdivision affect the above theoretical results? As an example, consider the case of the island model with no extinction and zygotic migration. According to Equation 44 from Roze and Rousset (2003), the G function becomes

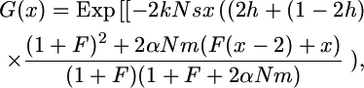(30)

where k is the number of demes and m the migration rate. Here, N stands for the local population size. First, it is worth noting that for complete selfing, , which is independent on m and h. In panmictic populations, G(x) depends both on m and on h. As shown by Roze and Rousset (2003), subdivision increases the probability of fixation of recessive advantageous mutations but decreases it for dominant ones (the reverse is expected for deleterious mutations).

Using (30) in (12), (15) and (22) allow us to explore the effect of subdivision on f₀ and ω. Figure 6 shows that for recessive deleterious mutations, f₀ and ω increase with migration rate, except under complete selfing when they are independent on m as predicted above. For advantageous recessive mutations, migration reduces ω. More importantly, Figure 6 shows that subdivision lessens the differences between self-fertilizing and outcrossing species. Subdivision has a strong effect in outcrossers by increasing local homozygosity, but a limited one in selfers, and even a null effect under complete selfing (see also Roze and Rousset 2003). Consequently α_limit should be higher in subdivided populations than in single ones. As an example, we give the case of weakly advantageous mutations:

(31)

(see appendix). As Nm tends toward 0, α_limit tends toward 1, while it tends toward , the single-population value, when Nm tends toward infinity. If both self-fertilizing and outcrossing species are similarly subdivided (same Nm) it would be easier to detect relaxed selection than in single large populations (because α_limit is higher and close to 1 in the former case). If self-fertilizing species are more subdivided than outcrossing ones, intermediate results are expected (α_limit taking intermediate values between the subdivided and the single-population cases). Anyway, the conclusions based on single population models appear robust.

Figure 6.—

f₀ (A) and ω (B) for deleterious mutations and ω for advantageous mutations (C) as a function of the migration rate, m, under the k-island model. N = 100, k = 10, h = 0, s = 0.002. From bottom to top (A and B) or from top to bottom (C): F = 0, F = 0.2, F = 0.5, F = 0.7, and F = 1.

DISCUSSION

Detecting reduced selection efficacy in selfers at the molecular level:

It has been claimed that reduced N_e in selfers should leave a signature of relaxed selection against deleterious mutations at the molecular level (Charlesworth and Wright 2001). This intuitive expectation comes from the idea that slightly deleterious mutations, which contribute more to polymorphism and divergence than strongly deleterious ones, should be nearly codominant and weakly affected by increased homozygosity in selfers (see also Charlesworth 1992). Here, we give a theoretical and quantitative basis to this hypothesis.

For realistic mutation parameters, f₀ and ω very slightly decrease as F increases for constant α. Thus only low N_e reduction is necessary to make f₀ and ω increase with F, as expected under the commonly accepted hypothesis. This study also shows that a stronger effect of mating system should be detectable using divergence rather than polymorphism statistics. The dominance level of deleterious mutations has a strong impact on polymorphism, somewhat compensating for genetic drift, but a weaker one on substitution rates, which are mainly governed by N_e. However, this is true at steady state. If mating systems evolve quickly and if self-fertilizing species are of recent origin (for example, A. thaliana; Charlesworth and Vekemans 2005; Bechsgaard et al. 2006), differences in ω between selfers and outcrossers should be weak because measures of ω along phylogenies correspond to averages over the mating system evolutionary path. Comparing f₀ and ω to test the previous predictions should be done on species or groups of species for which evidence for the relative stability of mating systems exists.

Both polymorphism and divergence data can be summarized by the so-called McDonald–Kreitman table (Mcdonald and Kreitman 1991) or by the neutrality index (NI) (Rand and Kann 1996). For instance, Bustamante et al. (2002) found an excess of nonsynonymous polymorphism compared with divergence, which can also be summarized by a NI ≫ 1. However, assuming only deleterious mutations we expect NI closer to 1 in selfers (with low N_e) than in outcrossers (with large N_e). But it is worth noting that this prediction does not hold if we assume a fraction of purely neutral mutations. Using (3a) and (3b) without adaptive mutations (c_a = 0), an equivalent to the NI index is given by 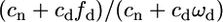. As selection against deleterious alleles increases (outcrossers with large N_e) this ratio tends toward 1 because f_d and ω_d tend toward 0, while it is >1 with weak or moderate selection (selfers with small N_e). If selection against deleterious alleles is relaxed in selfers, we thus expect to detect higher NI in selfers than in outcrossers.

Finally, a way to disentangle the effect of reduced N_e from that of increased homozygosity would be to compare nuclear and cytoplasmic genes. The second category is influenced only by hitchhiking and bottleneck effects affecting N_e. A related result has been reported in Daphnia where average mitochondrial ω is significantly higher in asexual lineages than in sexual ones (Paland and Lynch 2006). However, such a signature of relaxed selection on an organelle genome due to N_e reduction through a hitchhiking effect has not been reported yet in self-fertilizing species.

Adaptive evolution in selfers:

The difference in substitution rates of advantageous mutations between outcrossers and selfers critically depends on the dominance coefficients, which are poorly known. However, assuming that advantageous new mutations are either recessive or dominant with equal probability, no or low reduction in N_e is necessary to detect a signature of relaxed selection in selfers. Because adaptive mutations are supposed to be much less frequent than deleterious mutations, the average pattern at the gene level can be misleading. For example, the combination of strong selection against deleterious mutations with few adaptive substitutions in outcrossing species can lead to ω-values higher than those in self-fertilizing species where selection is weak both against deleterious mutations and in favor of advantageous ones. Depending on ω being higher or <1, opposite conclusions could be reached.

To test previous predictions, sites evolving under positive and purifying selection should be analyzed separately. Phylogenetic methods taking account of heterogeneous selection pressure among sites (Yang et al. 2000; Guindon et al. 2004) can help partition sites into different categories. Removing sites evolving under positive selection can reinforce the detection of relaxed selection against deleterious mutations in selfers. On the contrary, to test whether adaptive evolution is more or less frequent in selfers than in outcrossers, only sites detected as evolving under positive selection should be used. However, because such sites are supposed to be rare, specific genes like resistance genes should be used.

How small is α in natural populations?

The main results of this study critically depend on α-values. It is difficult to predict these values from biological data, as already mentioned. Under the BS hypothesis, however, predictions can be made provided genomic deleterious mutation parameters are known. Assuming complete selfing (17) becomes

(32)

Using data available in self-fertilizing species, α_BS spans between 0.48 and 0.98 but most values are close to one (Table 5). At least in those species, BS seems not sufficient to cause a strong decrease in N_e. However, strong reductions in N_e have been documented in the self-fertilizing nematodes Caenorhabditis elegans and C. briggsae, suggesting recurrent bottlenecks and/or frequent selective sweeps (Graustein et al. 2002). Irrespective of the underlying causes, a gross estimation of α can be inferred through π_s comparison between self-fertilizing and outcrossing related species,

(33)

with k = 2 for nuclear genes, k = 1 for cytoplasmic genes in hermaphrodite species, and k = for cytoplasmic genes in gonochoric species. Applying (33) to Graustein et al. (2002) data gives α-values between 0.04 and 0.28 for nuclear genes and ∼0.4 for the mitochondrial gene they used. On the contrary, in A. thaliana, α is close to or even >1 (Wright et al. 2003). This could explain why no effect of selfing was detected on the D_n/D_s ratio in this species (Wright et al. 2002).

TABLE 5.

Estimation of α in self-fertilizing species under the background selection model using Equation 32

Species	U	s	αBS	References
Amsinckia gloriosa	0.128	0.078	0.440	Schoen (2005)
	0.416	0.026	0.0003
Arabidopsis thaliana	0.05	0.23	0.897	Schultz et al. (1999)
Caenorhabditis briggsae	0.074	0.051	0.484	Baer et al. (2005)
	0.025	0.099	0.881
C. elegans	0.0083	0.126	0.968	Baer et al. (2005)
	0.0066	0.182	0.982
Oscheius myriophila	0.0055	0.219	0.988	Baer et al. (2005)
Triticum turgidum ssp. Durum	0.04	0.2	0.905	Bataillon (2000)

Evolutionary rate and long-term evolution in selfers:

On short timescales, selfers can efficiently purge strongly deleterious mutations causing inbreeding depression (Ohta and Cockerham 1974; Lande and Schemske 1985), preventing reverse transition to allogamy (Lande and Schemske 1985). On longer timescales, reduction in N_e may increase drift load and preclude adaptation, suggesting that self-fertilization could be an evolutionary dead end (Takebayashi and Morrell 2001). The results presented here confirm that reduction in N_e in natural populations of self-fertilizing species should be large enough to allow higher rates of fixation of weakly deleterious mutations than in outcrossing species, even for fully recessive mutations. Phylogenetic analyses offer tools to quantify drift load in self-fertilizing species and investigate further the evolutionary dead-end hypothesis. However, the claim of reduced adaptation in selfers is less clear from a theoretical point of view and crucially depends on dominance levels of new advantageous mutations. A few adaptive events can prevent an extinction vortex (Whitlock 2000) and could help maintain selfing lineages over a long timescale as observed in the Medicago genus (Bena et al. 1998).

APPENDIX: COMPUTATION OF α_LIMIT

The details of the approximation for α_limit that are not fully derived in the main text are given here.

Case i—ω, strong positive selection with recessive and dominant mutations:

Assume that half of the advantageous mutations are recessive and half are dominant. In fully self-fertilizing populations (F = 1), ω is independent of dominance levels. For strong selection, according to (26)

(A1)

In outcrossing populations (F = 0 and α = 1), for recessive mutations ω is given by (26) (and see Kimura 1962). For dominant ones, (22) becomes

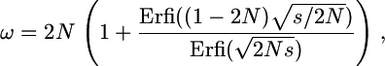(A2)

where Erfi is the imaginary error function (Abramowitz and Stegun 1970).

Using the approximation 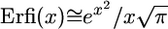for large x and assuming N ≫ 1, we get 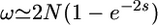. The average ω over half of the mutations being dominant and the other half being recessive is thus given by

(A3)

Solving for ω_self = ω_out in α gives

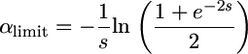(A4)

Case ii—ω, weak positive selection in subdivided populations:

For new advantageous mutations,

(A5)

with

where

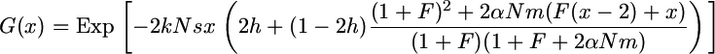in the k-island model (Roze and Rousset 2003). For α = 1 and F = 0,

(A6)

where Erf is the error function (Abramowitz and Stegun 1970).

For any α and F = 1,

(A7)

Assuming weak selection Ns < 1, Taylor expansions of (A6) and (A7) in Ns ∼ 0, and further simplification assuming N ≫ 1 give

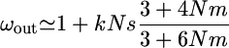(A8)

(A9)

which leads to

(A10)